Real-Time Identification Algorithm of Daylight Space Debris Laser Ranging Data Based on Observation Data Distribution Model
Abstract
Highlights
- A statistical distribution-based algorithm is proposed to distinguish weak echo signals from intense daylight background noise, achieving real-time identification of space debris laser ranging data within 1 s.
- The method successfully detects echo signals with intensities as low as 0.09 photons per pulse under high-noise conditions (background noise rate: 2 × 107 photons/s), surpassing the traditional intensity threshold constraints.
- Enables continuous daylight tracking and precise orbit determination of space debris in low signal-to-noise ratio (SNR) environments, which is critical for spacecraft safety.
- Leverages statistical distribution disparities instead of signal intensity, offering a universal framework for weak signal extraction in photon-starved regimes.
Abstract
1. Introduction
2. Establishment and Analysis of Observation Data Distribution Model
2.1. Sky Background Noise and System Model
- : Background brightness,
- : Receiving field-of-view angle,
- : Bandwidth of the narrowband filter,
- : Wavelength,
- : Planck’s constant,
- : Speed of light in vacuum,
- : Effective area of the receiving mirror,
- : Efficiency of the receiving optical system,
- : Echo photon detection efficiency (quantum efficiency),
- : Detector’s intrinsic noise.
2.2. Echo Distribution Model
- : Average number of photoelectrons per laser pulse,
- : Laser pulse width,
- r: Wavelength of the emitted laser,
- : Laser power,
- : Reflective cross-sectional area of the target,
- : Target reflectivity,
- : Lambertian cosine factor ( is the angle between the Lambertian radiation direction and the target surface normal),
- : Laser beam divergence angle,
- : Radial distance to the target,
- : Single-pass atmospheric transmittance,
- : Efficiency of the transmitting system,
- : Efficiency of the receiving system.
2.3. Measurement Data Distribution Model
2.4. Analysis of Measurement Data Distribution Model
- 1.
- Convert the observed O-C data into the relative time data , referenced to the range gate activation moment ().
- 2.
- Divide the time axis into intervals of the length . Assuming negligible pulse broadening due to the target shape effects, the echo duration matches the laser pulse width . When , the echo signals may disperse across multiple intervals, leading to the failure of distribution deviation detection. Conversely, when , the signals concentrate in a single interval, but the geometric properties of the noise distribution may be contaminated by the signals within the interval. Experimental results show that the optimal should satisfy , balancing the signal concentration and noise distribution stability. To ensure the echo falls within one or two intervals, set .
- 3.
- Define the detector’s operational time window as . This window is partitioned into intervals: , yielding the dataset .
- Pre-Echo Intervals
- Echo-Active Interval
- Post-Echo Intervals
Practical Implications
- After partitioning the data into intervals, the ratio remains constant at under noise-only conditions.
- At a specific adjusted range deviation time of , the data distribution pattern deviates due to the echo interference.
- Distribution Fitting: Use the measurement data to empirically fit the noise distribution.
- Deviation Detection: Identify the intervals where the data significantly deviate from the fitted distribution. These intervals (typically one or two) indicate the presence of echo signals.
- Back-to-O-C Conversion: Map the identified time regions back to the O-C data to obtain the coarse measurements.
3. Algorithm Design
3.1. Chi-Square Test and Echo Identification
- Critical Value Determination:
- Confidence Interval via Normal Approximation:
- 1.
- Deviation Detection:
- 2.
- O-C Conversion:
3.2. Operational Workflow
- 1.
- Data Acquisition:
- 2.
- Distribution Testing:
- 3.
- Decision Logic:
- Consistent with Noise: If the chi-square test validates the geometric distribution, proceed with the noise-only parameter updates.
- Echo Detected: If the deviations are significant,
- Extract the interval with the highest chi-square contribution.
- Compute the corresponding O-C values and output results.
- Validate the results by checking the consistency over consecutive time windows.
- 4.
- Real-Time Output:
4. Verification and Result Analysis
4.1. Noise Model Verification
4.2. Simulated Echo Validation
- 1.
- Equal Echo and Noise Intensities
- Simulated data were generated with (i.e., 0.16 echo photons per pulse) under varying laser pulse intensities.
- As shown in Figure 3, the algorithm’s identification performance degrades as the range gate duration increases. This occurs because the probability of the echo signals falling within a single interval diminishes, reducing their impact on the overall distribution.
- 2.
- Varying Echo-to-Noise Ratios
- Monte Carlo simulations were conducted for .
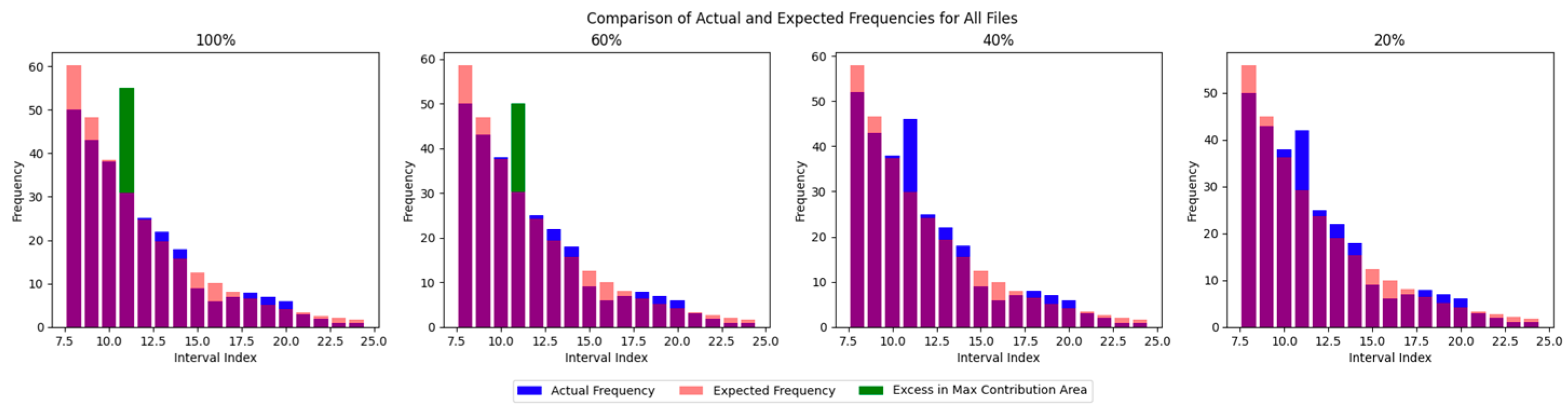
- Figure 4 demonstrates that the algorithm reliably identifies echo signals when
- The echo photon intensity exceeds 60% of the noise intensity ( > 0.09 photons/pulsene),
- The local noise density surpasses the echo density.
4.3. Data Segmentation and Analysis
- 1.
- Data Selection
- A segment of the measurement data containing both manually identified echo regions and noise-only regions was extracted (Figure 5).
- The vertical axis represents the O-C values, with the red horizontal lines marking the range gate activation times.
- 2.
- Manual Validation
- A post hoc manual analysis confirmed valid echo signals between 07:56:18 and 07:56:25, during which the system continued adjusting the range gate due to the lack of real-time feedback.
- 3.
- Algorithm Testing:
- Noise-Only Data: Four 4 s noise segments were processed.
- Echo-Containing Data: Four groups of echo data (post-range gate adjustment) were analyzed.
- 4.
- Results
4.4. Comparative Analysis of Methods
- 1.
- Comparison with Traditional Threshold-Based Methods
- Failure in High-Noise Scenarios: At a background noise rate of photons/s, the traditional threshold-based methods fail completely (false detection rate > 90%) due to the signal intensity ( photons/pulse) being overwhelmed by the noise. In contrast, the proposed algorithm successfully identifies weak signals by analyzing the statistical distribution deviations.
- Adaptability to Dynamic Noise: Threshold methods rely on manual parameter tuning and cannot adapt to dynamically changing noise (e.g., fluctuations caused by varying Sun–target angles). The proposed method, however, achieves adaptive recognition through real-time distribution fitting and chi-square testing.
- 2.
- Complementary Potential with Machine Learning
- Generalization vs. Data Scarcity: Machine learning (e.g., deep learning) exhibits superior generalization for complex noise patterns, but requires large labeled datasets (currently scarce for daytime ranging) and high computational resources (e.g., GPU acceleration).
- Lightweight Advantage: The proposed algorithm demonstrates efficiency in data-scarce scenarios (processing within 1 s), making it suitable for real-time applications. Future integration with lightweight online learning frameworks (e.g., incremental neural networks) could further enhance robustness.
- 3.
- Experimental Validation
- Detection Limits: The statistical distribution method achieves the reliable detection of photons/pulse under photons/s, whereas threshold-based methods fail entirely in such conditions.
- Real-Time Feasibility: With a processing time of ≤1 s at 400 Hz, the proposed method outperforms machine learning approaches in latency-critical applications.
- 4.
- Key Takeaways
- Performance Boundaries: The statistical distribution method breaks the detection bottleneck in high-noise regimes (), which traditional methods cannot address.
- Practical Trade-Offs: While machine learning holds theoretical promise, its reliance on labeled data and computational resources limits its practicality for the current daylight ranging scenarios.
- Synergy Opportunities: Hybrid frameworks combining statistical models with lightweight machine learning could balance adaptability and real-time performance.
5. Conclusions
- 1.
- Joint Noise–Echo Distribution Model
- The noise data strictly follow a geometric distribution,
- The hybrid noise–echo data deviate from geometric regularity due to the echo interference.
- 2.
- Algorithm Performance
- Real-time echo interval identification within 1 s data windows at a laser frequency of 400 Hz,
- Reliable detection under echo-to-noise intensity ratios as low as 0.6 (minimum ne > 0.09 photons/pulse),
- Coarse ranging outputs with errors < 3 m (10 ns), meeting real-time operational requirements.
- 3.
- Methodological Advancement
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krisko, P.H. The new NASA orbital debris engineering model ORDEM 3.0. In Proceedings of the 2014 AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 4–7 August 2014; p. 4227. [Google Scholar]
- Sun, H.; Zhang, H.F.; Zhang, Z.P.; Wu, B. Experiment of diffuse reflection laser ranging to space debris and data analysis. Res. Astron. Astrophys. 2015, 15, 909–917. [Google Scholar] [CrossRef][Green Version]
- Cordelli, E.; Vananti, A.; Schildknecht, T. Analysis of laser ranges and angular measurements data fusion for space debris orbit determination. Adv. Space Res. 2020, 65, 419–434. [Google Scholar] [CrossRef]
- Bennett, J.C.; Sang, J.; Smith, C.; Zhang, K. An analysis of very short—Arc orbit determination for low—Earth objects using sparse optical and laser tracking data. Adv. Space Res. 2015, 55, 617–629. [Google Scholar]
- Jianli, D.; Bin, L.; Lijuan, C.; Xiangxu, L.; Manyi, W.; Jizhang, S. Space debris orbit determination performance analysis using accurate simulated angular and ranging data. Infrared Laser Eng. 2016, 45, 0229004. [Google Scholar]
- Liang, Z.P.; Song, Q.L.; Wen, G.Y.; Liu, C.Z.; Han, X.W. Orbit determination research of high reflectivity CZ—2C upper stage. J. Space Sci. Exp. 2017, 13–19. Available online: http://www.journalofsse.com/EN/home (accessed on 1 April 2025).
- Steindorfer, M.A.; Kirchner, G.; Koidl, F.; Wang, P.; Jilete, B.; Flohrer, T. Daylight space debris laser ranging. Nat. Commun. 2020, 11, 3735. [Google Scholar] [CrossRef] [PubMed]
- Esmiller, B.; Jacquelard, C.; Eckel, H.A.; Wnuk, E. Space debris removal by ground-based lasers: Main conclusions of the European project CLEANSPACE. Appl. Opt. 2014, 53, I45–I54. [Google Scholar] [CrossRef] [PubMed]
- Lejba, P.; Suchodolski, T.; Michałek, P.; Bartoszak, J.; Schillak, S.; Zapaśnik, S. First laser measurements to space debris in Poland. Adv. Space Res. 2018, 61, 2609–2616. [Google Scholar] [CrossRef]
- Zhang, H.; Long, M.; Deng, H.; Cheng, S.; Wu, Z.; Zhang, Z.; Zhang, A.; Sun, J. Developments of Space Debris Laser Ranging Technology Including the Applications of Picosecond Lasers. Appl. Sci. 2021, 11, 10080. [Google Scholar] [CrossRef]
- Zhan, Z.Q.; Hu, M.Q.; Man, Y.Y. Multi-scale region growing point cloud filtering method based on surface fitting. Acta Geod. Cartogr. Sin. 2020, 49, 757–766. [Google Scholar]
- Kirchner, G.; Koidl, F.; Friederich, F.; Buske, I.; Völker, U.; Riede, W. Laser measurements to space debris from graz SLR station. Adv. Space Res. 2013, 51, 21–24. [Google Scholar]
- Luck, J.; Moore, C.; Greene, B. Autonomous laser ranging results from mount Stromlo. In Proceedings of the 12th International Workshop on Laser Ranging, Matera, Italy, 13–17 November 2000; pp. 2–12. [Google Scholar]
- Zhao, P.; Zhang, Y.; Zhang, X. Echo online extraction for diffuse reflection laser ranging. Acta Opt. Sin. 2015, 35, 288–296. [Google Scholar]
- Zhang, Y.; Shi, Q.Q.; Wang, K.P. Real—Time echo—Photon detection method based on motion compensation and robust estimation. Acta Opt. Sin. 2017, 37, 134–143. [Google Scholar]
- Rodríguez, J.; Appleby, G.; Otsubo, T.; Sherwood, R.; Wilkinson, M. Assessing and enforcing single-photon returns: Poisson filtering. In Proceedings of the 20th International Workshop on Laser Ranging Instrumentation, Potsdam, Germany, 9–14 October 2016. [Google Scholar]
- Liu, Y.; An, N.; Fan, C.; Liu, C.; Ma, L.; Song, Q.; Dong, X. Influence of Shape Effect of Angle Reflector on Ranging Precision of Satellite Laser Ranging System. Laser Optoelectron. Prog. 2018, 55, 110101. [Google Scholar]
- Degnan, J.J. Millimeter accuracy satellite laser ranging: A review. Contrib. Space Geod. Geodyn. Technol. AGU Geodyn. Ser. 1993, 25, 133–162. [Google Scholar]

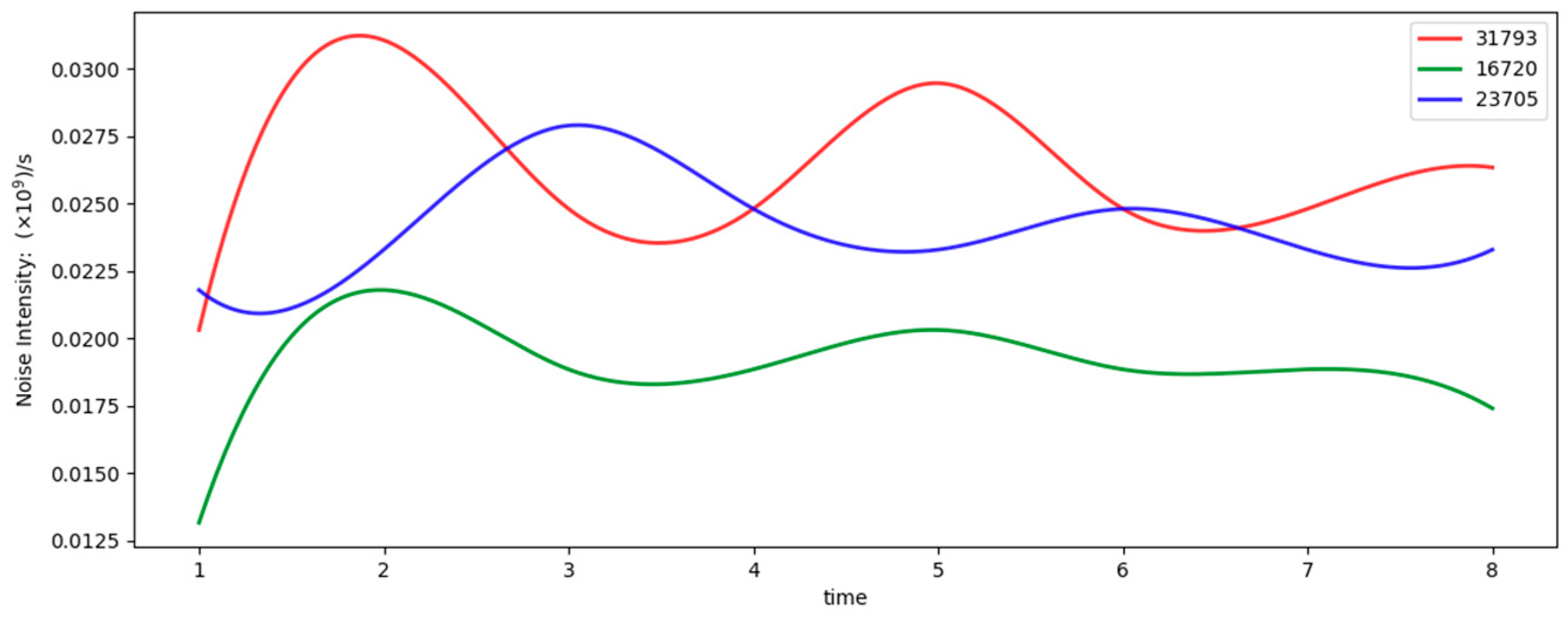




| Nord ID | Time (UTC) | Ranges (°) |
|---|---|---|
| 31793 | 07:30:02–07:30:09 | 93.83–94.74 |
| 16720 | 08:09:40–08:09:47 | 105.57–107.38 |
| 23705 | 08:20:18–08:20:25 | 68.18–68.37 |
| Statistical Distribution Method (Proposed) | Traditional Threshold-Based Method | Machine Learning Method (e.g., Deep Learning) | |
|---|---|---|---|
| Core Principles | Detects anomalies via statistical distribution differences (geometric vs. hybrid distribution) using chi-square tests. | Sets fixed intensity thresholds; signals above thresholds are classified as valid. | Learns complex noise–signal patterns through data-driven models for classification/regression. |
| Advantages | 1. No reliance on signal intensity thresholds; works when noise density > signal density. 2. Real-time (≤1 s processing). 3. No training data required. | 1. Simple implementation. 2. Effective in stable, high-SNR environments (e.g., nighttime). | 1. Captures nonlinear noise patterns. 2. Adapts to dynamic environments (e.g., nonlinear noise variations). |
| Limitations | 1. Assumes noise follows geometric/Poisson distribution. 2. Sensitive to model mismatch (e.g., nonstationary noise). | 1. Fails when noise density > signal density. 2. Manual threshold tuning; poor generalization. | 1. Requires large labeled datasets (scarce for daytime ranging). 2. High computational costs. |
| Applicable Scenarios | Low SNR, dynamic noise (e.g., daylight space debris tracking). | High SNR, stable noise (e.g., nighttime satellite ranging). | Complex noise patterns with sufficient labeled data. |
| Data Requirements | No training data; relies on real-time observations. | No training data; requires empirical threshold tuning. | Large labeled datasets (noise–signal spatiotemporal labels). |
| Computational Complexity | Low (suitable for embedded systems). | Extremely low (threshold comparison). | High (GPU acceleration needed for training/inference). |
| Future Directions | Adaptive windowing and online parameter updates for dynamic noise robustness. | Dynamic threshold adjustment (e.g., adaptive filtering). | Lightweight models (e.g., online learning), synthetic data augmentation, multimodal fusion. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Dong, X.; Gao, J.; Guan, B.; Zheng, Y.; Liang, Z.; Han, X.; Dong, H. Real-Time Identification Algorithm of Daylight Space Debris Laser Ranging Data Based on Observation Data Distribution Model. Sensors 2025, 25, 2281. https://doi.org/10.3390/s25072281
Liu Y, Dong X, Gao J, Guan B, Zheng Y, Liang Z, Han X, Dong H. Real-Time Identification Algorithm of Daylight Space Debris Laser Ranging Data Based on Observation Data Distribution Model. Sensors. 2025; 25(7):2281. https://doi.org/10.3390/s25072281
Chicago/Turabian StyleLiu, Yang, Xue Dong, Jian Gao, Bowen Guan, Yanning Zheng, Zhipeng Liang, Xingwei Han, and He Dong. 2025. "Real-Time Identification Algorithm of Daylight Space Debris Laser Ranging Data Based on Observation Data Distribution Model" Sensors 25, no. 7: 2281. https://doi.org/10.3390/s25072281
APA StyleLiu, Y., Dong, X., Gao, J., Guan, B., Zheng, Y., Liang, Z., Han, X., & Dong, H. (2025). Real-Time Identification Algorithm of Daylight Space Debris Laser Ranging Data Based on Observation Data Distribution Model. Sensors, 25(7), 2281. https://doi.org/10.3390/s25072281






