Multi-View Stereo Using Perspective-Aware Features and Metadata to Improve Cost Volume
Abstract
1. Introduction
- (1)
- We propose a powerful FMLT approach that leverages both internal and external attention mechanisms to integrate long-range contextual information both within individual images and across multiple images. This methodology reimagines MVS as a fundamental feature matching task and takes advantage of the remarkable feature representation capabilities offered by the Transformer architecture. By using attention mechanisms and position coding, the FMLT approach can perceive global and position-related contextual information, enhancing the robustness of depth assessments in challenging MVS scenarios.
- (2)
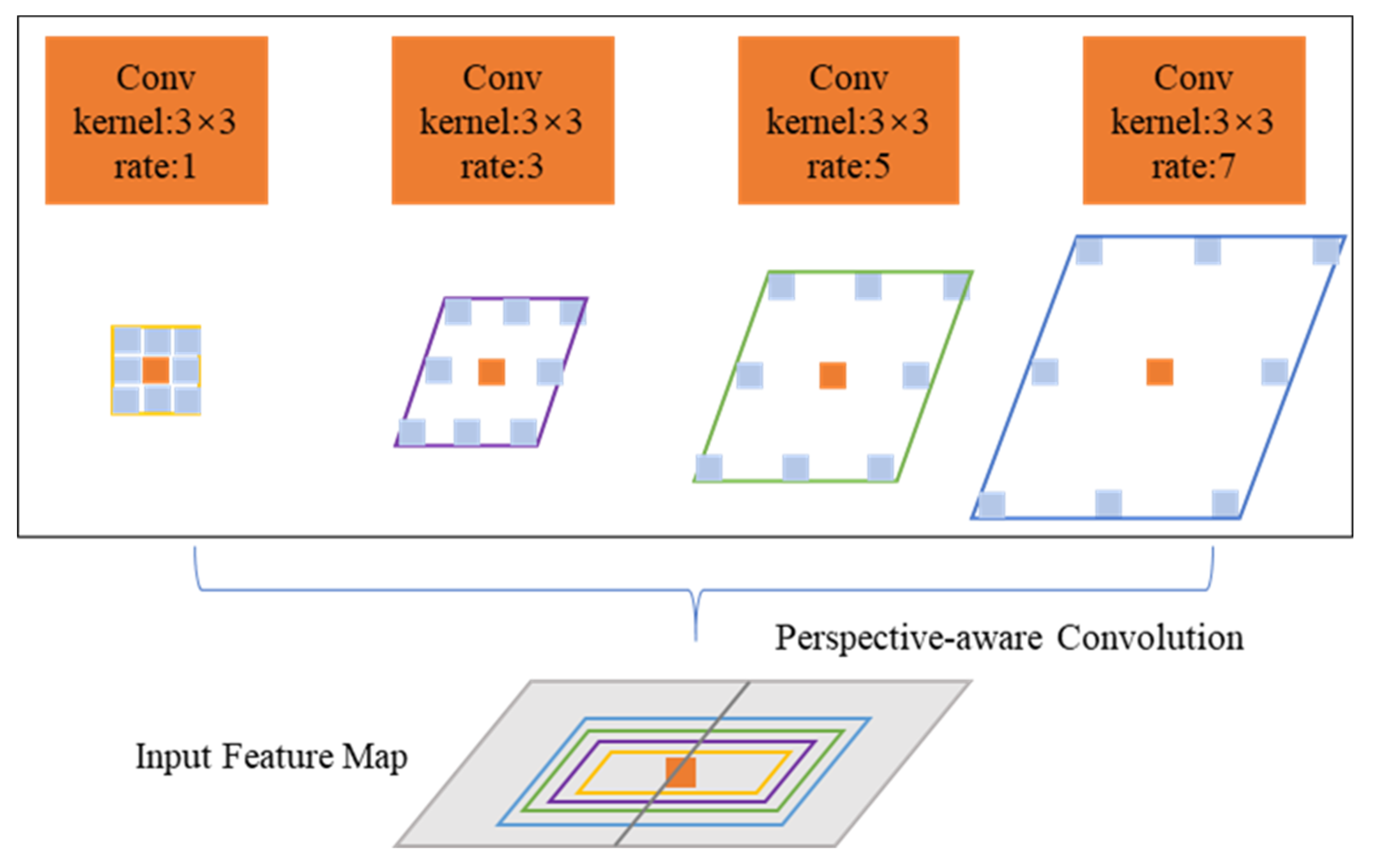
- We introduce a novel module called PAC that was designed to augment the capacity to capture features related to perspective. PAC derives features along the depth dimension by modifying the shape of the convolution kernel and facilitates the parallel integration of multiple dilation rates within convolutional branches. By embedding PAC modules within MVS networks, the resulting feature maps become sensitized to the viewpoint, enhancing the analysis of objects within scene structures specific to the view. This innovation addresses the issues related to feature search and alignment, providing a more accurate and detailed reconstruction of the scene.
- (3)
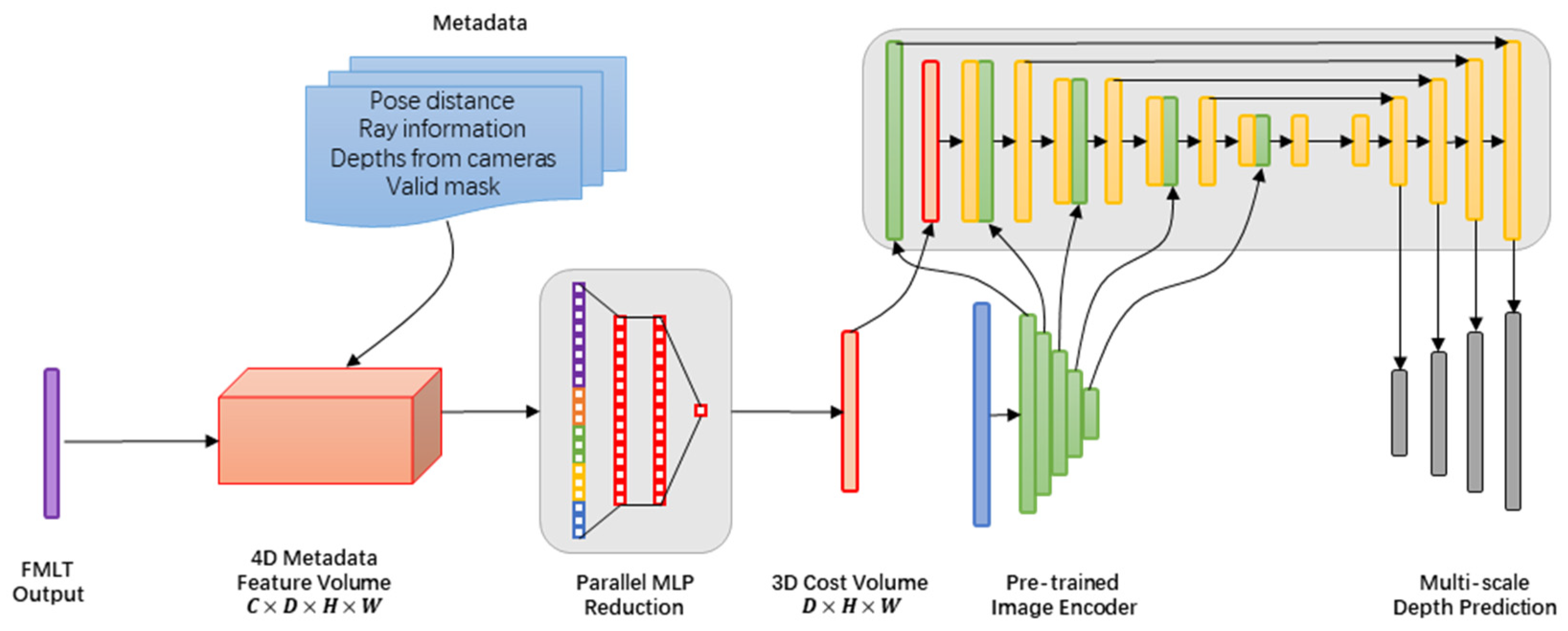
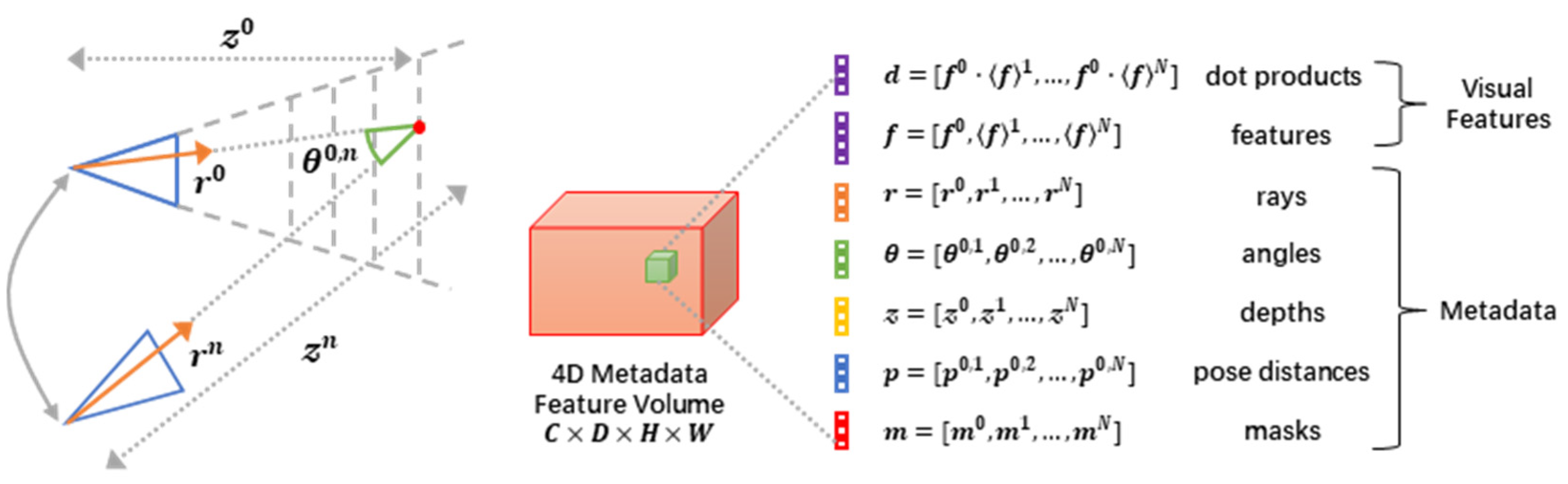
- We revisited fundamental principles and discovered that incorporating straightforward, cost-effective 2D CNNs can achieve high precision in depth determination. In contrast to resource-intensive 3D convolutions, this approach demonstrated comparable performance in 3D scene reconstruction utilizing standard TSDF fusion. The fundamental approach involves seamlessly integrating obtainable metadata within the cost volume, substantially improving the depth estimation and reconstruction quality. By eliminating the computational burden linked to 3D convolutions, this innovation is ideally suited for embedded systems and resource-limited environments.
2. Related Work
2.1. Learning-Based MVS Method
2.2. Transformer for Feature Matching
2.3. Cost Volume
3. Method
3.1. Overall Architecture Diagram
3.2. Perspective-Aware Convolution
3.3. Feature Matching with Long-Range Tracking
3.4. Cost Volume Architecture
3.5. Loss Function
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Experimental Results
5. Discussion
5.1. Ablation Discussion
- (1)
- Complementary Effects: Using both PAC and metadata contributed positively to 3D reconstruction, with each providing unique benefits. PAC enhances the model’s understanding of spatial relationships, resulting in improved accuracy. The use of metadata, on the other hand, offers additional context that aids in capturing finer details. When combined (Ours (PAC + Metadata)), these strategies complement each other, leading to significant improvements in reconstruction quality across all the evaluated datasets.
- (2)
- Performance Across Datasets: Our method with PAC + Metadata consistently outperformed the other two methods in terms of key metrics such as mean distance, percentage of points within certain error thresholds, and F-score. This robust performance indicates the method’s strong generalization capability across diverse scenarios, including indoor scenes (DTU), outdoor landmarks (Tanks and Temples), and urban environments (ETH3D and UrbanScene3D).
- (3)
- Individual Contributions: While our method with PAC generally outperformed the model with Metadata in terms of overall accuracy, the latter showed competitive results in capturing finer details, particularly in certain scenes. This suggests that PAC is crucial for improving the overall precision of the reconstruction, while the use of metadata plays a more nuanced role in enhancing surface textures and edge details. Table 1, Table 2, Table 3 and Table 4 confirmed that the use of PAC and metadata synergistically improved accuracy and completeness. PAC contributed most significantly (+12.6% F-score), validating its role in perspective alignment.
5.2. Inference Memory and Time Costs
5.3. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, X.; Fan, Z.; Zhu, S.; Dai, Z.; Tan, F.; Tan, P. Cascade Cost Volume for High-Resolution Multi-View Stereo and Stereo Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2495–2504. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. MVSNet: Depth Inference for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Recurrent MVSNet for High-Resolution Multi-View Stereo Depth Inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5525–5534. [Google Scholar]
- Collins, R. A Space-Sweep Approach to True Multi-Image Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 358–363. [Google Scholar]
- Zhou, T.; Matthew, B.; Noah, S.; Lowe, D. Unsupervised Learning of Depth and Ego-Motion from Video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1851–1858. [Google Scholar]
- Paul-Edouard, S.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning Feature Matching with Graph Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4938–4947. [Google Scholar]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-Free Local Feature Matching with Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 8922–8931. [Google Scholar]
- Dijk, T.; Guido, C. How Do Neural Networks See Depth in Single Images? In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2183–2191. [Google Scholar]
- Mohamed, S.; Gibson, J.; Watson, J.; Prisacariu, V.; Firman, M.; Godard, C. SimpleRecon: 3D Reconstruction without 3D Convolutions. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 1–19. [Google Scholar]
- Newcombe, R.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.; Kohi, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A. Kinectfusion: Real-time Dense Surface Mapping and Tracking. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 127–136. [Google Scholar]
- Henrik, A.; Jensen, R.; Vogiatzis, G.; Tola, E.; Dahl, A. Large-scale Data for Multiple-View Stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar]
- Thomas, S.; Schonberger, J.; Galliani, S.; Sattler, T.; Schindler, K.; Pollefeys, M.; Geiger, A. A Multi-View Stereo Benchmark with High-Resolution Images and Multi-Camera Videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3260–3269. [Google Scholar]
- Knapitsch, A.; Park, J.; Zhou, Q.; Koltun, V. Tanks and temples: Benchmarking Large-Scale Scene Reconstruction. ACM Trans. Graph. 2017, 36, 78. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Y.; Hu, Y.; Yan, X.; Xie, K.; Huang, H. Capturing, Reconstructing, And Simulating: The Urbanscene3d Dataset. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 93–109. [Google Scholar]
- Wei, Z.; Zhu, Q.; Min, C.; Chen, Y.; Wang, G. Aa-rmvsnet: Adaptive aggregation recurrent multi-view stereo network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6187–6196. [Google Scholar]
- Yan, J.; Wei, Z.; Yi, H.; Ding, M.; Zhang, R.; Chen, Y. Dense hybrid recurrent multi-view stereo net with dynamic consistency checking. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 674–689. [Google Scholar]
- Sotiris, K.; Gkika, I.; Gkitsas, V.; Konstantoudakis, K.; Zarpalas, D. A Survey of Deep Learning-Based Image Restoration Methods for Enhancing Situational Awareness at Disaster Sites: The Cases of Rain, Snow and Haze. Sensors 2022, 22, 4707. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Xu, Z.; Zhu, S.; Li, Z.; Li, E.; Ramamoorthi, R.; Su, H. Deep stereo using adaptive thin volume representation with uncertainty awareness. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2524–2534. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017; Volume 30, pp. 5998–6008. [Google Scholar]
- Nicolas, C.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Elashry, A.; Toth, C. Feature Matching Enhancement Using the Graph Neural Network. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2022, 46, 83–89. [Google Scholar] [CrossRef]
- Collings, S.; Botha, E.J.; Anstee, J.; Campbell, N. Depth from Satellite Images: Depth Retrieval Using a Stereo and Radiative Transfer-Based Hybrid Method. Remote Sens. 2018, 10, 1247. [Google Scholar] [CrossRef]
- Yamins, D.; DiCarlo, J. Using Goal-Driven Deep Learning Models to Understand Sensory Cortex. Nat. Neurosci. 2016, 19, 356–365. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Yao, G.; Yilmaz, A.; Zhang, L.; Meng, F.; Ai, H.; Jin, F. Matching Large Baseline Oblique Stereo Images Using an End-to-End Convolutional Neural Network. Remote Sens. 2021, 13, 274. [Google Scholar] [CrossRef]
- Nikolaus, M.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A Large Dataset to Train Convolutional Networks for Disparity, Optical Flow, and Scene Flow Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 4040–4048. [Google Scholar]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Van, P.; Smagt, D.; Cremers, D.; Brox, T. Flownet: Learning Optical Flow with Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2758–2766. [Google Scholar]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-End Learning of Geometry and Context for Deep Stereo Regression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 66–75. [Google Scholar]
- Lin, L.; Zhang, Y.; Wang, Z.; Zhang, L.; Liu, X.; Wang, Q. A-SATMVSNet: An Attention-Aware Multi-View Stereo Matching Network Based on Satellite Imagery. Front. Earth Sci. 2023, 11, 1108403. [Google Scholar]
- Zhu, Z.; Stamatopoulos, C.; Fraser, C.S. Accurate and Occlusion-Robust Multi-View Stereo. ISPRS J. Photogramm. Remote Sens. 2015, 109, 47–61. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J. Structure-from-Motion Revisited. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 4104–4113. [Google Scholar]
- Park, S.Y.; Seo, D.; Lee, M.J. GEMVS: A Novel Approach for Automatic 3D Reconstruction from Uncalibrated Multi-View Google Earth Images Using Multi-View Stereo and Projective to Metric 3D Homography Transformation. Int. J. Remote Sens. 2023, 44, 3005–3030. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Zheng, E.; Frahm, J.; Pollefeys, M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 501–518. [Google Scholar]
- Ji, M.; Gall, J.; Zheng, H.; Liu, Y.; Fang, L. SurfaceNet: An End-to-End 3d Neural Network for Multiview Stereopsis. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2307–2315. [Google Scholar]
- Abhishek, K.; Häne, C.; Malik, J. Learning a Multi-View Stereo Machine. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017; pp. 121–132. [Google Scholar]
- Liu, J.; Gao, J.; Ji, S. Deep Learning Based Multi-View Stereo Matching and 3D Scene Reconstruction from Oblique Aerial Images. ISPRS J. Photogramm. Remote Sens. 2023, 204, 42–60. [Google Scholar] [CrossRef]
- Ibrahimli, N.; Ledoux, H.; Kooij, J.F.P.; Nan, L. DDL-MVS: Depth Discontinuity Learning for Multi-View Stereo Networks. Remote Sens. 2023, 15, 2970. [Google Scholar] [CrossRef]
- Jin, J.; Hou, J. Occlusion-Aware Unsupervised Learning of Depth From 4-D Light Fields. IEEE Trans. Image Process. 2022, 31, 2216–2228. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, Y.; Guo, J.; Zhao, X.; Gao, M.; Lei, B. Attention-Based Monocular Depth Estimation Considering Global and Local Information in Remote Sensing Images. Remote Sens. 2024, 16, 585. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, K.; Zhang, F.; Sun, J.; Wan, W.; Zhang, H. Multiview Hypergraph Fusion Network for Change Detection in High-Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4597–4610. [Google Scholar]
- Vaishakh, P.; Van, W.; Dai, D.; Van, G. Don’t Forget the Past: Recurrent Depth Estimation from Monocular Video. IEEE Robot. Autom. Lett. 2020, 5, 6813–6820. [Google Scholar]
- Vincent, C.; Pirk, S.; Mahjourian, R.; Angelova, A. Depth Prediction without the Sensors: Leveraging Structure for Unsupervised Learning from Monocular Videos. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8001–8008. [Google Scholar]
- Jung, H.; Oh, Y.; Jeong, S.; Lee, C.; Jeon, T. Contrastive Self-Supervised Learning with Smoothed Representation for Remote Sensing. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8010105. [Google Scholar]
- Wang, X.; Wang, S.; Ning, C.; Zhou, H. Enhanced Feature Pyramid Network with Deep Semantic Embedding for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7918–7932. [Google Scholar] [CrossRef]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Katharopoulos, A.; Vyas, A.; Pappas, N.; Fleuret, F. Transformers are rnns: Fast autoregressive transformers with linear attention. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5156–5165. [Google Scholar]
- Clevert, D.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units. In Proceedings of the International Conference on Learning Representations, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Liu, Z.; Feng, R.; Wang, L.; Han, W.; Zeng, T. Dual Learning-Based Graph Neural Network for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5628614. [Google Scholar]
- Facil, J.M.; Ummenhofer, B.; Zhou, H.; Montesano, L.; Brox, T.; Civera, J. CAM-Convs: Camera-Aware Multi-Scale Convolutions for Single-View Depth. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11826–11835. [Google Scholar]
- Zhao, Y.; Kong, S.; Fowlkes, C. Camera Pose Matters: Improving Depth Prediction by Mitigating Pose Distribution Bias. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 15759–15768. [Google Scholar]
- Wei, Y.; Zhang, J.; Wang, O.; Niklaus, S.; Mai, L.; Chen, S.; Shen, C. Learning to Recover 3D Scene Shape from a Single Image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 204–213. [Google Scholar]
- Advances in Neural Information Processing Systems, C.; Fergus, R. Depth Map Prediction from a Single Image Using a Multi-Scale Deep Network. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2014; pp. 232–243. [Google Scholar]
- Fisher, A.; Cannizzaro, R.; Cochrane, M.; Nagahawatte, C.; Palmer, L. ColMap: A Memory-Efficient Occupancy Grid Mapping Framework. Robot. Auton. Syst. 2021, 142, 1232–1245. [Google Scholar]
- Wang, F.; Galliani, S.; Vogel, C.; Speciale, P.; Pollefeys, M. PatchMatchNet: Learned Multi-View PatchMatch Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 14194–14203. [Google Scholar]
- Ding, Y. TransMVSNet: Global Context-aware Multi-view Stereo Network with Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022; pp. 8575–8584. [Google Scholar]









| Method | Mean Distance (mm) | Percentage (<1 mm) | Percentage (<2 mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc. ↓ | Comp. ↓ | Overall ↓ | Acc. ↑ | Comp. ↑ | F-Score ↑ | Acc. ↑ | Comp. ↑ | F-Score ↑ | |
| Colmap | 0.400 | 0.664 | 0.532 | 71.75 | 64.94 | 68.20 | 84.83 | 67.82 | 75.27 |
| CasMVSNet | 0.325 | 0.385 | 0.355 | 69.55 | 61.52 | 65.30 | 78.99 | 67.88 | 72.99 |
| PatchMatchNet | 0.427 | 0.277 | 0.352 | 90.49 | 57.83 | 70.67 | 91.07 | 63.88 | 75.01 |
| TransMVSNet | 0.321 | 0.289 | 0.305 | 83.81 | 63.38 | 72.09 | 87.15 | 67.99 | 76.47 |
| Ours (PAC) | 0.342 | 0.262 | 0.302 | 84.45 | 68.37 | 75.52 | 91.72 | 73.16 | 80.78 |
| Ours (Metadata) | 0.353 | 0.283 | 0.318 | 83.99 | 66.52 | 74.57 | 89.82 | 72.67 | 79.86 |
| Ours (PAC + Metadata) | 0.331 | 0.255 | 0.293 | 86.46 | 71.13 | 77.92 | 93.94 | 75.31 | 83.47 |
| Method | Mean | Family | Francis | Horse | Lighthouse | M60 | Panther | Playground | Train |
|---|---|---|---|---|---|---|---|---|---|
| Colmap | 42.14 | 50.41 | 22.25 | 26.63 | 56.43 | 44.83 | 46.97 | 48.53 | 42.04 |
| CasMVSNet | 56.84 | 76.37 | 58.45 | 46.26 | 55.81 | 56.11 | 54.06 | 58.18 | 49.51 |
| PatchMatchNet | 54.03 | 76.50 | 47.74 | 47.07 | 55.12 | 57.28 | 54.28 | 57.43 | 47.54 |
| TransMVSNet | 63.52 | 80.92 | 65.83 | 56.94 | 62.54 | 63.06 | 60.00 | 60.20 | 58.67 |
| Ours (PAC) | 64.83 | 82.32 | 66.93 | 61.04 | 64.28 | 64.62 | 62.57 | 61.05 | 58.97 |
| Ours (Metadata) | 63.71 | 80.95 | 65.75 | 58.71 | 63.81 | 63.71 | 60.39 | 60.17 | 58.50 |
| Ours (PAC + Metadata) | 65.76 | 82.43 | 67.29 | 61.72 | 65.32 | 65.71 | 62.96 | 61.28 | 59.35 |
| Method | Acc. ↑ | Comp. ↑ | F-Score ↑ |
|---|---|---|---|
| Colmap | 91.97 | 62.98 | 74.76 |
| CasMVSNet | 66.32 | 72.05 | 69.64 |
| PatchMatchNet | 69.71 | 77.46 | 73.38 |
| TransMVSNet | 82.23 | 83.75 | 82.98 |
| Ours (PAC) | 86.61 | 84.92 | 85.76 |
| Ours (Metadata) | 82.87 | 83.94 | 83.40 |
| Ours (PAC + Metadata) | 88.37 | 85.67 | 86.99 |
| Method | Mean Distance (mm) | Percentage (<50 mm) | Percentage (<100 mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc. ↓ | Comp. ↓ | Overall ↓ | Acc. ↑ | Comp. ↑ | F-Score ↑ | Acc. ↑ | Comp. ↑ | F-Score ↑ | |
| Colmap | 79.80 | 89.15 | 84.48 | 68.57 | 54.49 | 60.69 | 81.83 | 62.85 | 71.15 |
| CasMVSNet | 58.52 | 84.58 | 71.55 | 65.44 | 57.25 | 61.18 | 76.55 | 65.78 | 70.61 |
| PatchMatchNet | 47.67 | 72.25 | 59.96 | 78.94 | 56.38 | 65.78 | 85.66 | 61.44 | 71.67 |
| TransMVSNet | 52.77 | 53.27 | 53.02 | 78.18 | 61.83 | 69.72 | 91.23 | 66.31 | 76.89 |
| Ours (PAC) | 45.52 | 42.15 | 43.84 | 81.79 | 71.26 | 76.12 | 90.51 | 74.27 | 81.84 |
| Ours (Metadata) | 52.03 | 48.76 | 50.40 | 79.63 | 65.34 | 71.58 | 90.23 | 68.21 | 77.56 |
| Ours (PAC + Metadata) | 45.91 | 42.38 | 44.15 | 82.26 | 73.33 | 77.59 | 90.66 | 75.31 | 82.38 |
| Method | Memory ↓ (MB) | Time ↓ (s) | Params. (Overall/Trainable) ↓ (Unit) |
|---|---|---|---|
| Colmap | 4326 (9107) | 0.7125 (2.9276) | --- |
| CasMVSNet | 6672 (12,351) | 0.7747 (0.8311) | 0.93 M/0.93 M |
| PatchMatchNet | 6320 (11,935) | 1.4975 (2.0652) | 1.15 M/1.15 M |
| TransMVSNet | 5136 (9673) | 0.4931 (0.5598) | 29.03 M/7.03 M |
| Ours (PAC + Metadata) | 4842 (9251) | 0.4630 (0.4972) | 26.45 M/4.79 M |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Z.; Li, Y.; Zhou, Y.; Mo, F. Multi-View Stereo Using Perspective-Aware Features and Metadata to Improve Cost Volume. Sensors 2025, 25, 2233. https://doi.org/10.3390/s25072233
Zuo Z, Li Y, Zhou Y, Mo F. Multi-View Stereo Using Perspective-Aware Features and Metadata to Improve Cost Volume. Sensors. 2025; 25(7):2233. https://doi.org/10.3390/s25072233
Chicago/Turabian StyleZuo, Zongcheng, Yuanxiang Li, Yu Zhou, and Fan Mo. 2025. "Multi-View Stereo Using Perspective-Aware Features and Metadata to Improve Cost Volume" Sensors 25, no. 7: 2233. https://doi.org/10.3390/s25072233
APA StyleZuo, Z., Li, Y., Zhou, Y., & Mo, F. (2025). Multi-View Stereo Using Perspective-Aware Features and Metadata to Improve Cost Volume. Sensors, 25(7), 2233. https://doi.org/10.3390/s25072233






