A Robust Method Based on Deep Learning for Compressive Spectrum Sensing
Abstract
1. Introduction
2. System Model
2.1. Compressive Sampling
2.2. Compressed Signal Reconstruction
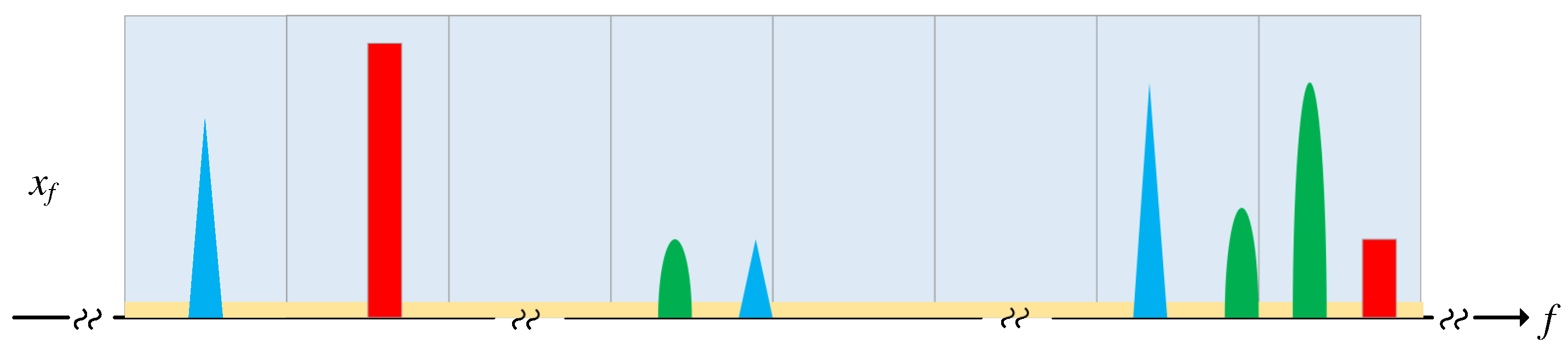
2.3. Wideband Spectrum Sensing
3. The Proposed CSS Method
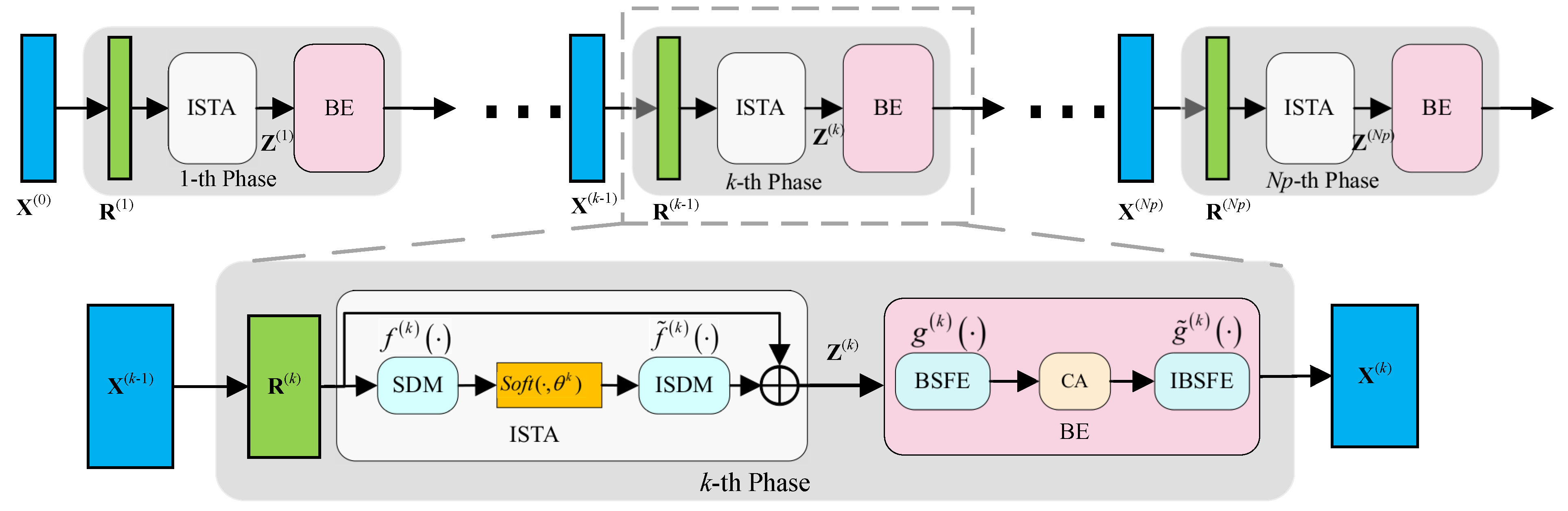
3.1. Beista-Net Architecture
- Module: This module corresponds to Equation (4) and is used to generate the instantaneous reconstruction result . Note that is actually the gradient of the data-fidelity term . To improve the reconstruction performance and increase its capacity, we permit the step size to vary during iterations. The input to this layer is , and the output is defined as
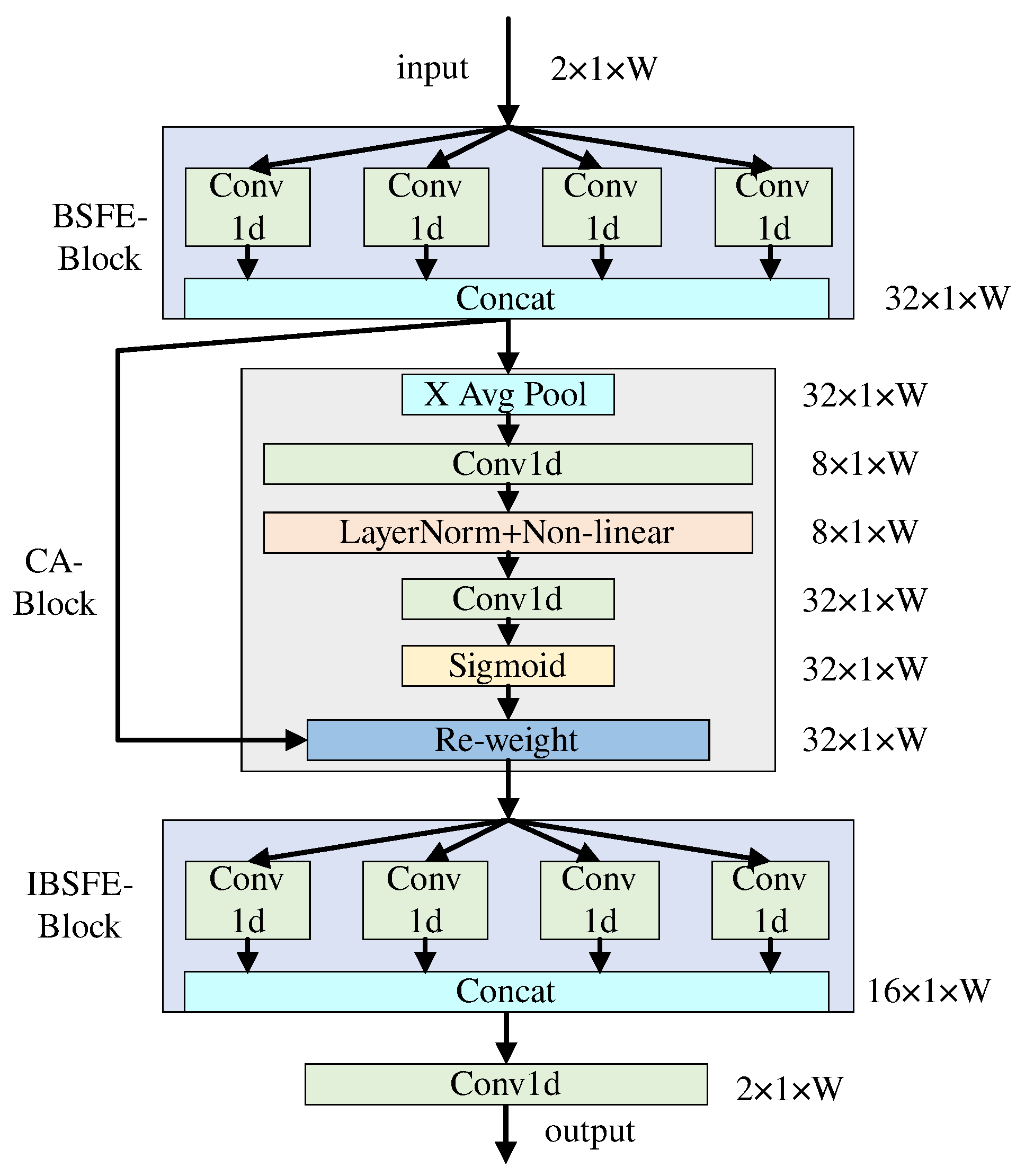
- Module: The network expansion diagram of the module is shown in Figure 4. First, this module extracts the BSF of the wideband spectrum signals by the BSFE-Block. Then, it enhances these features by the CA-Block. Finally, it maps the enhanced signals back to the original dimensions by the IBSFE-Block. The CA-Block transforms the captured features into corresponding coefficients and multiplies them with their original data to obtain the enhanced signals. The output of the feature enhancement module is
3.2. BSWSS-Net Architecture
3.3. Training Methodology
4. Datasets and Performance Metrics
4.1. Two Datasets
4.2. Performance Metrics
5. Experiment Results
5.1. BEISTA-Net
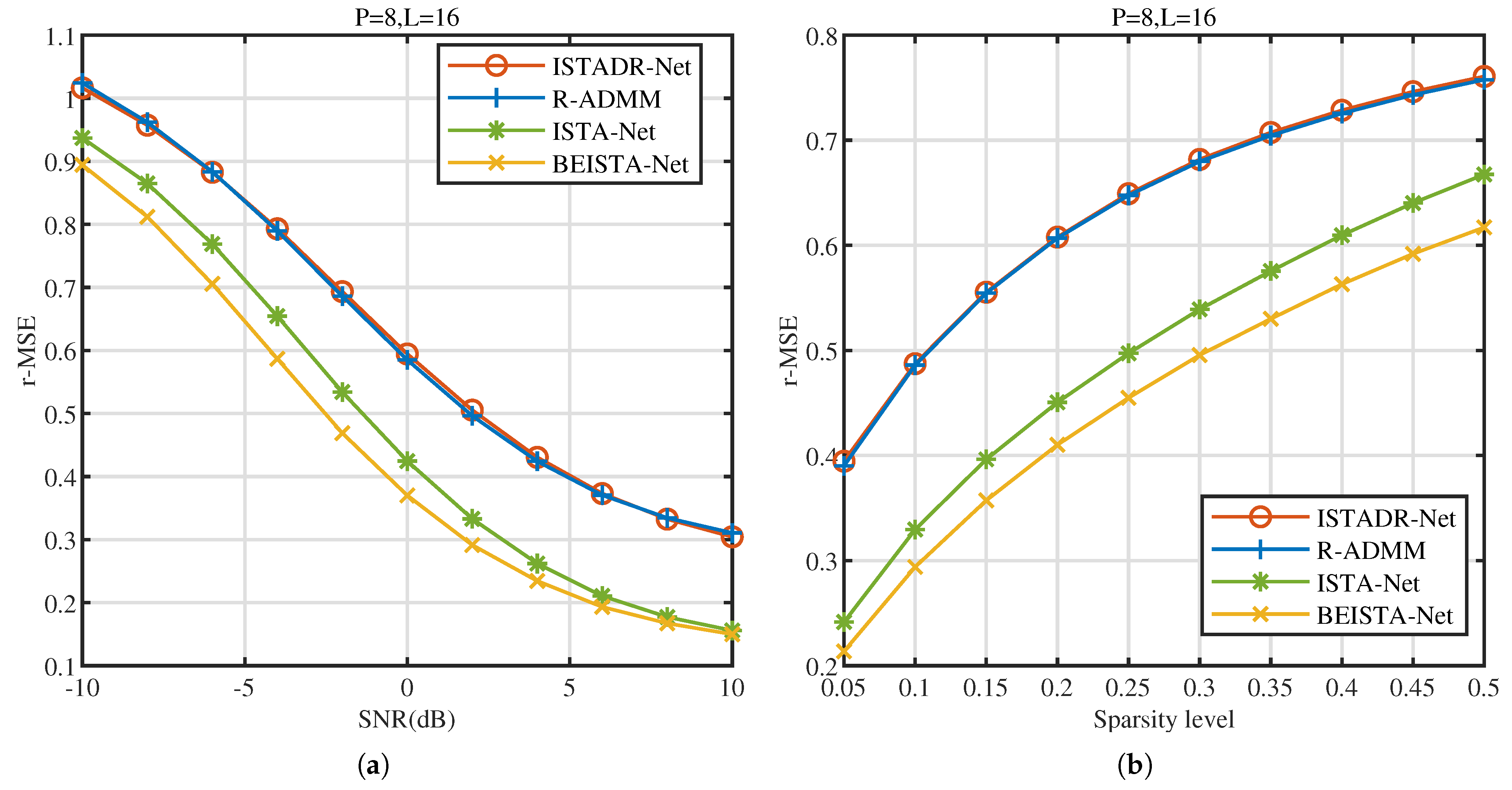
5.1.1. Reconstruction Accuracy
5.1.2. Complexity Analysis of Reconstruction Algorithms
5.2. BSWSS-Net
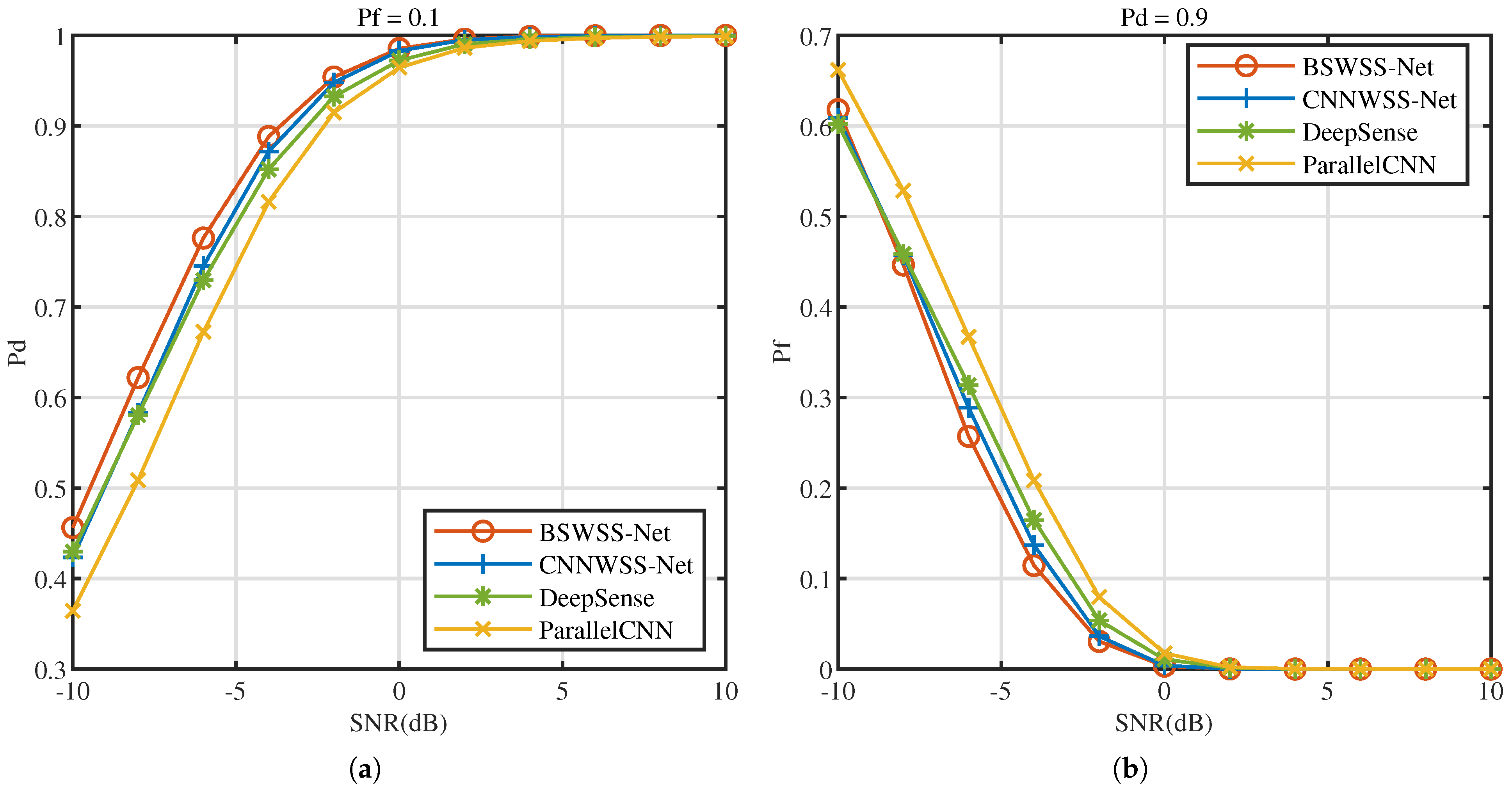
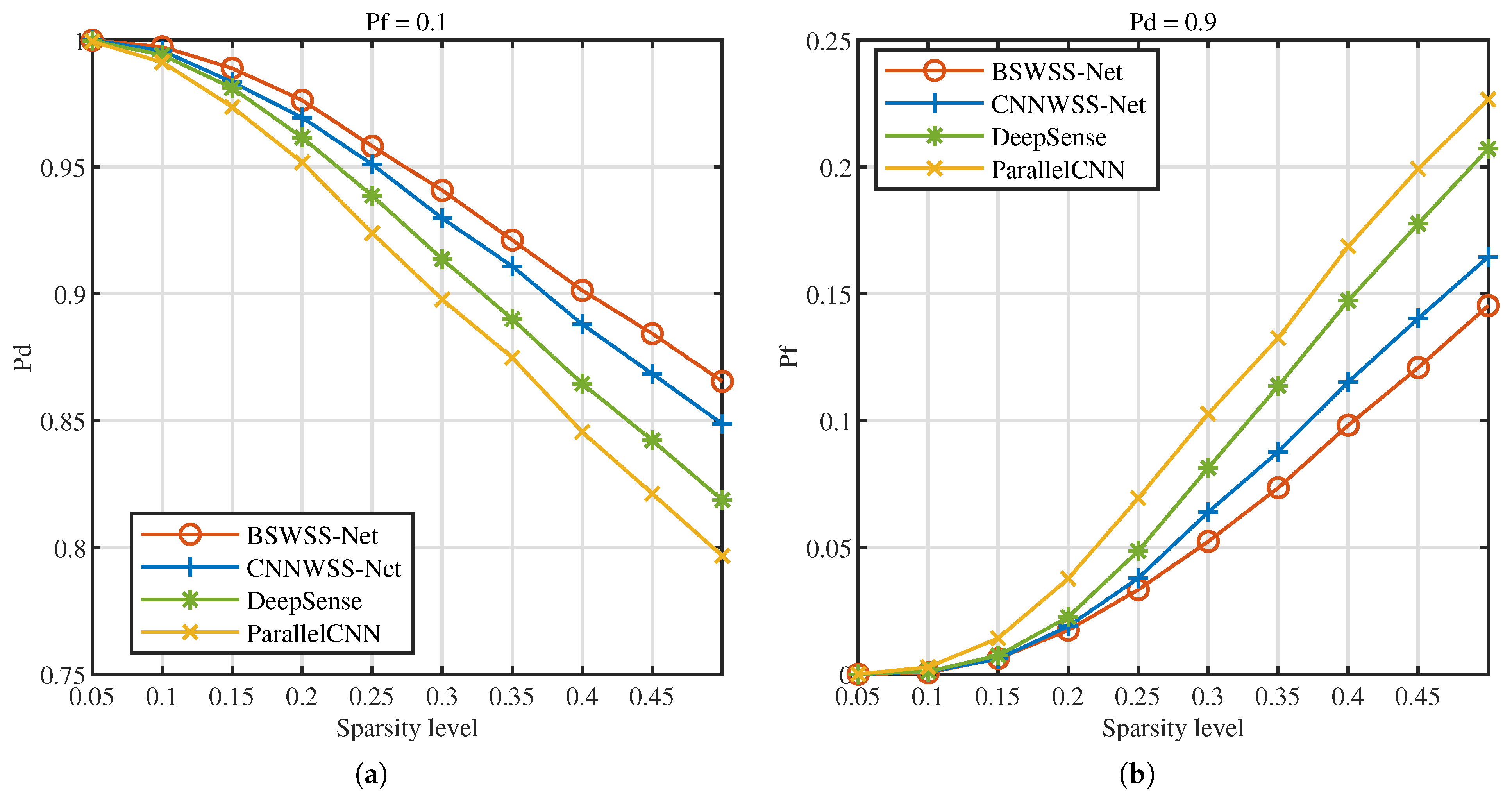
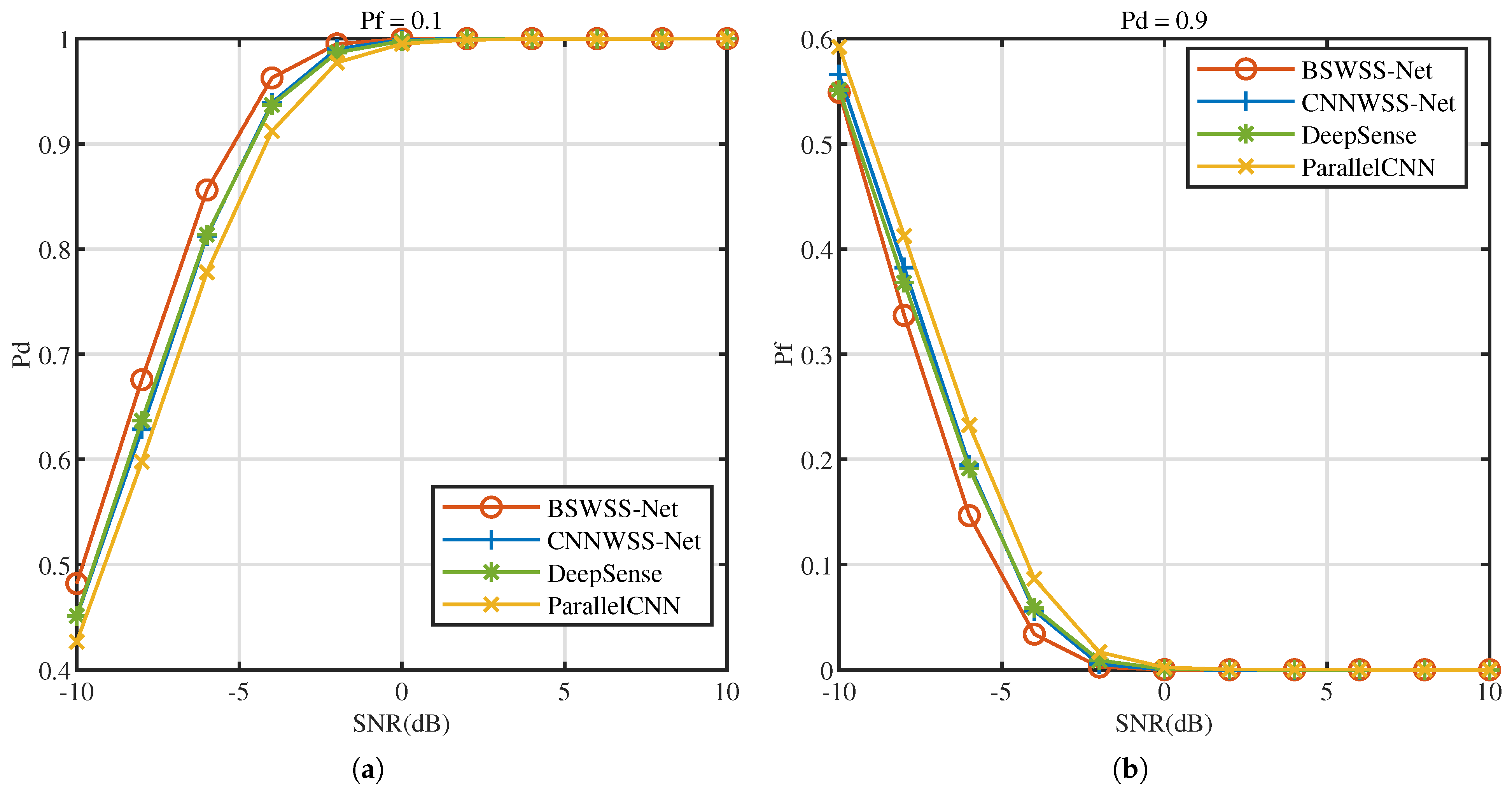
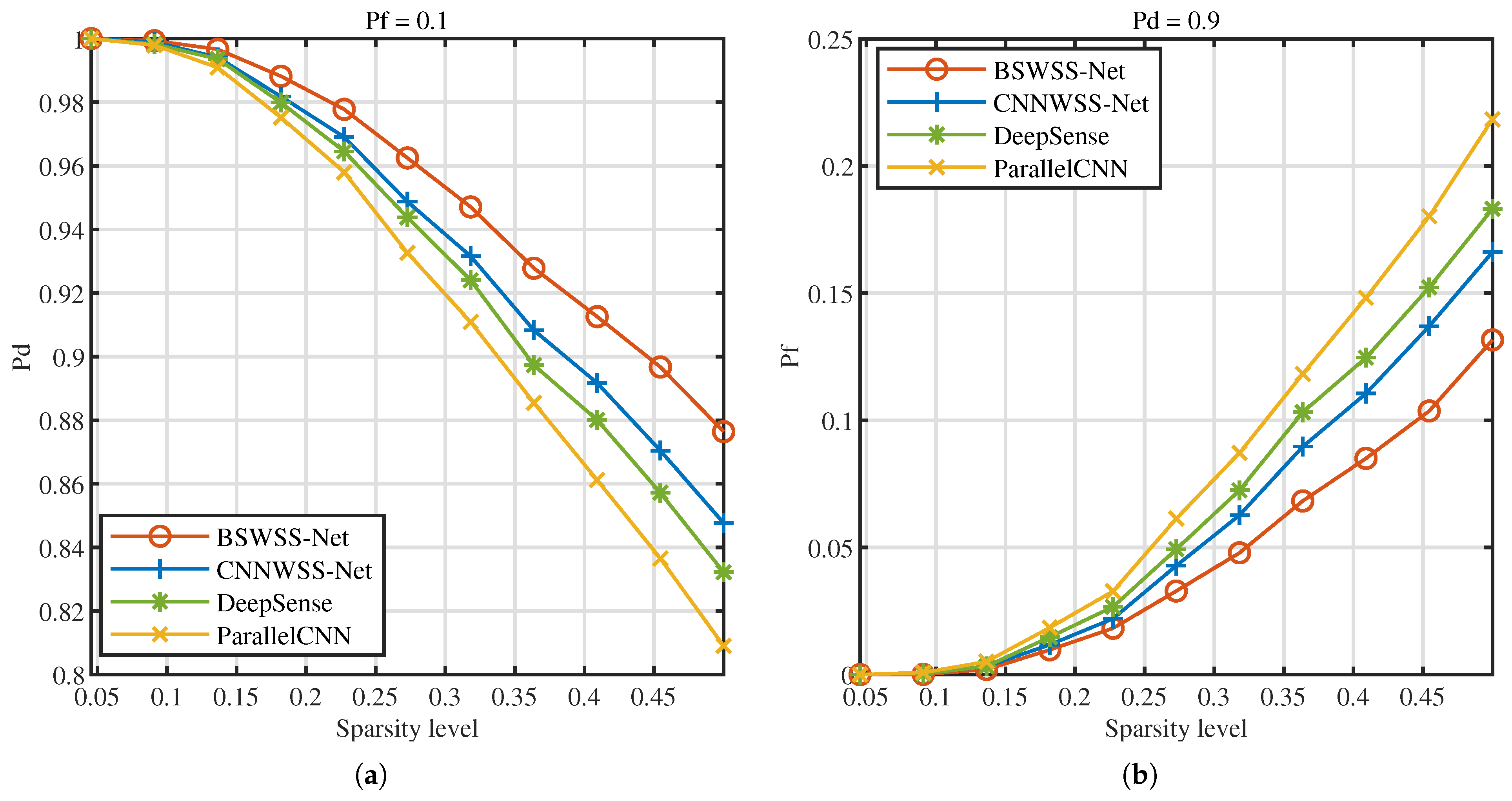
5.2.1. Sense Accuracy
5.2.2. Complexity Analysis of WSS Algorithms
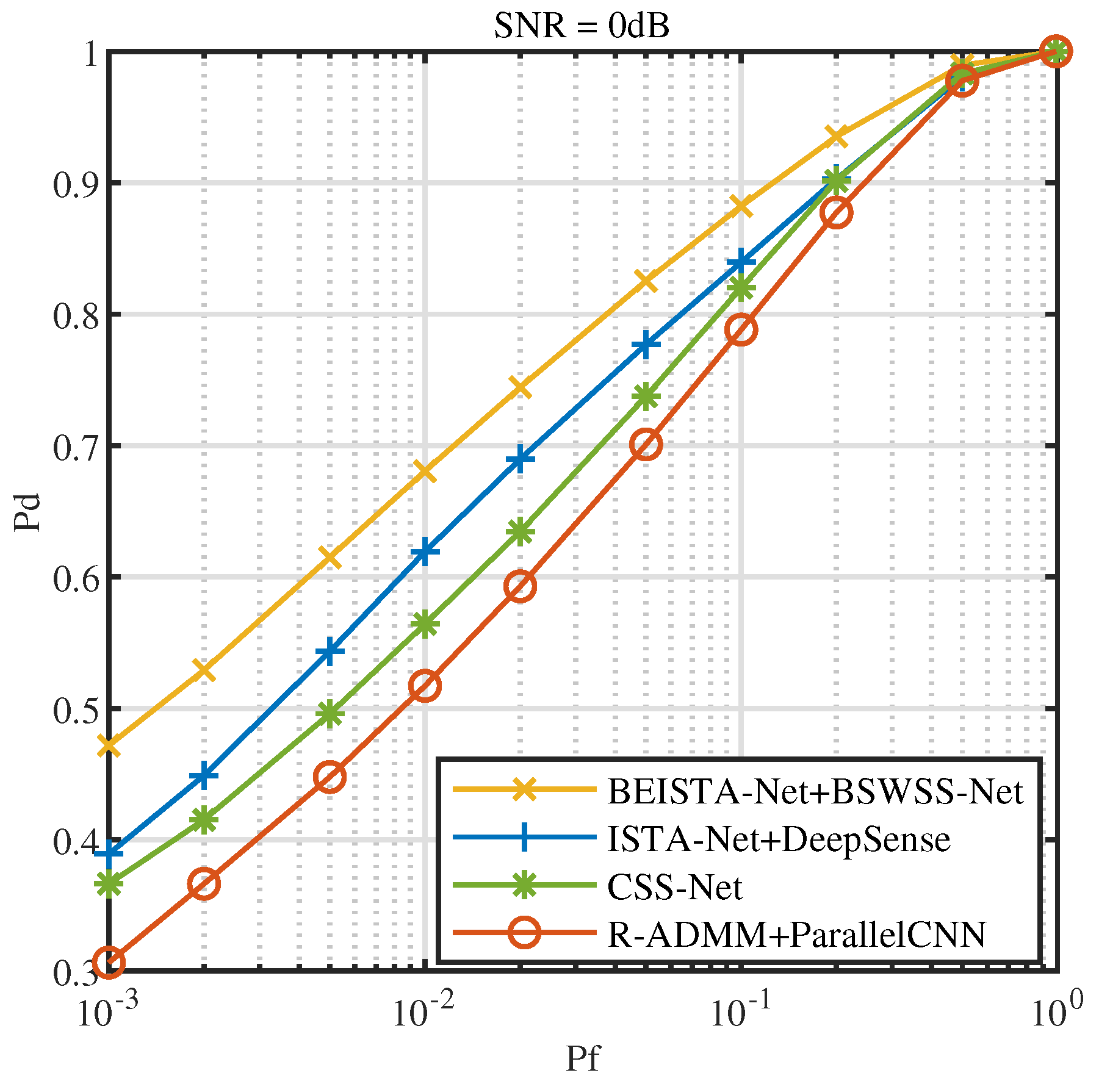
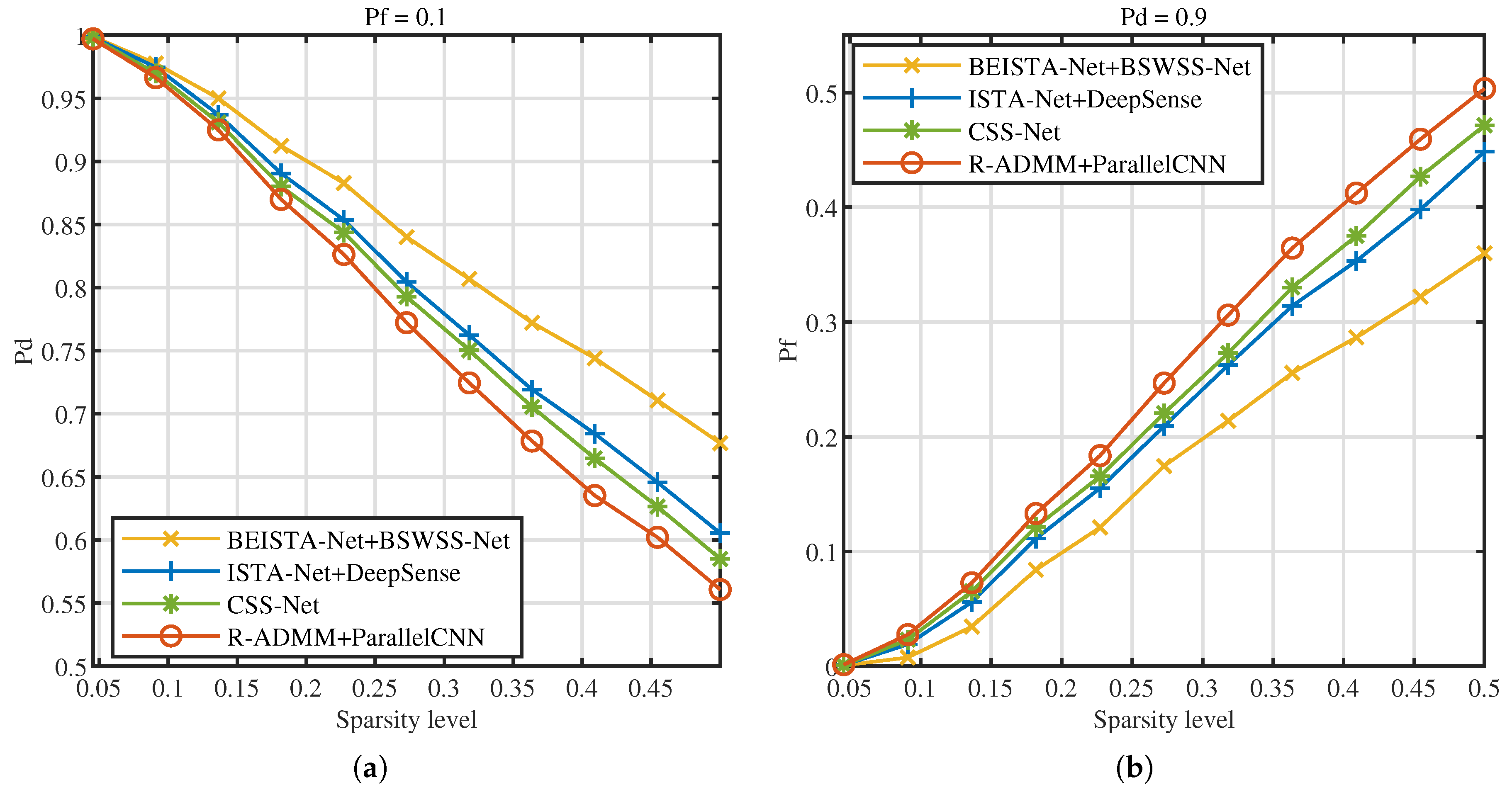
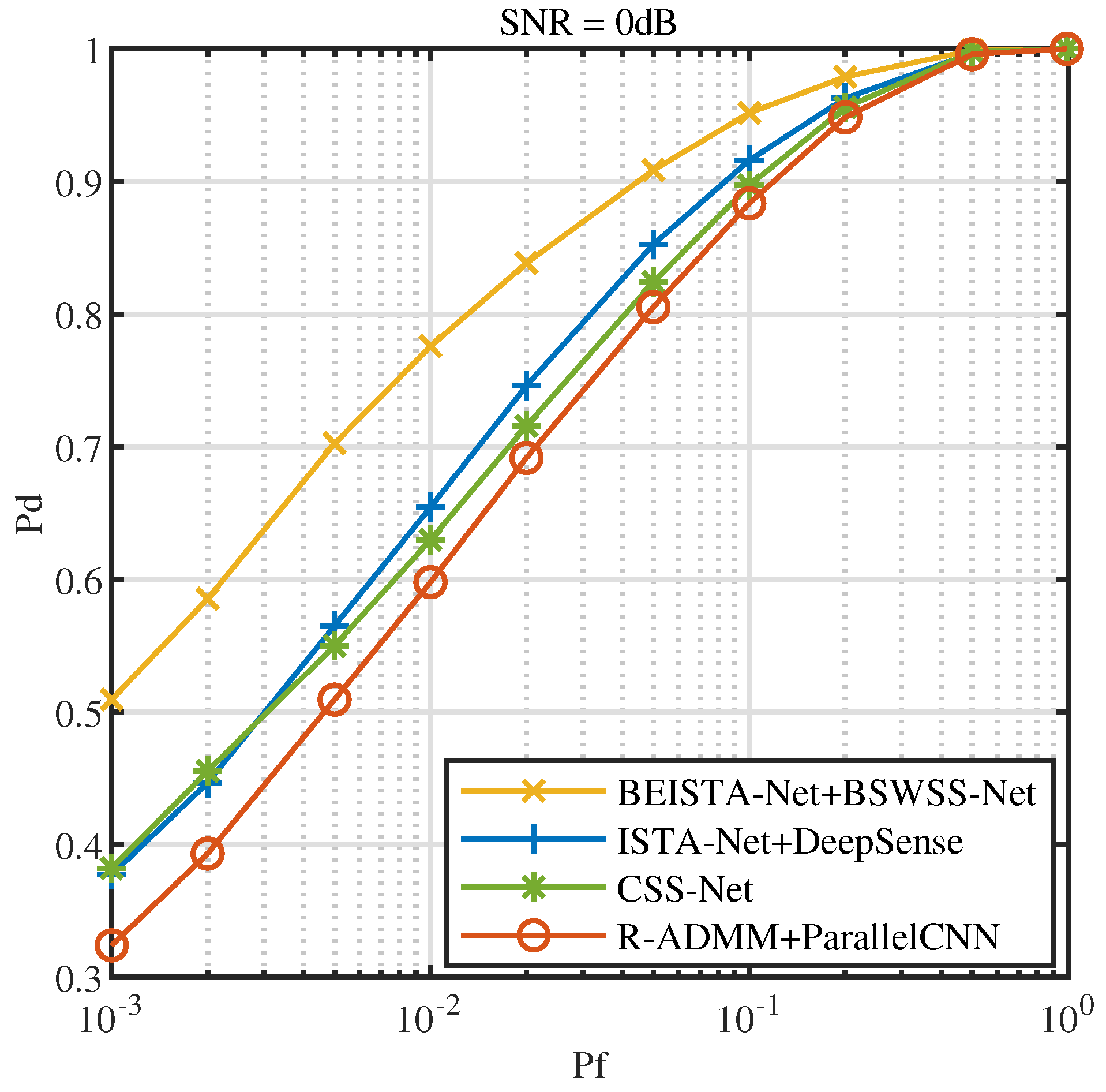
5.3. Joint CSS Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Hu, Z.; Shen, C.; Wu, H.; Zhao, Y. TFF_aDCNN: A Pre-Trained Base Model for Intelligent Wideband Spectrum Sensing. IEEE Trans. Veh. Technol. 2023, 72, 12912–12926. [Google Scholar]
- Qin, Z.; Zhou, X.; Zhang, L.; Gao, Y.; Liang, Y.C.; Li, G.Y. 20 Years of Evolution From Cognitive to Intelligent Communications. IEEE Trans. Cogn. Commun. Netw. 2019, 6, 6–20. [Google Scholar] [CrossRef]
- Ghadyani, M.; Shahzadi, A. Adaptive Data-Driven Wideband Compressive Spectrum Sensing for Cognitive Radio Networks. J. Commun. Inf. Netw. 2018, 3, 84–92. [Google Scholar]
- Wang, H.; Fang, J.; Duan, H.; Li, H. Compressive Wideband Spectrum Sensing and Signal Recovery with Unknown Multipath Channels. IEEE Trans. Wirel. Commun. 2022, 21, 5305–5316. [Google Scholar]
- Zhang, H.; Yang, J.; Gao, Y. Machine Learning Empowered Spectrum Sensing Under a Sub-Sampling Framework. IEEE Trans. Wirel. Commun. 2022, 21, 8205–8215. [Google Scholar]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar]
- Cai, T.T.; Wang, L. Orthogonal Matching Pursuit for Sparse Signal Recovery with Noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonalmatching pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; Mol, C.D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Zhang, X. Robust DNN-Based Recovery of Wideband Spectrum Signals. IEEE Wirel. Commun. Lett. 2023, 12, 1712–1715. [Google Scholar]
- Pavitra, V.; Dutt, V.B.S.S.I.; Raj Kumar, G.V.S. Deep Learning Based Compressive Sensing for Image Reconstruction and Inference. In Proceedings of the 2022 IEEE 7th International Conference for Convergence in Technology (I2CT), Mumbai, India, 7–9 April 2022; pp. 1–7. [Google Scholar]
- Michael, I.; Leonidas, S.; Aggelos, K.K. Deep fully-connected networks for video compressive sensing. Digit. Signal Process. 2018, 72, 9–18. [Google Scholar]
- Mousavi, A.; Patel, A.B.; Baraniuk, R.G. A deep learning approach to structured signal recovery. In Proceedings of the 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September– October 2015; pp. 1336–1343. [Google Scholar]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1828–1837. [Google Scholar]
- Mei, R.; Wang, Z. Compressed Spectrum Sensing of Sparse wideband spectrum signals Based on Deep Learning. IEEE Trans. Veh. Technol. 2024, 73, 8434–8444. [Google Scholar]
- Fu, R.; Monardo, V.; Huang, T.; Liu, Y. Deep Unfolding Network for Block-Sparse Signal Recovery. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 2880–2884. [Google Scholar]
- Gao, J.; Yi, X.; Zhong, C.; Chen, X.; Zhang, Z. Deep Learning for Spectrum Sensing. IEEE Wirel. Commun. Lett. 2019, 8, 1727–1730. [Google Scholar]
- Uvaydov, D.; D’Oro, S.; Restuccia, F.; Melodia, T. DeepSense: Fast Wideband Spectrum Sensing Through Real-Time In-the-Loop Deep Learning. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar]
- Mei, R.; Wang, Z. Deep Learning-Based Wideband Spectrum Sensing: A Low Computational Complexity Approach. IEEE Commun. Lett. 2023, 27, 2633–2637. [Google Scholar]
- Chen, Z.; Xu, Y.Q.; Wang, H.; Guo, D. Deep STFT-CNN for Spectrum Sensing in Cognitive Radio. IEEE Commun. Lett. 2021, 25, 864–868. [Google Scholar]
- Sabrina, Z.; Camel, T.; Djamal, T.; Ammar, M.; Said, S.; Belqassim, B. Spectrum Sensing based on an improved deep learning classification for cognitive radio. In Proceedings of the 2022 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Maldives, Maldives, 16–18 November 2022; pp. 1–5. [Google Scholar]
- Zhang, W.; Wang, Y.; Chen, X.; Cai, Z.; Tian, Z. Spectrum Transformer: An Attention-Based Wideband Spectrum Detector. IEEE Trans. Wirel. Commun. 2024, 23, 12343–12353. [Google Scholar]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13708–13717. [Google Scholar]
- Lu, L.; Xu, W.; Cui, Y.; Dai, M.; Long, J. Block spectrum sensing based on prior information in cognitive radio networks. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–19 April 2019; pp. 1–5. [Google Scholar]
- Li, F.; Zhao, X. Block-Structured Compressed Spectrum Sensing with Gaussian Mixture Noise Distribution. IEEE Wirel. Commun. Lett. 2019, 8, 1183–1186. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Part IV 13. pp. 184–199. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]

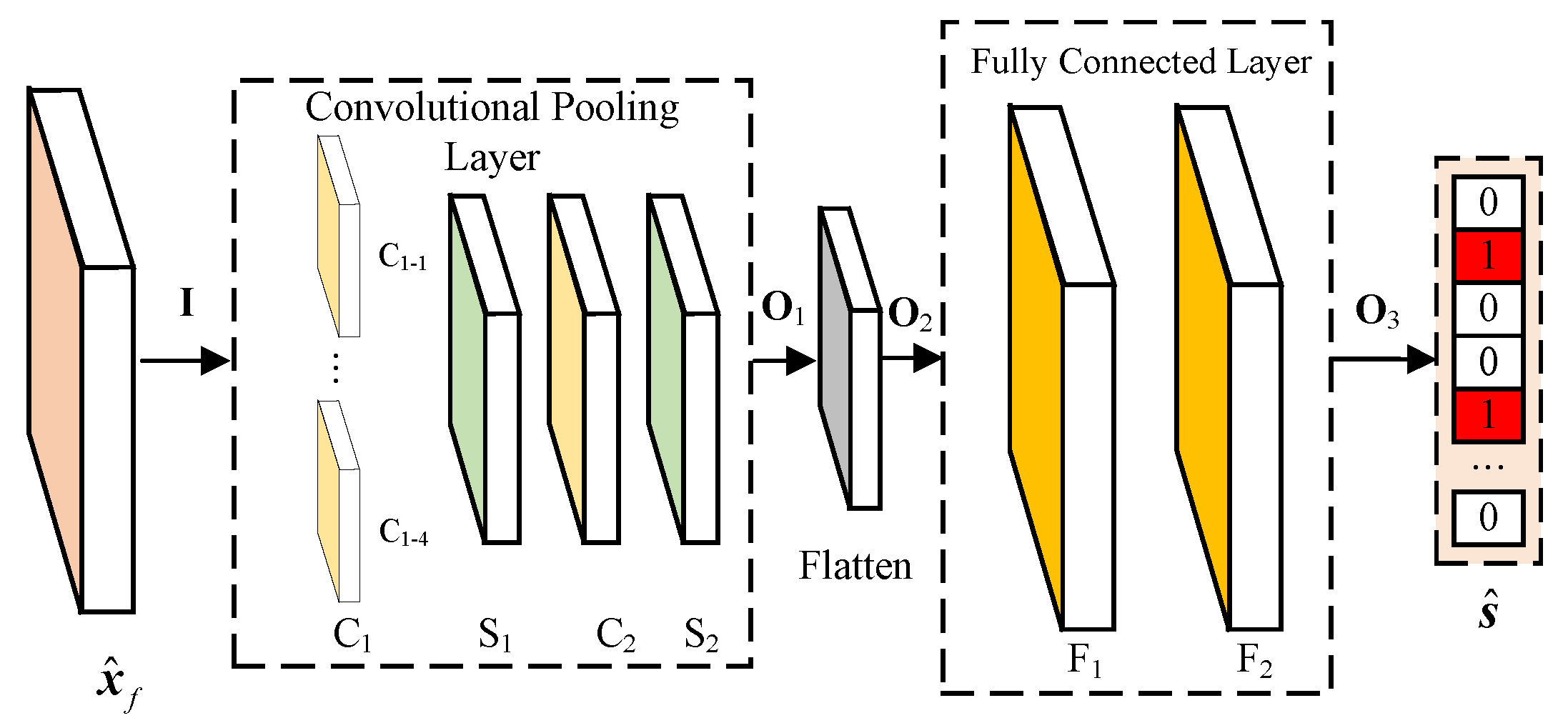






| Layer | Filter | Stride | Padding | |
|---|---|---|---|---|
| Convolutional Pooling Layer | 4 | 2 | 1 | |
| 8 | 2 | 3 | ||
| 12 | 2 | 5 | ||
| 16 | 2 | 7 | ||
| 4 | 4 | 0 | ||
| 8 | 2 | 3 | ||
| 4 | 4 | 0 | ||
| Layer | Out features | |||
| Fully Connected Layer | 256 | |||
| Algorithm | # of FLOPs | # of Learnable Parameters | Execution Time (ms) | Video Memory Usage (MB) |
|---|---|---|---|---|
| ISTADR-Net | 64 | |||
| R-ADMM | ||||
| ISTA-Net | ||||
| BEISTA-Net |
| Dataset | Algorithm | # of FLOPs | # Learnable Parameters | Execution Time (ms) | Video Memory Usage (MB) |
|---|---|---|---|---|---|
| NR dataset | DeepSense | ||||
| ParalellCNN | |||||
| CNNWSS-Net | |||||
| BSWSS-Net | |||||
| TVWS dataset | DeepSense | ||||
| ParalellCNN | |||||
| CNNWSS-Net | |||||
| BSWSS-Net |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, H.; Yu, Y.; Liu, G.; Wu, Y. A Robust Method Based on Deep Learning for Compressive Spectrum Sensing. Sensors 2025, 25, 2187. https://doi.org/10.3390/s25072187
Zeng H, Yu Y, Liu G, Wu Y. A Robust Method Based on Deep Learning for Compressive Spectrum Sensing. Sensors. 2025; 25(7):2187. https://doi.org/10.3390/s25072187
Chicago/Turabian StyleZeng, Haoye, Yantao Yu, Guojin Liu, and Yucheng Wu. 2025. "A Robust Method Based on Deep Learning for Compressive Spectrum Sensing" Sensors 25, no. 7: 2187. https://doi.org/10.3390/s25072187
APA StyleZeng, H., Yu, Y., Liu, G., & Wu, Y. (2025). A Robust Method Based on Deep Learning for Compressive Spectrum Sensing. Sensors, 25(7), 2187. https://doi.org/10.3390/s25072187





