Edge_MVSFormer: Edge-Aware Multi-View Stereo Plant Reconstruction Based on Transformer Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Preparation
2.1.1. Public Dataset
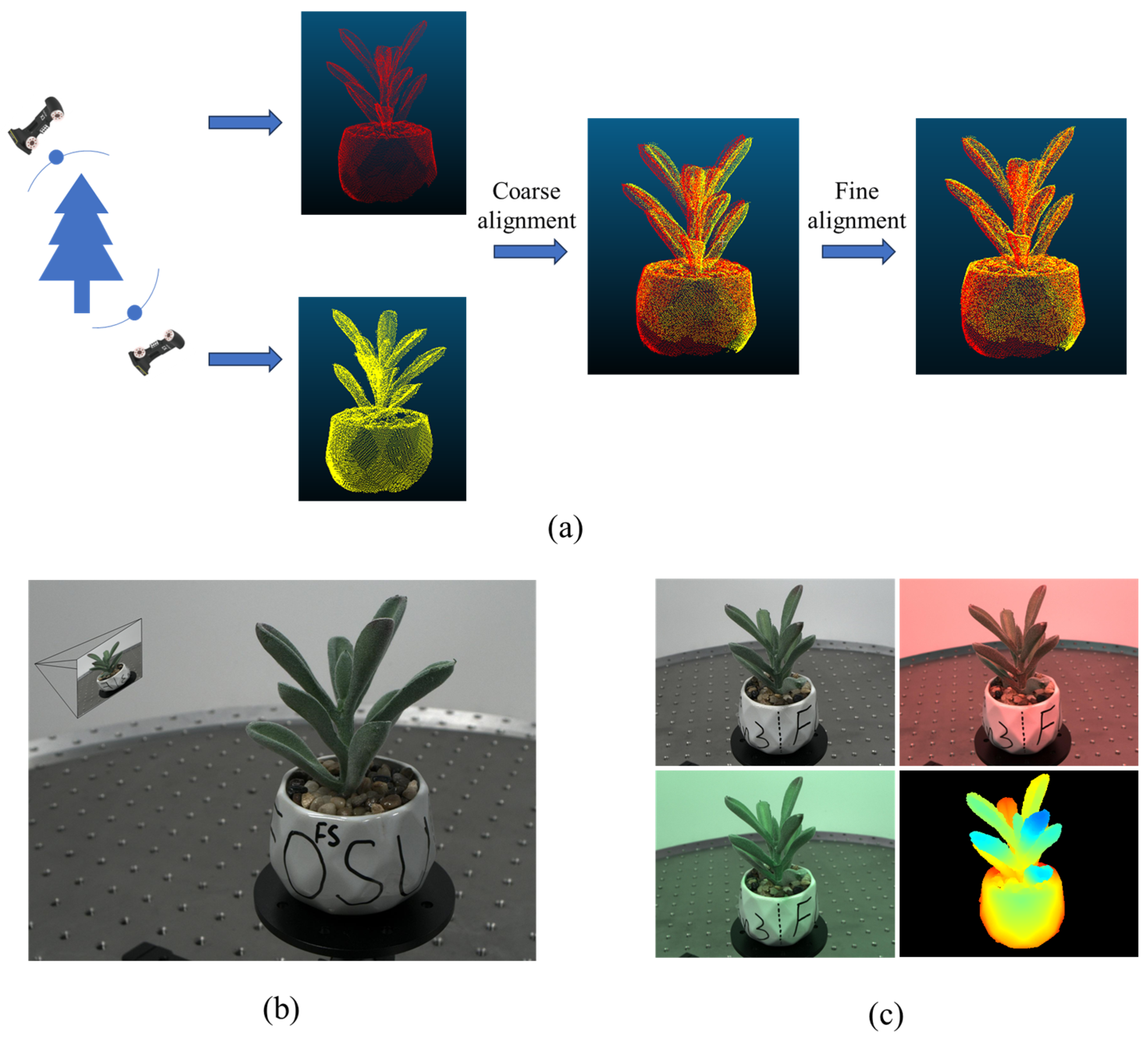
2.1.2. Private Dataset and Preparation
2.2. 3D Plant Reconstruction Method
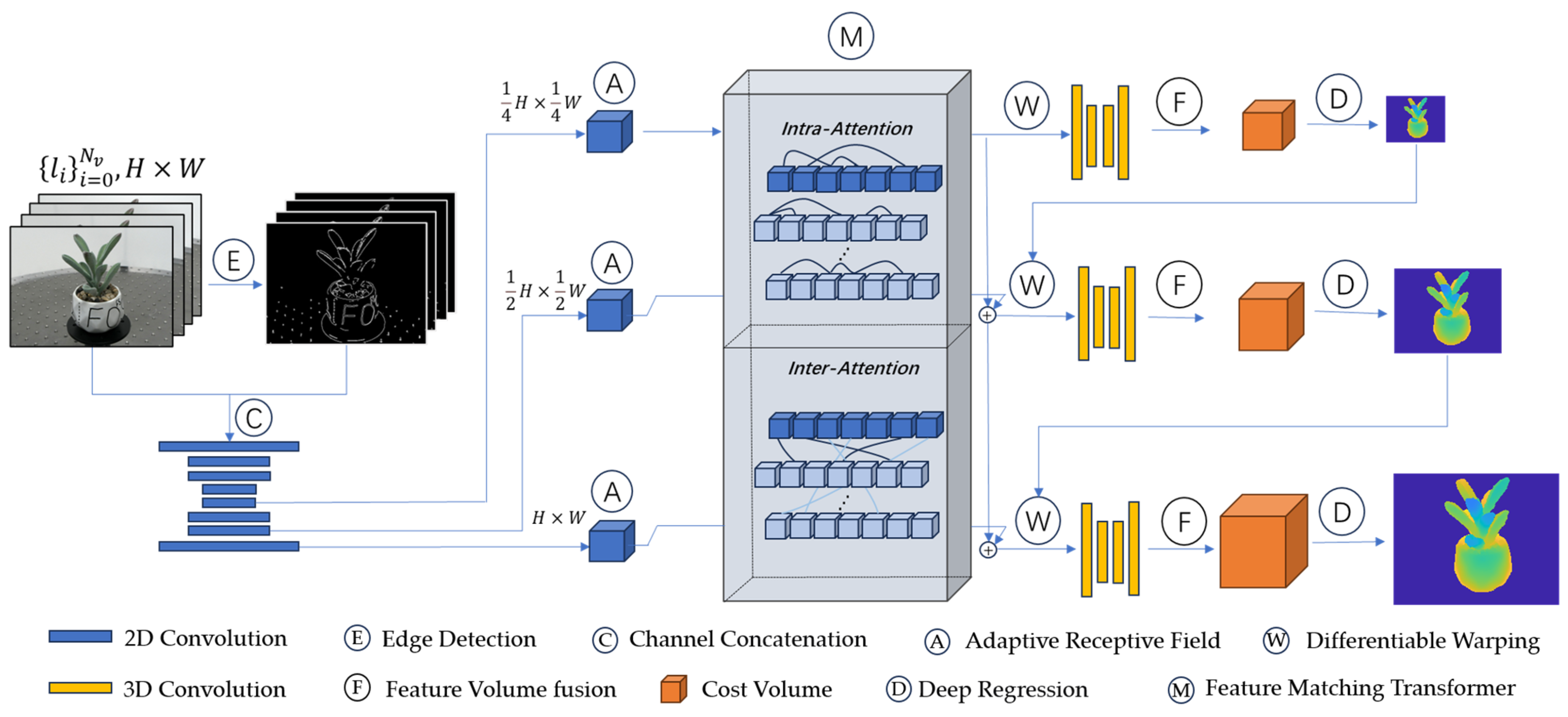
2.2.1. Network Model
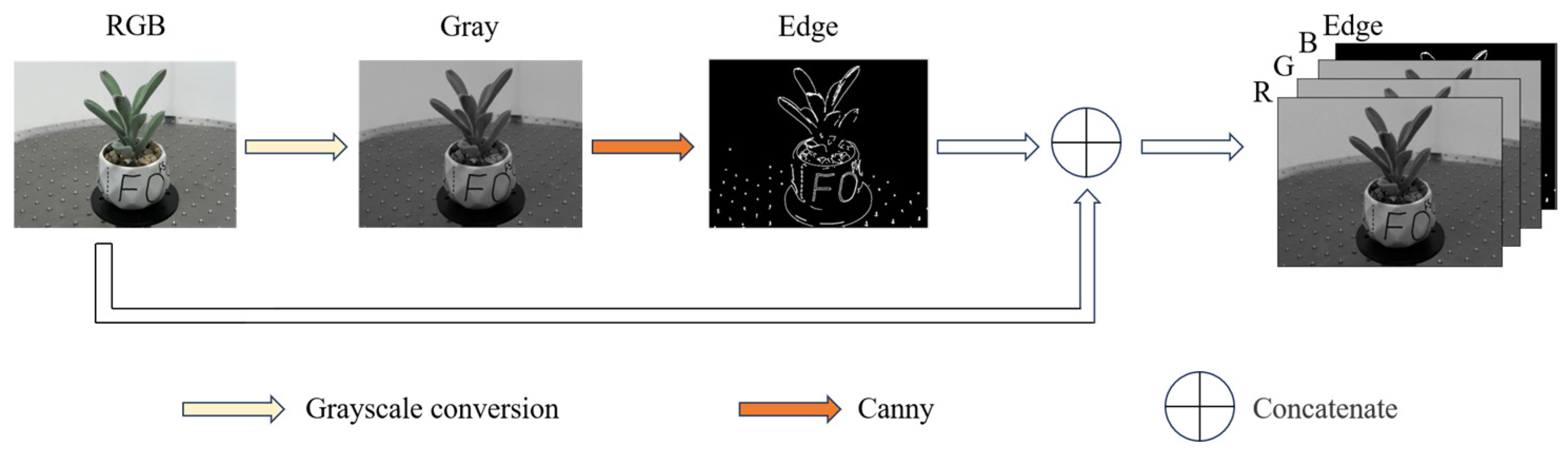
2.2.2. Edge Detection
2.2.3. Loss Function
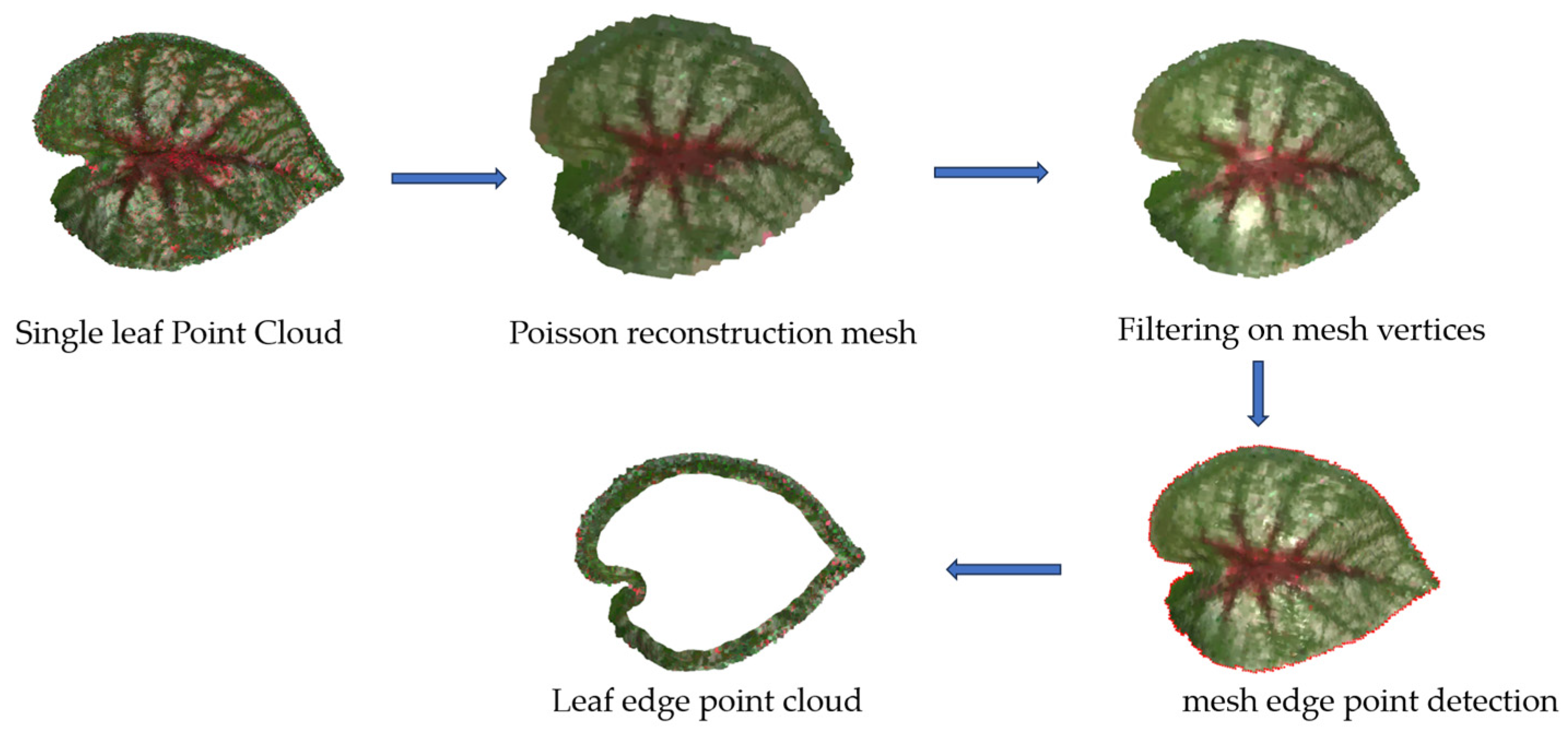
2.2.4. Point Cloud Generation
2.3. Experimental Validation
2.3.1. Experiment and Algorithm Implementation
2.3.2. Evaluation Metrics
Evaluation of Reconstructed Depth Images
Evaluation of Reconstructed Point Clouds
Evaluation of Phenotypic Parameters
Evaluation of Runtime Performance
3. Results
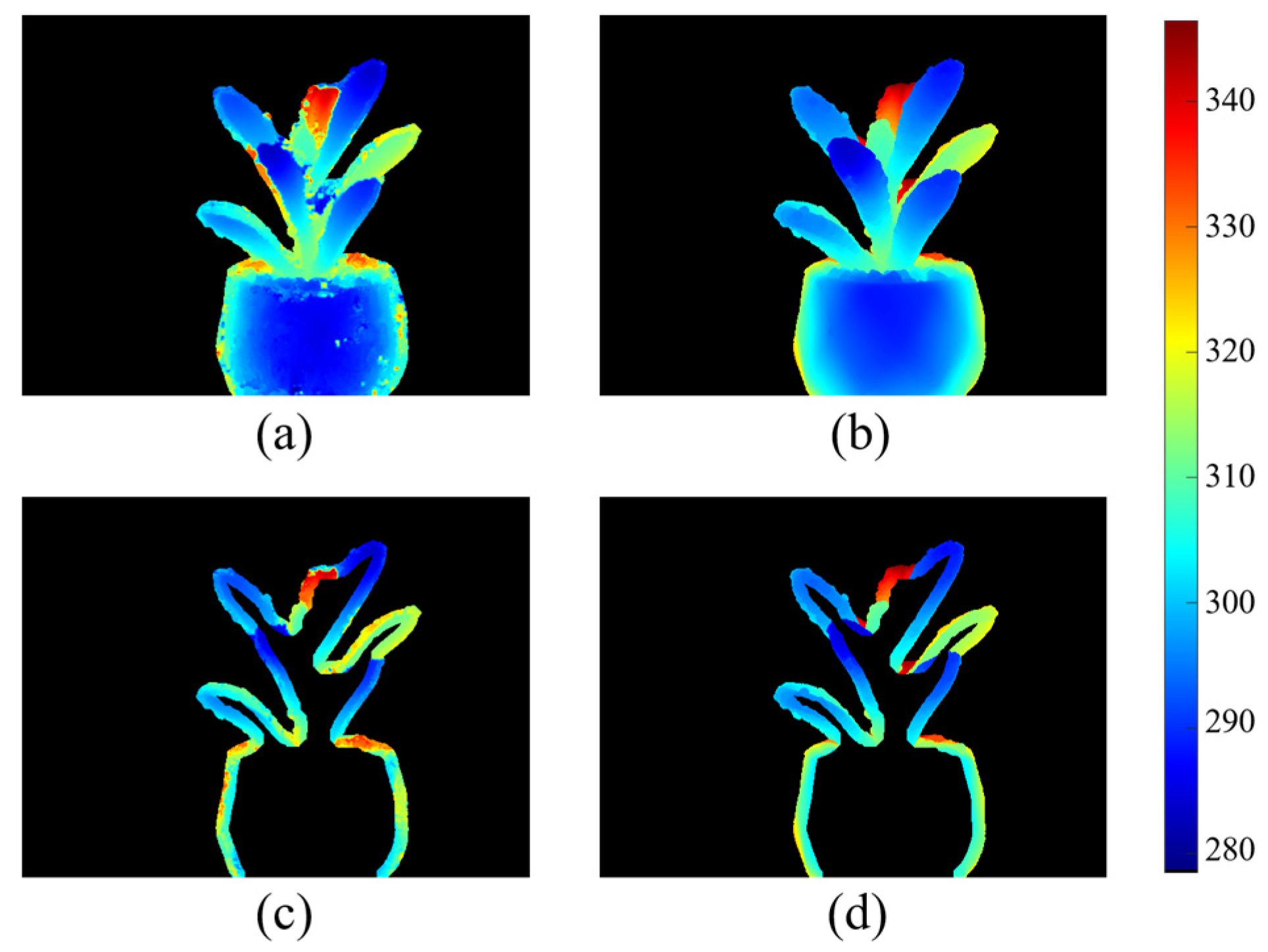
3.1. Results of Depth Map Evaluation
3.2. Results of Point Clouds Evaluation
3.3. Results of Phenotypic Parameters Evaluation
3.4. Results of Runtime Performance Evaluation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Okura, F. 3D modeling and reconstruction of plants and trees: A cross-cutting review across computer graphics, vision, and plant phenotyping. Breed. Sci. 2022, 72, 31–47. [Google Scholar] [CrossRef] [PubMed]
- Kochi, N.; Hayashi, A.; Shinohara, Y.; Tanabata, T.; Kodama, K.; Isobe, S. All-around 3D plant modeling system using multiple images and its composition. Breed. Sci. 2022, 72, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Phattaralerphong, J.; Sinoquet, H.J.T.P. A method for 3D reconstruction of tree crown volume from photographs: Assessment with 3D-digitized plants. Tree Physiol. 2005, 25, 1229–1242. [Google Scholar] [CrossRef]
- Paturkar, A.; Gupta, G.S.; Bailey, D. Non-destructive and cost-effective 3D plant growth monitoring system in outdoor conditions. Multimed. Tools Appl. 2020, 79, 34955–34971. [Google Scholar] [CrossRef]
- Ubbens, J.; Cieslak, M.; Prusinkiewicz, P.; Stavness, I. The use of plant models in deep learning: An application to leaf counting in rosette plants. Plant Methods 2018, 14, 1–10. [Google Scholar] [CrossRef]
- Yang, D.; Yang, H.; Liu, D.; Wang, X.J.C. Research on automatic 3D reconstruction of plant phenotype based on Multi-View images. Comput. Electron. Agric. 2024, 220, 108866. [Google Scholar] [CrossRef]
- He, Y.; Yu, Z.; Deng, Y.; Deng, J.; Cai, R.; Wang, Z.; Tu, W.; Zhong, W. AHP-based welding position decision and optimization for angular distortion and weld collapse control in T-joint multipass GMAW. J. Manuf. Process. 2024, 121, 246–259. [Google Scholar] [CrossRef]
- Andujar, D.; Calle, M.; Fernandez-Quintanilla, C.; Ribeiro, A.; Dorado, J. Three-Dimensional Modeling of Weed Plants Using Low-Cost Photogrammetry. Sensors 2018, 18, 1077. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, Q.; Chang, D.; Gao, Q.; Han, J.; Zhang, T.; Hartley, R.; Pollefeys, M. Learning-based Multi-View Stereo: A Survey. arXiv 2024, arXiv:2408.15235. [Google Scholar]
- Bi, R.; Gan, S.; Yuan, X.; Li, R.; Gao, S.; Yang, M.; Luo, W.; Hu, L. Multi-View Analysis of High-Resolution Geomorphic Features in Complex Mountains Based on UAV–LiDAR and SfM–MVS: A Case Study of the Northern Pit Rim Structure of the Mountains of Lufeng, China. Appl. Sci. 2023, 13, 738. [Google Scholar] [CrossRef]
- Sun, S.; Li, C.; Chee, P.W.; Paterson, A.H.; Meng, C.; Zhang, J.; Ma, P.; Robertson, J.S.; Adhikari, J.J.C. High resolution 3D terrestrial LiDAR for cotton plant main stalk and node detection. Comput. Electron. Agric. 2021, 187, 106276. [Google Scholar]
- Nguyen, T.T.; Slaughter, D.C.; Max, N.; Maloof, J.N.; Sinha, N. Structured Light-Based 3D Reconstruction System for Plants. Sensors 2015, 15, 18587–18612. [Google Scholar] [CrossRef] [PubMed]
- Teng, X.; Zhou, G.; Wu, Y.; Huang, C.; Dong, W.; Xu, S. Three-Dimensional Reconstruction Method of Rapeseed Plants in the Whole Growth Period Using RGB-D Camera. Sensors 2021, 21, 4628. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, L.; Xiang, L.; Wu, Q.; Jiang, H. Automatic non-destructive growth measurement of leafy vegetables based on kinect. Sensors 2018, 18, 806. [Google Scholar] [CrossRef] [PubMed]
- Aanæs, H.; Jensen, R.R.; Vogiatzis, G.; Tola, E.; Dahl, A.B. Large-Scale Data for Multiple-View Stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively parallel multiview stereopsis by surface normal diffusion. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 873–881. [Google Scholar]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Collins, R.T. A space-sweep approach to true multi-image matching. In Proceedings of the CVPR IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 358–363. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Mvsnet: Depth inference for unstructured multi-view stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Gu, X.; Fan, Z.; Zhu, S.; Dai, Z.; Tan, F.; Tan, P. Cascade cost volume for high-resolution multi-view stereo and stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2495–2504. [Google Scholar]
- Zhang, Z.; Peng, R.; Hu, Y.; Wang, R. Geomvsnet: Learning multi-view stereo with geometry perception. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21508–21518. [Google Scholar]
- Vaswani, A.; Shazeer, N.M.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ding, Y.; Yuan, W.; Zhu, Q.; Zhang, H.; Liu, X.; Wang, Y.; Liu, X. Transmvsnet: Global context-aware multi-view stereo network with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8585–8594. [Google Scholar]
- Cao, C.; Ren, X.; Fu, Y. MVSFormer: Multi-view stereo by learning robust image features and temperature-based depth. arXiv 2022, arXiv:2208.02541. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Zhang, J.; Ren, Y.; Zhou, L.; Fang, T.; Quan, L. Blendedmvs: A large-scale dataset for generalized multi-view stereo networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1790–1799. [Google Scholar]
- Xue, S.; Li, G.; Lv, Q.; Meng, X.; Tu, X. Point Cloud Registration Method for Pipeline Workpieces Based On NDT and Improved ICP Algorithms. IOP Conf. Ser. Mater. Sci. Eng. 2019, 677, 2131. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Luo, Z.; Fang, T.; Yao, Y. Vis-MVSNet: Visibility-Aware Multi-view Stereo Network. Int. J. Comput. Vis. 2022, 131, 199–214. [Google Scholar] [CrossRef]
- Zhu, X.; Huang, Z.; Li, B.J.P. Three-Dimensional Phenotyping Pipeline of Potted Plants Based on Neural Radiation Fields and Path Segmentation. Plants 2024, 13, 3368. [Google Scholar] [CrossRef]
- Knapitsch, A.; Park, J.; Zhou, Q.Y.; Koltun, V. Tanks and temples. ACM Trans. Graph. 2017, 36, 1–13. [Google Scholar]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1180–1189. [Google Scholar]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar]




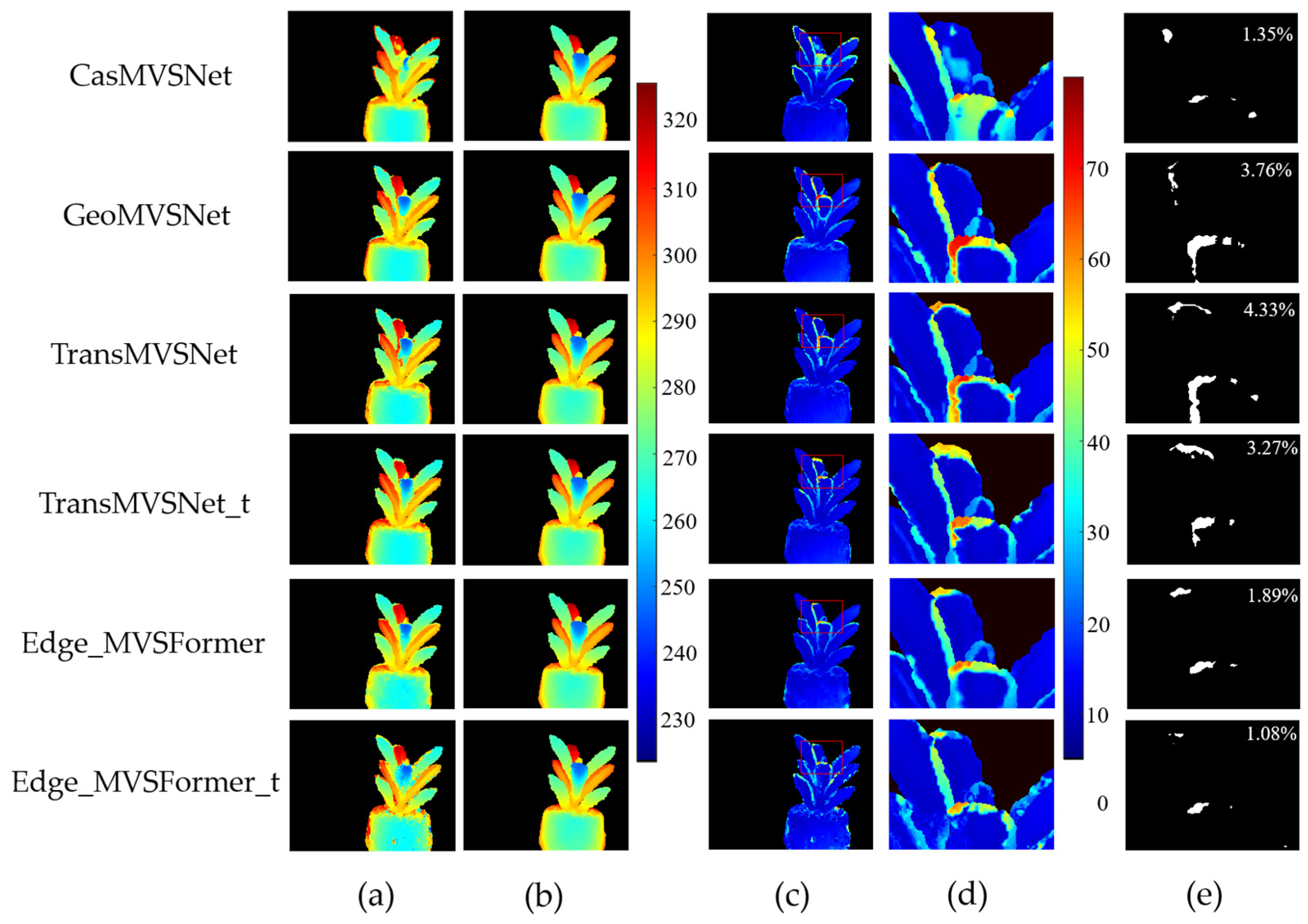

| Method | MAE_Depth (mm) | |||||
|---|---|---|---|---|---|---|
| Overall | Edge | Overall | Edge | Overall | Edge | |
| CasMVSNet | 7.37 ± 1.37 | 12.47 ± 1.95 | 36.97% | 22.15% | 53.68% | 41.26% |
| GeoMVSNet | 4.91 ± 0.79 | 8.71 ± 1.43 | 43.64% | 33.19% | 64.01% | 53.46% |
| TransMVSNet | 5.01 ± 0.81 | 9.18 ± 1.51 | 43.48% | 28.13% | 63.76% | 52.37% |
| TransMVSNet_t | 4.87 ± 0.78 | 8.74 ± 1.43 | 43.91% | 28.67% | 63.99% | 52.89% |
| Edge_MVSFormer | 4.50 ± 0.73 | 6.80 ± 1.06 | 44.54% | 38.65% | 65.44% | 58.05% |
| Edge_MVSFormer_t | 4.41 ± 0.71 | 6.54 ± 1.07 | 45.11% | 39.89% | 65.75% | 59.32% |
| Model | Normal (mm) | Red (mm) | Green (mm) |
|---|---|---|---|
| CasMVSNet | 7.34 ± 1.36 | 7.42 ± 1.47 | 7.44 ± 1.40 |
| GeoMVSNet | 5.04 ± 0.83 | 5.13 ± 0.81 | 5.08 ± 0.85 |
| TransMVSNet | 5.05 ± 0.82 | 5.23 ± 0.88 | 5.14 ± 0.84 |
| Edge_MVSFormer | 4.57 ± 0.73 | 4.76 ± 0.78 | 4.74 ± 0.81 |
| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| Overall | Edge | Overall | Edge | Overall | Edge | Overall | Edge | |
| CasMVSNet | 1.36 ± 0.20 | 0.67 ± 0.11 | 38.27% | 28.69% | 44.69% | 46.31% | 41.48% | 37.50% |
| GeoMVSNet | 1.11 ± 0.17 | 0.52 ± 0.08 | 41.49% | 39.36% | 53.67% | 58.17% | 47.58% | 48.77% |
| TransMVSNet | 1.16 ± 0.17 | 0.54 ± 0.09 | 42.72% | 35.08% | 52.36% | 57.55% | 47.54% | 46.32% |
| TransMVSNet_t | 1.14 ± 0.18 | 0.55 ± 0.09 | 42.65% | 35.61% | 52.14% | 57.96% | 47.40% | 46.79% |
| Edge_MVSFormer | 1.08 ± 0.16 | 0.43 ± 0.07 | 43.23% | 41.37% | 50.83% | 56.33% | 47.70% | 48.85% |
| Edge_MVSFormer_t | 1.09 ± 0.16 | 0.42 ± 0.07 | 43.41% | 42.83% | 51.22% | 55.18% | 47.83% | 49.01% |
| Model | Params (M) | GPU Mem (MB) | Inference Time (s) |
|---|---|---|---|
| CasMVSNet | 0.93 | 5487 | 0.17 |
| GeoMVSNet | 15.31 | 7235 | 0.46 |
| TransMVSNet | 1.15 | 5513 | 0.53 |
| Edge_MVSFormer | 1.15 | 5572 | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Liu, Z.; Lan, G.; Xu, J.; Chen, R.; Huang, Y. Edge_MVSFormer: Edge-Aware Multi-View Stereo Plant Reconstruction Based on Transformer Networks. Sensors 2025, 25, 2177. https://doi.org/10.3390/s25072177
Cheng Y, Liu Z, Lan G, Xu J, Chen R, Huang Y. Edge_MVSFormer: Edge-Aware Multi-View Stereo Plant Reconstruction Based on Transformer Networks. Sensors. 2025; 25(7):2177. https://doi.org/10.3390/s25072177
Chicago/Turabian StyleCheng, Yang, Zhen Liu, Gongpu Lan, Jingjiang Xu, Ren Chen, and Yanping Huang. 2025. "Edge_MVSFormer: Edge-Aware Multi-View Stereo Plant Reconstruction Based on Transformer Networks" Sensors 25, no. 7: 2177. https://doi.org/10.3390/s25072177
APA StyleCheng, Y., Liu, Z., Lan, G., Xu, J., Chen, R., & Huang, Y. (2025). Edge_MVSFormer: Edge-Aware Multi-View Stereo Plant Reconstruction Based on Transformer Networks. Sensors, 25(7), 2177. https://doi.org/10.3390/s25072177







