Degradation Prediction of PEMFCs Based on Discrete Wavelet Transform and Decoupled Echo State Network
Abstract
1. Introduction
- (1)
- The degradation of the PEMFC is separated into a low-frequency signal that is shielded and a high-frequency signal that is retained to obtain smooth degradation curve characterization.
- (2)
- A method that involves a decoupled echo state network with a mechanism for decreasing inhibition is proposed. This approach further decouples the network structure to enable accurate prediction.
- (3)
- The degradation is precisely predicted by optimizing parameters using PSO, ensuring that the structural and weight superposition parameters of the sub-reservoir are optimal.
2. Experimental Platform and Implementation Plan
2.1. Experimental Platform
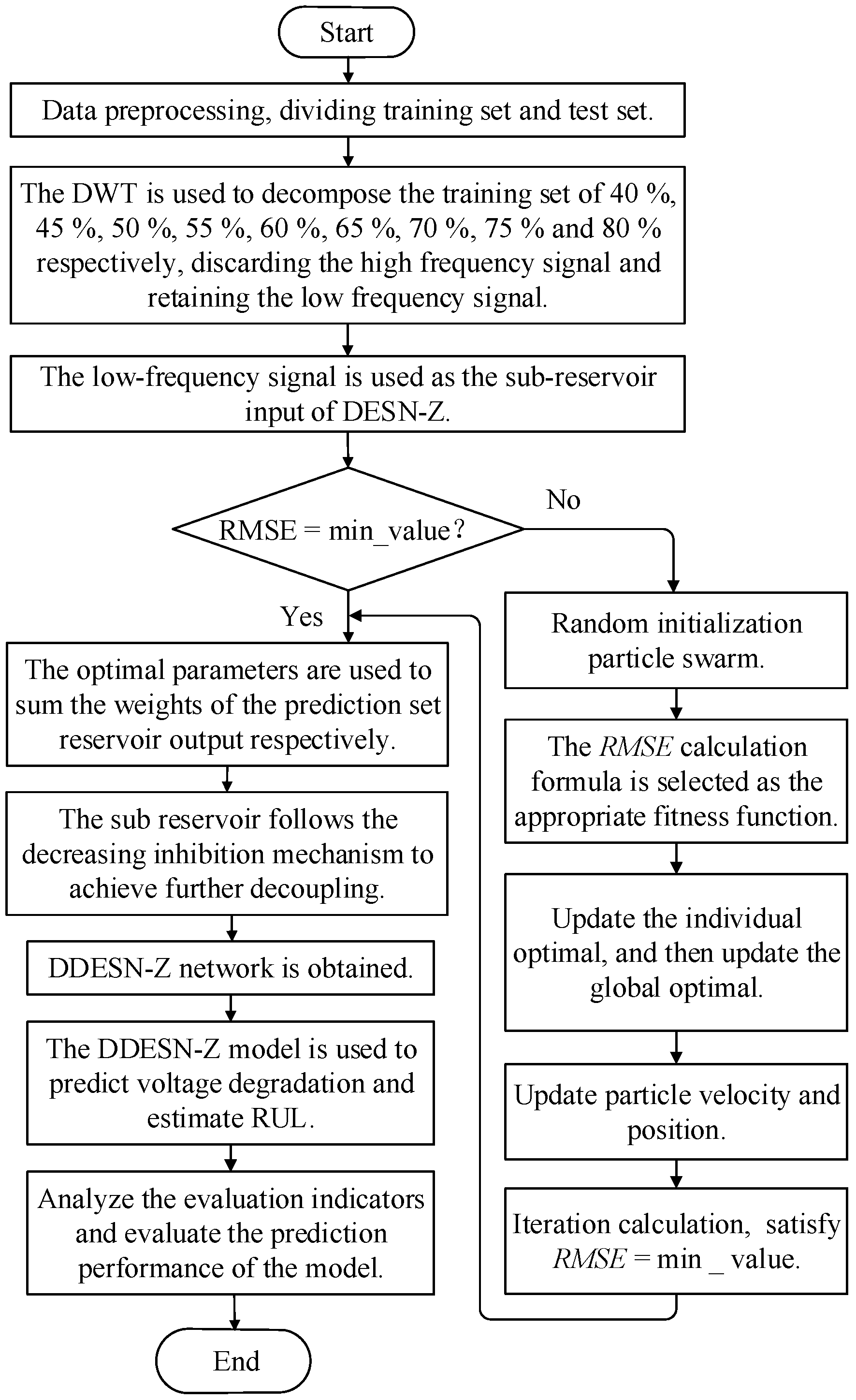
2.2. Implementation Plan
2.3. Evaluation Index
3. Mathematical Model
3.1. Discrete Wavelet Transform
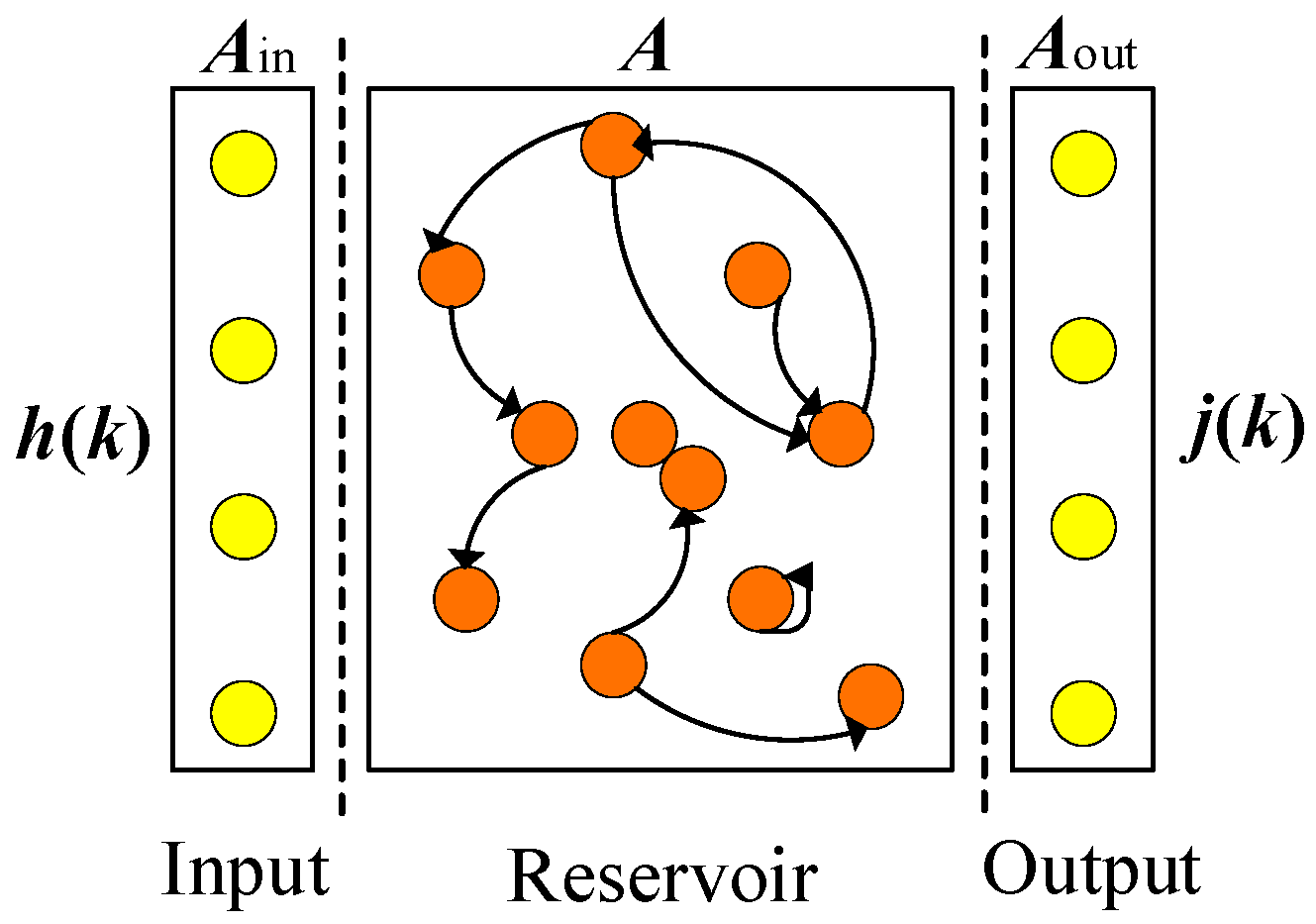
3.2. Echo State Network
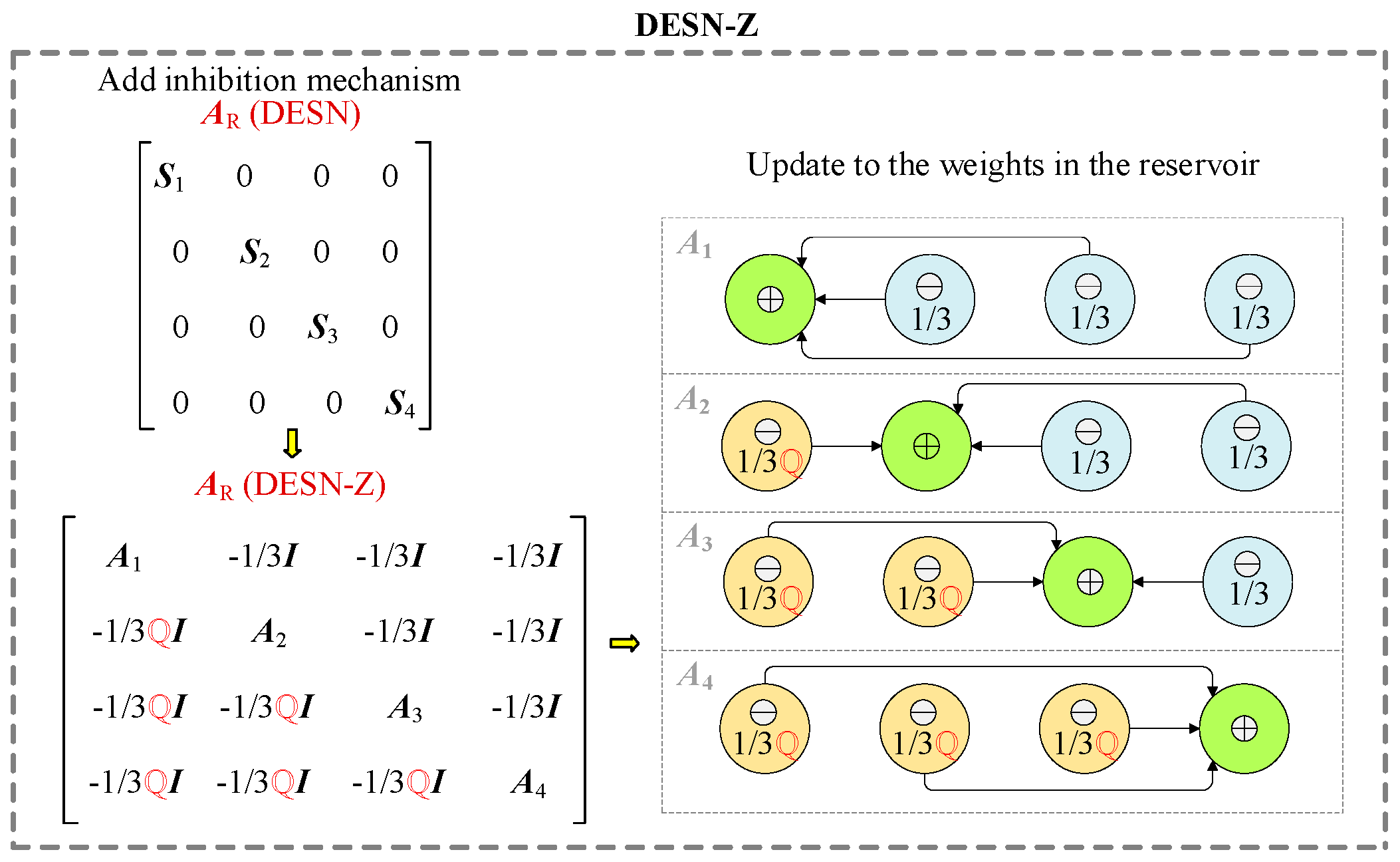
3.3. Decoupled Echo State Network
3.4. Decoupled Echo State Network with Z-Scheme
4. Result and Discussion
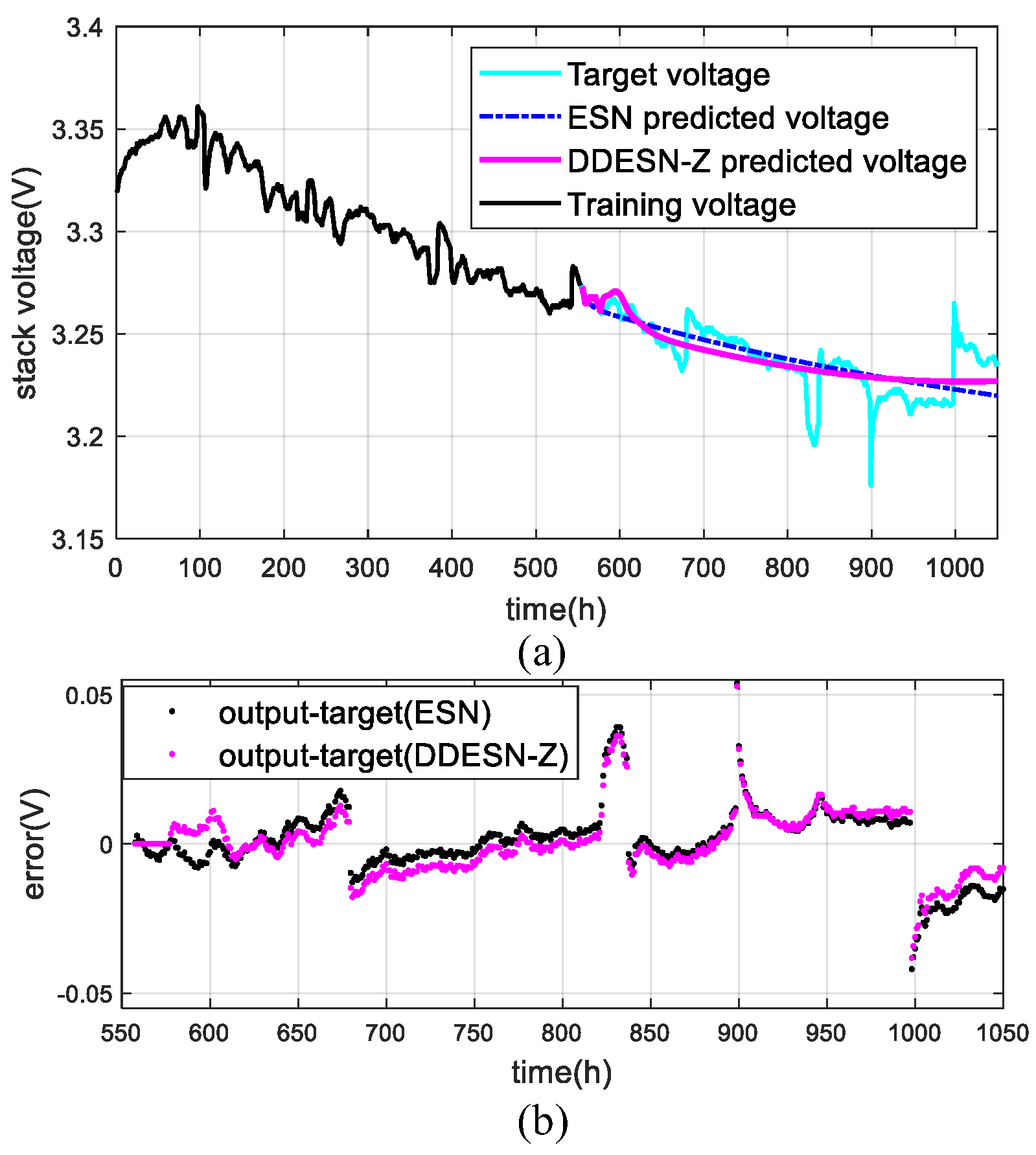
4.1. Under Steady Conditions (FC1)
4.2. Under Quasi-Dynamic Conditions (FC2)
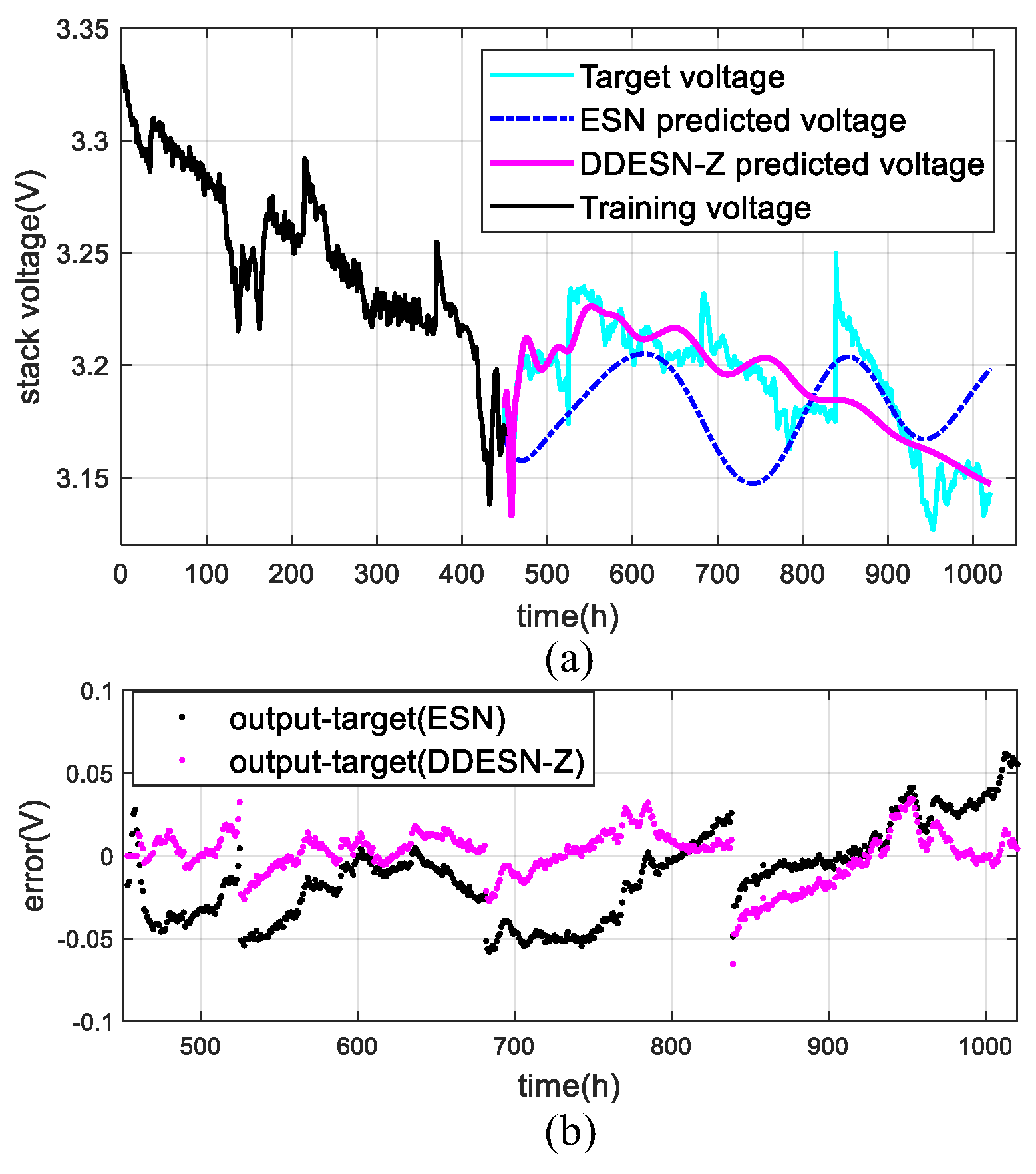
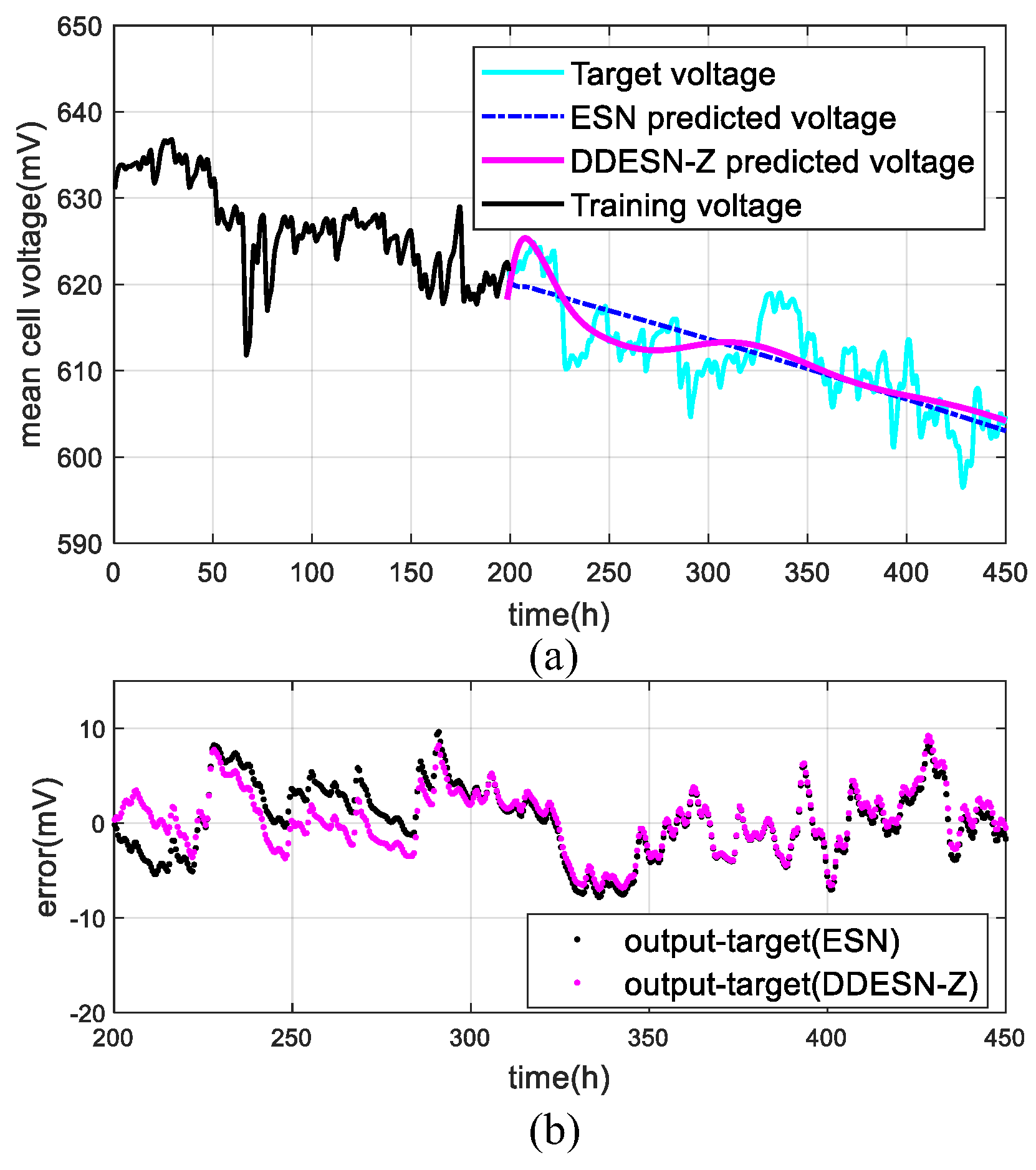
4.3. Under Dynamic Conditions (FC3)
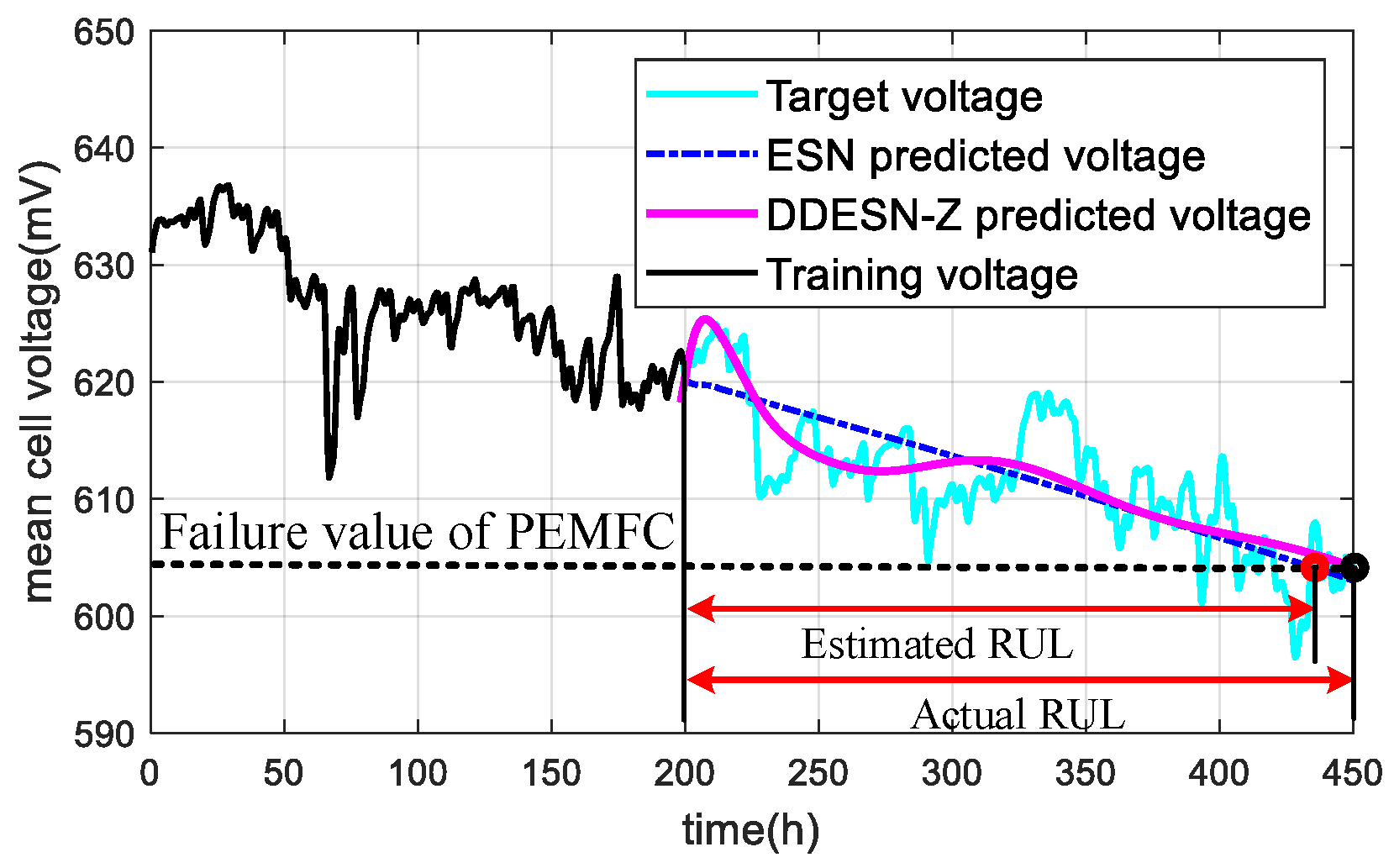
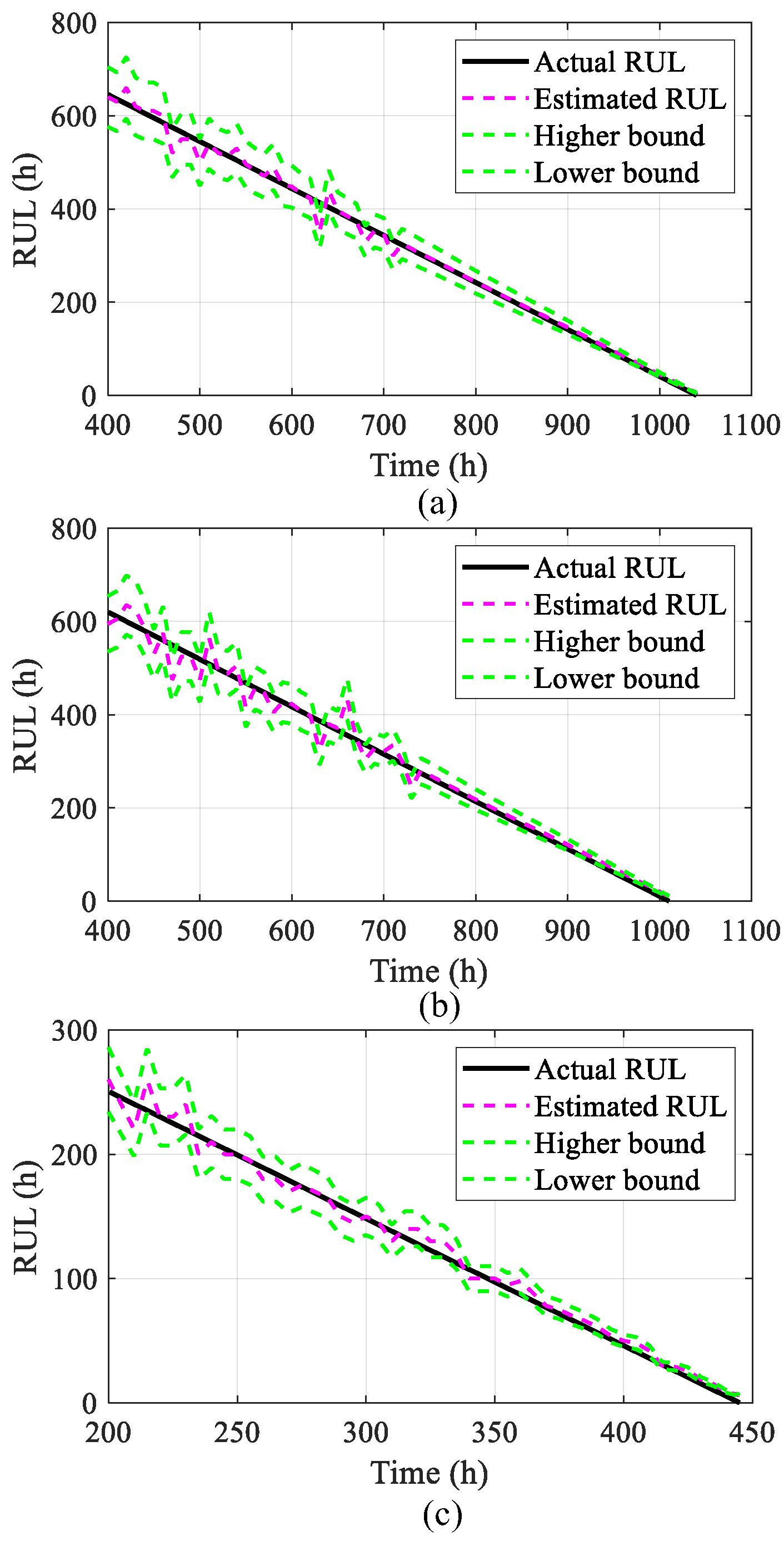
4.4. Estimation of Remaining Useful Life
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.H.; He, P.; Cai, S.J.; He, Z.H.; Zhu, H.N.; Yu, Z.Y.; Yang, L.Z.; Tao, W.Q. Modeling and temperature control of a water-cooled PEMFC system using intelligent algorithms. Appl. Energy 2024, 372, 123790. [Google Scholar] [CrossRef]
- Wang, Y.; Seo, B.; Wang, B.; Zamel, N.; Jiao, K.; Adroher, X.C. Fundamentals, materials, and machine learning of polymer electrolyte membrane fuel cell technology. Energy AI 2020, 1, 100014. [Google Scholar] [CrossRef]
- Moslehi, A.; Kandidayeni, M.; Hébert, M.; Kelouwani, S. Investigating the impact of a fuel cell system air supply control on the performance of an energy management strategy. Energy Convers. Manag. 2025, 325, 119374. [Google Scholar] [CrossRef]
- Hua, Z.; Yang, Q.; Chen, J.; Lan, T.; Zhao, D.; Dou, M.; Liang, B. Degradation prediction of PEMFC based on BiTCN-BiGRU-ELM fusion prognostic method. Int. J. Hydrogen Energy 2024, 87, 361–372. [Google Scholar]
- Hua, Z.; Zheng, Z.; Péra, M.-C.; Gao, F. Statistical analysis on random matrices of echo state network in PEMFC system’s lifetime prediction. Appl. Sci. 2022, 12, 3421. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, L.; Lyu, X.; Ning, W.; Liu, W.; Tao, W.-Q. Modeling and optimization of a residential PEMFC-based CHP system under different operating modes. Appl. Energy 2024, 353, 122066. [Google Scholar] [CrossRef]
- Wu, J.; Peng, J.; Li, M.; Wu, Y. Enhancing fuel cell electric vehicle efficiency with TIP-EMS: A trainable integrated predictive energy management approach. Energy Convers. Manag. 2024, 310, 118499. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Shum, C.; McPhee, J. A Review of physics-based and data-driven models for real-time control of polymer electrolyte membrane fuel cells. Energy AI 2021, 6, 100114. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, J.; Yi, F.; Feng, C.; Wu, G.; Li, Y.; Zhang, C.; Wang, C. A real-time prediction method for PEMFC life under actual operating conditions. Sustain. Energy Technol. Assess. 2024, 70, 103949. [Google Scholar] [CrossRef]
- Lee, J.; Ko, S.; Kim, B.-K.; Ryu, J.-H.; Baek, J.D.; Kang, S.-W. Empirical lifetime prediction through deterioration evaluation of high-power PEMFC for railway vehicle applications. Int. J. Hydrogen Energy 2024, 71, 972–981. [Google Scholar] [CrossRef]
- He, W.; Liu, T.; Ming, W.; Li, Z.; Du, J.; Li, X.; Guo, X.; Sun, P. Progress in prediction of remaining useful life of hydrogen fuel cells based on deep learning. Renew. Sustain. Energy Rev. 2024, 192, 114193. [Google Scholar] [CrossRef]
- Zhu, W.; Guo, B.; Li, Y.; Yang, Y.; Xie, C.; Jin, J.; Gooi, H.B. Uncertainty quantification of proton-exchange-membrane fuel cells degradation prediction based on bayesian-gated recurrent unit. eTransportation 2023, 16, 100230. [Google Scholar] [CrossRef]
- Allal, Z.; Noura, H.N.; Chahine, K. Efficient health indicators for the prediction of the remaining useful life of proton exchange membrane fuel cells. Energy Convers. Manag. X 2024, 21, 100503. [Google Scholar] [CrossRef]
- Pang, Y.; Hao, L.; Wang, Y. Convolutional neural network analysis of radiography images for rapid water quantification in PEM fuel cell. Appl. Energy 2022, 321, 119352. [Google Scholar] [CrossRef]
- Nnabuife, S.G.; Udemu, C.; Hamzat, A.K.; Darko, C.K.; Quainoo, K.A. Smart monitoring and control systems for hydrogen fuel cells using AI. Int. J. Hydrogen Energy 2024, 110, 704–726. [Google Scholar] [CrossRef]
- Li, K.; Hong, J.; Zhang, C.; Liang, F.; Yang, H.; Ma, F.; Wang, F. Health state monitoring and predicting of proton exchange membrane fuel cells: A review. J. Power Sources 2024, 612, 234828. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, D.; Xiao, Y.; Zheng, C. A non-stationary transformer-based remaining useful life prediction method for proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2024, 60, 1121–1133. [Google Scholar] [CrossRef]
- Song, K.; Huang, X.; Huang, P.; Sun, H.; Chen, Y.; Huang, D. Data-driven health state estimation and remaining useful life prediction of fuel cells. Renew. Energy 2024, 227, 120491. [Google Scholar] [CrossRef]
- Yu, X.; Yang, Y.; Liu, Y.; Zhu, W.; Xie, C. A novel method of long-term aging prediction for proton exchange membrane fuel cell under the dynamic load cycling condition. Int. J. Hydrogen Energy 2024, in press. [Google Scholar] [CrossRef]
- Chen, C.; Wei, J.; Yin, C.; Qiao, Z.; Zhan, W. Development of an optimized proton exchange membrane fuel cell model based on the artificial neural network. Energy Convers. Manag. 2025, 323, 119215. [Google Scholar] [CrossRef]
- He, K.; Mao, L.; Yu, J.; Huang, W.; He, Q.; Jackson, L. Long-Term Performance Prediction of PEMFC Based on LASSO-ESN. IEEE Trans. Instrum. Meas. 2021, 70, 3511611. [Google Scholar] [CrossRef]
- Jin, J.; Chen, Y.; Xie, C.; Wu, F. Degradation prediction of PEMFC based on data-driven method with adaptive fuzzy sampling. IEEE Trans. Transp. Electrif. 2023, 10, 3363–3372. [Google Scholar] [CrossRef]
- Mezzi, R.; Morando, S.; Steiner, N.Y.; Péra, M.C.; Hissel, D.; Larger, L. Multi-reservoir echo state network for proton exchange membrane fuel cell remaining useful life prediction. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1872–1877. [Google Scholar]
- Morando, S.; Jemei, S.; Hissel, D.; Gouriveau, R.; Zerhouni, N. ANOVA method applied to proton exchange membrane fuel cell ageing forecasting using an echo state network. Math. Comput. Simul. 2017, 131, 283–294. [Google Scholar] [CrossRef]
- Li, S.; Luan, W.; Wang, C.; Chen, Y.; Zhuang, Z. Degradation prediction of proton exchange membrane fuel cell based on Bi-LSTM-GRU and ESN fusion prognostic framework. Int. J. Hydrogen Energy 2022, 47, 33466–33478. [Google Scholar] [CrossRef]
- Gibey, G.; Pahon, E.; Zerhouni, N.; Hissel, D. Diagnostic and prognostic for prescriptive maintenance and control of PEMFC systems in an industrial framework. J. Power Sources 2024, 613, 234864. [Google Scholar] [CrossRef]
- Hua, Z.; Zheng, Z.; Péra, M.-C.; Gao, F. Remaining useful life prediction of PEMFC systems based on the multi-input echo state network. Appl. Energy 2020, 265, 114791. [Google Scholar] [CrossRef]
- Ibrahim, M.; Jemei, S.; Wimmer, G.; Steiner, N.Y.; Kokonendji, C.C.; Hissel, D. Selection of mother wavelet and decomposition level for energy management in electrical vehicles including a fuel cell. Int. J. Hydrogen Energy 2015, 40, 15823–15833. [Google Scholar] [CrossRef]
- Steiner, N.Y.; Hissel, D.; Moçotéguy, P.; Candusso, D. Non intrusive diagnosis of polymer electrolyte fuel cells by wavelet packet transform. Int. J. Hydrogen Energy 2010, 36, 740–746. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, Z.; Outbib, R. Adaptive prognostic of fuel cells by implementing ensemble echo state networks in time-varying model space. IEEE Trans. Ind. Electron. 2019, 67, 379–389. [Google Scholar] [CrossRef]
- Xue, Y.; Yang, L.; Haykin, S. Decoupled echo state networks with lateral inhibition. Neural Netw. 2007, 20, 365–376. [Google Scholar] [CrossRef]


| Parameters | FC1 | FC2 | FC3 |
|---|---|---|---|
| Number of single cells | 5 | 5 | 96 |
| Operating power (kW) | 1 | 1 | 1~5 |
| Activation area (cm2) | 100 | 100 | 100 |
| Operating current (A) | 70 | 70 ± 7 | 20~99 |
| Time (h) | 1154 | 1020 | 450 |
| Hydrogen input/output temperature (°C) | 29/41 | 27/37 | 58 |
| Air input/output temperature (°C) | 42/51 | 43/51 | 58 |
| Training Time (FC1) | RMSE | MAPE | ||
|---|---|---|---|---|
| ESN | DDESN-Z | ESN | DDESN-Z | |
| 400 h | 0.01039 | 0.00970 | 0.00216 | 0.00216 |
| 450 h | 0.01050 | 0.01125 | 0.00229 | 0.00237 |
| 500 h | 0.01098 | 0.01180 | 0.00243 | 0.00254 |
| 550 h | 0.01128 | 0.01084 | 0.00244 | 0.00251 |
| 600 h | 0.01207 | 0.01145 | 0.00264 | 0.00250 |
| 650 h | 0.01228 | 0.01012 | 0.00276 | 0.00254 |
| 700 h | 0.01161 | 0.01114 | 0.00270 | 0.00281 |
| 750 h | 0.01222 | 0.01195 | 0.00301 | 0.00299 |
| 800 h | 0.01228 | 0.00897 | 0.00307 | 0.00213 |
| Training Time (FC2) | RMSE | MAPE | ||
|---|---|---|---|---|
| ESN | DDESN-Z | ESN | DDESN-Z | |
| 400 h | 0.01934 | 0.01745 | 0.00437 | 0.00407 |
| 450 h | 0.02972 | 0.01480 | 0.00763 | 0.00353 |
| 500 h | 0.02475 | 0.01522 | 0.00653 | 0.00329 |
| 550 h | 0.02072 | 0.01591 | 0.00536 | 0.00353 |
| 600 h | 0.01973 | 0.01574 | 0.00496 | 0.00359 |
| 650 h | 0.019 66 | 0.017 14 | 0.004 83 | 0.004 13 |
| 700 h | 0.01924 | 0.01640 | 0.00453 | 0.00397 |
| 750 h | 0.01799 | 0.01750 | 0.00477 | 0.00458 |
| 800 h | 0.01862 | 0.01076 | 0.00441 | 0.00260 |
| Training Time (FC3) | RMSE | MAPE | ||
|---|---|---|---|---|
| ESN | DDESN-Z | ESN | DDESN-Z | |
| 200 h | 3.69178 | 3.28850 | 0.00483 | 0.00432 |
| 225 h | 3.81518 | 3.51380 | 0.00509 | 0.00450 |
| 250 h | 3.49377 | 3.25630 | 0.00468 | 0.00405 |
| 275 h | 4.69151 | 3.44200 | 0.00609 | 0.00437 |
| 300 h | 3.38791 | 2.64380 | 0.00435 | 0.00359 |
| 325 h | 3.29354 | 2.40670 | 0.00432 | 0.00307 |
| 350 h | 3.16738 | 2.42800 | 0.00431 | 0.00298 |
| 375 h | 2.825 85 | 2.61900 | 0.00370 | 0.00332 |
| 400 h | 2.89835 | 2.04930 | 0.00375 | 0.00267 |
| Training Time (h) | RMSE | MAPE | |||
|---|---|---|---|---|---|
| DESN-Z | DDESN-Z | DESN-Z | DDESN-Z | ||
| FC1 | 400 | 0.01001 | 0.00970 | 0.00216 | 0.00216 |
| 600 | 0.01168 | 0.01145 | 0.00255 | 0.00250 | |
| 800 | 0.01108 | 0.00897 | 0.00278 | 0.00213 | |
| FC2 | 400 | 0.01849 | 0.01745 | 0.00430 | 0.00407 |
| 500 | 0.02047 | 0.01522 | 0.00477 | 0.00329 | |
| 600 | 0.01732 | 0.01574 | 0.00394 | 0.00359 | |
| FC3 | 200 | 3.58188 | 3.28850 | 0.00469 | 0.00432 |
| 300 | 3.38001 | 2.64380 | 0.00410 | 0.00359 | |
| 400 | 2.80106 | 2.04930 | 0.00353 | 0.00267 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Li, W.; He, M.; Pan, S.; Hua, Z.; Zhao, D.; Gong, L.; Lan, T. Degradation Prediction of PEMFCs Based on Discrete Wavelet Transform and Decoupled Echo State Network. Sensors 2025, 25, 2174. https://doi.org/10.3390/s25072174
Sun J, Li W, He M, Pan S, Hua Z, Zhao D, Gong L, Lan T. Degradation Prediction of PEMFCs Based on Discrete Wavelet Transform and Decoupled Echo State Network. Sensors. 2025; 25(7):2174. https://doi.org/10.3390/s25072174
Chicago/Turabian StyleSun, Jie, Wenshuo Li, Mengying He, Shiyuan Pan, Zhiguang Hua, Dongdong Zhao, Lei Gong, and Tianyi Lan. 2025. "Degradation Prediction of PEMFCs Based on Discrete Wavelet Transform and Decoupled Echo State Network" Sensors 25, no. 7: 2174. https://doi.org/10.3390/s25072174
APA StyleSun, J., Li, W., He, M., Pan, S., Hua, Z., Zhao, D., Gong, L., & Lan, T. (2025). Degradation Prediction of PEMFCs Based on Discrete Wavelet Transform and Decoupled Echo State Network. Sensors, 25(7), 2174. https://doi.org/10.3390/s25072174







