Abstract
The growing urgency to address urban air quality and climate change has intensified the need for sustainable mobility solutions that mitigate vehicular emissions. Bike-sharing systems (BSSs) represent a viable alternative; however, their precise environmental impact remains insufficiently explored. This study quantifies and forecasts reductions in CO2 and NOx emissions resulting from BSS usage in Madrid by integrating real-time IoT sensor data with an advanced predictive model. The proposed framework effectively captures nonlinear and seasonal mobility and emission patterns, achieving high predictive accuracy while demonstrating significant energy savings. These findings confirm the environmental benefits of BSSs and provide urban planners and policymakers with a robust tool to extend and replicate this analysis in other cities, fostering sustainable urban mobility and improved air quality.
1. Introduction
Urban mobility significantly influences the environmental impact of transportation, especially in densely populated cities where traffic congestion and greenhouse gas (GHG) emissions exacerbate climate change and air pollution. Growing concerns about urban air quality have led to the search for efficient and eco-friendly transportation solutions [1,2,3,4]. Among these, bike-sharing systems (BSSs) have proven to be an effective strategy for reducing private vehicle dependency and promoting low-carbon mobility [1].
Despite the benefits of BSSs, challenges such as inefficient station distribution, fluctuating demand, and limited integration with other transport modes remain critical. Recent advances in IoT-enabled environmental monitoring have demonstrated the potential of wireless sensor networks to provide real-time data for urban air quality assessment, optimize fleet distribution, and improve operational efficiency [5,6,7,8]. In particular, Puyol and Baeza [8] demonstrated how IoT networks can enhance the real-time monitoring and optimization of bike-sharing systems, ensuring more efficient usage, reduced operational costs, and improved safety on journeys by rewarding good user behavior with a reduction in rental cost. Their work highlights the importance of integrating sensor data with predictive models, which aligns closely with this study’s approach to quantifying emission reductions through BSSs. Furthermore, the integration of machine learning models has facilitated the prediction of mobility patterns and environmental impact, allowing for data-driven decision-making in urban planning [9,10]. Beyond operational enhancements, AI and IoT technology are also being leveraged for security improvements. Karthika et al. [11] introduced a security framework that combines IoT tracking with Support Vector Machine (SVM) models to detect and prevent bicycle theft, thereby increasing system reliability. This approach demonstrates how IoT applications in BSSs extend beyond mobility optimization to ensure secure and sustainable operations.
Sustainability in urban environments and its relationship with the use of bike-sharing services is a topic of great interest, not only for our daily environment, as a key element of urban sustainability policies, but also in the scientific literature. Various environmental, economic, and social factors shape this relationship. BSSs generate large datasets that can be analyzed to understand urban mobility patterns, supporting infrastructure planning and policy-making [9]. Guo et al. [12] examined how the integration of bicycle docking stations with public transport can influence passenger attitudes and facilitate greater use of public transport, fostering a more sustainable transport system. Similarly, Guo and He [13] analyzed how the built environment affects the integration of dockless bike-sharing with subway systems, highlighting the importance of urban design in promoting bicycle use in Shenzhen (China). Another key study by Zhang et al. [14] proposed a model to optimize the distribution of shared bicycles during morning peak hours, improving traffic efficiency and reducing carbon emissions. Research by Wang et al. [15] explored the influence of built environment factors on bike-sharing usage through geographic detector models, using 6.5 million bike-share orders in Shanghai (China). Their findings provided urban designers with strategies to enhance bicycle use by integrating key environmental variables.
Beyond mobility efficiency, studies have quantified the broader impacts of bike-sharing programs on the economy, energy consumption, environmental protection, and public health [16]. These programs contribute significantly to carbon neutrality by reducing dependence on fossil fuels [17]. Furthermore, Tao and zuo Zhou [18] identified several sustainability benefits of dockless bike-sharing services, such as improved resource utilization and reduced GHG emissions. In a study of Shanghai’s bike-sharing program, Zhang and Mi [19] estimated that in 2016, the system saved 8358 tons of gasoline and reduced CO2 emissions by 25,240 tons and NOx emissions by 64 tons. Similarly, Chen et al. [20] conducted a retrospective analysis of bike-sharing in New York (USA), estimating energy savings and emission reductions from historical data (2014–2017), albeit without predictive modeling. Using service usage data from Lisbon (Portugal), Raposo and Silva [21] estimated that the e-bike sharing system could prevent 36 tons of GHG emissions annually and reduce energy consumption by 451 GJ. Beyond emissions reduction, Sun and Ertz [22] analyzed how free-flowing bike-sharing (FFBS) optimized resource use compared to station-based bike-sharing (SBBS) and privately owned bicycles, revealing significant reductions in aluminum, steel, plastic, and rubber consumption. Finally, Lu et al. [23] conducted simulations showing that integrating free bikesharing with transit systems could save USD 1.5 million per year in transportation damage costs and prevent 22 premature deaths annually by shifting mobility towards cycling and walking in Taipei (Taiwan).
Those studies highlight the multifaceted benefits of bike-sharing: (i) improving resource utilization, (ii) reducing greenhouse gas emissions, (iii) decreasing energy consumption, and (iv) enhancing public health. Unlike previous studies that have assessed the environmental impact of BSSs using historical data or indirect estimations, this work integrates real-time IoT sensor data with advanced predictive models to capture nonlinear mobility patterns and their effects on pollution. Additionally, the proposed approach enables the replicability of the model in other cities, providing an adaptable framework for decision-making in sustainable urban planning. The study presented in this article quantified the environmental impact of the bike-sharing system in Madrid (Spain) by leveraging IoT sensors and predictive machine learning models to quantify reductions in CO2 and NOx emissions. Through mobility data analysis, this research sought to assess the influence of BSS infrastructure on air quality and explore measures to enhance its environmental benefits. Accordingly, this study formulated the following research questions (RQ):
- RQ1: What is the state-of-the-art of machine learning models for estimating GHG emissions in large cities?
- RQ2: How can IoT sensors and predictive machine learning models be used to accurately quantify the environmental impact of the bike-sharing system in Madrid, specifically in terms of CO2 and NOx emission reductions?
This research is structured as follows: Section 2 addresses RQ1, reviewing the literature related to the use of IoT in urban mobility and the modeling of GHG emissions. Section 3 and Section 4 address RQ2, analyzing mobility patterns to explore the potential of BSS data to anticipate GHG emissions in large cities. Finally, Section 5 discusses the findings and provides insights for further research.
2. Machine Learning Models for Urban GHG Prediction
The growing concern about greenhouse gas emissions in urban areas has led to the development of advanced modeling techniques for their prediction and mitigation. Among sustainable mobility solutions, bicycle-sharing services have gained prominence due to their potential to reduce transportation-related emissions. However, accurately estimating their real impact remains a challenge, necessitating robust predictive models. This chapter explores the state of the art in the predictive modeling of GHG emissions in urban settings, with a specific focus on integrating BSSs into these models.
Following the first research question (RQ1), this review follows three main research paths: (i) the application of artificial intelligence in urban pollution prediction, (ii) the use of neural networks to model air pollution in cities with BSSs, and (iii) AI-driven applications specifically designed for BSSs. To identify relevant studies, a literature review was conducted using the terms “predictive model”, “bicycle sharing service”, and “artificial intelligence” across major academic databases, covering research published between 1995 and 2024. While extensive research has applied big data to quantify urban pollutants, no studies were found that explicitly leveraged predictive models to estimate GHG emissions in large cities through BSSs.
Figure 1 provides an overview of the classification of existing models based on four key dimensions: the machine learning model used (Y-axis), the accuracy of the model (color gradient from 0/red to 1/blue), the pollutants observed (X-axis), and the number of citations in Google Scholar. Additional details, including specific references and model performance metrics, are presented in Table A1 in Appendix A. Analysis of Figure 1 shows that modeling efforts are predominantly focused on , which emerged as the most studied pollutant, reflecting a strong research interest and a high number of citations for related studies. Other pollutants such as , , and have also been the subject of research, though to a lesser extent. In terms of model performance, techniques like XGBoost, VMD-MAEGA-NARX, UK2, and TS-LSTM demonstrate outstanding accuracy, particularly in predicting and , achieving values close to 0.75. This suggests that advanced machine learning methods, including neural networks and hybrid models, are well suited for handling these pollutants in urban settings. The number of citations associated with each study further indicates that while many high-accuracy models receive substantial academic recognition—especially those focusing on and —some high-performing models remain undercited, potentially pointing to gaps in dissemination or emerging areas for further exploration. Interestingly, only one of the models incorporates satellite-based prediction, underscoring a prevailing trend in the literature favoring machine learning-driven approaches over remote sensing techniques for urban pollution modeling.
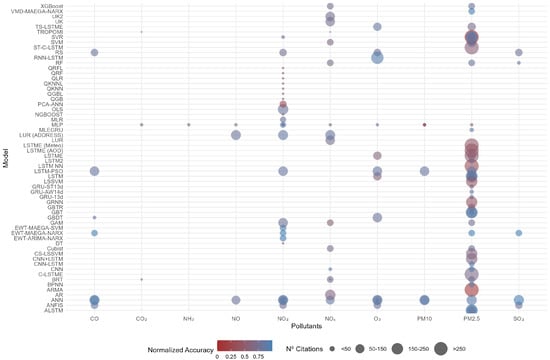
Figure 1.
ML models assessing urban pollutants.
Comparative Analysis of Predictive Models for Urban Air Pollution
Models based on satellite observations [24] have proven to be a reliable approach for estimating and emissions in large urban areas. In a recent study, researchers successfully reduced the uncertainty of daily and emission estimates in Wuhan (China) to 31% and 43%, respectively. Furthermore, these estimates were validated against bottom-up emission inventories, revealing deviations of less than 3% on average for the model year. Magazzino et al. [25] highlighted the potential of machine learning models in analyzing the relationship between renewable energy production and emissions, emphasizing AI’s capacity to model complex environmental systems. This approach also facilitates the quantification of environmental benefits associated with sustainable transportation solutions. Among machine learning techniques, algorithms such as Random Forest (RF) and Boosted Regression Trees (BRTs) have demonstrated high efficacy in predicting hourly PM2.5 and concentrations in Hong Kong (China), with RF exhibiting the best performance [26]. Additionally, the application of Gradient Boosting regression models has enabled highly accurate predictions of and emissions from diesel vehicles under different driving scenarios [27]. ANFIS (Adaptive Neuro-Fuzzy Inference System) and semi-experimental nonlinear regression models have been applied in air pollution prediction. In this context, Zeinalnezhad et al. [28] demonstrated that the ANFIS model exhibited superior accuracy compared to the semi-experimental regression model across all pollutants, achieving higher values and indicating a better alignment between the predicted and observed data.
Artificial Neural Networks (ANNs), when combined with uncertainty analysis using Monte Carlo simulations, have also demonstrated a strong correlation in predicting pollutants such as , , and CO in urban environments [29]. In Münster (Germany), ANNs have been successfully implemented to forecast hourly concentrations of multiple pollutants, particularly achieving reliable results for NO, , and [30].
Ordinary regression and time series autocorrelation models have also been employed to estimate the hourly concentrations of and , emphasizing the role of meteorological factors such as wind speed and chemical reactions in London (UK) [31]. However, these models have yielded suboptimal results, particularly in the case of the autoregressive model, which reported an value of only 0.65.
Regarding quantile regression methods, Vasseur and Aznarte [32] conducted a study in Madrid (Spain), concluding that quantile gradient boosted trees were the most effective model for predicting pollution levels. Nevertheless, they also found that simpler approaches, such as quantile nearest neighbors combined with linear regression, provided comparable results while reducing computational complexity and training time.
Liu et al. [33] introduced a hybrid approach combining three algorithms—Empirical Wavelet Transform (EWT), Modified Adaptive Genetic Algorithm (MAEGA), and Nonlinear Autoregressive with Exogenous Inputs (NARX)—resulting in the EWT-MAEGA-NARX model, which demonstrated effective performance in predicting air pollutant concentrations in Beijing (China). Similarly, Mao et al. [34] proposed the TS-LSTME (Temporal Sliding Long Short-Term Memory Extended) model for air quality prediction in the Jing-Jin-Ji region of (China), focusing on and concentrations. The results indicated that TS-LSTME achieved high predictive accuracy, with an coefficient of 0.72 for and 0.86 for , outperforming other models such as LSTME and LSTM. This deep learning approach, which integrates meteorological and temporal data, has proven to be effective for long-term forecasting and can be extended to the prediction of multiple air pollutants.
Predictive models such as linear regression and random forest have been employed to estimate spatial variations in air pollution within urban environments. However, improvements in evaluation methods and interpretability remain necessary [35]. Among the recent advancements, the proposed C-LSTME model has demonstrated superior performance compared to state-of-the-art models for air pollution forecasting across different temporal scales and regional contexts [36]. Similarly, Chang et al. [37] introduced a hybrid machine learning approach aimed at enhancing the predictive accuracy of and concentrations. Their study evaluated multiple models, including Gradient-Boosted Tree Regression (GBT), Support Vector Regression (SVR), and Long Short-Term Memory (LSTM), along with an optimized variant, LSTM2. The results indicated that GBT exhibited the highest accuracy, achieving an of 0.83 for predictions, followed by SVR and LSTM2, which attained values of 0.73, whereas the original LSTM model recorded an of 0.71. Expanding on their research, the same authors further developed and compared advanced machine learning models for prediction in Kaohsiung city (Taiwan) [38]. Several techniques were assessed, including Gradient-Boosted Tree (GBT), Support Vector Regression (SVR), Long Short-Term Memory (LSTM), and an enhanced model called Aggregated LSTM (ALSTM). Their findings revealed that ALSTM outperformed all other models, achieving an coefficient of 0.88. In a similar vein, Masih [39] underscored the effectiveness of advanced neural networks, particularly ALSTM, in refining air pollution prediction accuracy, particularly for concentrations. These results further reinforce the potential of deep learning methodologies in addressing urban air quality challenges.
Deep learning architectures, such as LSTM (Long Short-Term Memory) and ConvLSTM (Convolutional LSTM), have been developed to enhance the predictive accuracy of air pollutants, including , , , and . A notable application of these models in Beijing is presented in the work of Mokhtari et al. [40], where data from local monitoring stations were utilized to train and evaluate various predictive approaches. Comparisons were conducted between traditional models, such as Support Vector Regression (SVR) and Random Forest (RF), and more advanced deep learning techniques.
Gated Recurrent Unit (GRU)-based models have also been employed to predict concentrations across different regions, utilizing data from 67 monitoring stations in Taiwan. These GRU models were further enhanced through adaptive weighting techniques and spatio-temporal feature integration, leading to improved predictive performance. The findings of Lin et al. [41] highlight the effectiveness of GRU models in forecasting air pollution in urban areas.
Various air quality prediction models have been developed using advanced artificial intelligence techniques, including Long Short-Term Memory (LSTM) and Particle Swarm Optimization (PSO), in conjunction with traditional models such as Support Vector Machine (SVM) and Generalized Additive Model (GAM). These methodologies have been applied to estimate pollutant concentrations, including PM2.5, PM10, , CO, , and [42]. The results indicate that the LSTM-PSO model achieved superior accuracy compared to other models, such as Gradient-Boosted Decision Trees (GBDT).
For short-term forecasts ranging from 1 to 24 h, concentration prediction models have also been developed using deep neural networks, including Convolutional Neural Networks (CNNs), LSTM, and CNN-LSTM [43]. The findings demonstrate that deep learning models significantly outperform traditional approaches in predictive accuracy, with LSTM and CNN-LSTM models achieving the highest performance, yielding values exceeding 0.92. An insightful study was conducted in Ahvaz (Iran), a city notorious for its high pollution levels due to frequent dust storms [44]. This research analyzed a full year of data to evaluate the effectiveness of an Artificial Neural Network (ANN) model in estimating pollutant concentrations, including , , , PM10, PM2.5, and CO. The results demonstrated that the ANN model achieved a mean accuracy of across all pollutants, proving to be particularly effective in predicting the Air Quality Health Index (AQHI). Consequently, the study concluded that air quality authorities could leverage ANN-based models to forecast spatial and temporal pollution patterns, thereby mitigating adverse public health effects.
In a related study conducted in Tehran (Iran), the predictive accuracy of Multiple Linear Regression (MLR) and Artificial Neural Network (ANN) models for daily concentrations was assessed [45]. This analysis incorporated meteorological, urban traffic, and green space data collected over a one-year period. The findings indicated that the ANN model significantly outperformed the MLR model in predictive accuracy. Furthermore, the study highlighted the crucial role of urban green spaces in reducing concentrations, demonstrating their effectiveness as a more impactful factor than traffic volume. Another significant study conducted in Los Angeles (USA) compared the performance of Land-Use Regression (LUR) and a 2-step approach (UK2) in predicting summertime concentrations [46]. This research represented one of the pioneering applications of land-use regression models for traffic-related , , and air pollution in Los Angeles. The study achieved a prediction accuracy of 87–91% by incorporating remotely sensed variables as effective surrogates, ultimately surpassing the accuracy of traditional land use-based regression models [47].
3. Methods
Building on the previous comparative analysis, this chapter addresses RQ2 by applying predictive models to quantify and anticipate the reduction in air pollution resulting from the implementation of the bicycle-sharing system in Madrid. This approach provides a data-driven framework for assessing the environmental benefits of sustainable urban mobility solutions, offering valuable insights for policymakers and urban planners. The city of Madrid is the most populous urban center in Spain, with approximately 3.4 million inhabitants, while the greater Madrid region has a population of around 7.0 million. This accounts for approximately 7.0% and 14.2% of the total Spanish population, respectively. Given this demographic concentration, Madrid is a significant contributor to national emissions from transportation. Since cycling presents a viable and sustainable alternative to conventional road transport, it becomes essential to estimate the reduction in greenhouse gas emissions facilitated by the adoption of bicycle-sharing systems.
The model described below follows a structured process. First, the raw travel data are preprocessed by filtering out extreme durations and estimating distances. They are then aggregated on a weekly basis. Next, a univariate time series is constructed and the seasonal pattern is estimated. Then, the ARNN model is configured by means of grid search and cross-validation to capture non-linear trends. Finally, after validation, the bike-sharing usage is forecasted, translating the results into estimated CO2 and NOx emission savings.
3.1. Data
The dataset utilized in this study was sourced from the open data portal of the transport company of Madrid [48]. This repository provides regularly updated data with the latest available records. To facilitate a comprehensive temporal analysis, a full-year dataset was selected, making 2022 the most recent complete year for evaluation. The dataset comprised a total of 3,277,177 observations across 17 variables (cf. Table A2).
For the initial data exploration, analysis, and predictive modeling, RStudio (version 4.2.3) was chosen due to its open-source nature and specialization in handling large-scale data analysis. Additionally, RMarkdown was employed for integrating textual documentation with R code, allowing for seamless reproducibility. This interface is based on the Markdown language, designed to efficiently convert plain text into HTML format with minimal complexity. To analyze and visualize the bike-sharing system network structure, the Gephi (version 0.10) API was utilized. This open-source, Java-based interactive tool is well suited for managing large datasets and analyzing complex systems characterized by dynamic and hierarchical graphs [49]. Gephi was selected for its ability to enable real-time interaction, allowing users to modify both the properties and visual representations of the studied graphs. This feature is particularly valuable for optimizing the routing and operational efficiency of the bike-sharing service [50].
The study population included all users who utilized the bike-sharing service during the selected period. To ensure methodological consistency, it was estimated that urban bicycle trips typically last between 2 and 30 min. Trips with durations shorter than 2 min were presumed to be due to user errors in undocking the bicycle as reaching another station within such a short time was highly improbable. Conversely, trips exceeding 30 min were excluded to ensure that the entire journey was conducted solely by bicycle, without prolonged stops, aligning with the characteristics of urban mobility patterns.
Before the models were trained, the dataset was preprocessed. This included (i) the exclusion of anomalous records, specifically trips of less than 2 min (often caused by decoupling errors) and more than 30 min (to ensure that complete trips were made only by bicycle); (ii) the transformation of time stamps into categorical variables such as time of day and day of the week; and (iii) the estimation of distance traveled based on trip duration and an average bicycle speed of 12 km/h, as recommended by [51].
3.2. Materials
Artificial neural networks (ANNs) are fundamental algorithms for analyzing the relationship between logistics performance, energy consumption, and environmental degradation [52]. The model developed in this study is based on a multilayer perceptron (MLP) architecture, which is widely employed for nonlinear time series prediction [53]. This specific configuration of autoregressive neural networks (ARNNs) is derived by integrating a linear autoregressive model with an MLP [54]. The model relies on a statistical nonlinearity contrast, where both models are compared to determine their effectiveness [55,56,57]. In an ARNN framework, the dependent variable () is obtained as a nonlinear function of its P past values: , for , as expressed in the following equation:
where is the sigmoid function [58,59,60]. The parameters of the model—, , , , and for and —are estimated by minimizing the regularization error: . It should be noted that is a user-predefined external parameter; represents the errors between the forecast and the desired value . Also, is a function of the model parameters:
The model described in Equation (1) can be reduced to a standard multilayer perception if the constraint is imposed. Conversely, the neural network simplifies to an autoregressive model when the condition is enforced. Finally, during the model estimation process, several statistical measures are calculated, including variance (), the logarithm of the likelihood function of errors, and the values of the Akaike and Schwartz information criteria. The model implementation is carried out using the BFGS optimization algorithm, which is executed multiple times with automatic restarts to ensure convergence to the optimal model.
The ARNN model combines the strengths of classical autoregressive models with nonlinear modeling capabilities of feedforward neural networks [53,58]. Unlike traditional models such as ARIMA, which assume linearity and stationarity, ARNN models can accommodate nonlinear dynamics and seasonal trends present in urban mobility patterns.
Hyperparameter tuning was conducted using a grid search procedure with 10-fold cross-validation. The key parameters optimized were the number of input lags (p), the number of neurons in the hidden layer (H), and the seasonal period (s). The seasonal component was set to 7, reflecting weekly usage patterns. The optimal configuration was determined by minimizing the mean absolute percentage error (MAPE) and maximizing R2 using 10-fold cross-validation on the training set. The results shown in Section 4 align with prior research that demonstrates the superiority of ARNNs and other ANN-based models for environmental and mobility time series forecasting [36,53,58].
3.3. Procedure
This chapter describes the method used to estimate the approximate amount of energy saved in fuel consumption due to the implementation of the new bike-sharing service. Additionally, the equivalent kilograms of and emissions avoided as a result of this service are quantified. The analysis was performed following the procedure by Chen et al. [20] in New York. Although the New York system recorded a significantly higher number of trips, approximately 8.1 million compared to 3.4 million in Madrid, the methodological approach remains valid. An effective approach to assessing the environmental benefits of a bike-sharing system is by estimating the fuel savings in gasoline and diesel consumption. Based on the work of Scheiner [51], the primary modes of transport were classified according to the distance traveled (cf. Table 1). The environmental impact of walking and using shared electric bicycles was considered negligible as these modes do not contribute to fuel consumption.

Table 1.
Distribution of the percentage of transportation mode usage based on distance traveled.
A series of parameters were considered that affected the calculation of the energy consumed, such as the average fuel consumption of a bus or car, the density of the fuel, and coefficients specific to each means of transport. In addition, the value of the kilograms of and generated for each kilogram of fuel consumed was known. The value of each of the parameters can be seen in Table 2.

Table 2.
Units of consumption and pollution for motorized vehicles: bus and car parameters. Source: Chen et al. [20].
From these two tables, Equation (3) was obtained, which calculated the energy consumed by each vehicle:
where N is the energy consumed by the vehicle, d refers to the total distance traveled in km, and is the amount of diesel in liters consumed by a bus per kilometer traveled, expressed in liters per kilometer (L/km). represents the density of diesel, measured in kilograms per liter (kg/L). These values differ between buses (diesel-powered) and private cars (gasoline-powered). Both and are dimensionless and express the energy efficiency produced by the fuel in the explosion in the engine and in the direct transmission to the vehicle’s transport. The second part of this expression (, , , and ) represents the same for gasoline combustion in cars. This study focused particularly on the reduction of and emissions. The kilograms saved of these pollutant gases could be calculated using Equation (4):
where E represents the amount of emissions in kilograms of and that is saved from being discharged into the atmosphere. d, p, and are the same parameters of the previous formula and refers to the contribution factor corresponding to each of the polluting gases, i.e., the amount of or emitted per kilogram of fuel consumed.
3.4. Analysis
The distance between stations along each route was calculated using the longitude and latitude coordinates of each station. Since this method does not account for actual urban routes, it provided only an approximate estimation. A more accurate measure was obtained by considering the duration of each trip (available with precise data) and the average speed of the bicycles. An average speed of 12 km/h was assumed, a value supported by various reports and media sources from the Madrid Transport Consortium [61]. Based on this speed and the recorded travel time, a reliable estimate of the actual distance traveled for each route was obtained. To estimate the equivalent trips that would have been made by car or bus, Table 1 was used, which provided the percentage of trips that in the absence of the bike-sharing service, would have relied on motorized vehicles. For example, if a trip lasted 13.5 min, the estimated distance was 2.7 km (assuming an average speed of 12 km/h). This distance falls within the 2–3 km range in Table 1, which corresponds to 7% of trips that would have been taken by bus and 68% by car.
Using these proportions, it was estimated that the avoided emissions corresponded to a 189-meter bus trip (7% of 2.7 km) and a 1.84 km car trip (68% of 2.7 km). The remaining 25% of trips were considered non-polluting as they would have been completed by bicycle or on foot. By applying these parameters and the proportion of distances traveled by different polluting vehicles, the values were incorporated into the pollution estimation equation. This method enabled the calculation of the equivalent amount of energy saved, as well as the reduction in and emissions for each trip. A sample of observations detailing the total distance of each trip and the corresponding emissions savings is presented in Figure A1 Appendix B.
4. Results
Understanding the travel patterns and usage profiles of a bike-sharing system is essential for optimizing its operation and expanding its impact on urban mobility. This chapter analyzes various trip characteristics, such as duration, distance, and frequency, as well as the times of day and days of the week when the BSS was most frequently used. By examining these factors, we aim to identify key patterns that inform user behavior and reveal opportunities for improving service efficiency.
The histogram in Figure 2 shows the distribution of BSS trip durations in Madrid. The shape of the histogram reveals that most trips lasted between 10 and 15 min, with a peak in that range. After 15 min, the frequency of trips gradually decreased, with very few trips exceeding 30 min. This suggests that most users take relatively short trips. A closer analysis indicates that 50% of trips lasted between approximately 7 and 15 min, with a median of around 10 min. Additionally, the majority of trips fell within the range of 5 to 25 min. Trips lasting around 30 min were considered unusually long and treated as outliers. These results may have been influenced by the fact that the BSS in Madrid offers a flat rate of EUR 10 per month, provided that trips last less than 30 min. Any trip exceeding this duration incurs additional charges for the extra time. An exhaustive analysis of the BSS in Madrid is given in Appendix D.
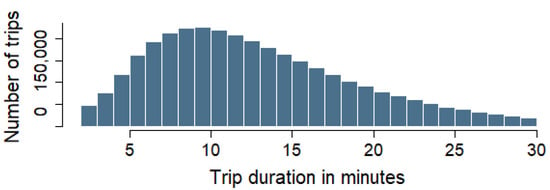
Figure 2.
Histogram of trip duration.
4.1. Quantifying Greenhouse Gas Emission Savings
The distribution of energy and pollutant gas savings throughout the day was examined. Figure 3 illustrates how these savings were concentrated during peak bicycle usage hours, which coincided with the peak demand for other motorized transport modes. The results highlight that the BSS not only contributed to reducing GHG emissions but also prevented additional emissions from being generated during periods of high traffic and pollution. This method quantified savings at individual and grouped docking station levels, offering valuable insights for urban mobility planning.
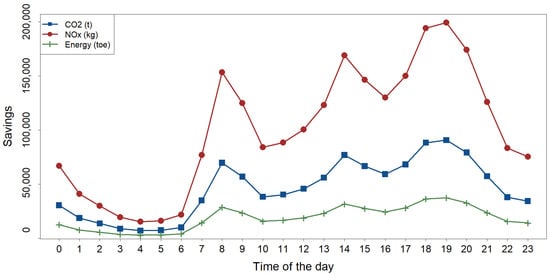
Figure 3.
Equivalent energy savings for and distributed by time of day.
The use of electric bicycles in Madrid’s bike-sharing system resulted in savings of approximately 451.8 tons of oil equivalent, corresponding to 1095.7 tons of CO2 and approximately 2.4 tons of NOx in 2023. Our method enabled us to estimate the reduction in greenhouse gas emissions for groups of docking stations. For instance, an analysis of the stations located near university schools and faculties in Ciudad Universitaria quarter revealed a total reduction of 5440 kg of emissions.
4.2. Anticipating Greenhouse Gas Emission Savings
The review in Section 2 shows that the ARNN model is well suited for predicting GHG emissions in bike-sharing systems due to its ability to handle non-linear time series, capture seasonal patterns, and adapt to dynamic data. Its flexibility in configuring input delays and hidden neurons allows for accurate short- and long-term forecasts. Additionally, it effectively predicts peaks in bicycle usage, which coincide with reduced motorized vehicle emissions, thereby providing a reliable tool for quantifying environmental benefits from BSS. Figure 4 shows that the resulting model was an NNAR(15,1,8)[7], meaning that the model had 15 input lags, one output unit, and eight neurons in the hidden layer. The series pattern had weekly stationarity (seven periods). Examining the forecasts for the next seven weeks, it was evident that the model performed well. In general, ARNN models effectively capture the asymmetry of cycles better than classical models such as ARIMA. The use of ARNN models in this study enabled the capture of nonlinear patterns and seasonal trends in emission reductions attributable to the BSS. Compared to traditional regression-based approaches, our model enhances prediction accuracy and provides a scalable methodology for other cities with available IoT data.
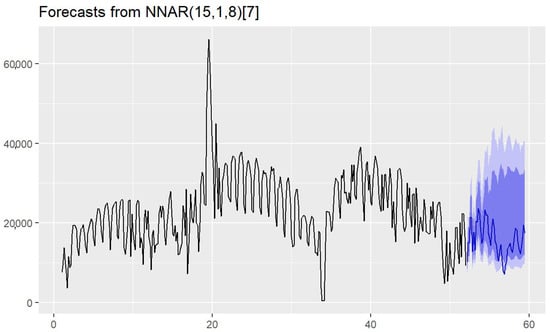
Figure 4.
Y-axis: predicted values; X-axis: time in weeks. NNAR(15,1,8)[7] model prediction.
The prediction obtained with the model proved to be highly accurate. The large amount of data available for training significantly improved the results of the analysis. In this case, the model had a low mean absolute percentage error (MAPE = 7%), suggesting that it performed quite well in percentage terms. The mean scaled absolute error (MASE) below 1 indicates that the model is better than a naive model. Finally, the fit of the model to the data was good () and the value of the residual variance showed that the errors were small ().
The predictive model enabled the calculation of the total distance expected to be covered in the forecasted weeks. According to this model, based on 52 weeks, the total estimated distance was nearly 200 km. From this data, further estimates of energy savings and greenhouse gas emissions could be calculated. Hence, it was estimated that in the first two weeks of 2023, approximately 10.8 tons of oil equivalent, 58 kg of , and 26.2 tons of were saved.
5. Discussion and Conclusions
This work investigated the state of the art of predictive models for GHG emissions in large cities, with a focus on bike-sharing systems. The literature review highlighted four key benefits of bike-sharing systems: (i) a reduction in air pollution through decreased emissions of carbon-based pollutants (CO and CO2), nitrogen oxides (NO and NO2), sulfur dioxide (SO2), and particulate matter (PM10 and PM2.5), which are primarily generated by fossil fuel combustion; (ii) a decrease in urban traffic congestion and associated energy consumption costs (e.g., fuel savings); (iii) improved urban space organization; and (iv) a decline in accidents, reducing both human injuries and material damages. Despite the increasing availability of mobility data and advances in machine learning, limited research has focused on predicting the impact of BSSs on greenhouse gas (GHG) emissions using machine learning techniques [19]. However, machine learning has been extensively applied to predict urban GHG emissions without explicitly considering BSSs.
This study builds upon previous research by (i) identifying key patterns in BSS usage, (ii) quantifying energy savings and reductions in GHG emissions, (iii) forecasting energy and emission savings, and (iv) presenting a scalable modeling framework applicable to various cities and emission types. A significant contribution of this research is the classification of the scientific literature into four dimensions (RQ1): (1) predictive models utilized (), (2) reported accuracy levels, (3) analyzed emissions, and (4) citation frequency per study (Figure 1 and Table A1).
The findings indicate that the most frequently used predictive models include ANN, ANFIS, LSTM-PSO, MLP, and random forest models. These models are widely adopted due to their ability to handle the complexity and non-linearity of urban data, effectively capturing intricate relationships between traffic patterns, meteorological conditions, and energy consumption, key factors in GHG emissions estimation. In particular, models such as LSTM, designed for time-series forecasting, excel in both short- and long-term predictions, which is essential in dynamic urban environments where emissions fluctuate over time. Moreover, MLP and random forest are particularly well suited for processing large-scale datasets generated by urban sensors and monitoring systems without excessive data simplification. ANFIS facilitates the integration of heterogeneous data sources, improving model robustness, while LSTM-PSO enhances predictive accuracy through optimization techniques. The widespread use of these models underscores their adaptability and effectiveness in urban GHG forecasting.
The selection of the autoregressive neural network (ARNN) model in this study was not based on its novelty in algorithmic development but on its strategic suitability for this study. ARNN models are particularly effective at capturing complex temporal dependencies and nonlinear patterns in univariate time series data. This makes them well suited to modeling the dynamic behavior of bike-sharing demand and its relationship to greenhouse gas emission reduction. While ARNN architecture is not new in the machine learning literature [53,58], its application in the context of environmental forecasting for urban bike-sharing systems remains limited. Existing studies have largely focused on retrospective analyses using regression models or traditional ANNs. In contrast, this study adopted the ARNN framework to enable short-term forecasting of CO2 and NOx emission reductions, incorporating both trend and seasonality in mobility data. This application demonstrates the model’s flexibility in real-world environmental assessment scenarios and offers a replicable approach for similar urban contexts.
Regarding the accuracy (R2 and RMSE) of predictive models, it is noteworthy that some studies with lower accuracy levels have a high number of citations. This discrepancy may indicate a research gap and presents an opportunity for further investigation into model refinement and validation.
In terms of GHG emissions, the most frequently studied pollutants are, in descending order, PM2.5, NOx, NO2, and O3, whereas pollutants such as NH3, CO2, and PM10 receive less attention. The prioritization of PM2.5, NOx, NO2, and O3 in GHG research is likely influenced by the relative ease and cost-effectiveness of monitoring these pollutants compared to CO2 and NH3, which require more sophisticated measurement techniques. Advanced sensor technologies readily capture PM2.5 and NOx, making them highly accessible for urban monitoring, especially given their well-documented impacts on public health and the environment. In contrast, CO2 is a global pollutant with diffuse sources, while NH3 emissions are more closely associated with agricultural rather than urban activities. Although PM10 is monitored, its health impact is generally considered less severe than PM2.5, which may contribute to its lower research frequency.
Using the ARNN model, this study accurately predicted greenhouse gas emission reductions attributed to the BSS (RQ2). The predictions demonstrated high accuracy using only data from the 12 weeks preceding the forecast period. Compared to other classical models, the ARIMA model produced values of R2 = 0.78 and MAPE = 13.4%, significantly lower than the R2 = 0.94 and MAPE = 7% of the ARNN model. Similarly, linear regression models performed even worse due to their inability to model temporal dependencies (R2 = 0.61; MAPE = 18.2%). These results are consistent with those of [19,27], who found that deep learning and neural autoregressive models outperform traditional statistical approaches in urban mobility and pollution forecasting.
The proposed predictive model is adaptable to different contexts while accounting for specific limitations in each case. For instance, it can be applied to aggregated areas (e.g., commercial centers, universities, residential zones, or business districts) and trained with varied time spans (e.g., the last 12 weeks, one year, or five years) to generate tailored predictions (e.g., for the next day, week, or two weeks). Additionally, the model can be extended to analyze alternative variables beyond NOx and CO2 emissions. This study introduced a significant innovation in predicting the environmental impact of BSSs by integrating real-time IoT sensor data with advanced machine learning models. While previous research has estimated emission reductions retrospectively, this methodology enables forecasting trends and improving sustainable urban planning. Moreover, the combination of prediction and real-time sensors offers a replicable tool for policymakers in other cities.
Future research could leverage this approach to predict and quantify reductions in other GHG emissions (e.g., CH4, O3, CO, PM) or additional pollutants such as noise pollution. The models explored in this study provide a robust framework for quantifying the impact of sustainable mobility policies implemented by regional governments. This analysis can aid in identifying streets requiring infrastructure improvements, such as the installation of additional bike lanes, docking stations, or bicycles, and aligns closely with machine learning-based models used to assess transportation policies aimed at reducing GHG emissions.
The findings of this study highlight several key areas where machine learning and AI contribute significantly. Heat maps displaying the most active stations (Figure A2 and Figure A3) enable the identification and prediction of stations that may require additional bicycles at specific times of the day. This information facilitates the optimal redistribution of bicycles across stations, helping maintenance personnel minimize periods when stations either run out of bicycles or lack available docking spaces. Moreover, route optimization for maintenance staff could reduce travel time and operational costs. Time-series data on bicycle usage throughout the day also assist in determining optimal time frames for infrastructure maintenance.
Finally, this study acknowledges a limitation in the dataset as BSS data lack GPS traceability throughout each bicycle’s journey, capturing only pickup and drop-off locations. This restriction limits the ability to cross-reference data with additional sources (e.g., real-time traffic conditions, air or noise pollution levels, green routes, tourist areas, or accident-prone locations), constraining the full potential of machine learning and IoT applications in this context. In addition, possible sources of prediction bias must be taken into account. Although the model was trained with data from an entire year and performed well, certain patterns (such as night-time use or certain user groups) may have been captured with less precision. Furthermore, the use of average values for vehicle type, fuel efficiency, and emission factors introduced generalizations that may not have fully reflected real-world variability. Future research could integrate geolocated mobile and ubiquitous sensing from users’ smartphones [62], incorporating additional parameters such as noise levels, light exposure, and GPS tracking. Furthermore, enabling users to annotate routes based on their experiences (e.g., labeling routes as safe/unsafe, conducive to physical activity, cyclist-adapted, or tourist-friendly) [63] could provide valuable insights into urban mobility preferences and enhance the functionality of bike-sharing systems.
Author Contributions
Conceptualization, M.U.-S. and B.T.; methodology, M.U.-S., B.T. and G.H.-G.; software, M.U.-S. and G.H.-G.; validation, M.U.-S., B.T., G.H.-G. and Y.N.-G.; formal analysis, M.U.-S. and B.T.; investigation, M.U.-S., B.T. and G.H.-G.; resources, M.U.-S. and B.T.; data curation, M.U.-S. and G.H.-G.; writing—original draft preparation, M.U.-S. and B.T.; writing—review and editing, M.U.-S. and B.T.; visualization, M.U.-S. and B.T.; supervision, M.U.-S., B.T. and Y.N.-G.; project administration, M.U.-S., B.T. and Y.N.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This work received partial support from the European Commission through Erasmus+ Cooperation partnerships in school education through the project SUTEE (2023-1-ES01-KA220-SCH-000153498).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Machine Learning Models Anticipating Pollutants in Urban Areas

Table A1.
Review of ML models that evaluate urban pollutants and their accuracy.
Table A1.
Review of ML models that evaluate urban pollutants and their accuracy.
| Reference | Model | Pollutants | Accuracy /RMSE |
|---|---|---|---|
| Zhang et al. [24] | TROPOMI | 0.97 / — | |
| TROPOMI | 0.97 / — | ||
| Li et al. [26] | SVM | PM2.5 | 0.75 / — |
| GAM | 0.76 / — | ||
| RF | 0.83 / — | ||
| BRT | 0.83 / — | ||
| XGBoost | 0.82 / — | ||
| Cubist | 0.81 / — | ||
| SVM | 0.69 / — | ||
| GAM | 0.59 / — | ||
| RF | 0.71 / — | ||
| BRT | 0.71 / — | ||
| XGBoost | 0.70 / — | ||
| Cubist | 0.70 / — | ||
| Wen et al. [27] | BRT | 0.93 / — | |
| BRT | 0.9 / — | ||
| Zeinalnezhad et al. [28] | ANFIS | CO | 0.8693 / — |
| RS | CO | 0.8445 / — | |
| ANFIS | 0.8011 / — | ||
| RS | 0.8001 / — | ||
| ANFIS | O3 | 0.8350 / — | |
| RS | O3 | 0.7830 / — | |
| ANFIS | NO2 | 0.7640 / — | |
| RS | NO2 | 0.7602 / — | |
| Arhami et al. [29] | ANN | CO | 0.92 / — |
| ANN | O3 | 0.77 / — | |
| ANN | 0.87 / — | ||
| ANN | 0.87 / — | ||
| ANN | 0.85 / — | ||
| ANN | NO | 0.82 / — | |
| Goulier et al. [30] | MLP | 0.685 / — | |
| MLP | 0.648 / — | ||
| MLP | NO | 0.751 / — | |
| MLP | 0.915 / — | ||
| MLP | 0.751 / — | ||
| MLP | O3 | 0.871 / — | |
| MLP | 0.315 / — | ||
| MLP | 0.587 / — | ||
| MLP | 0.536 / — | ||
| MLP | 0.449 / — | ||
| Shi and Harrison [31] | OLS | 0.83 / — | |
| AR | 0.65 / — | ||
| Vasseur and Aznarte [32] | QRF | — / 22.62 | |
| QRFL | — / 19.12 | ||
| QKNN | — / 20.73 | ||
| QKNNL | — / 18.4 | ||
| QGB | — / 16.09 | ||
| QGBL | — / 16.14 | ||
| QLR | — / 19.44 | ||
| MLP | — / 18.16 | ||
| NGBOOST | — / 18.52 | ||
| DT | — / 18.69 | ||
| Liu et al. [33] | EWT-MAEGA-NARX | — / 0.1793 | |
| EWT-MAEGA-NARX | — / 0.0347 | ||
| EWT-MAEGA-NARX | — / 0.0969 | ||
| EWT-MAEGA-NARX | CO | — / 0.0041 | |
| VMD-MAEGA-NARX | — / 0.3361 | ||
| EWT-MAEGA-SVM | — / 0.9451 | ||
| EWT-ARIMA-NARX | — / 0.3548 | ||
| Mercer et al. [47] | UK | 0.75 / — | |
| LUR | 0.74 / — | ||
| UK2 | 0.75 / — | ||
| Su et al. [46] | LUR (ADDRESS) | NO | 0.81 / — |
| LUR (ADDRESS) | 0.86 / — | ||
| LUR (ADDRESS) | 0.85 / — | ||
| Wen et al. [36] | C-LSTME | — / 12.08 | |
| ST-C-LSTM | — / 17.76 | ||
| LSTME | — / 18.25 | ||
| LSTME (AOD) | — / 21.17 | ||
| LSTME (Meteo) | — / 22.22 | ||
| LSTM NN | — / 25.95 | ||
| ARMA | — / 34.40 | ||
| SVR | — / 39.92 | ||
| Mao et al. [34] | TS-LSTME | 0.72 / — | |
| TS-LSTME | O3 | 0.86 / — | |
| LSTME | 0.52 / — | ||
| LSTME | O3 | 0.63 / — | |
| LSTM | 0.52 / — | ||
| LSTM | O3 | 0.60 / — | |
| Chang et al. [37] | GBT | 0.83 / — | |
| SVR | 0.73 / — | ||
| LSTM | 0.71 / — | ||
| LSTM2 | 0.73 / — | ||
| Chang et al. [38] | GBT | 0.86 / — | |
| SVR | 0.87 / — | ||
| LSTM | 0.85 / — | ||
| ALSTM | 0.88 / — | ||
| Rybarczyk and Zalakeviciute [64] | GBT | — / 1.59 | |
| SVR | — / 2.77 | ||
| LSTM | — / 1.59 | ||
| ALSTM | — / 0.44 | ||
| Masih [39] | LSTM | 0.78 / — | |
| SVR | 0.73 / — | ||
| GBTR | 0.76 / — | ||
| ALSTM | 0.82 / — | ||
| Mokhtari et al. [40] | LSTM | 0.91 / — | |
| SVR | 0.85 / — | ||
| ANN | O3 | 0.89 / — | |
| RF | 0.82 / — | ||
| GBDT | CO | 0.87 / — | |
| CNN | 0.88 / — | ||
| Lin et al. [41] | GRU-13d | 0.91 / — | |
| GRU-AW14d | 0.85 / — | ||
| GRU-ST13d | 0.78 / — | ||
| MLEGRU | 0.88 / — | ||
| Al-Janabi et al. [65] | LSTM-PSO | 0.85 / — | |
| LSTM-PSO | 0.85 / — | ||
| LSTM-PSO | 0.85 / — | ||
| LSTM-PSO | CO | 0.85 / — | |
| LSTM-PSO | O3 | 0.85 / — | |
| SVM | 0.78 / — | ||
| GAM | 0.81 / — | ||
| GBDT | O3 | 0.82 / — | |
| Mishra and Goyal [66] | PCA-ANN | 0.318 / — | |
| Freeman et al. [67] | RNN-LSTM | O3 | — / 2.5 |
| Qin et al. [68] | CNN+LSTM | — / 14.3 | |
| Sun and Sun [69] | CS-LSSVM | — / 14.47 | |
| LSSVM | — / 21.75 | ||
| GRNN | — / 22.89 | ||
| Yang et al. [43] | CNN | 0.931 / — | |
| LSTM | 0.92 / — | ||
| CNN-LSTM | 0.92 / — | ||
| BPNN | 0.875 / — | ||
| Maleki et al. [44] | ANN | O3 | 0.90 / — |
| ANN | 0.91 / — | ||
| ANN | 0.99 / — | ||
| ANN | 0.91 / — | ||
| ANN | 0.91 / — | ||
| ANN | CO | 0.94 / — | |
| Shams et al. [45] | ANN | 0.89 / — | |
| MLR | 0.81 / — | ||
| MLP | 0.89 / — |
Appendix B. Equivalent Energy Savings
Figure A1 is a sample of observations showing the total distance traveled and the different emissions saved on each of these trips. If all the individual observations are added up, the total savings in terms of energy and pollutant emissions can be arrived at, thanks to the BSS (cf. Figure 3).
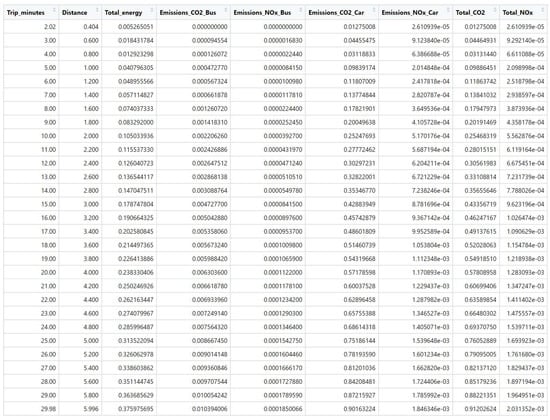
Figure A1.
Sample of equivalent energy savings of and .
Appendix C. Structure of the Working Dataset

Table A2.
Summary of study variables.
Table A2.
Summary of study variables.
| CHARACTER | ||||
|---|---|---|---|---|
| skim_variable | n_missing | complete_rate | min | max |
| geolocation_unlock | 0 | 1.0 | 53 | 75 |
| address_unlock | 0 | 1.0 | 15 | 68 |
| geolocation_lock | 0 | 1.0 | 53 | 75 |
| address_lock | 0 | 1.0 | 15 | 68 |
| unlock_station_name | 0 | 1.0 | 10 | 58 |
| lock_station_name | 0 | 1.0 | 10 | 58 |
| day | 0 | 1.0 | 2 | 2 |
| hour | 0 | 1.0 | 2 | 2 |
| daysweek | 0 | 1.0 | 5 | 9 |
| DATE | ||||
| skim_variable | n_missing | complete_rate | min | max |
| date | 0 | 1.0 | 2023-01-01 | 2023-01-31 |
| FACTOR | ||||
| skim_variable | n_missing | complete_rate | ordered | n_unique |
| station_unlock | 0 | 1.0 | FALSE | 260 |
| dock_unlock | 0 | 1.0 | FALSE | 30 |
| station_lock | 0 | 1.0 | FALSE | 260 |
| dock_lock | 0 | 1.0 | FALSE | 30 |
| NUMERIC | ||||
| skim_variable | n_missing | complete_rate | mean | sd |
| trip_minutes | 0 | 1.0 | 12.20849 | 5.980459 |
| POSIXCT | ||||
| skim_variable | n_missing | complete_rate | min | max |
| unlock_date | 0 | 1.0 | 2022-01-01 00:01:45 | 2022-12-31 23:59:44 |
| lock_date | 0 | 1.0 | 2022-01-01 00:10:05 | 2022-12-31 19:02:43 |
Appendix D. Extended Analysis of BSS in Madrid
Appendix D.1. Docking Station Usage Distribution
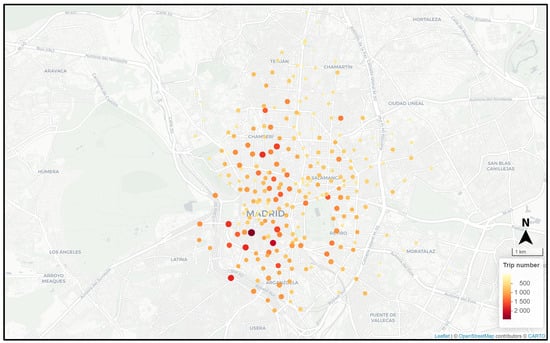
Figure A2.
Madrid BSS station distribution (monthly data).
Appendix D.2. Connectivity of Docking Stations
Hubs, or better-connected stations, are those that serve as the origin or destination for routes involving a larger number of distinct stations.
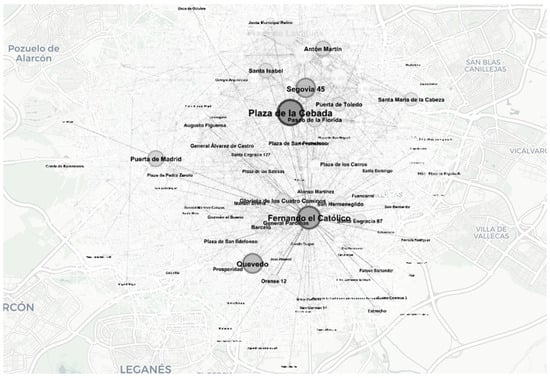
Figure A3.
Hubs in BSS Madrid: best-connected docking stations.
Appendix D.3. Weekly and Monthly Usage Patterns
Figure A4 illustrates the distribution of trips from Sunday to Saturday (grouped by color) in terms of total trips over the course of a year. The data also reflect the evolution of trips across the 4–5 weeks within each month.
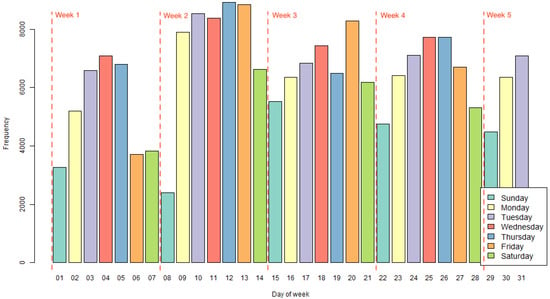
Figure A4.
Number of trips on each day of the month colored according to the day of the week.
Appendix D.4. Daily Usage Patterns
Figure A5 illustrates the total number of trips made throughout the day and their hourly distribution. Additionally, differences in usage patterns across the days of the week are explored to identify variations in the timing and frequency of trips.
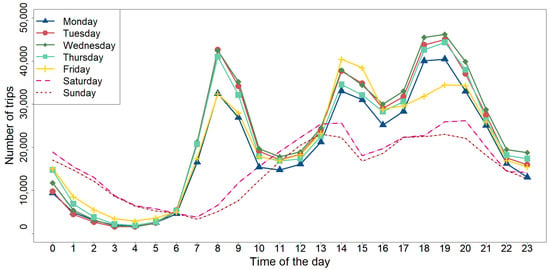
Figure A5.
Frequency divided by hours per day.
Appendix D.5. Leisure and Working Days
Figure A6 shows usage patterns throughout the day, distinguishing between weekdays (Monday to Friday) and non-working days (weekends). Additionally, it explores the dimension of trip duration, analyzing how travel times vary across different days of the week and time periods.
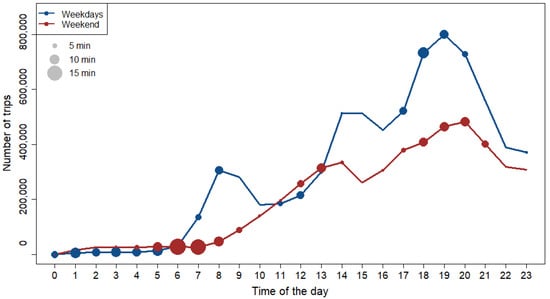
Figure A6.
Average weekday and weekend frequency divided by hours per day and duration.
References
- GrowLondon. Smart Mobility—Grow London. 2024. Available online: https://www.grow.london/set-up-in-london/sectors/urban/smart-mobility (accessed on 6 September 2024).
- AytoMadrid. Movilidad Sostenible—Madrid 360. 2024. Available online: https://www.madrid360.es/movilidad-sostenible/ (accessed on 6 September 2024).
- NYCityDept. New York City Mobility Report. 2024. Available online: https://www.nyc.gov/html/dot/html/about/mobilityreport.shtml (accessed on 6 September 2024).
- ParisRegion. Mobility & Transportation—Choose Paris Region. 2024. Available online: https://www.chooseparisregion.org/industries/Mobility-Transportation (accessed on 6 September 2024).
- Drosouli, I.; Voulodimos, A.; Mastorocostas, P.; Miaoulis, G.; Ghazanfarpour, D. A Spatial-Temporal Graph Convolutional Recurrent Network for Transportation Flow Estimation. Sensors 2023, 23, 7534. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Chen, Z.H.; Hong, Y. Enhancing Urban Mobility with Self-Tuning Fuzzy Logic Controllers for Power-Assisted Bicycles in Smart Cities. Sensors 2024, 24, 1552. [Google Scholar] [CrossRef]
- Zguira, Y.; Rivano, H.; Meddeb, A. Internet of Bikes: A DTN Protocol with Data Aggregation for Urban Data Collection. Sensors 2018, 18, 2819. [Google Scholar] [CrossRef] [PubMed]
- Puyol, J.L.M.; Baeza, V.M. Bicycle sharing system using an iot network. In Proceedings of the 2021 Global Congress on Electrical Engineering (GC-ElecEng), Valencia, Spain, 10–12 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 131–135. [Google Scholar]
- Kon, F.; Ferreira, É.C.; de Souza, H.A.; Duarte, F.; Santi, P.; Ratti, C. Abstracting mobility flows from bike-sharing systems. Public Transp. 2022, 14, 545–581. [Google Scholar]
- Gao, P.; Li, J. Understanding sustainable business model: A framework and a case study of the bike-sharing industry. J. Clean. Prod. 2020, 267, 122229. [Google Scholar]
- Karthika, K.; Nithya, A.; Sujatha, M.; Kovarasan, R.K.; Mahesh, A.; Murugan, S. Advancing Bike Sharing Security with SVM and IoT-Enabled Tracking and Anti-Theft Measures. In Proceedings of the 2024 2nd International Conference on Sustainable Computing and Smart Systems (ICSCSS), Coimbatore, India, 10–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 351–356. [Google Scholar]
- Guo, D.; Yao, E.; Liu, S.; Chen, R.; Hong, J.; Zhang, J. Exploring the role of passengers’ attitude in the integration of dockless bike-sharing and public transit: A hybrid choice modeling approach. J. Clean. Prod. 2023, 384, 135627. [Google Scholar]
- Guo, Y.; He, S.Y. Built environment effects on the integration of dockless bike-sharing and the metro. Transp. Res. Part D Transp. Environ. 2020, 83, 102335. [Google Scholar]
- Zhang, H.; Zhuge, C.; Jia, J.; Shi, B.; Wang, W. Green travel mobility of dockless bike-sharing based on trip data in big cities: A spatial network analysis. J. Clean. Prod. 2021, 313, 127930. [Google Scholar]
- Wang, L.; Zhou, K.; Zhang, S.; Moudon, A.V.; Wang, J.; Zhu, Y.G.; Sun, W.; Lin, J.; Tian, C.; Liu, M. Designing bike-friendly cities: Interactive effects of built environment factors on bike-sharing. Transp. Res. Part D Transp. Environ. 2023, 117, 103670. [Google Scholar]
- Qiu, L.Y.; He, L. Bike Sharing and the Economy, the Environment, and Health-Related Externalities. Sustainability 2018, 10, 1145. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, L.; Chen, Y. Bike Share Usage and the Built Environment: A Review. Front. Public Health 2022, 10, 848169. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Zhou, Z. Evaluation of Potential Contribution of Dockless Bike-sharing Service to Sustainable and Efficient Urban Mobility in China. Sustain. Prod. Consum. 2021, 27, 921–932. [Google Scholar] [CrossRef]
- Zhang, Y.; Mi, Z. Environmental benefits of bike sharing: A big data-based analysis. Appl. Energy 2018, 220, 296–301. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Coffman, D.; Mi, Z. An environmental benefit analysis of bike sharing in New York City. Cities 2022, 121, 103475. [Google Scholar] [CrossRef]
- Raposo, M.; Silva, C. City-Level E-Bike Sharing System Impact on Final Energy Consumption and GHG Emissions. Energies 2022, 15, 672. [Google Scholar] [CrossRef]
- Sun, S.; Ertz, M. Contribution of bike-sharing to urban resource conservation: The case of free-floating bike-sharing. J. Clean. Prod. 2021, 280, 124416. [Google Scholar] [CrossRef]
- Lu, M.; Hsu, S.; Chen, P.C.; yu Lee, W. Improving the sustainability of integrated transportation system with bike-sharing: A spatial agent-based approach. Sustain. Cities Soc. 2018, 41, 44–51. [Google Scholar] [CrossRef]
- Zhang, Q.; Boersma, K.F.; Zhao, B.; Eskes, H.; Chen, C.; Zheng, H.; Zhang, X. Quantifying daily NOx and CO2 emissions from Wuhan using satellite observations from TROPOMI and OCO-2. Atmos. Chem. Phys. 2023, 23, 551–563. [Google Scholar] [CrossRef]
- Magazzino, C.; Mele, M.; Schneider, N. A machine learning approach on the relationship among solar and wind energy production, coal consumption, GDP, and CO2 emissions. Renew. Energy 2021, 167, 99–115. [Google Scholar] [CrossRef]
- Li, Z.; Yim, S.; Ho, K. High temporal resolution prediction of street-level PM2.5 and NOx concentrations using machine learning approach. J. Clean. Prod. 2020, 268, 121975. [Google Scholar] [CrossRef]
- Wen, H.T.; Lu, J.H.; Jhang, D. Features Importance Analysis of Diesel Vehicles’ NOx and CO2 Emission Predictions in Real Road Driving Based on Gradient Boosting Regression Model. Int. J. Environ. Res. Public Health 2021, 18, 13044. [Google Scholar] [CrossRef] [PubMed]
- Zeinalnezhad, M.; Chofreh, A.G.; Goni, F.A.; Klemeš, J. Air pollution prediction using semi-experimental regression model and Adaptive Neuro-Fuzzy Inference System. J. Clean. Prod. 2020, 261, 121218. [Google Scholar] [CrossRef]
- Arhami, M.; Kamali, N.; Rajabi, M. Predicting hourly air pollutant levels using artificial neural networks coupled with uncertainty analysis by Monte Carlo simulations. Environ. Sci. Pollut. Res. 2013, 20, 4777–4789. [Google Scholar] [CrossRef]
- Goulier, L.; Paas, B.; Ehrnsperger, L.; Klemm, O. Modelling of Urban Air Pollutant Concentrations with Artificial Neural Networks Using Novel Input Variables. Int. J. Environ. Res. Public Health 2020, 17, 2025. [Google Scholar] [CrossRef]
- Shi, J.P.; Harrison, R. Regression modelling of hourly NOx and NO2 concentrations in urban air in London. Atmos. Environ. 1997, 31, 4081–4094. [Google Scholar] [CrossRef]
- Vasseur, S.P.; Aznarte, J. Comparing quantile regression methods for probabilistic forecasting of NO2 pollution levels. Sci. Rep. 2021, 11, 11592. [Google Scholar] [CrossRef]
- Liu, H.; Wu, H.; Lv, X.; Zhiren, R.; Liu, M.; Li, Y.; Shi, H. An intelligent hybrid model for air pollutant concentrations forecasting: Case of Beijing in China. Sustain. Cities Soc. 2019, 47, 101471. [Google Scholar] [CrossRef]
- Mao, W.; Wang, W.; Jiao, L.; Zhao, S.; Liu, A. Modeling air quality prediction using a deep learning approach: Method optimization and evaluation. Sustain. Cities Soc. 2020, 65, 102567. [Google Scholar] [CrossRef]
- Gu, J.; Yang, B.J.; Brauer, M.; Zhang, K.M. Enhancing the Evaluation and Interpretability of Data-Driven Air Quality Models. Atmos. Environ. 2021, 246, 118125. [Google Scholar] [CrossRef]
- Wen, C.; Liu, S.; Yao, X.; Peng, L.; Li, X.; Hu, Y.; Chi, T. A novel spatiotemporal convolutional long short-term neural network for air pollution prediction. Sci. Total. Environ. 2019, 654, 1091–1099. [Google Scholar] [CrossRef]
- Chang, Y.S.; Abimannan, S.; Chiao, H.T.; Lin, C.Y.; Huang, Y.P. An ensemble learning based hybrid model and framework for air pollution forecasting. Environ. Sci. Pollut. Res. 2020, 27, 38155–38168. [Google Scholar] [CrossRef]
- Chang, Y.S.; Chiao, H.T.; Abimannan, S.; Huang, Y.P.; Tsai, Y.T.; Lin, K.M. An LSTM-based aggregated model for air pollution forecasting. Atmos. Pollut. Res. 2020, 11, 1451–1463. [Google Scholar] [CrossRef]
- Masih, A. Machine learning algorithms in air quality modeling. Glob. J. Environ. Sci. Manag. 2019, 5, 515–534. [Google Scholar] [CrossRef]
- Mokhtari, I.; Bechkit, W.; Rivano, H.; Yaici, M.R. Uncertainty-Aware Deep Learning Architectures for Highly Dynamic Air Quality Prediction. IEEE Access 2021, 9, 14765–14778. [Google Scholar] [CrossRef]
- Lin, C.Y.; Chang, Y.S.; Abimannan, S. Ensemble multifeatured deep learning models for air quality forecasting. Atmos. Pollut. Res. 2021, 12, 101045. [Google Scholar] [CrossRef]
- Liu, H.; Yan, G.; Duan, Z.; Chen, C. Intelligent modeling strategies for forecasting air quality time series: A review. Appl. Soft Comput. 2021, 102, 106957. [Google Scholar]
- Yang, J.; Yan, R.; Nong, M.; Liao, J.; Li, F.; Sun, W. PM2.5 concentrations forecasting in Beijing through deep learning with different inputs, model structures and forecast time. Atmos. Pollut. Res. 2021, 12, 101168. [Google Scholar]
- Maleki, H.; Sorooshian, A.; Goudarzi, G.; Baboli, Z.; Birgani, Y.T.; Rahmati, M. Air pollution prediction by using an artificial neural network model. Clean Technol. Environ. Policy 2019, 21, 1341–1352. [Google Scholar] [CrossRef]
- Shams, S.R.; Jahani, A.; Kalantary, S.; Moeinaddini, M.; Khorasani, N. Artificial intelligence accuracy assessment in NO2 concentration forecasting of metropolises air. Sci. Rep. 2021, 11, 1805. [Google Scholar] [CrossRef]
- Su, J.G.; Jerrett, M.; Beckerman, B.; Wilhelm, M.; Ghosh, J.; Ritz, B. Predicting traffic-related air pollution in Los Angeles using a distance decay regression selection strategy. Environ. Res. 2009, 109 6, 657–670. [Google Scholar] [CrossRef]
- Mercer, L.; Szpiro, A.; Sheppard, L.; Lindström, J.; Adar, S.; Allen, R.; Avol, E.; Oron, A.; Larson, T.; Liu, L.; et al. Comparing universal kriging and land-use regression for predicting concentrations of gaseous oxides of nitrogen (NOx) for the Multi-Ethnic Study of Atherosclerosis and Air Pollution (MESA Air). Atmos. Environ. 2011, 45, 4412–4420. [Google Scholar] [CrossRef] [PubMed]
- EMT Madrid. BICIMAD Static Data. 2024. Available online: https://opendata.emtmadrid.es (accessed on 6 September 2024).
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the International AAAI Conference on Web and Social Media, San Jose, CA, USA, 17–20 May 2009; Volume 3, pp. 361–362. [Google Scholar]
- DatosGob. Análisis de Redes Sobre Viajes en BICIMAD. 2023. Available online: https://datos.gob.es/es/documentacion/analisis-de-redes-sobre-viajes-en-bicimad (accessed on 7 September 2024).
- Scheiner, J. Interrelations between travel mode choice and trip distance: Trends in Germany 1976–2002. J. Transp. Geogr. 2010, 18, 75–84. [Google Scholar] [CrossRef]
- Magazzino, C.; Mele, M.; Schneider, N. A new artificial neural networks algorithm to analyze the nexus among logistics performance, energy demand, and environmental degradation. Struct. Change Econ. Dyn. 2022, 60, 315–328. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- White, H. An additional hidden unit test for neglected nonlinearity in multilayer feedforward networks. In Advances in Econometric Theory; Edward Elgar Publishing: Cheltenham, UK, 1998; pp. 212–225. [Google Scholar]
- Lee, T.H.; White, H.; Granger, C.W. Testing for neglected nonlinearity in time series models: A comparison of neural network methods and alternative tests. J. Econom. 1993, 56, 269–290. [Google Scholar] [CrossRef]
- Teräsvirta, T.; Lin, C.F.; Granger, C.W. Power of the neural network linearity test. J. Time Ser. Anal. 1993, 14, 209–220. [Google Scholar] [CrossRef]
- Velásquez, J.D.; Zambrano, C.; Vélez, L. ARNN: Un paquete para la predicción de series de tiempo usando redes neuronales autorregresivas. Rev. Av. Sist. Inform. 2011, 8, 177–181. [Google Scholar]
- Chandra, P.; Singh, Y. An activation function adapting training algorithm for sigmoidal feedforward networks. Neurocomputing 2004, 61, 429–437. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- EMT. Resumen Ejecutivo BiciMAD. 2017. Available online: https://www.emtmadrid.es/Ficheros/Informes-Anuales/resumen_ejectutivo_2017_ESP.aspx (accessed on 17 May 2024).
- Song, J.; Han, K.; Stettler, M.E.J. Deep-MAPS: Machine-Learning-Based Mobile Air Pollution Sensing. IEEE Internet Things J. 2021, 8, 7649–7660. [Google Scholar] [CrossRef]
- Bergantino, A.S.; Intini, M.; Tangari, L. Influencing factors for potential bike-sharing users: An empirical analysis during the COVID-19 pandemic. Res. Transp. Econ. 2021, 86, 101028. [Google Scholar] [CrossRef]
- Rybarczyk, Y.; Zalakeviciute, R. Machine Learning Approaches for Outdoor Air Quality Modelling: A Systematic Review. Appl. Sci. 2018, 8, 2570. [Google Scholar] [CrossRef]
- Al-Janabi, S.; Mohammad, M.; Al-Sultan, A. A new method for prediction of air pollution based on intelligent computation. Soft Comput. 2020, 24, 661–680. [Google Scholar] [CrossRef]
- Mishra, D.; Goyal, P. Development of artificial intelligence based NO2 forecasting models at Taj Mahal, Agra. Atmos. Pollut. Res. 2015, 6, 99–106. [Google Scholar] [CrossRef]
- Freeman, B.S.; Taylor, G.; Gharabaghi, B.; Thé, J. Forecasting air quality time series using deep learning. J. Air Waste Manag. Assoc. 2018, 68, 866–886. [Google Scholar]
- Qin, D.; Yu, J.; Zou, G.; Yong, R.; Zhao, Q.; Zhang, B. A novel combined prediction scheme based on CNN and LSTM for urban PM 2.5 concentration. IEEE Access 2019, 7, 20050–20059. [Google Scholar]
- Sun, W.; Sun, J. Daily PM2. 5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm. J. Environ. Manag. 2017, 188, 144–152. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).