Very-Large-Scale Integration-Friendly Method for Vital Activity Detection with Frequency-Modulated Continuous Wave Radars
Abstract
1. Introduction
Related Work
2. Materials and Methods
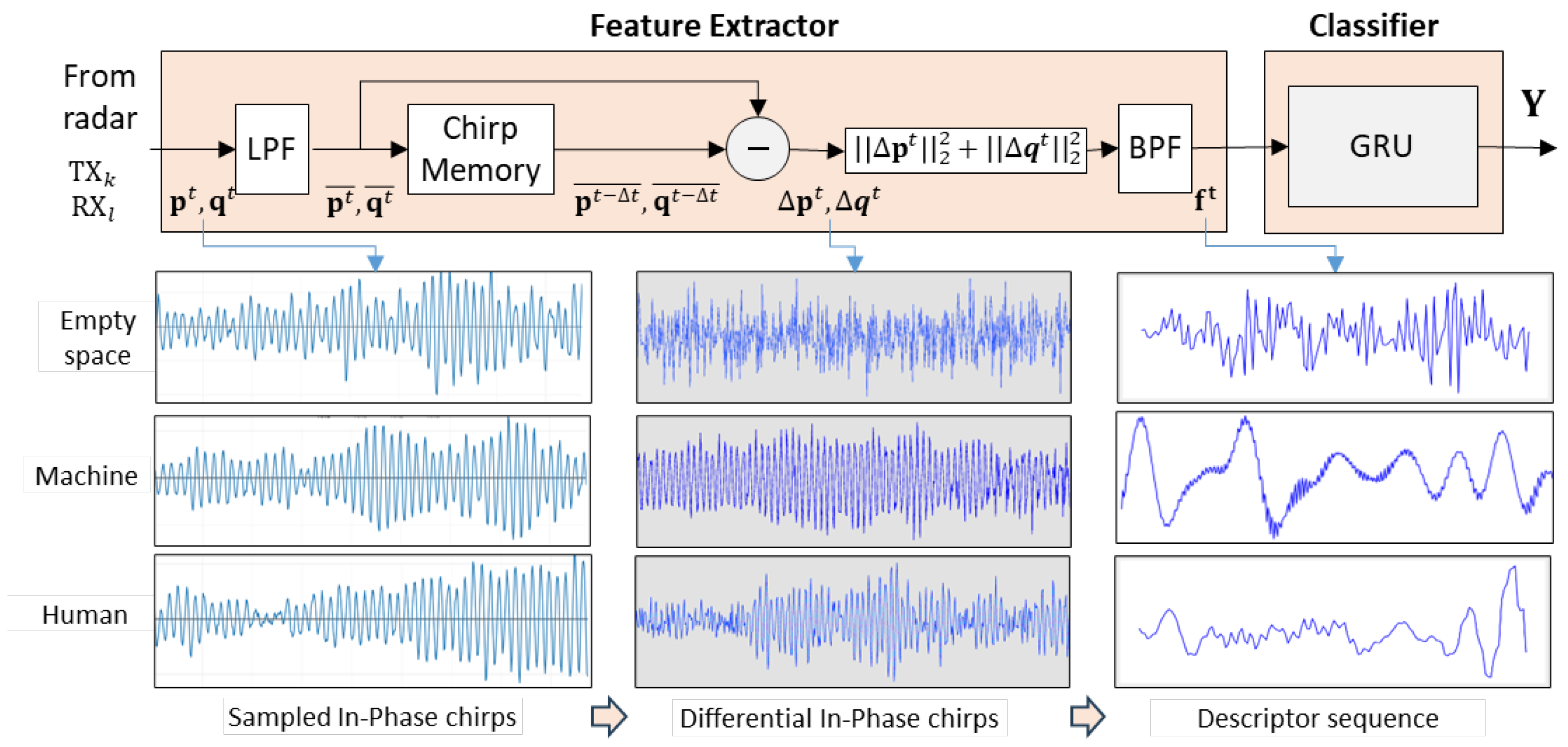
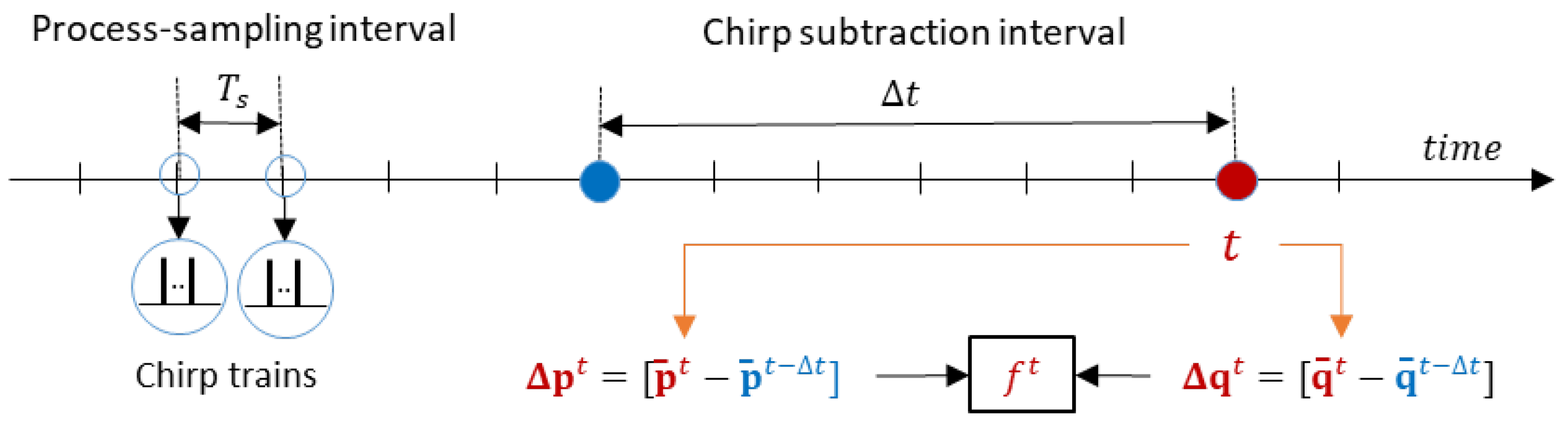
2.1. Descriptor Derivation
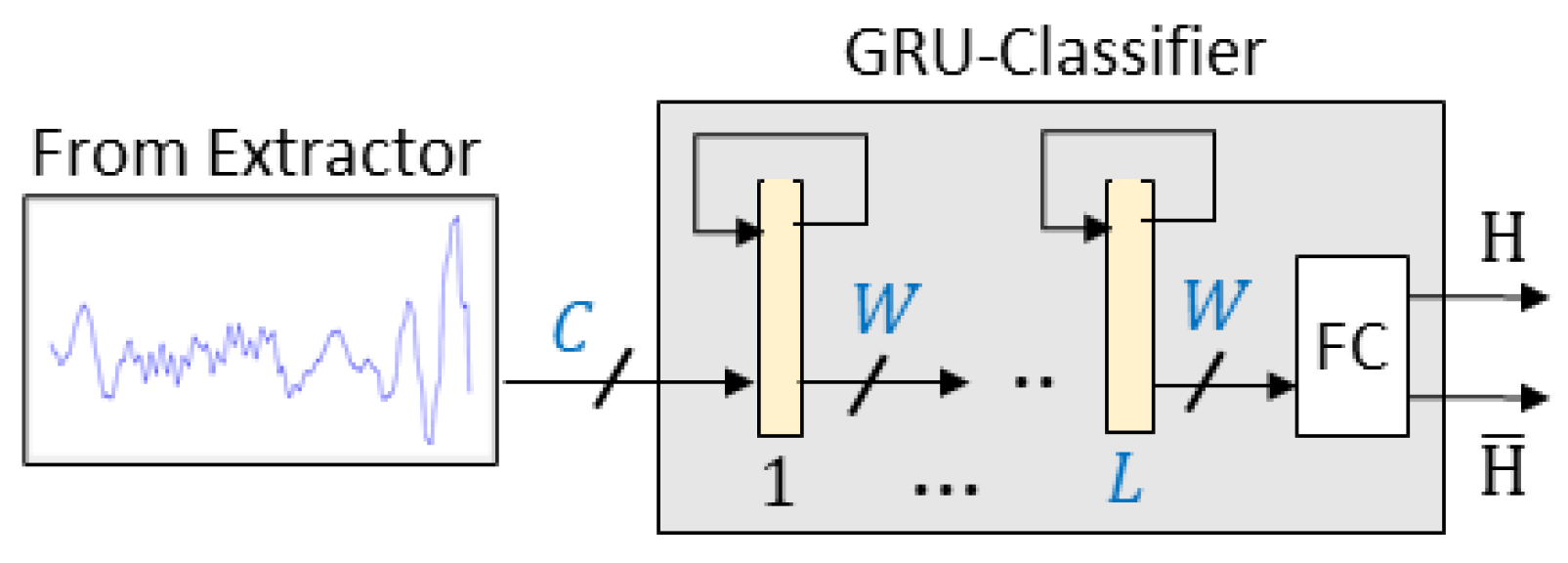
2.2. Sequence Classifier
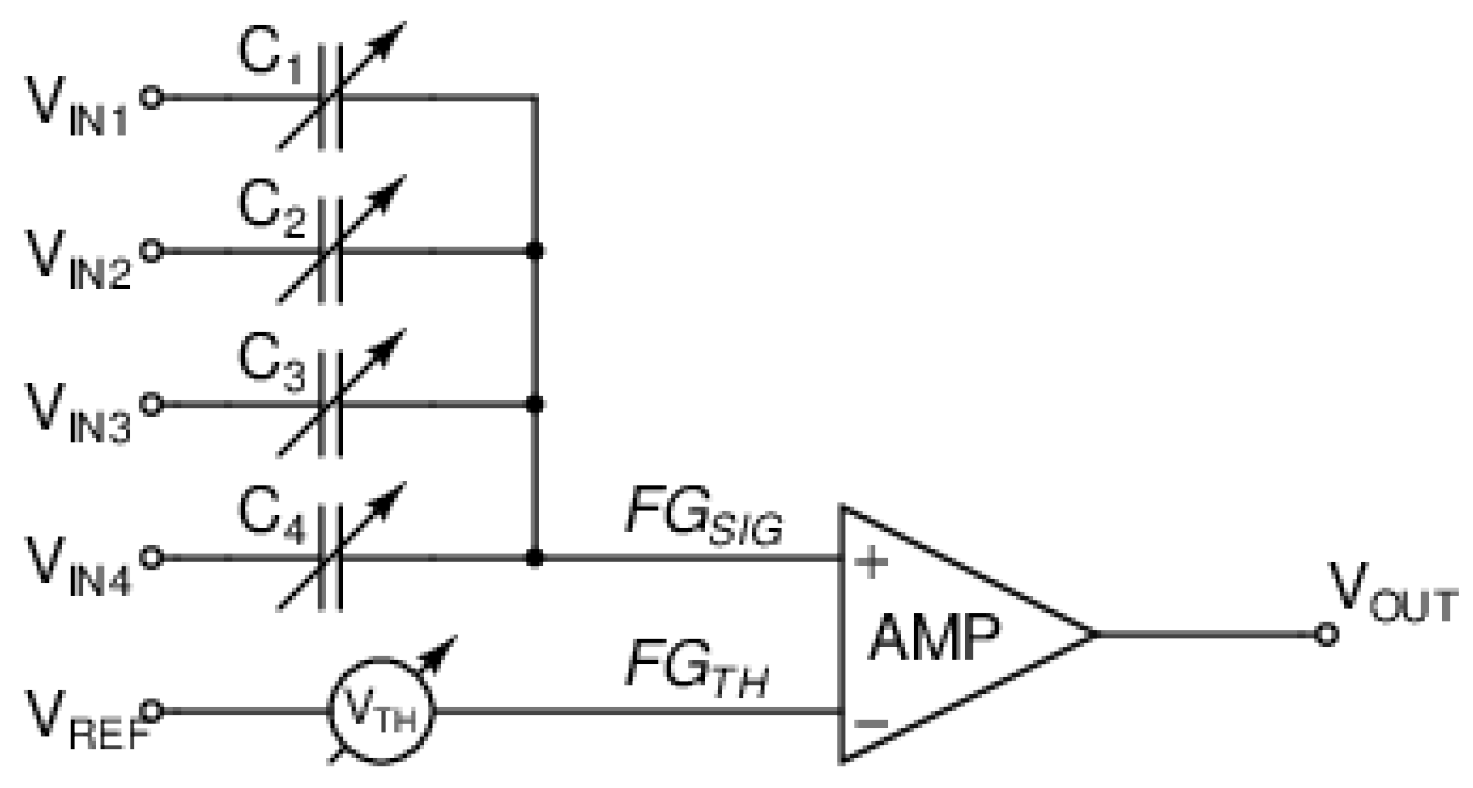
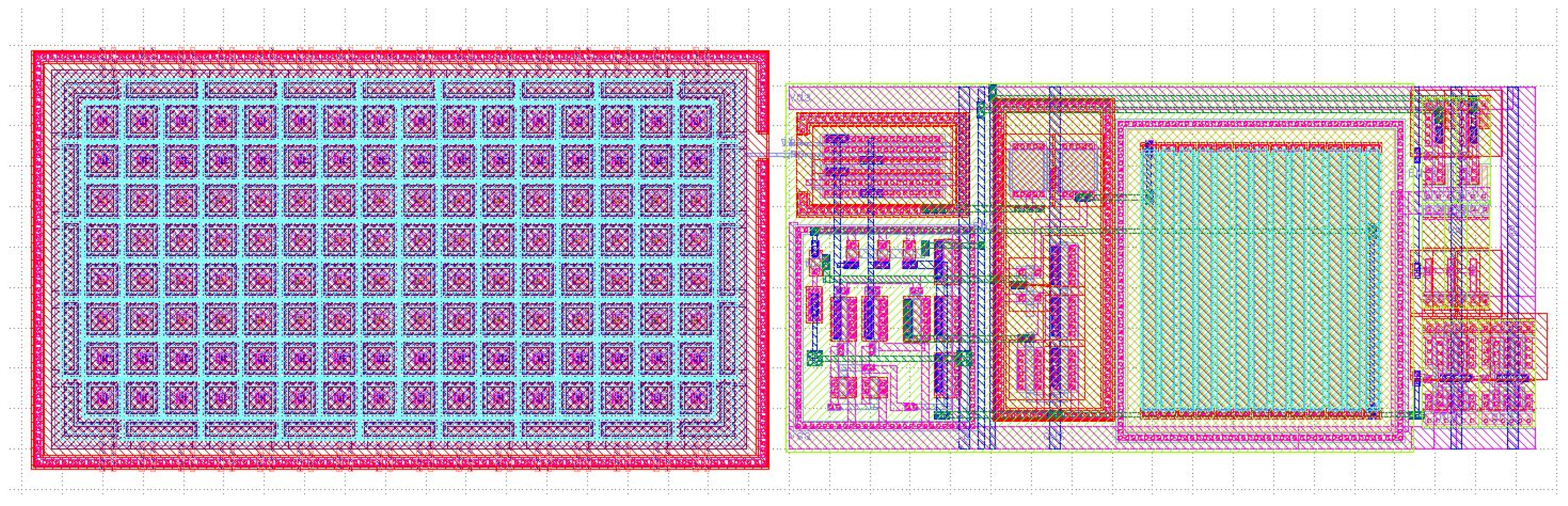
VLSI Implementation of Classifier Components
3. Results
3.1. Experimental Scenarios
3.2. Feature Extraction Procedure
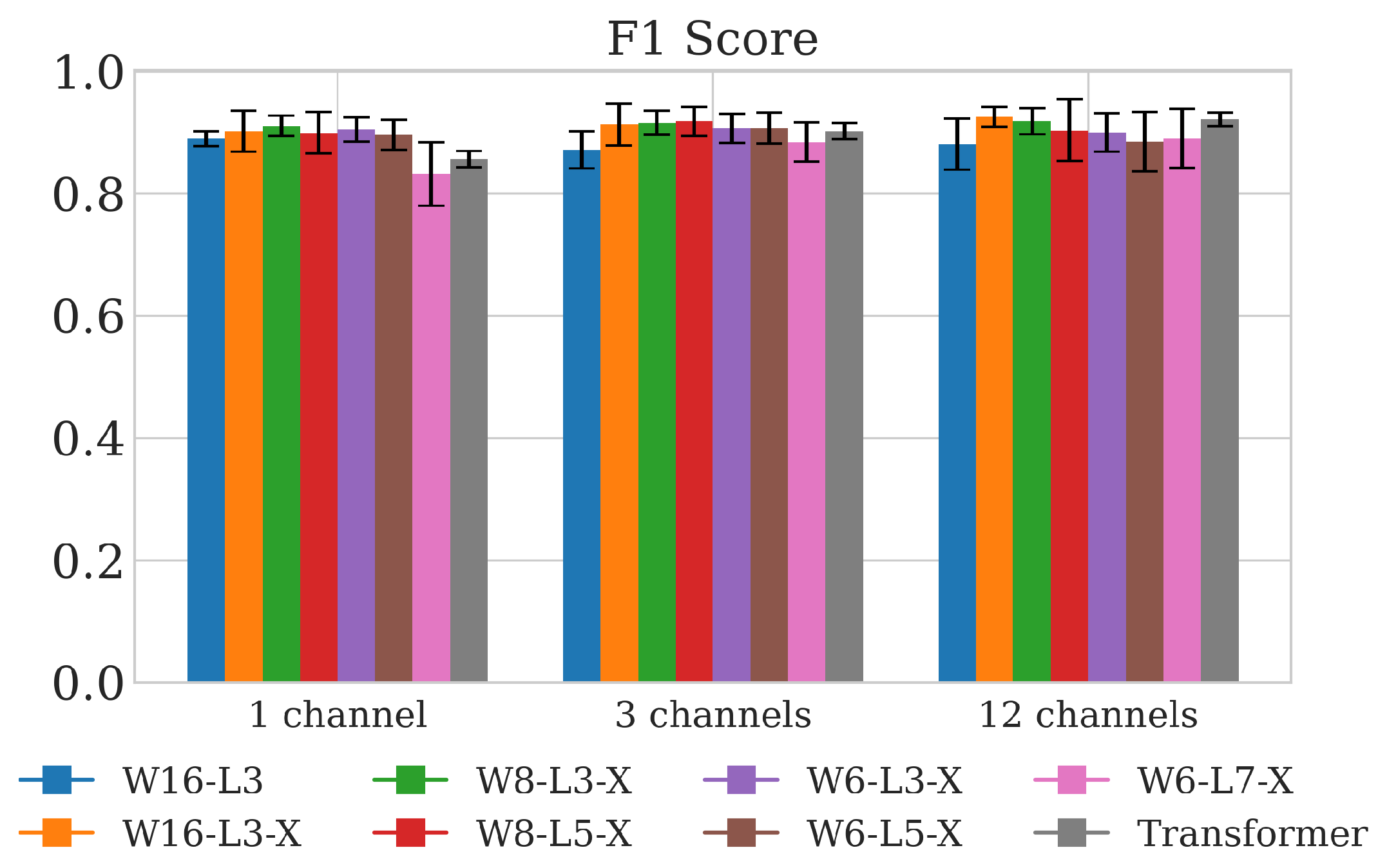
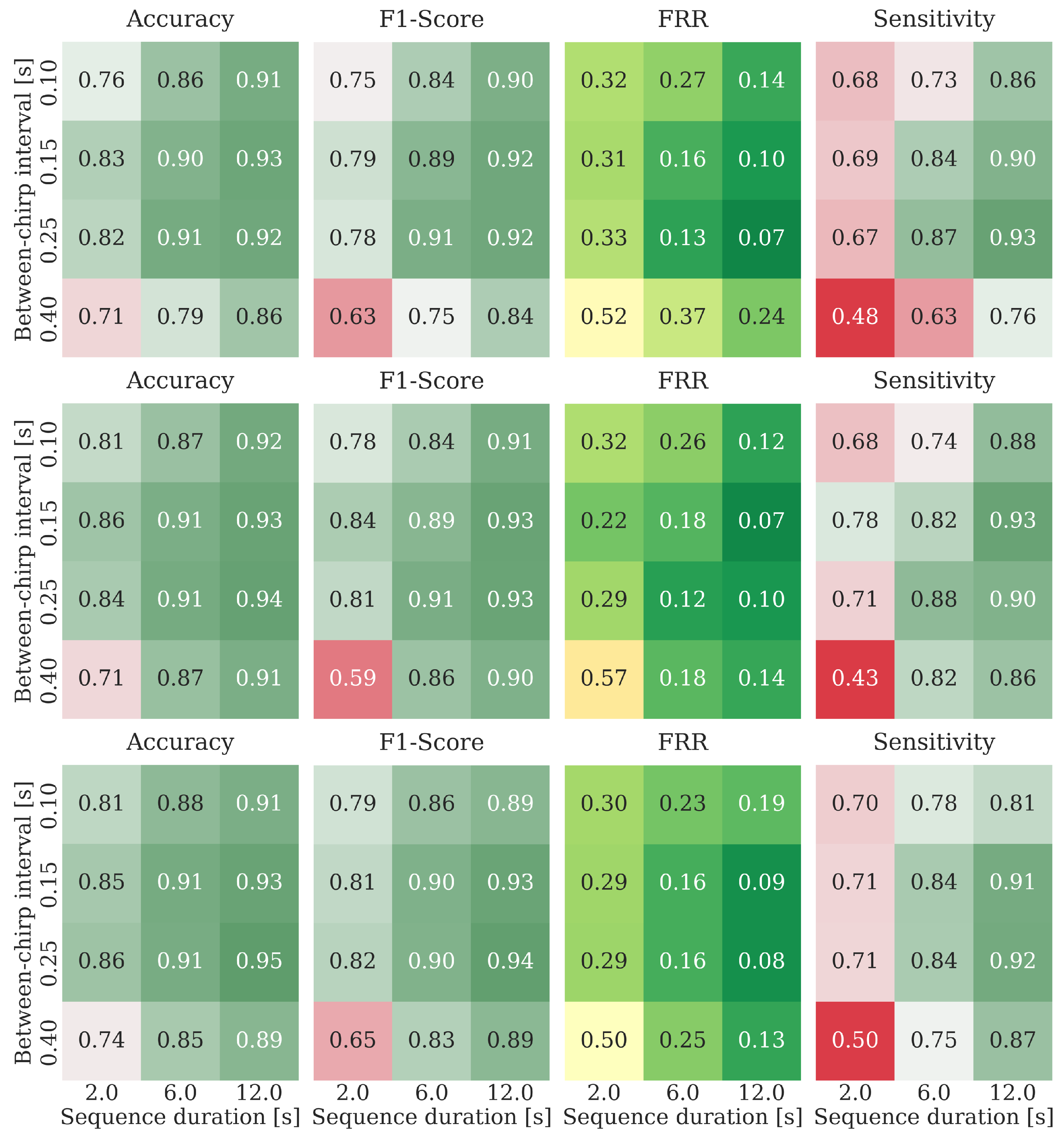
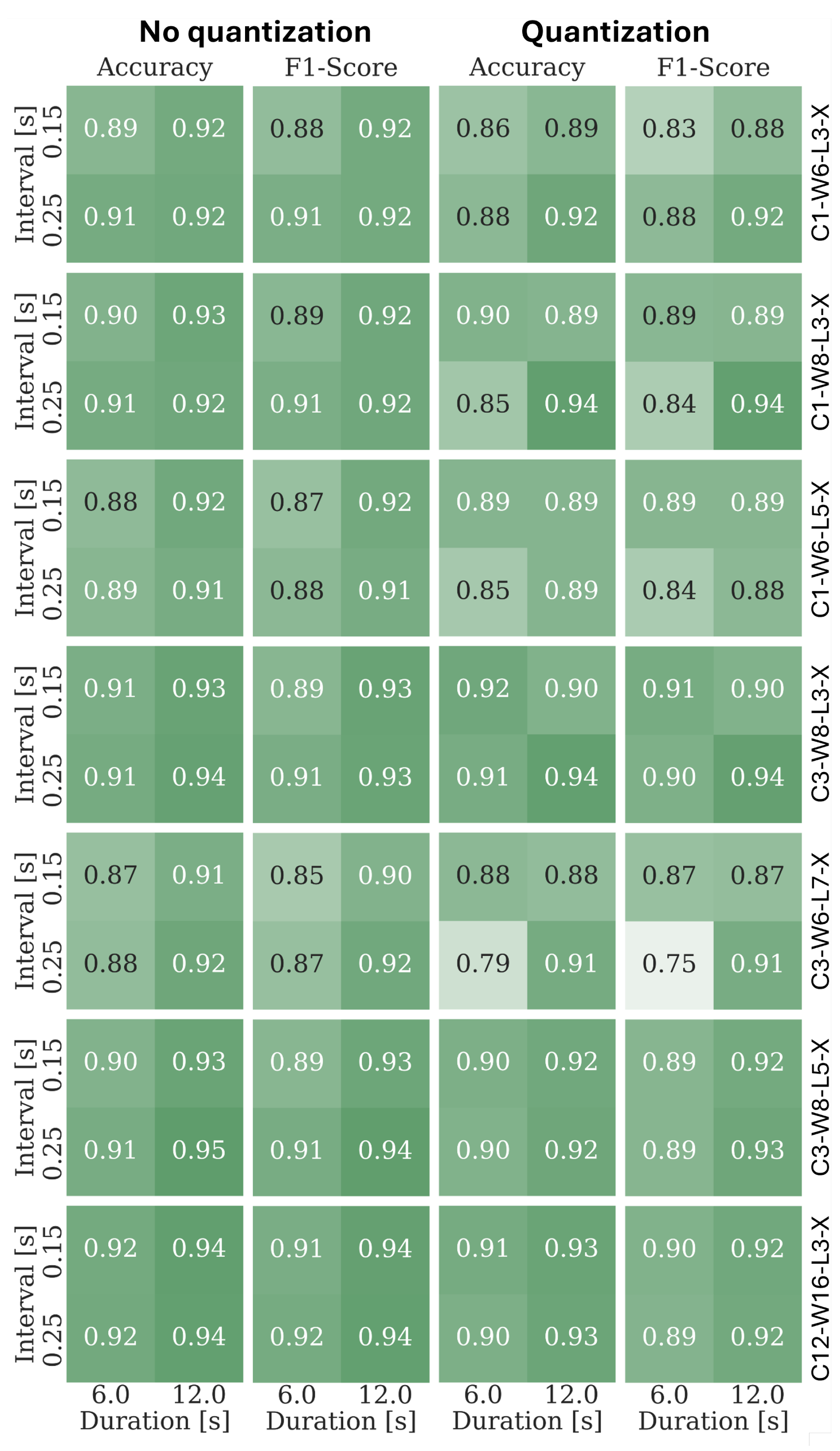
3.3. Vital Activity Detection Results
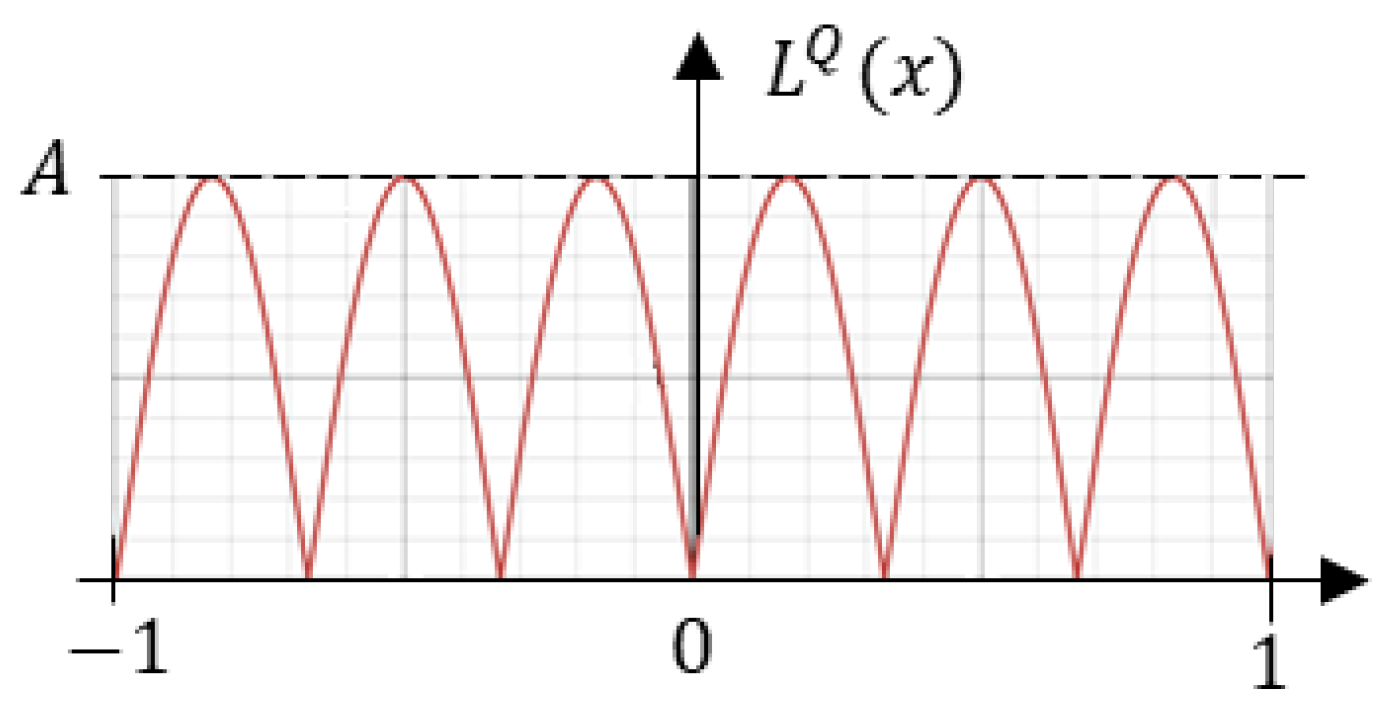
3.4. Parameter Quantization
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adib, F.; Mao, H.; Kabelac, Z.; Katabi, D.; Miller, R.C. Smart Homes that Monitor Breathing and Heart Rate. In Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems, CHI’ 15, New York, NY, USA, 13–17 August 2015. [Google Scholar] [CrossRef]
- Ślot, K.; Łuczak, P.; Hausman, S. Neuromorphic approach for breathing rate monitoring using data produced by FMCW radar. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e143552. [Google Scholar] [CrossRef]
- Rohman, B.P.A.; Nishimoto, M. Remote Human Respiration Detection Using Ultra-Wideband Impulse Radar Mounted on a Linearly Flying Platform. Prog. Electromagn. Res. M 2021, 99, 13–22. [Google Scholar] [CrossRef]
- Wang, S.; Pohl, A.; Jaeschke, T.; Czaplik, M.; Köny, M.; Leonhardt, S.; Pohl, N. A novel ultra-wideband 80 GHz FMCW radar system for contactless monitoring of vital signs. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015. [Google Scholar] [CrossRef]
- Lin, J. Microwave sensing of physiological movement and volume change: A review. Bioelectromagnetics 1992, 13, 557–565. [Google Scholar] [PubMed]
- Ahmad, A.; Roh, J.C.; Wang, D.; Dubey, A. Vital signs monitoring of multiple people using a FMCW millimeter-wave sensor. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018. [Google Scholar] [CrossRef]
- Hao, Z.; Gao, Y.; Tang, Y.; Wang, Y.; Fan, K.; Li, F. FMCW-based contactless heart rate monitoring. Sci. Rep. 2025, 15, 2616. [Google Scholar]
- Wang, F.; Zeng, X.; Wu, C.; Wang, B.; Liu, K.R. mmHRV: Contactless Heart Rate Variability Monitoring Using Millimeter-Wave Radio. IEEE Internet Things J. 2021, 8, 16623–16636. [Google Scholar] [CrossRef]
- Arsalan, M.; Santra, A.; Will, C. Improved Contactless Heartbeat Estimation in FMCW Radar via Kalman Filter Tracking. IEEE Sensors Lett. 2020, 4, 7001304. [Google Scholar] [CrossRef]
- Ahmed, S.; Park, J.; Cho, S.H. FMCW Radar Sensor Based Human Activity Recognition using Deep Learning. In Proceedings of the 2022 International Conference on Electronics, Information, and Communication (ICEIC), Jeju, Republic of Korea, 6–9 February 2022. [Google Scholar]
- Tschopp, S.; Borner, U.; Caversaccio, M.; Tschopp, K. Long-term night-to-night variability of sleep-disordered breathing using a radar-based home sleep apnea test: A prospective cohort study. J. Clin. Sleep Med. 2024, 20, 1079–1086. [Google Scholar]
- Li, F.; Guan, Y.; Ye, W. A Hardware and Software Co-Design for Energy-Efficient Neural Network Accelerator with Multiplication-Less Folded-Accumulative PE for Radar-Based Hand Gesture Recognition. IEEE Trans. Very Large Scale Integr. Syst. 2024, 32, 1964–1968. [Google Scholar] [CrossRef]
- Pereira-Rial, Ó.; García-Lesta, D.; Vaquero, L.; López, P.; Brea, V.; Cabello, D. Live Demonstration: 5-bit signed SRAM-based DNN CIM for Image Recognition. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024. [Google Scholar] [CrossRef]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Klauder, J.R.; Price, A.C.; Darlington, S.; Albersheim, W.J. The theory and design of chirp radars. Bell Syst. Tech. J. 1960, 39, 745–808. [Google Scholar] [CrossRef]
- Rao, S. Introduction to Mmwave Sensing: FMCW Radars; Technical Report; Texas Instruments: Dallas, TX, USA, 2017. [Google Scholar]
- Zhao, P.; Lu, C.X.; Wang, J.; Chen, C.; Wang, W.; Trigoni, N.; Markham, A. mID: Tracking and Identifying People with Millimeter Wave Radar. In Proceedings of the 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini Island, Greece, 29–31 May 2019. [Google Scholar]
- Kong, H.; Xu, X.; Yu, J.; Chen, Q.; Ma, C.; Chen, Y.; Chen, Y.C.; Kong, L. m3Track: mm wave-based multi-user 3D posture tracking. In Proceedings of the 20th Annual International Conference on Mobile Systems, Applications and Services, MobiSys’ 22, Portland, Oregon, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Nocera, A.; Senigagliesi, L.; Ciattaglia, G.; Gambi, E. Walking Pattern Identification of FMCW Radar Data based on a Combined CNN and bi-LSTM Approach. In Proceedings of the 2023 IEEE 36th International Symposium on Computer-Based Medical Systems (CBMS), L’Aquila, Italy, 22–24 June 2023. [Google Scholar] [CrossRef]
- Nocera, A.; Ciattaglia, G.; Raimondi, M.; Senigagliesi, L.; Gambi, E. Identification of Smartphone Zombies and Normal Pedestrians Using FMCW Radar and Machine Learning. In Proceedings of the 2024 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 6–8 January 2024. [Google Scholar] [CrossRef]
- Vogginger, B.; Kreutz, F.; López-Randulfe, J.; Liu, C.; Dietrich, R.; Gonzalez, H.A.; Scholz, D.; Reeb, N.; Auge, D.; Hille, J.; et al. Automotive Radar Processing with Spiking Neural Networks: Concepts and Challenges. Front Neurosci. 2022, 16, 851774. [Google Scholar] [CrossRef] [PubMed]
- Lien, J.; Gillian, N.; Karagozler, M.E.; Amihood, P.; Schwesig, C.; Olson, E.; Raja, H.; Poupyrev, I. Soli: Ubiquitous gesture sensing with millimeter wave radar. ACM Trans. Graph. 2016, 35, 142. [Google Scholar] [CrossRef]
- Dore, A.; Pasquaretta, C.; Henry, D.; Ricard, E.; Bompa, J.F.; Bonneau, M.; Boissy, A.; Hazard, D.; Lihoreau, M.; Aubert, H. A Non-Invasive Millimetre-Wave Radar Sensor for Automated Behavioural Tracking in Precision Farming—Application to Sheep Husbandry. Sensors 2021, 21, 8140. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Park, J.Y.; Choi, Y.W.; Park, H.K.; Cho, S.H.; Cho, S.H.; Lim, Y.H. A Novel Non-contact Heart Rate Monitor Using Impulse-Radio Ultra-Wideband (IR-UWB) Radar Technology. Sci. Rep. 2018, 8, 13053. [Google Scholar] [CrossRef]
- Kiuru, T.; Metso, M.; Jardak, S.; Pursula, P.; Hakli, J.; Hirvonen, M.; Sepponen, R. Movement and Respiration Detection Using Statistical Properties of the FMCW Radar Signal. In Proceedings of the 2016 Global Symposium on Millimeter Waves, GSMM 2016 and ESA Workshop on Millimetre-Wave Technology and Applications, Espoo, Finland, 6–8 June 2016. [Google Scholar] [CrossRef]
- Turppa, E.; Kortelainen, J.M.; Antropov, O.; Kiuru, T. Vital Sign Monitoring Using FMCW Radar in Various Sleeping Scenarios. Sensors 2020, 20, 6505. [Google Scholar] [CrossRef]
- Fu, S.; Ling, M.; Li, Z.; Pan, L. A new method for vital sign detection using FMCW radar based on random body motion cancellation. Biomed. Eng. Biomed. Tech. 2023, 68, 617–632. [Google Scholar] [CrossRef]
- Purnomo, A.T.; Lin, D.B.; Adiprabowo, T.; Hendria, W.F. Non-Contact Monitoring and Classification of Breathing Pattern for the Supervision of People Infected by COVID-19. Sensors 2021, 21, 3172. [Google Scholar] [CrossRef]
- Hsu, P.; Liu, G.; Fang, S.H.; Wu, H.C.; Yan, K. Novel Robust On-Line Indoor Occupancy Counting System Using mmWave Radar. IEEE Sens. J. 2023, 23, 12159–12170. [Google Scholar] [CrossRef]
- Mattos, A.B.R.C.D.; Brante, G.; Moritz, G.L.; Souza, R.D. Human and Small Animal Detection Using Multiple Millimeter-Wave Radars and Data Fusion: Enabling Safe Applications. Sensors 2024, 24, 1901. [Google Scholar] [CrossRef]
- Kahya, S.M.; Yavuz, M.S.; Steinbach, E. HOOD: Real-Time Human Presence and Out-of-Distribution Detection Using FMCW Radar. IEEE Trans. Radar Syst. 2025, 3, 44–56. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Qu, Y.; Zhang, S.; Xiao, W. mmRH: Noncontact Vital Sign Detection with an FMCW mm-Wave Radar. IEEE Sens. J. 2023, 23, 8856–8866. [Google Scholar] [CrossRef]
- Bazzi, A.; Bomfin, R.; Mezzavilla, M.; Rangan, S.; Rappaport, T.; Chafii, M. Upper Mid-Band Spectrum for 6G: Vision, Opportunity and Challenges. arXiv 2025, arXiv:2502.17914. [Google Scholar] [CrossRef]
- Guo, M.; Zhao, D.; Wu, Q.; Wu, J.; Li, D.; Zhang, P. An Integrated Real-Time FMCW Radar Baseband Processor in 40-nm CMOS. IEEE Access 2023, 11, 36041–36051. [Google Scholar] [CrossRef]
- Heo, J.; Jung, Y.; Lee, S.; Jung, Y. FPGA Implementation of an Efficient FFT Processor for FMCW Radar Signal Processing. Sensors 2021, 21, 6443. [Google Scholar] [CrossRef] [PubMed]
- Odame, K.; Nyamukuru, M.; Shahghasemi, M.; Bi, S.; Kotz, D. Analog Gated Recurrent Unit Neural Network for Detecting Chewing Events. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 1106–1115. [Google Scholar] [CrossRef]
- Haensch, W.; Gokmen, T.; Puri, R. The Next Generation of Deep Learning Hardware: Analog Computing. Proc. IEEE 2019, 107, 108–122. [Google Scholar] [CrossRef]
- Pan, C.H.; Hsieh, H.Y.; Tang, K.T. An Analog Multilayer Perceptron Neural Network for a Portable Electronic Nose. Sensors 2013, 13, 193. [Google Scholar] [CrossRef]
- Han, J.K.; Yun, S.Y.; Lee, S.W.; Yu, J.M.; Choi, Y.K. A Review of Artificial Spiking Neuron Devices for Neural Processing and Sensing. Adv. Funct. Mater. 2022, 32, 2204102. [Google Scholar] [CrossRef]
- Lee, J.; Cha, M.; Kwon, M.W. Capacitor-Less Low-Power Neuron Circuit with Multi-Gate Feedback Field Effect Transistor. Appl. Sci. 2023, 13, 2628. [Google Scholar] [CrossRef]
- Pereira-Rial, Ó.; García-Lesta, D.; Brea, V.; López, P.; Cabello, D. Design of a 5-Bit Signed SRAM-based In-Memory Computing Cell for Deep Learning Models. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 27 May–1 June 2022. [Google Scholar] [CrossRef]
- Odame, K.; Nyamukuru, M. Analog LSTM for Keyword Spotting. In Proceedings of the 2022 IEEE 4th International Conference on Artificial Intelligence Circuits and Systems (AICAS), Incheon, Republic of Korea, 13–15 June 2022. [Google Scholar] [CrossRef]
- Amoh, J.; Odame, K.M. An Optimized Recurrent Unit for Ultra-Low-Power Keyword Spotting. ACM J. 2019, 3, 1–17. [Google Scholar] [CrossRef]
- Hasler, J. Energy-Efficient Programable Analog Computing: Analog computing in a standard CMOS process. IEEE Solid-State Circuits Mag. 2024, 16, 32–40. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 37–45. [Google Scholar] [CrossRef]
- Hasler, J.; Basu, A. Historical perspective and opportunity for computing in memory using floating-gate and resistive non-volatile computing including neuromorphic computing. Neuromorphic Comput. Eng. 2025, 5, 012001. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]





| ‘Humans’ | ‘No Humans’ | |||
|---|---|---|---|---|
| Empty Space | Fan | Robotic Arm | ||
| No of recordings | 43 | 18 | 20 | 9 |
| Total duration [s] | 16,108 | 1310 | 6494 | 1590 |
| C1-W6-L3-X | C1-W8-L3-X | C1-W6-L5-X | C3-W8-L3-X | C3-W6-L7-X | C3-W8-L5-X | C12-W16-L3-X | |
|---|---|---|---|---|---|---|---|
| Parameters | 888 | 1362 | 1368 | 1410 | 1872 | 2226 | 4602 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ślot, K.; Łuczak, P.; Kapusta, P.; Hausman, S.; Rantala, A.; Flak, J. Very-Large-Scale Integration-Friendly Method for Vital Activity Detection with Frequency-Modulated Continuous Wave Radars. Sensors 2025, 25, 2151. https://doi.org/10.3390/s25072151
Ślot K, Łuczak P, Kapusta P, Hausman S, Rantala A, Flak J. Very-Large-Scale Integration-Friendly Method for Vital Activity Detection with Frequency-Modulated Continuous Wave Radars. Sensors. 2025; 25(7):2151. https://doi.org/10.3390/s25072151
Chicago/Turabian StyleŚlot, Krzysztof, Piotr Łuczak, Paweł Kapusta, Sławomir Hausman, Arto Rantala, and Jacek Flak. 2025. "Very-Large-Scale Integration-Friendly Method for Vital Activity Detection with Frequency-Modulated Continuous Wave Radars" Sensors 25, no. 7: 2151. https://doi.org/10.3390/s25072151
APA StyleŚlot, K., Łuczak, P., Kapusta, P., Hausman, S., Rantala, A., & Flak, J. (2025). Very-Large-Scale Integration-Friendly Method for Vital Activity Detection with Frequency-Modulated Continuous Wave Radars. Sensors, 25(7), 2151. https://doi.org/10.3390/s25072151






