An Enhanced, Real-Time, Low-Cost GNSS/INS Integrated Navigation Algorithm and Its Platform Design
Abstract
1. Introduction
2. Materials and Methods
2.1. Observation Equation with Position Constraints
2.2. Observation Equation with Position and Velocity Constraints
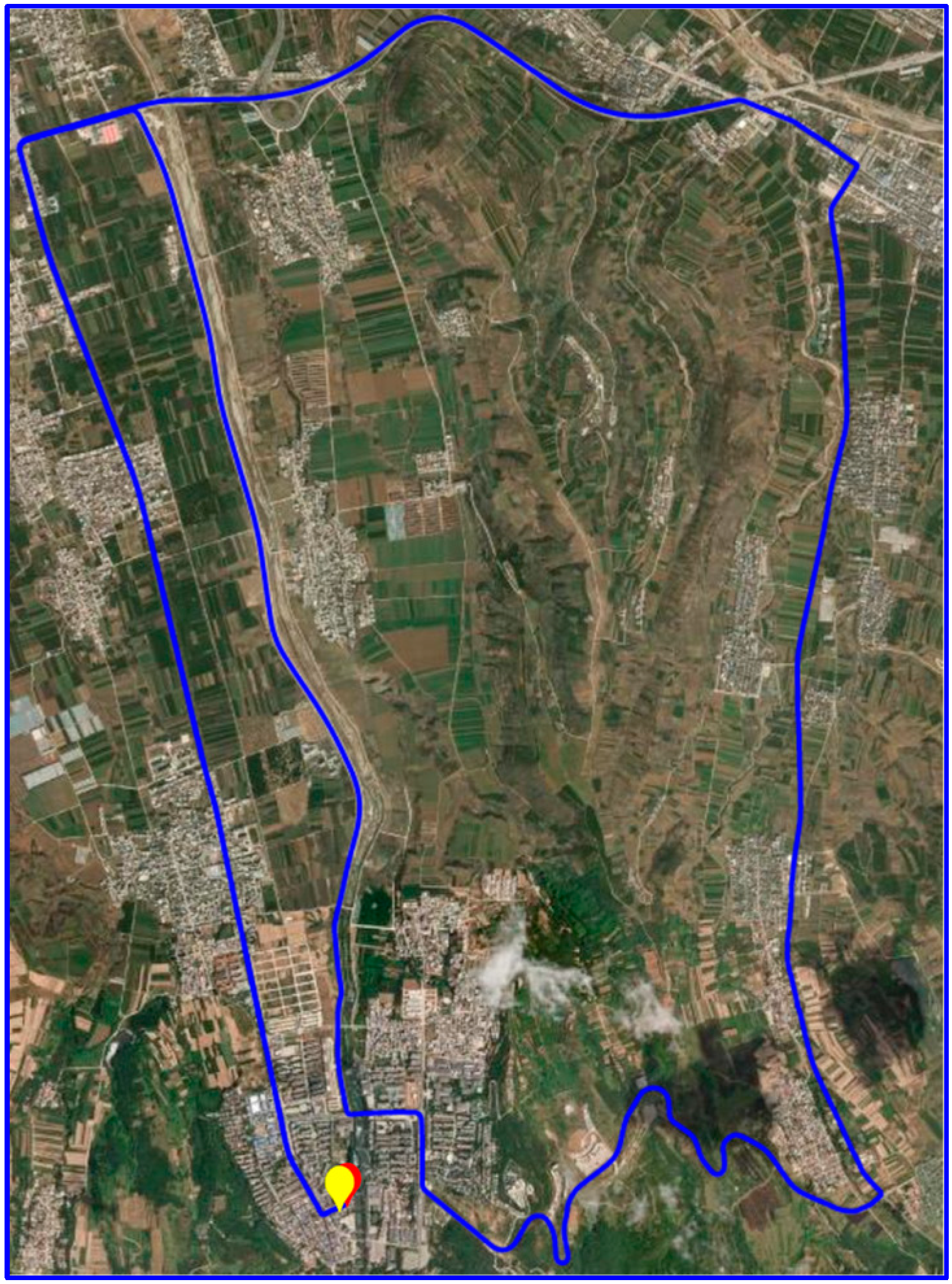
3. Experimental Setting and Data Collection
4. Results
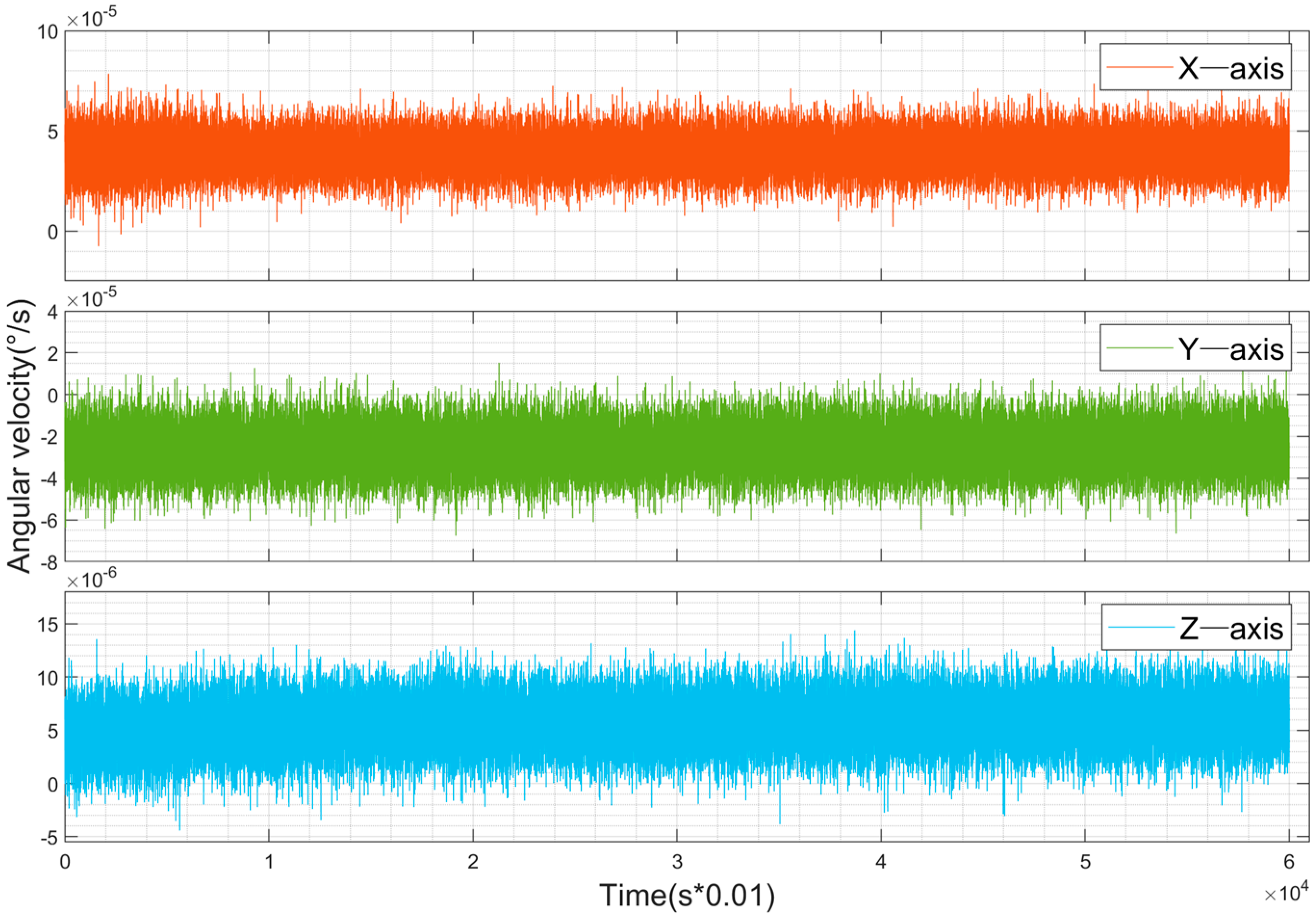
4.1. Error Compensation for Low-Cost IMUs
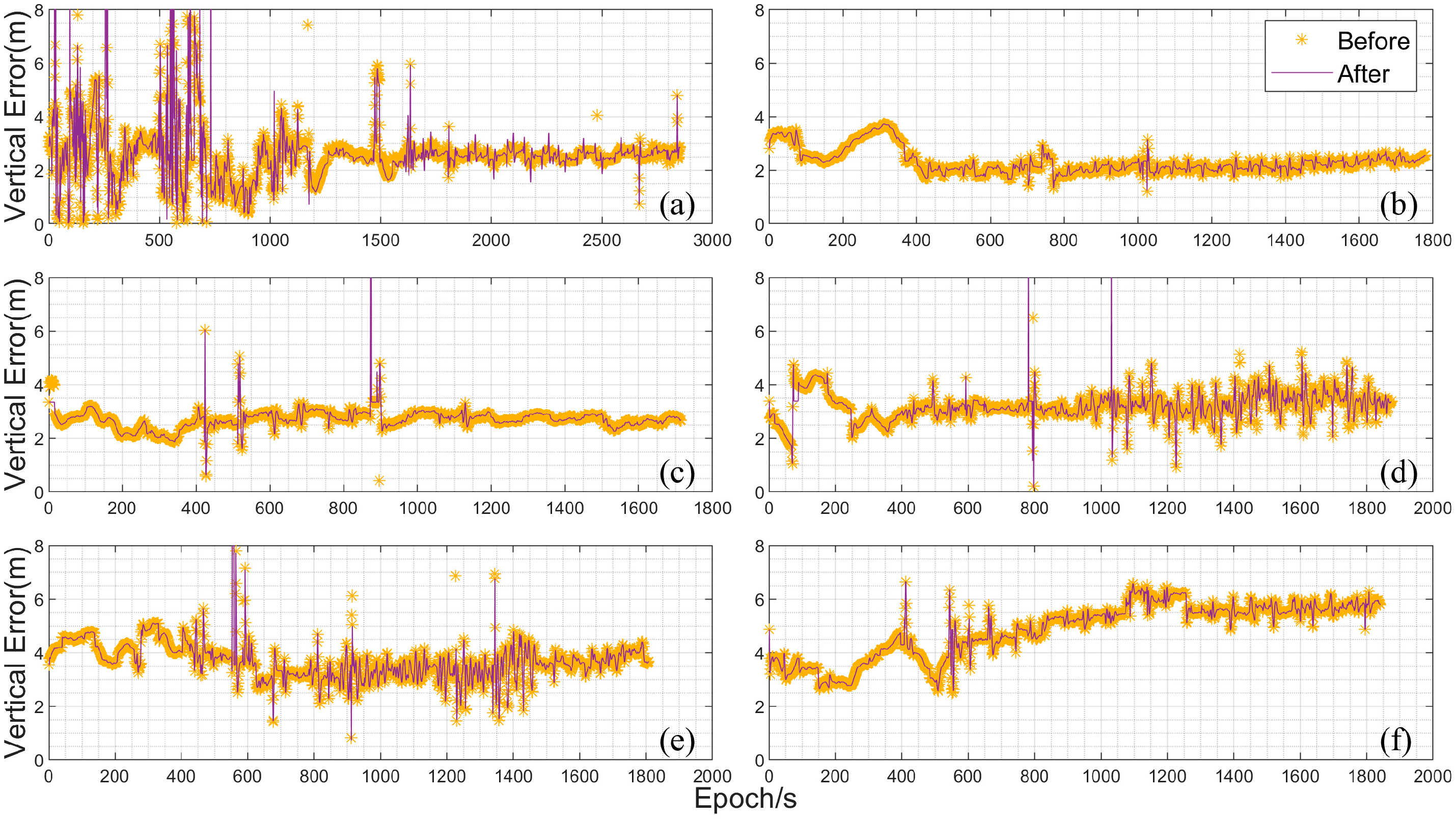
4.2. Ground Vehicle Experiment Analysis
4.3. UAV Onboard Experiment Analysis
5. Conclusions
- (1)
- The proposed algorithm platform is capable of real-time wireless transmission and processing of raw GNSS and IMU data. By integrating GNSS velocity information, it effectively mitigates the drift caused by low-cost inertial sensors, thereby improving the positioning accuracy of the integrated navigation system.
- (2)
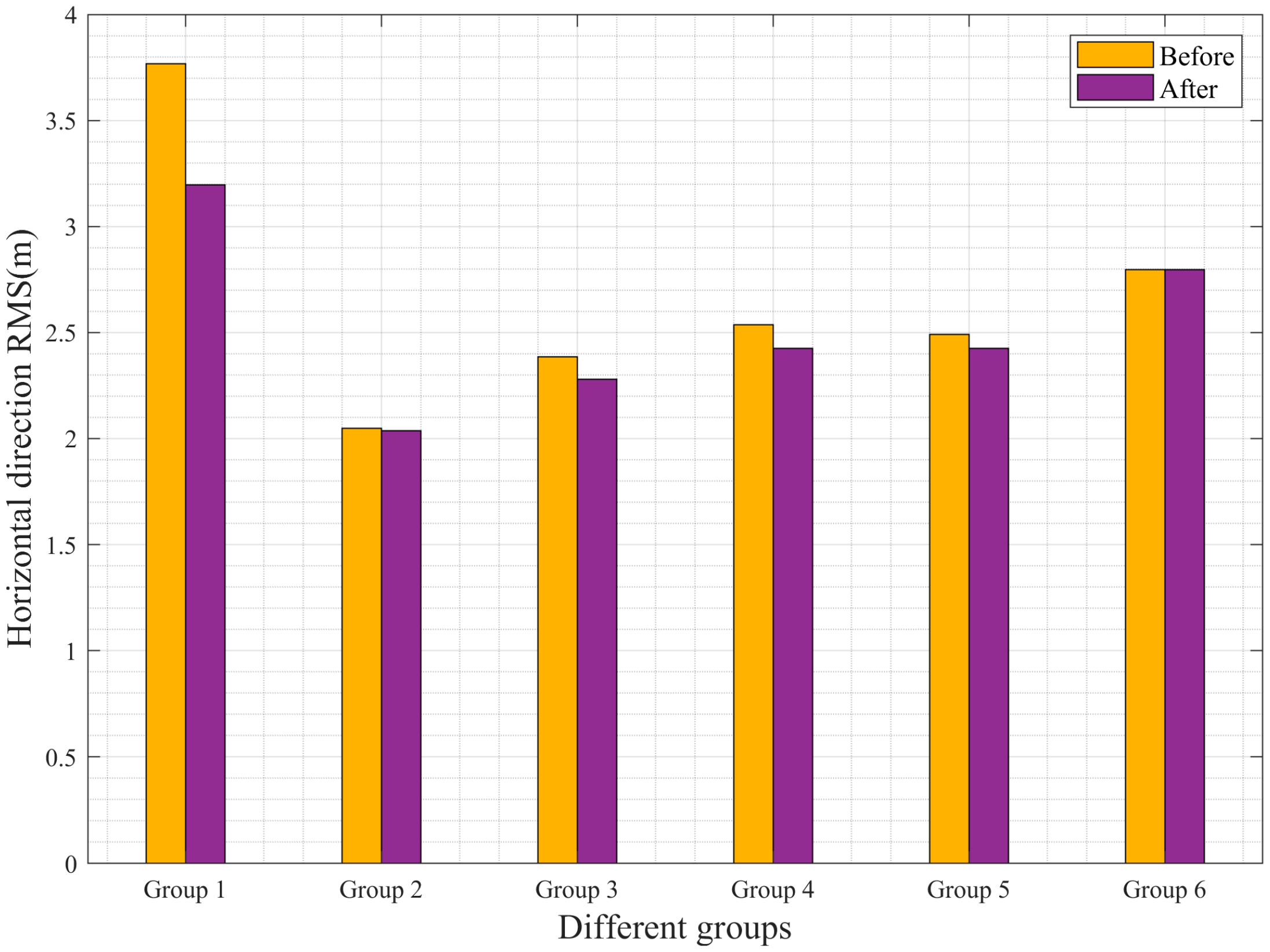
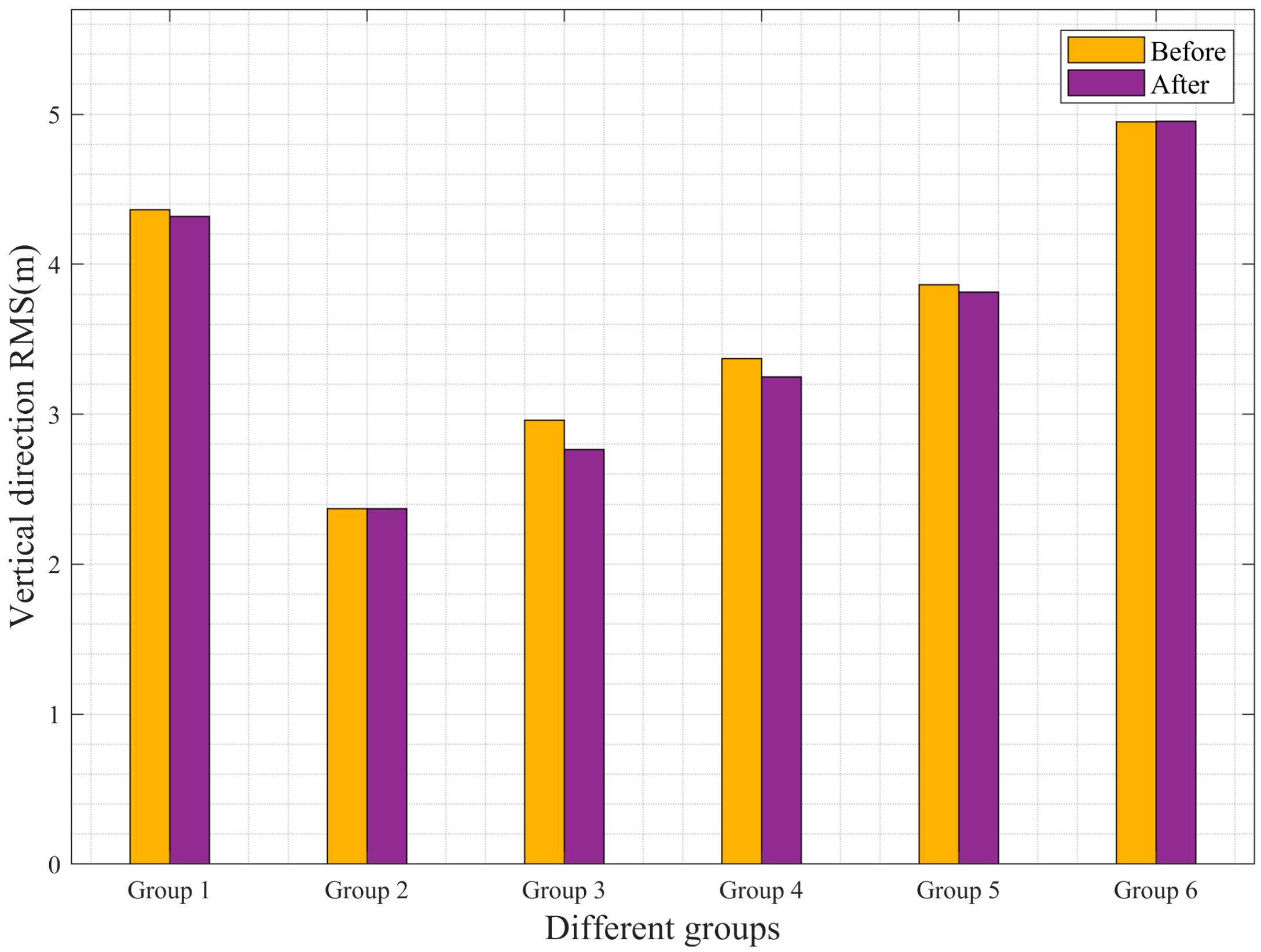
- The improved software demonstrates enhanced positioning accuracy in both the horizontal and vertical directions. In the UAV experiments, the RMSE in the horizontal direction was reduced by up to 58 cm, representing an improvement rate of 15.38%. In the vertical direction, the RMSE was reduced by a maximum of 20 cm, with an improvement rate of 6.76%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abd Rabbou, M.; El-Rabbany, A. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems. GPS Solut. 2015, 19, 601–609. [Google Scholar]
- Yue, Z.; Tang, C.; Gao, Y.A. Novel Three-Stage Robust Adaptive Filtering Algorithm for Visual-Inertial Odometry in GNSS-Denied Environments. IEEE Sens. J. 2023, 23, 17499–17509. [Google Scholar] [CrossRef]
- Yang, X. Unmanned visual localization based on satellite and image fusion. J. Phys. Conf. Ser. 2019, 1187, 042026. [Google Scholar] [CrossRef]
- Guo, H.; Chen, X.; Yu, M.; Uradziński, M.; Cheng, L. The usefulness of sensor fusion for unmanned aerial vehicle indoor positioning. Int. J. Intell. Unmanned Syst. 2023, 12, 1–18. [Google Scholar] [CrossRef]
- Lee, H.; Yoon, J.; Jang, M.-S.; Park, K.-J. A Robot Operating System Framework for Secure UAV Communications. Sensors 2021, 21, 1369. [Google Scholar] [CrossRef]
- Battiston, A.; Sharf, I.; Nahon, M. Attitude estimation for collision recovery of a quadcopter unmanned aerial vehicle. Int. J. Robot. Res. 2019, 38, 1286–1306. [Google Scholar] [CrossRef]
- Liu, R.; Greve, K.; Cui, P.; Jiang, N. Collaborative positioning method via GPS/INS and RS/MO multi-source data fusion in multi-target navigation. Surv. Rev. 2021, 54, 95–105. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Z. Research Status and Progress in MEMS Gyroscopes (Continued). Micronanoelectron. Technol. 2021, 58, 851–859, 934. [Google Scholar] [CrossRef]
- Chai, D. Study on the Theory and Method in Integrated Navigation of Multi-Constellation GNSS/INS. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2020. [Google Scholar] [CrossRef]
- Ma, L.; Guan, B. SINS/GPS integrated navigation system using an improved particle filter based on state reconstruction. J. Control Eng. Appl. Inform. 2011, 13, 58–64. [Google Scholar]
- Ni, S.; Li, S.; Xie, Y.; Deng, D. Overview of GNSS /INS ultra-tight integrated navigation. J. Natl. Univ. Def. Technol. 2023, 45, 48–59. [Google Scholar]
- Li, W.; Zhang, R.; Lei, H. Navigation Switching Strategy-Based SINS/GPS/ADS/DVL Fault-Tolerant Integrated Navigation System. J. Sens. 2021, 2021, 9943370. [Google Scholar]
- Gao, Z. Research on Algorithms and Applications of Multi-mode GNSS PPP/INS Integrated System. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Li, X.; Li, H.; Huang, G.; Zhang, Q.; Meng, S. Non-holonomic constraint (NHC)-assisted GNSS/SINS positioning using a vehicle motion state classification (VMSC)-based convolution neural network. GPS Solut. 2023, 27, 1–15. [Google Scholar] [CrossRef]
- Dai, H.-F.; Bian, H.-W.; Wang, R.-Y.; Ma, H. An INS/GNSS integrated navigation in GNSS denied environment using recurrent neural network. Def. Technol. 2020, 16, 334–340. [Google Scholar] [CrossRef]
- Shi, B.; Wang, M.; Wang, Y.; Bai, Y.; Lin, K.; Yang, F. Effect Analysis of GNSS/INS Processing Strategy for Sufficient Utilization of Urban Environment Observations. Sensors 2021, 21, 620. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Chang, G. Low-cost GNSS/INS integration for enhanced land vehicle performance. Meas. Sci. Technol. 2019, 31, 035009. [Google Scholar] [CrossRef]
- Ding, W.; Sun, W.; Yan, H.; Li, W.; Jiang, Y.; Gao, Y. Low-cost dual-antenna GNSS-based heading and pitch angles estimation considering baseline length constraint. Measurement 2024, 239, 115492. [Google Scholar] [CrossRef]
- Vanek, B.; Farkas, M.; Rózsa, S. Position and Attitude Determination in Urban Canyon with Tightly Coupled Sensor Fusion and a Prediction-Based GNSS Cycle Slip Detection Using Low-Cost Instruments. Sensors 2023, 23, 2141. [Google Scholar] [CrossRef]
- Chen, K.; Chang, G.; Chen, C. GINav: A MATLAB-based software for the data processing and analysis of a GNSS/INS integrated navigation system. GPS Solut. 2021, 25, 108. [Google Scholar] [CrossRef]
- Zhang, Q.; Niu, X.; Gong, L.; Zhang, H.; Shi, C.; Liu, C.; Wang, J.; Coleman, M. Development and Evaluation of GNSS/INS Data Processing Software; China Satellite Navigation Conference (CSNC); Springer: Berlin/Heidelberg, Germany, 2013; pp. 685–696. [Google Scholar]
- Niu, X.; Zhang, Q.; Gong, L.; Liu, C.; Zhang, H.; Shi, C.; Wang, J.; Coleman, M. Development and evaluation of GNSS/INS data processing software for position and orientation systems. Surv. Rev. 2015, 47, 87–98. [Google Scholar] [CrossRef]
- Gyagenda, N.; Hatilima, J.V.; Roth, H.; Zhmud, V. A review of GNSS-independent UAV navigation techniques. Robot. Auton. Syst. 2022, 152, 104069. [Google Scholar] [CrossRef]
- Chi, C.; Zhan, X.; Wang, S.; Zhai, Y. Enabling robust and accurate navigation for UAVs using real-time GNSS precise point positioning and IMU integration. Aeronaut. J. 2020, 125, 87–108. [Google Scholar] [CrossRef]
- Solomon, P.D.; Wang, J.; Rizos, C. Latency determination and compensation in real-time GNSS/INS integrated navigation systems. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 303–307. [Google Scholar] [CrossRef]
- Wu, H. Research on the Key Technology of Integrated Navigation for Multi-Rotor UAV Based on Low-Cost Inertial/GNSS/Vision. Ph.D. Thesis, University of Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences), Beijing, China, 2020. [Google Scholar] [CrossRef]
- Yan, G.; Weng, J. Principles Handout on Strapdown Inertial Navigation and Integrated Navigation; Northwestern Polytechnical University Press: Xi’an, China, 2019. [Google Scholar]




| Device | M22 | |
|---|---|---|
| gyroscope | Range (°/s) | ±300 (XY)/±460 (Z) |
| Bias stability (°/h) | 5 | |
| accelerometer | Range (g) | ±16 |
| Bias stability (µg) | 50 | |
| GNSS receivers | System and frequency | BDS: B1I/B2I/B3I/B2a GPS: L1/L2/L5 GALILEO: E1/E5a/E5b GLONASS: L1/L2 |
| Price (yuan) | ¥8000 | |
| Data | Bias (m) | |||
|---|---|---|---|---|
| Horizontal Direction | Vertical Direction | |||
| Before | After | Before | After | |
| Group 1 | 2.98 | 2.82 | 2.38 | 2.37 |
| Group 2 | 1.94 | 1.93 | 2.32 | 2.32 |
| Group 3 | 2.27 | 2.23 | 2.74 | 2.71 |
| Group 4 | 2.39 | 2.32 | 3.23 | 3.20 |
| Group 5 | 2.23 | 2.19 | 3.61 | 3.60 |
| Group 6 | 2.68 | 2.68 | 4.85 | 4.85 |
| Data | RMSE (m) | |||
|---|---|---|---|---|
| Horizontal Direction | Vertical Direction | |||
| Before | After | Before | After | |
| Group 1 | 3.77 | 3.19 | 4.37 | 4.32 |
| Group 2 | 2.05 | 2.03 | 2.37 | 2.36 |
| Group 3 | 2.39 | 2.27 | 2.96 | 2.76 |
| Group 4 | 2.54 | 2.43 | 3.37 | 3.24 |
| Group 5 | 2.49 | 2.42 | 3.87 | 3.81 |
| Group 6 | 2.80 | 2.79 | 4.95 | 4.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Gao, Y.; Zhao, Q.; Wang, Y.; Zhou, F.; Zhang, D. An Enhanced, Real-Time, Low-Cost GNSS/INS Integrated Navigation Algorithm and Its Platform Design. Sensors 2025, 25, 2119. https://doi.org/10.3390/s25072119
Wang P, Gao Y, Zhao Q, Wang Y, Zhou F, Zhang D. An Enhanced, Real-Time, Low-Cost GNSS/INS Integrated Navigation Algorithm and Its Platform Design. Sensors. 2025; 25(7):2119. https://doi.org/10.3390/s25072119
Chicago/Turabian StyleWang, Pengcheng, Yuting Gao, Qingzhi Zhao, Yalong Wang, Feng Zhou, and Dengxiong Zhang. 2025. "An Enhanced, Real-Time, Low-Cost GNSS/INS Integrated Navigation Algorithm and Its Platform Design" Sensors 25, no. 7: 2119. https://doi.org/10.3390/s25072119
APA StyleWang, P., Gao, Y., Zhao, Q., Wang, Y., Zhou, F., & Zhang, D. (2025). An Enhanced, Real-Time, Low-Cost GNSS/INS Integrated Navigation Algorithm and Its Platform Design. Sensors, 25(7), 2119. https://doi.org/10.3390/s25072119








