LSEWOA: An Enhanced Whale Optimization Algorithm with Multi-Strategy for Numerical and Engineering Design Optimization Problems
Abstract
1. Introduction
| Algorithm | Year | Author | Source of Inspiration |
|---|---|---|---|
| COGWO2D [19] | 2018 | Ibrahim R A et al. | Opposition-Based Learning, Differential Evolution, and disruption operator. |
| MEGWO [20] | 2019 | Tu Q et al. | Adaptable cooperative strategy and disperse foraging strategy. |
| QMPA [21] | 2021 | Abd Elaziz M et al. | Schrodinger wave function. |
| ISSA [22] | 2023 | Xue Z et al. | Circle chaotic mapping, GWO and chaotic sine cosine mechanism |
| ACRIME [23] | 2024 | Abdel-Salam M et al. | Symbiotic Organism Search (SOS) and restart strategy |
| BWOA [24] | 2019 | H Chen et al. | Levy flight and chaotic local search. |
| SMWOA [25] | 2020 | W Guo et al. | Linear incremental probability, social learning principle and Morlet wavelet mutation |
| HSWOA [26] | 2021 | VKRA Kalanandan et al. | Social Group Optimization algorithm (SGO) |
| ImWOA [27] | 2022 | S Chakraborty et al. | Cooperative hunting strategy and improving the exploration-exploitation logic |
2. Development History and Current Research of Engineering Design
3. Organization of the Paper
4. Major Contributions
5. WOA
5.1. Encircling Prey
5.2. Bubble-Net Attacking Method
5.2.1. Shrinking Encircling
5.2.2. Spiral Updating
5.3. Searching for Prey
5.4. Population Initialization
5.5. Pseudo-Code of WOA
| Algorithm 1 WOA |
|
5.6. Advantages and Disadvantages of WOA
6. LSEWOA
6.1. Good Nodes Set Initialization
6.2. Leader-Followers Search-for-Prey Strategy
6.3. Spiral-Based Encircling Prey Strategy
6.4. Enhanced Spiral Updating Strategy
6.4.1. Inertia Weight
6.4.2. Tangent Flight
6.5. Calculation of Enhanced Spiral Updating Strategy
6.6. Redesigned Convergence Factor a
6.7. Pseudo-Code of LSEWOA
| Algorithm 2 LSEWOA |
|
6.8. Time Complexity Analysis
6.8.1. Time Complexity of WOA
6.8.2. Time Complexity of LSEWOA
7. Experiments
- A parameter sensitivity analysis experiment was performed on different LSEWOAs with various and , aiming at choosing the perfect option of and for parameter a and inertia weight respectively to better balance exploration and exploitation.
- A qualitative analysis experiment was performed by applying LSEWOA on the 23 benchmark functions to comprehensively evaluate the performance, robustness and exploration-exploitation balance of LSEWOA in different types of problems, by assessing search behavior, exploration-exploitation capability and population diversity.
- An ablation study was performed by removing each of the five improvement strategies from LSEWOA and testing on 23 benchmark functions.
- LSEWOA was tested against five excellent WOA variants on the benchmark functions.
- LSEWOA was compared with the canonical WOA and several state-of-the-art algorithms on the benchmark functions.
7.1. Parameter Sensitivity Analysis Experiment
7.2. Ablation Study
- LSEWOA1: We replaced the Good Nodes Set Initialization with pseudo-random number initialization in LSEWOA, which is referred to as LSEWOA1;
- LSEWOA2: We replaced the Leader-Followers Search-for-Prey Strategy with the original WOA’s Search-for-prey strategy, referred to as LSEWOA2;
- LSEWOA3: We replaced the Spiral-based Encircling Prey Strategy with the original WOA’s encircling prey strategy, referred to as LSEWOA3;
- LSEWOA4: We replaced the Enhanced Spiral Updating Strategy with the original WOA’s spiral updating mechanism, referred to as LSEWOA4;
- LSEWOA5: We replaced the proposed update mechanism of parameter a with the one in classical WOA, referred to as LSEWOA5.
7.3. Qualitative Analysis Experiment
- the landscape of benchmark functions;
- the search history of the whale population;
- the exploration-exploitation ratio;
- the changes in population diversity;
- the iteration curves.
7.4. Comparative Experiment with State-of-the-Art WOA Variants
- WOAV1: The WOA variant (eWOA) that introduces adaptive parameter adjustment, multi-strategy search mechanisms, and elite retention strategies is referred to as WOAV1 [32];
- WOAV2: The WOA variant (NHWOA) that incorporates multiple subpopulations, dynamically adjusted control parameters, adaptive position update mechanisms, and Levy flight perturbations is referred to as WOAV2 [33];
- WOAV3: The WOA variant (MSWOA) that introduces adaptive weights, dynamic convergence factors, and Levy flight is referred to as WOAV3 [34];
- WOAV4: The WOA variant (MWOA) that uses an iteration-based cosine function and exponential decay adjustment for parameters, hybrid mutation strategies, Levy flight, and hybrid update mechanisms is referred to as WOAV4 [35];
- WOAV5: The WOA variant (WOA_LFDE) that introduces Levy flight and Differential Evolution strategies is referred to as WOAV5 [36].
7.4.1. Parametric Analysis
7.4.2. Non-Parametric Wilcoxon Rank-Sum Test
7.4.3. Non-Parametric Friedman Test
7.5. Scalability Experiment of LSWOA
Overall Effectiveness of LSEWOA
7.6. Comparative Experiment with State-of-the-Art Metaheuristic Algorithms in 30 Dimension
7.7. Comparative Experiment with State-of-the-Art Metaheuristic Algorithms in Higher Dimensions
8. Engineering Optimization
8.1. Three-Bar Truss
8.2. Tension/Compression Spring
8.3. Speed Reducer
8.4. Cantilever Beam
8.5. I-Beam
8.6. Piston Lever
8.7. Multi-Disc Clutch Brake
8.8. Gas Transmission System
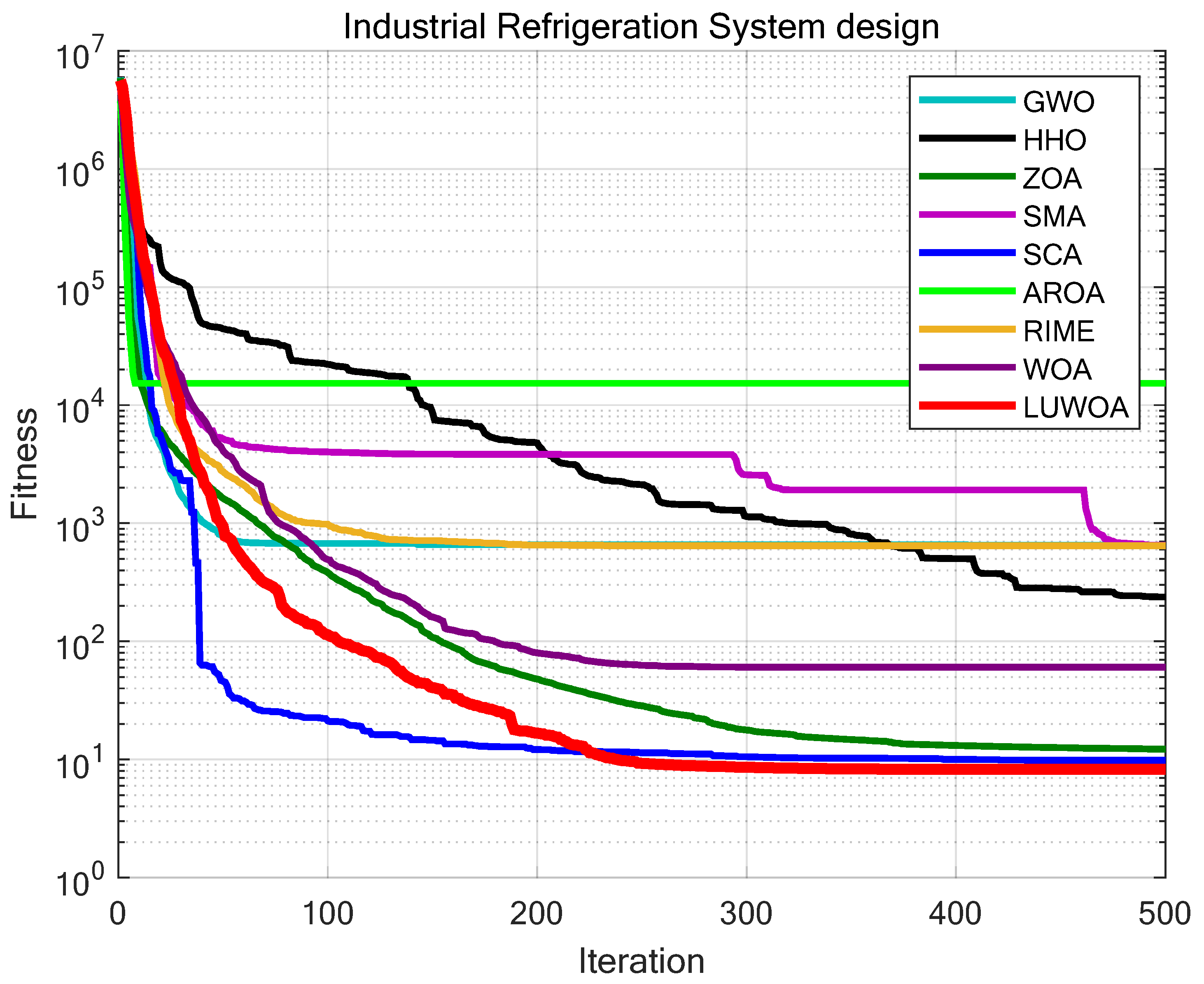
8.9. Industrial Refrigeration System
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ave | Average fitness |
| Std | Standard deviation |
| OE | overall effectiveness |
Appendix A
| Function | Function’s Name | Best Value |
|---|---|---|
| Sphere | 0 | |
| Schwefel’s Problem 2.22 | 0 | |
| Schwefel’s Problem 1.2 | 0 | |
| Schwefel’s Problem 2.21 | 0 | |
| Generalized Rosenbrock’s Function | 0 | |
| Step Function | 0 | |
| Quartic Function | 0 | |
| Generalized Schwefel’s Function | −12,569.5 | |
| Generalized Rastrigin’s Function | 0 | |
| Ackley’s Function | 0 | |
| Generalized Griewank’s Function | 0 | |
| Generalized Penalized Function 1 | 0 | |
| Generalized Penalized Function 2 | 0 | |
| Shekel’s Foxholes Function | 0.998 | |
| Kowalik’s Function | 0.0003075 | |
| Six-Hump Camel-Back Function | −1.0316 | |
| Branin Function | 0.398 | |
| Goldstein-Price Function | 3 | |
| Hartman’s Function 1 | −3.8628 | |
| Hartman’s Function 2 | −3.32 | |
| Shekel’s Function 1 | −10.1532 | |
| Shekel’s Function 1 | −10.1532 | |
| Shekel’s Function 2 | −10.4029 | |
| Shekel’s Function 1 | −10.1532 | |
| Shekel’s Function 3 | −10.5364 |
References
- Laarhoven, P.J.M.V.; Aarts, E.H.L. Simulated Annealing; Springer: Eindhoven, The Netherlands, 1987. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27–31 March 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Cai, J.; Wan, H.; Sun, Y.; Qin, T. Artificial bee colony algorithm-based self-optimization of base station antenna azimuth and down-tilt angle. Telecommun. Sci. 2021, 37, 69–75. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Jia, H.; Rao, H.; Wen, C.; Mirjalili, S. Crayfish optimization algorithm. Artif. Intell. Rev. 2023, 56 (Suppl. S2), 1919–1979. [Google Scholar] [CrossRef]
- Hvolby, H.H.; Steger-Jensen, K. Technical and industrial issues of Advanced Planning and Scheduling (APS) systems. Comput. Ind. 2010, 61, 845–851. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Abualigah, L. An improved moth-flame optimization algorithm with adaptation mechanism to solve numerical and mechanical engineering problems. Entropy 2021, 23, 1637. [Google Scholar] [CrossRef]
- Kabir, M.M.; Shahjahan, M.; Murase, K. A new hybrid ant colony optimization algorithm for feature selection. Expert Syst. Appl. 2012, 39, 3747–3763. [Google Scholar] [CrossRef]
- Masoomi, Z.; Mesgari, M.S.; Hamrah, M. Allocation of urban land uses by Multi-Objective Particle Swarm Optimization algorithm. Int. J. Geogr. Inf. Sci. 2013, 27, 542–566. [Google Scholar] [CrossRef]
- Wei, J.; Gu, Y.; Law, K.L.E.; Zhang, X.; Li, Z.; Wang, Q.; Liu, Y.; Chen, P.; Zhang, L.; Wang, R.; et al. Adaptive Position Updating Particle Swarm Optimization for UAV Path Planning. In Proceedings of the 2024 22nd International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Athens, Greece, 14–17 May 2024; pp. 124–131. [Google Scholar]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, Q.X. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Feda, A.K.; Ishaya, M.M.; Agyekum, E.B.; Kim, K.-C.; Mbasso, W.F.; Kamel, S. Antenna S-parameter optimization based on golden sine mechanism based honey badger algorithm with tent chaos. Heliyon 2023, 9, e13087. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Abd Elaziz, M.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Tu, Q.; Chen, X.; Liu, X. Multi-strategy ensemble grey wolf optimizer and its application to feature selection. Appl. Soft Comput. 2019, 76, 16–30. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Mohammadi, D.; Oliva, D.; Gandomi, A.H.; Al-qaness, M.A.A.; Ewees, A.A. Quantum marine predators algorithm for addressing multilevel image segmentation. Appl. Soft Comput. 2021, 110, 107598. [Google Scholar] [CrossRef]
- Xue, Z.; Yu, J.; Zhao, A.; Zong, Y.; Yang, S.; Wang, M. Optimal chiller loading by improved sparrow search algorithm for saving energy consumption. J. Build. Eng. 2023, 67, 105980. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Hu, G.; Çelik, E.; Gharehchopogh, F.S.; El-Hasnony, I.M. Chaotic RIME optimization algorithm with adaptive mutualism for feature selection problems. Comput Biol Med. 2024, 179, 108803. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Xu, Y.; Wang, M.; Zhao, X. A Balanced Whale Optimization Algorithm for Constrained Engineering Design Problems. Appl. Math. Model. 2019, 71, 45–59. [Google Scholar] [CrossRef]
- Guo, W.; Liu, T.; Dai, F.; Xu, P. An improved whale optimization algorithm for forecasting water resources demand. Appl. Soft Comput. 2020, 86, 105925. [Google Scholar] [CrossRef]
- Kalananda, V.K.R.A.; Komanapalli, V.L.N. A combinatorial social group whale optimization algorithm for numerical and engineering optimization problems. Appl. Soft Comput. 2021, 99, 106903. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sharma, S.; Saha, A.K.; Saha, A. A novel improved whale optimization algorithm to solve numerical optimization and real-world applications. Artif. Intell. Rev. 2022, 55, 4605–4716. [Google Scholar] [CrossRef]
- Xiao, C.; Cai, Z.; Wang, Y. A good nodes set evolution strategy for constrained optimization. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 943–950. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Layeb, A. Tangent search algorithm for solving optimization problems. Neural Comput. Appl. 2022, 34, 8853–8884. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.-P.; Auger, A.; Tiwari, S. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. Kangal Rep. 2005, 2005, 2005005. [Google Scholar]
- Chakraborty, S.; Saha, A.K.; Chakraborty, R.; Saha, S. An enhanced whale optimization algorithm for large scale optimization problems. Knowl.-Based Syst. 2021, 233, 107543. [Google Scholar] [CrossRef]
- Lin, X.; Yu, X.; Li, W. A heuristic whale optimization algorithm with niching strategy for global multi-dimensional engineering optimization. Comput. Ind. Eng. 2022, 171, 108361. [Google Scholar] [CrossRef]
- Yang, W.; Xia, K.; Fan, S.; Wang, L.; Li, T.; Zhang, J.; Feng, Y. A Multi-Strategy Whale Optimization Algorithm and Its Application. Eng. Appl. Artif. Intell. 2022, 108, 104558. [Google Scholar] [CrossRef]
- Anitha, J.; Pian, S.I.A.; Agnes, S.A. An efficient multilevel color image thresholding based on modified whale optimization algorithm. Expert Syst. Appl. 2021, 178, 115003. [Google Scholar] [CrossRef]
- Liu, M.; Yao, X.; Li, Y. Hybrid whale optimization algorithm enhanced with Lévy flight and differential evolution for job shop scheduling problems. Appl. Soft Comput. 2020, 87, 105954. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Faris, H. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020, 97, 106761. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Cymerys, K.; Oszust, M. Attraction-Repulsion Optimization Algorithm for Global Optimization Problems. Swarm Evol. Comput. 2024, 84, 101459. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Yildiz, B.S.; Pholdee, N.; Bureerat, S.; Yildiz, A.R.; Sait, S.M. Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems. Eng. Comput. 2022, 38, 4207–4219. [Google Scholar] [CrossRef]































| Algorithm | Year | Author | Source of Inspiration |
|---|---|---|---|
| Simulated annealing (SA) [1] | 1953 | Metropolis et al. | The annealing process. |
| Genetic Algorithm (GA) [2] | 1975 | John Holland et al. | Darwin’s theory of evolution and Mendel’s genetic. |
| Ant Colony Optimization (ACO) [3] | 1991 | Dorigo et al. | Foraging behavior of ants. |
| Particle Swarm Optimization (PSO) [4] | 1995 | Kennedy et al. | Foraging behavior of birds. |
| Differential Evolution (DE) [5] | 1997 | Rainer Storn et al. | Mutation, crossover and selection. |
| Artificial Bee Colony (ABC) [6] | 2005 | Karaboga et al. | Honeybee’s foraging behavior. |
| Harris Hawks Optimization (HHO) [7] | 2019 | Elhamifar et al. | Hunting behavior of Harris hawks. |
| Aquila Optimizer (AO) [8] | 2021 | Laith Abualigah et al. | Hunting behavior of aquila eagles. |
| Beluga Whale Optimization (BWO) [9] | 2022 | C Zhong et al. | Swimming, foraging and whale fall phenomena of beluga white whales. |
| Crayfish Optimization (COA) [10] | 2023 | H Jia et al. | foraging, cooling and competitive behaviors of crayfish. |
| Function | Function’s Name | Type | Dimension (Dim) | Best Value |
|---|---|---|---|---|
| F1 | Sphere | Uni-modal, Scalable | 30/50/100 | 0 |
| F2 | Schwefel’s Problem 2.22 | Uni-modal, Scalable | 30/50/100 | 0 |
| F3 | Schwefel’s Problem 1.2 | Uni-modal, Scalable | 30/50/100 | 0 |
| F4 | Schwefel’s Problem 2.21 | Uni-modal, Scalable | 30/50/100 | 0 |
| F5 | Generalized Rosenbrock’s Function | Uni-modal, Scalable | 30/50/100 | 0 |
| F6 | Step Function | Uni-modal, Scalable | 30/50/100 | 0 |
| F7 | Quartic Function | Uni-modal, Scalable | 30/50/100 | 0 |
| F8 | Generalized Schwefel’s Function | Multi-modal, Scalable | 30/50/100 | −418.98·Dim |
| F9 | Generalized Rastrigin’s Function | Multi-modal, Scalable | 30/50/100 | 0 |
| F10 | Ackley’s Function | Multi-modal, Scalable | 30/50/100 | 0 |
| F11 | Generalized Griewank’s Function | Multi-modal, Scalable | 30/50/100 | 0 |
| F12 | Generalized Penalized Function 1 | Multi-modal, Scalable | 30/50/100 | 0 |
| F13 | Generalized Penalized Function 2 | Multi-modal, Scalable | 30/50/100 | 0 |
| F14 | Shekel’s Foxholes Function | Multi-modal, Unscalable | 2 | 0.998 |
| F15 | Kowalik’s Function | Composition, Unscalable | 4 | 0.0003075 |
| F16 | Six-Hump Camel-Back Function | Composition, Unscalable | 2 | −1.0316 |
| F17 | Branin Function | Composition, Unscalable | 2 | 0.398 |
| F18 | Goldstein-Price Function | Composition, Unscalable | 2 | 3 |
| F19 | Hartman’s Function 1 | Composition, Unscalable | 3 | −3.8628 |
| F20 | Hartman’s Function 2 | Composition, Unscalable | 6 | −3.32 |
| F21 | Shekel’s Function 1 | Composition, Unscalable | 4 | −10.1532 |
| F22 | Shekel’s Function 2 | Composition, Unscalable | 4 | −10.4029 |
| F23 | Shekel’s Function 3 | Composition, Unscalable | 4 | −10.5364 |
| Function | LSEWOA(15, 15) | LSEWOA(15, 20) | LSEWOA(15, 25) | LSEWOA(20, 15) | LSEWOA(20, 20) | LSEWOA(20, 25) | LSEWOA(25, 15) | LSEWOA(25, 20) | LSEWOA(25, 25) |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 |
| F2 | 5.1500 | 5.0600 | 4.9700 | 4.9700 | 4.9700 | 4.9700 | 4.9700 | 4.9700 | 4.9700 |
| F3 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 |
| F4 | 5.6200 | 5.0100 | 4.9100 | 4.9100 | 4.9100 | 4.9100 | 4.9100 | 4.9100 | 4.9100 |
| F5 | 7.0200 | 4.9600 | 3.1200 | 6.7200 | 4.1000 | 3.7800 | 7.1000 | 4.3200 | 3.8800 |
| F6 | 7.9200 | 4.5600 | 3.1000 | 7.2800 | 4.6600 | 2.7000 | 7.7400 | 4.2400 | 2.8000 |
| F7 | 4.4000 | 4.6800 | 4.8800 | 5.1400 | 6.2200 | 4.6000 | 4.9800 | 5.1400 | 4.9600 |
| F8 | 7.9800 | 5.0000 | 2.3000 | 7.9800 | 4.8200 | 2.0800 | 7.7600 | 4.8800 | 2.2000 |
| F9 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 |
| F10 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 |
| F11 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 5.0000 |
| F12 | 6.4600 | 3.8800 | 4.3000 | 6.6400 | 4.0400 | 4.4000 | 6.6800 | 3.8200 | 4.7800 |
| F13 | 7.1600 | 3.9800 | 4.2400 | 7.0600 | 4.2600 | 3.6600 | 6.8200 | 3.9000 | 3.9200 |
| F14 | 7.6400 | 4.5600 | 2.9500 | 7.5900 | 5.1300 | 2.5800 | 7.4200 | 4.7900 | 2.3400 |
| F15 | 4.7000 | 4.3800 | 5.5400 | 4.4200 | 4.8800 | 5.7200 | 4.8600 | 4.9400 | 5.5600 |
| F16 | 7.6000 | 5.0900 | 2.1100 | 8.0000 | 5.2000 | 2.2000 | 7.8400 | 4.8100 | 2.1500 |
| F17 | 8.1200 | 5.2400 | 2.2600 | 7.7800 | 5.0000 | 2.0700 | 7.7000 | 4.9200 | 1.9100 |
| F18 | 4.2800 | 4.3000 | 5.9600 | 4.0000 | 5.4000 | 5.2000 | 4.2800 | 5.4800 | 6.1000 |
| F19 | 5.8400 | 4.4800 | 4.9000 | 6.4000 | 4.0800 | 4.9800 | 6.0400 | 4.0200 | 4.2600 |
| F20 | 7.6600 | 5.2600 | 7.8600 | 7.8800 | 4.8400 | 2.2200 | 2.2400 | 2.2600 | 4.7800 |
| F21 | 7.9800 | 4.8800 | 1.7400 | 8.1400 | 5.1000 | 2.2000 | 7.8600 | 5.0400 | 2.0600 |
| F22 | 8.1800 | 4.9800 | 2.1400 | 7.8200 | 5.1600 | 1.8600 | 7.9400 | 4.9200 | 2.0000 |
| F23 | 8.1000 | 4.7600 | 1.8200 | 7.8400 | 5.1000 | 2.1200 | 8.0600 | 5.0600 | 2.1400 |
| Average | 6.3830 | 4.7852 | 4.0913 | 6.3291 | 4.9074 | 3.7935 | 6.0957 | 4.6704 | 3.9443 |
| Rank | 9 | 5 | 3 | 8 | 6 | 1 | 7 | 4 | 2 |
| Function | Metrics | WOAV1 | WOAV2 | WOAV3 | WOAV4 | WOAV5 | LSEWOA |
|---|---|---|---|---|---|---|---|
| F1 | Ave | 0.0000E+00 | 9.8638E-17 | 1.3408E-149 | 0.0000E+00 | 5.6634E-30 | 0.0000E+00 |
| Std | 0.0000E+00 | 2.5718E-16 | 3.8808E-149 | 0.0000E+00 | 1.3704E-29 | 0.0000E+00 | |
| F2 | Ave | 2.0330E-169 | 2.1140E-14 | 4.1665E-81 | 1.9041E-229 | 4.4123E-23 | 0.0000E+00 |
| Std | 2.6530E-169 | 2.2621E-14 | 9.4838E-81 | 2.0640E-229 | 5.8699E-23 | 0.0000E+00 | |
| F3 | Ave | 9.7597E-283 | 1.1229E+04 | 2.2191E-138 | 0.0000E+00 | 1.1728E+03 | 0.0000E+00 |
| Std | 9.9857E-283 | 4.4476E+03 | 8.0227E-138 | 0.0000E+00 | 8.1830E+02 | 0.0000E+00 | |
| F4 | Ave | 1.2894E-165 | 2.7553E+01 | 8.5275E-71 | 1.7281E-200 | 3.4477E+01 | 0.0000E+00 |
| Std | 1.6534E-165 | 1.4118E+01 | 6.5641E-71 | 1.8576E-200 | 1.2159E+01 | 0.0000E+00 | |
| F5 | Ave | 2.8434E+01 | 2.5671E+01 | 3.9129E+00 | 2.8674E+01 | 2.5411E+01 | 7.0226E-04 |
| Std | 1.9274E-01 | 9.7131E-01 | 9.8399E+00 | 1.5929E-01 | 1.6234E+00 | 7.1473E-04 | |
| F6 | Ave | 3.0652E-01 | 1.0685E-04 | 1.0465E-03 | 1.5137E+00 | 1.8336E-02 | 4.4627E-07 |
| Std | 1.5010E-01 | 6.0965E-05 | 9.1790E-04 | 4.0534E-01 | 6.2416E-02 | 8.5647E-07 | |
| F7 | Ave | 1.2704E-04 | 1.8777E-02 | 1.6854E-04 | 1.0146E-04 | 3.6796E-02 | 9.0617E-05 |
| Std | 1.6348E-04 | 8.9501E-03 | 1.1422E-04 | 1.0148E-04 | 2.7993E-02 | 9.8754E-05 | |
| F8 | Ave | −1.1587E+04 | −5799.7097 | −9.6835E+03 | −5071.082 | −6.2135E+03 | −1.2569E+04 |
| Std | 8.6513E+02 | 1.7944E+02 | 1.4073E+03 | 1.9181E+03 | 3.0826E+02 | 8.8190E-03 | |
| F9 | Ave | 0.0000E+00 | 4.3725E+01 | 7.2948E-02 | 0.0000E+00 | 1.0214E+02 | 0.0000E+00 |
| Std | 0.0000E+00 | 3.5049E+01 | 3.9955E-01 | 0.0000E+00 | 3.3930E+01 | 0.0000E+00 | |
| F10 | Ave | 4.4409E-16 | 5.5139E-10 | 4.4409E-16 | 4.4409E-16 | 3.4122E+00 | 4.4409E-16 |
| Std | 0.0000E+00 | 7.5953E-10 | 0.0000E+00 | 0.0000E+00 | 4.4409E-16 | 0.0000E+00 | |
| F11 | Ave | 0.0000E+00 | 6.5879E-03 | 0.0000E+00 | 0.0000E+00 | 9.8103E-03 | 0.0000E+00 |
| Std | 0.0000E+00 | 1.7301E-02 | 0.0000E+00 | 0.0000E+00 | 1.6744E-02 | 0.0000E+00 | |
| F12 | Ave | 2.1045E-02 | 1.5641E+00 | 2.0810E-02 | 8.2819E-02 | 4.5985E+00 | 1.1056E-06 |
| Std | 1.0780E-02 | 1.6340E+00 | 1.1291E-01 | 3.0729E-02 | 4.2231E+00 | 3.3784E-06 | |
| F13 | Ave | 4.0665E-01 | 8.1110E-02 | 7.6209E-03 | 7.0082E-01 | 7.7391E+00 | 1.1074E-03 |
| Std | 1.9499E-01 | 8.3807E-02 | 1.9818E-02 | 2.2757E-01 | 1.2779E+01 | 3.3682E-03 | |
| F14 | Ave | 4.7805E+00 | 1.3287E+00 | 1.5967E+00 | 6.6164E+00 | 3.4841E+00 | 9.9800E-01 |
| Std | 4.4631E+00 | 7.5207E-01 | 1.3094E+00 | 4.6380E+00 | 3.5220E+00 | 1.5423E-16 | |
| F15 | Ave | 3.2035E-04 | 5.6925E-04 | 1.6779E-03 | 6.0438E-04 | 2.4352E-03 | 3.1131E-04 |
| Std | 4.057E-05 | 3.4712E-04 | 3.6112E-03 | 2.2205E-04 | 6.0863E-03 | 8.9892E-06 | |
| F16 | Ave | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 | −9.9542E-01 | −1.0316E+00 | −1.0316E+00 |
| Std | 6.3208E-16 | 6.7122E-16 | 1.5322E-05 | 3.5053E-02 | 6.3208E-16 | 6.1358E-16 | |
| F17 | Ave | 3.9789E-01 | 3.9789E-01 | 3.9807E-01 | 4.1714E-01 | 3.9789E-01 | 3.9789E-01 |
| Std | 1.8233E-09 | 0.0000E+00 | 2.4150E-04 | 2.1294E-02 | 0.0000E+00 | 3.0227E-14 | |
| F18 | Ave | 3.0000E+00 | 3.0000E+00 | 3.0003E+00 | 9.7182E+00 | 3.9000E+00 | 3.0000E+00 |
| Std | 1.4523E-14 | 1.5003E-15 | 2.6184E-04 | 1.0779E+01 | 4.9295E+00 | 9.1567E-05 | |
| F19 | Ave | −3.8628E+00 | −3.8628E+00 | −3.8610E+00 | −3.7703E+00 | −3.8628E+00 | −3.8628E+00 |
| Std | 1.6154E-12 | 2.7101E-15 | 1.4594E-03 | 8.7085E-02 | 2.5684E-15 | 4.5466E-05 | |
| F20 | Ave | −3.2970E+00 | −3.2705E+00 | 3.1149E+00 | −2.8895E+00 | −3.2546E+00 | −3.3139E+00 |
| Std | 5.0399E-02 | 5.9923E-02 | 2.3645E-02 | 2.2151E-01 | 5.9923E-02 | 1.0705E-02 | |
| F21 | Ave | −1.0153E+01 | −8.0347E+00 | −8.3530E+00 | −4.7618E+00 | −7.1336E+00 | −1.0153E+01 |
| Std | 1.2439E-03 | 2.6741E+00 | 2.3778E+00 | 1.0865E+00 | 3.3901E+00 | 9.4998E-11 | |
| F22 | Ave | −1.0402E+01 | −8.3325E+00 | −6.9258E+00 | −4.7869E+00 | −6.9124E+00 | −1.0403E+01 |
| Std | 4.1015E-03 | 2.8050E+00 | 3.5457E+00 | 8.6837E-01 | 3.4437E+00 | 1.0354E-10 | |
| F23 | Ave | −1.0536E+01 | −9.0041E+00 | −8.3377E+00 | −4.7300E+00 | −6.2289E+00 | −1.0536E+01 |
| Std | 1.2232E-04 | 2.6270E+00 | 3.4851E+00 | 8.9833E-01 | 2.9646E+00 | 1.5291E-10 |
| Algorithm | Rank | Average Friedman Value | +/=/− |
|---|---|---|---|
| WOAV1 | 2 | 3.2188 | 19/4/0 |
| WOAV2 | 4 | 3.8783 | 23/0/0 |
| WOAV3 | 3 | 3.8370 | 21/2/0 |
| WOAV4 | 6 | 4.3645 | 18/5/0 |
| WOAV5 | 2 | 4.0304 | 23/0/0 |
| LSEWOA | 1 | 1.6710 | − |
| Metrics | WOAV1 (w/t/l) | WOAV2 (w/t/l) | WOAV3 (w/t/l) | WOAV4 (w/t/l) | WOAV5 (w/t/l) | LSEWOA (w/t/l) |
|---|---|---|---|---|---|---|
| D = 30 | 0/4/19 | 0/0/23 | 0/2/21 | 0/5/18 | 0/0/23 | 18/5/0 |
| D = 50 | 1/4/18 | 0/0/23 | 1/2/20 | 1/5/17 | 0/0/23 | 17/5/1 |
| D = 100 | 1/4/18 | 0/0/23 | 1/2/20 | 1/5/17 | 0/0/23 | 17/5/1 |
| Total | 2/12/55 | 0/0/69 | 2/6/61 | 2/15/52 | 0/0/69 | 52/15/2 |
| 20.29% | 0.00% | 11.59% | 24.64% | 0.00% | 97.10% |
| Dimension | Algorithm | Rank | Average Friedman Value | +/=/− |
|---|---|---|---|---|
| D = 50 | WOAV1 | 2 | 3.1717 | 22/0/1 |
| WOAV2 | 5 | 4.0130 | 19/3/1 | |
| WOAV3 | 3 | 3.7203 | 20/3/0 | |
| WOAV4 | 6 | 4.3406 | 19/3/1 | |
| WOAV5 | 4 | 3.8754 | 22/0/1 | |
| LSEWOA | 1 | 1.7790 | − | |
| D = 100 | WOAV1 | 6 | 3.1717 | 22/0/1 |
| WOAV2 | 4 | 4.0130 | 19/3/1 | |
| WOAV3 | 3 | 3.7203 | 20/3/0 | |
| WOAV4 | 2 | 4.3406 | 19/3/1 | |
| WOAV5 | 9 | 3.8754 | 22/0/1 | |
| LSEWOA | 1 | 1.5551 | − |
| Algorithm | Year | Author(s) | Source of Inspiration |
|---|---|---|---|
| Grey Wolf Optimizer (GWO) [38] | 2014 | Seyedali Mirjalili et al. | The leadership hierarchy and |
| hunting system of gray wolves. | |||
| Harris Hawk Optimization | 2019 | AA Heidari et al. | The predatory behavior |
| algorithm (HHO) [7] | of Harris’s hawks. | ||
| Zebra Optimization Algorithm | 2022 | E Trojovská et al. | Foraging and Defense Strategy |
| (ZOA) [39] | of zebras. | ||
| Slime Mould Algorithm (SMA) [40] | 2020 | S Li et al. | Foraging behavior of slime molds. |
| Sine Cosine Algorithm | 2022 | Seyedali Mirjalili | Mathematical model of the |
| (SCA) [41] | tangent function. | ||
| Attraction-Repulsion Optimization | 2024 | K Cymerys | Attraction-repulsion phenomenon. |
| Algorithm (AROA) [42] | |||
| Rime optimization algorithm | 2023 | Su Hang et al. | The formation process of rime |
| (RIME) [43] | in nature. | ||
| Whale Optimization Algorithm | 2016 | Seyedali Mirjalili et al. | The hunting behavior of |
| (WOA) [18] | humpback whales. |
| Algorithm | Parameter | Value |
|---|---|---|
| GWO | Convergence factor a | 2 decrease to 0 |
| HHO | Threshold | 0.5 |
| ZOA | R | 0.1 |
| SMA | z | 0.03 |
| 1 decrease to 0 | ||
| SCA | a | 2 |
| AROA | Attraction factor c | 0.95 |
| Local search scaling factor 1 | 0.15 | |
| Local search scaling factor 2 | 0.6 | |
| Attraction probability 1 | 0.2 | |
| Local search probability | 0.8 | |
| Expansion factor | 0.4 | |
| Local search threshold 1 | 0.9 | |
| Local search threshold 2 | 0.85 | |
| Local search threshold 3 | 0.9 | |
| RIME | 5 | |
| WOA | Convergence factor a | 2 decrease to 0 |
| Spiral factor b | 1 | |
| LSEWOA | Convergence factor a | 2 decrease to 0 |
| Inertia weight | 0 increase to 0.9 | |
| Spiral factor k | 1 |
| Function | Metrics | GWO | HHO | ZOA | SMA | SCA | AROA | RIME | WOA | LSEWOA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 2.0895E-27 | 1.6901E-56 | 1.3535E-249 | 3.4272E-319 | 1.1493E+01 | 3.9851E+00 | 2.1360E+00 | 3.122E-72 | 0.0000E+00 |
| Std | 3.4562E-27 | 9.2573E-56 | 1.4325E-249 | 3.653E-319 | 1.2787E+01 | 2.7759E+00 | 1.2179E+00 | 1.4327E-71 | 0.0000E+00 | |
| F2 | Ave | 9.8045E-17 | 7.2027E-38 | 2.4225E-130 | 6.1088E-142 | 1.5330E-02 | 7.2023E-01 | 1.5665E+00 | 1.0548E-49 | 0.0000E+00 |
| Std | 6.078E-17 | 2.6592E-37 | 8.6167E-130 | 3.3458E-141 | 2.0414E-02 | 2.2962E-01 | 1.0821E+00 | 4.055E-49 | 0.0000E+00 | |
| F3 | Ave | 2.6528E-05 | 6.4586E-66 | 2.317E-154 | 9.577E-296 | 7.5000E+03 | 1.9846E+02 | 1.4642E+03 | 4.7902E+04 | 0.0000E+00 |
| Std | 1.1192E-04 | 3.5282E-65 | 1.2691E-153 | 9.5432E-296 | 5.2636E+03 | 2.7161E+02 | 4.5706E+02 | 1.6365E+04 | 0.0000E+00 | |
| F4 | Ave | 6.8653E-07 | 1.2801E-36 | 4.223E-114 | 3.4892E-159 | 3.7443E+01 | 1.8233E+00 | 7.5008E+00 | 5.4785E+01 | 0.0000E+00 |
| Std | 7.816E-07 | 5.0091E-36 | 1.4688E-113 | 1.9017E-158 | 1.2096E+01 | 8.0749E-01 | 3.2426E+00 | 2.5634E+01 | 0.0000E+00 | |
| F5 | Ave | 2.7214E+01 | 1.2597E+01 | 2.8435E+01 | 7.9363E+00 | 8.2844E+04 | 9.4260E+01 | 3.8156E+02 | 2.7943E+01 | 2.1804E-04 |
| Std | 7.6933E-01 | 1.4341E+01 | 4.6934E-01 | 1.1387E+01 | 1.4598E+05 | 6.3976E+01 | 5.9200E+02 | 4.7547E-01 | 1.9583E-04 | |
| F6 | Ave | 7.5490E-01 | 1.1604E-01 | 2.6854E+00 | 5.6277E-03 | 2.3240E+01 | 1.0211E+01 | 2.0228E+00 | 3.7597E-01 | 2.4235E-07 |
| Std | 4.1382E-01 | 2.0970E-01 | 5.4786E-01 | 2.7533E-03 | 3.3771E+01 | 3.0057E+00 | 6.5657E-01 | 1.9799E-01 | 3.0661E-07 | |
| F7 | Ave | 2.1070E-03 | 1.6577E-04 | 1.2183E-04 | 2.0192E-04 | 1.3017E-01 | 3.3554E-02 | 4.2646E-02 | 3.3823E-03 | 9.2310E-05 |
| Std | 1.1727E-03 | 2.0006E-04 | 9.8147E-05 | 1.4495E-04 | 1.2503E-01 | 2.6544E-02 | 1.7281E-02 | 3.4709E-03 | 9.4816E-05 | |
| F8 | Ave | −6.0646E+03 | −12569.413 | −6.5366E+03 | −12569.0803 | −3.7756E+03 | −4.5711E+03 | −9.9880E+03 | −1.0387E+04 | −12569.4810 |
| Std | 8.6178E+02 | 1.8809E-01 | 6.6667E+02 | 2.4234E-01 | 2.9546E+02 | 7.0335E+02 | 4.8839E+02 | 1.9207E+03 | 7.1526E-03 | |
| F9 | Ave | 2.5289E+00 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 3.6167E+01 | 5.1770E+01 | 6.7959E+01 | 1.8948E-15 | 0.0000E+00 |
| Std | 4.8781E+00 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 3.2372E+01 | 6.5822E+01 | 1.2253E+01 | 1.0378E-14 | 0.0000E+00 | |
| F10 | Ave | 1.0501E-13 | 4.4409E-16 | 4.4409E-16 | 4.4409E-16 | 1.2727E+01 | 8.2919E-01 | 2.1549E+00 | 3.76E-15 | 4.4409E-16 |
| Std | 2.0391E-14 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 9.4703E+00 | 3.8480E-01 | 5.0321E-01 | 2.6279E-15 | 0.0000E+00 | |
| F11 | Ave | 4.0717E-03 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 8.5792E-01 | 9.8457E-01 | 9.9393E-01 | 3.7007E-18 | 0.0000E+00 |
| Std | 9.2179E-03 | 0.0000E+00 | 0.0000E+00 | 0.0000E+00 | 2.4644E-01 | 1.1340E-01 | 3.4509E-02 | 2.027e-17 | 0.0000E+00 | |
| F12 | Ave | 4.5354E-02 | 7.6756E-04 | 1.6897E-01 | 8.3303E-03 | 1.3194E+04 | 1.3013E+00 | 3.3013E+00 | 2.5013E-02 | 1.1132E-06 |
| Std | 2.4764E-02 | 1.6439E-03 | 6.6607E-02 | 9.6578E-03 | 4.3933E+04 | 3.2708E-01 | 2.1232E+00 | 2.5786E-02 | 1.8246E-06 | |
| F13 | Ave | 6.1504E-01 | 4.8366E-02 | 2.2662E+00 | 6.2369E-03 | 1.2142E+05 | 4.0630E+00 | 2.1907E-01 | 4.5703E-01 | 7.3709E-04 |
| Std | 2.3088E-01 | 9.7235E-02 | 2.7059E-01 | 6.4921E-03 | 2.2536E+05 | 4.7363E-01 | 6.5521E-02 | 2.0359E-01 | 2.7942E-03 | |
| F14 | Ave | 4.2279E+00 | 1.4941E+00 | 2.7431E+00 | 9.9800E-01 | 1.6626E+00 | 6.4242E+00 | 9.9800E-01 | 1.9840E+00 | 9.9800E-01 |
| Std | 4.2406E+00 | 8.5423E-01 | 2.0626E+00 | 1.1416E-12 | 9.4904E-01 | 4.4124E+00 | 6.8753E-12 | 2.0261E+00 | 4.2751E-16 | |
| F15 | Ave | 4.4172E-03 | 3.8813E-04 | 1.7074E-03 | 5.4518E-04 | 9.5536E-04 | 4.2943E-03 | 7.1893E-03 | 7.4320E-04 | 3.0960E-04 |
| Std | 8.1125E-03 | 7.6667E-05 | 5.0750E-03 | 2.4870E-04 | 3.4759E-04 | 6.0518E-03 | 1.2544E-02 | 5.6744E-04 | 5.1968E-06 | |
| F16 | Ave | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 | −1.0316E+00 |
| Std | 2.5294E-08 | 1.1537E-06 | 3.6246E-10 | 1.0767E-09 | 6.1383E-05 | 2.8188E-05 | 9.1271E-08 | 2.3332E-09 | 1.19E-15 | |
| F17 | Ave | 3.9791E-01 | 3.9817E-01 | 3.9789E-01 | 3.9789E-01 | 3.9913E-01 | 3.9889E-01 | 3.9789E-01 | 3.9791E-01 | 3.9789E-01 |
| Std | 1.0285E-04 | 1.0967E-03 | 2.5577E-08 | 8.5519E-08 | 9.2873E-04 | 3.1123E-03 | 7.8052E-07 | 3.9929E-05 | 1.8276E-14 | |
| F18 | Ave | 3.0001E+00 | 3.9007E+00 | 5.7000E+00 | 3.0000E+00 | 3.0001E+00 | 3.9922E+00 | 3.0000E+00 | 3.9004E+00 | 3.0000E+00 |
| Std | 9.6496E-05 | 4.9298E+00 | 8.2385E+00 | 1.0303E-10 | 1.6082E-04 | 4.9382E+00 | 6.9447E-07 | 4.9312E+00 | 5.6509E-05 | |
| F19 | Ave | −3.8615E+00 | −3.8024E+00 | −3.8623E+00 | −3.8628E+00 | −3.8549E+00 | −3.8591E+00 | −3.8628E+00 | −3.8535E+00 | −3.8628E+00 |
| Std | 2.5697E-03 | 7.5654E-02 | 4.5151E-04 | 1.9366E-07 | 3.3445E-03 | 5.6257E-03 | 2.5256E-07 | 1.5083E-02 | 4.59E-05 | |
| F20 | Ave | −3.2599E+00 | −2.5371E+00 | −3.3178E+00 | −3.2583E+00 | −2.9681E+00 | −3.2171E+00 | −3.2665E+00 | −3.2337E+00 | 3.3220E+00 |
| Std | 7.5667E-02 | 4.3035E-01 | 2.1897E-02 | 6.0626E-02 | 2.8675E-01 | 7.5154E-02 | 6.0327E-02 | 1.2029E-01 | 2.5098E-12 | |
| F21 | Ave | −9.3930E+00 | −2.9686E+00 | −9.8132E+00 | −1.0153E+01 | −2.3603E+00 | −6.5719E+00 | −7.0419E+00 | −7.8461E+00 | −1.0153E+01 |
| Std | 2.0038E+00 | 1.4372E+00 | 1.2934E+00 | 3.6940E-04 | 1.9595E+00 | 3.2936E+00 | 3.0763E+00 | 2.6970E+00 | 6.4992E-11 | |
| F22 | Ave | −1.0401E+01 | −3.6079E+00 | −9.6935E+00 | −1.0403E+01 | −3.0380E+00 | −6.9924E+00 | −8.8560E+00 | −7.5651E+00 | −1.0403E+01 |
| Std | 1.3707E-03 | 1.1968E+00 | 1.8374E+00 | 3.3640E-04 | 1.5471E+00 | 3.3121E+00 | 2.9167E+00 | 2.8153E+00 | 8.9896E-11 | |
| F23 | Ave | −1.0264E+01 | −3.0811E+00 | −9.6350E+00 | −1.0536E+01 | −3.5309E+00 | −6.0164E+00 | −9.0563E+00 | −6.6449E+00 | −1.0536E+01 |
| Std | 1.4812E+00 | 1.4661E+00 | 2.0499E+00 | 2.5217E-04 | 2.1461E+00 | 3.3571E+00 | 2.7900E+00 | 3.6057E+00 | 1.1943E-10 |
| Algorithm | Rank | Average Friedman Value | +/=/− |
|---|---|---|---|
| GWO | 5 | 5.2312 | 23/0/0 |
| HHO | 4 | 4.9297 | 20/3/0 |
| ZOA | 3 | 3.8956 | 20/3/0 |
| SMA | 2 | 2.7565 | 20/3/0 |
| SCA | 9 | 8.0783 | 23/0/0 |
| AROA | 8 | 7.2913 | 23/0/0 |
| RIME | 7 | 6.0000 | 22/0/1 |
| WOA | 6 | 5.2587 | 23/0/0 |
| LSEWOA | 1 | 1.5587 | − |
| Metrics | GWO (w/t/l) | HHO (w/t/l) | ZOA (w/t/l) | SMA (w/t/l) | SCA (w/t/l) | AROA (w/t/l) | RIME (w/t/l) | WOA (w/t/l) | LSEWOA (w/t/l) |
|---|---|---|---|---|---|---|---|---|---|
| D = 30 | 0/0/23 | 0/3/20 | 0/3/20 | 0/3/20 | 0/0/23 | 0/0/23 | 1/0/22 | 0/0/23 | 22/1/0 |
| D = 50 | 1/0/22 | 1/3/19 | 0/3/20 | 1/3/19 | 1/0/22 | 0/0/23 | 1/0/22 | 1/1/21 | 19/3/1 |
| D = 100 | 1/0/22 | 1/3/19 | 0/3/20 | 1/3/19 | 1/0/22 | 0/0/23 | 1/0/22 | 1/2/20 | 19/3/1 |
| Total | 2/0/67 | 2/9/58 | 0/9/60 | 2/9/58 | 2/0/67 | 0/0/69 | 3/0/66 | 2/3/64 | 60/7/2 |
| 2.90% | 15.94% | 13.04% | 15.94% | 2.90% | 0.00% | 4.35% | 7.25% | 97.10% |
| Dimension | Algorithm | Rank | Average Friedman Value | +/=/− |
|---|---|---|---|---|
| D = 50 | GWO | 6 | 5.2225 | 22/0/1 |
| HHO | 4 | 4.9471 | 19/3/1 | |
| ZOA | 3 | 3.8826 | 20/3/0 | |
| SMA | 2 | 2.8232 | 19/3/1 | |
| SCA | 9 | 8.1261 | 22/0/1 | |
| AROA | 8 | 7.1536 | 23/0/0 | |
| RIME | 7 | 6.0232 | 22/0/1 | |
| WOA | 5 | 5.1471 | 22/0/1 | |
| LSEWOA | 1 | 1.6746 | − | |
| D = 100 | GWO | 6 | 5.3551 | 22/0/1 |
| HHO | 4 | 4.8101 | 19/3/1 | |
| ZOA | 3 | 3.8442 | 20/3/0 | |
| SMA | 2 | 2.7645 | 19/3/1 | |
| SCA | 9 | 8.3072 | 22/0/1 | |
| AROA | 8 | 6.9710 | 23/0/0 | |
| RIME | 7 | 6.2884 | 22/0/1 | |
| WOA | 5 | 5.1043 | 22/1/0 | |
| LSEWOA | 1 | 1.5551 | − |
| Challenges | Metrics | GWO | HHO | ZOA | SMA | SCA | AROA | RIME | WOA | LSEWOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Three-bar Truss | Ave | 259.805063 | 259.815011 | 259.805048 | 263.072647 | 259.820148 | 259.832780 | 259.806407 | 259.863959 | 259.805047 |
| Std | 0.000015 | 0.014659 | 0.000001 | 2.666551 | 0.012243 | 0.083901 | 0.001547 | 0.081753 | 0.000000 | |
| Tension/Compression Spring | Ave | 0.121526 | 0.121522 | 0.121523 | 0.121522 | 0.121740 | 0.124473 | 0.122241 | 0.121921 | 0.121522 |
| Std | 0.000005 | 0.000000 | 0.000001 | 0.000000 | 0.000231 | 0.009336 | 0.003592 | 0.001725 | 0.000000 | |
| Speed Reducer | Ave | 2638.848210 | 2638.824969 | 2638.820667 | 2638.819863 | 2647.800460 | 2640.757902 | 2638.866459 | 2638.820024 | 2638.819842 |
| Std | 0.025308 | 0.023320 | 0.000996 | 0.000062 | 6.014099 | 2.752896 | 0.101059 | 0.000388 | 0.000020 | |
| Cantilever Beam | Ave | 13.360394 | 13.390888 | 13.360290 | 13.360645 | 13.963792 | 20.620153 | 13.584452 | 15.444253 | 13.360259 |
| Std | 0.000108 | 0.021638 | 0.000050 | 0.000308 | 0.212685 | 4.997151 | 0.179248 | 1.779201 | 0.000000 | |
| I-beam | Ave | 6.702705 | 6.702689 | 6.702962 | 6.703047 | 6.664008 | 5.782476 | 6.457600 | 6.365987 | 6.703048 |
| Std | 0.000320 | 0.000531 | 0.000105 | 0.000001 | 0.035199 | 0.995907 | 0.289582 | 0.322097 | 0.000000 | |
| Piston Lever | Ave | 12.179036 | 274.057852 | 2.953538 | 34.340337 | 1.219121 | 281.004695 | 52.942343 | 28.643545 | 1.057195 |
| Std | 42.317243 | 238.155716 | 7.405989 | 67.704274 | 0.071245 | 202.116656 | 132.158718 | 79.421364 | 0.000099 | |
| Multi-disc Clutch Brake | Ave | 0.235302 | 0.235243 | 0.235258 | 0.235243 | 0.237668 | 0.236633 | 0.235452 | 0.235244 | 0.235242 |
| Std | 0.000082 | 0.000001 | 0.000015 | 0.000001 | 0.002042 | 0.002617 | 0.000278 | 0.000009 | 0.000000 | |
| Gas Transmission System | Ave | 1224745.959830 | 1224745.937224 | 1224745.938295 | 1224745.937223 | 1224901.598433 | 1226318.258250 | 1224745.952955 | 1224745.937227 | 1224745.937222 |
| Std | 0.017907 | 0.000005 | 0.001656 | 0.000002 | 118.092819 | 3538.385964 | 0.022237 | 0.000007 | 0.000000 | |
| Industrial Refrigeration System | Ave | 642.809538 | 897.655989 | 13.111876 | 642.333923 | 9.729020 | 23312.391077 | 8.430037 | 868.334558 | 8.249197 |
| Std | 3477.950844 | 3927.456866 | 5.330660 | 3475.959550 | 1.070188 | 24530.767002 | 2.012544 | 4131.221271 | 0.496502 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Gu, Y.; Yan, Y.; Li, Z.; Lu, B.; Pan, S.; Cheong, N. LSEWOA: An Enhanced Whale Optimization Algorithm with Multi-Strategy for Numerical and Engineering Design Optimization Problems. Sensors 2025, 25, 2054. https://doi.org/10.3390/s25072054
Wei J, Gu Y, Yan Y, Li Z, Lu B, Pan S, Cheong N. LSEWOA: An Enhanced Whale Optimization Algorithm with Multi-Strategy for Numerical and Engineering Design Optimization Problems. Sensors. 2025; 25(7):2054. https://doi.org/10.3390/s25072054
Chicago/Turabian StyleWei, Junhao, Yanzhao Gu, Yuzheng Yan, Zikun Li, Baili Lu, Shirou Pan, and Ngai Cheong. 2025. "LSEWOA: An Enhanced Whale Optimization Algorithm with Multi-Strategy for Numerical and Engineering Design Optimization Problems" Sensors 25, no. 7: 2054. https://doi.org/10.3390/s25072054
APA StyleWei, J., Gu, Y., Yan, Y., Li, Z., Lu, B., Pan, S., & Cheong, N. (2025). LSEWOA: An Enhanced Whale Optimization Algorithm with Multi-Strategy for Numerical and Engineering Design Optimization Problems. Sensors, 25(7), 2054. https://doi.org/10.3390/s25072054






