The Impact of Probe Angle and Swivel Length on Contact Point Identification in Coordinate Measuring Machine Measurements: A Case Study
Abstract
1. Introduction
2. Materials and Methods
- All repetitions were performed at the same point on the shaft surface;
- All repetitions were conducted from one CMM start, without resetting it;
- After the intial start, calibration was performed once for all the repetitions;
- All measurements were carried out in the same Part Coordinate System, defined at the beginning and closely connected with the measurement conditions;
- The fixation and orientation of the measured object were not changed;
- The tested probing point was placed in a position usually applied in measurements due to its convenience.
2.1. Measured Object
2.2. Coordinate Measuring Machine
2.3. Measurement Strategy
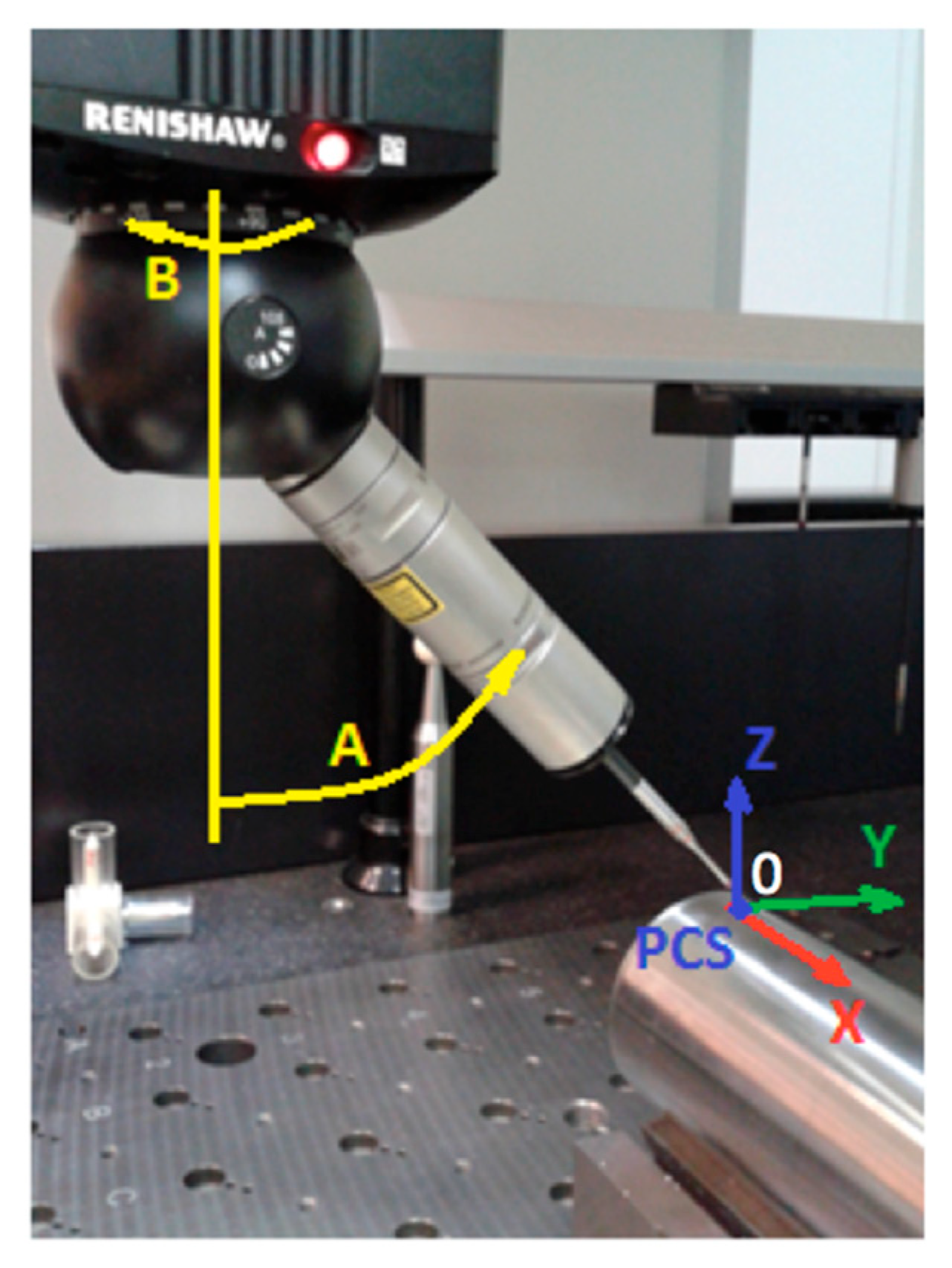
2.3.1. Part Coordinate System
2.3.2. Measurement Procedure
- Movement speed of 520 mm/s;
- Measurement speed of 1.5 mm/s;
- Safety distance of 0.5 mm;
- Starting point of (0,0,5);
- Loop measurement along the PCS axis.
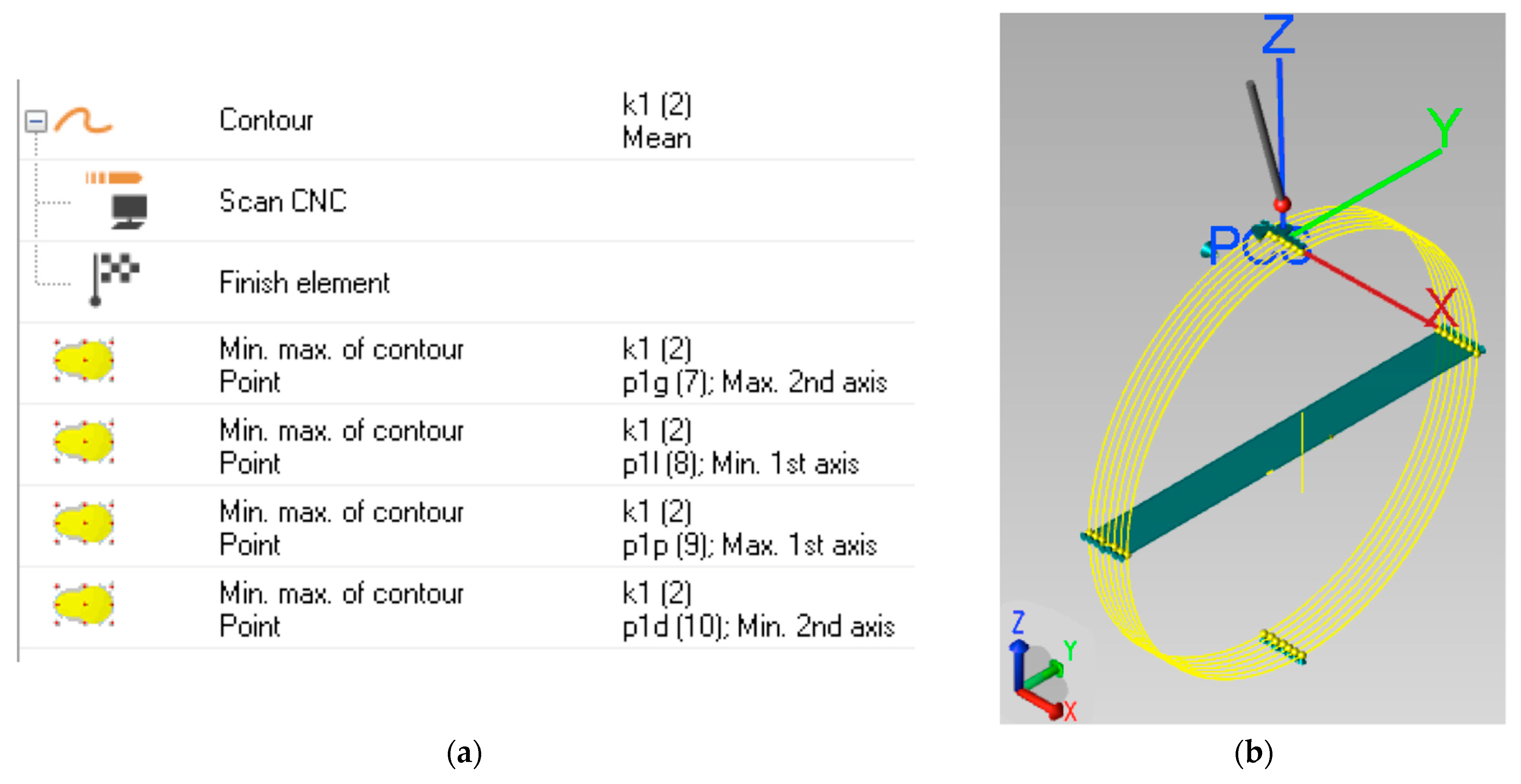
2.3.3. Data Processing
3. Results and Discussion
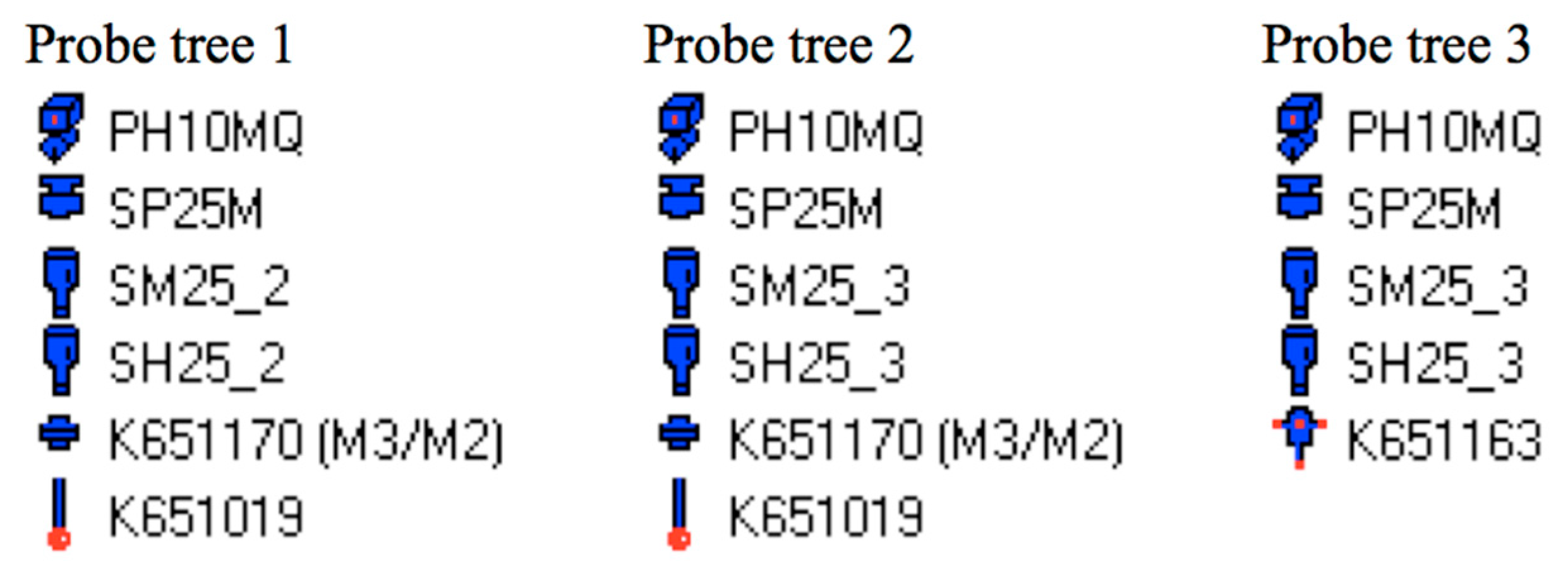
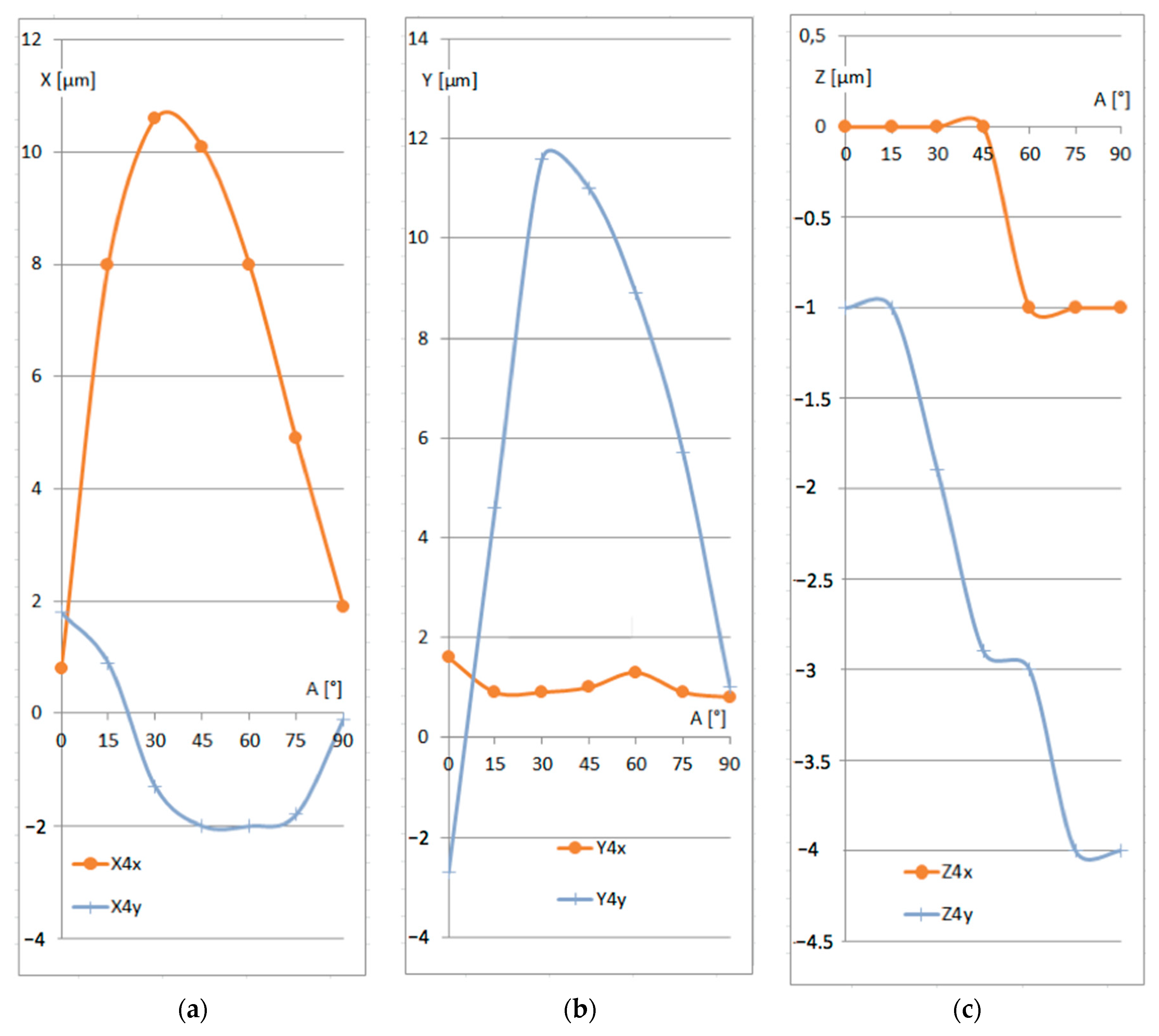
- The first character corresponds to the respective coordinate (X, Y, or Z).
- The second character denotes the respective probe tree (1, 2, or 3), as specified in Figure 2.
- The third character indicates the direction of the probe: x—along the x-axis of the PCS (along the shaft axis), with B = 180°; y—along the y-axis of the PCS, perpendicular to the shaft axis, with B = 90°.
4. Additional Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schulze, F.; Dallasega, P. Industry 4.0 Concepts and Lean Methods Mitigating Traditional Losses in Engineer-to-Order Manufacturing with Subsequent Assembly On-Site: A Framework. Procedia Manuf. 2020, 51, 1363–1370. [Google Scholar] [CrossRef]
- Rucki, M. Recent Development of Air Gauging in Industry 4.0 Context. Sensors 2023, 23, 2122. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, R.; Möhring, M.; Härting, R.C.; Reichstein, C.; Neumaier, P.; Jozinović, P. Industry 4.0—Potentials for Creating Smart Products: Empirical Research Results. In Business Information Systems; Abramowicz, W., Ed.; Springer: Cham, Switzerland, 2015; pp. 16–27. [Google Scholar] [CrossRef]
- Wu, K.; Xu, J.; Zheng, M. Industry 4.0: Review and proposal for implementing a smart factory. Int. J. Adv. Manuf. Technol. 2024, 133, 1331–1347. [Google Scholar] [CrossRef]
- Wu, W.; Lu, J.; Zhang, H. Smart Factory Reference Architecture Based on CPS Fractal. IFAC Pap. 2019, 52, 2776–2781. [Google Scholar] [CrossRef]
- Shi, Z.; Xie, Y.; Xue, W.; Chen, Y.; Fu, L.; Xu, X. Smart factory in Industry 4.0. Syst. Res. Behav. Sci. 2020, 37, 607–617. [Google Scholar] [CrossRef]
- Fortoul-Diaz, J.A.; Carrillo-Martinez, L.A.; Centeno-Tellez, A.; Cortes-Santacruz, F.; Olmos-Pineda, I.; Flores-Quintero, R.R. A Smart Factory Architecture Based on Industry 4.0 Technologies: Open-Source Software Implementation. IEEE Access 2023, 11, 101727–101749. [Google Scholar] [CrossRef]
- Kapp, V.; May, M.C.; Lanza, G.; Wuest, T. Pattern Recognition in Multivariate Time Series: Towards an Automated Event Detection Method for Smart Manufacturing Systems. J. Manuf. Mater. Process. 2020, 4, 88. [Google Scholar] [CrossRef]
- Ritter, T.; Pedersen, C. Digitization capability and the digitalization of business models in business-to-business firms: Past, present, and future. Ind. Mark. Manag. 2020, 86, 180–190. [Google Scholar] [CrossRef]
- Minea, M.; Dumitrescu, C.M.; Dima, M. Robotic Railway Multi-Sensing and Profiling Unit Based on Artificial Intelligence and Data Fusion. Sensors 2021, 21, 6876. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M. Applying Sensor-Based Information Systems to Identify Unplanned Downtime in Mining Machinery Operation. Sensors 2022, 22, 2127. [Google Scholar] [CrossRef]
- Gorski, E.G.; Loures, E.D.F.R.; Santos, E.A.P.; Kondo, R.E.; Martins, G.R.D.N. Towards a smart workflow in CMMS/EAM systems: An approach based on ML and MCDM. J. Ind. Inf. Integr. 2022, 26, 100278. [Google Scholar] [CrossRef]
- Ciancio, V.; Homri, L.; Dantan, J.Y.; Siadat, A.; Convain, P. Development of a flexible predictive maintenance system in the context of Industry 4.0. IFAC Pap. 2022, 55, 1576–1581. [Google Scholar] [CrossRef]
- Wieczorowski, M.; Trojanowska, J. Towards Metrology 4.0 in Dimensional Measurements. J. Mach. Eng. 2023, 23, 100–113. [Google Scholar] [CrossRef]
- De Groot, P.; Schmidt, M. Metrology & industry 4.0: Deploying optical technology and process control solutions to the smart factory floor. PhotonicsViews 2021, 18, 73–75. [Google Scholar] [CrossRef]
- Catalucci, S.; Thompson, A.; Piano, S.; Branson, D.T., III; Leach, R. Optical metrology for digital manufacturing: A review. Int. J. Adv. Manuf. Technol. 2022, 120, 4271–4290. [Google Scholar] [CrossRef]
- Wieczorowski, M.; Kucharski, D.; Sniatala, P.; Pawlus, P.; Krolczyk, G.; Gapinski, B. A novel approach to using artificial intelligence in coordinate metrology including nano scale. Measurement 2023, 217, 113051. [Google Scholar] [CrossRef]
- Kubátová, D.; Melichar, M.; Kutlwašer, J. Evaluation of Repeatability and reproducibility of CMM equipment. Procedia Manuf. 2017, 13, 558–564. [Google Scholar] [CrossRef]
- Iglesias, I.; Sanchez, A.; Silva, F.J.G. Robotic path compensation training method for optimizing face milling operations based on non-contact CMM techniques. Robot. Comput. Integr. Manuf. 2024, 85, 102623. [Google Scholar] [CrossRef]
- Kaarlela, T.; Niemi, T.; Pitkäaho, T.; Harjula, J. Retrofitting enables sustainability, Industry 4.0 connectivity, and improved usability. Adv. Ind. Manuf. Eng. 2024, 9, 100146. [Google Scholar] [CrossRef]
- Majstorovic, V.; Stojadinovic, S.; Jakovljevic, Z.; Zivkovic, S.; Djurdjanovic, D.; Kostic, J.; Gligorijevic, N. Cyber-Physical Manufacturing Metrology Model (CPM3)—Big Data Analytics Issue. Procedia CIRP 2018, 72, 503–508. [Google Scholar] [CrossRef]
- Emmer, C.; Glaesner, K.H.; Pfouga, A.; Stjepandić, J. Advances in 3D Measurement Data Management for Industry 4.0. Procedia Manuf. 2017, 11, 1335–1342. [Google Scholar] [CrossRef]
- Franco, P.; Jodar, J. Theoretical Analysis of Measuring Accuracy of Three Linear Axis CMMs from Position Errors. Int. J. Precis. Eng. Manuf. 2020, 21, 2235–2247. [Google Scholar] [CrossRef]
- Mazur, T.; Cepova, L.; Szymanski, T.; Rucki, M. Analysis of the Planar Point Identification Accuracy in CMM Measurements. Sensors 2022, 22, 7005. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, X.; Zhang, X.; Shen, Y.; Ling, T. A LS-SVM method for CMM geometric error identification based on spatially integrated measurement. Measurement 2025, 242 Pt B, 115952. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, Y.; Yan, L.; Huang, N.; Zhang, X.; Zhang, Y.; Zhu, L. Dynamic Error Modeling and Compensation of a Scanning Probe on CMM. IEEE Trans. Instrum. Meas. 2024, 73, 1009109. [Google Scholar] [CrossRef]
- Ito, S.; Tsutsumi, D.; Kamiya, K.; Matsumoto, K.; Kawasegi, N. Measurement of form error of a probe tip ball for coordinate measuring machine (CMM) using a rotating reference sphere. Precis. Eng. 2020, 61, 41–47. [Google Scholar] [CrossRef]
- Mazur, T.; Rucki, M.; Jakubowicz, M.; Cepova, L. Analysis of the Direction-Dependent Point Identification Accuracy in CMM Measurement. In Advances in Manufacturing III; Diering, M., Wieczorowski, M., Harugade, M., Pereira, A., Eds.; Springer: Cham, Switzerland, 2022; pp. 48–56. [Google Scholar] [CrossRef]
- Gu, Y.; Wu, J.; Liu, C. Error analysis and accuracy evaluation method for coordinate measurement in transformed coordinate system. Measurement 2025, 242 Pt A, 115860. [Google Scholar] [CrossRef]
- Mazur, T.; Rucki, M.; Gutsalenko, Y. Accuracy analysis of the curved profile measurement with CMM: A case study. Facta Univ. Ser. Mech. Eng. 2023, 21, 121–135. [Google Scholar] [CrossRef]
- He, G.; Sang, Y.; Wang, H.; Sun, G. A profile error evaluation method for freeform surface measured by sweep scanning on CMM. Precis. Eng. 2019, 56, 280–292. [Google Scholar] [CrossRef]
- Zelinka, J.; Čepová, L.; Gapiński, B.; Čep, R.; Mizera, O.; Hrubý, R. The Effect of a Stylus Tip on Roundness Deviation with Different Roughness. In Advances in Manufacturing II; Diering, M., Wieczorowski, M., Brown, C., Eds.; Springer: Cham, Switzerland, 2019; pp. 147–157. [Google Scholar] [CrossRef]
- Watanabe, M.; Sato, O.; Matsuzaki, K.; Kajima, M.; Watanabe, T.; Bitou, Y.; Takatsuji, T. Accurate surface profile measurement using CMM without estimating tip correction vectors. Precis. Eng. 2024, 91, 233–241. [Google Scholar] [CrossRef]
- Urban, J.; Resl, J.; Beránek, L.; Koptiš, M.; Petrášek, Š. Optimizing coordinate measuring machine measurement plans: Economic benefits and environmental impact. J. Clean. Prod. 2024, 477, 143891. [Google Scholar] [CrossRef]
- Mazur, T. Effects of Part Coordinate System Appointment on CMM Measurement. In Proceedings of 23rd International Scientific Conference Engineering for Rural Development, Jelgava, Latvia, 22–24 May 2024; pp. 769–774. [Google Scholar] [CrossRef]
- PH10 Legacy Probe Heads. Available online: https://www.renishaw.com/cmmsupport/knowledgebase/en/ph10-legacy-probe-heads--38818?srsltid=AfmBOooFOyofcLOwI5J7OWINzFyFVNOyYRAT8MCDmfxrMbjpbPVUHO1i (accessed on 10 December 2024).
- BIPM/JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty of Measurement. Joint Committee for Guides in Metrology/BIPM: Sèvres, France, 2008.
- Stojadinovic, S.M.; Majstorovic, V.D.; Gąska, A.; Sładek, J.; Durakbasa, N.M. Development of a Coordinate Measuring Machine—Based Inspection Planning System for Industry 4.0. Appl. Sci. 2021, 11, 8411. [Google Scholar] [CrossRef]
- Psarommatis, F.; Azamfirei, V. Customized quality inspection cycles for achieving sustainable manufacturing in the era of Zero Defect Manufacturing. Procedia CIRP 2023, 120, 141–146. [Google Scholar] [CrossRef]

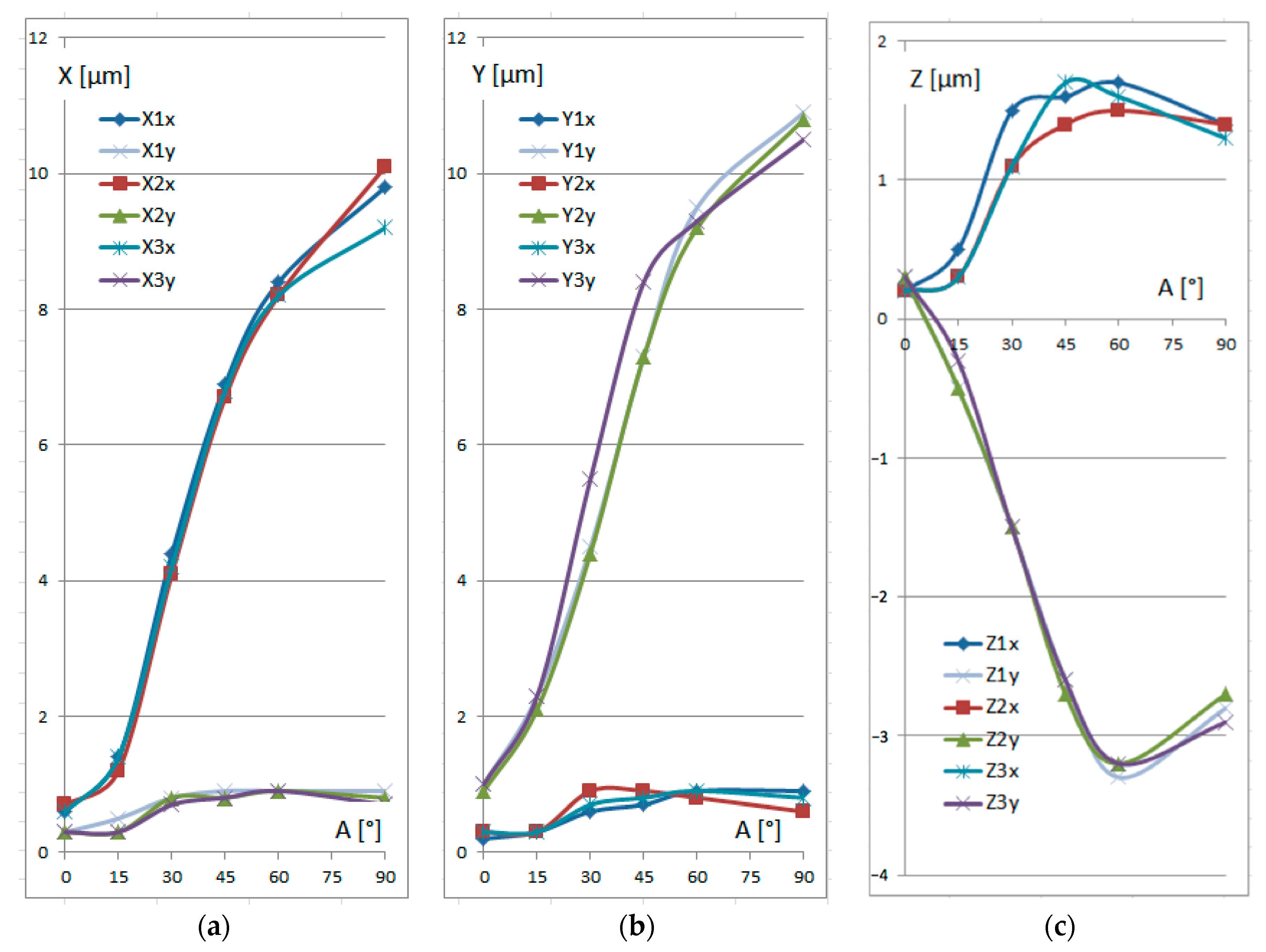


| Experiment Code | A = 0° | A = 15° | A = 30° | A = 45° | A = 60° | A = 90° |
|---|---|---|---|---|---|---|
| X1x | 0.6 | 1.4 | 4.4 | 6.9 | 8.4 | 9.8 |
| X1y | 0.3 | 0.5 | 0.8 | 0.9 | 0.9 | 0.9 |
| X2x | 0.7 | 1.2 | 4.1 | 6.7 | 8.2 | 10.1 |
| X2y | 0.3 | 0.3 | 0.8 | 0.8 | 0.9 | 0.8 |
| X3x | 0.6 | 1.4 | 4.2 | 6.8 | 8.2 | 9.2 |
| X3y | 0.3 | 0.3 | 0.7 | 0.8 | 0.9 | 0.7 |
| Y1x | 0.2 | 0.3 | 0.6 | 0.7 | 0.9 | 0.9 |
| Y1y | 1.0 | 2.3 | 4.5 | 7.3 | 9.5 | 10.9 |
| Y2x | 0.3 | 0.3 | 0.9 | 0.9 | 0.8 | 0.6 |
| Y2y | 0.9 | 2.1 | 4.4 | 7.3 | 9.2 | 10.8 |
| Y3x | 0.3 | 0.3 | 0.7 | 0.8 | 0.9 | 0.8 |
| Y3y | 1.0 | 2.3 | 5.5 | 8.4 | 9.3 | 10.5 |
| Z1x | 0.2 | 0.5 | 1.5 | 1.6 | 1.7 | 1.4 |
| Z1y | 0.3 | −0.5 | −1.5 | −2.6 | −3.3 | −2.8 |
| Z2x | 0.2 | 0.3 | 1.1 | 1.4 | 1.5 | 1.4 |
| Z2y | 0.3 | −0.5 | −1.5 | −2.7 | −3.2 | −2.7 |
| Z3x | 0.2 | 0.3 | 1.1 | 1.7 | 1.6 | 1.3 |
| Z3y | 0.3 | −0.3 | −1.5 | −2.6 | −3.2 | −2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazur, T.; Szymanski, T.; Samociuk, W.; Rucki, M.; Ryba, T. The Impact of Probe Angle and Swivel Length on Contact Point Identification in Coordinate Measuring Machine Measurements: A Case Study. Sensors 2025, 25, 2008. https://doi.org/10.3390/s25072008
Mazur T, Szymanski T, Samociuk W, Rucki M, Ryba T. The Impact of Probe Angle and Swivel Length on Contact Point Identification in Coordinate Measuring Machine Measurements: A Case Study. Sensors. 2025; 25(7):2008. https://doi.org/10.3390/s25072008
Chicago/Turabian StyleMazur, Tomasz, Tomasz Szymanski, Waldemar Samociuk, Miroslaw Rucki, and Tomasz Ryba. 2025. "The Impact of Probe Angle and Swivel Length on Contact Point Identification in Coordinate Measuring Machine Measurements: A Case Study" Sensors 25, no. 7: 2008. https://doi.org/10.3390/s25072008
APA StyleMazur, T., Szymanski, T., Samociuk, W., Rucki, M., & Ryba, T. (2025). The Impact of Probe Angle and Swivel Length on Contact Point Identification in Coordinate Measuring Machine Measurements: A Case Study. Sensors, 25(7), 2008. https://doi.org/10.3390/s25072008








