Tent–PSO-Based Unmanned Aerial Vehicle Path Planning for Cooperative Relay Networks in Dynamic User Environments
Abstract
1. Introduction
1.1. DRL
1.2. Bio-Inspired Optimization Algorithms
1.3. Chaotic Map
2. System Model and Problem Description
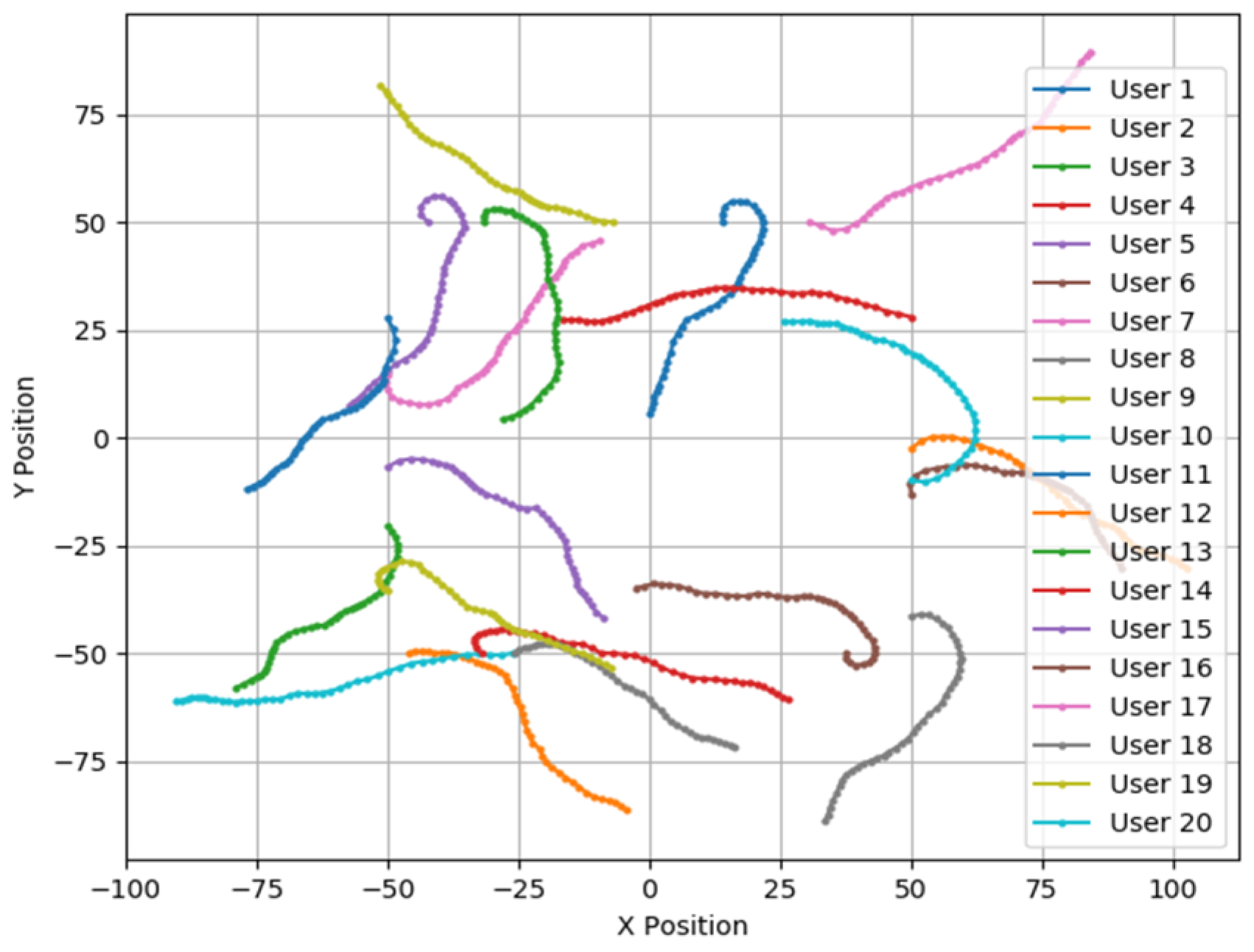
2.1. User Mobility Model
2.2. UAV Dynamic Constraints
2.3. Environmental Threats
2.4. Joint Optimization Objective
2.5. Path Smoothing Algorithm
3. Algorithm Improvement
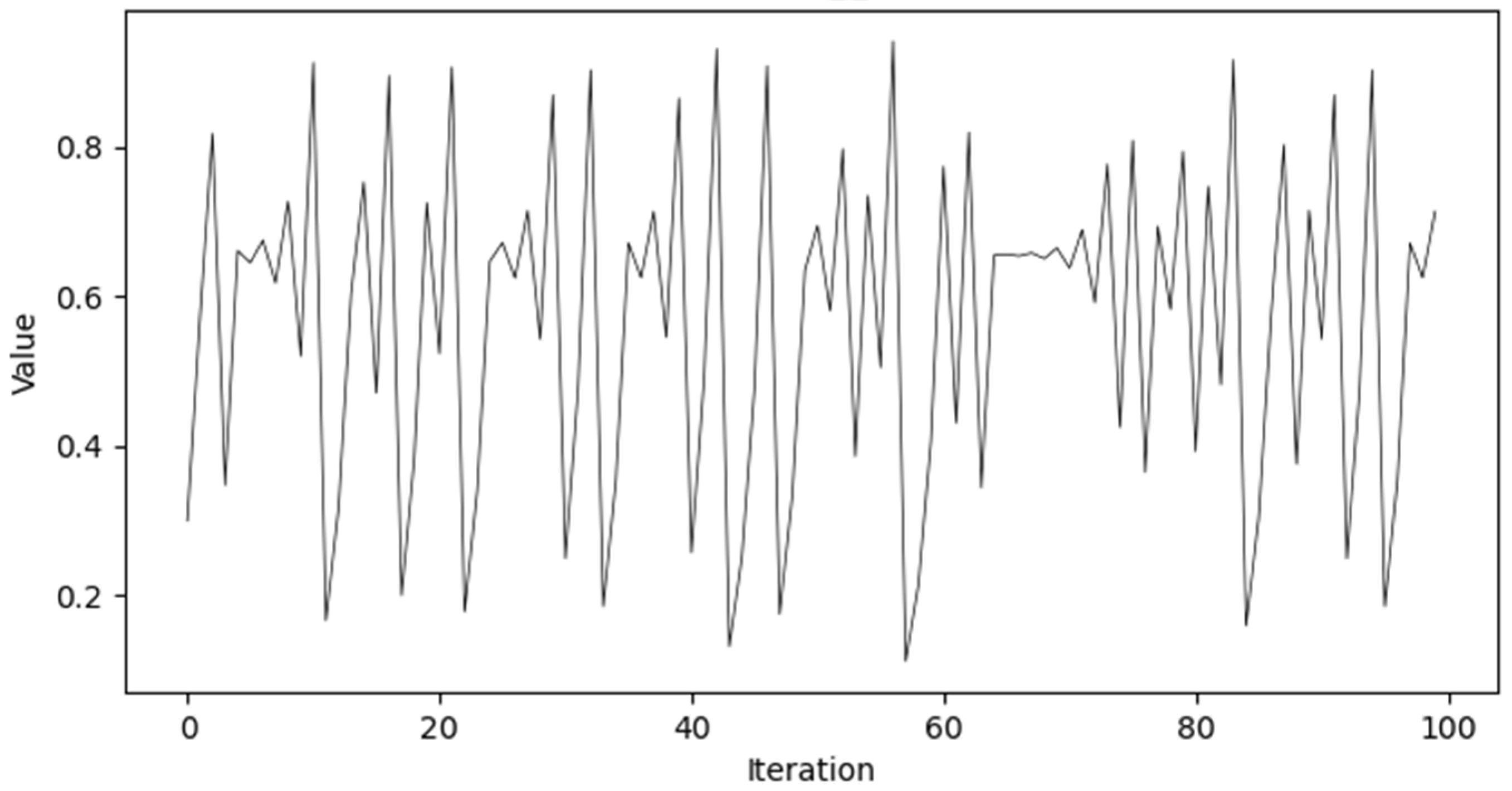
3.1. Tent Mapping Initialization
3.2. Adaptive Inertia Weight Adjustment
3.3. Learning Factor Adjustment
3.4. UAV Speed and Position Update Formulas
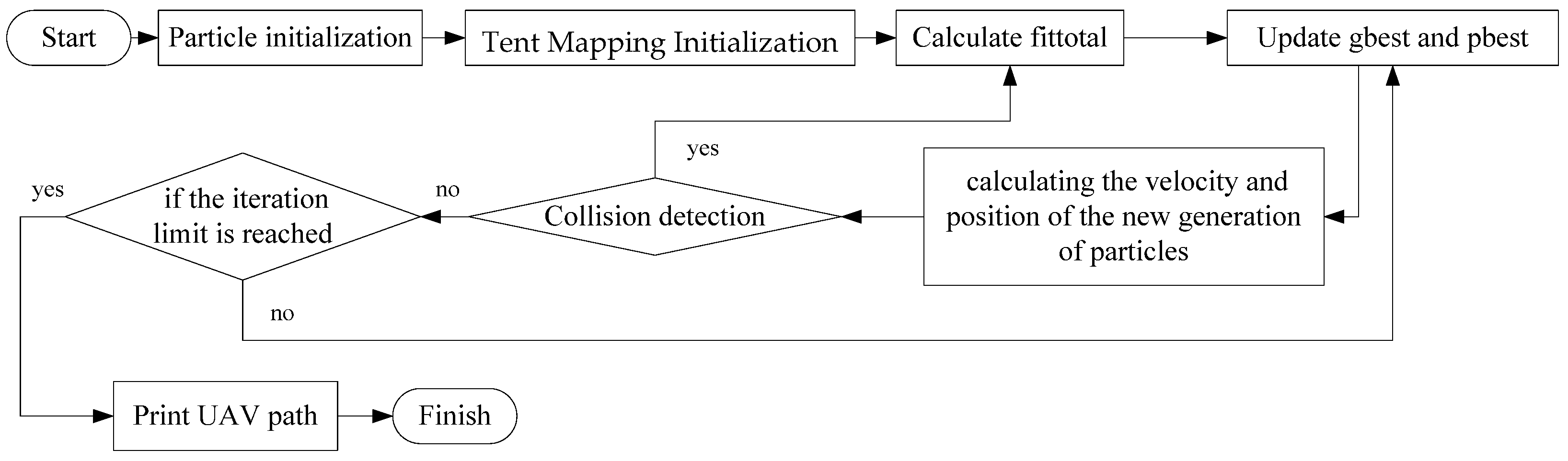
3.5. Tent–PSO Procedure
| Algorithm 1 Tent–PSO | |
| 1: | Input: ; |
| 2: | Output: final UAV positions and paths; |
| 3: | for each do |
| 4: | ; |
| 5: | Evaluate and set ; |
| 6: | ; |
| 7: | end for |
| 8: | for < do |
| 9: | for each do |
| 10: | Update and by (19)–(21); |
| 11: | Update and by (22) and (23); |
| 12: | Update by (13–15); |
| 13: | if |
| 14: | ; |
| 15: | else |
| 16: | ; |
| 17: | end if |
| 18: | end for |
| 19: | end for |
| 20: | |
4. Experimental Results
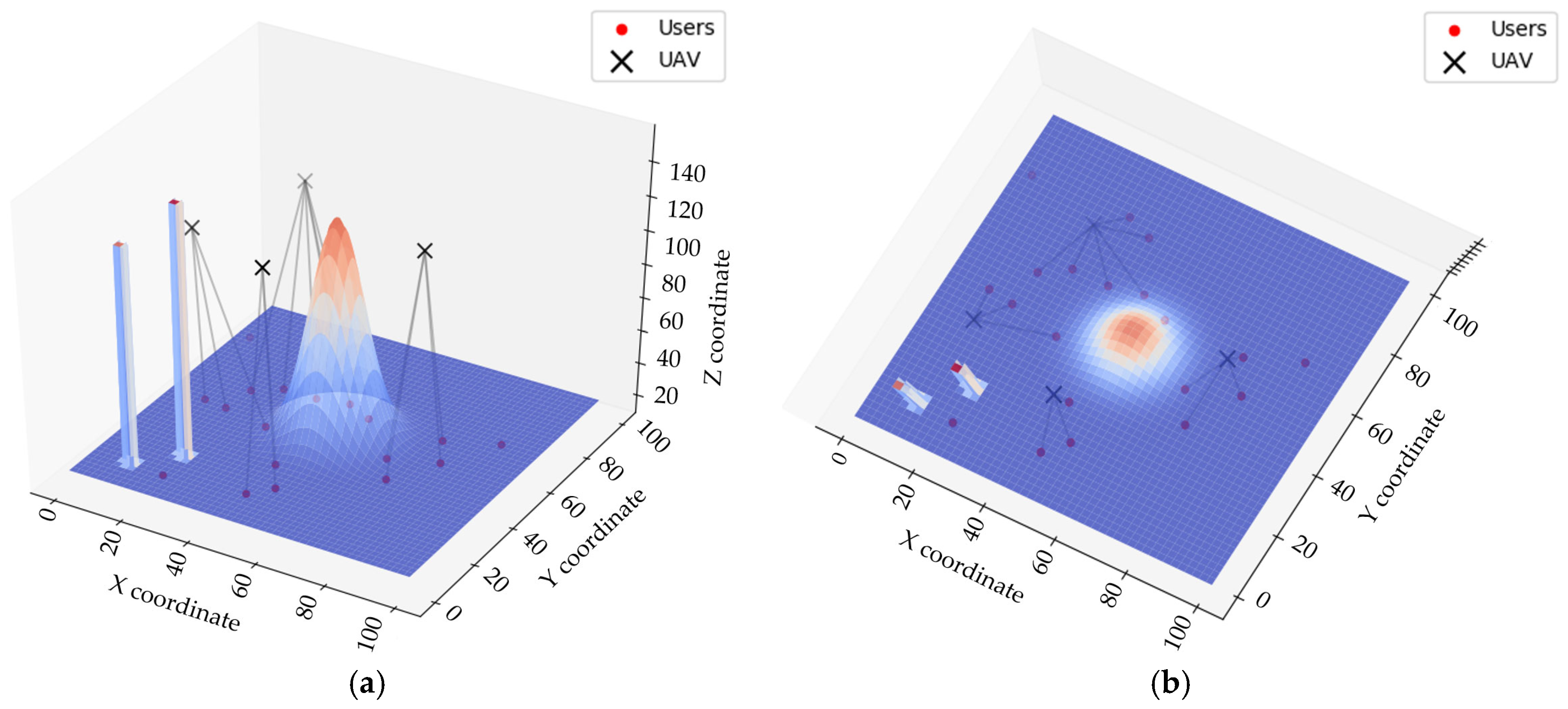
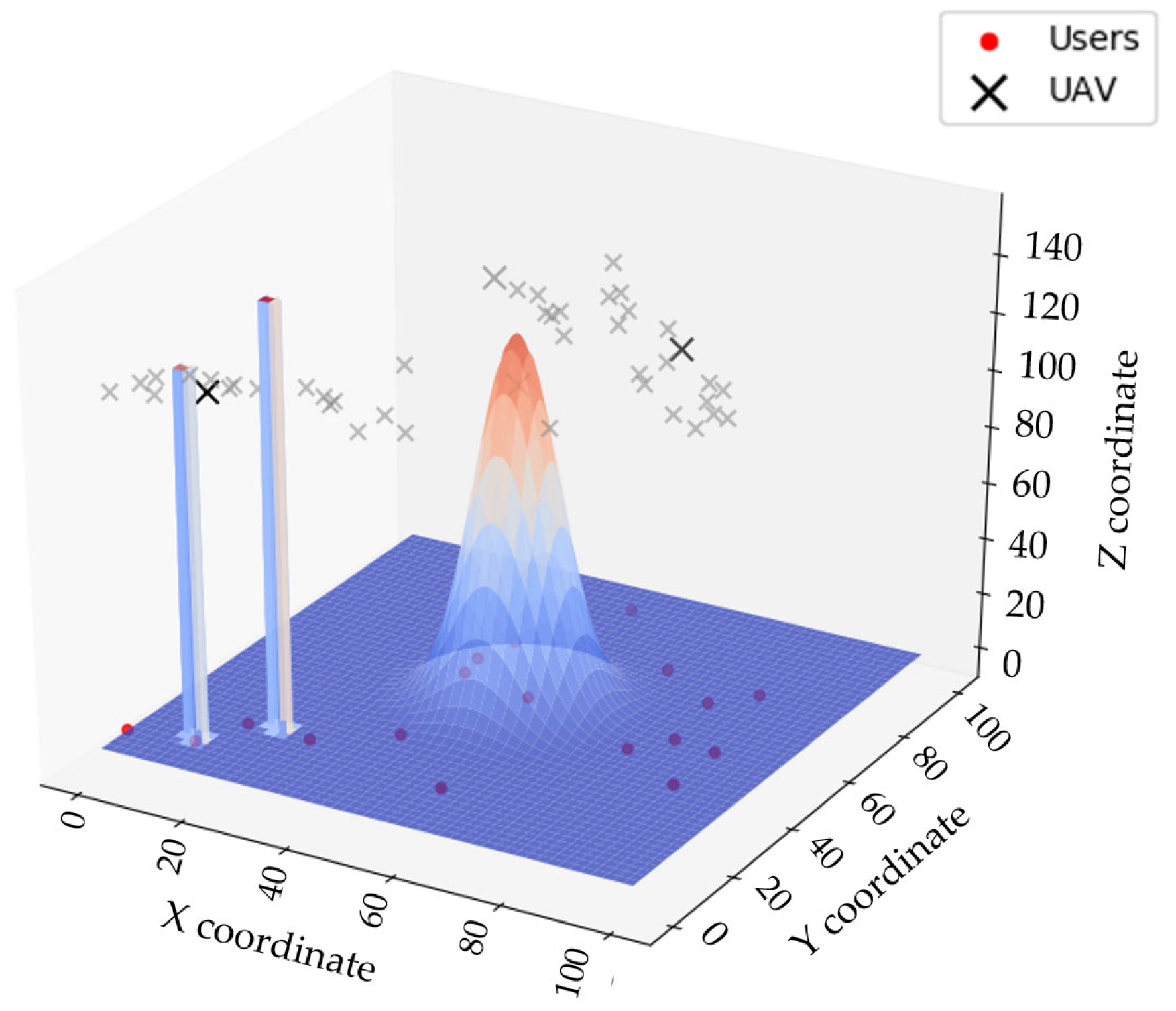
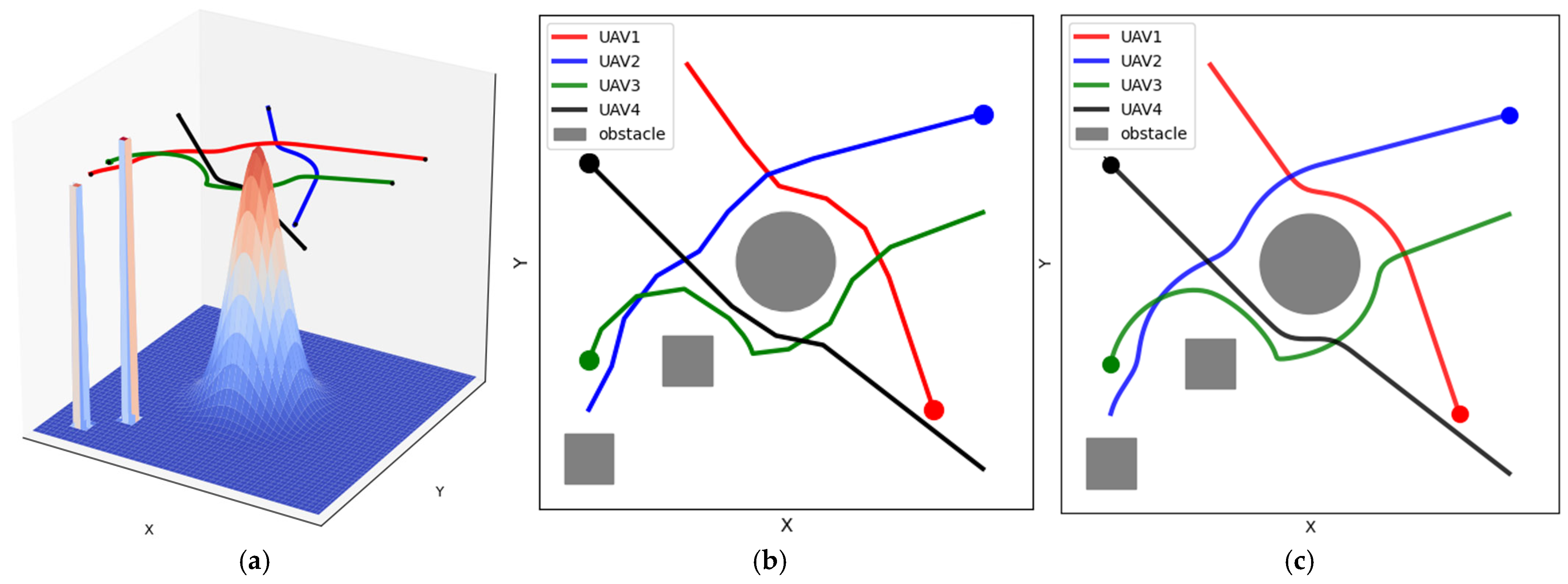
4.1. Simulation Parameter Design and UAV Path
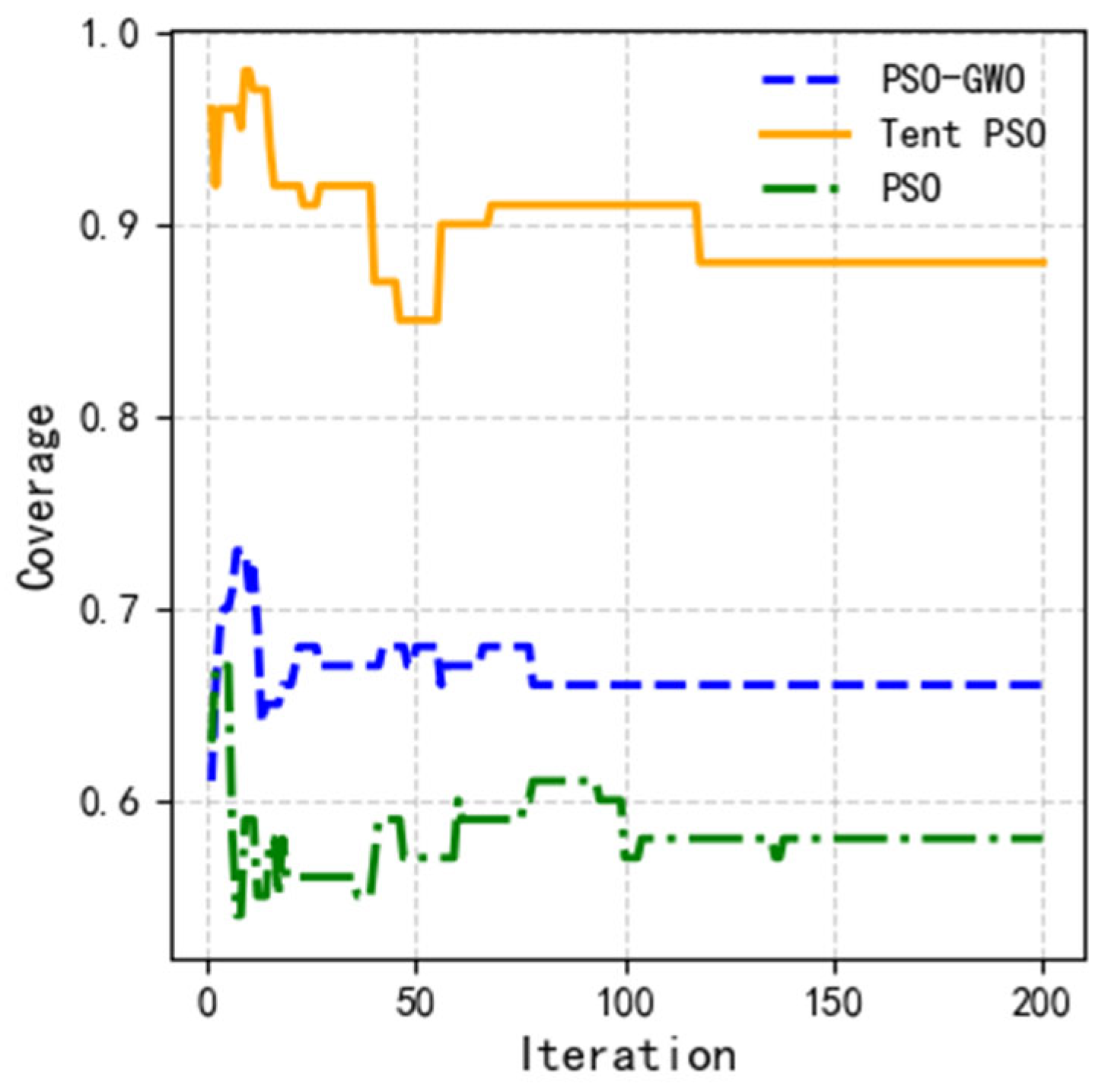
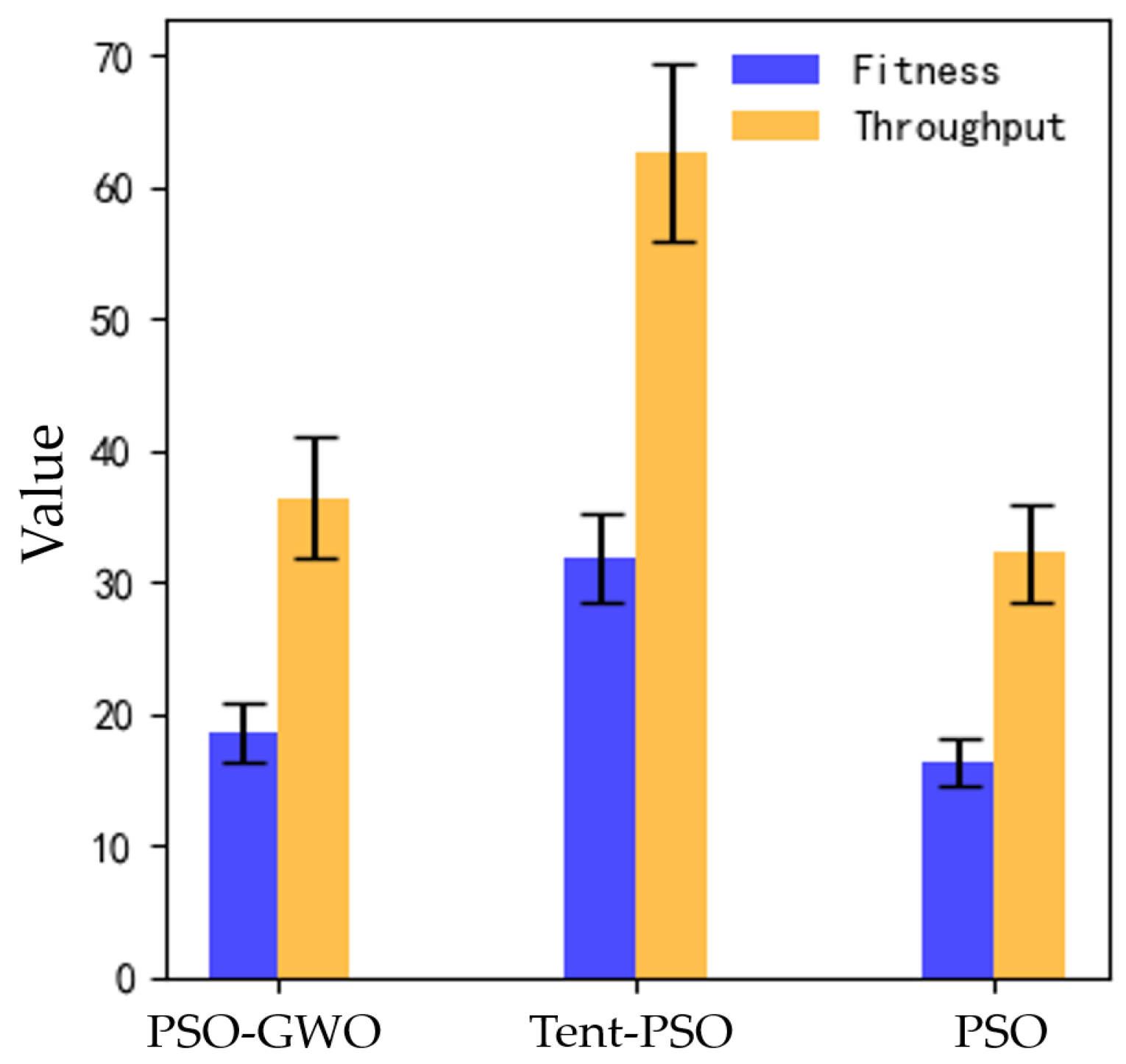
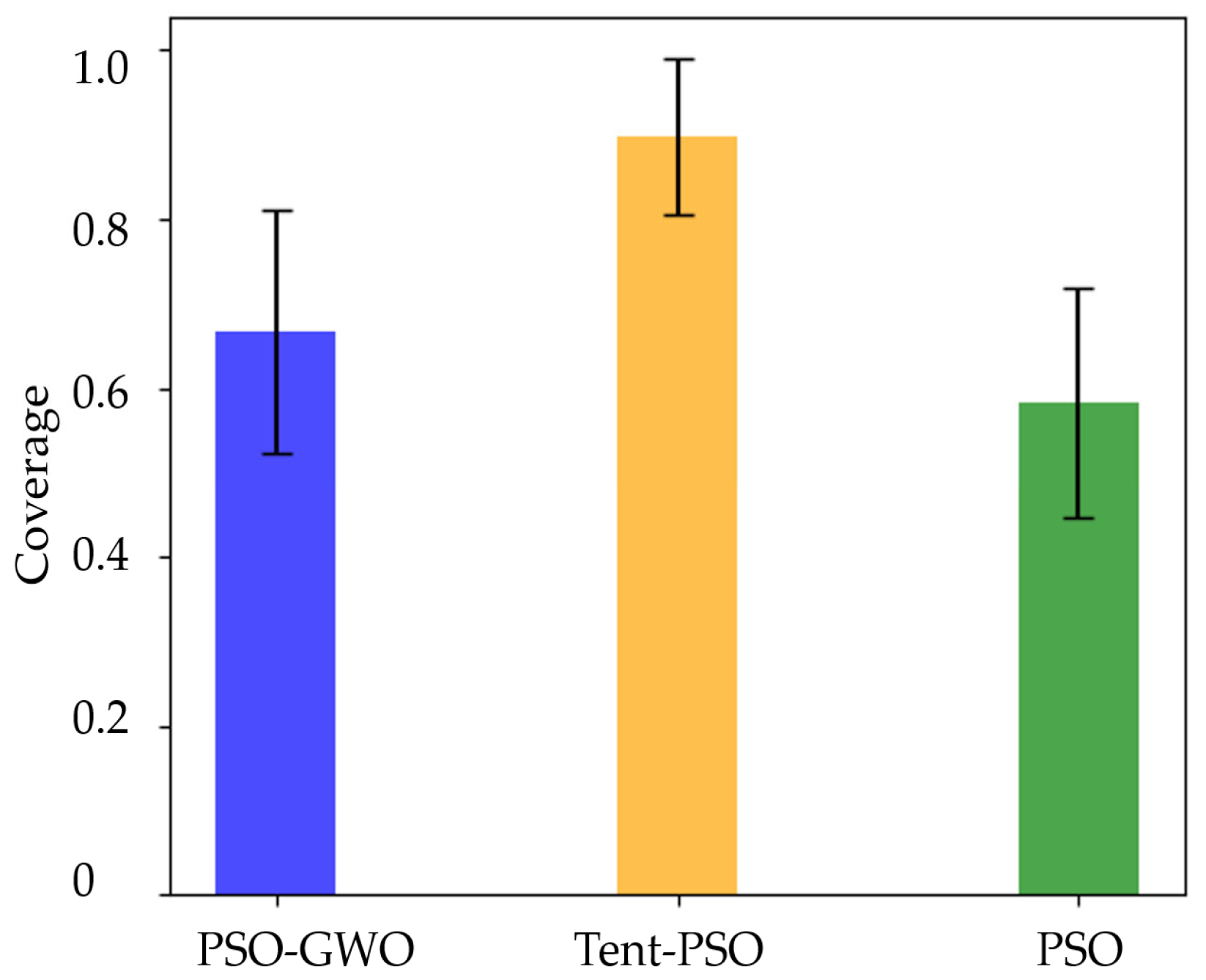
4.2. Comparison of Experimental Data
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, T.; Jiang, Z.; Sun, R.; Cheng, N.; Feng, H. Maritime Search and Rescue Based on Group Mobile Computing for Unmanned Aerial Vehicles and Unmanned Surface Vehicles. IEEE Trans. Ind. Inform. 2020, 16, 7700–7708. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Xu, M. The Coverage Problem in UAV Network: A Survey. In Proceedings of the Fifth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Hefei, China, 11–13 July 2014; pp. 1–5. [Google Scholar]
- Greenberg, E.; Bar, A.; Klodzh, E. LOS Classification of UAV-to-Ground Links in Built-up Areas. In Proceedings of the 2019 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel-Aviv, Israel, 4–6 November 2019; pp. 1–5. [Google Scholar]
- Ahmed, S.; Chowdhury, M.Z.; Jang, Y.M. Energy-Efficient UAV Relaying Communications to Serve Ground Nodes. IEEE Commun. Lett. 2020, 24, 849–852. [Google Scholar] [CrossRef]
- Dai, T.; Li, A.; Wang, H. Design and Implementation of a Relay Mechanism in Restricted UAVs Ad-hoc Networks. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; pp. 605–611. [Google Scholar]
- Huang, H.; Savkin, A.V.; Ding, M.; Kaafar, M.A. Optimized Deployment of Drone Base Station to Improve User Experience in Cellular Networks. J. Netw. Comput. Appl. 2019, 144, 49–58. [Google Scholar] [CrossRef]
- Li, X.; Xu, X. UAV Comprehensive Coverage to Users in Urban Environment. In Proceedings of the 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 November 2018; pp. 503–506. [Google Scholar]
- Khuwaja, A.A.; Chen, Y. 3D Mobility Models and Their Impact on the Outage Performance of UAV Communications. IEEE Wirel. Commun. Lett. 2024, 13, 3129–3132. [Google Scholar] [CrossRef]
- Hou, X.; Liu, F.; Wang, R.; Yu, Y. A UAV Dynamic Path Planning Algorithm. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Zhanjiang, China, 16–18 October 2020; pp. 127–131. [Google Scholar]
- Ladosz, P.; Oh, H.; Zheng, G.; Chen, W.-H. A Hybrid Approach of Learning and Model-based Channel Prediction for Communication Relay UAVs in Dynamic Urban Environments. IEEE Robot. Autom. Lett. 2019, 4, 2370–2377. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R.; Lim, T.J. Placement Optimization of UAV-Mounted Mobile Base Stations. IEEE Commun. Lett. 2017, 21, 604–607. [Google Scholar] [CrossRef]
- Agrawal, S.; Patle, B.K.; Sanap, S. Path Planning of UAV in Uncertain Static Environment Using Matrix Based Genetic Algorithm (MGA). In Proceedings of the 2023 International Conference on Integration of Computational Intelligent System (ICICIS), Pune, India, 1–4 November 2023; pp. 1–7. [Google Scholar]
- Mehmood, D.; Ali, A.; Ali, S.; Kulsoom, F.; Chaudhry, H.N.; Haider, A.Z.U. A Novel Hybrid Genetic and A-star Algorithm for UAV Path Optimization. In Proceedings of the 2024 IEEE 1st Karachi Section Humanitarian Technology Conference (KHI-HTC), Tandojam, Pakistan, 8–9 January 2024; pp. 1–5. [Google Scholar]
- Zheng, J.; Sun, X.; Ji, Y.; Wu, J. Research on UAV Path Planning Based on Improved ACO Algorithm. In Proceedings of the 2023 IEEE 11th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 8–10 December 2023; Volume 11, pp. 762–770. [Google Scholar]
- Li, J.; Xiong, Y.; She, J. UAV Path Planning for Target Coverage Task in Dynamic Environment. IEEE Internet Things J. 2023, 10, 17734–17745. [Google Scholar] [CrossRef]
- Sonny, A.; Yeduri, S.R.; Cenkeramaddi, L.R. Autonomous UAV Path Planning Using Modified PSO for UAV-Assisted Wireless Networks. IEEE Access 2023, 11, 70353–70367. [Google Scholar] [CrossRef]
- Yu, Z.; Si, Z.; Li, X.; Wang, D.; Song, H. A Novel Hybrid Particle Swarm Optimization Algorithm for Path Planning of UAVs. IEEE Internet Things J. 2022, 9, 22547–22558. [Google Scholar] [CrossRef]
- Zhang, H.; Gan, X.; Li, S.; Chen, Z. UAV Safe Route Planning Based on PSO-BAS Algorithm. J. Syst. Eng. Electron. 2022, 33, 1151–1160. [Google Scholar] [CrossRef]
- Korneev, D.A.; Leonov, A.V.; Litvinov, G.A. Estimation of Mini-UAVs Network Parameters for Search and Rescue Operation Scenario With Gauss-Markov Mobility Model. In Proceedings of the 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO), Minsk, Belarus, 4–5 July 2018; pp. 1–7. [Google Scholar]
- Hata, Y.; Iwai, H.; Ibi, S. Estimation Formula of UAV-BS Density for Required LOS Coverage in Urban Environments. In Proceedings of the 2023 IEEE International Symposium On Antennas and Propagation (ISAP), Kuala Lumpur, Malaysia, 30 October–2 November 2023; pp. 1–2. [Google Scholar]
- Patel, A.K.; Joshi, R.D. Area Coverage Analysis of Low Altitude UAV Bases Station Using Statistical Channel Model. In Proceedings of the 2022 International Conference on Signal and Information Processing (IConSIP), Pune, India, 26–27 August 2022; pp. 1–6. [Google Scholar]
- Li, B.; Zhang, Y.; Zhang, T.; Acarman, T.; Ouyang, Y.; Li, L.; Dong, H.; Cao, D. Embodied Footprints: A Safety-Guaranteed Collision-Avoidance Model for Numerical Optimization-Based Trajectory Planning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 2046–2060. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Nayeem, G.M.; Fan, M.; Daiyan, G.M.; Fahad, K.S. UAV Path Planning with an Adaptive Hybrid PSO. In Proceedings of the 2023 International Conference on Information and Communication Technology for Sustainable Development (ICICT4SD), Dhaka, Bangladesh, 21–23 September 2023; pp. 139–143. [Google Scholar]





| Parameter | Description | Value |
|---|---|---|
| UAV number | 4 | |
| Users number | 20 | |
| UAV safe distance | 10 | |
| path loss exponent under LOS | 3 | |
| path loss exponent under NLOS | 3.5 | |
| weight coefficient | 0.3 | |
| weight coefficient | 0.4 | |
| weight coefficient | 0.1 | |
| weight coefficient | 0.1 | |
| weight coefficient | 0.1 | |
| decay factor | 0.9 | |
| initial value of the inertia weight | 1.2 | |
| final value of the inertia weight | 0.3 | |
| UAV’s transmission power | 1 MHz | |
| carrier frequency | 2 GHz | |
| noise power | −20 dBm | |
| channel bandwidth | 10 MHz | |
| channel constant factor | 1 | |
| chaotic coefficient | 0.5 | |
| maximum value of individual factor | 2.5 | |
| maximum value of social factor | 1 |
| PSO | PSO-GWO | Tent–PSO | |
|---|---|---|---|
| fitness | 1.76 | 2.28 | 3.37 |
| throughput | 3.64 | 4.65 | 6.71 |
| Coverage | 0.12 | 0.16 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhou, W.; Qin, M.; Peng, X. Tent–PSO-Based Unmanned Aerial Vehicle Path Planning for Cooperative Relay Networks in Dynamic User Environments. Sensors 2025, 25, 2005. https://doi.org/10.3390/s25072005
Liu S, Zhou W, Qin M, Peng X. Tent–PSO-Based Unmanned Aerial Vehicle Path Planning for Cooperative Relay Networks in Dynamic User Environments. Sensors. 2025; 25(7):2005. https://doi.org/10.3390/s25072005
Chicago/Turabian StyleLiu, Shuyue, Wenmao Zhou, Mingwei Qin, and Xin Peng. 2025. "Tent–PSO-Based Unmanned Aerial Vehicle Path Planning for Cooperative Relay Networks in Dynamic User Environments" Sensors 25, no. 7: 2005. https://doi.org/10.3390/s25072005
APA StyleLiu, S., Zhou, W., Qin, M., & Peng, X. (2025). Tent–PSO-Based Unmanned Aerial Vehicle Path Planning for Cooperative Relay Networks in Dynamic User Environments. Sensors, 25(7), 2005. https://doi.org/10.3390/s25072005





