Estimating Tea Plant Physiological Parameters Using Unmanned Aerial Vehicle Imagery and Machine Learning Algorithms
Abstract
:1. Introduction
2. Materials and Methods
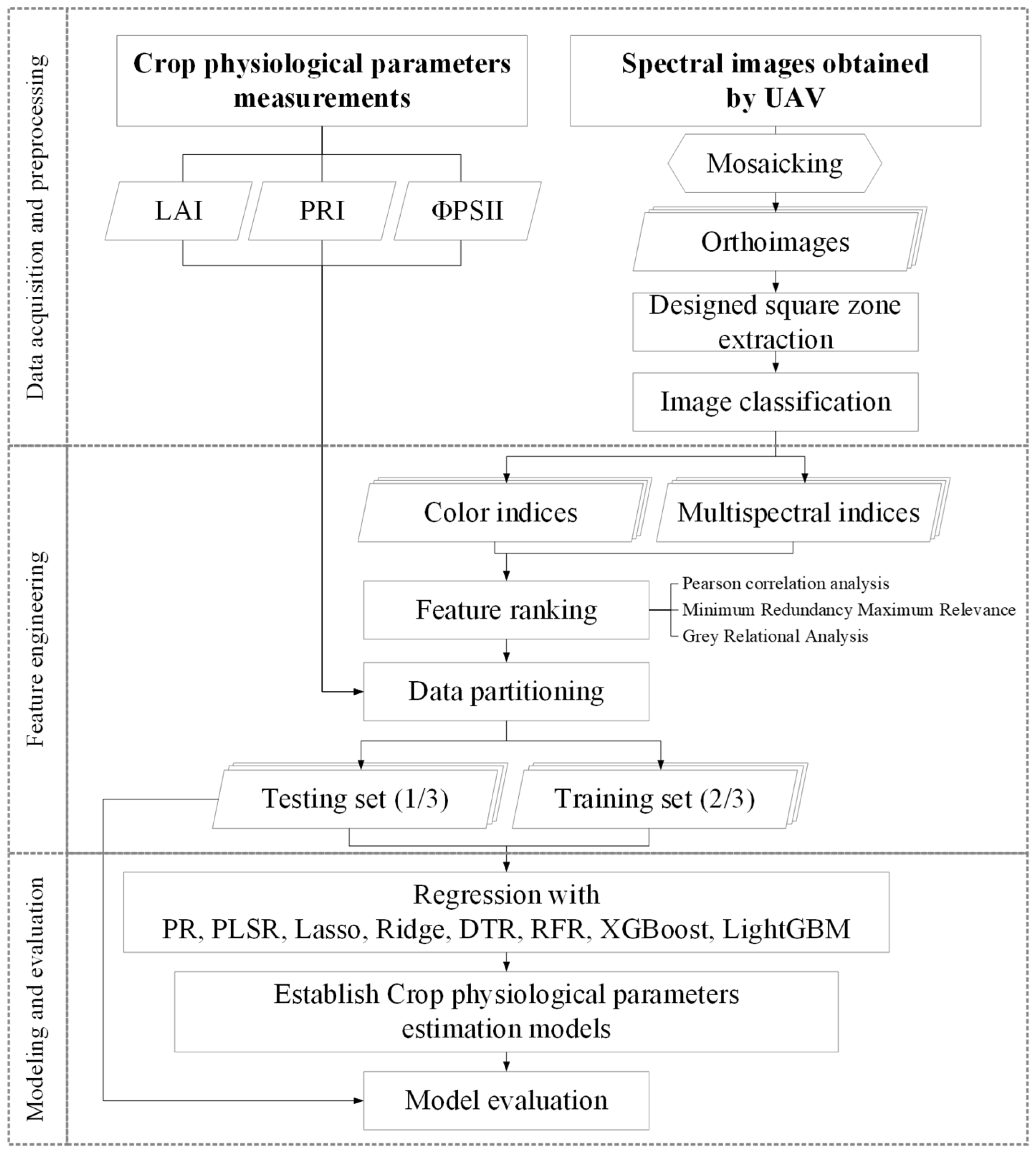
2.1. Overview
2.2. Experimental Site and Design
2.3. Data Acquisition
2.3.1. Tea Plant Physiological Parameter Acquisition
2.3.2. UAV Image Acquisition
2.4. Image Processing
2.4.1. Canopy Part Segmentation
2.4.2. Calculation of Color Indices and Multispectral Indices
2.5. Feature Ranking Methods
2.5.1. Pearson Correlation Analysis
2.5.2. Minimum Redundancy Maximum Relevance
2.5.3. Gray Relational Analysis
2.6. Model Training and Evaluation Metrics
3. Results
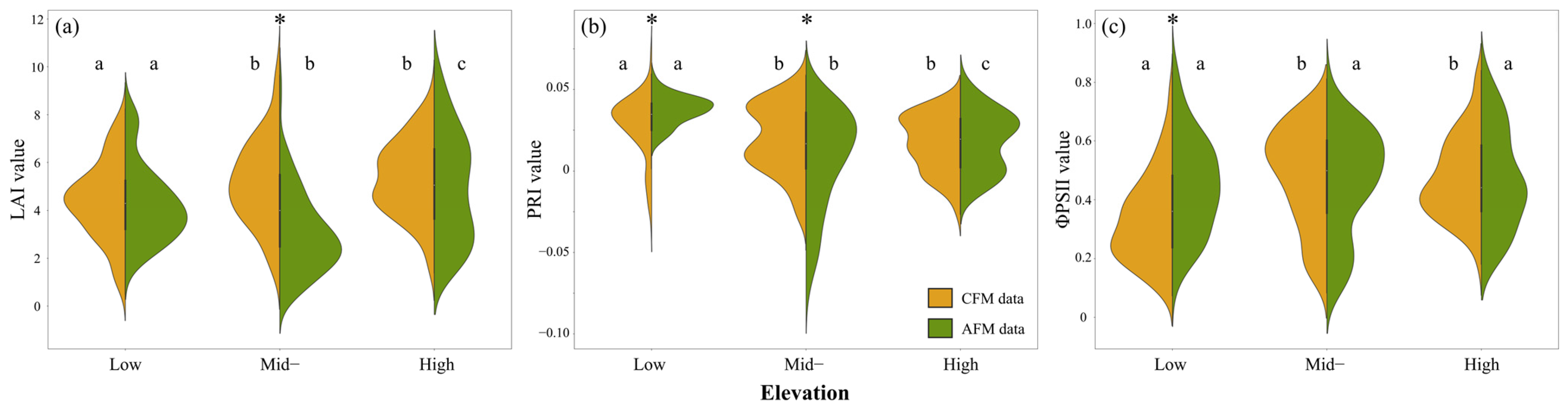
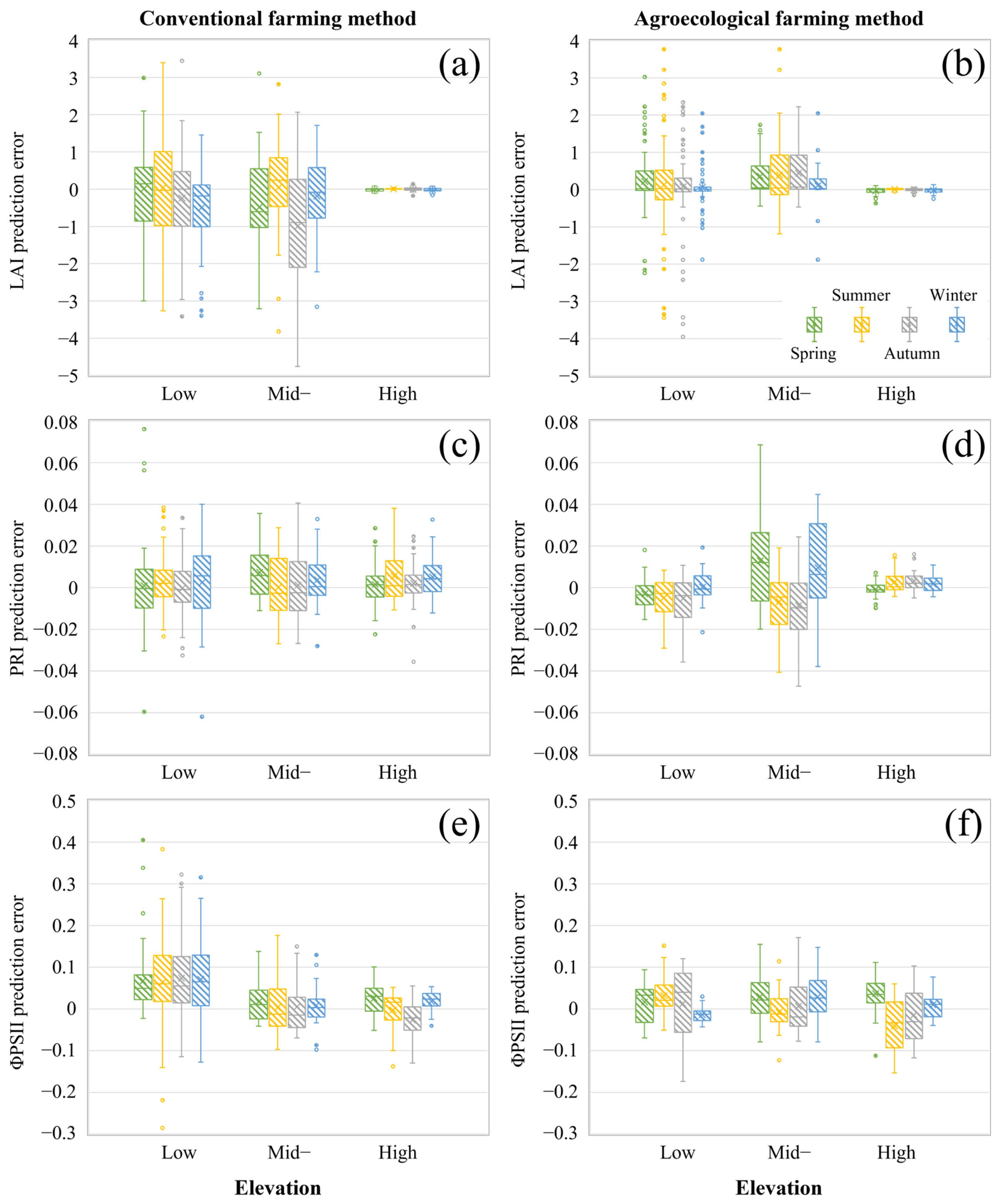
3.1. Effects of Elevation Distribution and Farming Method Differences on Tea Plant Physiology
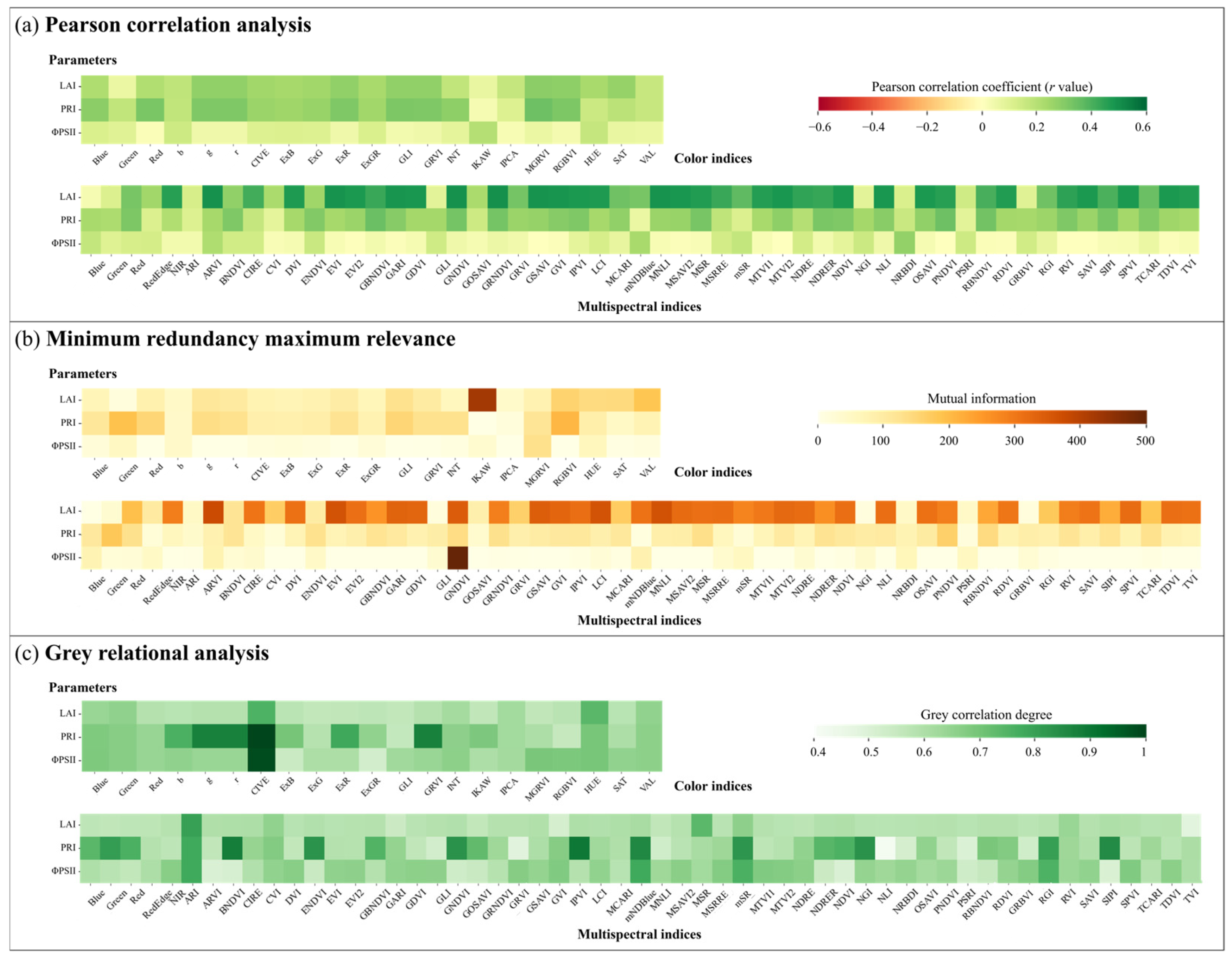
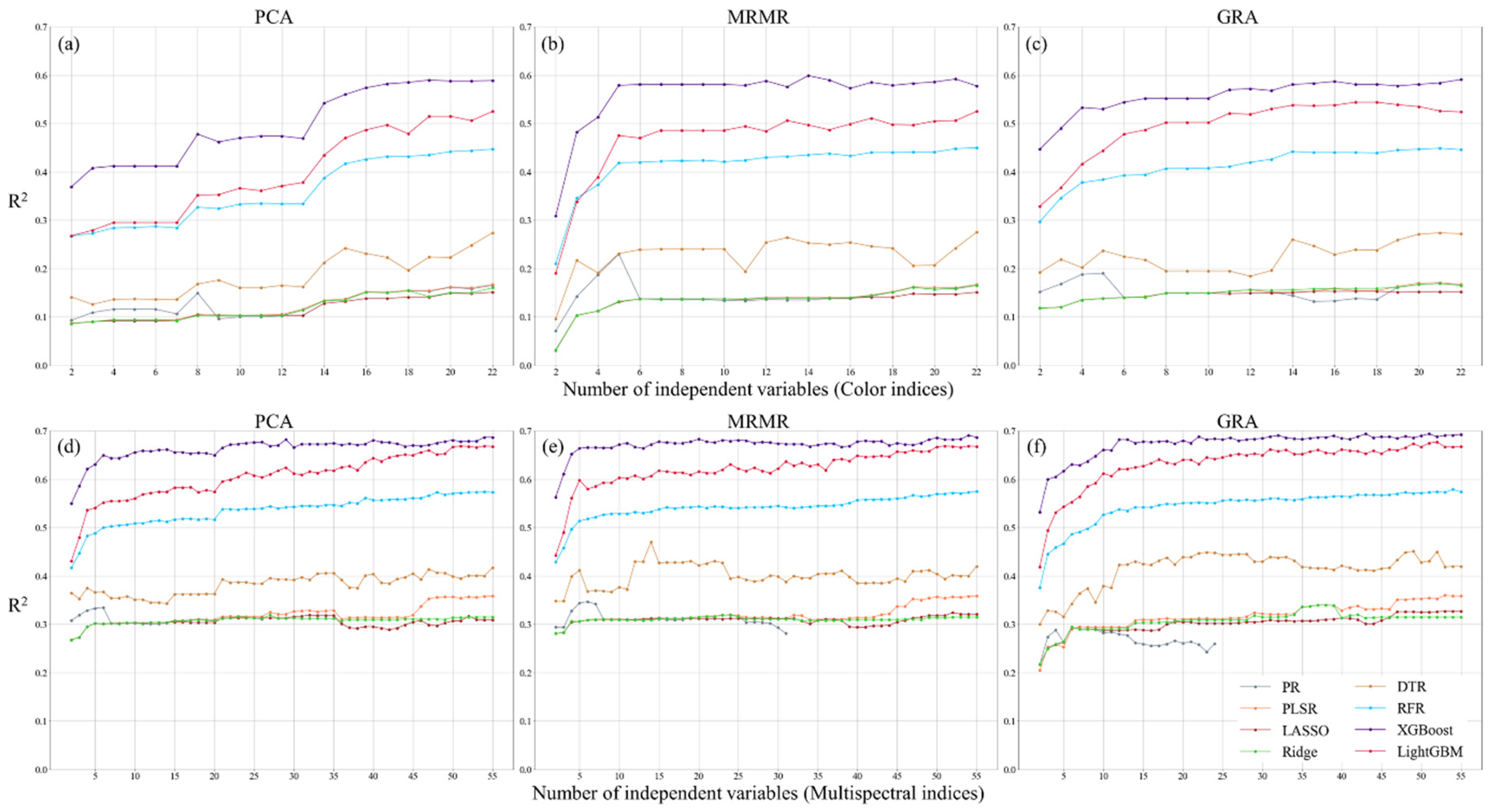
3.2. Feature Ranking of Image Indices
3.3. Comparison of Regression Model Accuracy for Tea Plant Physiological Parameter Estimation
3.4. Effects of Elevation and Seasonal Conditions on Prediction Accuracy
4. Discussion
4.1. Differences in Tea Plant Physiological Parameters Across Elevations and Farming Methods
4.2. Effects of Feature Ranking Methods and Image Indices on Prediction Models
4.3. Applicability Analysis of Regression Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| Low elev. | Field | CLS001 | CLS002 | CLS003 | CLS004 | CLJ001 | ALS001 | ALS002 | ALS003 | |||||||||
| Area | 3399 | 1142 | 1616 | 1110 | 6499 | 1651 | 2697 | 3065 | ||||||||||
| Slope | 1.74 | 3.04 | 4.12 | 1.96 | 4.17 | 1.74 | 1.36 | 4.19 | ||||||||||
| Elev. | 329 | 279 | 388 | 324 | 371 | 315 | 348 | 288 | ||||||||||
| Mid-elev. | Field | CMC001 | CMJ001 | CMJ002 | AMC001 | AMJ001 | AMJ002 | |||||||||||
| Area | 1131 | 1658 | 1911 | 1131 | 1658 | 1911 | ||||||||||||
| Slope | 1.04 | 16.87 | 3.70 | 1.04 | 16.87 | 3.70 | ||||||||||||
| Elev. | 565 | 826~833 | 924~926 | 565 | 826~833 | 924~926 | ||||||||||||
| High elev. | Field | CHO001 | CHO002 | CHO003 | AHO001 | AHO002 | AHO003 | AHJ001 | ||||||||||
| Area | 28,749 | 5122 | 16,138 | 3412 | 10,744 | 4805 | 2082 | |||||||||||
| Slope | 42.35 | 36.83 | 24.35 | 18.19 | 35.65 | 20.63 | 27.25 | |||||||||||
| Elev. | 1510~1572 | 1406~1451 | 1381~1414 | 1523~1536 | 1476~1508 | 1452~1467 | 1471~1478 | |||||||||||
| Color Indices (CIs) | |
| Normalized Blue | |
| Normalized Green | |
| Normalized Red | |
| Color Index of Vegetation | |
| Excess Blue Vegetation Index | |
| Excess Green Vegetation Index | |
| Excess Red Vegetation Index | |
| Excess Green Minus Excess Red Index | |
| Green Leaf Index | |
| Green–Red Vegetation Index | |
| Color Intensity Index | |
| Kawashima Index | |
| Principal Component Analysis Index | |
| Modified Green–Red Vegetation Index | |
| Red–Green–Blue Vegetation Index | |
| Hue | |
| Saturation | |
| Value | |
| Multispectral indices (MIs) | |
| Anthocyanin Reflectance Index | |
| Atmospherically Resistant Vegetation Index | |
| Blue Normalized Difference Vegetation Index | |
| Chlorophyll Index Red Edge | |
| Chlorophyll Vegetation Index | |
| Difference Vegetation Index | |
| Enhanced Normalized Difference Vegetation Index | |
| Enhanced Vegetation Index | |
| Enhanced Vegetation Index 2 | |
| Green–Blue Normalized Difference Vegetation Index | |
| Green Atmospherically Resistant Index | |
| Green Difference Vegetation Index | |
| Green Leaf Index | |
| Green Normalized Difference Vegetation Index | |
| Green Optimized Soil-Adjusted Vegetation Index | |
| Green–Red Normalized Difference Vegetation Index | |
| Green–Red Vegetation Index | |
| Green Soil-Adjusted Vegetation Index | |
| Green Vegetation Index | |
| Infrared Percentage Vegetation Index | |
| Leaf Chlorophyll Index | |
| Modified Chlorophyll Absorption in Reflectance Index | |
| Modified Normalized Difference Blue Index | |
| Modified Nonlinear Vegetation Index | |
| Modified Soil-Adjusted Vegetation Index 2 | |
| Modified Simple Ratio | |
| Red Edge Modified Simple Ratio | |
| Modified Red Edge Simple Ratio | |
| Modified Triangular Vegetation Index 1 | |
| Modified Triangular Vegetation Index | |
| Normalized Difference Red Edge Index | |
| Normalized Difference Red Edge/Red | |
| Normalized Difference Vegetation Index | |
| Normalized Green Intensity | |
| Nonlinear Vegetation Index | |
| Normalized Red–Blue Difference Index | |
| Optimized Soil-Adjusted Vegetation Index | |
| Pan Normalized Difference Vegetation Index | |
| Plant Senescence Reflectance Index | |
| Red–Blue Normalized Difference Vegetation Index | |
| Renormalized Difference Vegetation Index | |
| Red–Green–Blue Vegetation Indices | |
| Red–Green Index | |
| Ratio Vegetation Index | |
| Soil-Adjusted Vegetation Index | |
| Structure Insensitive Pigment Index | |
| Spectral Polygon Vegetation Index | |
| Transformed Chlorophyll Absorption in Reflectance Index | |
| Transformed Difference Vegetation Index | |
| Triangular Vegetation Index | |
References
- Li, S.; Wu, X.; Xue, H.; Gu, B.; Cheng, H.; Zeng, J.; Peng, C.; Ge, Y.; Chang, J. Quantifying carbon storage for tea plantations in China. Agric. Ecosyst. Environ. 2011, 141, 390–398. [Google Scholar]
- Pramanik, P.; Phukan, M. Potential of tea plants in carbon sequestration in North-East India. Environ. Monit. Assess. 2020, 192, 211. [Google Scholar] [PubMed]
- Chettri, V.; Ghosh, C. Tea Gardens, A Potential Carbon-Sink for Climate Change Mitigation. Curr. Agric. Res. J. 2023, 11, 695–704. [Google Scholar]
- Debnath, B.; Haldar, D.; Purkait, M.K. Potential and sustainable utilization of tea waste: A review on present status and future trends. J. Environ. Chem. Eng. 2021, 9, 106179. [Google Scholar] [CrossRef]
- Pan, S.Y.; Nie, Q.; Tai, H.C.; Song, X.L.; Tong, Y.F.; Zhang, L.J.F.; Wu, X.-W.; Lin, Z.-H.; Zhang, Y.-Y.; Ye, D.-Y.; et al. Tea and tea drinking: China’s outstanding contributions to the mankind. Chin. Med. 2022, 17, 27. [Google Scholar] [CrossRef]
- Eitzinger, A.; Läderach, P.; Quiroga, A.; Pantoja, A.; Gordon, J. Future Climate Scenarios for Kenya’s Tea Growing Areas; International Center for Tropical Agriculture: Palmira, Colombia; Consultative Group on International Agricultural Research: Montpellier, France, 2011. [Google Scholar]
- Zhong, C.; Cheng, S.; Kasoar, M.; Arcucci, R. Reduced-order digital twin and latent data assimilation for global wildfire prediction. Nat. Hazards Earth Syst. Sci. 2023, 23, 1755–1768. [Google Scholar]
- Xu, Z.; Li, J.; Cheng, S.; Rui, X.; Zhao, Y.; He, H.; Xu, L. Wildfire risk prediction: A review. arXiv 2024, arXiv:2405.01607. [Google Scholar]
- Hussain, S.; Ulhassan, Z.; Brestic, M.; Zivcak, M.; Zhou, W.; Allakhverdiev, S.I.; Yang, X.; Safdar, M.E.; Yang, W.; Liu, W. Photosynthesis research under climate change. Photosynth. Res. 2021, 150, 5–19. [Google Scholar]
- RM. Climate Change and the Tea Industry. Assignment: Climate Change Challenge. 2016. Available online: https://d3.harvard.edu/platform-rctom/submission/climate-change-and-the-tea-industry/ (accessed on 21 December 2024).
- Ahmed, S.; Stepp, J.R.; Orians, C.; Griffin, T.; Matyas, C.; Robbat, A.; Cash, S.; Xue, D.; Long, C.; Unachukwu, U.; et al. Effects of extreme climate events on tea (Camellia sinensis) functional quality validate indigenous farmer knowledge and sensory preferences in tropical China. PLoS ONE 2014, 9, e109126. [Google Scholar]
- Jayasinghe, S.L.; Kumar, L. Climate change may imperil tea production in the four major tea producers according to climate prediction models. Agronomy 2020, 10, 1536. [Google Scholar] [CrossRef]
- De Costa, W.A.; Mohotti, A.J.; Wijeratne, M.A. Ecophysiology of tea. Braz. J. Plant Physiol. 2007, 19, 299–332. [Google Scholar]
- Calzadilla, P.I.; Carvalho FE, L.; Gomez, R.; Neto, M.L.; Signorelli, S. Assessing photosynthesis in plant systems: A cornerstone to aid in the selection of resistant and productive crops. Environ. Exp. Bot. 2022, 201, 104950. [Google Scholar]
- Chen, J.M.; Ju, W.; Ciais, P.; Viovy, N.; Liu, R.; Liu, Y.; Lu, X. Vegetation structural change since 1981 significantly enhanced the terrestrial carbon sink. Nat. Commun. 2019, 10, 4259. [Google Scholar] [PubMed]
- Li, X.; Liu, Q.; Yang, R.; Zhang, H.; Zhang, J.; Cai, E. The design and implementation of the leaf area index sensor. Sensors 2015, 15, 6250–6269. [Google Scholar] [CrossRef] [PubMed]
- Koetz, B.; Baret, F.; Poilvé, H.; Hill, J. Use of coupled canopy structure dynamic and radiative transfer models to estimate biophysical canopy characteristics. Remote Sens. Environ. 2005, 95, 115–124. [Google Scholar]
- Asner, G.P.; Scurlock, J.M.; Hicke, J.A. Global synthesis of leaf area index observations: Implications for ecological and remote sensing studies. Glob. Ecol. Biogeogr. 2003, 12, 191–205. [Google Scholar]
- Cao, X.; Zhou, Z.; Chen, X.; Shao, W.; Wang, Z. Improving leaf area index simulation of IBIS model and its effect on water carbon and energy—A case study in Changbai Mountain broadleaved forest of China. Ecol. Model. 2015, 303, 97–104. [Google Scholar]
- Trotter, G.M.; Whitehead, D.; Pinkney, E.J. The photochemical reflectance index as a measure of photosynthetic light use efficiency for plants with varying foliar nitrogen contents. Int. J. Remote Sens. 2002, 23, 1207–1212. [Google Scholar]
- Lu, Y.; Zhu, X. Response of mangrove carbon fluxes to drought stress detected by photochemical reflectance index. Remote Sens. 2021, 13, 4053. [Google Scholar] [CrossRef]
- He, H.; Yang, R.; Jia, B.; Chen, L.; Fan, H.; Cui, J.; Yang, D.; Li, M.; Ma, F.Y. Rice photosynthetic productivity and PSII photochemistry under nonflooded irrigation. Sci. World J. 2014, 2014, 839658. [Google Scholar]
- Hasan, U.; Sawut, M.; Chen, S. Estimating the leaf area index of winter wheat based on unmanned aerial vehicle RGB-image parameters. Sustainability 2019, 11, 6829. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Lelong, C.C.; Burger, P.; Jubelin, G.; Roux, B.; Labbé, S.; Baret, F. Assessment of unmanned aerial vehicles imagery for quantitative monitoring of wheat crop in small plots. Sensors 2008, 8, 3557–3585. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Sun, L.; Shu, M.; Gu, X.; Yang, G.; Zhou, L. Monitoring maize lodging grades via unmanned aerial vehicle multispectral image. Plant Phenomics 2019, 2019, 5704154. [Google Scholar] [PubMed]
- Jiang, Q.; Huang, Z.; Xu, G.; Su, Y. MIoP-NMS: Perfecting crops target detection and counting in dense occlusion from high-resolution UAV imagery. Smart Agric. Technol. 2023, 4, 100226. [Google Scholar]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of Remote Sensing in Precision Agriculture: A Review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A review on UAV-based applications for precision agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef]
- Velusamy, P.; Rajendran, S.; Mahendran, R.K.; Naseer, S.; Shafiq, M.; Choi, J.G. Unmanned Aerial Vehicles (UAV) in precision agriculture: Applications and challenges. Energies 2021, 15, 217. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Ata-UI-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining color indices and textures of UAV-based digital imagery for rice LAI estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef]
- Qiao, L.; Zhao, R.; Tang, W.; An, L.; Sun, H.; Li, M.; Wang, N.; Liu, Y.; Liu, G. Estimating maize LAI by exploring deep features of vegetation index map from UAV multispectral images. Field Crops Res. 2022, 289, 108739. [Google Scholar]
- Duan, B.; Liu, Y.; Gong, Y.; Peng, Y.; Wu, X.; Zhu, R.; Fang, S. Remote estimation of rice LAI based on Fourier spectrum texture from UAV image. Plant Methods 2019, 15, 124. [Google Scholar] [CrossRef] [PubMed]
- Gong, Y.; Yang, K.; Lin, Z.; Fang, S.; Wu, X.; Zhu, R.; Peng, Y. Remote estimation of leaf area index (LAI) with unmanned aerial vehicle (UAV) imaging for different rice cultivars throughout the entire growing season. Plant Methods 2021, 17, 88. [Google Scholar] [PubMed]
- Ochiai, S.; Kamada, E.; Sugiura, R. Comparative analysis of RGB and multispectral UAV image data for leaf area index estimation of sweet potato. Smart Agric. Technol. 2024, 9, 100579. [Google Scholar]
- Na, S.I.; Park, C.W.; So, K.H.; Ahn, H.Y.; Lee, K.D. Photochemical Reflectance Index (PRI) mapping using drone-based hyperspectral image for evaluation of crop stress and its application to multispectral Imagery. Korean J. Remote Sens. 2019, 35, 637–647. [Google Scholar]
- Garrity, S.R.; Eitel, J.U.; Vierling, L.A. Disentangling the relationships between plant pigments and the photochemical reflectance index reveals a new approach for remote estimation of carotenoid content. Remote Sens. Environ. 2011, 115, 628–635. [Google Scholar]
- Clemente, A.A.; Maciel, G.M.; Siquieroli AC, S.; de Araujo Gallis, R.B.; Pereira, L.M.; Duarte, J.G. High-throughput phenotyping to detect anthocyanins, chlorophylls, and carotenoids in red lettuce germplasm. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102533. [Google Scholar]
- Candiago, S.; Remondino, F.; De Giglio, M.; Dubbini, M.; Gattelli, M. Evaluating multispectral images and vegetation indices for precision farming applications from UAV images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef]
- Tubuxin, B.; Rahimzadeh-Bajgiran, P.; Ginnan, Y.; Hosoi, F.; Omasa, K. Estimating chlorophyll content and photochemical yield of photosystem II (ΦPSII) using solar-induced chlorophyll fluorescence measurements at different growing stages of attached leaves. J. Exp. Bot. 2015, 66, 5595–5603. [Google Scholar]
- Zou, T.; Zhang, J. A new fluorescence quantum yield efficiency retrieval method to simulate chlorophyll fluorescence under natural conditions. Remote Sens. 2020, 12, 4053. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar]
- Barclay, H.J. Convert the total leaf area to the projected leaf area in lodgepole pine and Douglas-fir. Tree Physiol. 1998, 18, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Gong, Y.; Fang, S.; Duan, B.; Yuan, N.; Peng, Y.; Wu, X.; Zhu, R. Combining Spectral and Texture Features of UAV Images for the Remote Estimation of Rice LAI throughout the Entire Growing Season. Remote Sens. 2021, 13, 3001. [Google Scholar] [CrossRef]
- Gamon, J.A. The Dynamic 531-Nanometer A Reflectance Si qlnal: A Survey of Twenty Angiosperm Species. In Proceedings of the Photosynthetic Responses to the Environment, Honolulu, HI, USA, 24–27 August 1992; American Society of Plant Physiologists: Rockville, MD, USA, 1993; p. 172. [Google Scholar]
- Peñuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Sukhova, E.; Sukhov, V. Relation of photochemical reflectance indices based on different wavelengths to the parameters of light reactions in photosystems I and II in pea plants. Remote Sens. 2020, 12, 1312. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Bilger, W.; Björkman, O.; Fredeen, A.L.; Peñuelas, J. Remote sensing of the xanthophyll cycle and chlorophyll fluorescence in sunflower leaves and canopies. Oecologia 1990, 85, 1–7. [Google Scholar] [CrossRef]
- Nakamura, Y.; Tsujimoto, K.; Ogawa, T.; Noda, H.M.; Hikosaka, K. Correction of photochemical reflectance index (PRI) by optical indices to predict non-photochemical quenching (NPQ) across various species. Remote Sens. Environ. 2024, 305, 114062. [Google Scholar] [CrossRef]
- Zhang, C.; Filella, I.; Garbulsky, M.F.; Peñuelas, J. Affecting factors and recent improvements of the photochemical reflectance index (PRI) for remotely sensing foliar, canopy and ecosystemic radiation-use efficiencies. Remote Sens. 2016, 8, 677. [Google Scholar] [CrossRef]
- Thénot, F.; Méthy, M.; Winkel, T. The Photochemical Reflectance Index (PRI) as a water-stress index. Int. J. Remote Sens. 2002, 23, 5135–5139. [Google Scholar] [CrossRef]
- Winkel, T.; Méthy, M.; Thénot, F. Radiation use efficiency, chlorophyll fluorescence, and reflectance indices associated with ontogenic changes in water-limited Chenopodium quinoa leaves. Photosynthetica 2002, 40, 227–232. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies: A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Genty, B.; Briantais, J.M.; Baker, N.R. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Biophys. Acta (BBA)-Gen. Subj. 1989, 990, 87–92. [Google Scholar] [CrossRef]
- Maxwell, K.; Johnson, G.N. Chlorophyll fluorescence—A practical guide. J. Exp. Bot. 2000, 51, 659–668. [Google Scholar] [PubMed]
- Zhuang, Z.H.; Tsai, H.P.; Chen, C.I.; Yang, M.D. Subtropical region tea tree LAI estimation integrating vegetation indices and texture features derived from UAV multispectral images. Smart Agric. Technol. 2024, 9, 100650. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar]
- Bai, J.; Zhou, Z.; Zou, Y.; Pulatov, B.; Siddique, K.H. Watershed drought and ecosystem services: Spatiotemporal characteristics and gray relational analysis. ISPRS Int. J. Geo-Inf. 2021, 10, 43. [Google Scholar] [CrossRef]
- Aixiang, T. Grey Relation Analysis on Agriculture Energy Consumption and Its Affecting Factors. In Proceedings of the 2010 International Conference on Digital Manufacturing & Automation, Changcha, China, 18–20 December 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 1, pp. 786–789. [Google Scholar]
- Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of crop growth parameters using UAV-based hyperspectral remote sensing data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef]
- Luo, D.; Gao, Y.; Wang, Y.; Shi, Y.; Chen, S.; Ding, Z.; Fan, K. Using UAV image data to monitor the effects of different nitrogen application rates on tea quality. J. Sci. Food Agric. 2022, 102, 1540–1549. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar]
- Zhu, C.; Ding, J.; Zhang, Z.; Wang, Z. Exploring the potential of UAV hyperspectral image for estimating soil salinity: Effects of optimal band combination algorithm and random forest. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 279, 121416. [Google Scholar]
- Shafiee, S.; Lied, L.M.; Burud, I.; Dieseth, J.A.; Alsheikh, M.; Lillemo, M. Sequential forward selection and support vector regression in comparison to LASSO regression for spring wheat yield prediction based on UAV imagery. Comput. Electron. Agric. 2021, 183, 106036. [Google Scholar]
- Qun’ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval model for total nitrogen concentration based on UAV hyper spectral remote sensing data and machine learning algorithms—A case study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar]
- Zhang, Y.; Jiang, Y.; Xu, B.; Yang, G.; Feng, H.; Yang, X.; Yang, H.; Liu, C.; Cheng, Z.; Feng, Z. Study on the Estimation of Leaf Area Index in Rice Based on UAV RGB and Multispectral Data. Remote Sens. 2024, 16, 3049. [Google Scholar] [CrossRef]
- Sun, C.; Feng, L.; Zhang, Z.; Ma, Y.; Crosby, T.; Naber, M.; Wang, Y. Prediction of end-of-season tuber yield and tuber set in potatoes using in-season UAV-based hyperspectral imagery and machine learning. Sensors 2020, 20, 5293. [Google Scholar] [CrossRef]
- Zhai, W.; Li, C.; Cheng, Q.; Mao, B.; Li, Z.; Li, Y.; Ding, F.; Qin, S.; Fei, S.; Chen, Z. Enhancing wheat above-ground biomass estimation using UAV RGB images and machine learning: Multi-feature combinations, flight height, and algorithm implications. Remote Sens. 2023, 15, 3653. [Google Scholar] [CrossRef]
- Xu, M.; Watanachaturaporn, P.; Varshney, P.K.; Arora, M.K. Decision tree regression for soft classification of remote sensing data. Remote Sens. Environ. 2005, 97, 322–336. [Google Scholar]
- Balogun, A.L.; Tella, A. Modelling and investigating the impacts of climatic variables on ozone concentration in Malaysia using correlation analysis with random forest, decision tree regression, linear regression, and support vector regression. Chemosphere 2022, 299, 134250. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Liu, Y.; Liu, S.; Li, J.; Guo, X.; Wang, S.; Lu, J. Estimating biomass of winter oilseed rape using vegetation indices and texture metrics derived from UAV multispectral images. Comput. Electron. Agric. 2019, 166, 105026. [Google Scholar]
- Yang, X.; Yang, R.; Ye, Y.; Yuan, Z.; Wang, D.; Hua, K. Winter wheat SPAD estimation from UAV hyperspectral data using cluster-regression methods. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102618. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Xiaosong, Z.; Qiangfu, Z. Stock prediction using optimized LightGBM based on cost awareness. In Proceedings of the 2021 5th IEEE International Conference on Cybernetics (CYBCONF), Sendai, Japan, 8–10 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 107–113. [Google Scholar]
- Welch, B.L. On the comparison of several mean values: An alternative approach. Biometrika 1951, 38, 330–336. [Google Scholar] [CrossRef]
- Reganold, J.P.; Elliott, L.F.; Unger, Y.L. Long-term effects of organic and conventional farming on soil erosion. Nature 1987, 330, 370–372. [Google Scholar] [CrossRef]
- Schrama, M.; De Haan, J.J.; Kroonen, M.; Verstegen, H.; Van der Putten, W.H. Crop yield gap and stability in organic and conventional farming systems. Agric. Ecosyst. Environ. 2018, 256, 123–130. [Google Scholar] [CrossRef]
- De Ponti, T.; Rijk, B.; Van Ittersum, M.K. The crop yield gap between organic and conventional agriculture. Agric. Syst. 2012, 108, 1–9. [Google Scholar] [CrossRef]
- Wortman, S.E.; Galusha, T.D.; Mason, S.C.; Francis, C.A. Soil fertility and crop yields in long-term organic and conventional cropping systems in Eastern Nebraska. Renew. Agric. Food Syst. 2012, 27, 200–216. [Google Scholar]
- Schärer, M.L.; Dietrich, L.; Kundel, D.; Mäder, P.; Kahmen, A. Reduced plant water use can explain higher soil moisture in organic compared to conventional farming systems. Agric. Ecosyst. Environ. 2022, 332, 107915. [Google Scholar]
- Petcu, E.; Toncea, I.; Mustăţea, P.; Petcu, V. Effect of organic and conventional farming systems on some physiological indicators of winter wheat. Org. Farming 2009, 2010, 131–135. [Google Scholar]
- Han, W.Y.; Wang, D.H.; Fu, S.W.; Ahmed, S. Tea from organic production has higher functional quality characteristics compared with tea from conventional management systems in China. Biol. Agric. Hortic. 2018, 34, 120–131. [Google Scholar] [CrossRef]
- Olsen, J.; Weiner, J. The influence of Triticum aestivum density, sowing pattern and nitrogen fertilization on leaf area index and its spatial variation. Basic Appl. Ecol. 2007, 8, 252–257. [Google Scholar]
- Chen, C.I.; Lin, K.H.; Huang, M.Y.; Yang, C.K.; Lin, Y.H.; Hsueh, M.L.; Lee, L.-H.; Lin, S.-R.; Wang, C.W. Gas exchange and chlorophyll fluorescence responses of Camellia sinensis grown under various cultivations in different seasons. Bot. Stud. 2024, 65, 10. [Google Scholar]
- Liu, W.; Cui, S.; Wu, L.; Qi, W.; Chen, J.; Ye, Z.; Ma, J.; Liu, D. Effects of bio-organic fertilizer on soil fertility, yield, and quality of tea. J. Soil Sci. Plant Nutr. 2023, 23, 5109–5121. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Liu, L.; Myint, S.W.; Wang, S.; Liu, H.; He, Z. Exploring the potential of worldview-2 red-edge band-based vegetation indices for estimation of mangrove leaf area index with machine learning algorithms. Remote Sens. 2017, 9, 1060. [Google Scholar] [CrossRef]
- Shahsavari, M.; Mohammadi, V.; Alizadeh, B.; Alizadeh, H. Application of machine learning algorithms and feature selection in rapeseed (Brassica napus L.) breeding for seed yield. Plant Methods 2023, 19, 57. [Google Scholar] [CrossRef]
- Fang, S.; Yao, X.; Zhang, J.; Han, M. Grey correlation analysis on travel modes and their influence factors. Procedia Eng. 2017, 174, 347–352. [Google Scholar] [CrossRef]
- Shao, G.; Han, W.; Zhang, H.; Zhang, L.; Wang, Y.; Zhang, Y. Prediction of maize crop coefficient from UAV multisensor remote sensing using machine learning methods. Agric. Water Manag. 2023, 276, 108064. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, K.; Xiao, C.; Wei, D.; Zhao, X.; Lan, J.; Wei, X.; Yao, Y.; Wang, B.; Sun, Y.; et al. Leaf area index estimation algorithm for GF-5 hyperspectral data based on different feature selection and machine learning methods. Remote Sens. 2020, 12, 2110. [Google Scholar] [CrossRef]
- Zhang, C.; Yi, Y.; Wang, L.; Zhang, X.; Chen, S.; Su, Z.; Zhang, S.; Xue, Y. Estimation of the Bio-Parameters of Winter Wheat by Combining Feature Selection with Machine Learning Using Multi-Temporal Unmanned Aerial Vehicle Multispectral Images. Remote Sens. 2024, 16, 469. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. Multi-scale object-based image analysis and feature selection of multi-sensor earth observation imagery using random forests. Int. J. Remote Sens. 2012, 33, 4502–4526. [Google Scholar] [CrossRef]
- Nagy, A.; Szabó, A.; Elbeltagi, A.; Nxumalo, G.S.; Bódi, E.B.; Tamás, J. Hyperspectral indices data fusion-based machine learning enhanced by MRMR algorithm for estimating maize chlorophyll content. Front. Plant Sci. 2024, 15, 1419316. [Google Scholar] [CrossRef]
- Wu, S.; Deng, L.; Guo, L.; Wu, Y. Wheat leaf area index prediction using data fusion based on high-resolution unmanned aerial vehicle imagery. Plant Methods 2022, 18, 68. [Google Scholar] [PubMed]
- Wittstruck, L.; Jarmer, T.; Trautz, D.; Waske, B. Estimating LAI from winter wheat using UAV data and CNNs. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Li, H.; Yan, X.; Su, P.; Su, Y.; Li, J.; Xu, Z.; Gao, C.; Zhao, Y.; Feng, M.; Shafiq, F.; et al. Estimation of winter wheat LAI based on color indices and texture features of RGB images taken by UAV. J. Sci. Food Agric. 2025, 105, 189–200. [Google Scholar] [PubMed]
- Liu, S.; Zeng, W.; Wu, L.; Lei, G.; Chen, H.; Gaiser, T.; Srivastava, A.K. Simulating the leaf area index of rice from multispectral images. Remote Sens. 2021, 13, 3663. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar]




| Model | Hyperparameter |
|---|---|
| Polynomial Regression | Polynomial Terms: 2nd degree |
| Partial Least Squares Regression | n_components: from 2 to N based on the input features |
| Lasso Regression | Regularization strength (α): 0, 0.01, 0.1, 1, 10, 100 |
| Ridge Regression | Regularization strength (α): 0, 0.01, 0.1, 1, 10, 100 |
| Decision Tree Regression | max_depth: 4~100 min_samples_split: 5~50, increasing in increments of 5 |
| Random Forest Regression | n_estimators: 50~150, increasing in increments of 25 max_depth: 3~50 min_samples_split: 5~50, increasing in increments of 5 |
| eXtreme Gradient Boosting | max_depth: 3~25 learning_rate: 0.001, 0.005, 0.01, 0.05, 0.1 n_estimators: 50~150, increasing in increments of 25 |
| Light Gradient Boosting Machine | num_leaves: 50~150, increasing in increments of 10 learning_rate: 0.001, 0.005, 0.01, 0.05, 0.1 n_estimators: 50~150, increasing in increments of 25 |
| Parameter | Farming Method | Number | Min | Mean | Max | StDev | CV |
|---|---|---|---|---|---|---|---|
| LAI | CFM | 499 | 0.500 | 4.878 | 10.370 | 1.704 | 0.349 |
| AFM | 377 | 0.130 | 4.058 | 9.810 | 2.035 | 0.501 | |
| PRI | CFM | 503 | −0.0371 | 0.0228 | 0.0766 | 0.0196 | 0.860 |
| AFM | 378 | −0.0770 | 0.0201 | 0.0596 | 0.0251 | 1.249 | |
| ΦPSII | CFM | 477 | 0.0729 | 0.4121 | 0.8277 | 0.1671 | 0.405 |
| AFM | 350 | 0.0819 | 0.4586 | 0.8648 | 0.1717 | 0.374 |
| Parameter | Index | Feature Ranking | R2 | RMSE | MAE | Model |
|---|---|---|---|---|---|---|
| LAI | CI | PCA | 0.59 | 1.214 | 0.759 | XGBoost |
| MRMR | 0.599 | 1.2 | 0.752 | |||
| GRA | 0.591 | 1.212 | 0.751 | |||
| MI | PCA | 0.687 | 1.06 | 0.676 | XGBoost | |
| MRMR | 0.691 | 1.053 | 0.669 | |||
| GRA | 0.694 | 1.049 | 0.632 | |||
| PRI | CI | PCA | 0.281 | 0.019 | 0.014 | RFR |
| MRMR | 0.284 | 0.019 | 0.014 | |||
| GRA | 0.284 | 0.019 | 0.014 | |||
| MI | PCA | 0.603 | 0.014 | 0.009 | XGBoost | |
| MRMR | 0.607 | 0.014 | 0.009 | |||
| GRA | 0.643 | 0.013 | 0.009 | |||
| ΦPSII | CI | PCA | 0.92 | 0.048 | 0.013 | XGBoost |
| MRMR | 0.919 | 0.049 | 0.016 | |||
| GRA | 0.915 | 0.05 | 0.014 | |||
| MI | PCA | 0.909 | 0.052 | 0.021 | XGBoost | |
| MRMR | 0.913 | 0.05 | 0.024 | |||
| GRA | 0.919 | 0.049 | 0.015 |
| Parameter | Indices | Feature Ranking | Accuracy 1 | Model | # Variables 1 (Difference) |
|---|---|---|---|---|---|
| LAI | CI | MRMR | 0.599/0.569 | XGBoost | 14/5 (9) |
| MI | GRA | 0.716/0.680 | 43/11 (32) | ||
| PRI | CI | GRA | 0.284/0.270 | RFR | 19/17 (2) |
| MI | 0.643/0.611 | XGBoost | 55/53 (2) | ||
| ΦPSII | CI | PCA | 0.920/0.874 | XGBoost | 22/3 (19) |
| MI | GRA | 0.919/0.873 | 36/3 (33) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Z.-H.; Tsai, H.-P.; Chen, C.-I. Estimating Tea Plant Physiological Parameters Using Unmanned Aerial Vehicle Imagery and Machine Learning Algorithms. Sensors 2025, 25, 1966. https://doi.org/10.3390/s25071966
Zhuang Z-H, Tsai H-P, Chen C-I. Estimating Tea Plant Physiological Parameters Using Unmanned Aerial Vehicle Imagery and Machine Learning Algorithms. Sensors. 2025; 25(7):1966. https://doi.org/10.3390/s25071966
Chicago/Turabian StyleZhuang, Zhong-Han, Hui-Ping Tsai, and Chung-I Chen. 2025. "Estimating Tea Plant Physiological Parameters Using Unmanned Aerial Vehicle Imagery and Machine Learning Algorithms" Sensors 25, no. 7: 1966. https://doi.org/10.3390/s25071966
APA StyleZhuang, Z.-H., Tsai, H.-P., & Chen, C.-I. (2025). Estimating Tea Plant Physiological Parameters Using Unmanned Aerial Vehicle Imagery and Machine Learning Algorithms. Sensors, 25(7), 1966. https://doi.org/10.3390/s25071966






