Remaining Useful Life Prediction Method for Bearings Based on Pruned Exact Linear Time State Segmentation and Time–Frequency Diagram
Abstract
1. Introduction
- In the segmentation of the bearing degradation stage, the PELT algorithm is adopted. Compared with traditional methods (such as dynamic programming or binary search), the PELT algorithm significantly reduces computational complexity through a pruning strategy, enabling fast and accurate detection of multiple change points in time series and thereby achieving effective segmentation of feature curves.
- Unlike previous RUL prediction approaches that only consider time-domain features, this paper utilizes wavelet transform to convert the original vibration signal into time–frequency feature maps, which are then fed into a neural network model for bearing RUL prediction.
- The Informer model is selected for bearing life prediction. Due to its improved self-attention mechanism (ProbSparse Self-Attention) and distillation mechanism, Informer can effectively enhance the computational efficiency and prediction performance of traditional Transformer models.
2. Materials and Methods
2.1. Feature Extraction
2.2. Bearing Degradation State Segmentation Based on the PELT Method
2.3. Continuous Wavelet Transform
2.4. Informer
3. Experiments and Work
3.1. Dataset Introduction
3.2. Feature Extraction
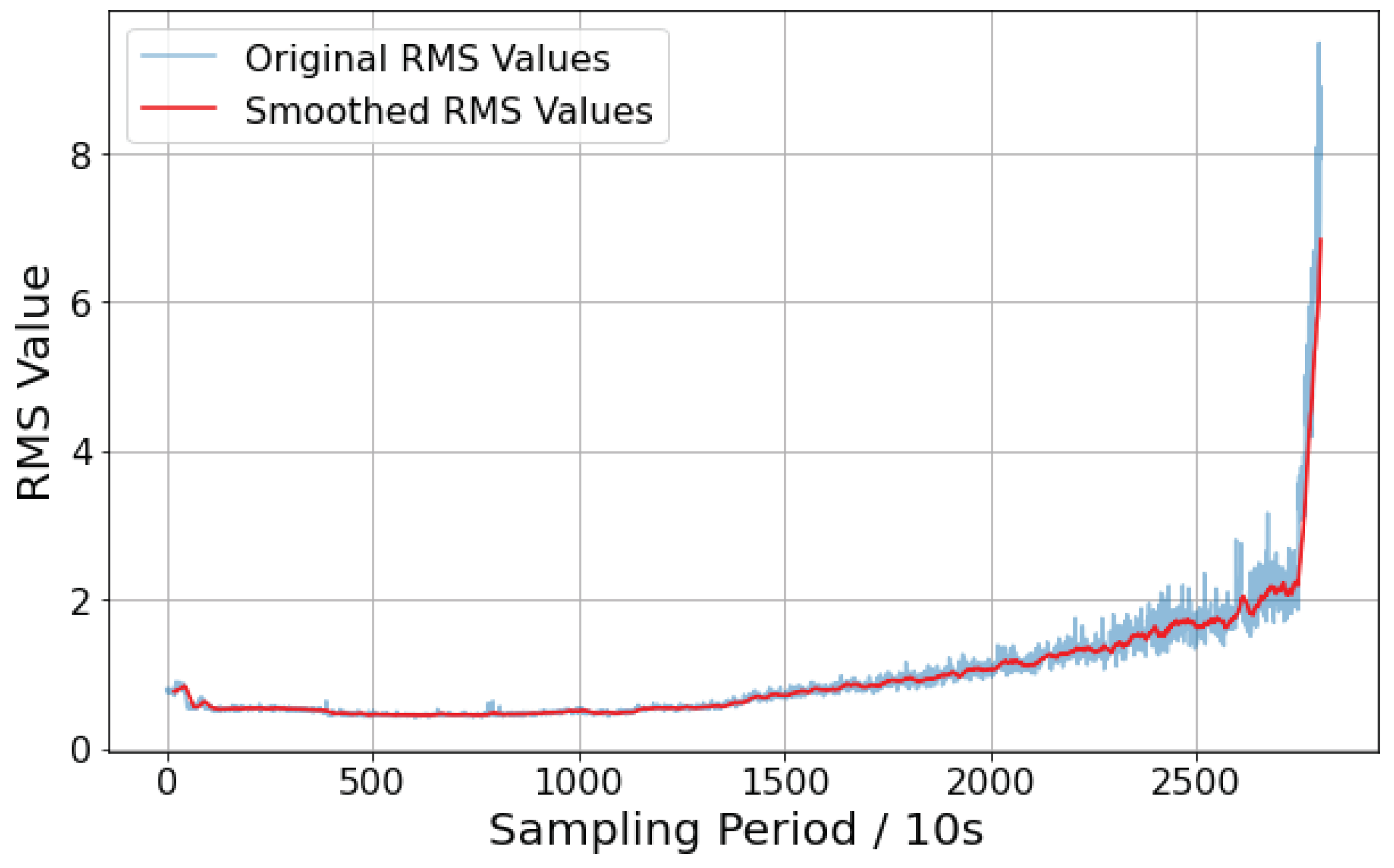
3.2.1. RMS Feature Extraction
3.2.2. Time–Frequency Image Feature Extraction
3.3. Bearing Degradation State Classification Based on the PELT Method
3.4. Bearing RUL Prediction Based on Informer
- -
- is the total number of pairs of samples;
- -
- is the indicator function, which returns 1 if the condition inside is true, and 0 otherwise;
- -
- is the sign function, which returns 1 if , if , and 0 if .
4. Conclusions
- The transformation of original bearing vibration signals into two-dimensional images through continuous wavelet transform (CWT) provides an effective visualization of the bearing degradation process. As the bearing deterioration advances, both energy impacts and bursts exhibit a marked increase. Notably, the energy distribution within the low-frequency region demonstrates more substantial variations compared to the medium- and high-frequency regions, accompanied by more pronounced impact characteristics, which warrants particular attention.
- The PELT algorithm can effectively segment the degradation stages of bearings based on the root mean square (RMS) value, providing a basis for piecewise fitting in the model network and improving the accuracy of predictions.
- The Informer network inherits the excellent feature extraction capabilities of the Transformer in time-series forecasting while using a sparse attention mechanism to reduce computational complexity. It demonstrates superior accuracy when handling long time-series bearing datasets, improving prediction accuracy by approximately 15.83% and computational efficiency by about 30.88%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Zhou, G.; Zhao, S.; Li, L.; Xie, W.; Su, B.; Li, Y.; Zhao, Z. A novel two-stage method via adversarial strategy for remaining useful life prediction of bearings under variable conditions. Reliab. Eng. Syst. Saf. 2025, 254, 110602. [Google Scholar]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. Trans. ASME 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Lundberg, G.; Palmgren, A. Dynamic capacity of rolling bearings. J. Appl. Mech. 1949, 16, 165–172. [Google Scholar]
- Huang, Y.; He, J. Study and Contrast of Some Kinds of Fatigue Reliability Models. Mech. Res. Appl. 2017, 30, 71–76. [Google Scholar]
- Zhu, J.; Chen, N.; Shen, C. A new data-driven transferable remaining useful life prediction approach for bearing under different working conditions. Mech. Syst. Signal Process. 2020, 139, 106602. [Google Scholar]
- Wang, H.; Liao, H.; Ma, X.; Bao, R. Remaining useful life prediction and optimal maintenance time determination for a single unit using isotonic regression and gamma process model. Reliab. Eng. Syst. Saf. 2021, 210, 107504. [Google Scholar]
- Huang, Z.; Xu, Z.; Ke, X.; Wang, W.; Sun, Y. Remaining useful life prediction for an adaptive skew-Wiener process model. Mech. Syst. Signal Process. 2017, 87, 294–306. [Google Scholar]
- Li, N.; Lei, Y.; Lin, J.; Ding, S.X. An improved exponential model for predicting remaining useful life of rolling element bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar]
- Nielsen, J.S.; Sørensen, J.D. Bayesian estimation of remaining useful life for wind turbine blades. Energies 2017, 10, 664. [Google Scholar] [CrossRef]
- Du, Y.; Duan, C.; Wu, T. Lubricating oil deterioration modeling and remaining useful life prediction based on hidden semi-Markov modeling. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 916–923. [Google Scholar]
- Lei, S.; Sun, J.; Liu, H. Cumulative Damage Index Model and Service Reliability Evaluation of Turbine Blades. Acta Aeronaut. Astronaut. Sin. 2022, 43, 252–268. [Google Scholar]
- Sayyad, S.; Kumar, S.; Bongale, A.; Kamat, P.; Patil, S.; Kotecha, K. Data-Driven Remaining Useful Life Estimation for Milling Process: Sensors, Algorithms, Datasets, and Future Directions. IEEE Access 2021, 9, 110255–110286. [Google Scholar] [CrossRef]
- Leite, D.; Andrade, E.; Rativa, D.; Maciel, A.M.A. Fault Detection and Diagnosis in Industry 4.0: A Review on Challenges and Opportunities. Sensors 2024, 25, 60. [Google Scholar] [CrossRef]
- He, Z.; He, Z.; Li, S.; Yu, Y.; Liu, K. A ship navigation risk online prediction model based on informer network using multi-source data. Ocean. Eng. 2024, 298, 117007. [Google Scholar] [CrossRef]
- Sun, B.; Hu, W.; Wang, H.; Wang, L.; Deng, C. Remaining Useful Life Prediction of Rolling Bearings Based on CBAM-CNN-LSTM. Sensors 2025, 25, 554. [Google Scholar] [CrossRef]
- Yin, C.; Li, Y.; Wang, Y.; Dong, Y. Physics-guided degradation trajectory modeling for remaining useful life prediction of rolling bearings. Mech. Syst. Signal Process. 2025, 224, 112192. [Google Scholar] [CrossRef]
- Shen, Y.; Tang, B.; Li, B.; Tan, Q.; Wu, Y. Remaining Useful Life Prediction of Rolling Bearings Based on Attention Mechanism and CNN-BiLSTM. Nucl. Power Eng. 2023, 44, 33–38. [Google Scholar]
- Yu, P.; Cao, J. Dual-Input Convolutional Neural Network for Graphical Features-Based Remaining Useful Life Prognosticating of Wind Turbine Bearings. Acta Energiae Solaris Sin. 2022, 43, 343–350. [Google Scholar]
- Qi, M.; Wang, G.; Shi, N.; Shi, N.; Li, C.; He, Y. Intelligent fault diagnosis method of rolling bearings based on the fusion of time-frequency diagram and visual Transformer. Bearing 2024, 10, 115–123. [Google Scholar] [CrossRef]
- Yan, J.; Yi, C.; Huang, T.; Xiao, H. Research on Remaining Useful Life Prediction of Rolling Bearings Based on CSPA-Informer. Comb. Modul. Mach. Autom. Manuf. Tech. 2023, 10, 85–90. [Google Scholar] [CrossRef]
- Liu, B.; Gao, Z.; Lu, B.; Dong, H.; An, Z. Deep learning-based remaining useful life estimation of bearings with time-frequency information. Sensors 2022, 22, 7402. [Google Scholar] [CrossRef] [PubMed]
- Kaji, M.; Parvizian, J.; van de Venn, H.W. Constructing a reliable health indicator for bearings using convolutional autoencoder and continuous wavelet transform. Appl. Sci. 2020, 10, 8948. [Google Scholar] [CrossRef]
- Li, Y.; Li, H.; Wang, B. Extraction of Degradation Feature for Rolling Bearings Based on Cointegration Theory. J. Vib. Meas. Diagn. 2021, 41, 385–391+417–418. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, J.; Wu, J.; Zhu, H.; Wang, Y. Abnormal symptom-triggered remaining useful life prediction for rolling element bearings. J. Vib. Control. 2023, 29, 2102–2115. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Zuo, M.J. Predicting remaining useful life of rolling bearings based on deep feature representation and transfer learning. IEEE Trans. Instrum. Meas. 2019, 69, 1594–1608. [Google Scholar]
- Shakya, P.; Kulkarni, M.S.; Darpe, A.K. A novel methodology for online detection of bearing health status for naturally progressing defect. J. Sound Vib. 2014, 333, 5614–5629. [Google Scholar]
- Alkaya, A.; Eker, İ. Variance sensitive adaptive threshold-based PCA method for fault detection with experimental application. ISA Trans. 2011, 50, 287–302. [Google Scholar] [PubMed]
- Liu, L. Remaining Useful Life Prediction of Rolling Bearing Based on Feature Fusion and LSTM. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2021. [Google Scholar]
- Zeng, L. Study on Multi-stage Prediction Method of Remaining Useful Life of Rolling Bearing Based on Transformer Health Indicator. Master’s Thesis, Chongqing University, Chongqing, China, 2022. [Google Scholar]
- Chen, D.; Hu, C.; Zheng, J.; Pei, H.; Zhang, J.; Pang, Z. Prediction of Bearing Residual Life Based on Bi-LSTM-Att Under State Partition. Aerosp. Control. Appl. 2023, 49, 29–39. [Google Scholar]
- Liu, S.; Fan, L. An adaptive prediction approach for rolling bearing remaining useful life based on multistage model with three-source variability. Reliab. Eng. Syst. Saf. 2022, 218, 108182. [Google Scholar]
- Killick, R.; Fearnhead, P.; Eckley, I.A. Optimal Detection of Changepoints with a Linear Computational Cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar]
- Han, Y.; Ding, X.; Gu, F.; Chen, X.; Xu, M. Dual-drive RUL prediction of gear transmission systems based on dynamic model and unsupervised domain adaption under zero sample. Reliab. Eng. Syst. Saf. 2025, 253, 110442. [Google Scholar]
- Xiao, P. An empirical Study on the Structural Change of Stock Volume and Price Level Based on PELT Algorithm. Master’s Thesis, Shanghai Normal University, Shanghai, China, 2020. [Google Scholar]
- Xie, Z.; Wei, H.; Zhu, H.; Yang, F.; Wu, S.; Zhao, L.; Li, C. HSR Curve Control Point Identification Method Based on PELT and Robust Estimation. Railw. Stand. Des. 2025, 1–9. [Google Scholar] [CrossRef]
- Elbakri, W.; Siraj, M.M.; Al-Rimy, B.A.S.; Qasem, S.N.; Al-Hadhrami, T. Adaptive cloud intrusion detection system based on pruned exact linear time technique. Comput. Mater. Contin. 2024, 79, 3725–3756. [Google Scholar]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [PubMed]
- Nguyen, T.-D.; Nguyen, P.-H. Improvements in the Wavelet Transform and Its Variations: Concepts and Applications in Diagnosing Gearbox in Non-Stationary Conditions. Appl. Sci. 2024, 14, 4642. [Google Scholar] [CrossRef]
- Rhif, M.; Abbes, A.B.; Farah, I.R.; Martínez, B.; Sang, Y. Wavelet transform application for/in non-stationary time-series analysis: A review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef]
- Chang, Y.; Li, F.; Chen, J.; Liu, Y.; Li, Z. Efficient temporal flow Transformer accompanied with multi-head probsparse self-attention mechanism for remaining useful life prognostics. Reliab. Eng. Syst. Saf. 2022, 226, 108701. [Google Scholar]
- Tay, Y.; Dehghani, M.; Bahri, D.; Metzler, D. Efficient transformers: A survey. ACM Comput. Surv. 2022, 55, 1–28. [Google Scholar]
- Lim, B.; Arık, S.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An Experimental Platform for Bearings Accelerated Life Test. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]









| Operating Conditions | Radial Force (N) | Rotational Speed (r/min) | Training Set | Test Set |
|---|---|---|---|---|
| Operating Condition 1 | 4000 | 1800 | Bearing1-1 Bearing1-2 | Bearing1-3 Bearing1-4 Bearing1-5 Bearing1-6 Bearing1-7 |
| Operating Condition 2 | 4200 | 1650 | Bearing2-1 Bearing2-2 | Bearing2-3 Bearing2-4 Bearing2-5 Bearing2-6 Bearing2-7 |
| Operating Condition 3 | 5000 | 1500 | Bearing3-1 Bearing3-2 | Bearing3-3 |
| RUL Prediction Method | MAE | MES | RMSE | C-Index |
|---|---|---|---|---|
| informer | 0.0649 | 0.0068 | 0.0827 | 0.9175 |
| Transformer | 0.0670 | 0.0079 | 0.0888 | 0.9297 |
| PELT+informer | 0.0403 | 0.0025 | 0.0501 | 0.9452 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Fan, J.; Wang, H.; Cai, L. Remaining Useful Life Prediction Method for Bearings Based on Pruned Exact Linear Time State Segmentation and Time–Frequency Diagram. Sensors 2025, 25, 1950. https://doi.org/10.3390/s25061950
Wei X, Fan J, Wang H, Cai L. Remaining Useful Life Prediction Method for Bearings Based on Pruned Exact Linear Time State Segmentation and Time–Frequency Diagram. Sensors. 2025; 25(6):1950. https://doi.org/10.3390/s25061950
Chicago/Turabian StyleWei, Xu, Jingjing Fan, Huahua Wang, and Lulu Cai. 2025. "Remaining Useful Life Prediction Method for Bearings Based on Pruned Exact Linear Time State Segmentation and Time–Frequency Diagram" Sensors 25, no. 6: 1950. https://doi.org/10.3390/s25061950
APA StyleWei, X., Fan, J., Wang, H., & Cai, L. (2025). Remaining Useful Life Prediction Method for Bearings Based on Pruned Exact Linear Time State Segmentation and Time–Frequency Diagram. Sensors, 25(6), 1950. https://doi.org/10.3390/s25061950





