Privacy-Preserving Multi-User Graph Intersection Scheme for Wireless Communications in Cloud-Assisted Internet of Things
Abstract
1. Introduction
1.1. Contributions
- We present a construction of privacy-preserving graph intersection computation. In our scheme, a TA initializes the system, and it generates public parameters for the system and re-encryption keys for the cloud server. Each data owner encrypts their graph before uploading it to the cloud server. Every time a data user sends a graph intersection query, the cloud server re-encrypts these encrypted graphs with a re-encryption key from the TA to the data user. After calculating the intersection of all these encrypted graphs, it sends the graph intersection to the query user. Following this procedure, our scheme can support data users to query for the graph intersection of data owners securely and flexibly.
- Our scheme supports multi-user scenarios. It allows multiple users to query for the graph intersection, while data owners only need encrypt their data once. On the one hand, it achieves flexible data sharing; on the other hand, it decreases the processing burden placed on data owners.
- In our scheme, the cloud server transforms the ciphertexts intended for TA to ciphertexts that can be decrypted by the query user by using proxy re-encryption, enabling data users to decrypt the result with their own keys, without exposing sensitive data. It reduces the complexity of key management.
- We present the theoretical analysis from aspects of security and performance. The results from our experiments confirm that the scheme is practical and efficient.
1.2. Paper Organization
2. Related Work
2.1. Graph Encryption
2.2. Outsourced Private Set Intersection
3. Preliminaries
3.1. Graph Intersection
- For each vertex , and .
- For each vertex , and .
3.2. Bilinear Pairings
- Bilinearity. , for all and .
- Non-degeneracy. .
- Computability. can be computed efficiently.
3.3. Proxy Re-Encryption
- . Given a security parameter , constructs a bilinear map where and are groups of prime order p, and generator , return the public parameters .
- . An entity chooses a random as the private key; their public key is .
- . The re-encryption key can be generated with delegator a’s private key and delegatee b’s public key as
- . To encrypt a message under : sample , , . The ciphertext .
- . Given the re-encryption key , ciphertext can be re-encrypted as follows: sample , , . The re-encrypted ciphertext .
- . Entity b can decrypt using their private key :
4. Problem Formalization
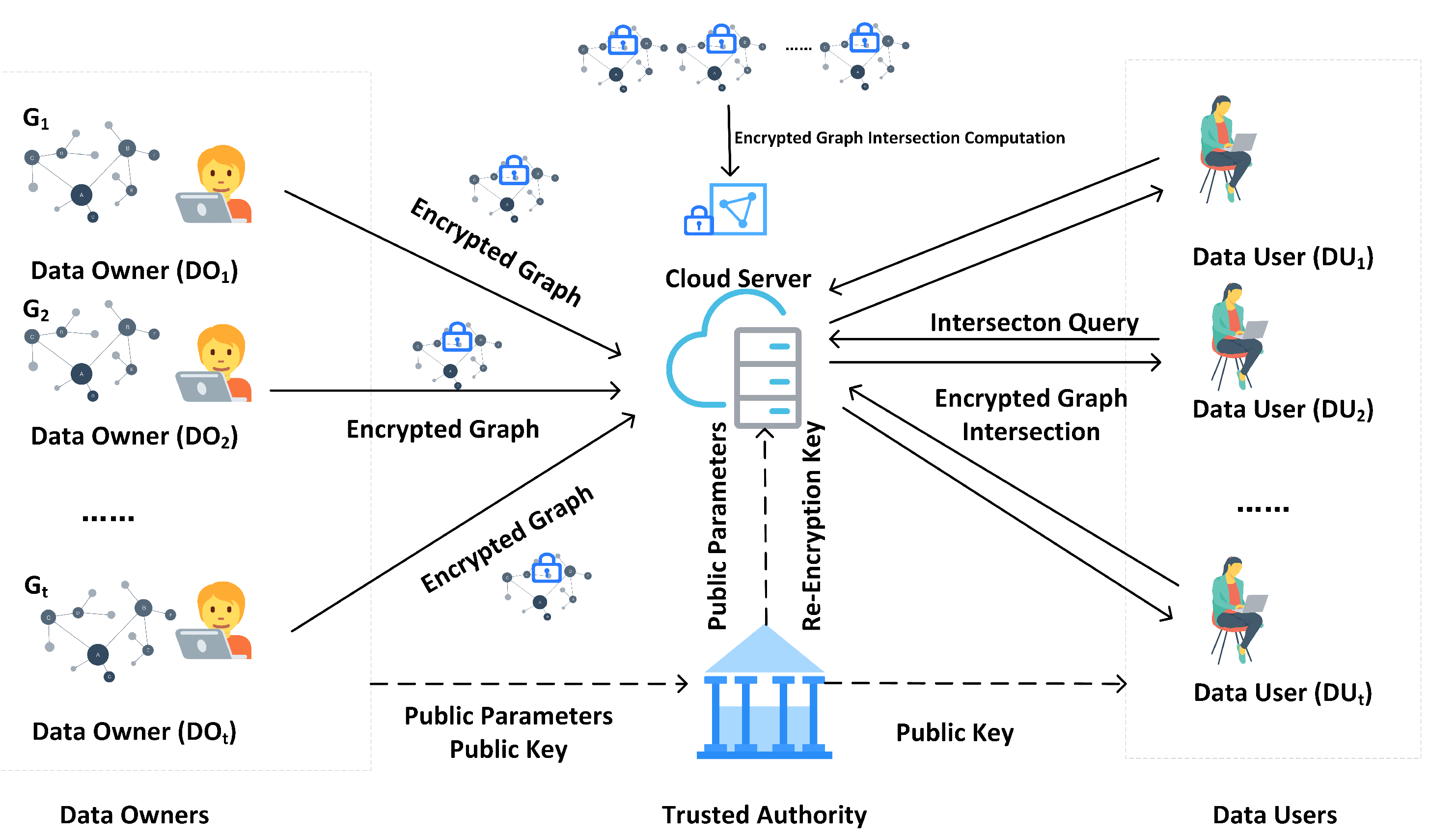
4.1. System Model
- Cloud Server. The cloud server possesses strong storage and computational capabilities: it receives and stores encrypted graph data uploaded by data owners, performs graph re-encryption and intersection operations, and finally it provides the results to the data user.
- Data Owner . Each data owner has a graph that participates in graph intersection computation. To ensure the confidentiality of the graph , they will encrypt before uploading it to the cloud server.
- Data User. A data user may query for the intersection of graphs from . In order to save storage and computational costs, they outsource the computational task to the cloud server, and finally obtains the encrypted result from the cloud server and decrypts it.
- Trusted Authority. As a trusted third party, the initializes the system with a security parameter , generates a set of public parameters . It is also responsible for generating re-encryption keys that enable the cloud server to convert the ciphertexts for them to be decryptable by the data user.
4.2. Threat Model
4.3. Security Goals
- Graph data confidentiality. Any information about original graphs except for information in leakage functions should not be obtainable by the cloud server or other adversaries; only the part in the intersection with graphs from other data owners can be learned by an authorized data user.
- Query result confidentiality. The graph intersection results in a ciphertext form that can only be decrypted by an authorized data user with their own key. It remains confidential from the cloud server, data owners, other data users, and adversaries.
4.4. Security Definition
- : outputs graphs . The experiment generates a pair of keys by and generates the re-encryption key by . Then, makes queries for intersections of randomly chosen t graphs , for each query, and the experiment computes computes and sends the encrypted graphs to . It then compute the encrypted intersection graph and gives it to . At the end of the experiment, outputs a bit as the experiment result.
- : outputs graphs . Then, makes queries for intersections of randomly chosen t graphs . Based on leakage functions and , produces encrypted graphs and sends them to , then simulates and sends the query results to . At the end of the experiment, outputs a bit as the experiment result.
5. Construction of Our Scheme
5.1. Construction Overview
- . The procedure is executed by the , the trusted third party, taking a secure parameter as input and producing a set of public parameters as output.
- . Upon input of a security parameter and public parameter , we use this algorithm to generate a pair of public–private keys .
- . Given the public parameter , ’s private key , and the public key of the data user , the algorithm outputs a re-encryption key that allows ciphertexts encrypted by data owners to be transformed into ciphertexts intended for the data user .
- . It is the graph encryption algorithm executed by data owner ; taking the graph , public key of the , and as inputs, it outputs the encrypted graph .
- . This algorithm takes public parameter , the re-encryption key , and ciphertexts uploaded by the data owner , and the cloud server performs re-encryption on , resulting in new ciphertexts . The cloud server calculates the graph intersections and outputs the encrypted result .
- .Taking the inputs of private key and re-encrypted ciphertext , this algorithm returns the subgraph G.
5.2. Concrete Construction
5.2.1. Setup
5.2.2. KeyGen
5.2.3. ReKeyGen
5.2.4. Enc
- Vertices Hashing. performs a hash computation on the vertices set to obtain the corresponding hashed set .
- Graph Encryption. encrypts using proxy re-encryption (PRE). To elaborate in detail, given , adjacency matrix , . For each element , choose randomly from , compute , where . For each element , choose randomly from , and compute where . The encrypted graph is , where the encrypted vertices set , and the encrypted adjacency matrix
| Algorithm 1 Enc. |
| Input: public parameter , ’s graph , ’s public key . Output: encrypted graph .
|
5.2.5. GraphIntersection
| Algorithm 2 GraphIntersection. |
| Input: public parameter , the re-encryption key , , , . Output: .
|
- Vertices Re-encryption. Given the hash sets , the cloud server computes their intersection. Denote the intersection by and the intersection of graph nodes as . The graph node corresponding to element actually has different ordinality in the original graphs. We denote the ordinality of the node of the original graph corresponding to by . There are t encrypted node sets, and since the t encrypted node sets can be decrypted to the same node intersection set, we only need to choose a random one to re-encrypt it, which can be written as . For each , we re-encrypt it using proxy re-encryption (PRE). Specifically, for , choose randomly from , and compute , with the re-encrypted . The cloud server can precompute for every node for the decryption phase. Finally, the cloud server obtains the re-encrypted vertices sets .
- Matrices Re-encryption. The cloud server continues to calculate the re-encrypted adjacency matrix. It chooses the elements in the encrypted matrix where and constructs the submatrixFor each , we re-encrypt it using proxy re-encryption (PRE). Specifically, for , we choose randomly from , and compute , with the re-encrypted . The cloud server can also precompute for every element for the decryption phase. Finally, the cloud server obtains the re-encrypted matrix
- Graph Intersection Computation. The cloud server then computes
5.2.6. Dec
- Vertices Decryption. According to the graph re-encryption in Algorithm 2, the re-encrypted node set corresponding to the intersection set is , where . It can be obtained that . Finally, we obtain the set of intersections of vertices .
- Matrix Decryption. The edges set intersection can be decrypted with as follows:
| Algorithm 3 Dec. |
| Input: , , . Output: G.
|
6. Correctness and Security Analysis
6.1. Correctness Analysis
6.2. Security Analysis
- Leakage function : Given a query , where , the leakage function reveals the information inferred from encrypted graphs and their encrypted intersection graph , including the vertex count of each individual graph and the vertex count of the graph intersection. Thus, where are formally described as follows:
- -
- . is is a t-sized array, where for .
- -
- . signifies the total vertices in the graph intersection which denoted as .
- Leakage function : The leakage function reveals information during multiple queries including query pattern leakage, which reveals whether a particular query has been issued previously, and intersection pattern leakage, which indicates the number of common vertices shared among different queries. Let be a sequence of graph intersection queries, where corresponds to a collection of graphs . They are formally stated as follows.
7. Performance Analysis
7.1. Theoretical Analysis
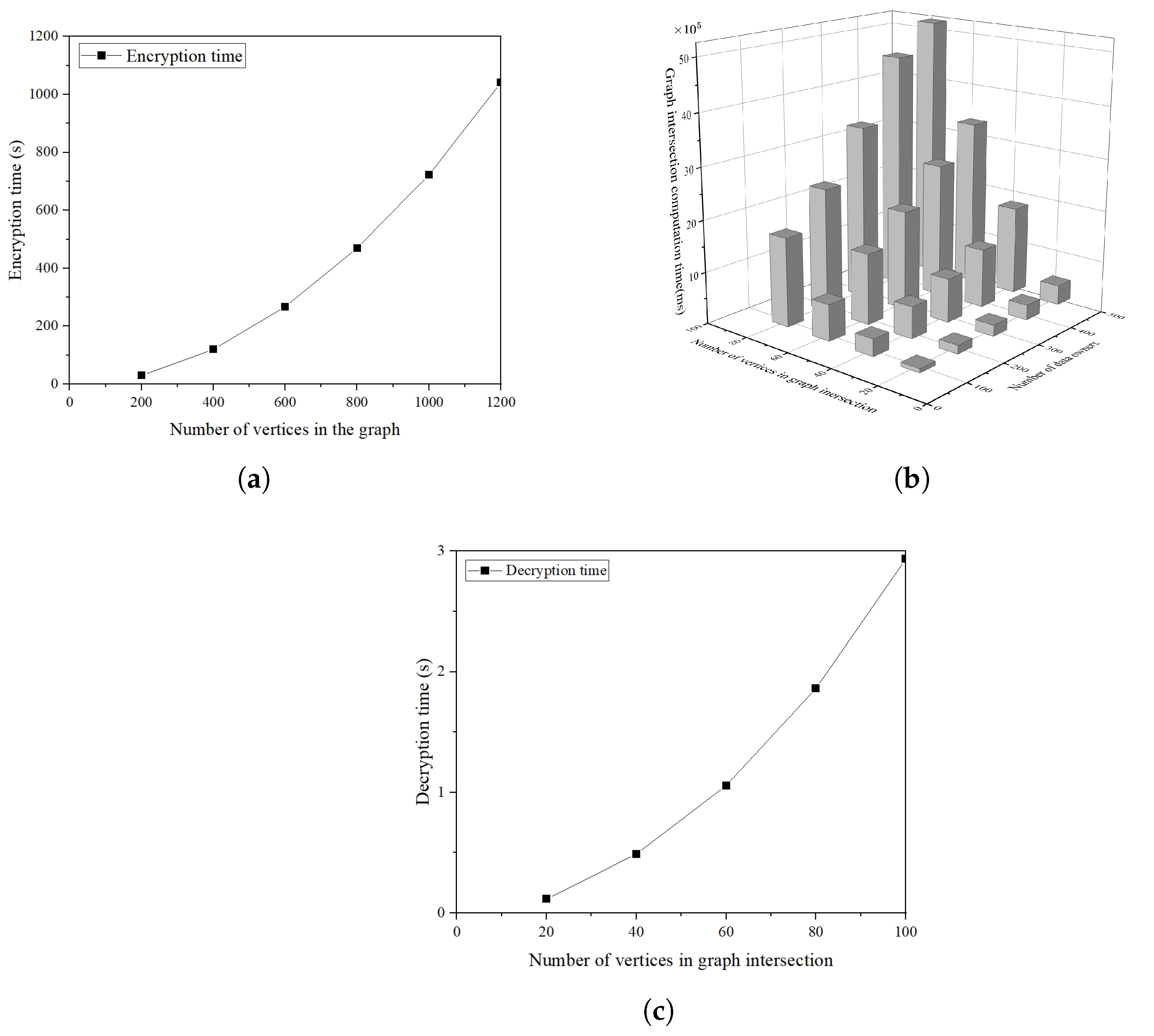
7.2. Experiments
7.2.1. Experimental Setting
7.2.2. Experimental Results
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, M.; Ma, B.; Zhu, L.; Mijumbi, R.; Du, X.; Hu, J. Cloud-Based Approximate Constrained Shortest Distance Queries Over Encrypted Graphs with Privacy Protection. arXiv 2018, arXiv:1809.07912. [Google Scholar] [CrossRef]
- Wang, W.; Jia, Z.; Xu, M.; Li, S. SPCS: Strong Privacy-Preserving-Constrained Shortest Distance Queries on Encrypted Graphs. IEEE Internet Things J. 2022, 9, 22516–22528. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, L.; Xu, C.; Sharif, K.; Zhang, C.; Liu, X. PGAS: Privacy-preserving Graph Encryption for Accurate Constrained Shortest Distance Queries. Inf. Sci. 2020, 506, 325–345. [Google Scholar] [CrossRef]
- Wang, Q.; Ren, K.; Du, M.; Li, Q.; Mohaisen, A. SecGDB: Graph Encryption for Exact Shortest Distance Queries with Efficient Updates. In Financial Cryptography and Data Security; Kiayias, A., Ed.; Springer International Publishing: Cham, Switzerland, 2017; Volume 10322, pp. 79–97. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, L.; He, X.; Chen, J. Enabling Privacy-Preserving Shortest Distance Queries on Encrypted Graph Data. IEEE Trans. Dependable Secur. Comput. 2021, 18, 192–204. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, M.; Jia, Z.; Li, S. Privacy-Preserving Any-Hop Cover Shortest Distance Queries on Encrypted Graphs. IEEE Internet Things J. 2024, 11, 16517–16528. [Google Scholar] [CrossRef]
- Sun, F.; Yu, J.; Hu, J. Privacy-Preserving Approximate Minimum Community Search on Large Networks. IEEE Trans. Inf. Forensics Secur. 2024, 19, 4146–4160. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Y.; Jia, X.; Wang, Q.; Wang, C. MAGO: Maliciously Secure Subgraph Counting on Decentralized Social Graphs. IEEE Trans. Inf. Forensics Secur. 2023, 18, 2929–2944. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Y.; Jia, X.; Huang, H.; Wang, C. OblivGM: Oblivious Attributed Subgraph Matching as a Cloud Service. arXiv 2022, arXiv:2209.03526. [Google Scholar] [CrossRef]
- Zuo, X.; Li, L.; Peng, H.; Luo, S.; Yang, Y. Privacy-Preserving Subgraph Matching Scheme with Authentication in Social Networks. IEEE Trans. Cloud Comput. 2022, 10, 2038–2049. [Google Scholar] [CrossRef]
- Ge, X.; Yu, J.; Hao, R. Privacy-Preserving Graph Matching Query Supporting Quick Subgraph Extraction. IEEE Trans. Dependable Secur. Comput. 2024, 21, 1286–1300. [Google Scholar] [CrossRef]
- Fan, Z.; Choi, B.; Chen, Q.; Xu, J.; Hu, H.; Bhowmick, S.S. Structure-Preserving Subgraph Query Services. IEEE Trans. Knowl. Data Eng. 2015, 27, 2275–2290. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Y.; Jia, X.; Wang, C. eGrass: An Encrypted Attributed Subgraph Matching System with Malicious Security. IEEE Trans. Inf. Forensics Secur. 2024, 19, 5999–6014. [Google Scholar] [CrossRef]
- Cao, N.; Yang, Z.; Wang, C.; Ren, K.; Lou, W. Privacy-Preserving Query over Encrypted Graph-Structured Data in Cloud Computing. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems, Minneapolis, MI, USA, 20–24 June 2011; pp. 393–402. [Google Scholar] [CrossRef]
- Zuo, X.; Li, L.; Luo, S.; Peng, H.; Yang, Y.; Gong, L. Privacy-Preserving Verifiable Graph Intersection Scheme with Cryptographic Accumulators in Social Networks. IEEE Internet Things J. 2021, 8, 4590–4603. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, Z.; Li, Y.; Xu, J.; Peng, S. Private Graph Intersection Protocol. In Information Security and Privacy; Pieprzyk, J., Suriadi, S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 10343, pp. 235–248. [Google Scholar] [CrossRef]
- Liu, X.; Tu, X.F.; Luo, D.; Xu, G.; Xiong, N.N.; Chen, X.B. Secure Multi-Party Computation of Graphs’ Intersection and Union under the Malicious Model. Electronics 2023, 12, 258. [Google Scholar] [CrossRef]
- Kerschbaum, F. Outsourced Private Set Intersection Using Homomorphic Encryption. In Proceedings of the 7th ACM Symposium on Information, Computer and Communications Security, Asan, Republic of Korea, 2–4 May 2012; pp. 85–86. [Google Scholar] [CrossRef]
- Kamara, S.; Mohassel, P.; Raykova, M.; Sadeghian, S. Scaling Private Set Intersection to Billion-Element Sets. In Financial Cryptography and Data Security; Christin, N., Safavi-Naini, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8437, pp. 195–215. [Google Scholar] [CrossRef]
- Abadi, A.; Terzis, S.; Metere, R.; Dong, C. Efficient Delegated Private Set Intersection on Outsourced Private Datasets. IEEE Trans. Dependable Secur. Comput. 2019, 16, 608–624. [Google Scholar] [CrossRef]
- Ali, M.; Mohajeri, J.; Sadeghi, M.R.; Liu, X. Attribute-Based Fine-Grained Access Control for Outscored Private Set Intersection Computation. Inf. Sci. 2020, 536, 222–243. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, S. Verifiable Delegated Set Intersection Operations on Outsourced Encrypted Data. In Proceedings of the 2015 IEEE International Conference on Cloud Engineering, Tempe, AZ, USA, 9–13 March 2015; pp. 175–184. [Google Scholar] [CrossRef]
- Qian, Y.; Shen, J.; Vijayakumar, P.; Sharma, P.K. Profile Matching for IoMT: A Verifiable Private Set Intersection Scheme. IEEE J. Biomed. Health Inform. 2021, 25, 3794–3803. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, F.; Xu, J.; Peng, S. Tag-Based Verifiable Delegated Set Intersection over Outsourced Private Datasets. IEEE Trans. Cloud Comput. 2022, 10, 1201–1214. [Google Scholar] [CrossRef]
- Chase, M.; Kamara, S. Structured Encryption and Controlled Disclosure. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 5–9 December 2010; pp. 577–594. [Google Scholar] [CrossRef]
- Meng, X.; Kamara, S.; Nissim, K.; Kollios, G. GRECS: Graph Encryption for Approximate Shortest Distance Queries. In Proceedings of the CCS, Denver, CO, USA, 12–16 October 2015. [Google Scholar]
- Ghosh, E.; Kamara, S.; Tamassia, R. Efficient Graph Encryption Scheme for Shortest Path Queries. In Proceedings of the 2021 ACM Asia Conference on Computer and Communications Security, Virtual Event, 7–11 June 2021; pp. 516–525. [Google Scholar] [CrossRef]
- Falzon, F.; Ghosh, E.; Paterson, K.G.; Tamassia, R. PathGES: An Efficient and Secure Graph Encryption Scheme for Shortest Path Queries. In Proceedings of the CCS, Salt Lake City, UT, USA, 14–18 October 2024. [Google Scholar]
- Wang, F.; Chen, Z.; Pan, L.; Zhang, L.Y.; Zhou, J. CryptGraph: An Efficient Privacy-Enhancing Solution for Accurate Shortest Path Retrieval in Cloud Environments. In Proceedings of the 19th ACM Asia Conference on Computer and Communications Security, Singapore, 1–5 July 2024; pp. 1660–1674. [Google Scholar] [CrossRef]
- Wu, D.J.; Zimmerman, J.; Planul, J.; Mitchell, J.C. Privacy-Preserving Shortest Path Computation. In Proceedings of the NDSS, San Diego, CA, USA, 21–24 February 2016. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Y.; Jia, X.; Yi, X. PeGraph: A System for Privacy-Preserving and Efficient Search Over Encrypted Social Graphs. IEEE Trans. Inf. Forensics Secur. 2022, 17, 3179–3194. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.; Xu, D.; Zhou, Y. Spidey: Secure Dynamic Encrypted Property Graph Search with Lightweight Access Control. IEEE Internet Things J. 2024. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, H.; Lu, R.; Guan, Y.; Zhang, S.; Wang, F.; Shao, J.; Li, H. PGSim: Efficient and Privacy-Preserving Graph Similarity Query Over Encrypted Data in Cloud. IEEE Trans. Inf. Forensics Secur. 2023, 18, 2030–2045. [Google Scholar] [CrossRef]
- Jiang, G.; Zhang, H.; Lin, J.; Kong, F.; Yu, L. Optimized Verifiable Delegated Private Set Intersection on Outsourced Private Datasets. Comput. Secur. 2024, 141, 103822. [Google Scholar] [CrossRef]
- Sharma, S.; Li, Y.; Mehrotra, S.; Panwar, N.; Gupta, P.; Ghosh, D. Prism: Privacy-preserving and Verifiable Set Computation over Multi-Owner Secret Shared Outsourced Databases. IEEE Trans. Dependable Secur. Comput. 2024, 21, 1355–1371. [Google Scholar] [CrossRef]
- Libert, B.; Vergnaud, D. Unidirectional Chosen-Ciphertext Secure Proxy Re-Encryption. In Proceedings of the PKC 2008: 11th International Workshop on Practice and Theory in Public-Key Cryptography, Barcelona, Spain, 9–12 March 2008; Proceedings 11. Springer: Berlin/Heidelberg, Germany, 2008; pp. 360–379. [Google Scholar]
- Nik-U. The PBC Go Wrapper. Available online: https://github.com/Nik-U/pbc (accessed on 5 December 2018).
- Rozemberczki, B.; Sarkar, R. Characteristic Functions on Graphs: Birds of a Feather, from Statistical Descriptors to Parametric Models. arXiv 2020, arXiv:2005.07959. [Google Scholar]

| Notations | Description |
|---|---|
| public parameters | |
| public–private key pair of data user | |
| public–private key pair of the trusted authority | |
| re-encryption key from trusted authority to data user | |
| graph of data owner | |
| the amount of vertices in | |
| vertex set of | |
| hashed vertex set of | |
| adjacency matrix of | |
| the vertex in | |
| the element in adjacency matrix | |
| the encrypted form of | |
| the encrypted graph intersection |
| Schemes | Cryptographic Primitives | Privacy | Cloud-Assisted Computation | Multi-Owners | Multi-Users |
|---|---|---|---|---|---|
| [16] | Paillier encryption | √ | × | × | × |
| [17] | Lifted-ElGamal threshold encryption | √ | × | √ | √ |
| [15] | ElGamal encryption | √ | √ | √ | × |
| Our scheme | Proxy re-encryption | √ | √ | √ | √ |
| Algorithms | Computational Cost | Output Size |
|---|---|---|
| (one data owner) | ||
| - |
| Operation () | Exponent in | Exponent in | Multiplication in | Bilinear Paring | H |
|---|---|---|---|---|---|
| time | ms | ms | µs | ms | µs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S. Privacy-Preserving Multi-User Graph Intersection Scheme for Wireless Communications in Cloud-Assisted Internet of Things. Sensors 2025, 25, 1892. https://doi.org/10.3390/s25061892
Yang S. Privacy-Preserving Multi-User Graph Intersection Scheme for Wireless Communications in Cloud-Assisted Internet of Things. Sensors. 2025; 25(6):1892. https://doi.org/10.3390/s25061892
Chicago/Turabian StyleYang, Shumei. 2025. "Privacy-Preserving Multi-User Graph Intersection Scheme for Wireless Communications in Cloud-Assisted Internet of Things" Sensors 25, no. 6: 1892. https://doi.org/10.3390/s25061892
APA StyleYang, S. (2025). Privacy-Preserving Multi-User Graph Intersection Scheme for Wireless Communications in Cloud-Assisted Internet of Things. Sensors, 25(6), 1892. https://doi.org/10.3390/s25061892





