Ensemble-Based Model-Agnostic Meta-Learning with Operational Grouping for Intelligent Sensory Systems
Abstract
1. Introduction
- An ensemble-based model, the agnostic meta-learning method (MAML), is proposed using majority voting and operational grouping to maximize information intake in a few-shot scenarios.
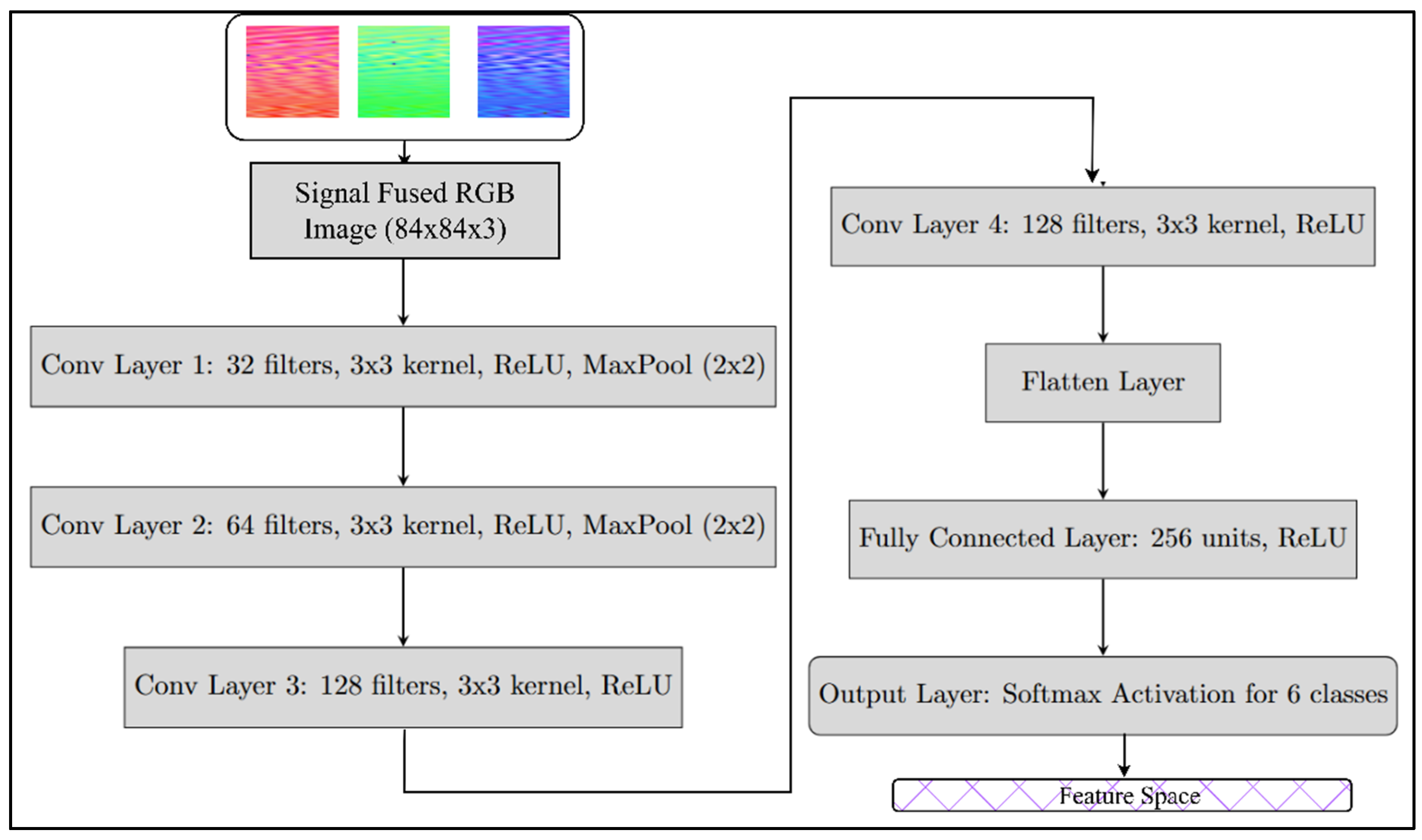
- A convolutional autoencoder-based multi-sensor to fused RGB image conversion method is implemented for converting senor signals to RGB images, and the images are later used for classifying different fault classes.
- To the best of our knowledge, this work is the first of its kind to implement ensemble-based MAML algorithms with such diverse classes in a synthetic dataset.
2. Related Work
3. Methodology and Overview
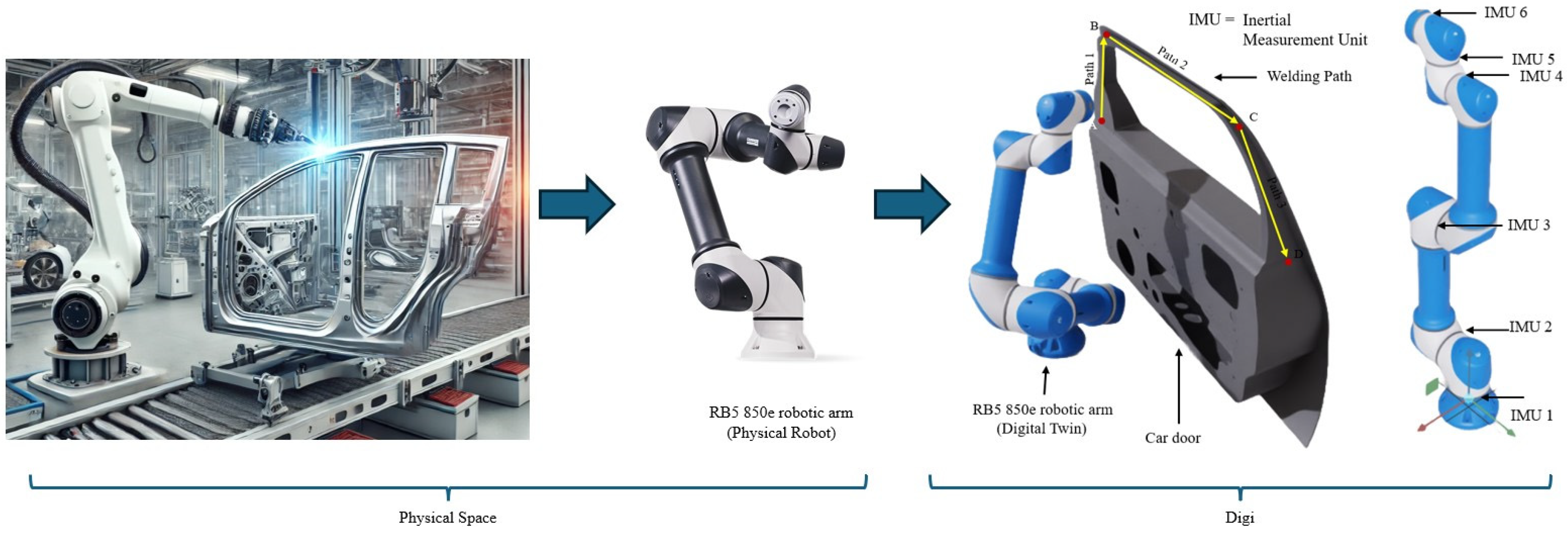
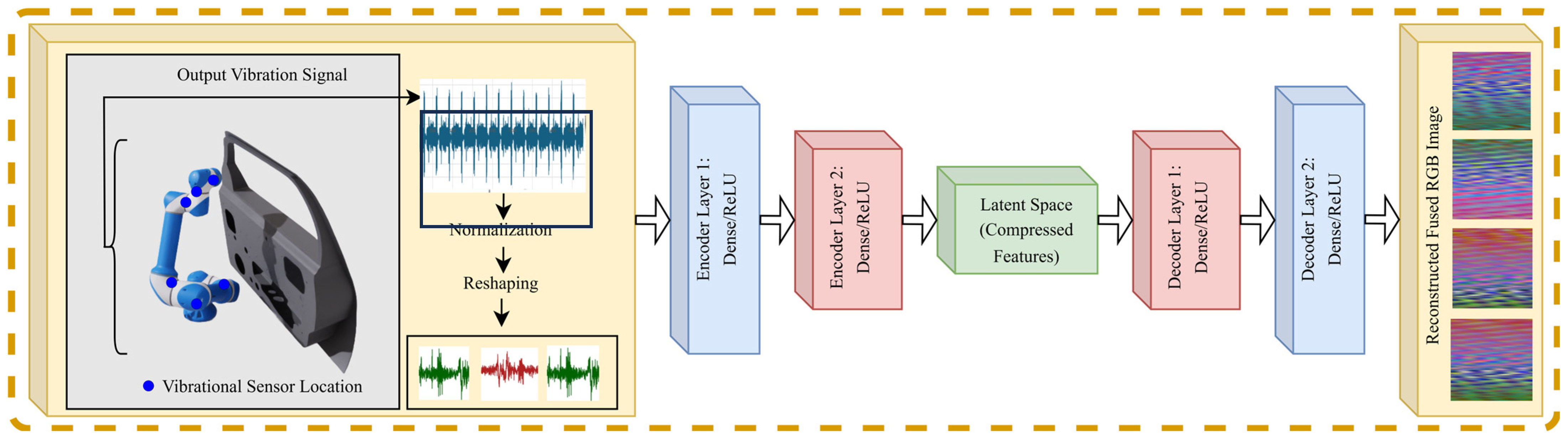
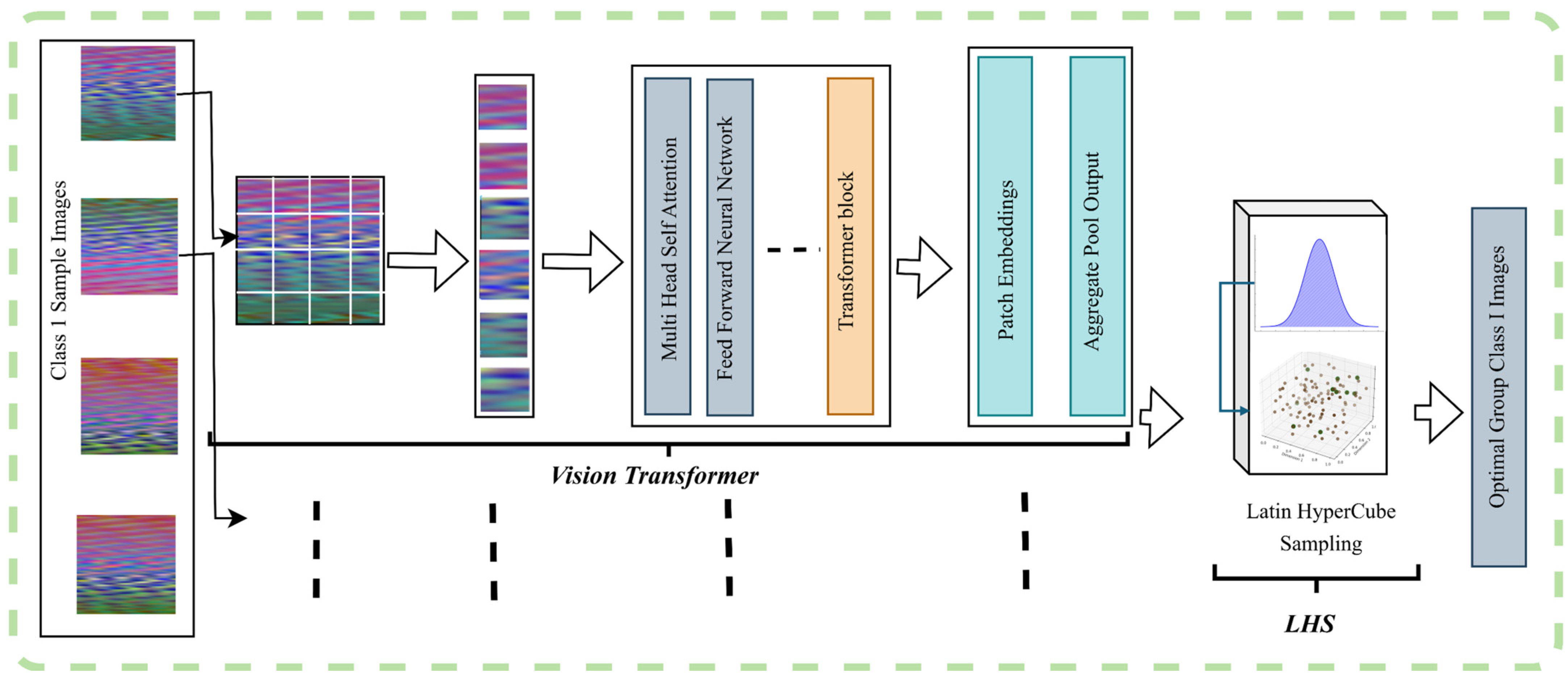
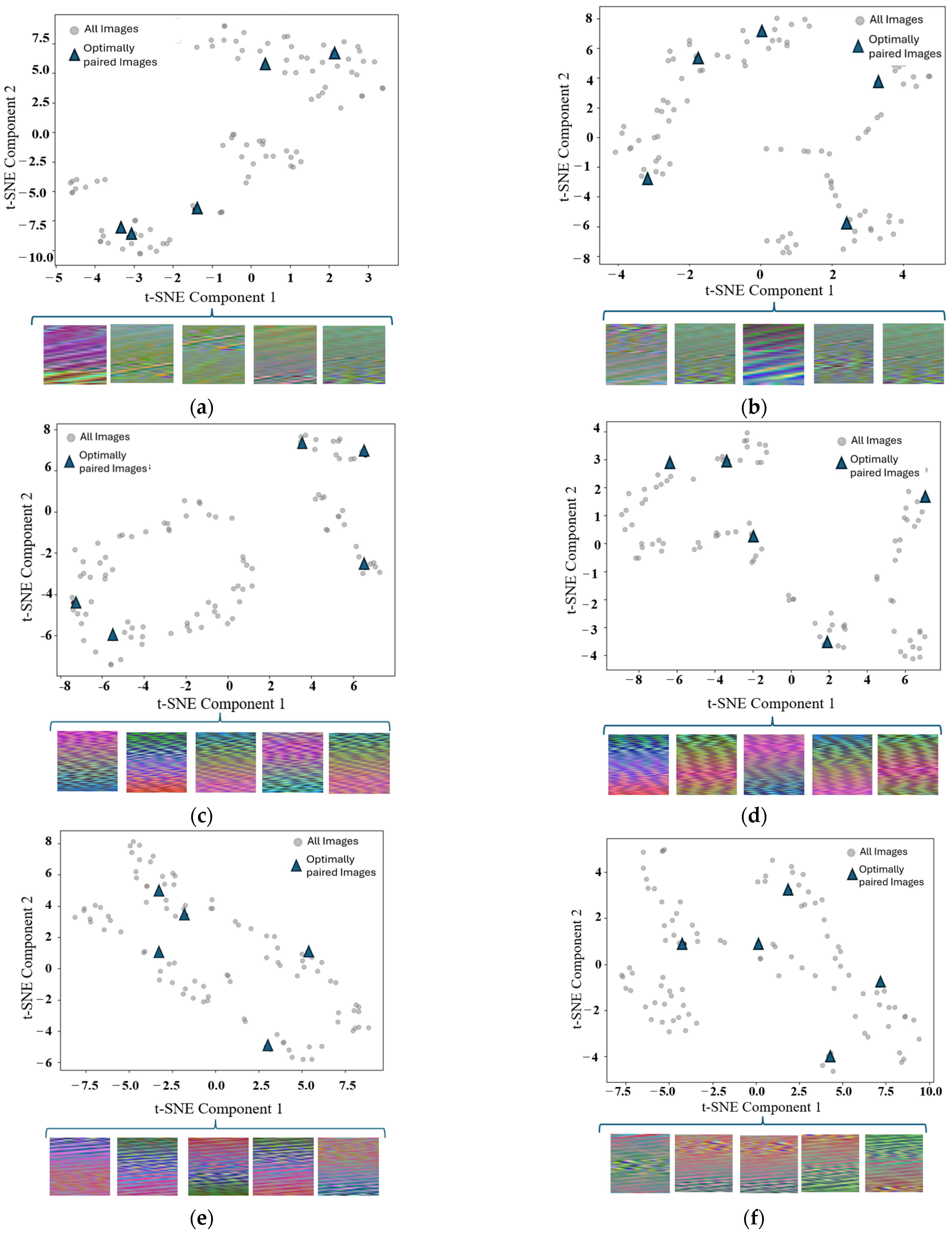
3.1. Dataset Generation and Operational Grouping Strategy
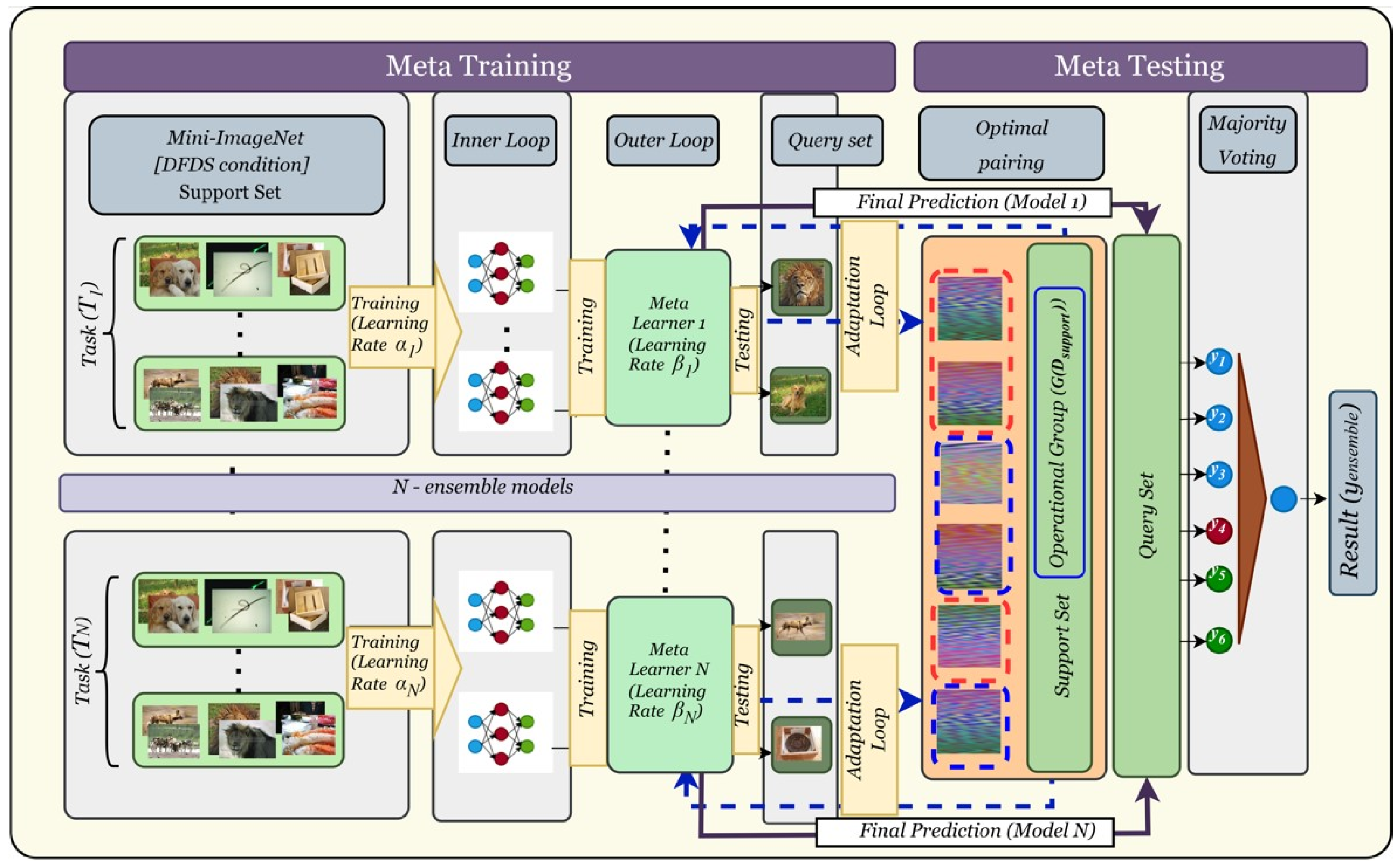
3.2. Ensemble MAML Framework
| Algorithm 1 Ensemble-Based MAML with Operational Grouping in Meta-Test Phase | |
| Require: Dataset of tasks , learning rates for ensemble models, number of inner loop steps , operational grouping strategy . | |
| Ensure: Final ensemble prediction . | |
| 1: | Meta-Train Phase: Initialize MAML models with random parameters . |
| 2: | for each task from the meta-training dataset do |
| 3: | Split into support set and query set . |
| 4: | for each model in the ensemble do |
| 5: | Compute loss . |
| 6: | Adapt via gradient steps: . |
| 7: | Evaluate loss . |
| 8: | Update meta-parameters: . |
| 9: | end for |
| 10: | end for |
| 11: | Meta-Test Phase: |
| 12: | for each task from the meta-test dataset do |
| 13: | Split into support set and query set . |
| 14: | Apply Operational grouping . |
| 15: | for each model in the ensemble do |
| 16: | Compute loss . |
| 17: | Adapt . |
| 18: | end for |
| 19: | Aggregate predictions via majority voting: . |
| 20: | end for |
| 21: | Return . |
4. Experimental Setup
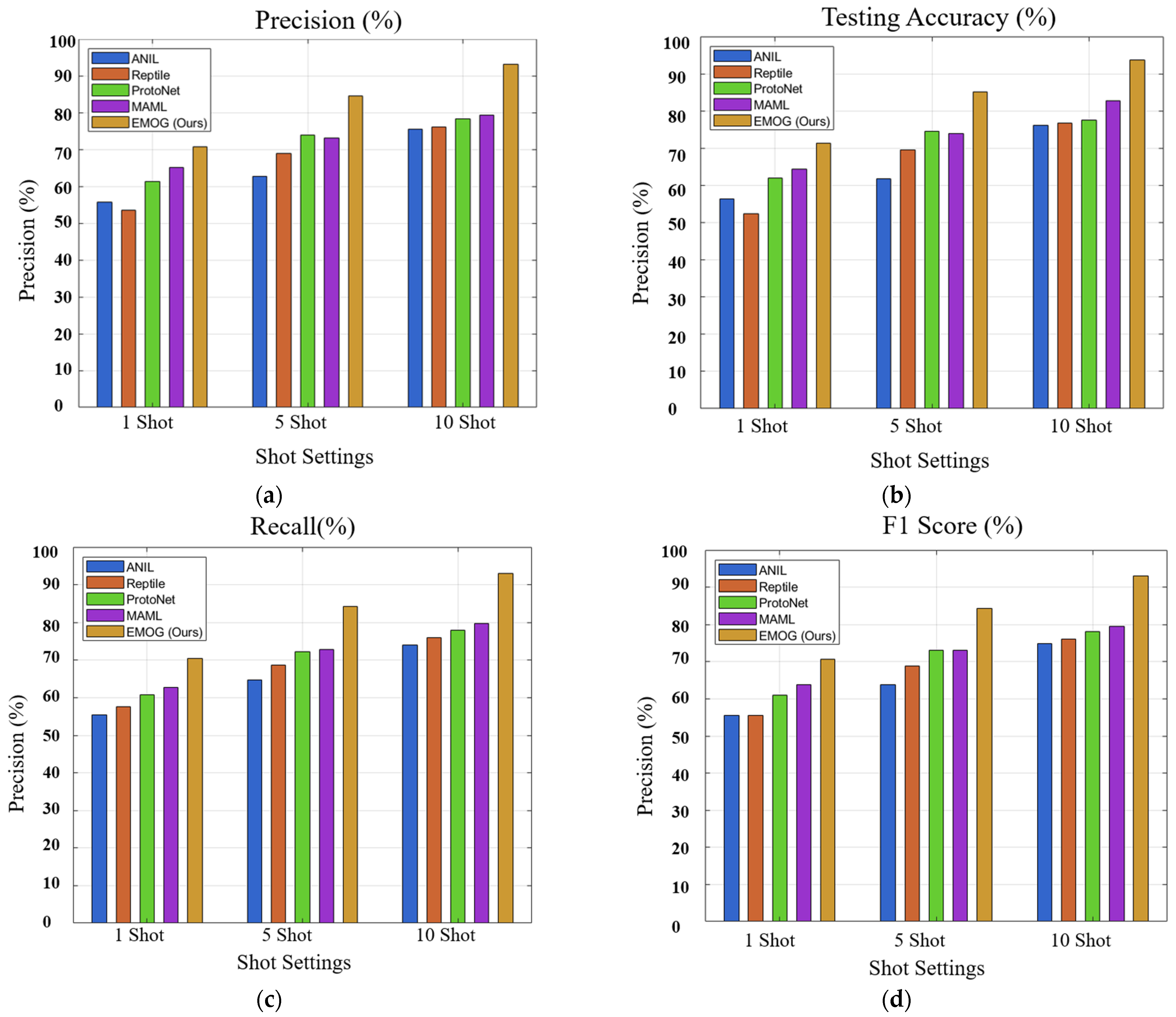
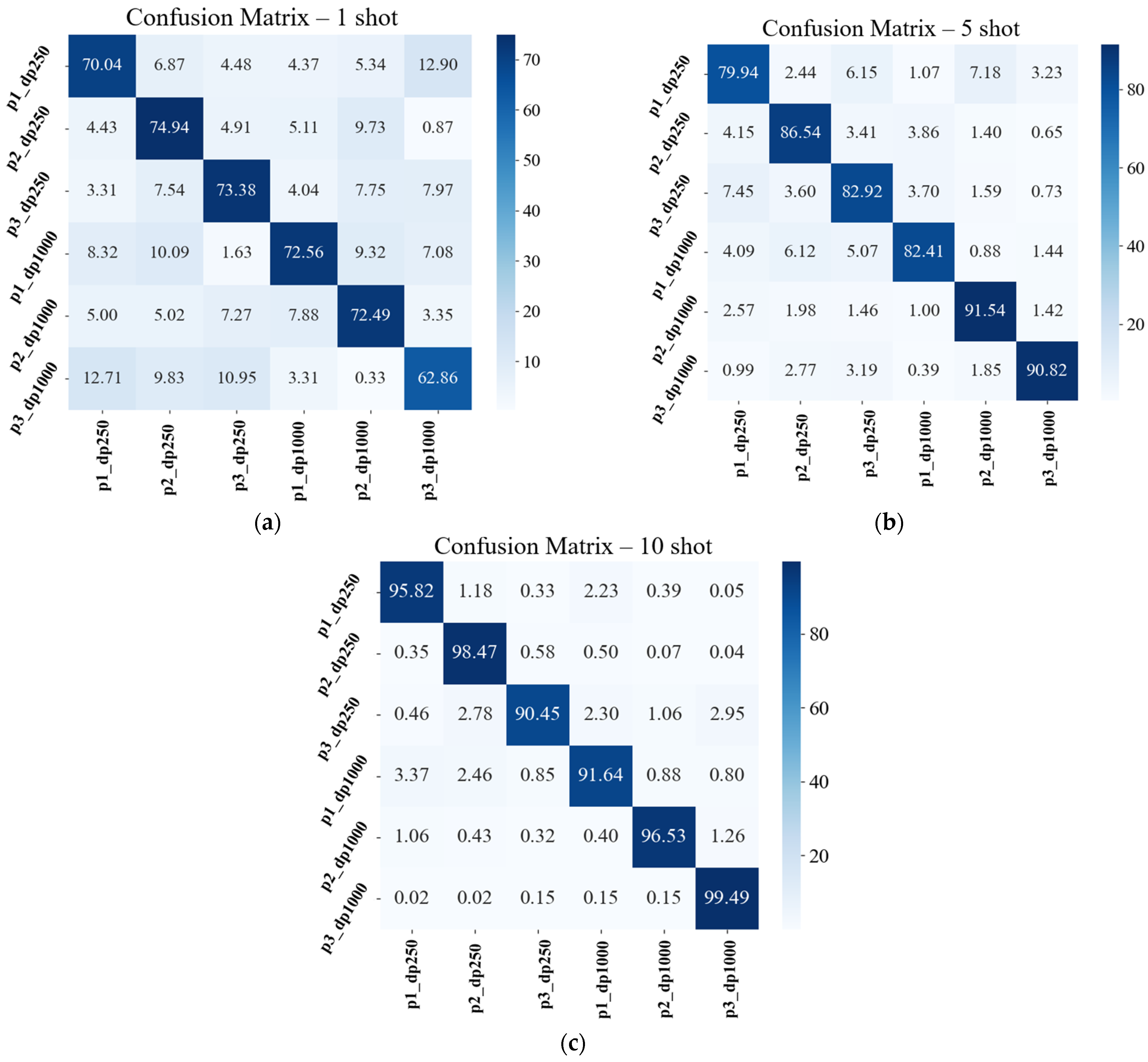
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shao, Y.; Du, S.; Huang, D. Advancements in Applications of Manufacturing and Measurement Sensors. Sensors 2025, 25, 454. [Google Scholar] [CrossRef] [PubMed]
- Saleem, J.; Raza, U.; Holderbaum, W. Transforming Industry 4.0 Security: Analysis of ABE and ABA Technologies. IECE Trans. Intell. Syst. 2024, 1, 127–144. [Google Scholar] [CrossRef]
- Ramolia, N.; Tank, P.P.; Ravikumar, R.N.; Zeb, B.; Kumar, M.; Singh, S.K. Futuristic Metaverse: Security and Counter Measures. IECE Transactions on Intelligent Systematics. IECE Trans. Intell. Syst. 2025, 2, 49–65. [Google Scholar]
- Xie, J.; Xiang, N.; Yi, S. Enhanced Recognition for Finger Gesture-Based Control in Humanoid Robots Using Inertial Sensors. IECE Trans. Sens. Commun. Control 2024, 1, 89–100. [Google Scholar] [CrossRef]
- Park, S.; Youm, M.; Kim, J. IMU Sensor-Based Worker Behavior Recognition and Construction of a Cyber–Physical System Environment. Sensors 2025, 25, 442. [Google Scholar] [CrossRef]
- Duan, J.; Cao, G.; Ma, G.; Yu, Z.; Shao, C. Research on On-Line Monitoring of Grinding Wheel Wear Based on Multi-Sensor Fusion. Sensors 2024, 24, 5888. [Google Scholar] [CrossRef]
- Izagirre, U.; Andonegui, I.; Landa-Torres, I.; Zurutuza, U. A Practical and Synchronized Data Acquisition Network Architecture for Industrial Robot Predictive Maintenance in Manufacturing Assembly Lines. Robot. Comput. Integr. Manuf. 2022, 74, 102287. [Google Scholar] [CrossRef]
- Borgi, T.; Hidri, A.; Neef, B.; Naceur, M.S. Data Analytics for Predictive Maintenance of Industrial Robots. In Proceedings of the 2017 International Conference on Advanced Systems and Electric Technologies (IC_ASET), Hammamet, Tunisia, 14–17 January 2017; pp. 412–417. [Google Scholar]
- Pookkuttath, S.; Rajesh Elara, M.; Sivanantham, V.; Ramalingam, B. AI-Enabled Predictive Maintenance Framework for Autonomous Mobile Cleaning Robots. Sensors 2022, 22, 13. [Google Scholar] [CrossRef]
- Xie, T.; Huang, X.; Choi, S.-K. Intelligent Mechanical Fault Diagnosis Using Multisensor Fusion and Convolution Neural Network. IEEE Trans. Ind. Inform. 2022, 18, 3213–3223. [Google Scholar] [CrossRef]
- Che, C.; Wang, H.; Xiong, M.; Ni, X. Few-Shot Fault Diagnosis of Rolling Bearing under Variable Working Conditions Based on Ensemble Meta-Learning. Digit. Signal Process. 2022, 131, 103777. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, S.; Luo, L.; Yang, J. Few-Shot Learning with Long-Tailed Labels. Pattern Recognit. 2024, 156, 110806. [Google Scholar] [CrossRef]
- Sabry, A.H.; Ungku Amirulddin, U.A.B. A Review on Fault Detection and Diagnosis of Industrial Robots and Multi-Axis Machines. Results Eng. 2024, 23, 102397. [Google Scholar] [CrossRef]
- Antoniou, A.; Edwards, H.; Storkey, A. How to Train Your MAML. In Proceedings of the Seventh International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 5 September 2019. [Google Scholar]
- Wang, H.; Li, C.; Ding, P.; Li, S.; Li, T.; Liu, C.; Zhang, X.; Hong, Z. A Novel Transformer-Based Few-Shot Learning Method for Intelligent Fault Diagnosis with Noisy Labels under Varying Working Conditions. Reliab. Eng. Syst. Saf. 2024, 251, 110400. [Google Scholar] [CrossRef]
- Xie, T.; Huang, X.; Choi, S.-K. Cross-Domain Health Conditions Identification Based on Joint Distribution Modeling of Fused Prototypes. In Proceedings of the ASME 2023 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 21 November 2023. [Google Scholar]
- Li, C.; Li, S.; Zhang, A.; He, Q.; Liao, Z.; Hu, J. Meta-Learning for Few-Shot Bearing Fault Diagnosis under Complex Working Conditions. Neurocomputing 2021, 439, 197–211. [Google Scholar] [CrossRef]
- Xiao, Y.; Shao, H.; Wang, J.; Cai, B.; Liu, B. Domain-Augmented Meta Ensemble Learning for Mechanical Fault Diagnosis from Heterogeneous Source Domains to Unseen Target Domains. Expert Syst. Appl. 2025, 259, 125345. [Google Scholar] [CrossRef]
- Billion Polak, P.; Prusa, J.D.; Khoshgoftaar, T.M. Low-Shot Learning and Class Imbalance: A Survey. J. Big Data 2024, 11, 1. [Google Scholar] [CrossRef]
- Ochal, M.; Patacchiola, M.; Vazquez, J.; Storkey, A.; Wang, S. Few-Shot Learning With Class Imbalance. IEEE Trans. Artif. Intell. 2023, 4, 1348–1358. [Google Scholar] [CrossRef]
- Song, H.; Deng, B.; Pound, M.; Özcan, E.; Triguero, I. A Fusion Spatial Attention Approach for Few-Shot Learning. Inf. Fusion 2022, 81, 187–202. [Google Scholar] [CrossRef]
- Siwek, K.; Osowski, S. Autoencoder versus PCA in Face Recognition. In Proceedings of the 2017 18th International Conference on Computational Problems of Electrical Engineering (CPEE), Kutna Hora, Czech Republic, 11–13 September 2017; pp. 1–4. [Google Scholar]
- Azarang, A.; Manoochehri, H.E.; Kehtarnavaz, N. Convolutional Autoencoder-Based Multispectral Image Fusion. IEEE Access 2019, 7, 35673–35683. [Google Scholar] [CrossRef]
- Hurtado, J.; Salvati, D.; Semola, R.; Bosio, M.; Lomonaco, V. Continual Learning for Predictive Maintenance: Overview and Challenges. Intell. Syst. Appl. 2023, 19, 200251. [Google Scholar] [CrossRef]
- Li, J.; Schaefer, D.; Milisavljevic-Syed, J. A Decision-Based Framework for Predictive Maintenance Technique Selection in Industry 4.0. Procedia CIRP 2022, 107, 77–82. [Google Scholar] [CrossRef]
- Pan, T.; Chen, J.; Zhang, T.; Liu, S.; He, S.; Lv, H. Generative Adversarial Network in Mechanical Fault Diagnosis under Small Sample: A Systematic Review on Applications and Future Perspectives. ISA Trans. 2022, 128, 1–10. [Google Scholar] [CrossRef]
- Lumer-Klabbers, G.; Hausted, J.O.; Kvistgaard, J.L.; Macedo, H.D.; Frasheri, M.; Larsen, P.G. Towards a Digital Twin Framework for Autonomous Robots. In Proceedings of the 2021 IEEE 45th Annual Computers, Software, and Applications Conference (COMPSAC), Madrid, Spain, 12–16 July 2021; pp. 1254–1259. [Google Scholar]
- Sahli, A.; Evans, R.; Manohar, A. Predictive Maintenance in Industry 4.0: Current Themes. Procedia CIRP 2021, 104, 1948–1953. [Google Scholar] [CrossRef]
- Wu, Y.; Su, Y.; Wang, Y.-L.; Shi, P. T-S Fuzzy Data-Driven ToMFIR With Application to Incipient Fault Detection and Isolation for High-Speed Rail Vehicle Suspension Systems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7921–7932. [Google Scholar] [CrossRef]
- Pu, Z.; Cabrera, D.; Bai, Y.; Li, C. Generative Adversarial One-Shot Diagnosis of Transmission Faults for Industrial Robots. Robot. Comput. Integr. Manuf. 2023, 83, 102577. [Google Scholar] [CrossRef]
- Xia, L.; Zheng, P.; Li, X.; Gao, R.X.; Wang, L. Toward Cognitive Predictive Maintenance: A Survey of Graph-Based Approaches. J. Manuf. Syst. 2022, 64, 107–120. [Google Scholar] [CrossRef]
- Wang, X.; Liu, M.; Liu, C.; Ling, L.; Zhang, X. Data-Driven and Knowledge-Based Predictive Maintenance Method for Industrial Robots for the Production Stability of Intelligent Manufacturing. Expert Syst. Appl. 2023, 234, 121136. [Google Scholar] [CrossRef]
- Raghu, A.; Raghu, M.; Bengio, S.; Vinyals, O. Rapid Learning or Feature Reuse? Towards Understanding the Effectiveness of MAML. In Proceedings of the Eighth International Conference on Learning Representations, Addis Ababa, Ethiopia, 19 September 2020. [Google Scholar]
- Nichol, A.; Achiam, J.; Schulman, J. On First-Order Meta-Learning Algorithms. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical Networks for Few-Shot Learning. In Proceedings of the NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 15 March 2017; pp. 4080–4090. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 9 March 2017. [Google Scholar]
- Garg, G.; Kuts, V.; Anbarjafari, G. Digital Twin for FANUC Robots: Industrial Robot Programming and Simulation Using Virtual Reality. Sustainability 2021, 13, 10336. [Google Scholar] [CrossRef]
- Yun, J.; Li, G.; Jiang, D.; Xu, M.; Xiang, F.; Huang, L.; Jiang, G.; Liu, X.; Xie, Y.; Tao, B.; et al. Digital Twin Model Construction of Robot and Multi-Object under Stacking Environment for Grasping Planning. Appl. Soft Comput. 2023, 149, 111005. [Google Scholar] [CrossRef]
- Erickson, D.; Weber, M.; Sharf, I. Contact Stiffness and Damping Estimation for Robotic Systems. Int. J. Robot. Res. 2003, 22, 41–57. [Google Scholar] [CrossRef]
- Bitz, T.; Zahedi, F.; Lee, H. Variable Damping Control of a Robotic Arm to Improve Trade-off between Agility and Stability and Reduce User Effort. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 11259–11265. [Google Scholar]
- Patiño, J.; Encalada-Dávila, Á.; Sampietro, J.; Tutivén, C.; Saldarriaga, C.; Kao, I. Damping Ratio Prediction for Redundant Cartesian Impedance-Controlled Robots Using Machine Learning Techniques. Mathematics 2023, 11, 1021. [Google Scholar] [CrossRef]
- Coleman, T.; Franzese, G.; Borja, P. Damping Design for Robot Manipulators. In Human-Friendly Robotics 2022—HFR: Proceedings of the 15th International Workshop on Human-Friendly Robotics; Springer: Cham, Switzerland, 2023; pp. 74–89. [Google Scholar]
| Model No. | Inner-Loop Learning Rate (α) | Outer-Loop Learning Rate (β) |
|---|---|---|
| M1 | 0.002264 | 0.040161 |
| M2 | 0.001987 | 0.046838 |
| M3 | 0.001475 | 0.001475 |
| M4 | 0.001008 | 0.036277 |
| M5 | 0.002848 | 0.029295 |
| M6 | 0.002592 | 0.024300 |
| Sample Number | Path 1 (A-B) | Path 2 (B-C) | Path 3 (C-D) |
|---|---|---|---|
| Correct damping (dp = 250) | 50 | 50 | 50 |
| Defective damping (dp = 1000) | 50 | 50 | 50 |
| Testing Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shot number | 1 | 5 | 10 | 1 | 5 | 10 | 1 | 5 | 10 | 1 | 5 | 10 |
| ANIL | 56.3 | 61.8 | 76.2 | 55.8 | 62.8 | 75.5 | 55.4 | 64.8 | 74.1 | 55.6 | 63.8 | 74.8 |
| Reptile | 52.4 | 69.6 | 76.8 | 53.5 | 69 | 76.2 | 57.6 | 68.6 | 76 | 55.5 | 68.8 | 76.1 |
| ProtoNet | 61.9 | 74.6 | 77.6 | 61.3 | 73.9 | 78.4 | 60.8 | 72.2 | 77.9 | 61.0 | 73.0 | 78.1 |
| MAML | 64.4 | 73.9 | 82.8 | 65.1 | 73.2 | 79.4 | 62.7 | 72.8 | 79.8 | 63.9 | 73.0 | 79.6 |
| EMOG (Ours) | 71.4 | 85.2 | 93.8 | 70.8 | 84.6 | 93.1 | 70.4 | 84.3 | 84.3 | 70.6 | 84.4 | 93.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallick, M.; Shim, Y.-D.; Won, H.-I.; Choi, S.-K. Ensemble-Based Model-Agnostic Meta-Learning with Operational Grouping for Intelligent Sensory Systems. Sensors 2025, 25, 1745. https://doi.org/10.3390/s25061745
Mallick M, Shim Y-D, Won H-I, Choi S-K. Ensemble-Based Model-Agnostic Meta-Learning with Operational Grouping for Intelligent Sensory Systems. Sensors. 2025; 25(6):1745. https://doi.org/10.3390/s25061745
Chicago/Turabian StyleMallick, Mainak, Young-Dae Shim, Hong-In Won, and Seung-Kyum Choi. 2025. "Ensemble-Based Model-Agnostic Meta-Learning with Operational Grouping for Intelligent Sensory Systems" Sensors 25, no. 6: 1745. https://doi.org/10.3390/s25061745
APA StyleMallick, M., Shim, Y.-D., Won, H.-I., & Choi, S.-K. (2025). Ensemble-Based Model-Agnostic Meta-Learning with Operational Grouping for Intelligent Sensory Systems. Sensors, 25(6), 1745. https://doi.org/10.3390/s25061745







