Enhanced DWT for Denoising Heartbeat Signal in Non-Invasive Detection
Abstract
1. Introduction
2. Principle
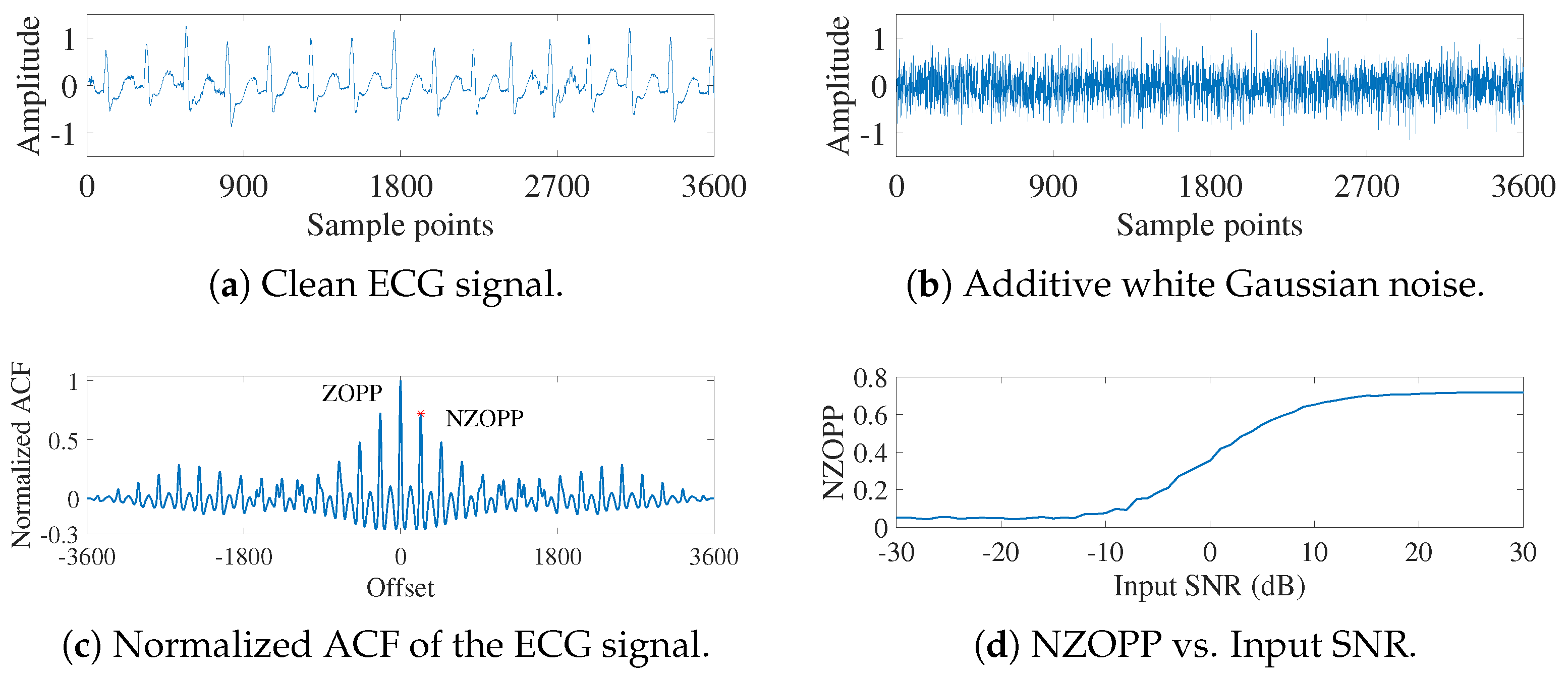
2.1. ACF Evaluation Indicator
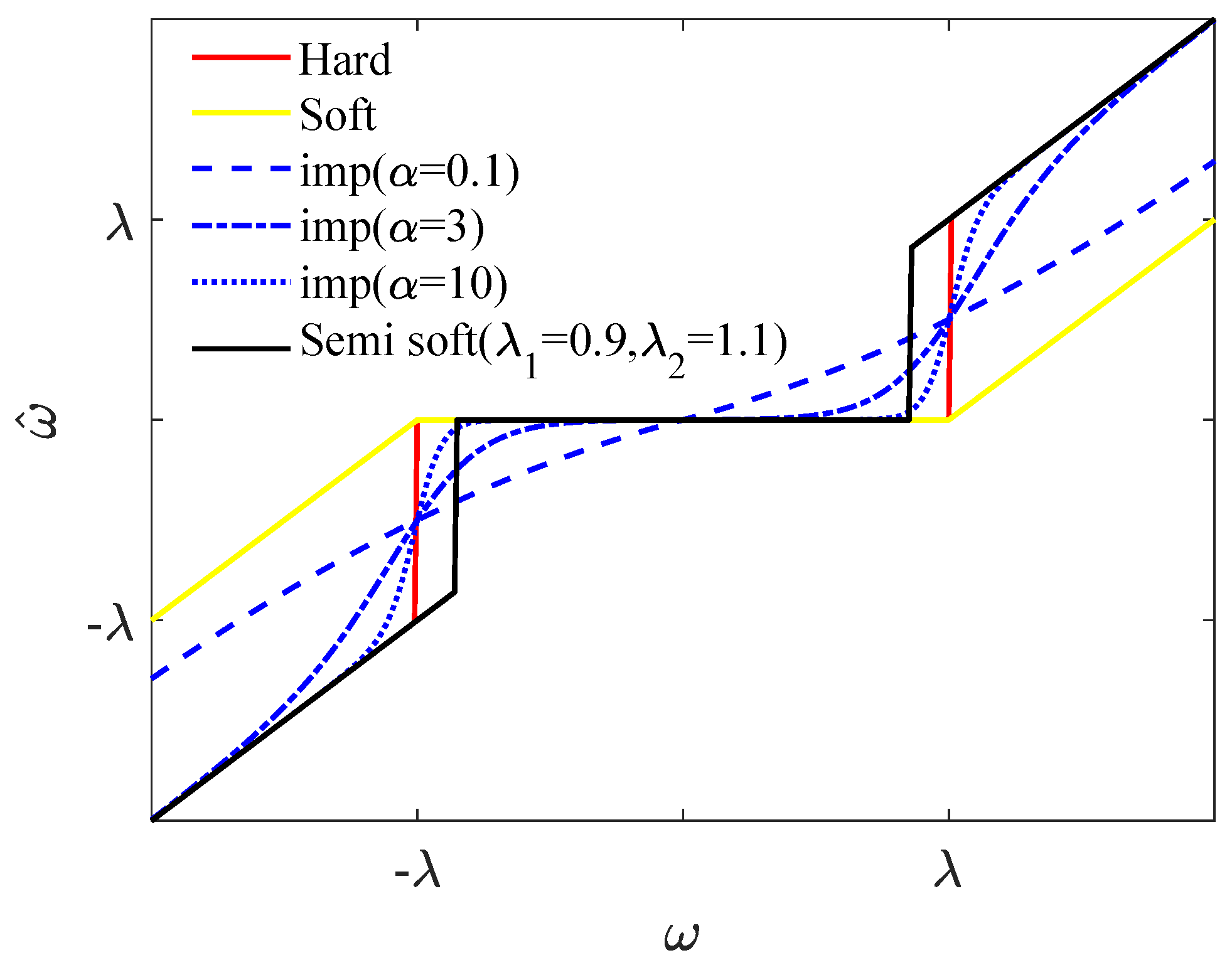
2.2. Improved Threshold and Threshold Function
2.3. Fast Algorithms for Thresholds and Threshold Function
- (1)
- Set the wavelet basis as db3, perform an 8-layer wavelet decomposition, and set a sufficiently wide tuning factor in the range [] with the interpolation , i.e., [], as shown in the step (1) of Figure 4;
- (2)
- Denoise the noisy signals with each tuning factor of threshold function in [] and calculate the NZOPP corresponding to each denoised signal to obtain [], i.e., [];
- (3)
- Find the maximum NZOPP. For example, and its corresponding ;
- (4)
- Interpolate both sides of to generate a new sequence [, ], i.e., [], as shown in the step (2) of Figure 4.
- (5)
- Denoise the noisy signals with each new tuning factor of threshold function () and calculate the NZOPP corresponding to each denoised signal to obtain [];
- (6)
- Find the maximum value in []. For example, and its corresponding ;
- (7)
- Interpolate on both sides of to obtain a new tuning factor sequence [, ], i.e., [], as shown in the step (3) of Figure 4;
- (8)
- Repeat steps (4)∼(7) until ;
- (9)
- Outputs the current as the optimal tuning factor.
3. Simulation Experiments
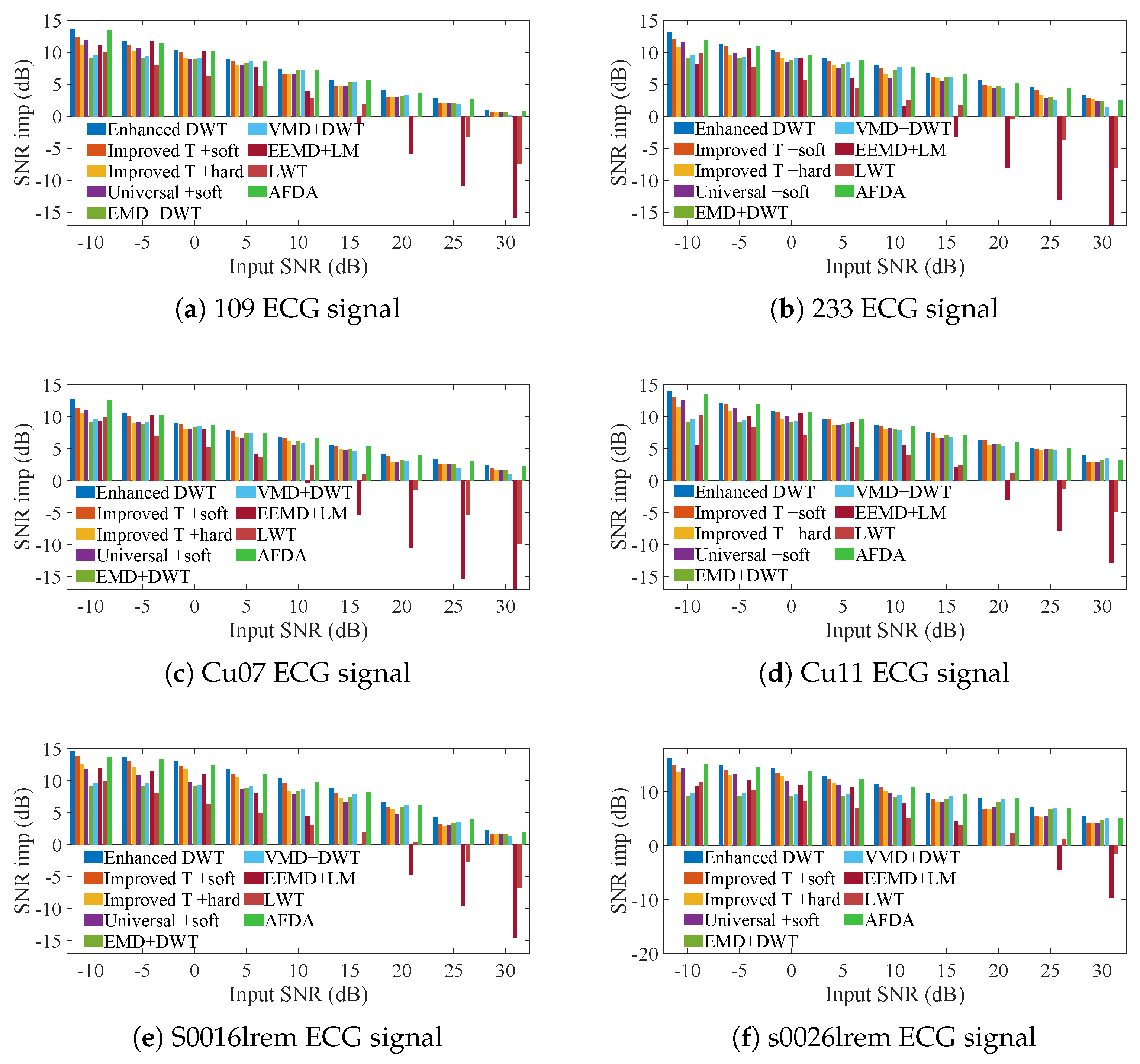
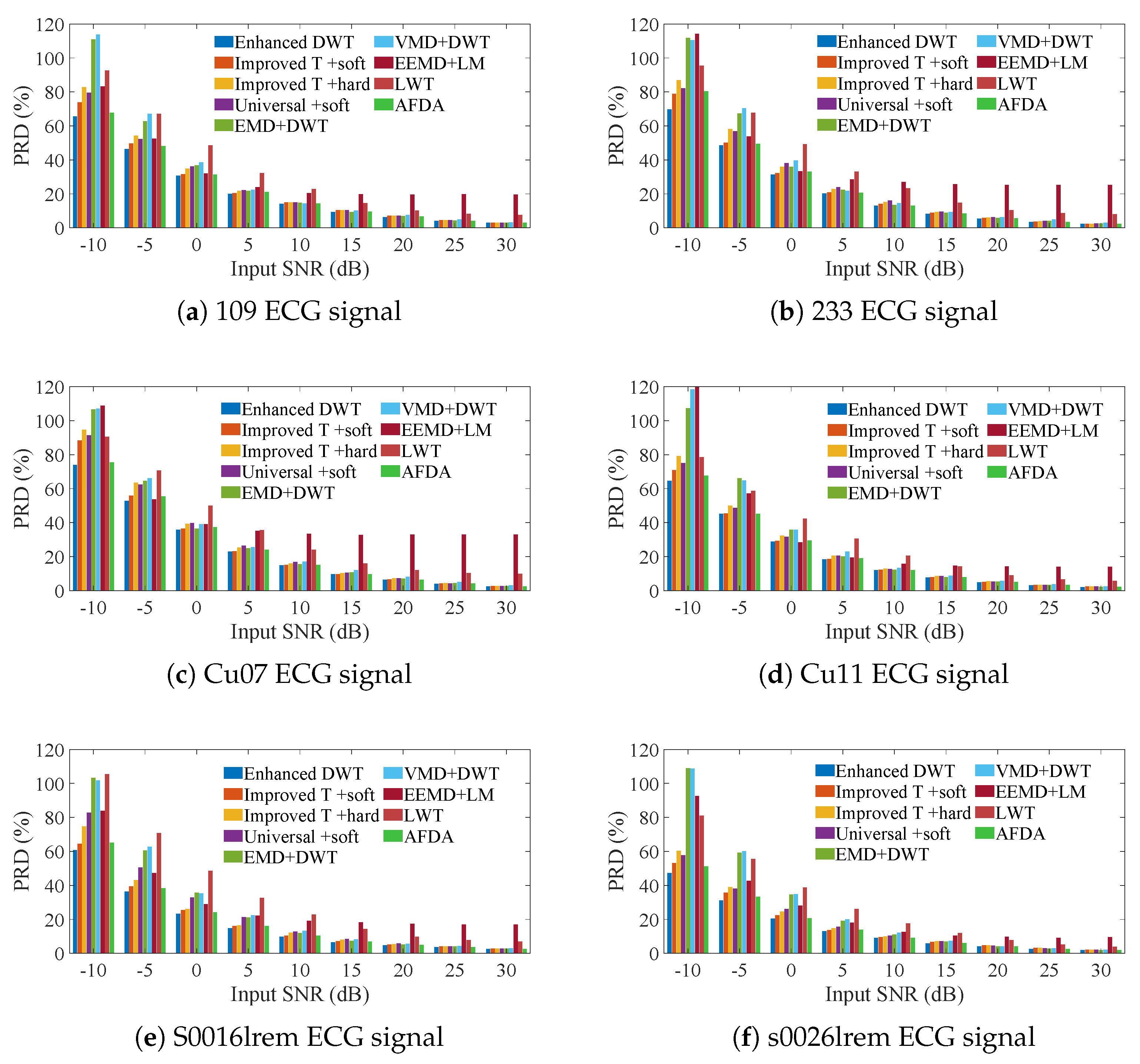
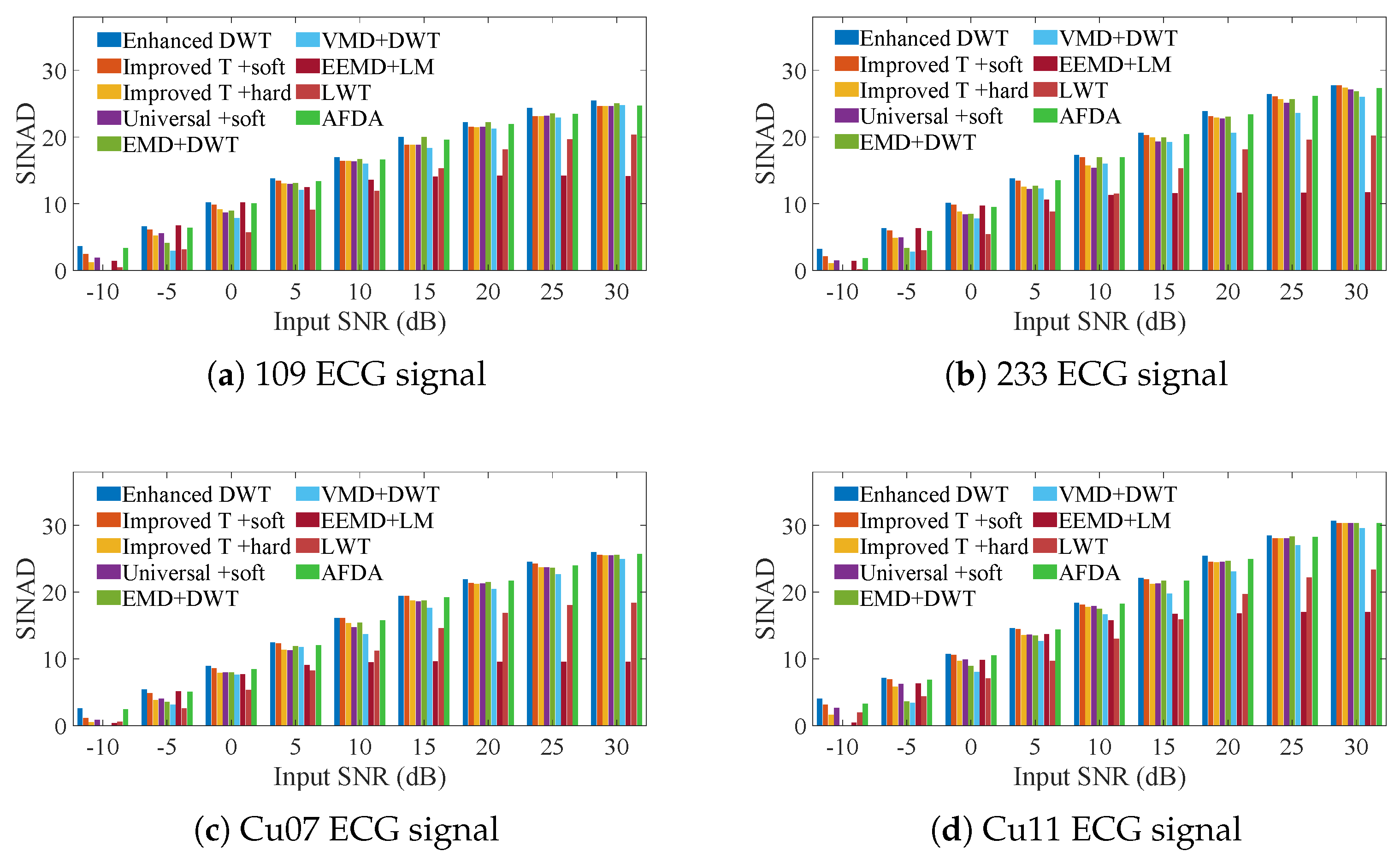
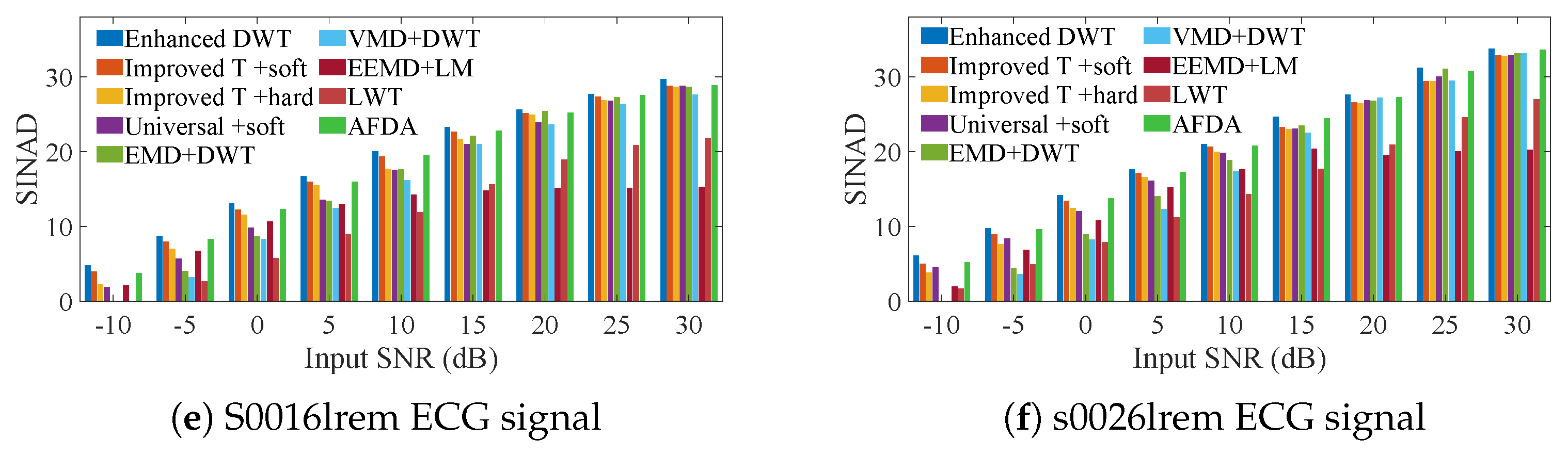
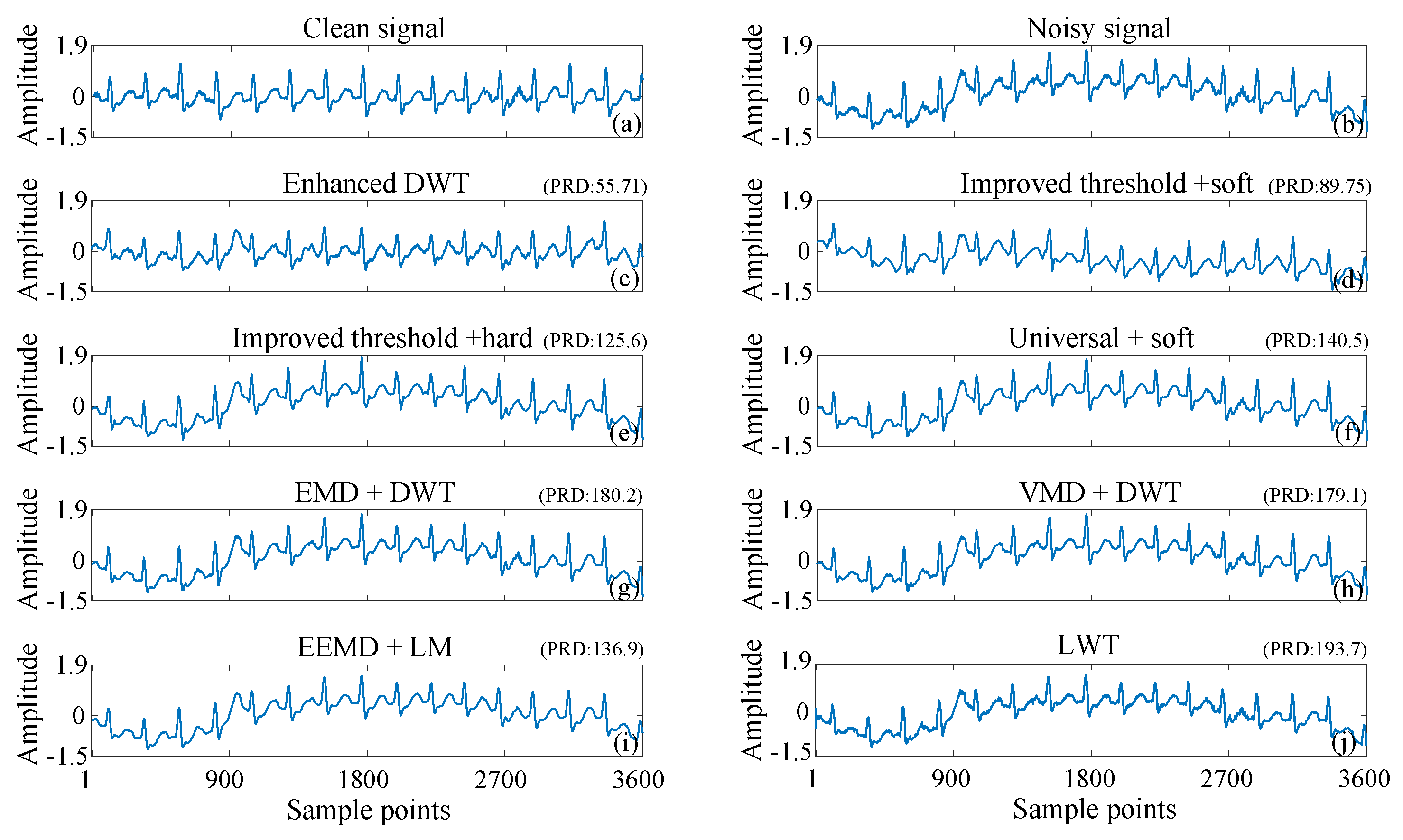
3.1. ECG Signals Contaminated by AGW Noise
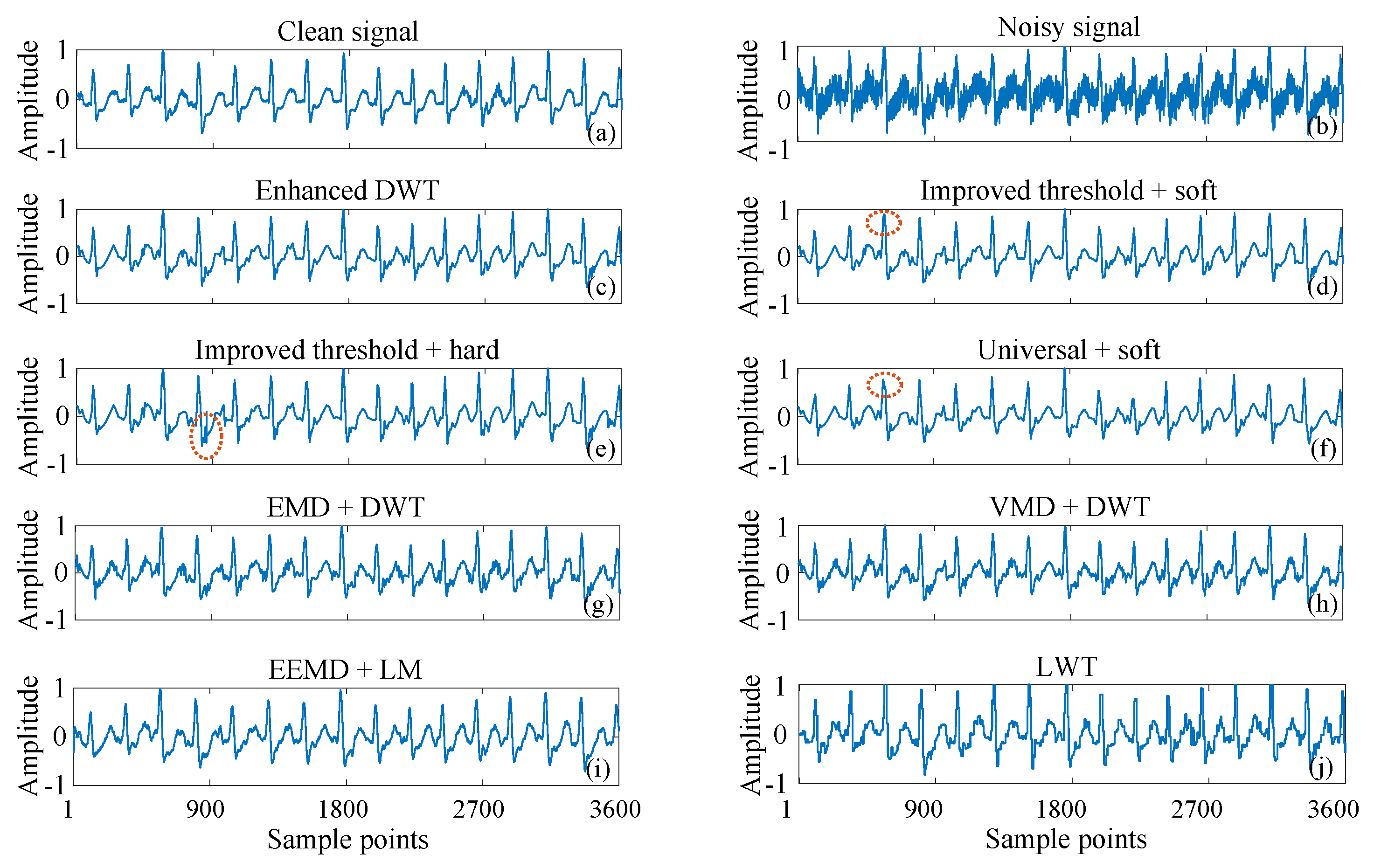
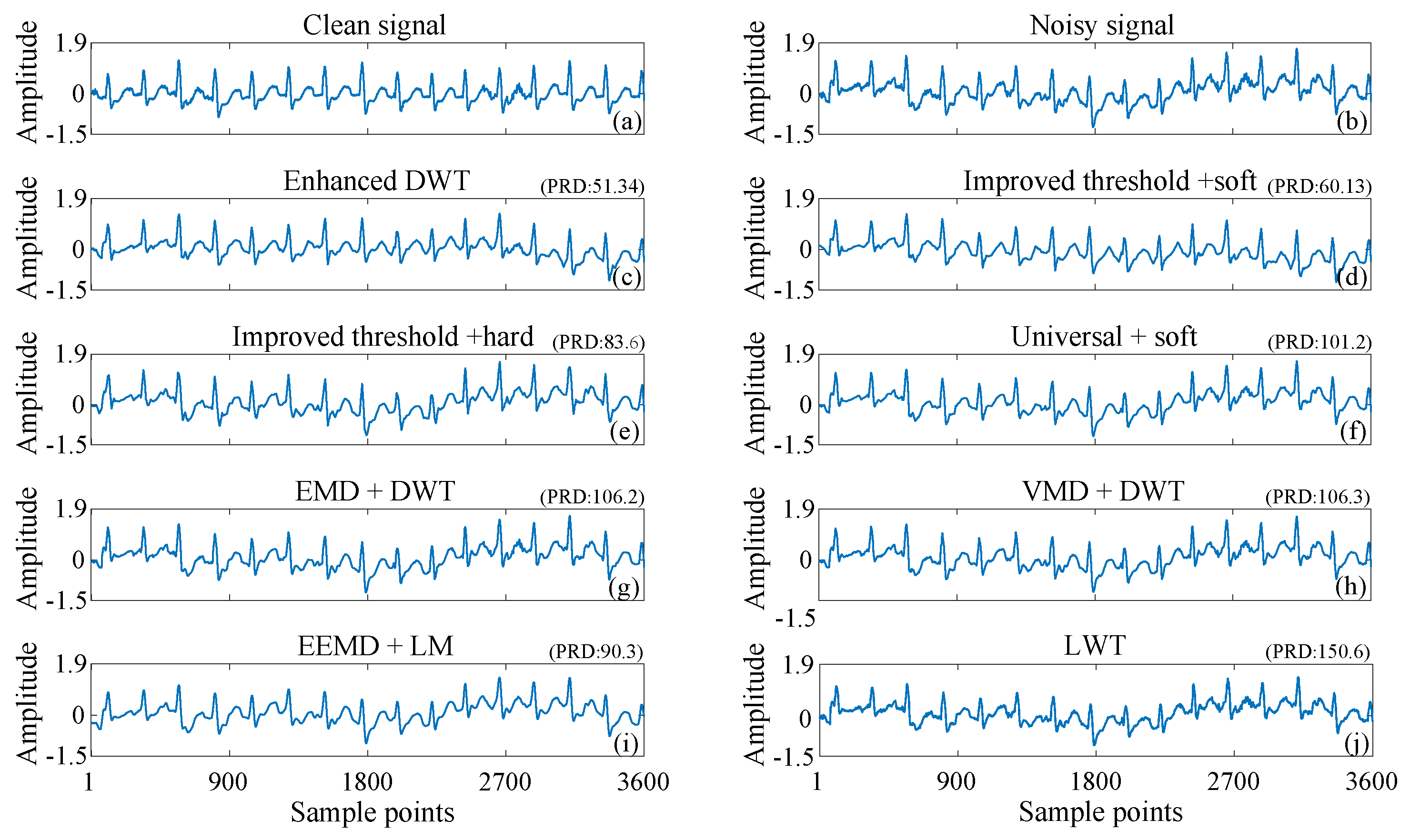
3.2. ECG Signals Contaminated by Real Noise
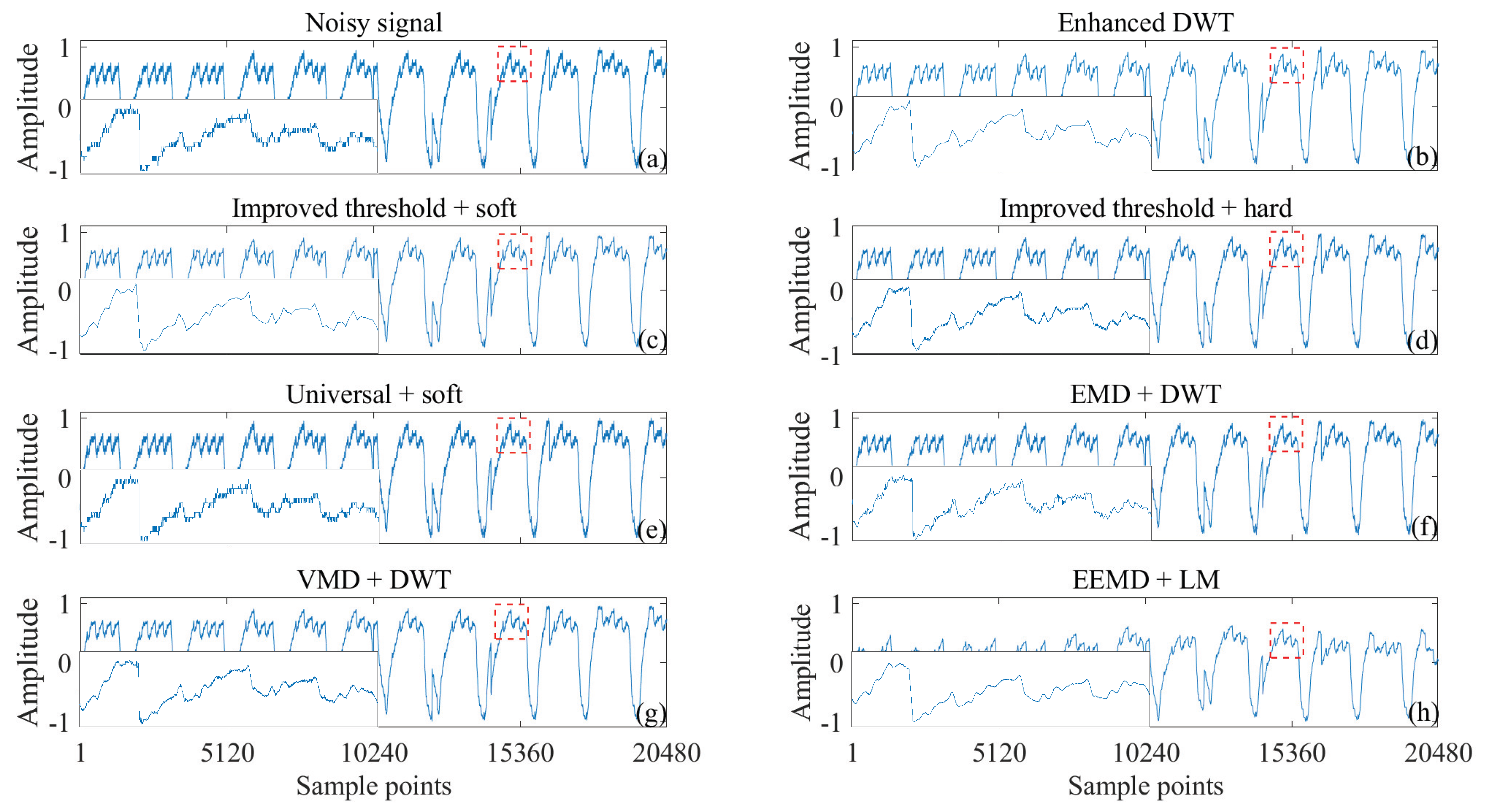
3.3. Heartbeat Signals Detected by Non-Invasive Technology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DWT | Discrete Wavelet Transform |
| AWG | Additive White Gaussian |
| AI | Artificial Intelligence |
| EMD | Empirical Mode Decomposition |
| VMD | Variable Mode Decomposition |
| SSA | Singular Spectrum Analysis |
| NLM | Non-Localized Mean Filtering |
| EEMD | Ensemble Empirical Mode Decomposition |
| CEEMD | Complementary Ensemble Empirical Mode Decomposition |
| IMF | Intrinsic Mode Functions |
| WT | Wavelet Transform |
| SDWT | Spcshrink’s Discrete Wavelet Transform |
| SWT | Stationary Wavelet Transform |
| SWPT | Stationary Wavelet Packet Transform |
| DTCWT | Dual Tree Complex Wavelet Transform |
| DDC | Double Density Complex |
| SBWT | Stationary Bionic Wavelet Transform |
| SNR | Signal-to-Noise Ratio |
| RMSE | Root Mean Square Error |
| MMF | Multimode Fiber |
| SMF | Single Mode Fiber |
| NZOPP | Nonzero-Order Periodic Peak |
| ACF | Autocorrelation Function |
| PRD | Root Mean Square Difference Percentage |
| SINAD | Signal-to-Noise and Distortion Ratio |
| ECG | Electrocardiogram |
References
- Malakouti, S.M. Heart disease classification based on ECG using machine learning models. Biomed. Signal Process. 2023, 84, 104796. [Google Scholar] [CrossRef]
- Liu, H.; Cui, S.; Zhao, X.; Cong, F. Detection of obstructive sleep apnea from single-channel ECG signals using a CNN-transformer architecture. Biomed. Signal Process. 2023, 82, 104581. [Google Scholar] [CrossRef]
- Siontis, K.; Noseworthy, P.; Attia, Z.; Friedman, P. Artificial intelligence-enhanced electrocardiography in cardiovascular disease management. Nat. Rev. Cardiol. 2021, 18, 465–478. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Hwang, H.; Tseng, V. Convolutional neural network based automatic screening tool for cardiovascular diseases using different intervals of ECG signals. Comput. Meth. Prog. Biomed. 2021, 203, 106035. [Google Scholar] [CrossRef]
- Rath, A.; Mishra, D.; Panda, G.; Satapathy, S. Heart disease detection using deep learning methods from imbalanced ECG samples. Biomed. Signal Process. 2021, 68, 102820. [Google Scholar] [CrossRef]
- Ertuğrul, Ö.; Acar, E.; Aldemir, E.; Öztekin, A. Automatic diagnosis of cardiovascular disorders by sub images of the ECG signal using multi-feature extraction methods and randomized neural network. Biomed. Signal Process. 2021, 64, 102260. [Google Scholar] [CrossRef]
- Cosoli, G.; Spinsante, S.; Scardulla, F.; D’Acquisto, L.; Scalise, L. Wireless ECG and cardiac monitoring systems: State of the art, available commercial devices and useful electronic components. Measurement 2021, 177, 109243. [Google Scholar] [CrossRef]
- Ribeiro, H.; Arnold, A.; Howard, J.; Shun-Shin, M.; Zhang, Y.; Francis, D.; Lim, P.; Whinnett, Z.; Zolgharni, M. ECG-based real-time arrhythmia monitoring using quantized deep neural networks: A feasibility study. Comput. Biol. Med. 2022, 143, 105249. [Google Scholar] [CrossRef]
- Rahul, J.; Sora, M.; Sharma, L.; Bohat, V. An improved cardiac arrhythmia classification using an RR interval-based approach. Biocybern. Biomed. Eng. 2022, 41, 656–666. [Google Scholar] [CrossRef]
- Saini, S.; Gupta, R. Artificial intelligence methods for analysis of electrocardiogram signals for cardiac abnormalities: State-of-the-art and future challenges. Artif. Intell. Rev. 2022, 55, 1519–1565. [Google Scholar] [CrossRef]
- Yin, C.; Zhou, X.; Zhao, Y.; Zheng, Y.; Shi, Y.; Yan, X.; Guo, X. Diagnosis of exercise-induced cardiac fatigue based on deep learning and heart sounds. Appl. Acoust. 2022, 197, 108900. [Google Scholar] [CrossRef]
- Ahmed, A.; Abbas, Q.; Daadaa, Y.; Qureshi, I.; Perumal, G.; Ibrahim, M. A residual-dense-based convolutional neural network architecture for recognition of cardiac health based on ECG signals. Sensors 2023, 23, 7204. [Google Scholar] [CrossRef] [PubMed]
- Madan, P.; Singh, V.; Singh, D.; Diwakar, M.; Kishor, A. Denoising of ECG signals using weighted stationary wavelet total variation. Biomed. Signal Process. 2022, 73, 103478. [Google Scholar] [CrossRef]
- Jiang, F.; Zhou, Y.; Ling, T.; Zhang, Y.; Zhu, Z. Recent research for unobtrusive atrial fibrillation detection methods based on cardiac dynamics signals: A survey. Sensors 2021, 21, 3814. [Google Scholar] [CrossRef]
- Houssein, E.H.; Ibrahim, I.E.; Hassaballah, M.; Wazery, Y.M. Integration of machine learning and optimization techniques for cardiac health recognition. In Integrating Meta-Heuristics and Machine Learning for Real-World Optimization Problems; Houssein, E.H., Elaziz, M.A., Oliva, D., Abualigah, L., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 121–148. [Google Scholar] [CrossRef]
- Boujnouni, I.; Zili, H.; Tali, A.; Tali, T.; Laaziz, Y. A wavelet-based capsule neural network for ECG biometric identification. Biomed. Signal Process. 2022, 76, 103692. [Google Scholar] [CrossRef]
- Hossain, M.; Bashar, S.; Lazaro, J.; Reljin, N.; Noh, Y.; Chon, K. A robust ECG denoising technique using variable frequency complex demodulation. Comput. Meth. Prog. Biomed. 2021, 200, 105856. [Google Scholar] [CrossRef]
- Mourad, T. ECG denoising based on 1-D double-density complex DWT and SBWT. In The Stationary Bionic Wavelet Transform and Its Applications for ECG and Speech Processing; Springer International Publishing: Cham, Switzerland, 2022; pp. 31–50. [Google Scholar] [CrossRef]
- Chen, C.; Shu, M.; Zhou, S.; Liu, Z.; Liu, R. Wavelet-domain group-sparse denoising method for ECG signals. Biomed. Signal Process. 2023, 83, 104702. [Google Scholar] [CrossRef]
- Sraitih, M.; Jabrane, Y. A denoising performance comparison based on ECG signal decomposition and local means filtering. Biomed. Signal Process. 2021, 69, 102903. [Google Scholar] [CrossRef]
- Gan, M.; Pan, H.; Chen, Y.; Pan, S. Application of the Variational Mode Decomposition (VMD) method to river tides. Estuar. Coast. Shelf Sci. 2021, 261, 107570. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, Z.; Zhang, H.; Wang, X.; Guo, Y. A short-term wind power prediction model based on CEEMD and WOA-KELM. Renew. Energy 2022, 189, 188–198. [Google Scholar] [CrossRef]
- Zhang, W.; Teng, F.; Li, J.; Zhang, Z.; Niu, L.; Zhang, D.; Song, Q.; Zhang, Z. Denoising method based on CNN-LSTM and CEEMD for LDV signals from accelerometer shock testing. Measurement 2023, 216, 112951. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, T.; Lim, E.; Lopez-Benitez, M.; Ma, F.; Yu, L. A review of wavelet analysis and its applications: Challenges and opportunities. IEEE Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Prashar, N.; Sood, M.; Jain, S. Design and implementation of a robust noise removal system in ECG signals using dual-tree complex wavelet transform. Biomed. Signal Process. 2021, 63, 102212. [Google Scholar] [CrossRef]
- Baldazzi, G.; Sulas, E.; Urru, M.; Tumbarello, R.; Raffo, L.; Pani, D. Wavelet denoising as a post-processing enhancement method for non-invasive foetal electrocardiography. Comput. Meth. Prog. Biomed. 2020, 195, 105558. [Google Scholar] [CrossRef]
- Kumar, A.; Tomar, H.; Mehla, V.K.; Komaragiri, R.; Kumar, M. Stationary wavelet transform based ECG signal denoising method. ISA Trans. 2021, 114, 251–262. [Google Scholar] [CrossRef]
- Mourad, N. ECG denoising based on successive local filtering. Biomed. Signal Process. 2022, 73, 103431. [Google Scholar] [CrossRef]
- Zaki, F.; Wang, Y.; Su, H.; Yuan, X.; Liu, X. Noise adaptive wavelet thresholding for speckle noise removal in optical coherence tomography. Biomed. Opt. Express 2017, 8, 2720. [Google Scholar] [CrossRef]
- Ghorat, M.; Gharehpetian, G.B.; Latifi, H.; Hejazi, M.A. A new partial discharge signal denoising algorithm based on adaptive dual-tree complex wavelet transform. IEEE Trans. Instrum. Meas. 2018, 67, 2262–2272. [Google Scholar] [CrossRef]
- Bayer, F.M.; Kozakevicius, A.J.; Cintra, R.J. An iterative wavelet threshold for signal denoising. Signal Process. 2019, 162, 10–20. [Google Scholar] [CrossRef]
- Chatterjee, S.; Thakur, R.S.; Yadav, R.N.; Gupta, L. Sparsity-based modified wavelet denoising autoencoder for ECG signals. Signal Process. 2022, 198, 108605. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, J.; Wang, R.; Xu, T. Improved wavelet thresholding function and adaptive thresholding for noise reduction. In Proceedings of the 2023 11th International Conference on Intelligent Computing and Wireless Optical Communications (ICWOC), Chongqing, China, 16–18 June 2023; pp. 25–30. [Google Scholar] [CrossRef]
- Malik, S.A.; Parah, S.A.; Aljuaid, H.; Malik, B.A. An ierative filtering based ECG denoising using lifting wavelet transform technique. Electronics 2023, 12, 387. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, P.; Yin, Y.; Wu, M.; Yu, K.; Feng, L.; Chen, W. Objective assessment of ipm denoising quality of Φ-OTDR signal. Measurement 2023, 214, 112775. [Google Scholar] [CrossRef]
- Yu, K.; Feng, L.; Chen, Y.; Wu, M.; Zhang, Y.; Zhu, P.; Chen, W.; Wu, Q.; Hao, J. Accurate wavelet thresholding method for ECG signals. Comput. Biol. Med. 2024, 169, 107835. [Google Scholar] [CrossRef]
- He, C.; Xing, J.; Li, J.; Yang, Q.; Wang, R. A new wavelet thresholding function based on hyperbolic tangent function. Math. Probl. Eng. 2015, 10, 528656. [Google Scholar] [CrossRef]
- Wang, J.; Sun, S.; Sun, Y. A muscle fatigue classification model based on LSTM and improved wavelet packet threshold. Sensors 2021, 21, 6369. [Google Scholar] [CrossRef]
- Sun, Z.; Lu, J. An ultrasonic signal denoising method for EMU wheel trackside fault diagnosis system based on improved threshold function. IEEE Access 2021, 9, 96244–96256. [Google Scholar] [CrossRef]
- Kong, X.; Xu, T.; Ji, J.; Zou, F.; Yuan, W.; Zhang, L. Wind turbine bearing incipient fault diagnosis based on adaptive exponential wavelet threshold function with improved CPSO. IEEE Access 2021, 9, 122457–122473. [Google Scholar] [CrossRef]
- Zhu, J.; Fu, Z.; Li, K.; Su, A. Chromatography denoising with improved wavelet thresholding based on modified genetic particle swarm optimization. Electronics 2023, 12, 4249. [Google Scholar] [CrossRef]
- Ming, F.; Long, H. Partial discharge de-noising based on hybrid particle swarm optimization SWT adaptive threshold. IEEE Access 2023, 99, 1–14. [Google Scholar] [CrossRef]
- Xie, B.; Xiong, Z.; Wang, Z.; Zhang, L.; Zhang, D.; Li, F. Gamma spectrum denoising method based on improved wavelet threshold. Nucl. Eng. Technol. 2020, 52, 1771–1776. [Google Scholar] [CrossRef]
- Li, G.; Han, Y.; Yang, H. A new underwater acoustic signal denoising method based on modified uniform phase empirical mode decomposition, hierarchical amplitude-aware permutation entropy, and optimized improved wavelet threshold denoising. Ocean. Eng. 2024, 293, 116629. [Google Scholar] [CrossRef]
- Chen, M.; Cheng, Q.; Feng, X.; Zhao, K.; Zhou, Y.; Xing, B.; Tang, S.; Wang, R.; Duan, J.; Wang, J.; et al. Optimized variational mode decomposition algorithm based on adaptive thresholding method and improved whale optimization algorithm for denoising magnetocardiography signal. Biomed. Signal Process. 2024, 88, 105681. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, C.; Wang, Y.; Cheng, X. A comprehensive diagnosis method of rolling bearing fault based on CEEMDAN-DFA-improved wavelet threshold function and QPSO-MPE-SVM. Entropy 2021, 23, 1142. [Google Scholar] [CrossRef] [PubMed]
- Yin, C.; Wang, Y.; Ma, G.; Wang, Y.; Sun, Y.; He, Y. Weak fault feature extraction of rolling bearings based on improved ensemble noise-reconstructed EMD and adaptive threshold denoising. Mech. Syst. Signal Process. 2022, 171, 108834. [Google Scholar] [CrossRef]
- Wang, L.; Xu, H.; Liu, Y. A novel dynamic load identification approach for multi-source uncertain structures based on the set-theoretical wavelet transform and layered noise reduction. Structures 2023, 51, 91–104. [Google Scholar] [CrossRef]
- Chegini, S.; Bagheri, A.; Najafi, F. Application of a new EWT-based denoising technique in bearing fault diagnosis. Measurement 2019, 144, 275–297. [Google Scholar] [CrossRef]
- Gao, L.; Gan, Y.; Shi, J. A novel intelligent denoising method of ECG signals based on wavelet adaptive threshold and mathematical morphology. Appl. Intell. 2022, 52, 10270–10284. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Qian, J. A novel denoising method of the hydro-turbine runner for fault signal based on WT-EEMD. Measurement 2023, 219, 113306. [Google Scholar] [CrossRef]
- Kaplun, D.; Voznesenskiy, A.; Romanov, S.; Nepomuceno, E.; Butusov, D. Optimal estimation of wavelet decomposition level for a matching pursuit algorithm. Entropy 2019, 21, 843. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, K.; Wu, M.; Feng, L.; Zhang, Y.; Zhu, P.; Chen, W.; Hao, J. Wavelet decomposition layer selection for the φ-OTDR signal. Photonics 2024, 11, 137. [Google Scholar] [CrossRef]
- Serhal, H.; Abdallah, N.; Marion, J.; Chauvet, P.; Oueidat, M.; Heurtier, A. Overview on prediction, detection, and classification of atrial fibrillation using wavelets and AI on ECG. Comput. Biol. Med. 2022, 142, 105168. [Google Scholar] [CrossRef] [PubMed]
- Phadikar, S.; Sinha, N.; Ghosh, R. Automatic eyeblink artifact removal from EEG signal using wavelet transform with heuristically optimized threshold. IEEE J. Biomed. Health 2021, 25, 475–484. [Google Scholar] [CrossRef] [PubMed]
- Meymandi, A.; Ghaffari, A. A deep learning-based framework for ECG signal denoising based on stacked cardiac cycle tensor. Biomed. Signal Process. 2022, 71, 103275. [Google Scholar] [CrossRef]
- Jin, Y.; Qin, C.; Liu, J.; Liu, Y.; Li, Z.; Liu, C. A novel deep wavelet convolutional neural network for actual ECG signal denoising. Biomed. Signal Process. 2024, 87, 105480. [Google Scholar] [CrossRef]
- Wu, M.; Chen, Y.; Zhu, P.; Chen, W. NLM parameter optimization for φ-OTDR signal. J. Light. Technol. 2022, 40, 6045–6051. [Google Scholar] [CrossRef]
- Miaou, S.G.; Lin, C.L. A quality-on-demand algorithm for wavelet-based compression of electrocardiogram signals. IEEE Trans. Biomed. Eng. 2002, 49, 233–239. [Google Scholar] [CrossRef]
- Strang, G.; Nguyen, T. Wavelets and Filter Banks; Wellesley-Cambridge Press: Wellesley, MA, USA, 1996. [Google Scholar]
- Zhang, K.; Tang, B.; Qin, Y.; Deng, L. Fault diagnosis of planetary gearbox using a novel semi-supervised method of multiple association layers networks. Mech. Syst. Sig. Process. 2019, 131, 243–260. [Google Scholar] [CrossRef]
- Beale, C.; Niezrecki, C.; Inalpolat, M. An adaptive wavelet packet denoising algorithm for enhanced active acoustic damage detection from wind turbine blades. Mech. Syst. Sig. Process. 2020, 142, 106754. [Google Scholar] [CrossRef]
- Gao, H.Y.; Bruce, A.G. Waveshrink with firm shrinkage. Stat. Sin. 1997, 7, 855–874. [Google Scholar]
- Bruce, A.G.; Gao, H.Y. WaveShrink: Shrinkage functions and thresholds. In Wavelet Applications in Signal and Image Processing III; SPIE: San Francisco, CA, USA, 1995; Volume 2569, pp. 270–281. [Google Scholar] [CrossRef]


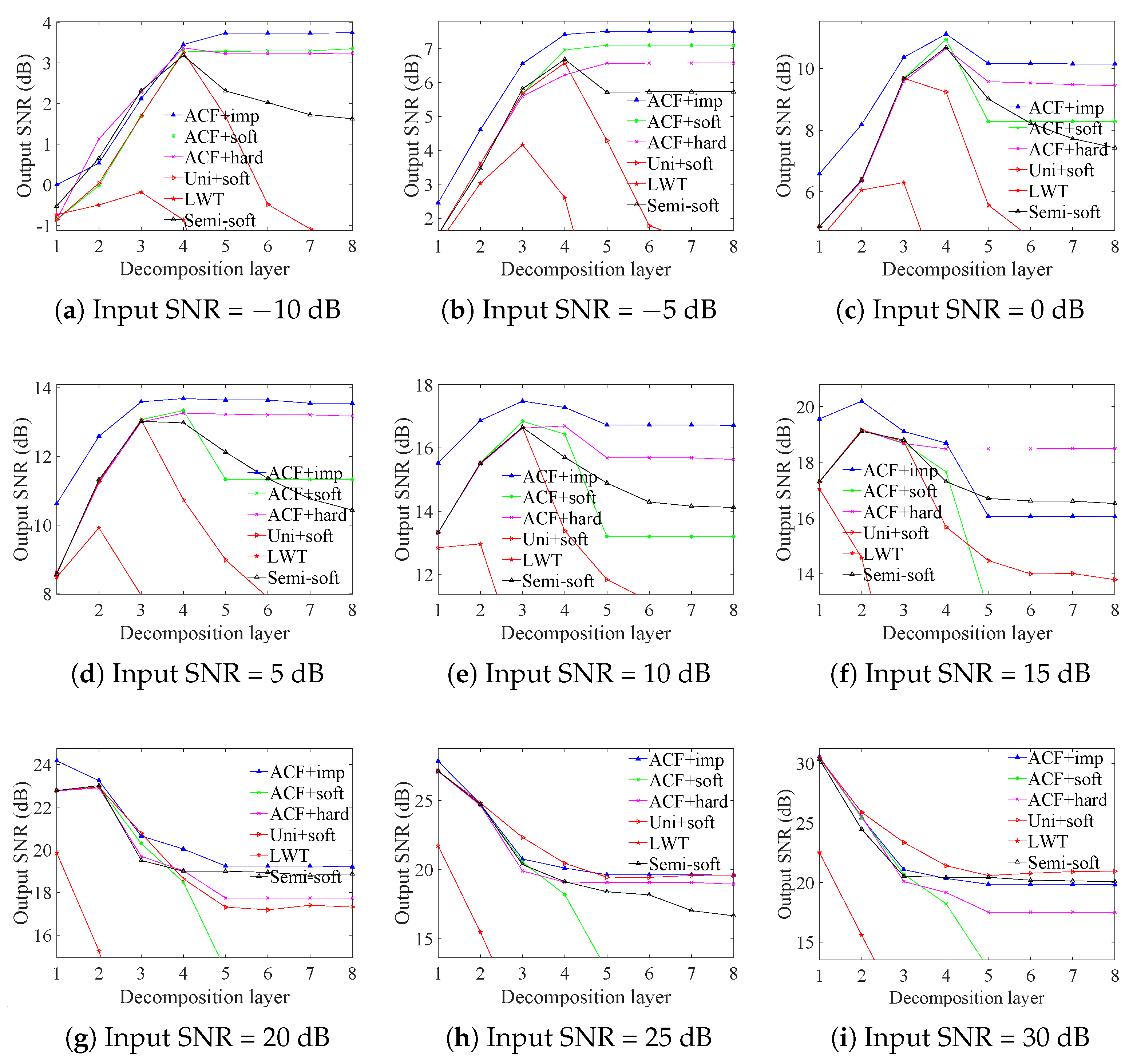


| Input SNR (dB) | Soft | Hard | Semisoft | Improved |
|---|---|---|---|---|
| −10 | 9.8933 | 9.4434 | 10.4166 | 10.7973 |
| −5 | 12.5791 | 12.7460 | 13.3488 | 13.6201 |
| 0 | 16.1215 | 15.8090 | 16.9137 | 17.5043 |
| 5 | 19.4142 | 19.6456 | 20.9539 | 21.7680 |
| 10 | 25.1601 | 25.1404 | 26.1945 | 26.8667 |
| 15 | 29.2865 | 29.2438 | 29.8761 | 30.4211 |
| Methods | Ehanced DWT | Improved T + Soft | Universal + Soft | EMD + DWT | VMD + DWT | EEMD + LM |
|---|---|---|---|---|---|---|
| Cost (s) | 0.2597 | 0.1724 | 0.0960 | 0.3162 | 3.2624 | 0.4786 |
| SNR (dB) | 14.4542 | 13.9492 | 13.6104 | 13.7961 | 13.2239 | 12.6712 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Feng, L.; Yu, K.; Zhang, Y.; Chen, W.; Hao, J. Enhanced DWT for Denoising Heartbeat Signal in Non-Invasive Detection. Sensors 2025, 25, 1743. https://doi.org/10.3390/s25061743
Zhu P, Feng L, Yu K, Zhang Y, Chen W, Hao J. Enhanced DWT for Denoising Heartbeat Signal in Non-Invasive Detection. Sensors. 2025; 25(6):1743. https://doi.org/10.3390/s25061743
Chicago/Turabian StyleZhu, Peibin, Lei Feng, Kaimin Yu, Yuanfang Zhang, Wen Chen, and Jianzhong Hao. 2025. "Enhanced DWT for Denoising Heartbeat Signal in Non-Invasive Detection" Sensors 25, no. 6: 1743. https://doi.org/10.3390/s25061743
APA StyleZhu, P., Feng, L., Yu, K., Zhang, Y., Chen, W., & Hao, J. (2025). Enhanced DWT for Denoising Heartbeat Signal in Non-Invasive Detection. Sensors, 25(6), 1743. https://doi.org/10.3390/s25061743










