Modeling and Parameter Analysis of Basic Single Channel Neuron Mass Model for SSVEP
Abstract
1. Introduction
- (1)
- We explore the mechanism for generating SSVEPs based on the NMM, which helps to construct the SSVEP by artificially generating virtual signals similar to actual EEGs. As a result, it does not need an experimental setup, subject recruitment, and equipment configuration, and the simulation modeling method provides a more cost-effective avenue for SSVEP-BCI research, which will improve repeatability.
- (2)
- The principle of the neural mass model for single-channel SSVEP is analyzed in detail, where the three basic dynamic waveforms are generated by the model, and the effects of key parameters are analyzed on the simulated signals.
- (3)
- We provide current study limitations and further research directions, which help to clarify the understanding of the physiological significance and functionality of the current NMM.
2. Neural Mass Model
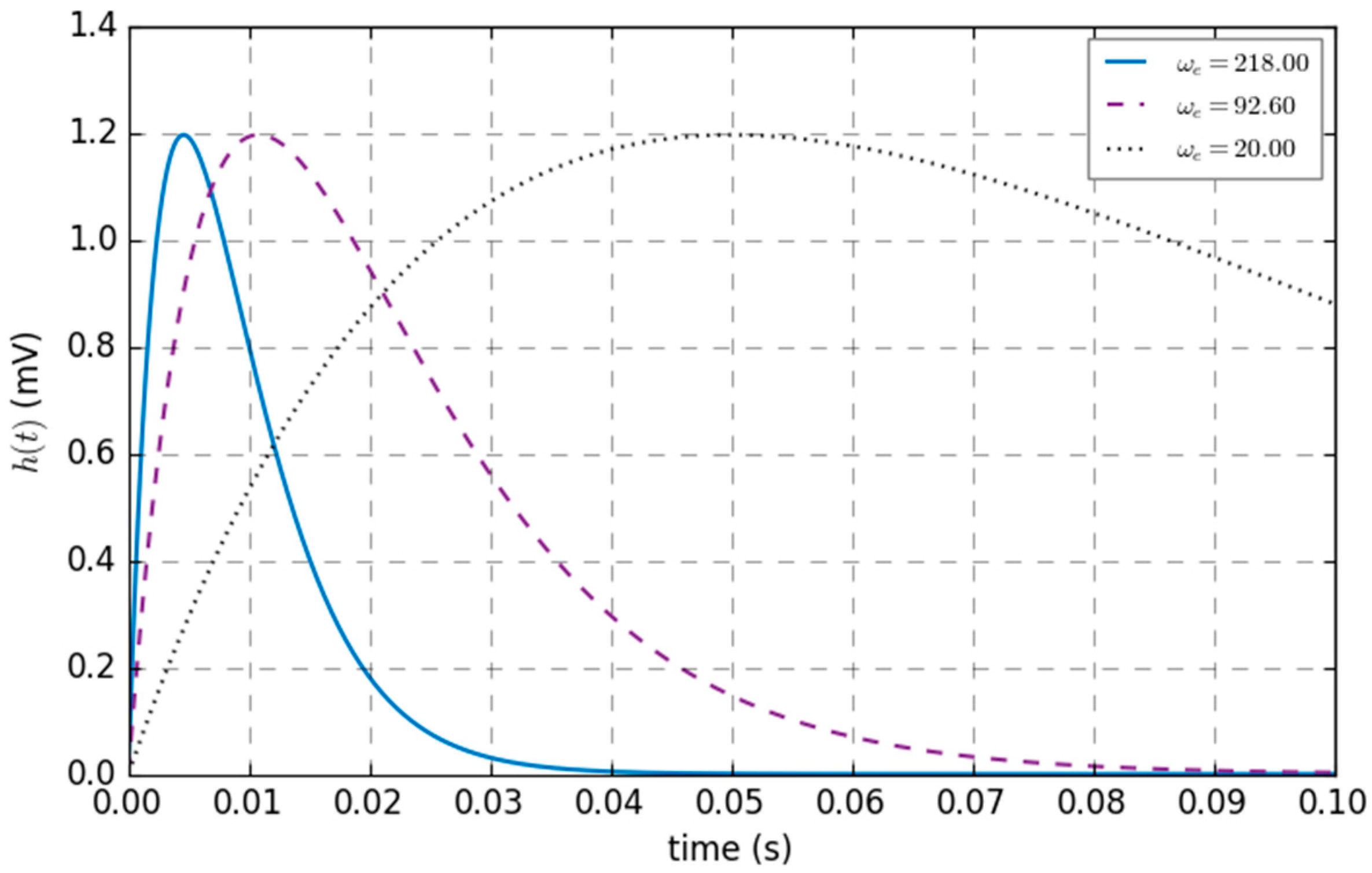
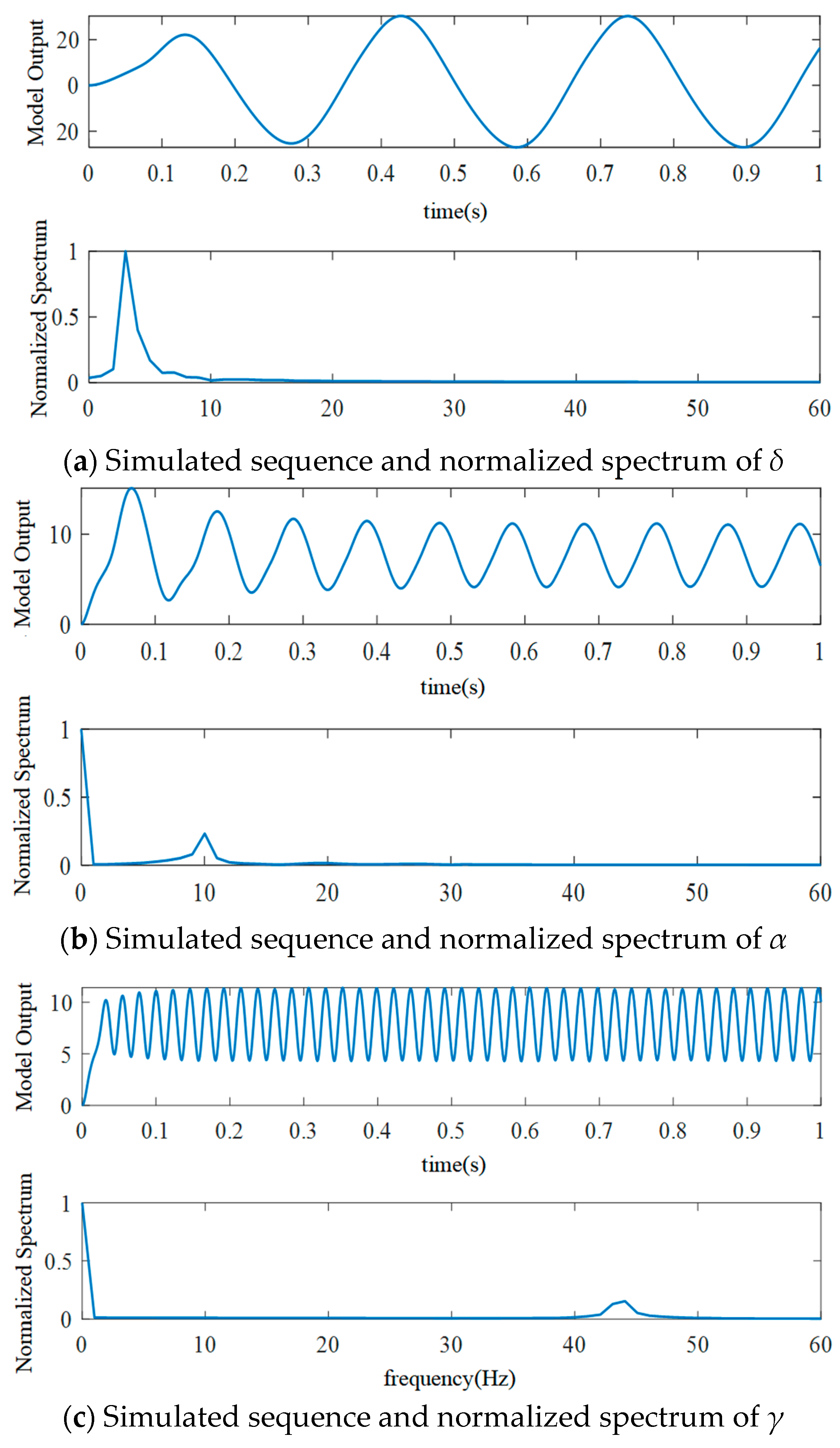
2.1. Single-Channel Basic Neuron Mass Model
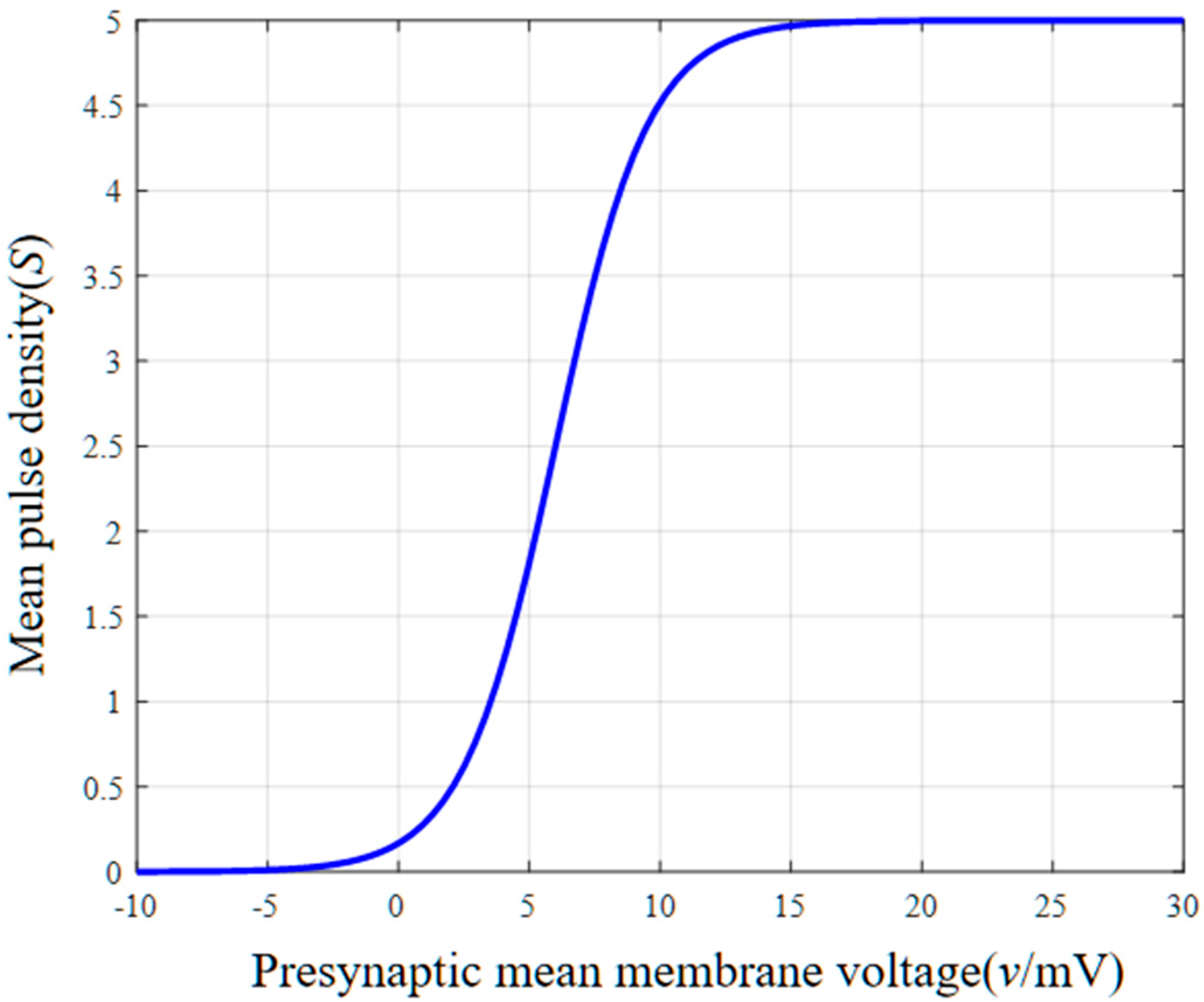
2.2. Parameters of a Single-Channel Basic Neuron Mass Model
3. Results
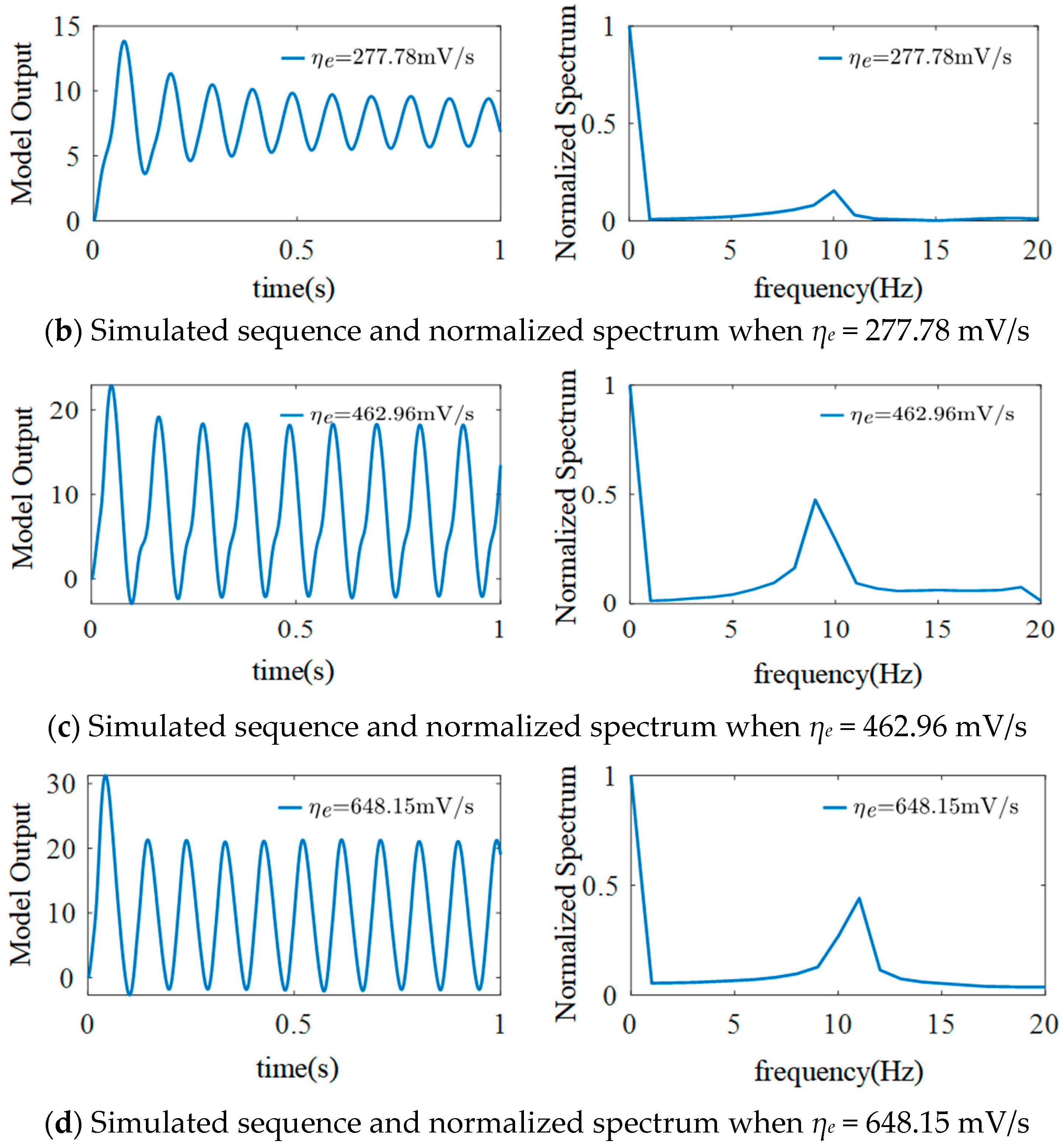
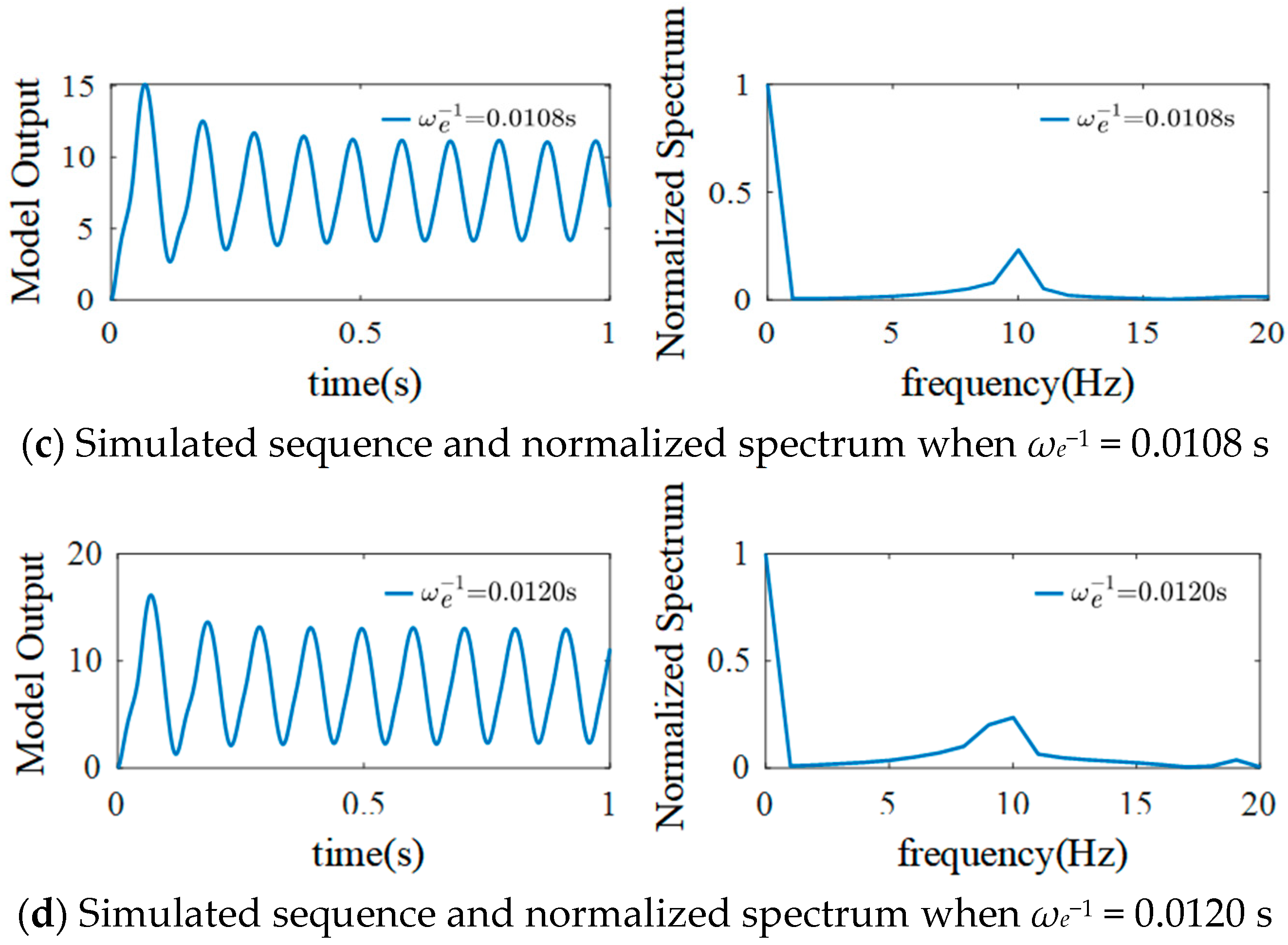
3.1. The Effect of ηe on the Model
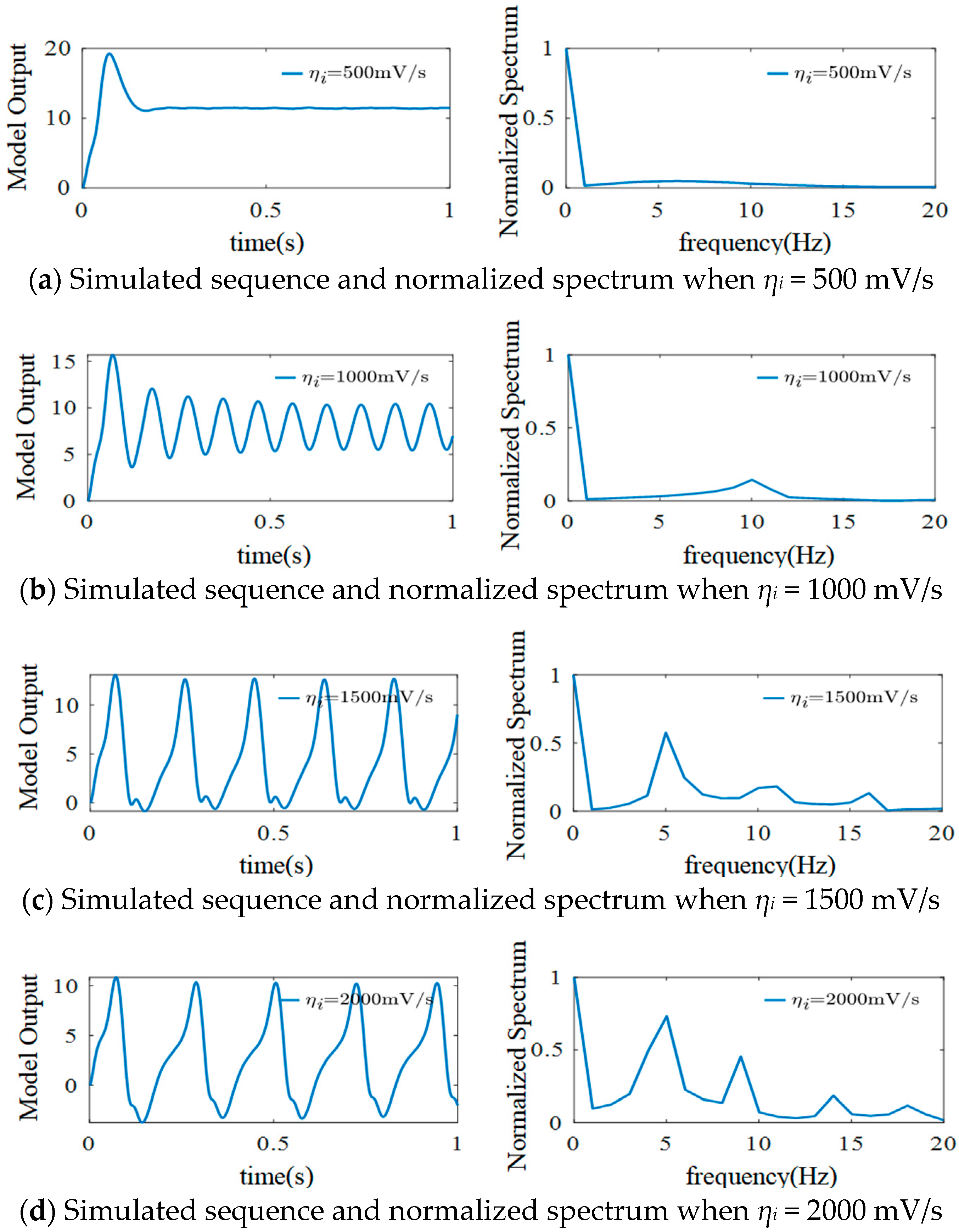
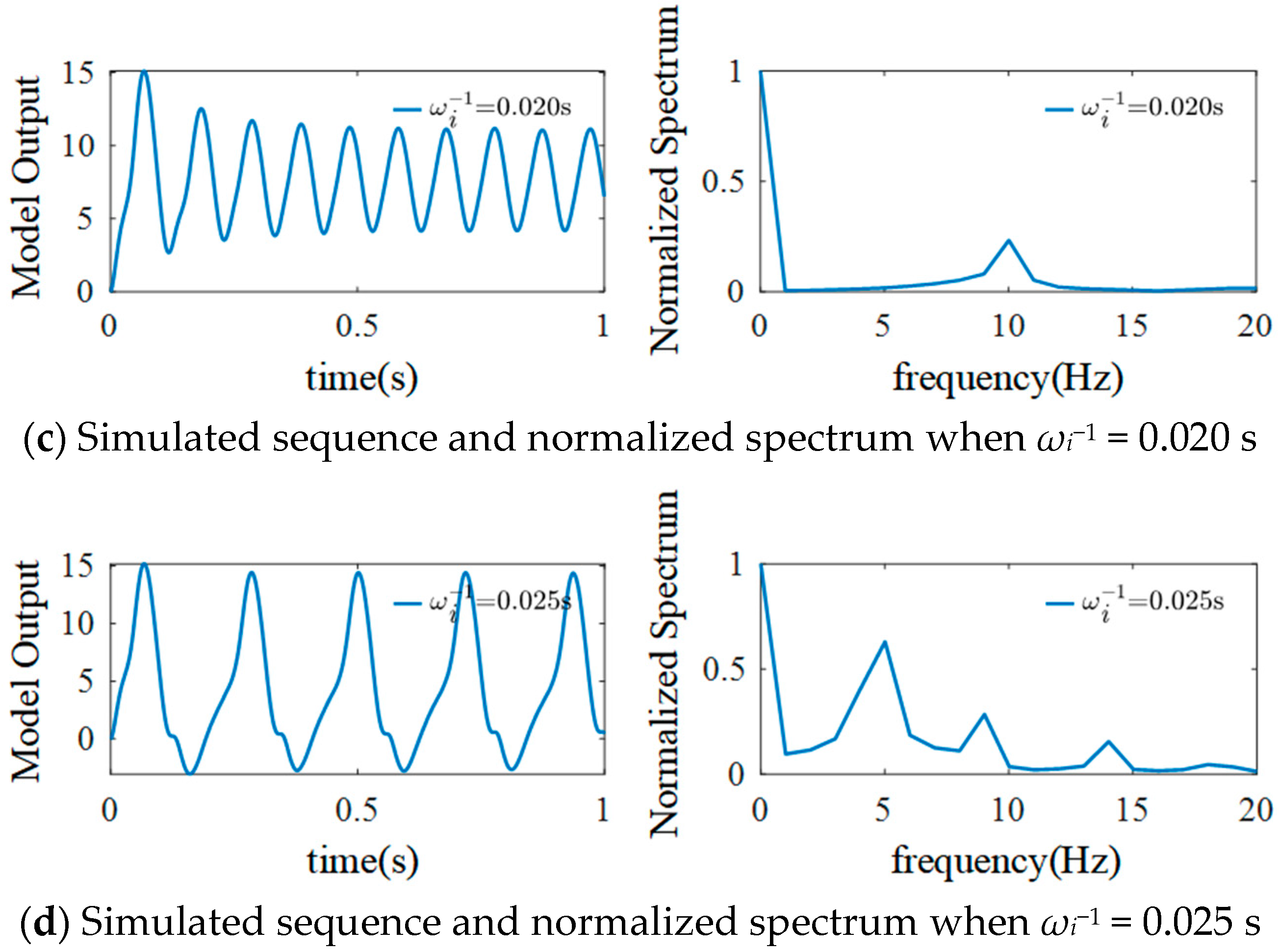
3.2. The Effect of ηi on the Model
3.3. The Effects of External Inputs on the Model
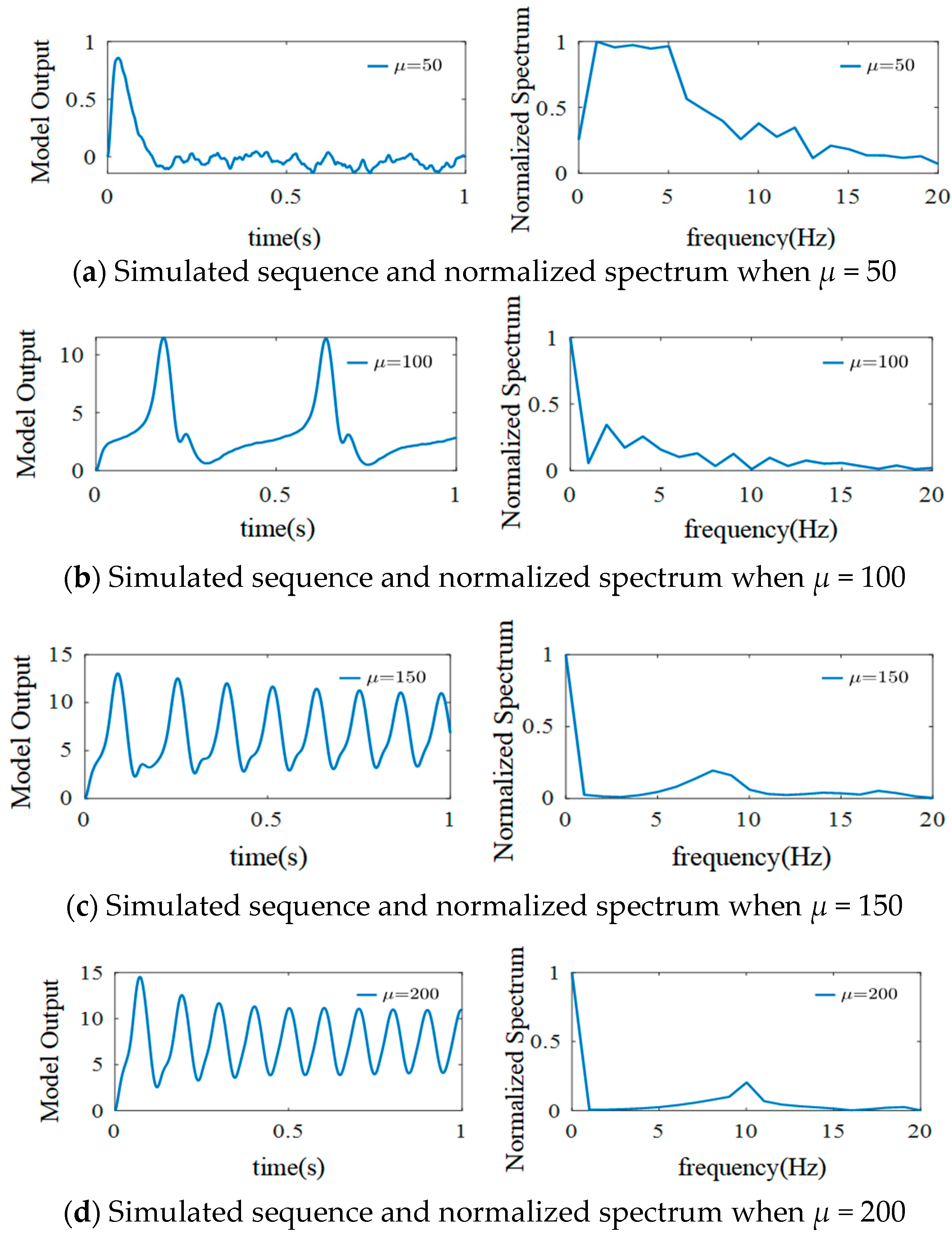
3.3.1. The Effect of External Inputs’ Mean Value
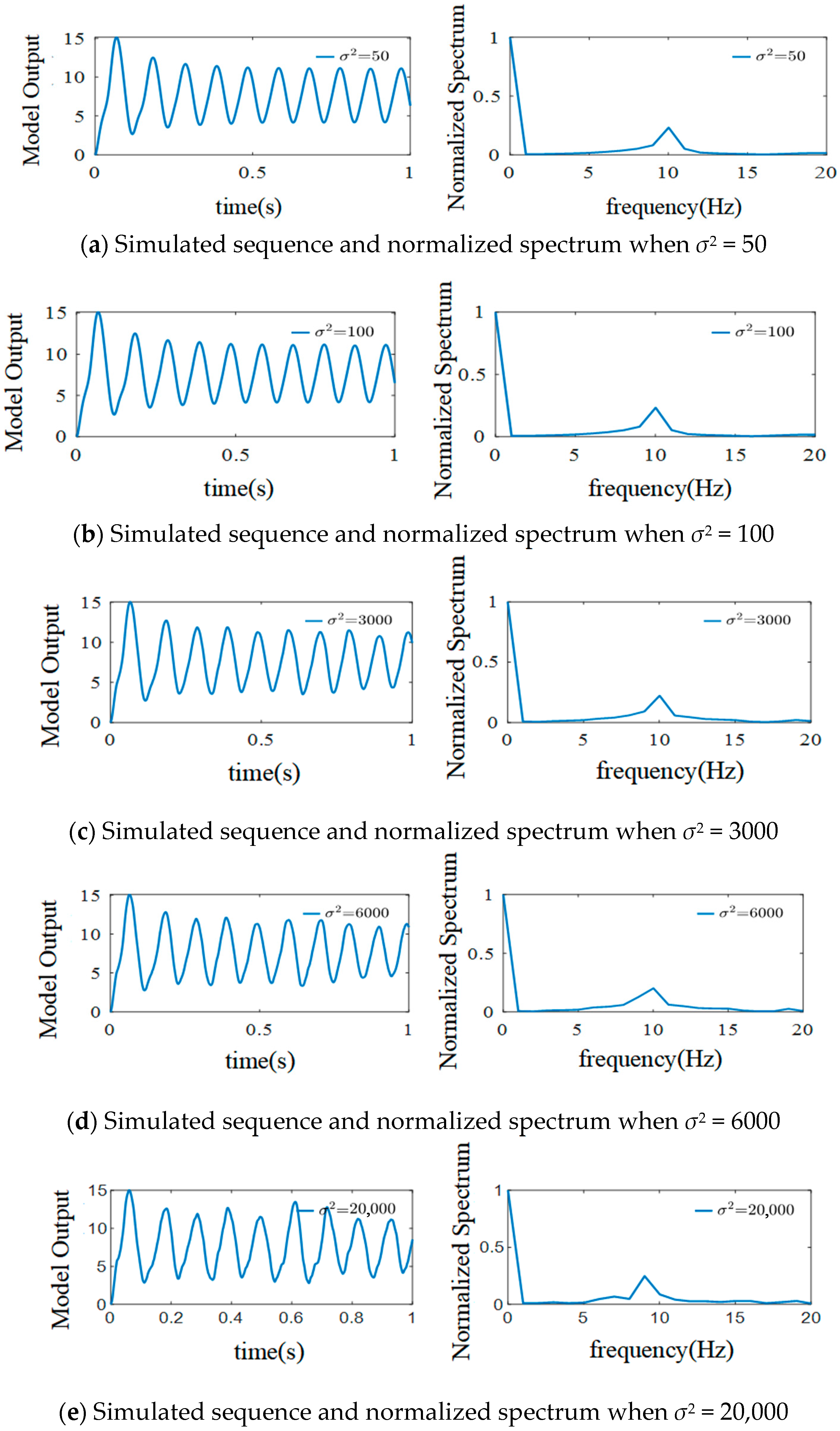
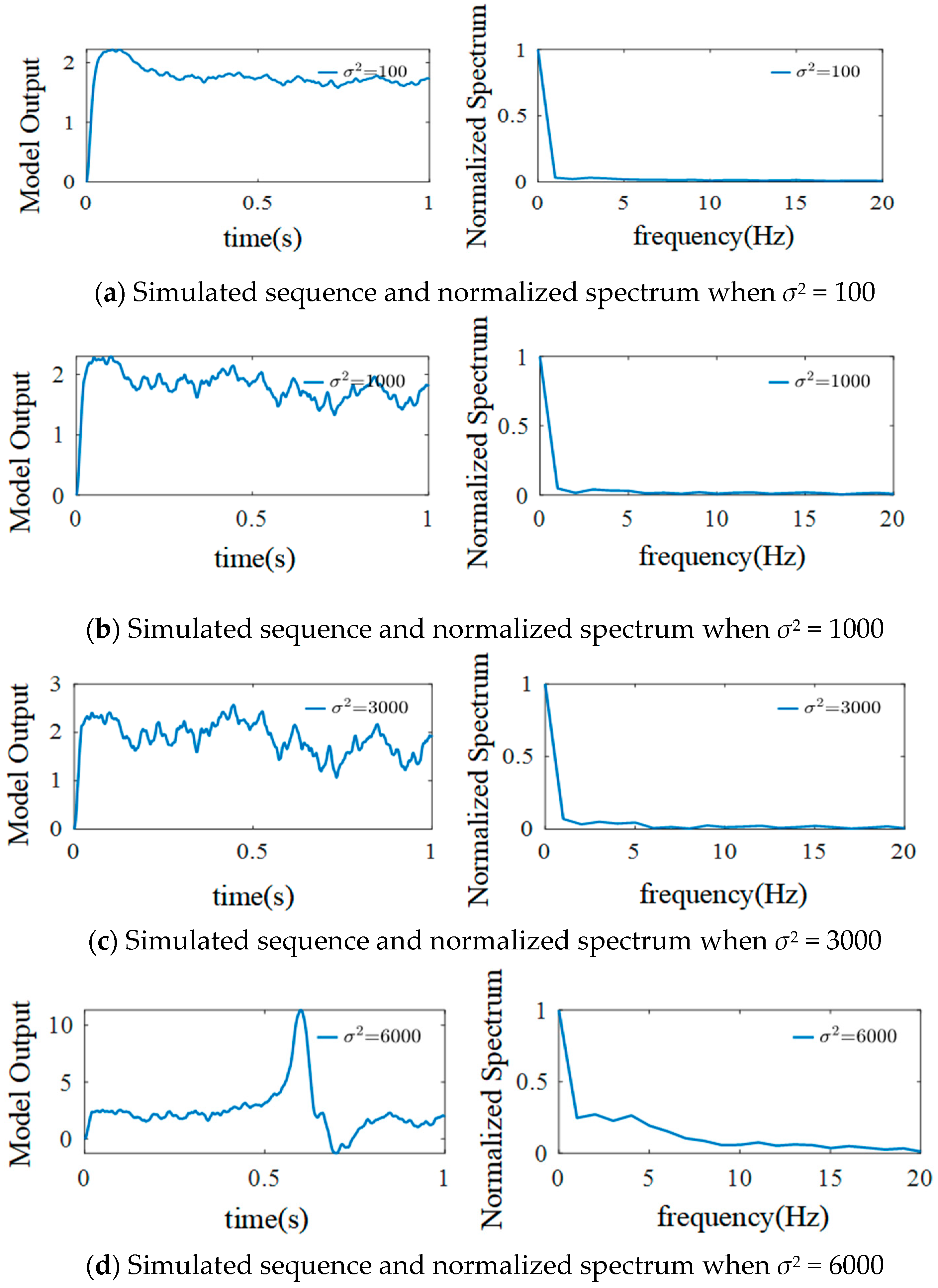
3.3.2. The Effect of External Inputs’ Variance
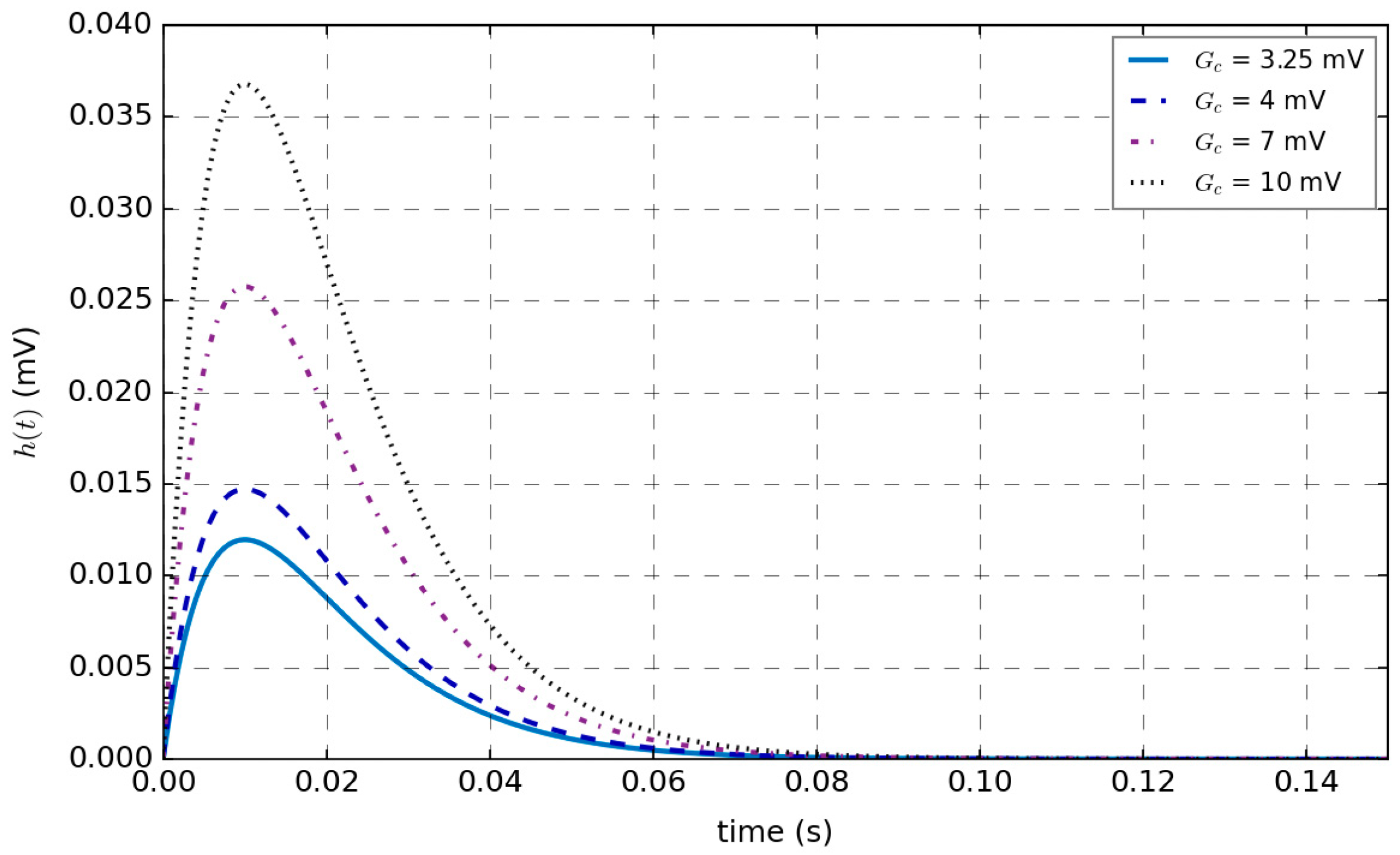
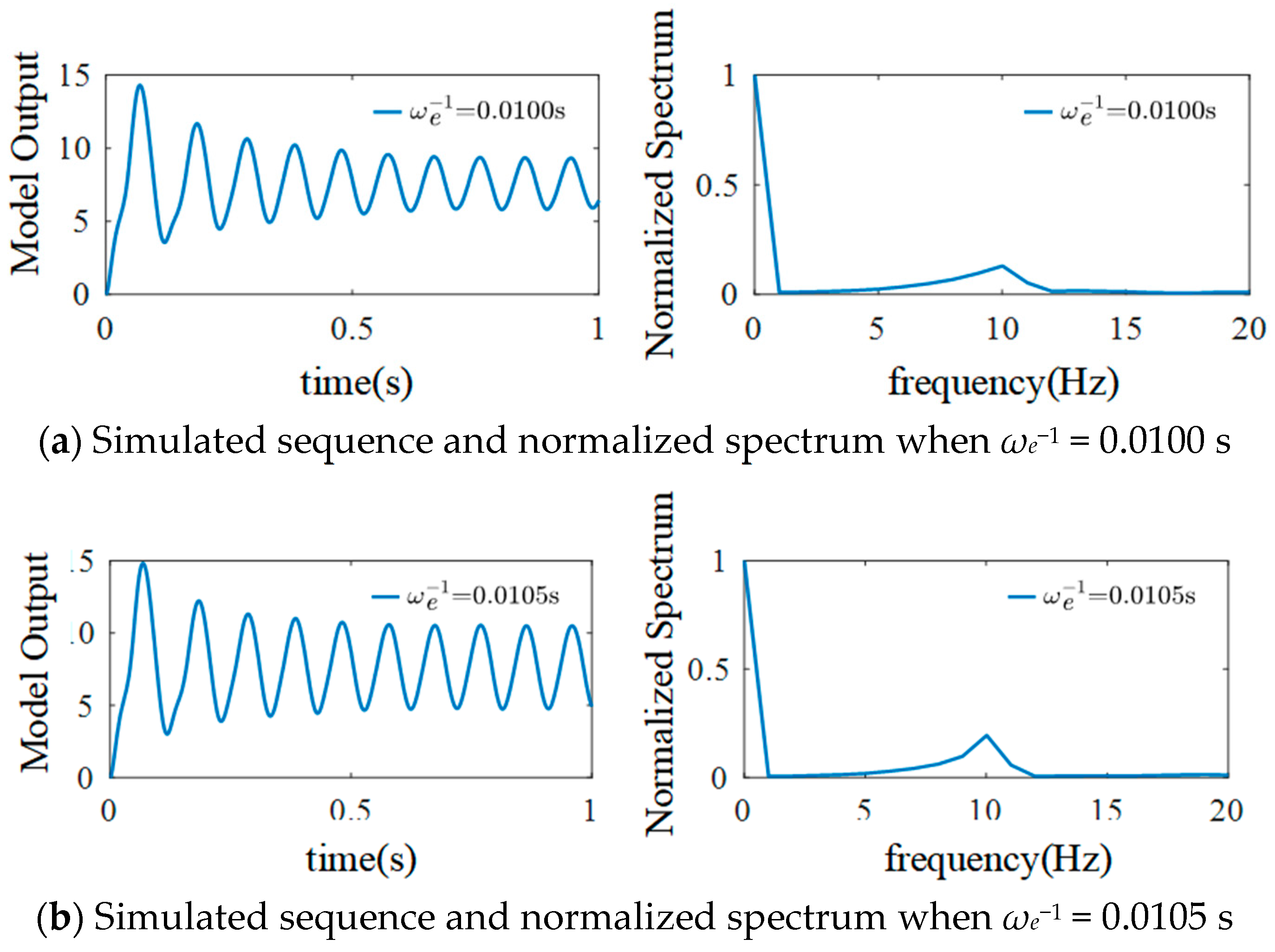
3.4. The Effect of Mean Time Constant on the Model
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hodgkin, A.L.; Huxley, A.F. A quantitatived escription of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Chay, T.R. Chaos in a three-variable excitable cell model. Phys. D Nonlinear Phenom. 1985, 16, 233–242. [Google Scholar] [CrossRef]
- Traub, R.D.; Contreras, D.; Cunningham, M.O.; Murray, H.; LeBeau, F.E.N.; Roopun, A.; Bibbig, A.; Wilent, W.B.; Higley, M.J.; Whittington, M.A. Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. J. Neurophysiol. 2005, 93, 2194–2232. [Google Scholar] [CrossRef] [PubMed]
- Schelter, B.; Mader, M.; Mader, W.; Sommerlade, L.; Platt, B.; Lai, Y.C.; Grebogi, C.; Thiel, M. Overarching framework for data-based modelling. Europhys. Lett. 2014, 105, 30004. [Google Scholar] [CrossRef][Green Version]
- Dong, E.; Liang, Z. The multi-frequency EEG rhythms modeling based on two-parameter bifurcation of neural mass model. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 1564–1569. [Google Scholar]
- Wilson, H.R.; Cowan, J.D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef] [PubMed]
- da Silva, F.H.L.; Hoeks, A.; Smits, H.; Zetterberg, L.H. Model of brain rhythmic activity. Kybernetik 1974, 15, 27–37. [Google Scholar] [CrossRef]
- da Silva, F.H.L.; Rotterdam, A.V.; Barts, P.; van Heusden, E.; Burr, W. Models of neuronal populations: The basic mechanisms of rhythmicity. Prog. Brain Res. 1976, 45, 281–308. [Google Scholar]
- Jansen, B.H.; Zouridakis, G.; Brandt, M.E. A neurophysiologically-based mathematical model of flash visual evoked potentials. Biol. Cybern. 1993, 68, 275–283. [Google Scholar] [CrossRef]
- Tsoneva, T.; Garcia-Molina, G.; Desain, P. SSVEP phase synchronies and propagation during repetitive visual stimulation at high frequencies. Sci. Rep. 2021, 11, 4975. [Google Scholar] [CrossRef]
- Ding, J.; Sperling, G.; Srinivasan, R. Attentional modulation of SSVEP power depends on the network tagged by the flicker frequency. Cereb. Cortex 2006, 16, 1016–1029. [Google Scholar] [CrossRef]
- Li, F.; Tian, Y.; Zhang, Y.; Qiu, K.; Tian, C.; Jing, W.; Liu, T.; Xia, Y.; Guo, D.; Yao, D.; et al. The enhanced information flow from visual cortex to frontal area facilitates SSVEP response: Evidence from model-driven and data-driven causality analysis. Sci. Rep. 2015, 5, 14765. [Google Scholar] [CrossRef] [PubMed]
- Fu, P.R.; Li, H.; Zhang, S. Review of latest noninvasive EEG-based robotic device. In Proceedings of the IEEE/ASME (AIM) International Conference on Advanced Intelligent Mechatronics, Sapporo, Japan, 11–15 July 2022; pp. 11–15. [Google Scholar]
- Lin, C.; Deng, X.; Yu, Z.L.; Gu, Z. A SSVEP-based BCI for controlling a 4-DOF robotic manipulator. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Bari, Italy, 6–9 October 2019; pp. 2174–2179. [Google Scholar]
- Ishizuka, K.; Kobayashi, N.; Saito, K. High accuracy and short delay 1ch-ssvep quadcopter-BMI using deep learning. J. Robot. Mechatron. 2020, 32, 738–744. [Google Scholar] [CrossRef]
- Shao, L.; Zhang, L.; Belkacem, A.N.; Zhang, Y.; Chen, X.; Li, J.; Liu, H. EEG-controlled wall-crawling cleaning robot using SSVEP-based brain-computer interface. J. Healthc. Eng. 2020, 2020, 6968713. [Google Scholar] [CrossRef] [PubMed]
- Jebri, A.; Madani, T.; Djouani, K. Neural adaptive integral-sliding-mode controller with a SSVEP-based BCI for exoskeletons. In Proceedings of the International Conference on Advanced Robotics, Belo Horizonte, Brazil, 2–6 December 2019; pp. 87–92. [Google Scholar]
- Na, R.; Hu, C.; Sun, Y.; Wang, S.; Zhang, S.; Han, M.; Yin, W.; Zhang, J.; Chen, X.; Zheng, D. An embedded lightweight SSVEP-BCI electric wheelchair with hybrid stimulator. Digit. Signal Process. 2021, 16, 103101. [Google Scholar] [CrossRef]
- Gao, Q.; Zhao, X.; Yu, X.; Song, Y.; Wang, Z. Controlling of smart home system based on brain-computer interface. Technol. Health Care 2018, 26, 769–783. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Millán, J.d.R. Noninvasive EEG-based intelligent mobile robots: A systematic review. IEEE Trans. Autom. Sci. Eng. 2024, 1–25. [Google Scholar] [CrossRef]
- Li, H.; Bi, L.; Li, X. Robust predictive control for EEG-based brain-robot teleoperation. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9130–9140. [Google Scholar] [CrossRef]
- Jansen, B.H.; Rit, V.G. Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biol. Cybern. 1995, 73, 357–366. [Google Scholar] [CrossRef]
- Braitenberg, V.; Schüz, A. Anatomy of the Cortex: Statistics and Geometry; Springer-Verlag Publishing: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Keller, A.; White, E.L. Triads: A synaptic network component in the cerebral cortex. Brain Res. 1989, 496, 105–112. [Google Scholar] [CrossRef]
- Elhanany, E.; White, E.L. Intrinsic circuitry: Synapses involving the local axon collaterals of corticocortical projection neurons in the mouse primary somatosensory cortex. J. Comp. Neurol. 1990, 291, 43–54. [Google Scholar] [CrossRef]
- Liu, X.B.; Zheng, Z.H.; Xi, M.C.; Wu, C.P. Distribution of synapses on an intracellularly labeled small pyramidal neuron in the cat motor cortex. Brain Struct. Funct. 1991, 184, 313–318. [Google Scholar] [CrossRef] [PubMed]
- Larkman, A.U. Dendritic morphology of pyramidal neurones of the visual cortex of the rat. J. Comp. Neurol. 1991, 306, 332–343. [Google Scholar] [CrossRef] [PubMed]
- White, E.L. Termination of Thalamic Afferents in the Cerebral Cortex. In Sensory-Motor Areas and Aspects of Cortical Connectivity; Springer: Berlin/Heidelberg, Germany, 1986; Volume 5, pp. 271–289. [Google Scholar]
- Schnepel, P.; Kumar, A.; Zohar, M.; Aertsen, A.; Boucsein, C. Physiology and impact of horizontal connections in rat neocortex. Cereb. Cortex 2015, 25, 3818–3835. [Google Scholar] [CrossRef]
- van Rotterdam, A.; da Silva, F.H.L.; van den Ende, J.; Viergever, M.A.; Hermans, A.J. A model of the spatial-temporal characteristics of the alpha rhythm. Bull. Math. Biol. 1982, 44, 283–305. [Google Scholar] [CrossRef]
- Dodt, H.U.; Pawelzik, H.; Zieglga, W. Actions of noradrenaline on neocortical neurons in vitro. Brain Res. 1991, 545, 307–311. [Google Scholar] [CrossRef]
- Mina, F.; Benquet, P.; Pasnicu, A.; Biraben, A.; Wendling, F. Modulation of epileptic activity by deep brain stimulation: A model-based study of frequency-dependent effects. Front. Comput. Neurosci. 2013, 7, 94. [Google Scholar] [CrossRef]
- McCormick, D.A.; Pape, H.C.; Williamson, A. Actions of norepinephrine in the cerebral cortex and thalamus: Implications for function of the central noradrenergic system. Prog. Brain Res. 1991, 88, 293–305. [Google Scholar]
- Terakado, M. Adrenergic regulation of GABA release from presynaptic terminals in rat cerebral cortex. J. Oral Sci. 2014, 56, 49–57. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Morikawa, M.; Nakamichi, A. A simple model for pink noise from amplitude modulations. Sci. Rep. 2023, 13, 8364. [Google Scholar] [CrossRef]
- Hatayama, A.; Matsubara, A.; Nakashima, S.; Nishifuji, S. Effect of pink noise on EEG and memory performance in memory task. In Proceedings of the 2021 IEEE 10th Global Conference on Consumer Electronics (GCCE), Kyoto, Japan, 12–15 October 2021; pp. 238–241. [Google Scholar]
- David, O.; Friston, K.J. A Neural Mass Model for MEG/EEG: Coupling and Neuronal Dynamics. NeuroImage 2003, 20, 1743–1755. [Google Scholar] [CrossRef]
- Zanto, T.P.; Rubens, M.T.; Thangavel, A.; Gazzaley, A. Causal role of the prefrontal cortex in top-down modulation of visual processing and working memory. Nat. Neurosci. 2011, 14, 656–661. [Google Scholar] [CrossRef] [PubMed]
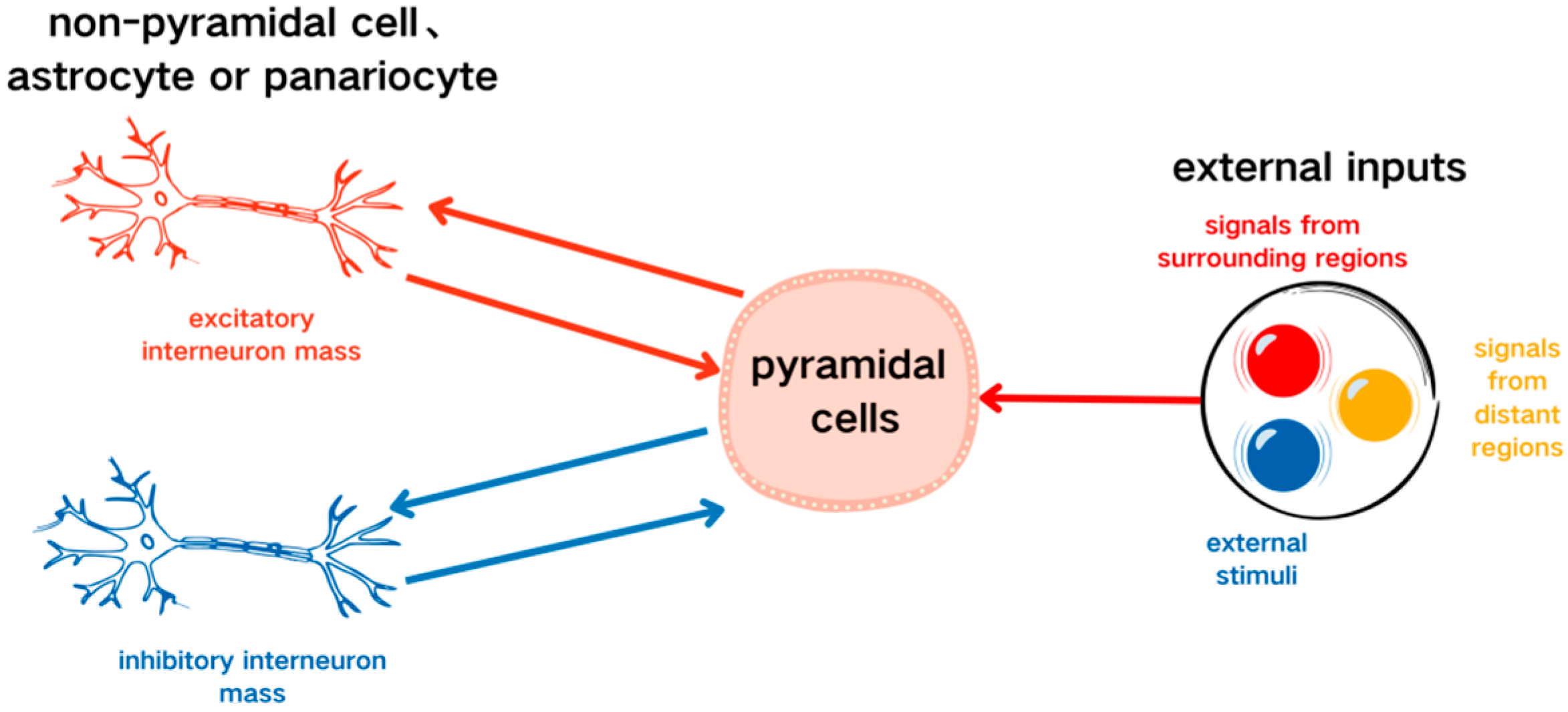
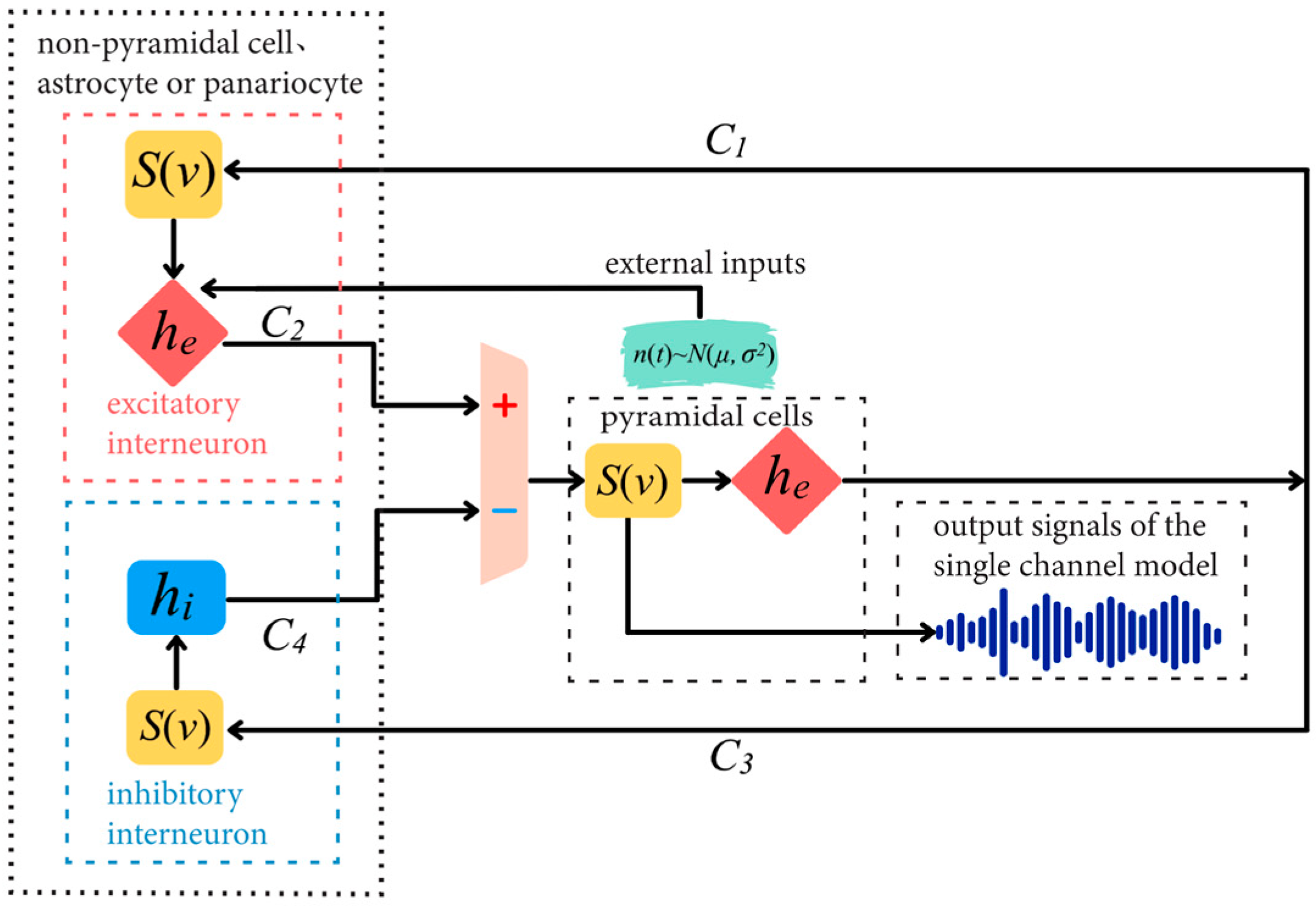



| Parameters | Physiological Significance | Typical Values | ||
|---|---|---|---|---|
| δ Waveform | α Waveform | γ Waveform | ||
| ηe | Ge * ωe | 40 mV/s | 325 mV/s | 1630.43 mV/s |
| ηi | Gi * ωi | 300 mV/s | 1100 mV/s | 51,724.14 mV/s |
| ωe−1 | Excitability time constant | 0.05 s | 0.0108 s | 0.0046 s |
| ωi−1 | Inhibitory time constant | 0.05 s | 0.02 s | 0.0029 s |
| C1, C2 | Excitatory mean synaptic connections | C1 = C, C2 = 0.8C (C = 135) | ||
| C3, C4 | Inhibitory mean synaptic connections | C3 = 0.25C C4 = 0.25C | ||
| v0, e0, r | Parameters of the nonlinear function | v0 = 6 mV, 0 = 2.5 s−1, r = 0.56 mV−1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, D.; Wang, Y.; Fu, P.; Qiu, J.; Li, H. Modeling and Parameter Analysis of Basic Single Channel Neuron Mass Model for SSVEP. Sensors 2025, 25, 1706. https://doi.org/10.3390/s25061706
Gao D, Wang Y, Fu P, Qiu J, Li H. Modeling and Parameter Analysis of Basic Single Channel Neuron Mass Model for SSVEP. Sensors. 2025; 25(6):1706. https://doi.org/10.3390/s25061706
Chicago/Turabian StyleGao, Depeng, Yujuan Wang, Peirong Fu, Jianlin Qiu, and Hongqi Li. 2025. "Modeling and Parameter Analysis of Basic Single Channel Neuron Mass Model for SSVEP" Sensors 25, no. 6: 1706. https://doi.org/10.3390/s25061706
APA StyleGao, D., Wang, Y., Fu, P., Qiu, J., & Li, H. (2025). Modeling and Parameter Analysis of Basic Single Channel Neuron Mass Model for SSVEP. Sensors, 25(6), 1706. https://doi.org/10.3390/s25061706





