Detection and Severity Classification of Sleep Apnea Using Continuous Wearable SpO2 Signals: A Multi-Scale Feature Approach
Abstract
1. Introduction
- RQ1: How do different timescales impact the relevance of features for sleep apnea severity?
- RQ2: Which features, derived from multiple timescales, are most useful for detecting sleep apnea and classifying its severity?
- RQ3: Which machine learning algorithms perform best with multi-scale feature engineering?
2. Materials and Methods
2.1. Dataset
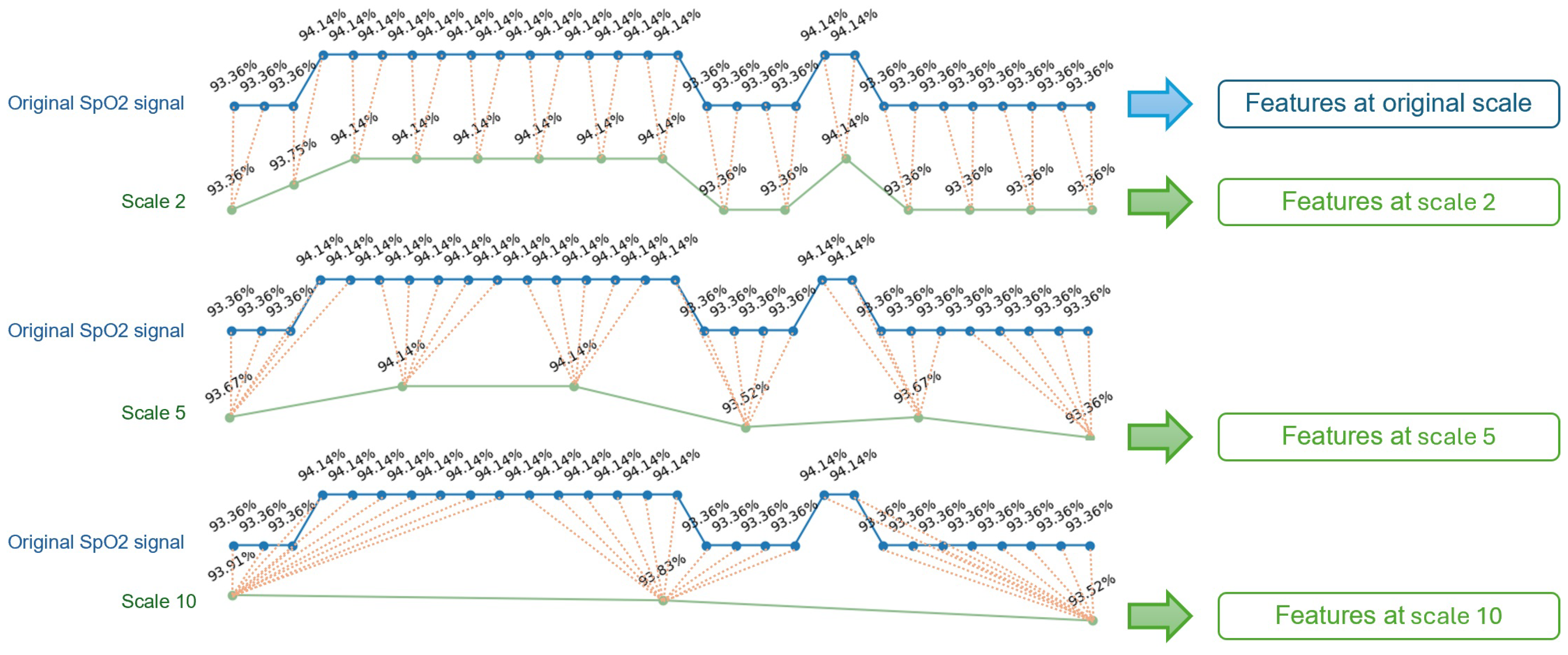
2.2. Multi-Scale Features Engineering
2.3. Model Training, Validation and Testing
3. Results
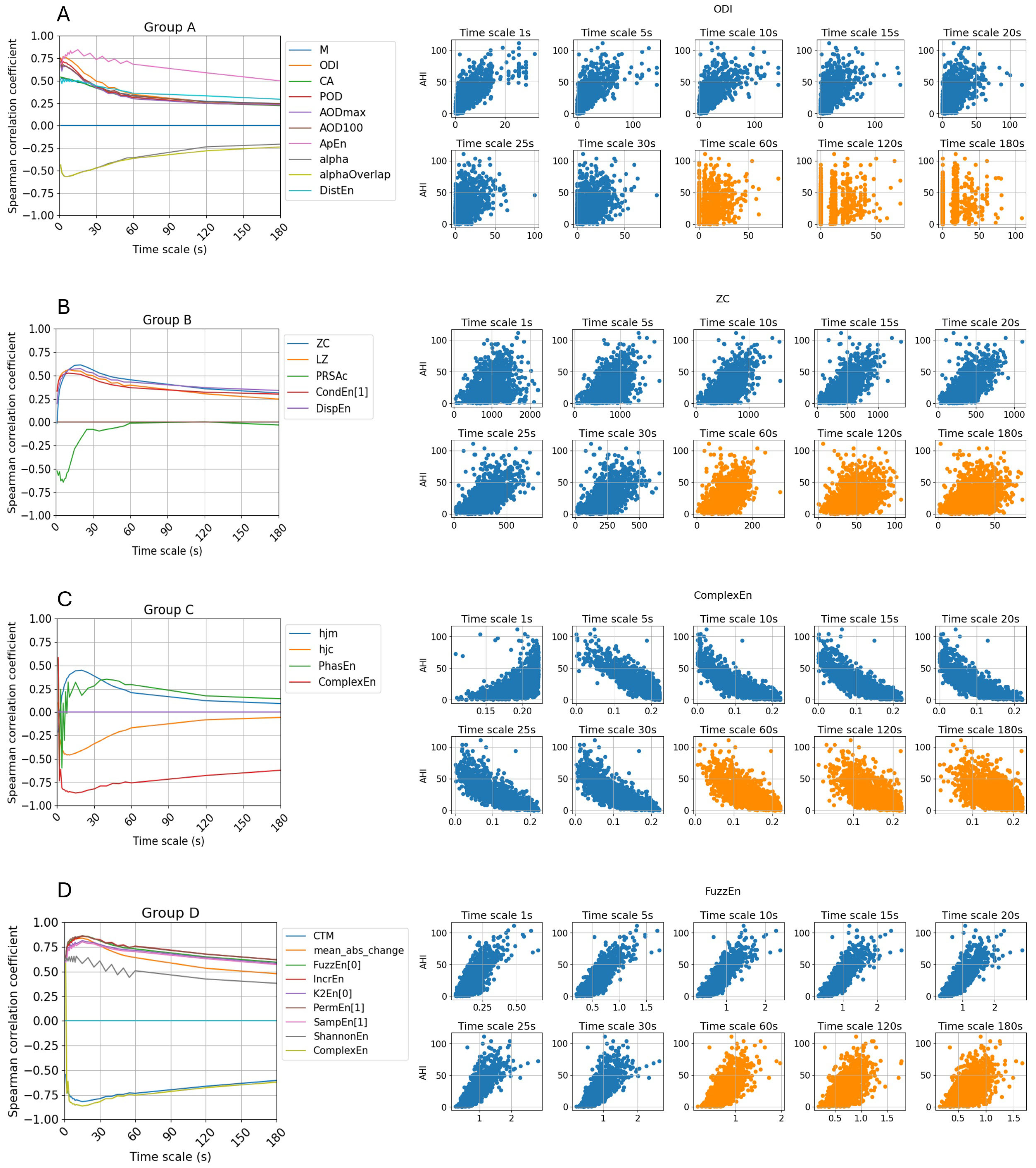
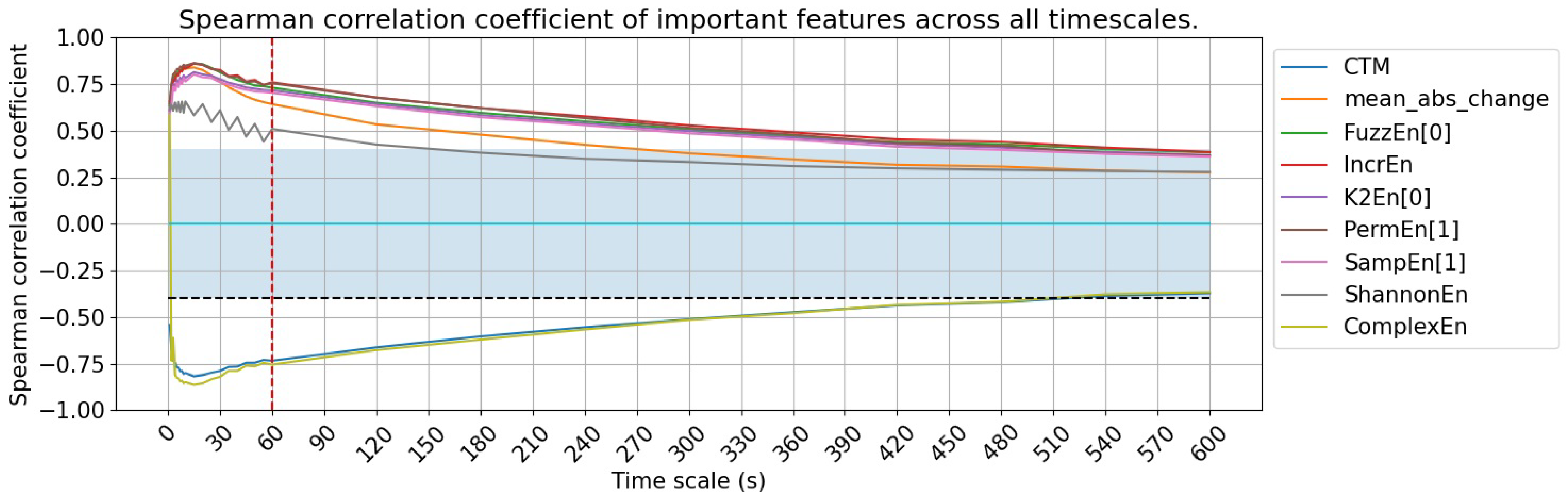
3.1. Feature Utility Across Different Signal Granularity Scales
3.2. Model Performance
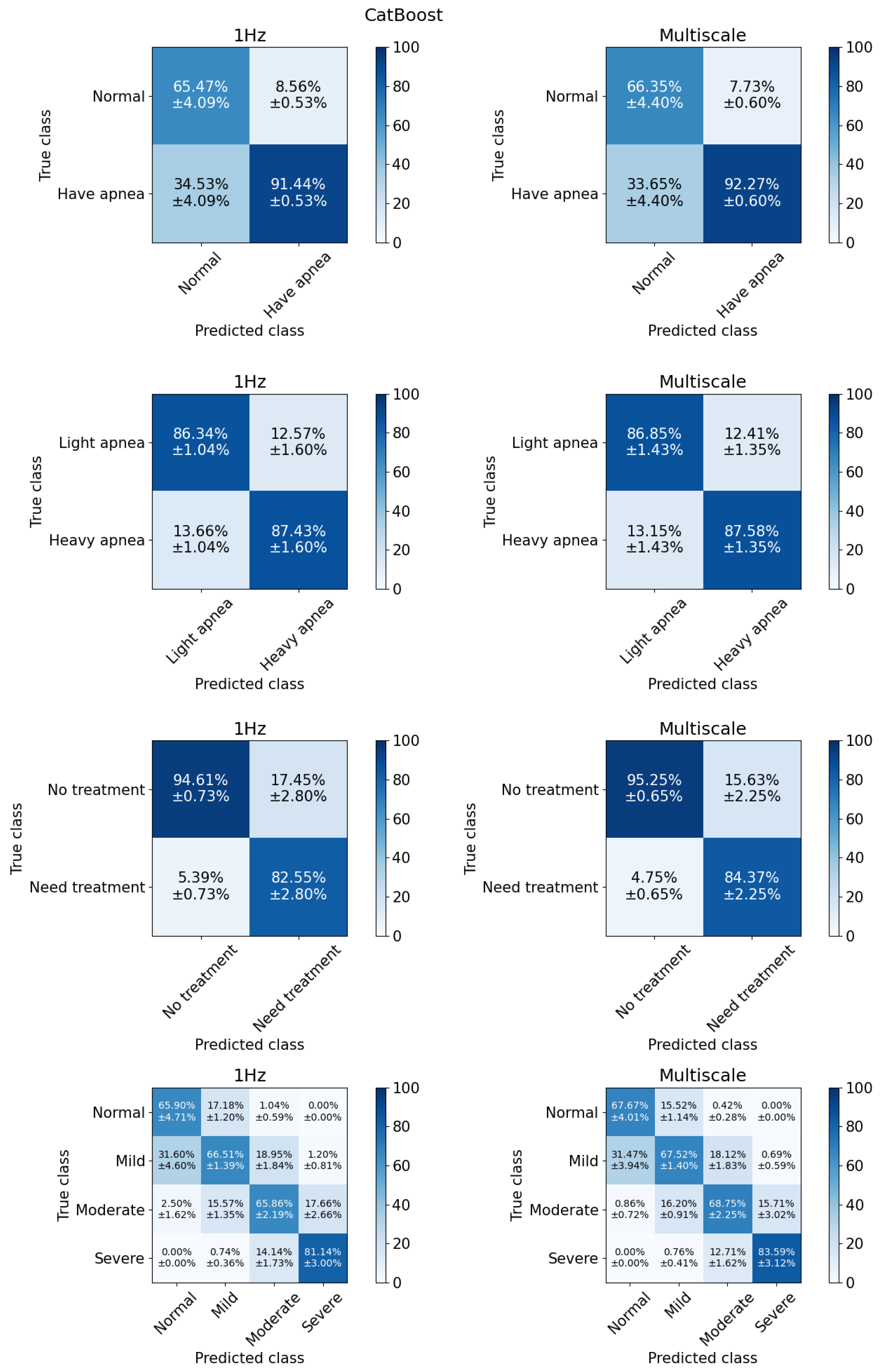
3.2.1. Binary Classification
3.2.2. Multiclass Classification
4. Discussion
4.1. Towards More Effective SpO2-Based Feature Extraction
4.2. A Closer Understanding of Model Performance
4.3. Comparison with Previous Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lupton, D. Self-tracking cultures: Towards a sociology of personal informatics. In Proceedings of the 26th Australian Computer-Human Interaction Conference on Designing Futures: The Future of Design, Sydney, Australia, 2–4 December 2014; pp. 77–86. [Google Scholar]
- Canali, S.; Schiaffonati, V.; Aliverti, A. Challenges and recommendations for wearable devices in digital health: Data quality, interoperability, health equity, fairness. PloS Digit. Health 2022, 1, e0000104. [Google Scholar] [CrossRef] [PubMed]
- De Zambotti, M.; Goldstein, C.; Cook, J.; Menghini, L.; Altini, M.; Cheng, P.; Robillard, R. State of the science and recommendations for using wearable technology in sleep and circadian research. Sleep 2024, 47, zsad325. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Chapa Martell, M.A. Validity of consumer activity wristbands and wearable EEG for measuring overall sleep parameters and sleep structure in free-living conditions. J. Healthc. Inform. Res. 2018, 2, 152–178. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Ploderer, B.; Liu, W.; Nagata, Y.; Bailey, J.; Kulik, L.; Li, Y. SleepExplorer: A visualization tool to make sense of correlations between personal sleep data and contextual factors. Pers Ubiquit Comput. 2016, 20, 985–1000. [Google Scholar] [CrossRef]
- Baron, K.G.; Duffecy, J.; Berendsen, M.A.; Mason, I.C.; Lattie, E.G.; Manalo, N.C. Feeling validated yet? A scoping review of the use of consumer-targeted wearable and mobile technology to measure and improve sleep. Sleep Med. Rev. 2018, 40, 151–159. [Google Scholar] [CrossRef]
- Retamales, G.; Gavidia, M.E.; Bausch, B.; Montanari, A.N.; Husch, A.; Goncalves, J. Towards automatic home-based sleep apnea estimation using deep learning. NPJ Digit. Med. 2024, 7, 144. [Google Scholar] [CrossRef]
- Tamaki, M.; Yamada, T.; Barnes-Diana, T.; Wang, Z.; Watanabe, T.; Sasaki, Y. First-night effect reduces the beneficial effects of sleep on visual plasticity and modifies the underlying neurochemical processes. Sci. Rep. 2024, 14, 14388. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Martell, M. A Multi-level Classification Approach for Sleep Stage Prediction with Processed Data Derived from Consumer Wearable Activity Trackers. Front. Digit. Health 2021, 3, 1–16. [Google Scholar] [CrossRef]
- Depner, C.M.; Cheng, P.C.; Devine, J.K.; Khosla, S.; De Zambotti, M.; Robillard, R.; Vakulin, A.; Drummond, S.P. Wearable technologies for developing sleep and circadian biomarkers: A summary of workshop discussions. Sleep 2020, 43, zsz254. [Google Scholar] [CrossRef]
- Rahman, M.J.; Morshed, B.I. A minimalist method toward severity assessment and progression monitoring of obstructive sleep apnea on the edge. Acm Trans. Comput. Healthc. 2021, 3, 1–16. [Google Scholar] [CrossRef]
- Pathinarupothi, R.K.; Rangan, E.S.; Gopalakrishnan, E.; Vinaykumar, R.; Soman, K. Single sensor techniques for sleep apnea diagnosis using deep learning. In Proceedings of the 2017 IEEE International Conference on Healthcare Informatics (ICHI), Park City, UT, USA, 23–27 August 2017; pp. 524–529. [Google Scholar]
- Ganglberger, W.; Bucklin, A.A.; Tesh, R.A.; Da Silva Cardoso, M.; Sun, H.; Leone, M.J.; Paixao, L.; Panneerselvam, E.; Ye, E.M.; Thompson, B.T.; et al. Sleep apnea and respiratory anomaly detection from a wearable band and oxygen saturation. Sleep Breath. 2021, 2021, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Minn, H. Real-time sleep apnea detection by classifier combination. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 469–477. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Wang, Y.; Qiu, C. A real-time auto-adjustable smart pillow system for sleep apnea detection and treatment. In Proceedings of the 12th International Conference on Information Processing in Sensor Networks, Hong Kong, China, 13–16 May 2013; pp. 179–190. [Google Scholar]
- Jeon, Y.; Heo, K.; Kang, S.J. Real-time sleep apnea diagnosis method using wearable device without external sensors. In Proceedings of the 2020 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Washington, DC, USA, 17–21 March 2020; pp. 1–5. [Google Scholar]
- Piorecky, M.; Bartoň, M.; Koudelka, V.; Buskova, J.; Koprivova, J.; Brunovsky, M.; Piorecka, V. Apnea detection in polysomnographic recordings using machine learning techniques. Diagnostics 2021, 11, 2302. [Google Scholar] [CrossRef] [PubMed]
- Deviaene, M.; Testelmans, D.; Buyse, B.; Borzée, P.; Van Huffel, S.; Varon, C. Automatic screening of sleep apnea patients based on the spo 2 signal. IEEE J. Biomed. Health Inform. 2018, 23, 607–617. [Google Scholar] [CrossRef] [PubMed]
- De Zambotti, M.; Cellini, N.; Goldstone, A.; Colrain, I.M.; Baker, F.C. Wearable sleep technology in clinical and research settings. Med. Sci. Sport. Exerc. 2019, 51, 1538. [Google Scholar] [CrossRef]
- Alvarez, D.; Hornero, R.; Marcos, J.V.; Penzel, T.; del Campo, F.; Wessel, N. Prospective evaluation of logistic regression models from overnight oximetry to assist in sleep apnea diagnosis. In Proceedings of the 2011 11th International Conference on Intelligent Systems Design and Applications, Cordoba, Spain, 22–24 November 2011; pp. 920–924. [Google Scholar]
- Mostafa, S.S.; Carvalho, J.P.; Morgado-Dias, F.; Ravelo-García, A. Optimization of sleep apnea detection using SpO2 and ANN. In Proceedings of the 2017 XXVI International Conference on Information, Communication and Automation Technologies (ICAT), Sarajevo, Bosnia and Herzegovina, 26–28 November 2017; pp. 1–6. [Google Scholar]
- Sánchez-Morillo, D.; López-Gordo, M.; León, A. Novel multiclass classification for home-based diagnosis of sleep apnea hypopnea syndrome. Expert Syst. Appl. 2014, 41, 1654–1662. [Google Scholar] [CrossRef]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Crespo, A.; Del Campo, F.; Hornero, R. Evaluation of machine-learning approaches to estimate sleep apnea severity from at-home oximetry recordings. IEEE J. Biomed. Health Inform. 2018, 23, 882–892. [Google Scholar] [CrossRef]
- Liang, Z. Multiscale attention entropy (MSAE) of overnight pulse oximetry for assessing sleep apnea. In Proceedings of the 2023 7th International Conference on Medical and Health Informatics, Kyoto, Japan, 12–14 March 2023; pp. 77–80. [Google Scholar]
- Levy, J.; Álvarez, D.; Rosenberg, A.A.; Alexandrovich, A.; Del Campo, F.; Behar, J.A. Digital oximetry biomarkers for assessing respiratory function: Standards of measurement, physiological interpretation, and clinical use. NPJ Digit. Med. 2021, 4, 1. [Google Scholar] [CrossRef]
- Bilge, P.C.; Fatma, E.K.; Cansu, S.; Haydar, S.; Deniz, K.; Alisher, K.; Sibel, C.; Ulufer, C.; Zuhal, A.; Ibrahim, O. Scanning of obstructive sleep apnea syndrome using smartwatch: A comparison of smartwatch and polysomnography. J. Clin. Neurosci. 2024, 119, 212–219. [Google Scholar] [CrossRef]
- Brennan, H.L.; Kirby, S.D. Barriers of artificial intelligence implementation in the diagnosis of obstructive sleep apnea. J.-Otolaryngol.-Head Neck Surg. 2022, 51, 16. [Google Scholar] [CrossRef]
- Quan, S.F.; Howard, B.V.; Iber, C.; Kiley, J.P.; Nieto, F.J.; O’Connor, G.T.; Rapoport, D.M.; Redline, S.; Robbins, J.; Samet, J.M.; et al. The sleep heart health study: Design, rationale, and methods. Sleep 1997, 20, 1077–1085. [Google Scholar]
- Zhang, G.Q.; Cui, L.; Mueller, R.; Tao, S.; Kim, M.; Rueschman, M.; Mariani, S.; Mobley, D.; Redline, S. The National Sleep Research Resource: Towards a sleep data commons. J. Am. Med. Inform. Assoc. 2018, 25, 1351–1358. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z. Novel method combining multiscale attention entropy of overnight blood oxygen level and machine learning for easy sleep apnea screening. Digit. Health 2023, 9, 20552076231211550. [Google Scholar] [CrossRef]
- Bernardini, A.; Brunello, A.; Gigli, G.L.; Montanari, A.; Saccomanno, N. OSASUD: A dataset of stroke unit recordings for the detection of Obstructive Sleep Apnea Syndrome. Sci. Data 2022, 9, 177. [Google Scholar] [CrossRef] [PubMed]
- Bark, B.; Nam, B.; Kim, I.Y. SelANet: Decision-assisting selective sleep apnea detection based on confidence score. Bmc Med. Inform. Decis. Mak. 2023, 23, 190. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2005, 71, 021906. [Google Scholar] [CrossRef]
- Pessa, A.A.B.; Ribeiro, H.V. ordpy: A Python package for data analysis with permutation entropy and ordinal network methods. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 063110. [Google Scholar] [CrossRef]
- Flood, M.W.; Grimm, B. EntropyHub: An open-source toolkit for entropic time series analysis. PloS ONE 2021, 16, e0259448. [Google Scholar] [CrossRef]
- De Winter, J.C.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273. [Google Scholar] [CrossRef]
- Berry, R.B.; Brooks, R.; Gamaldo, C.; Harding, S.M.; Lloyd, R.M.; Quan, S.F.; Troester, M.T.; Vaughn, B.V. The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology and Technical Specifications; Version 2.4; American Academy of Sleep Medicine: Darien, IL, USA, 2017. [Google Scholar]
- Iber, C. The AASM manual for the scoring of sleep and associated events: Rules, terminology, and technical specification. Am. Acad. Sleep Med. 2007, 176, 7. [Google Scholar]
- Alvarez, D.; Hornero, R.; Marcos, J.V.; del Campo, F.; Lopez, M. Obstructive sleep apnea detection using clustering classification of nonlinear features from nocturnal oximetry. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Piscataway, NJ, USA, 26–26 August 2007; pp. 1937–1940. [Google Scholar]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Vaquerizo-Villar, F.; Crespo, A.; Kheirandish-Gozal, L.; Gozal, D.; del Campo, F.; Hornero, R. Ensemble-learning regression to estimate sleep apnea severity using at-home oximetry in adults. Appl. Soft Comput. 2021, 111, 107827. [Google Scholar] [CrossRef] [PubMed]
- Levy, J.; Álvarez, D.; Del Campo, F.; Behar, J.A. Deep learning for obstructive sleep apnea diagnosis based on single channel oximetry. Nat. Commun. 2023, 14, 4881. [Google Scholar] [CrossRef] [PubMed]
- Varghese, L.; Rebekah, G.; Oliver, A.; Kurien, R. Oxygen desaturation index as alternative parameter in screening patients with severe obstructive sleep apnea. Sleep Sci. 2022, 15, 224–228. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.W.; Liu, C.M.; Wang, C.Y.; Lin, C.C.; Qiu, K.Y.; Yeh, C.Y.; Hwang, S.H. A deep neural network-based model for OSA severity classification using unsegmented peripheral oxygen saturation signals. Eng. Appl. Artif. Intell. 2023, 122, 106161. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Zhao, G.; Zhang, X.; Xu, W.; Han, D. A model for obstructive sleep apnea detection using a multi-layer feed-forward neural network based on electrocardiogram, pulse oxygen saturation, and body mass index. Sleep Breath. 2021, 25, 1–8. [Google Scholar] [CrossRef]
- Hwang, S.H.; Cho, J.G.; Choi, B.H.; Baek, H.J.; Lee, Y.J.; Jeong, D.U.; Park, K.S. Real-time automatic apneic event detection using nocturnal pulse oximetry. IEEE Trans. Biomed. Eng. 2017, 65, 706–712. [Google Scholar]
- Lyden, B.; Dair, Z.; O’Reilly, R. Classification of Sleep Apnea via SpO2 in a Simulated Smartwatch Environment. In Proceedings of the 2022 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Ioannina, Greek, 27–30 September 2022; pp. 1–5. [Google Scholar]
- Sharma, M.; Kumbhani, D.; Tiwari, J.; Kumar, T.S.; Acharya, U.R. Automated detection of obstructive sleep apnea in more than 8000 subjects using frequency optimized orthogonal wavelet filter bank with respiratory and oximetry signals. Comput. Biol. Med. 2022, 144, 105364. [Google Scholar] [CrossRef]
- Sharma, M.; Kumbhani, D.; Yadav, A.; Acharya, U.R. Automated Sleep apnea detection using optimal duration-frequency concentrated wavelet-based features of pulse oximetry signals. Appl. Intell. 2022, 52, 1325–1337. [Google Scholar] [CrossRef]



| Categories | SHHS1 | |
|---|---|---|
| Number of subject 1 | 4664 | |
| Age | 65.88 ± 11.01 | |
| BMI | 28.24 ± 5.04 | |
| Gender | Female | 2287 (49.04%) |
| Male | 2377 (50.96%) | |
| AHI | 18.66 ± 15.4 | |
| Binary (AHI cut-off = 5) | Normal | 634 (13.59%) |
| Patient/have apnea | 4030 (86.40%) | |
| Binary (AHI cut-off = 15) | Normal & mild | 2426 (52.02%) |
| Moderate & severe | 2238 (47.98%) | |
| Binary (AHI cut-off = 30) | Non-severe | 3 840 (82.33%) |
| Severe | 824 (17.67%) | |
| Multiclass | Normal | 634 (13.59%) |
| Mild | 1792 (38.42%) | |
| Moderate | 1414 (30.32%) | |
| (AHI cut-offs: 5, 15, 30) | Severe | 824 (17.67%) |
| Trend | Features | Description | Correlation Coefficient Score () | Timescale of Highest | ||
|---|---|---|---|---|---|---|
| Highest | Lowest | Median | ||||
| M | Percentage of the signal at least x% below median SpO2, by default x = 2 | 0.54 | 0.18 | 0.40 | 2 s | |
| ODI | The oxygen desaturation index | 0.77 | 0.2 | 0.48 | 3 s | |
| CA | Integral of SpO2 below the x SpO2 level normalized by the total recording time, by default x = AV, here 93 | 0.54 | 0.16 | 0.4 | 1 s | |
| POD | Time of oxygen desaturation event, normalized by the total recording time | 0.75 | 0.20 | 0.41 | 1 s | |
| Showing decreasing trend | AODmax | The area under the oxygen desaturation event curve, using the maximum SpO2 value as baseline and normalized by the total recording time | 0.68 | 0.20 | 0.40 | 1 s |
| AOD100 | Cumulative area of desaturations under the 100% SpO2 level as baseline and normalized by the total recording time | 0.71 | 0.20 | 0.42 | 1 s | |
| ApEn | Approximate entropy with, by default, m = 1, r = 0.25 times the standard deviation of the data | 0.85 | 0.11 | 0.72 | 5 s | |
| alpha | Long-term correlations for non-stationary process, using non-overlapping windows | −0.57 | −0.08 | −0.44 | 5 s | |
| alphaOverlap | Long-term correlations for non-stationary process, using overlapping windows | −0.57 | −0.12 | −0.43 | 5 s | |
| DistEn | Distribution entropy | 0.52 | 0.23 | 0.43 | 1 s | |
| Reach | ZC | Mean crossing | 0.61 | −0.01 | 0.45 | 20 s |
| stronger | LZ | Lempel–Zip complexity | 0.56 | 0.13 | 0.43 | 10 s |
| correlation at higher | PRSAc | Phase-rectified signal averaging capacity. With d the fragment duration, here d = 10 | −0.68 | 0.03 | −0.17 | 6 s |
| timescale | CondEn | Corrected conditional entropy | 0.53 | 0.24 | 0.42 | 10 s |
| DispEn | Dispersion entropy | 0.57 | 0.24 | 0.45 | 15 s | |
| Show | hjm | Hjorth mobility | 0.45 | −0.21 | 0.22 | 20 s |
| correlation | hjc | Hjorth complexity | −0.46 | 0.10 | −0.27 | 7 s |
| polarity | PhasEn | Phase entropy | −0.60 | 0.07 | 0.18 | 3 s |
| shifts | ComplexEn | Complex entropy | −0.86 | 0.31 | −0.76 | 10 s |
| CTM | Central tendency measure with radius , by default = 0.25 | −0.82 | −0.37 | −0.75 | 15 s | |
| Mean abs change | Average magnitude of change between consecutive SpO2 values | 0.84 | 0.28 | 0.71 | 15 s | |
| Constant high | FuzzEn | Fuzzy Entropy | 0.86 | 0.38 | 0.76 | 15 s |
| high | IncrEn | Increment entropy | 0.86 | 0.39 | 0.77 | 15 s |
| relationship | K2En | Kolmogorov (K2) entropy | 0.81 | 0.37 | 0.73 | 9 s |
| PermEn | Permutation entropy | 0.86 | 0.37 | 0.76 | 3 s | |
| SampEn | Sample entropy | 0.80 | 0.36 | 0.71 | 5 s | |
| ShannonEn | Shannon entropy | 0.66 | 0.28 | 0.55 | 4 s | |
| ComplexEn | Complex entropy | −0.86 | 0.31 | −0.76 | 10 s | |
| Acc (%) | Pre (%) | Sen (%) | F1-Score | MCC | AUC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Multi-Scale | Baseline | Multi-Scale | Baseline | Multi-Scale | Baseline | Multi-Scale | Baseline | Multi-Scale | Baseline | Multi-Scale | Baseline | |
| Cut_off_5 | ||||||||||||
| Bayes | 73.59 | 67.17 | 96.77 | 96.75 | 71.84 | 64.16 | 0.82 | 0.77 | 0.41 | 0.35 | 0.83 | 0.84 |
| DT | 85.38 | 84.35 | 91.91 | 91.67 | 91.10 | 90.07 | 0.92 | 0.91 | 0.39 | 0.37 | 0.65 | 0.69 |
| KNN | 87.50 | 87.11 | 88.21 | 87.68 | 98.73 | 98.99 | 0.93 | 0.93 | 0.29 | 0.24 | 0.87 | 0.85 |
| LG | 88.54 | 88.94 | 93.62 | 91.33 | 93.08 | 96.35 | 0.93 | 0.94 | 0.52 | 0.46 | 0.92 | 0.91 |
| XGB | 88.66 | 88.37 | 92.32 | 91.99 | 94.76 | 94.80 | 0.94 | 0.93 | 0.48 | 0.47 | 0.91 | 0.91 |
| CatBoost | 89.63 | 89.10 | 92.27 | 91.44 | 96.06 | 96.42 | 0.94 | 0.94 | 0.51 | 0.47 | 0.92 | 0.92 |
| MLP | 87.13 | 86.24 | 92.01 | 91.66 | 93.20 | 92.49 | 0.93 | 0.92 | 0.43 | 0.40 | 0.89 | 0.87 |
| Cut_off_15 | ||||||||||||
| Bayes | 79.58 | 77.17 | 84.12 | 87.66 | 70.92 | 61.08 | 0.77 | 0.72 | 0.60 | 0.56 | 0.86 | 0.86 |
| DT | 81.36 | 80.80 | 81.62 | 80.96 | 79.01 | 78.52 | 0.80 | 0.80 | 0.63 | 0.62 | 0.79 | 0.81 |
| KNN | 83.57 | 82.20 | 85.06 | 84.26 | 79.84 | 77.42 | 0.82 | 0.81 | 0.67 | 0.64 | 0.91 | 0.90 |
| LG | 87.05 | 86.49 | 87.69 | 87.24 | 85.01 | 84.20 | 0.86 | 0.86 | 0.74 | 0.73 | 0.94 | 0.94 |
| XGB | 86.11 | 86.08 | 86.31 | 86.56 | 84.49 | 84.09 | 0.85 | 0.85 | 0.72 | 0.72 | 0.94 | 0.94 |
| CatBoost | 87.17 | 86.82 | 87.59 | 87.43 | 85.42 | 84.79 | 0.87 | 0.86 | 0.74 | 0.74 | 0.95 | 0.94 |
| MLP | 84.89 | 82.85 | 84.47 | 82.72 | 84.00 | 81.33 | 0.84 | 0.82 | 0.70 | 0.66 | 0.93 | 0.91 |
| Cut_off_30 | ||||||||||||
| Bayes | 85.92 | 88.05 | 57.41 | 64.57 | 79.53 | 72.21 | 0.67 | 0.68 | 0.59 | 0.61 | 0.89 | 0.91 |
| DT | 90.53 | 89.47 | 74.38 | 71.45 | 71.10 | 67.67 | 0.73 | 0.69 | 0.67 | 0.63 | 0.79 | 0.83 |
| KNN | 90.74 | 91.07 | 87.94 | 83.85 | 55.20 | 61.47 | 0.68 | 0.71 | 0.65 | 0.67 | 0.94 | 0.94 |
| LG | 92.02 | 92.79 | 74.51 | 84.15 | 83.66 | 73.08 | 0.79 | 0.78 | 0.74 | 0.74 | 0.96 | 0.96 |
| XGB | 92.86 | 92.12 | 82.27 | 80.39 | 76.17 | 73.54 | 0.79 | 0.77 | 0.75 | 0.72 | 0.96 | 0.95 |
| CatBoost | 93.47 | 92.67 | 84.37 | 82.55 | 77.50 | 74.34 | 0.81 | 0.78 | 0.77 | 0.74 | 0.96 | 0.96 |
| MLP | 91.92 | 90.85 | 77.83 | 74.64 | 76.16 | 73.42 | 0.77 | 0.74 | 0.72 | 0.69 | 0.95 | 0.94 |
| Multiclass | ||||||||||||
| Bayes | 57.70 | 57.36 | 57.66 | 57.87 | 58.25 | 55.57 | 0.58 | 0.56 | 0.41 | 0.40 | ||
| DT | 60.85 | 58.67 | 60.87 | 58.24 | 60.02 | 57.55 | 0.60 | 0.58 | 0.45 | 0.42 | ||
| KNN | 62.32 | 60.91 | 66.13 | 63.07 | 55.05 | 53.92 | 0.57 | 0.55 | 0.46 | 0.44 | ||
| LG | 67.54 | 68.37 | 67.43 | 69.32 | 65.09 | 64.49 | 0.66 | 0.66 | 0.54 | 0.55 | ||
| XGB | 69.28 | 68.29 | 69.86 | 68.84 | 67.16 | 65.60 | 0.68 | 0.67 | 0.56 | 0.55 | ||
| CatBoost | 70.46 | 68.54 | 71.88 | 69.85 | 67.64 | 64.75 | 0.69 | 0.66 | 0.58 | 0.55 | ||
| MLP | 62.72 | 60.14 | 62.40 | 59.49 | 61.49 | 58.78 | 0.62 | 0.59 | 0.47 | 0.44 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoang, N.H.; Liang, Z. Detection and Severity Classification of Sleep Apnea Using Continuous Wearable SpO2 Signals: A Multi-Scale Feature Approach. Sensors 2025, 25, 1698. https://doi.org/10.3390/s25061698
Hoang NH, Liang Z. Detection and Severity Classification of Sleep Apnea Using Continuous Wearable SpO2 Signals: A Multi-Scale Feature Approach. Sensors. 2025; 25(6):1698. https://doi.org/10.3390/s25061698
Chicago/Turabian StyleHoang, Nhung H., and Zilu Liang. 2025. "Detection and Severity Classification of Sleep Apnea Using Continuous Wearable SpO2 Signals: A Multi-Scale Feature Approach" Sensors 25, no. 6: 1698. https://doi.org/10.3390/s25061698
APA StyleHoang, N. H., & Liang, Z. (2025). Detection and Severity Classification of Sleep Apnea Using Continuous Wearable SpO2 Signals: A Multi-Scale Feature Approach. Sensors, 25(6), 1698. https://doi.org/10.3390/s25061698







