An Analog Sensor Signal Processing Method Susceptible to Anthropogenic Noise Based on Improved Adaptive Singular Spectrum Analysis
Abstract
1. Introduction
2. Methodology
2.1. Basic Theory of Singular Spectrum Analysis and K-Means Clustering Algorithm
| Algorithm 1. Process of SSA combined with K-means clustering algorithm. |
| Input: Pending sequence Y(t) |
| 1: Start: Set window length L, if , , determine the value of clustering K; 2: Embed Y(t) into trajectory matrix X; 3: Perform singular value decomposition using Equation (1), and sort the singular values in descending order; 4: Perform K-means clustering, choose K singular values as clustering centroids; 5: When new centroid is different from the original one; 6: for i = 1 to m; 7: Calculate the distance between the ith sample and the centroids according to Equation (6), and take the centroid with the smallest dxiμi and denoted as ci; 8: end; 9: for i = 1 to K; 10: Calculate the mean of the coordinate of all sample points belonging to the current centroid, and take the mean value as the new centroid. 11: end; 12: end; 13: Screen for valid classifications based on correlations, selecting clusters with correlations greater than 0.99; 14: Filter the eigentriples corresponding to the singular values of each clustered cluster based on indexing; 15: Reconstruct the signal components with different frequencies according to Equation (4); 16: end. |
| Output: Reconstructed signals |
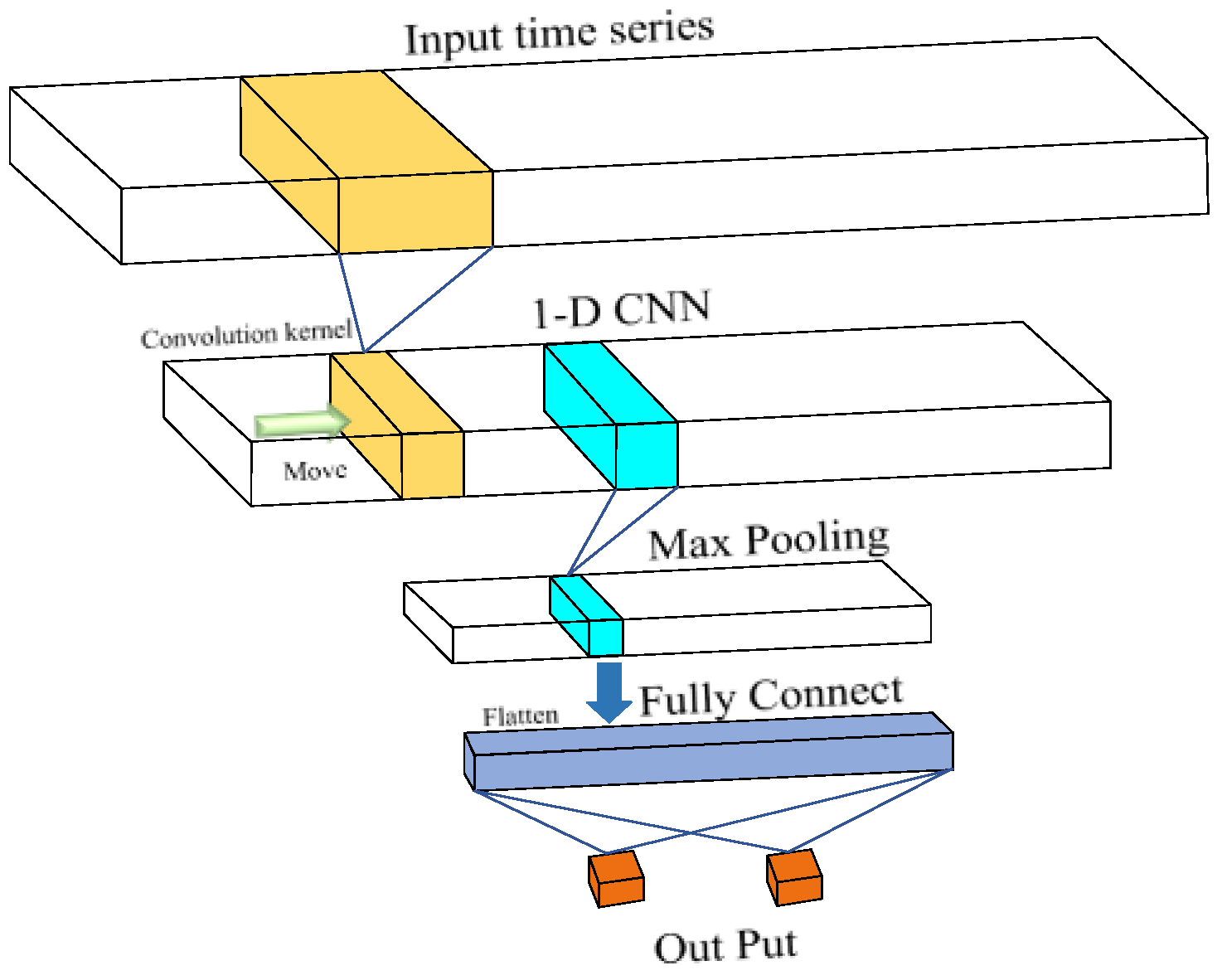
2.2. Deep Residual Neural Networks
| Algorithm 2. Overall workflow of the ASSA algorithm. |
| Input: Measured data sequence Y(t) |
| 1: Start: Deep Res-Net recognition process of Y(t); 2: Deep Res-Net outputs noise signal category K and target signal category T, respectively; 3: Set window length L, if ; 4: Embed Y(t) into trajectory matrix X; 5: Perform singular value decomposition using Equation (1), and sort the singular values in descending order; 6: Perform K-means clustering, choose K + T singular values as clustering centroids; 7: Obtain the clusters , calculate the mean Ci of i-th cluster , where cij is the j-th element of Ci, and sort in ascending order; 8: Set threshold Ts; 9: if ; 10: for i, j < K + T; 11: if 12: Correlation matrix ; 13: end 14: Valid cluster Cv = where (Cor_m < 0.01) 15: end 16: end 17: Filter the eigentriples corresponding to the singular values of each clustered cluster based on Cv; 18: Reconstruct the signal components with different frequencies, according to Equation (4); 19: end. |
| Output: Reconstructed signals |
3. Experiments and Result Analysis
3.1. Experiments of Frequency Resolution Performance
3.2. Experiments of Target Signal Recognition
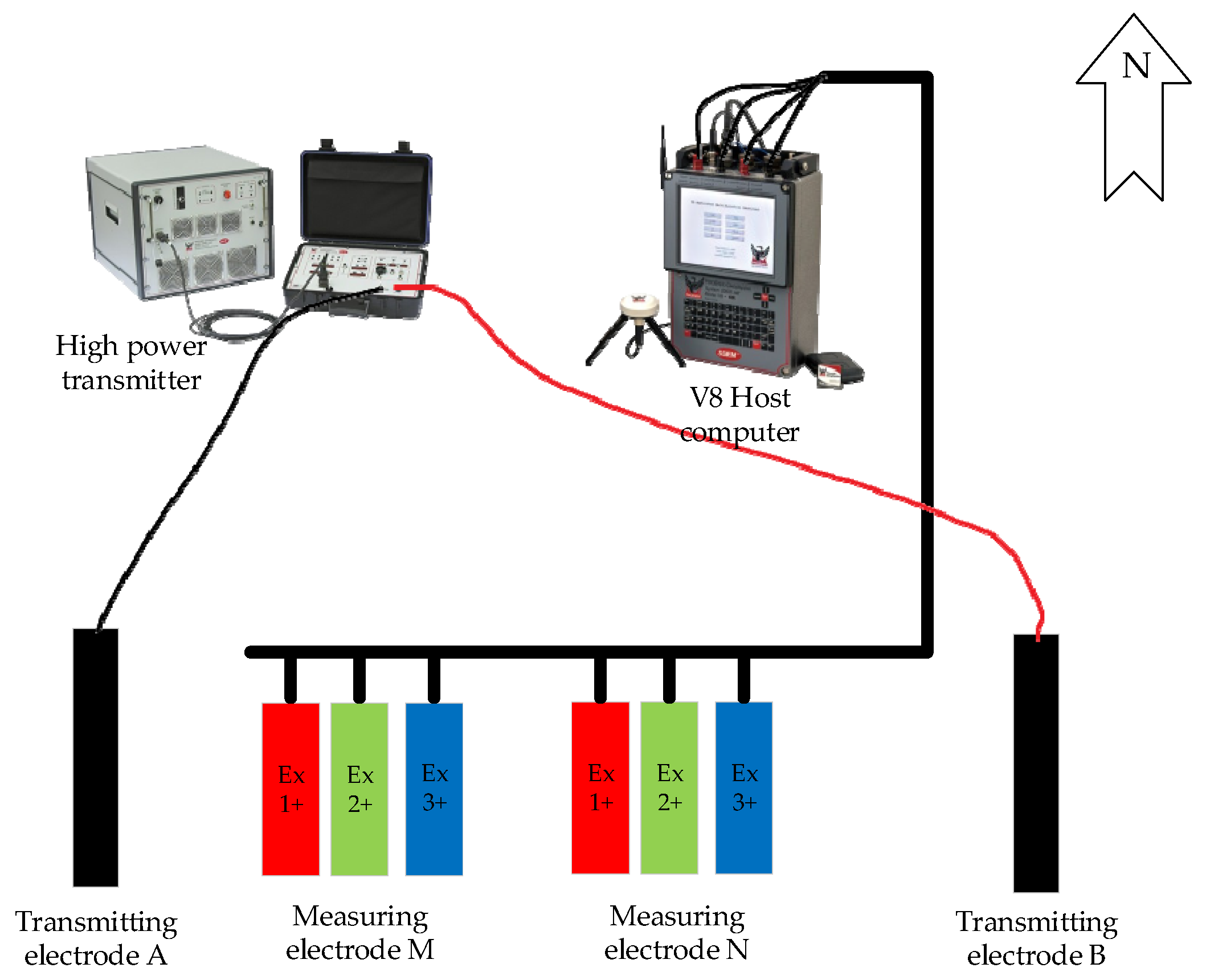
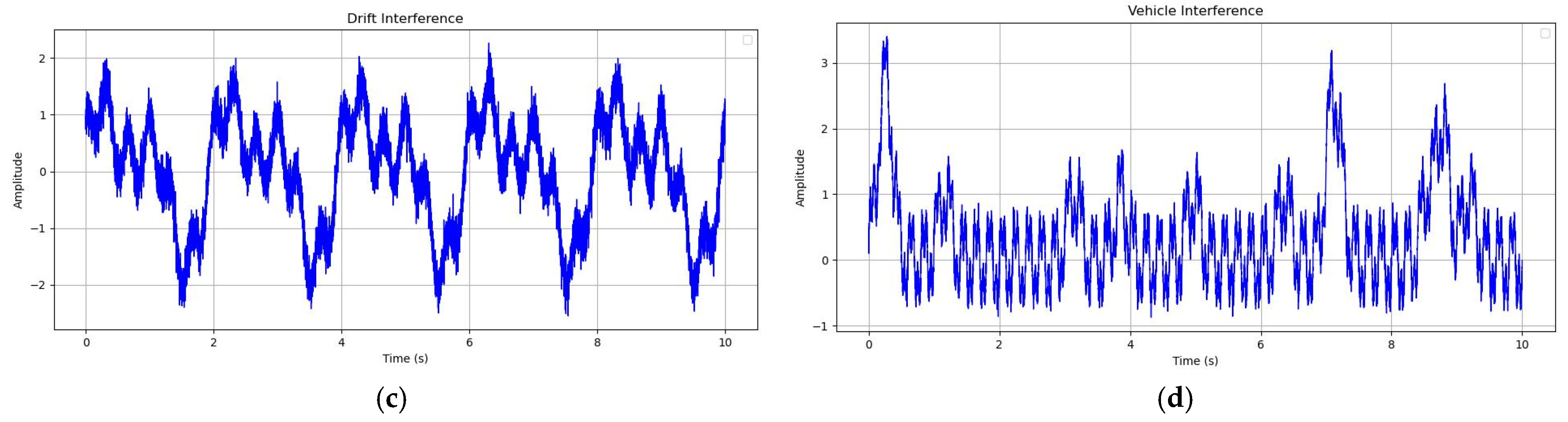
3.3. Measured Data Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, Z.; Ge, S.; Li, J.; Feng, K. Inertial Navigation Trajectory and Attitude Prediction Based on Improved Hidden Markov Model. In Proceedings of the 2023 IEEE 16th International Conference on Electronic Measurement & Instruments (ICEMI), Harbin, China, 9–11 August 2023; pp. 383–389. [Google Scholar]
- Cai, J. A de-noising method of magnetotelluric signals based on the generalized S-transform. J. Appl. Geophys. 2024, 223, 105349. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Tang, J.; Ma, F. Magnetotelluric noise suppression via convolutional neural network. Geophysics 2023, 88, WA361–WA375. [Google Scholar] [CrossRef]
- Pukhova, V.M.; Kustov, T.V.; Ferrini, G. Time-frequency analysis of non-stationary signals. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia, 29 January–1 February 2018; pp. 1141–1145. [Google Scholar]
- Akaniro, O.G.; Sanei, S. Singular Spectrum Analysis of Non-stationary Signals. In Proceedings of the 2020 3rd International Conference on Emerging Trends in Electrical, Electronic and Communications Engineering (ELECOM), Balaclava, Mauritius, 25–27 November 2020; pp. 18–21. [Google Scholar]
- Yang, D.; Wang, H.; Wang, T.; Lu, G. Piezoelectric Active Sensing-Based Pipeline Corrosion Monitoring Using Singular Spectrum Analysis. Sensors 2024, 24, 4192. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, X.; Tang, J. Noise suppression for magnetotelluric using variational mode decomposition and detrended fluctuation analysis. J. Appl. Geophys. 2020, 180, 104127. [Google Scholar] [CrossRef]
- Pal, U.; Chattopadhyay, P.B.; Sarraf, Y.; Halder, S. Optimizing noise reduction in layered-earth magnetotelluric data for generating smooth models with artificial neural networks. Acta Geophys. 2024, 1–31. [Google Scholar] [CrossRef]
- Lin, W.; Yang, B.; Han, B.; Hu, X. A Review of Subsurface Electrical Conductivity Anomalies in Magnetotelluric Imaging. Sensors 2023, 23, 1803. [Google Scholar] [CrossRef]
- Pedersen, J.; Hermance, J.F. Least squares inversion of one-dimensional magnetotelluric data: An assessment of procedures employed by Brown University. Surv. Geophys. 1986, 8, 45. [Google Scholar] [CrossRef]
- Cadzow, J.A. Least Squares, Modeling, and Signal Processing. Digit. Signal Process. 1994, 4, 19. [Google Scholar] [CrossRef]
- Sharma, L.D.; Bhattacharyya, A. A Computerized Approach for Automatic Human Emotion Recognition Using Sliding Mode Singular Spectrum Analysis. IEEE Sens. J. 2021, 21, 26931–26940. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Chen, S.; Hou, L.; Zhu, L. An Antijamming Method Based on Multichannel Singular Spectrum Analysis and Affinity Propagation for UWB Ranging Sensors. IEEE Sens. J. 2023, 23, 11869–11878. [Google Scholar] [CrossRef]
- Eriksen, T.; Rehman, N.U. Data-driven nonstationary signal decomposition approaches: A comparative analysis. Sci. Rep. 2023, 13, 1798. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H. Singular spectrum analysis: Methodology and comparison. J. Data Sci. 2007, 5, 19. [Google Scholar] [CrossRef]
- Jain, S.; Panda, R.; Tripathy, R.K. Multivariate Sliding-Mode Singular Spectrum Analysis for the Decomposition of Multisensor Time Series. IEEE Sens. Lett. 2020, 4, 7002404. [Google Scholar] [CrossRef]
- Bayati, F.; Trad, D. 3-D Data Interpolation and Denoising by an Adaptive Weighting Rank-Reduction Method Using Multichannel Singular Spectrum Analysis Algorithm. Sensors 2023, 23, 577. [Google Scholar] [CrossRef]
- Du, W.; Zhou, J.; Wang, Z.; Li, R.; Wang, J. Application of Improved Singular Spectrum Decomposition Method for Composite Fault Diagnosis of Gear Boxes. Sensors 2018, 18, 3804. [Google Scholar] [CrossRef]
- Liao, Z.; Song, L.; Chen, P.; Guan, Z.; Fang, Z.; Li, K. An Effective Singular Value Selection and Bearing Fault Signal Filtering Diagnosis Method Based on False Nearest Neighbors and Statistical Information Criteria. Sensors 2018, 18, 2235. [Google Scholar] [CrossRef]
- Gu, J.; Hung, K.; Ling, B.W.-K.; Chow, D.H.-K.; Zhou, Y.; Fu, Y.; Pun, S.H. Generalized singular spectrum analysis for the decomposition and analysis of non-stationary signals. J. Frankl. Inst. 2024, 361, 106696. [Google Scholar] [CrossRef]
- Zhou, R.; Han, J.; Guo, Z.; Li, T. De-Noising of Magnetotelluric Signals by Discrete Wavelet Transform and SVD Decomposition. Remote Sens. 2021, 13, 4932. [Google Scholar] [CrossRef]
- Harmouche, J.; Fourer, D.; Auger, F.; Borgnat, P.; Flandrin, P. The Sliding Singular Spectrum Analysis: A Data-Driven Nonstationary Signal Decomposition Tool. IEEE Trans. Signal Process. 2018, 66, 251–263. [Google Scholar] [CrossRef]
- Zhang, C.; Du, C.; Peng, X.; Han, Q.; Guo, H. An Aeromagnetic Compensation Method for Suppressing the Magnetic Interference Generated by Electric Current with Vector Magnetometer. Sensors 2022, 22, 6151. [Google Scholar] [CrossRef]
- Lin, C.-S.; Wu, Y.-X. Singular Spectrum Analysis for Modal Estimation from Stationary Response Only. Sensors 2022, 22, 2585. [Google Scholar] [CrossRef]
- Bonizzi, P.; Karel, J.M.H.; Meste, O.; Peeters, R.L.M. Singular spectrum decomposition: A new method for time series decomposition. Adv. Adapt. Data Anal. 2014, 06, 1450011. [Google Scholar] [CrossRef]
- Xu, W.; Shen, Y.; Jiang, Q.; Zhu, Q.; Xu, F. Rolling bearing fault feature extraction via improved SSD and a singular-value energy autocorrelation coefficient spectrum. Meas. Sci. Technol. 2022, 33, 085112. [Google Scholar] [CrossRef]
- Kazemi, M.; Rodrigues, P.C. Robust singular spectrum analysis: Comparison between classical and robust approaches for model fit and forecasting. Comput. Stat. 2023. [Google Scholar] [CrossRef]
- Golyandina, N. Particularities and commonalities of singular spectrum analysis as a method of time series analysis and signal processing. WIREs Comput. Stat. 2020, 12, e1487. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-D Convolutional Neural Networks for Signal Processing Applications. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8360–8364. [Google Scholar]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Zhao, M.; Kang, M.; Tang, B.; Pecht, M. Deep Residual Networks With Dynamically Weighted Wavelet Coefficients for Fault Diagnosis of Planetary Gearboxes. IEEE Trans. Ind. Electron. 2018, 65, 4290–4300. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; p. 8. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; p. 9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; p. 9. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep Residual Shrinkage Networks for Fault Diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 4681–4690. [Google Scholar] [CrossRef]




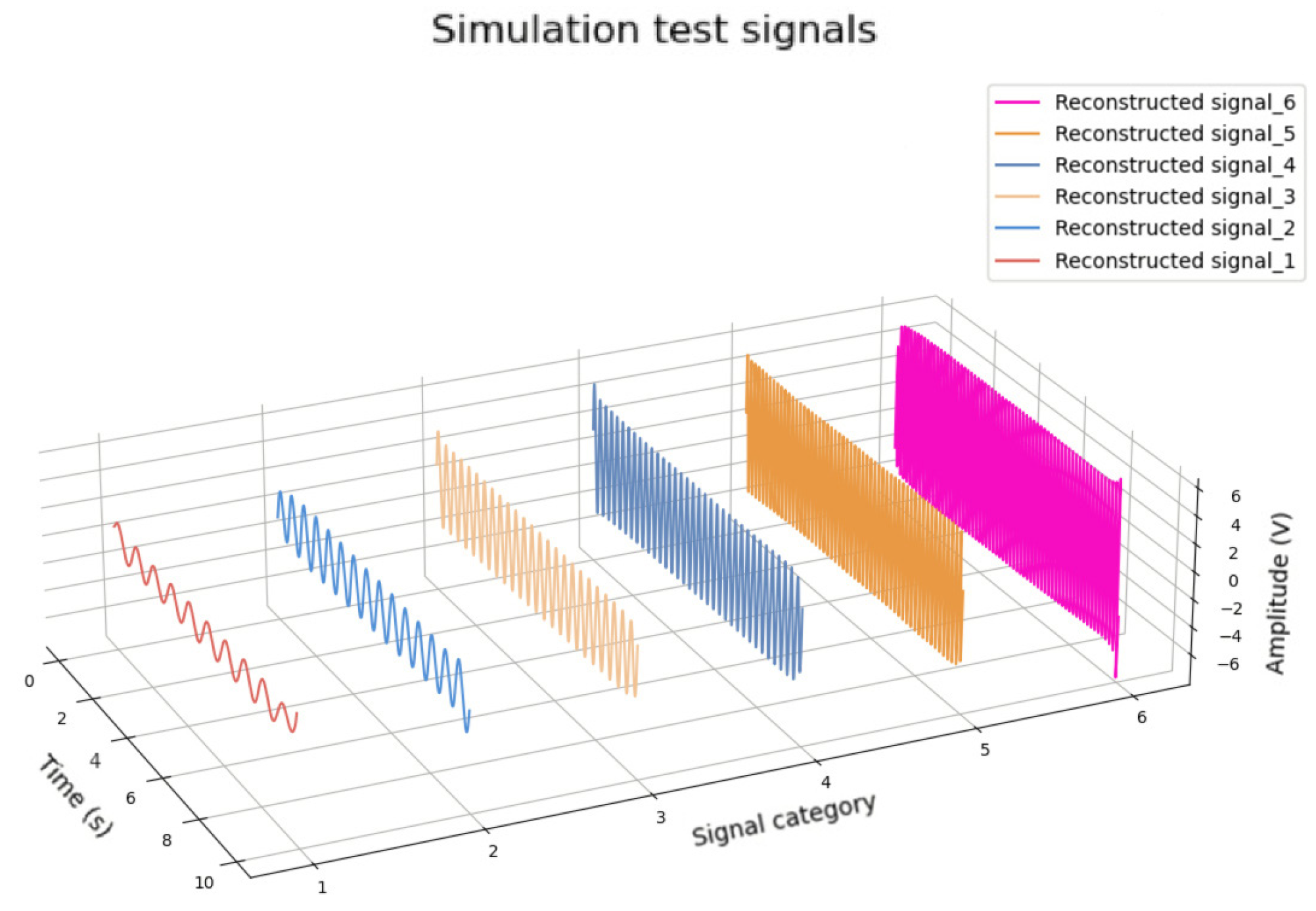



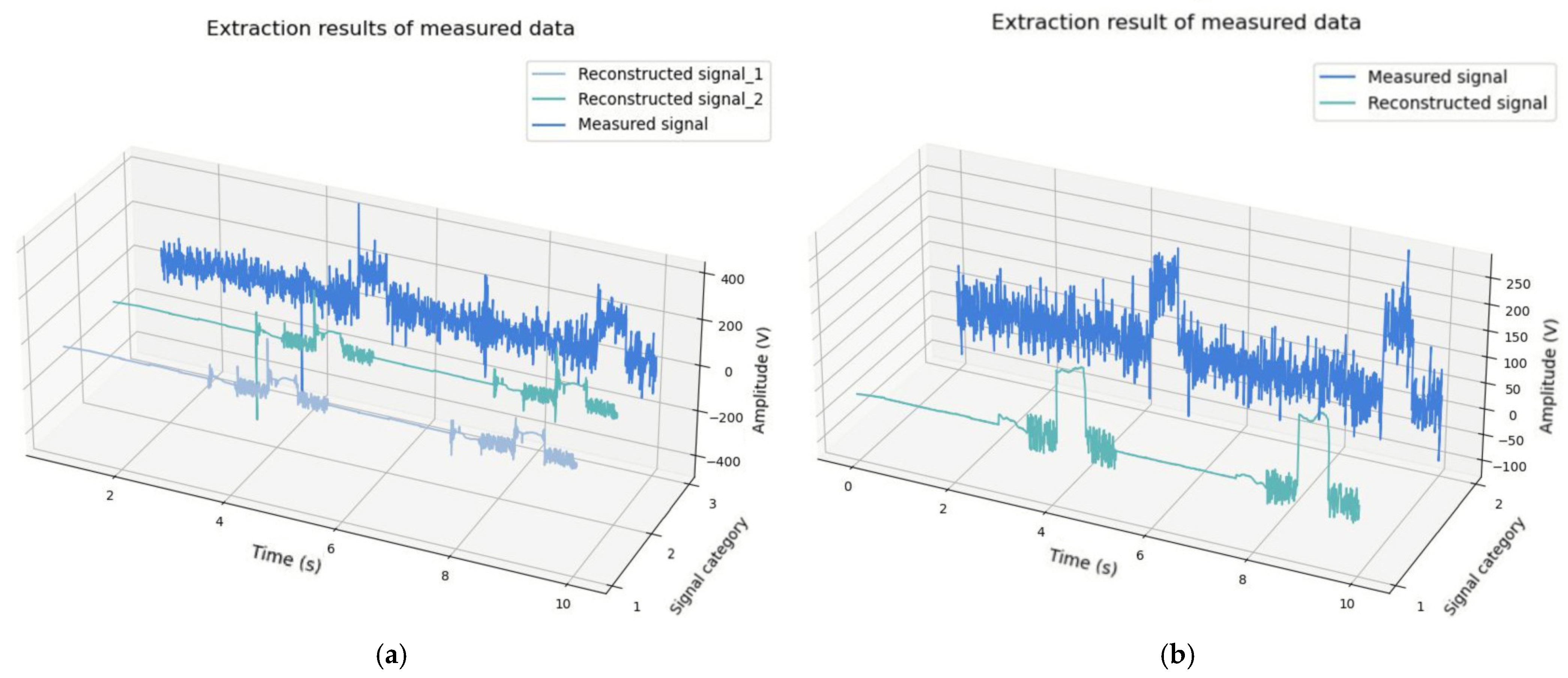


| Signal | RMSE | Processing Time (s) |
|---|---|---|
| Reconstructed signal 1 | 3.64 × 10−2 | 2.81 |
| Reconstructed signal 2 | 3.45 × 10−2 | 2.73 |
| Reconstructed signal 3 | 4.60 × 10−2 | 2.72 |
| Reconstructed signal 4 | 4.26 × 10−2 | 2.99 |
| Reconstructed signal 5 | 1.84 × 10−2 | 2.73 |
| Reconstructed signal 6 | 3.64 × 10−2 | 2.72 |
| Signal | RMSE | Processing Time (s) | ||||
|---|---|---|---|---|---|---|
| ASSA | SSA | OMP | ASSA | SSA | OMP | |
| Triangle wave | 0.1041 | 0.1512 | 0.4262 | 24.86 | 21.75 | 1075.91 |
| Oscillating attenuation | 0.0356 | 0.0473 | 0.0475 | 23.53 | 23.37 | 1075.91 |
| Pulstran | 0.1889 | 0.2163 | 0.2565 | 24.62 | 20.58 | 1075.91 |
| Dual-frequency | 0.1552 | 0.2367 | 0.2743 | 23.81 | 20.79 | 1075.91 |
| Reconstructed Signal | RMSE | SNR (dB) | Processing Time (s) |
|---|---|---|---|
| Reconstructed signal 1 (First time) | 0.2047 | 12 | 32.75 |
| Reconstructed signal 2 (First time) | 0.2902 | 11 | 32.68 |
| Reconstructed signal (Second time) | 0.2962 | 13 | 33.57 |
| Algorithm | RMSE | Processing Time (s) |
|---|---|---|
| Conventional SSA | 0.4906 | 29.36 |
| OMP | 0.1342 | 4347.62 |
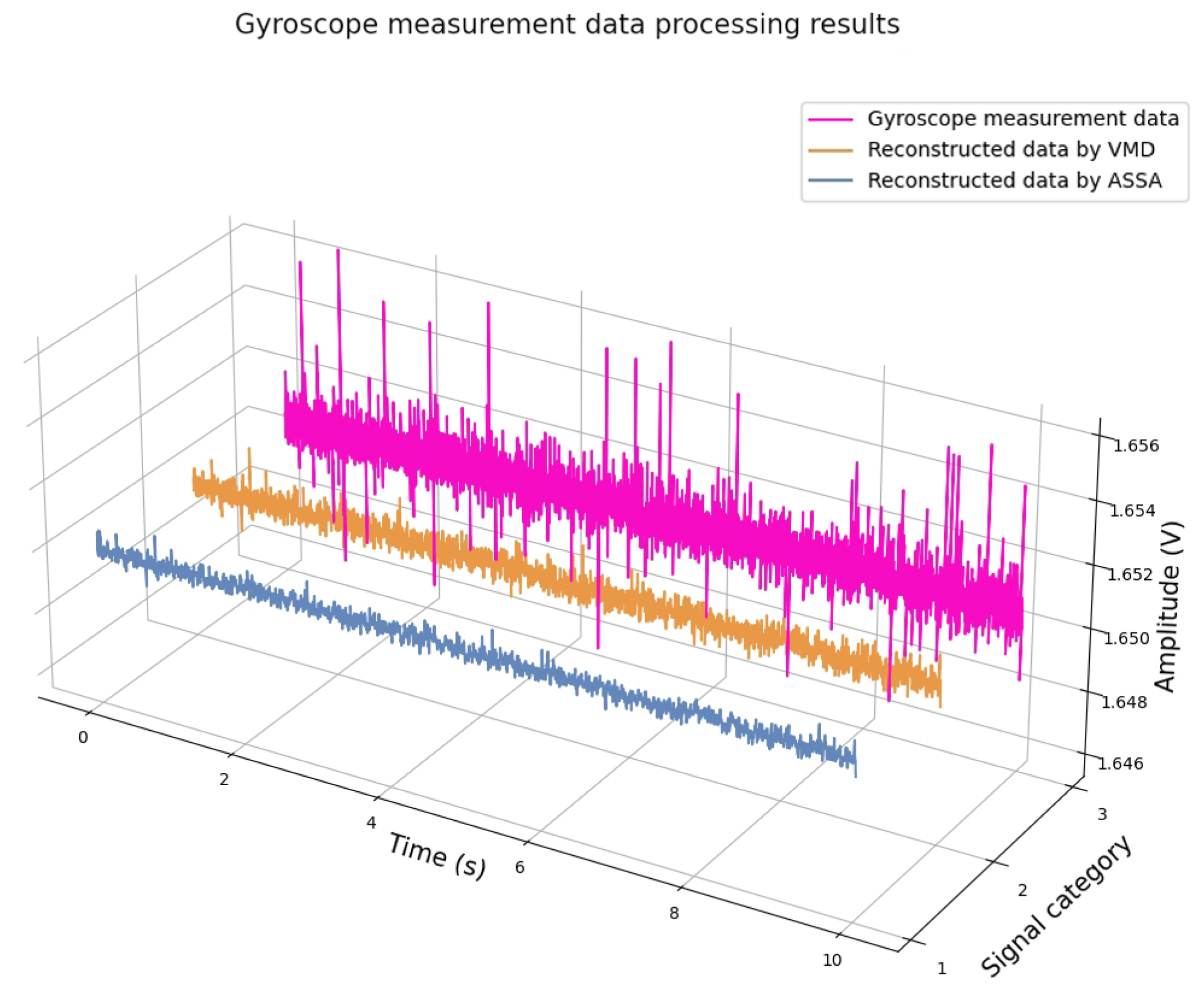
| Algorithm | RMSE | Processing Time (s) |
|---|---|---|
| ASSA | 3.57 × 10−4 | 4.2 |
| VMD | 4.02 × 10−4 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Ge, S.; Li, J.; Huang, W.; Feng, K.; Zhang, C.; Zhang, C.; Sun, J. An Analog Sensor Signal Processing Method Susceptible to Anthropogenic Noise Based on Improved Adaptive Singular Spectrum Analysis. Sensors 2025, 25, 1598. https://doi.org/10.3390/s25051598
Gao Z, Ge S, Li J, Huang W, Feng K, Zhang C, Zhang C, Sun J. An Analog Sensor Signal Processing Method Susceptible to Anthropogenic Noise Based on Improved Adaptive Singular Spectrum Analysis. Sensors. 2025; 25(5):1598. https://doi.org/10.3390/s25051598
Chicago/Turabian StyleGao, Zhengyang, Shuangchao Ge, Jie Li, Wentao Huang, Kaiqiang Feng, Chenming Zhang, Chunxing Zhang, and Jiaxin Sun. 2025. "An Analog Sensor Signal Processing Method Susceptible to Anthropogenic Noise Based on Improved Adaptive Singular Spectrum Analysis" Sensors 25, no. 5: 1598. https://doi.org/10.3390/s25051598
APA StyleGao, Z., Ge, S., Li, J., Huang, W., Feng, K., Zhang, C., Zhang, C., & Sun, J. (2025). An Analog Sensor Signal Processing Method Susceptible to Anthropogenic Noise Based on Improved Adaptive Singular Spectrum Analysis. Sensors, 25(5), 1598. https://doi.org/10.3390/s25051598








