Visual-Inertial-Wheel Odometry with Slip Compensation and Dynamic Feature Elimination
Abstract
1. Introduction
- (i)
- The use of a data-driven methodology employing GPR and LSTM networks to address wheel slippage. This integration of GPR and LSTM presents a substantial enhancement over prior approach by effectively mitigating errors induced by slippage; thus, it significantly improves the precision of wheel odometry measurements.
- (ii)
- The incorporation of a feature confidence estimator that utilizes additional sensory data. This ensures that only reliable sensor data influence the system’s state estimation.
2. The System Description and Preliminaries
2.1. IMU Kinematics Model
2.2. Camera Measurement Model
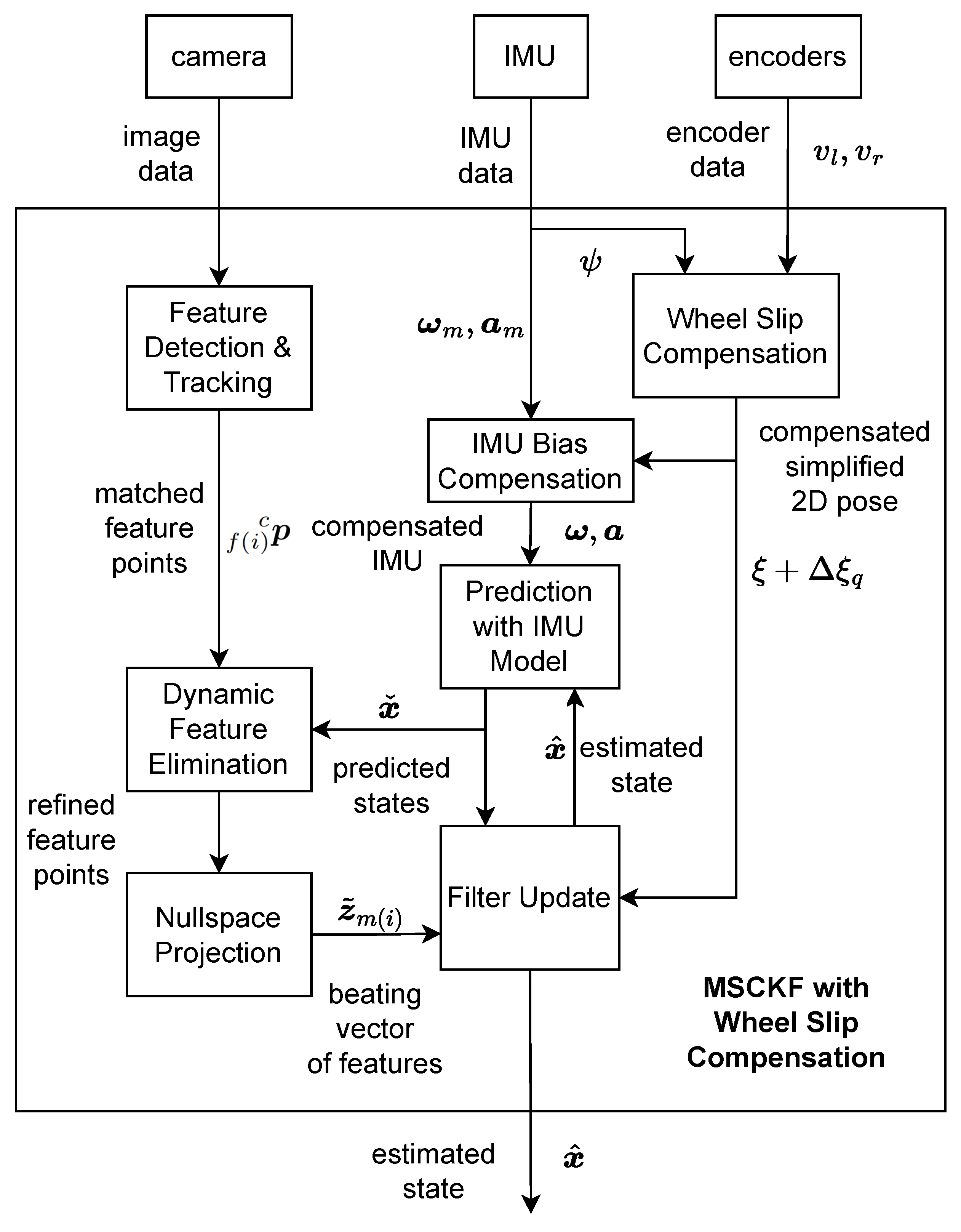
3. Overall Methodology
3.1. Robot State Vector
3.2. Process Model
3.3. Dynamic Feature Elimination
3.4. Measurement Update
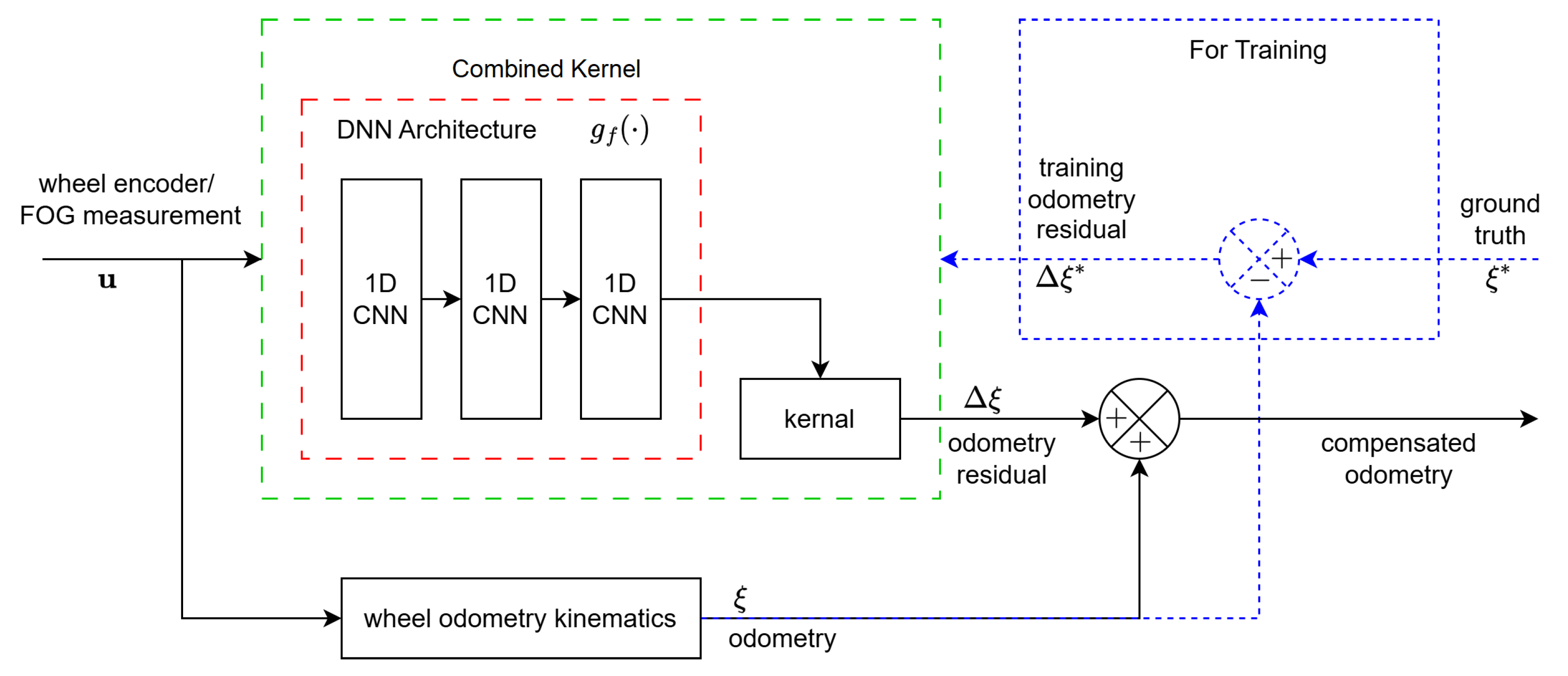
4. Slip Compensation
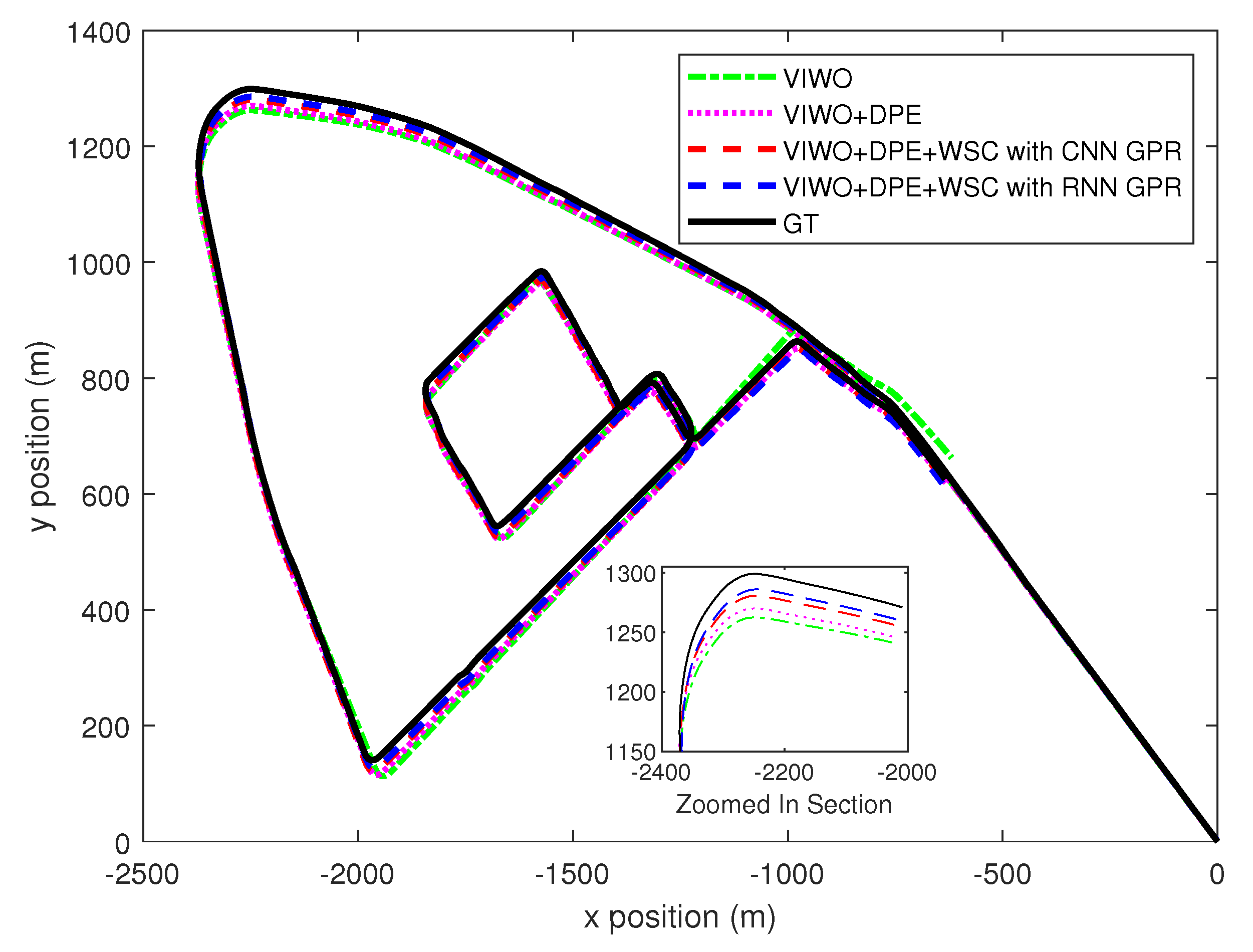
5. Real-World Data Simulation
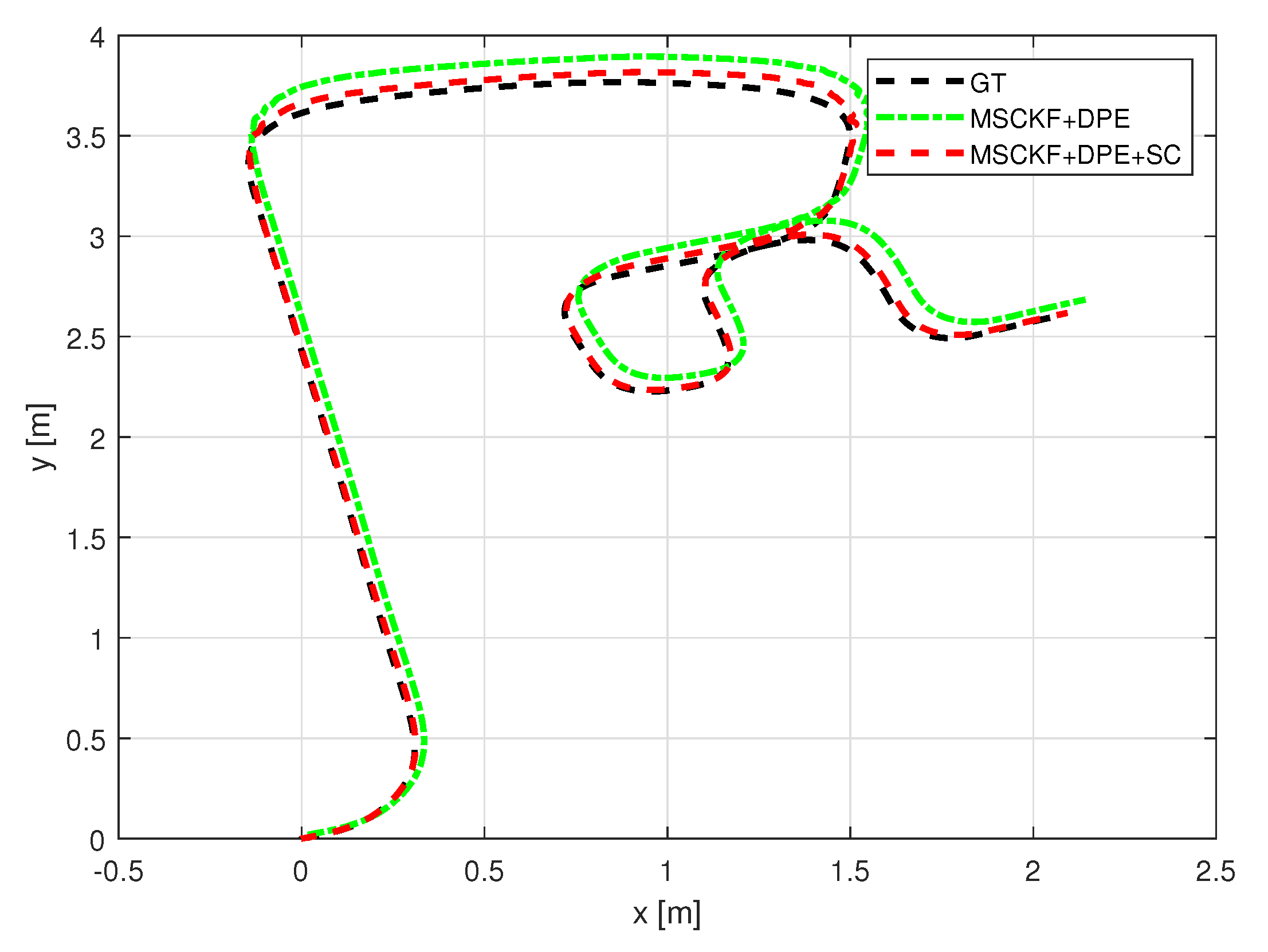
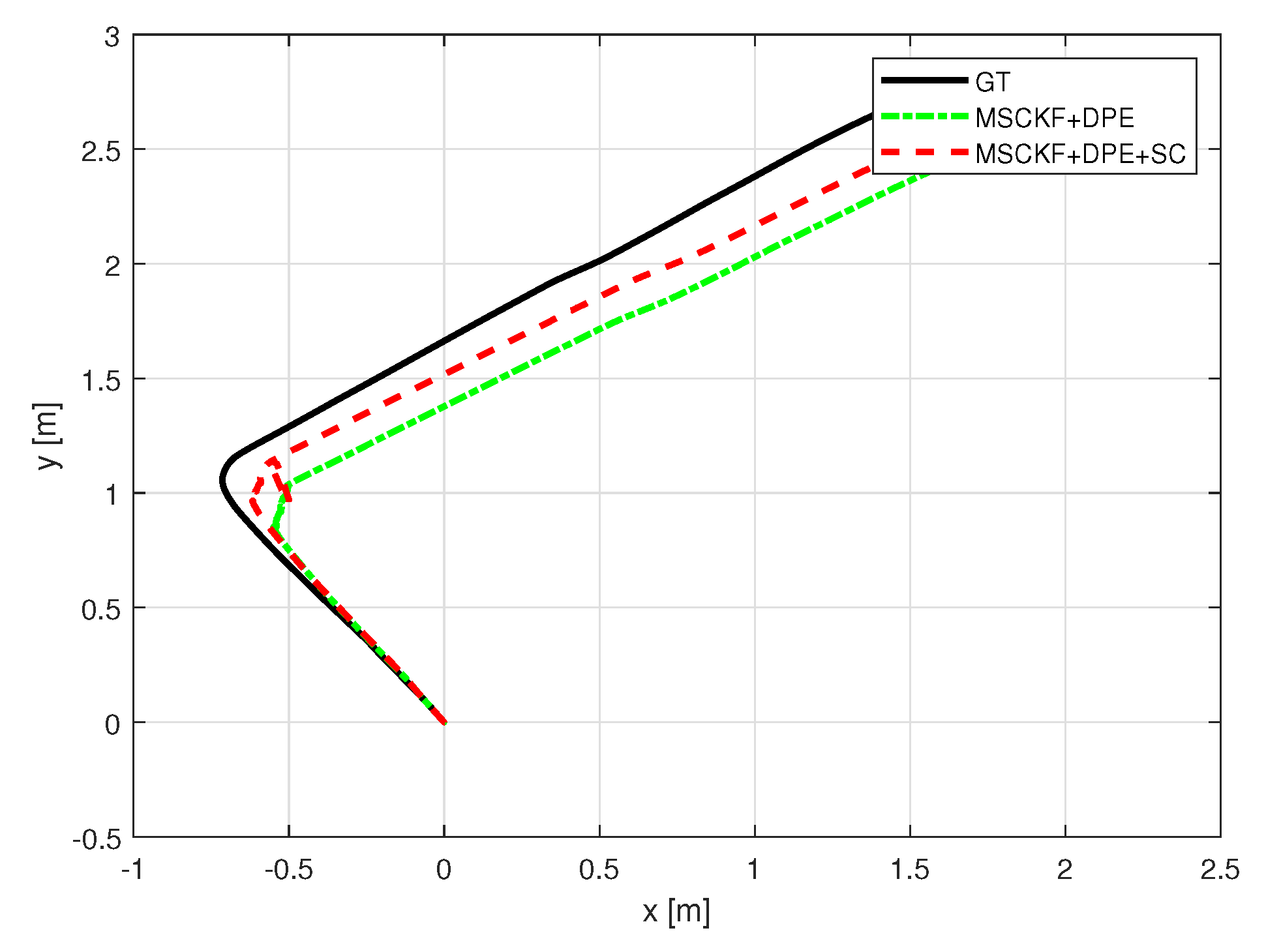
6. Indoor Experimentation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Category | Proposed Approach | VINS with WO [1,6,24] | Filter-Based VIWO [5,25,35] | VIWO with Slip Detection [20] |
|---|---|---|---|---|
| Objective | Compensate for wheel slippage and improve VIWO accuracy. | Refine inertial measurements and improve the accuracy of VIWO. | Fuse WO and VINS for improved localization. | Detect and mitigate slip in real time. |
| Methodology | GPR and LSTM to model and correct slip errors; integrates a feature confidence estimator. | Neural gyroscope calibration to reduce drift in localization. | Partial invariant EKF (PIEKF) to optimally fuse WO and VINS. | Threshold-based slip detection and rejection. |
| Key Innovation and Limitations | Integrates adaptive slip correction with dynamic feature elimination for robust VIWO. | Uses deep learning for enhanced gyroscope drift compensation. Affected by wheel slip and inherent IMU drifts, leading to localization errors. Ref. [24] has focused on reducing the gyroscope drift. | Leverages kinematic constraints to refine odometry accuracy but assumes minimal slip, causing errors in dynamic conditions. | Ensures real-time slip detection but does not model slip dynamics, leading to accumulated drift over time. |
| Feature | Proposed | GNSS-Free UAV Navigation [28] | VO Using RCNNs [29] | VO Using CNN and Bi-LSTM [30] |
|---|---|---|---|---|
| Objective | Uses GPR and LSTM to compensate for wheel slippage, enhancing VO accuracy. | LSTM-based GNSS-free UAV navigation using optical odometry and radar. | Monocular VO with deep RCNNs estimating poses from raw RGB images. | Monocular VO with CNN and Bi-LSTM for 6-DoF pose estimation. |
| Methodology | GPR-LSTM fusion to correct slippage-induced errors in VO. | LSTM for drift correction and radar for scale estimation. | CNN for feature extraction, RNN for sequential motion modeling. | Hybrid CNN for features, Bi-LSTM for sequence learning. |
| Key Innovation and Limitations | Combines GPR and LSTM for adaptive slippage compensation, improving localization. | Uses LSTM for velocity correction and radar for scale resolution. | End-to-end learning without explicit VO components. | Bi-LSTM utilizes past and future frames for improved estimation. |
| Main Contributions | Enhances wheel odometry with ML and sensor fusion. | Reliable UAV navigation in GNSS-denied areas. | VO without feature engineering or scale priors. | End-to-end VO without geometric constraints. |
| Technological Focus | Ground navigation with: (1) Slippage compensation, (2) Robust localization, (3) Improved odometry. | UAV navigation, GNSS signal loss mitigation. | Learning-based feature extraction and motion estimation. | Enhancing feature extraction and motion estimation. |
| Validation | Tested on KAIST dataset, showing robust performance in dynamic terrains. | Flight-tested, reducing velocity errors in GNSS outages. | Validated on KITTI dataset, competitive with traditional VO. | Tested on KITTI, ETH-asl-cla, suited for structured driving. |
| Advantages | Accurate slippage compensation, improving localization in uneven terrains. | Reliable UAV navigation under GNSS loss. | Adaptable VO without manual tuning. | No manual feature extraction, robust across environments. |
References
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Brasch, N.; Bozic, A.; Lallemand, J.; Tombari, F. Semantic Monocular SLAM for Highly Dynamic Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 393–400. [Google Scholar] [CrossRef]
- Huang, G.P. Visual-Inertial Navigation: A Concise Review. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9572–9582. [Google Scholar]
- Jung, J.H.; Heo, S.; Park, C. Observability Analysis of IMU Intrinsic Parameters in Stereo Visual–Inertial Odometry. IEEE Trans. Instrum. Meas. 2020, 69, 7530–7541. [Google Scholar] [CrossRef]
- Zhang, Z.; Scaramuzza, D. A Tutorial on Quantitative Trajectory Evaluation for Visual(-Inertial) Odometry. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7244–7251. [Google Scholar] [CrossRef]
- Campos, C.; Montiel, J.M.; Tardós, J.D. Inertial-only optimization for visual-inertial initialization. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 51–57. [Google Scholar]
- Yang, Y.; Geneva, P.; Eckenhoff, K.; Huang, G. Degenerate motion analysis for aided INS with online spatial and temporal sensor calibration. IEEE Robot. Autom. Lett. 2019, 4, 2070–2077. [Google Scholar] [CrossRef]
- Wu, K.; Guo, C.; Georgiou, G.; Roumeliotis, S. VINS on wheels. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 5155–5162. [Google Scholar]
- Liu, J.; Gao, W.; Hu, Z. Visual-Inertial Odometry Tightly Coupled with Wheel Encoder Adopting Robust Initialization and Online Extrinsic Calibration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019; pp. 5391–5397. [Google Scholar]
- Kang, R.; Xiong, L.; Xu, M.; Zhao, J.; Zhang, P. VINS-Vehicle: A Tightly-Coupled Vehicle Dynamics Extension to Visual-Inertial State Estimator. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Auckland, New Zealand, 27–30 October 2019; pp. 3593–3600. [Google Scholar]
- Lee, W.; Eckenhoff, K.; Yang, Y.; Geneva, P.; Huang, G. Visual-Inertial-Wheel Odometry with Online Calibration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020; pp. 4559–4566. [Google Scholar]
- Peng, G.; Lu, Z.; Chen, S.; He, D.; Xinde, L. Pose Estimation Based on Wheel Speed Anomaly Detection in Monocular Visual-Inertial SLAM. IEEE Sens. J. 2021, 21, 11692–11703. [Google Scholar] [CrossRef]
- Kim, J.; Kim, B.K. Cornering Trajectory Planning Avoiding Slip for Differential-Wheeled Mobile Robots. IEEE Trans. Ind. Electron. 2020, 67, 6698–6708. [Google Scholar] [CrossRef]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated Vehicle Sideslip Angle Estimation Considering Signal Measurement Characteristic. IEEE Sens. J. 2021, 21, 21675–21687. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Chen, J. Fusion Algorithm Design Based on Adaptive SCKF and Integral Correction for Side-Slip Angle Observation. IEEE Trans. Ind. Electron. 2018, 65, 5754–5763. [Google Scholar] [CrossRef]
- Kim, C.H.; Cho, D.I. DNN-Based Slip Ratio Estimator for Lugged-Wheel Robot Localization in Rough Deformable Terrains. IEEE Access 2023, 11, 53468–53484. [Google Scholar] [CrossRef]
- Sun, X.; Quan, Z.; Cai, Y.; Chen, L.; Li, B. Intelligent Tire Slip Angle Estimation Based on Sensor Targeting Configuration. IEEE Trans. Instrum. Meas. 2024, 73, 9503016. [Google Scholar] [CrossRef]
- Tang, T.Y.; Yoon, D.J.; Pomerleau, F.; Barfoot, T.D. Learning a Bias Correction for Lidar-Only Motion Estimation. In Proceedings of the 2018 15th Conference on Computer and Robot Vision, Toronto, ON, Canada, 8–10 May 2018; pp. 166–173. [Google Scholar]
- Yao, S.; Li, H.; Wang, K.; Zhang, X. High-Accuracy Calibration of a Visual Motion Measurement System for Planar 3-DOF Robots Using Gaussian Process. IEEE Sens. J. 2019, 19, 7659–7667. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, C.; Ren, M. An Enhanced Hybrid Visual–Inertial Odometry System for Indoor Mobile Robot. Sensors 2022, 22, 2930. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Wu, X.; Sun, J.; Qiao, N.; Sun, C. Multi-Stage Refinement Feature Matching Using Adaptive ORB Features for Robotic Vision Navigation. IEEE Sens. J. 2022, 22, 2603–2617. [Google Scholar] [CrossRef]
- Li, A.; Wang, J.; Xu, M.; Chen, Z. DP-SLAM: A visual SLAM with moving probability towards dynamic environments. Inf. Sci. 2021, 556, 128–142. [Google Scholar] [CrossRef]
- Reginald, N.; Al-Buraiki, O.; Fidan, B.; Hashemi, E. Confidence Estimator Design for Dynamic Feature Point Removal in Robot Visual-Inertial Odometry. In Proceedings of the 48th Annual Conf. of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Zhi, M.; Deng, C.; Zhang, H.; Tang, H.; Wu, J.; Li, B. RNGC-VIWO: Robust Neural Gyroscope Calibration Aided Visual-Inertial-Wheel Odometry for Autonomous Vehicle. Remote Sens. 2023, 15, 4292. [Google Scholar] [CrossRef]
- Hua, T.; Li, T.; Pei, L. PIEKF-VIWO: Visual-Inertial-Wheel Odometry using Partial Invariant Extended Kalman Filter. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 2083–2090. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Z.; Lv, Z.; Zhou, C.; Wu, P.; Zhu, C.; Liu, W. Research on Positioning Accuracy of Mobile Robot in Indoor Environment Based on Improved RTABMAP Algorithm. Sensors 2023, 23, 9468. [Google Scholar] [CrossRef]
- Onyekpe, U.; Palade, V.; Kanarachos, S.; Christopoulos, S.R.G. Learning Uncertainties in Wheel Odometry for Vehicular Localisation in GNSS Deprived Environments. In Proceedings of the 19th IEEE International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 14–17 December 2020; pp. 741–746. [Google Scholar] [CrossRef]
- Deraz, A.A.; Badawy, O.; Elhosseini, M.A.; Mostafa, M.; Ali, H.A.; El-Desouky, A.I. Deep learning based on LSTM model for enhanced visual odometry navigation system. Ain Shams Eng. J. 2023, 14, 102050. [Google Scholar] [CrossRef]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. Deepvo: Towards end-to-end visual odometry with deep recurrent convolutional neural networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2043–2050. [Google Scholar]
- Jiao, J.; Jiao, J.; Mo, Y.; Liu, W.; Deng, Z. MagicVO: An end-to-end hybrid CNN and bi-LSTM method for monocular visual odometry. IEEE Access 2019, 7, 94118–94127. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J.; Cheng, Y.; Ni, Q.; Wang, S. Short-Term Solar Power Forecasting Based on Weighted Gaussian Process Regression. IEEE Trans. Ind. Electron. 2018, 65, 300–308. [Google Scholar] [CrossRef]
- Saleem, H.; Malekian, R.; Munir, H. Neural Network-Based Recent Research Developments in SLAM for Autonomous Ground Vehicles: A Review. IEEE Sens. J. 2023, 23, 13829–13858. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Ding, W.; Zhao, J. A Novel Visual Inertial Odometry Based on Interactive Multiple Model and Multistate Constrained Kalman Filter. IEEE Trans. Instrum. Meas. 2024, 73, 5000110. [Google Scholar] [CrossRef]
- Castro-Toscano, M.J.; Rodríguez-Quiñonez, J.C.; Hernández-Balbuena, D.; Lindner, L.; Sergiyenko, O.; Rivas-Lopez, M.; Flores-Fuentes, W. A methodological use of inertial navigation systems for strapdown navigation task. In Proceedings of the IEEE 26th International Symposium on Industrial Electronics, Edinburgh, UK, 19–21 June 2017; pp. 1589–1595. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Quan, M.; Piao, S.; Tan, M.; Huang, S.S. Tightly-Coupled Monocular Visual-Odometric SLAM Using Wheels and a MEMS Gyroscope. IEEE Access 2019, 7, 97374–97389. [Google Scholar] [CrossRef]
- Li, M.; Mourikis, A.I. Improving the accuracy of EKF-based visual-inertial odometry. In Proceedings of the IEEE International Conference on Robotics and Automation (TCRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 828–835. [Google Scholar] [CrossRef]
- Chatfield, A.B. Fundamentals of High Accuracy Inertial Navigation; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1997. [Google Scholar]
- Geneva, P.; Eckenhoff, K.; Lee, W.; Yang, Y.; Huang, G. OpenVINS: A Research Platform for Visual-Inertial Estimation. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 4666–4672. [Google Scholar]
- Carlevaris-Bianco, N.; Ushani, A.K.; Eustice, R.M. University of Michigan North Campus long-term vision and lidar dataset. Int. J. Robot. Res. 2016, 35, 1023–1035. [Google Scholar] [CrossRef]
- Tronarp, F.; Karvonen, T.; Särkkä, S. Mixture representation of the Matern class with applications in state space approximations and Bayesian quadrature. In Proceedings of the IEEE 28th International Workshop on Machine Learning for Signal Processing, Aalborg, Denmark, 17–20 September 2018; pp. 1–6. [Google Scholar]
- Wilson, A.G.; Hu, Z.; Salakhutdinov, R.; Xing, E.P. Deep Kernel Learning. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; Gretton, A., Robert, C.C., Eds.; Proceedings of Machine Learning Research. Volume 51, pp. 370–378.
- Uber AI Labs. Pyro: Deep Universal Probabilistic Programming; Uber AI Labs: San Francisco, CA, USA, 2023. [Google Scholar]
- Jeong, J.; Cho, Y.; Shin, Y.S.; Roh, H.; Kim, A. Complex Urban Dataset with Multi-level Sensors from Highly Diverse Urban Environments. Int. J. Robot. Res. 2019, 38, 642–657. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; Bengio, Y., LeCun, Y., Eds.; [Google Scholar]
- Macenski, S.; Foote, T.; Gerkey, B.; Lalancette, C.; Woodall, W. Robot Operating System 2: Design, architecture, and uses in the wild. Sci. Robot. 2022, 7, eabm6074. [Google Scholar] [CrossRef]








| Training Parameter | Value |
|---|---|
| Optimizer | Adam |
| Learning rate | 0.01 |
| No. of epochs | 100 |
| sample rate | 100 Hz |
| Kernel length parameter | 1 |
| Sensor | Manufacturer | Model | Description | Freq. (Hz) |
|---|---|---|---|---|
| Camera | Pointgray | Flea3 | 1600 × 1200 color, 59 FPS | 10 |
| IMU | Xsens | MTi-300 | Enhanced AHRS Gyro | 100 |
| wheel encoder | RLS | LM13 | Magnetic rotary encoder | 100 |
| Method | MATE [m] | MRTE [Degree] |
|---|---|---|
| VIWO uncorrected | 11.45 | 2.526 |
| VIWO with DPE | 9.13 | 1.912 |
| VIWO with DPE and CNN GPR | 6.04 | 1.279 |
| VIWO with DPE and RNN GPR | 5.45 | 1.079 |
| Sensor | Description | Frequency |
|---|---|---|
| Camera | Intel realsense T265 | 10 fps |
| IMU | 400 Hz | |
| Wheel encoders | 78,000 pulses/m quadrature | 100 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reginald, N.; Al-Buraiki, O.; Choopojcharoen, T.; Fidan, B.; Hashemi, E. Visual-Inertial-Wheel Odometry with Slip Compensation and Dynamic Feature Elimination. Sensors 2025, 25, 1537. https://doi.org/10.3390/s25051537
Reginald N, Al-Buraiki O, Choopojcharoen T, Fidan B, Hashemi E. Visual-Inertial-Wheel Odometry with Slip Compensation and Dynamic Feature Elimination. Sensors. 2025; 25(5):1537. https://doi.org/10.3390/s25051537
Chicago/Turabian StyleReginald, Niraj, Omar Al-Buraiki, Thanacha Choopojcharoen, Baris Fidan, and Ehsan Hashemi. 2025. "Visual-Inertial-Wheel Odometry with Slip Compensation and Dynamic Feature Elimination" Sensors 25, no. 5: 1537. https://doi.org/10.3390/s25051537
APA StyleReginald, N., Al-Buraiki, O., Choopojcharoen, T., Fidan, B., & Hashemi, E. (2025). Visual-Inertial-Wheel Odometry with Slip Compensation and Dynamic Feature Elimination. Sensors, 25(5), 1537. https://doi.org/10.3390/s25051537







