A Comparative Study of Plantar Pressure and Inertial Sensors for Cross-Country Ski Classification Using Deep Learning
Abstract
1. Introduction
Related Works
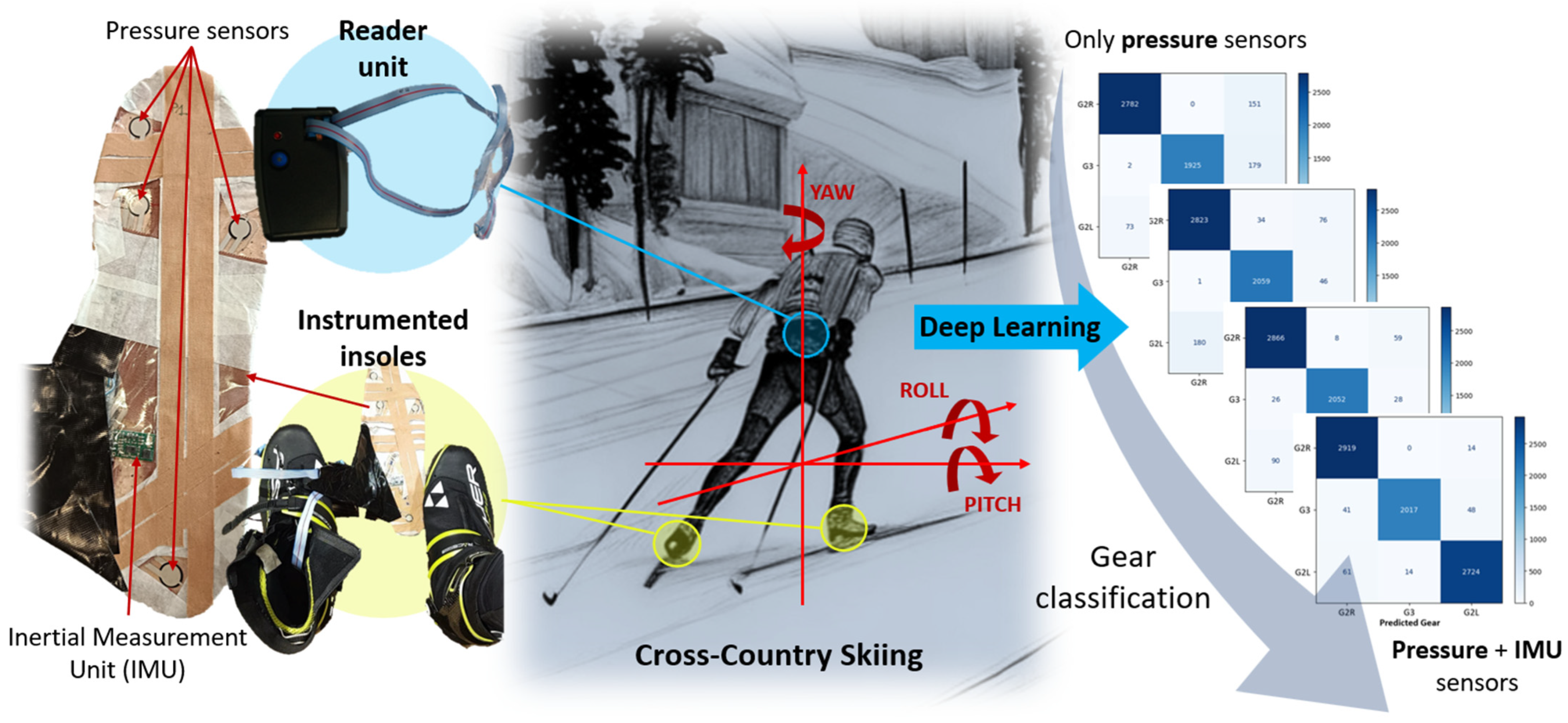
2. Materials and Methods
2.1. Experimental Setup
2.2. Sensor Combinations
- No pressure sensors (0P); only one (A), two (AG), or three (AGM) inertial sensors:
- ○
- 0P + A: The input to the deep learning model is the output of the 3D accelerometer (A).
- ○
- 0P + AG: The outputs of the accelerometer (A) and gyroscope (G) were considered.
- ○
- 0P + AGM: All the inertial sensors: accelerometer (A), gyroscope (G), and magnetometer (M), were considered.
- Combinations of two pressure sensors (2P) without inertial sensors:
- ○
- 2P.1m5m: Involving the first (1 m) and fifth metatarsals (5 m) sensors.
- ○
- 2P.1mH: Considering the first metatarsal (1 m) and heel (H) sensors.
- ○
- 2P.5mH: Considering the fifth metatarsal (5 m) and heel (H) sensors.
- Combinations of two pressure sensors on the first and fifth metatarsals (2P.1m5m) with one, two, or three inertial sensors:
- ○
- 2P.1m5m + A: Combination of 2P.1m5m plus A.
- ○
- 2P.1m5m + AG: Combination 2P.1m5m plus A and G.
- ○
- 2P.1m5m + AGM: Combination 2P.1m5m plus A, G, and M.
- Combinations of two pressure sensors on the first metatarsal and heel (2P.1mH) with one, two, or three inertial sensors:
- ○
- 2P.1mH + A: Combination of 2P.1mH plus A.
- ○
- 2P.1mH + AG: Combination 2P.1mH plus A and G.
- ○
- 2P.1mH + AGM: Combination 2P.1mH plus A, G, and M.
- Combinations of two pressure sensors on the fifth metatarsal and the heel (2P.5mH) with one, two, or three inertial sensors (A, AG, or AGM):
- ○
- 2P.5mH + A: Combination of 2P.5mH plus A.
- ○
- 2P.5mH + AG: Combination 2P.5mH plus A and G.
- ○
- 2P.5mH + AGM: Combination 2P.5mH plus A, G, and M.
- Three pressure sensors (3P) without inertial sensors:
- ○
- 3P.1m5mH: Involving the first and fifth metatarsals and the heel sensor.
- Three pressure sensors on the first and fifth metatarsals and the heel (3P.1m5mH) with one, two, or three inertial sensors:
- ○
- 3P.1m5mH + A: Combination of 3P.1m5mH plus A.
- ○
- 3P.1m5mH + AG: Combination of 3P.1m5mH plus A and G.
- ○
- 3P.1m5mH + AGM: Combination of 3P.1m5mH plus A, G, and M.
- Four pressure sensors (4P) without inertial sensors:
- ○
- 4P: All pressure sensors, involving the first and the fifth metatarsals, heel, and big toe sensors.
- Four pressure sensors (4P) with one, two, or three inertial sensors:
- ○
- 4P + A: Combination of 4P plus A.
- ○
- 4P + AG: Combination of 4P plus A and G.
- ○
- 4P + AGM: Combination of 4P plus A, G, and M.
2.3. Data Curation and Segmentation
2.4. Deep Learning Model for Ski-Gear Classification
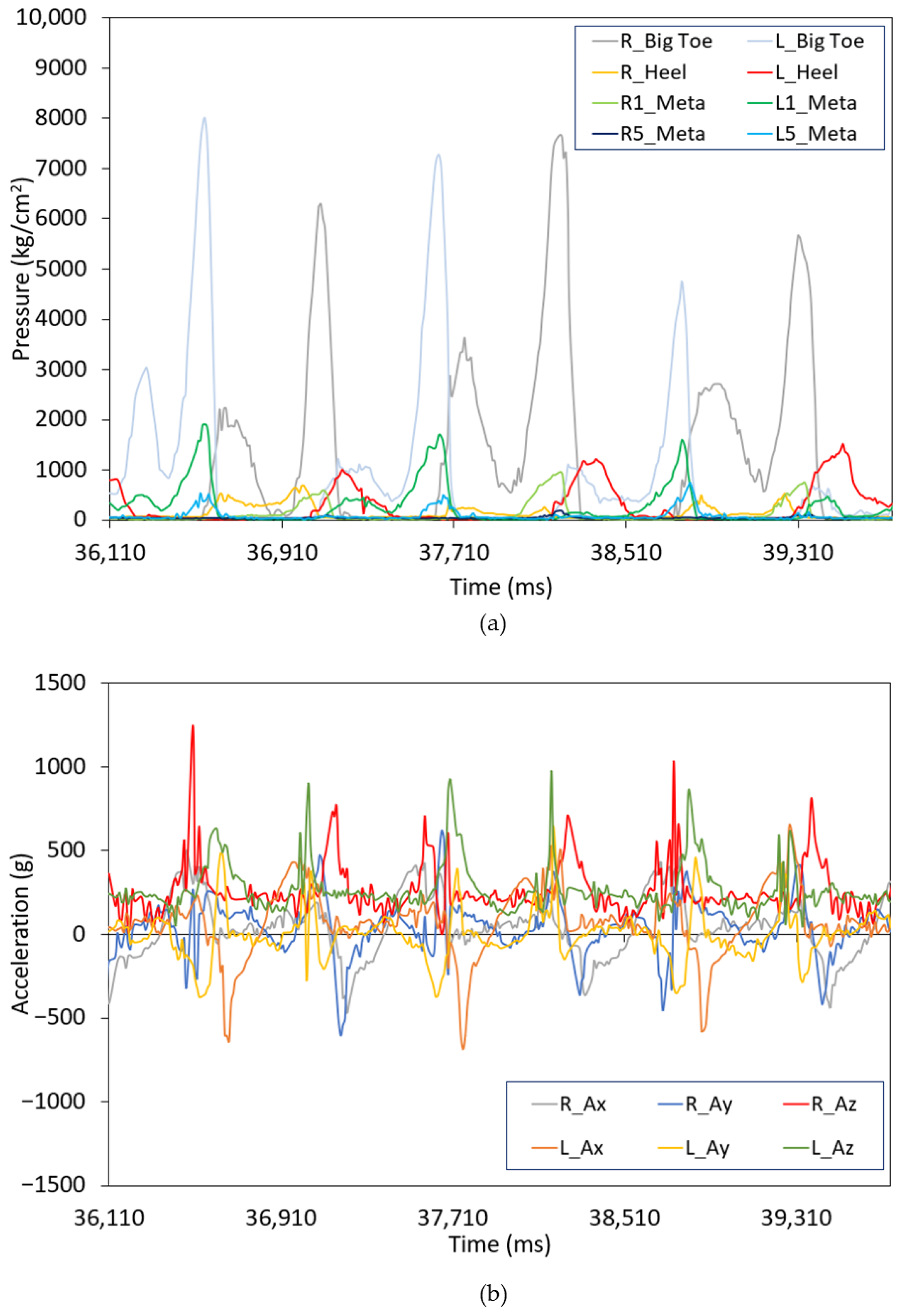
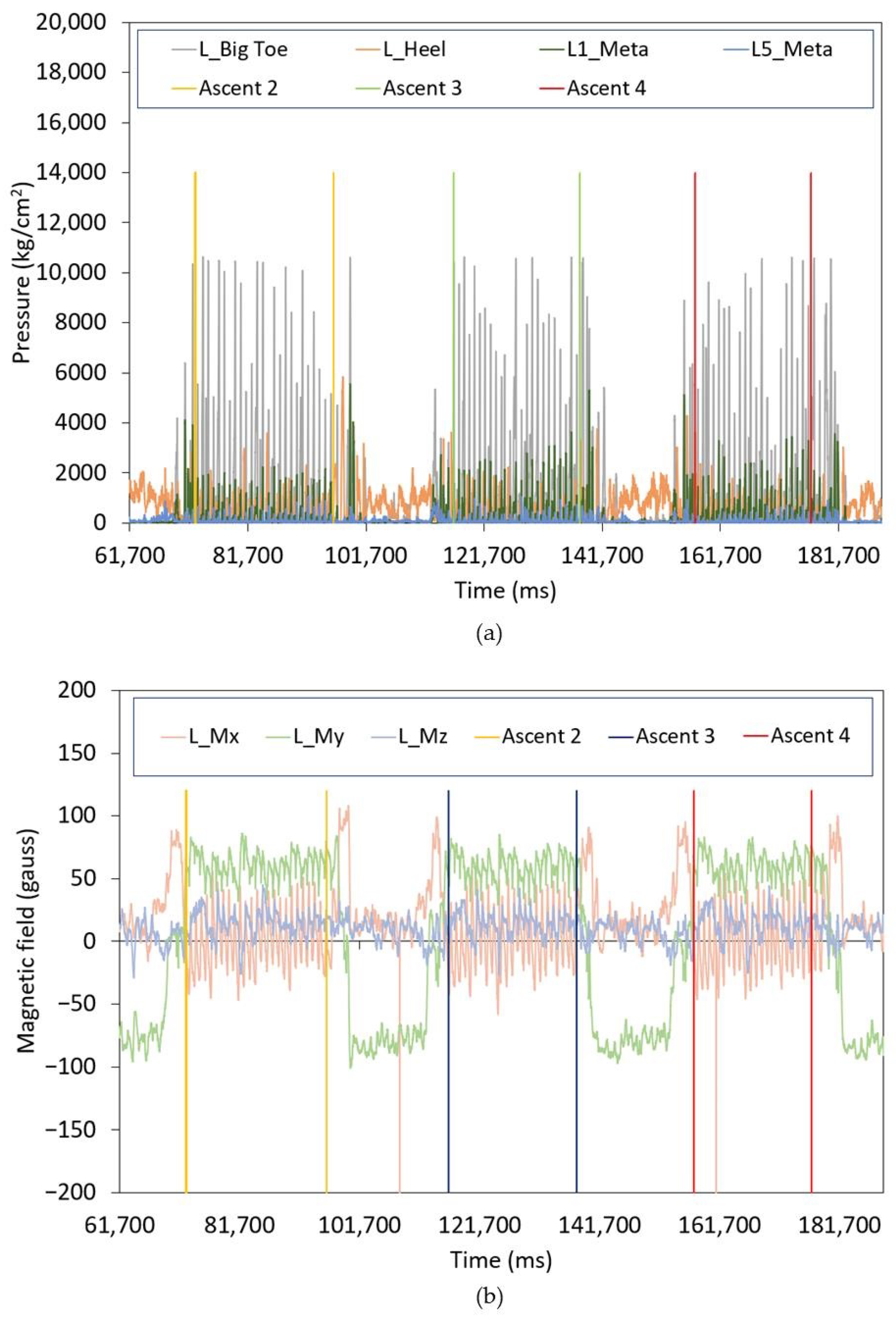
- R1_Meta and L1_Meta: Pressure data from the first metatarsal for the right and left foot, respectively.
- R5_Meta or L5_Meta: Pressure data from the fifth metatarsal for the right and left foot, respectively.
- R_Heel or L_Heel: Pressure data from the heel for the right and left foot, respectively.
- R_Big Toe or L_Big Toe: Pressure data from the big toe for the right and left foot, respectively (measured in kg/cm2).
- R_Gx, R_Gy, R_Gz, L_Gx, L_Gy and L_Gz: Gravitational acceleration components along the X, Y, and Z axes for the right and left foot, respectively.
- R_Ax, R_Ay, R_Az, L_Ax, L_Ay and L_Az: Dynamic acceleration components along the X, Y, and Z axes for the right and left foot, respectively.
- R_Mx, R_My, R_Mz, L_Mx, L_My and L_Mz: Acceleration components of the foot in relation to the magnetic field along the X, Y, and Z axes for the right and left foot, respectively, during activity.
- 1.
- Temporal alignment: All signals were resampled to a fixed frequency using linear interpolation.
- 2.
- Normalization: The pressure sensor values were normalized using min-max scaling.
- 3.
- Feature concatenation: The computed features from both sensor modalities were merged into a single feature vector per time window, which was then input into the deep learning model.
3. Results
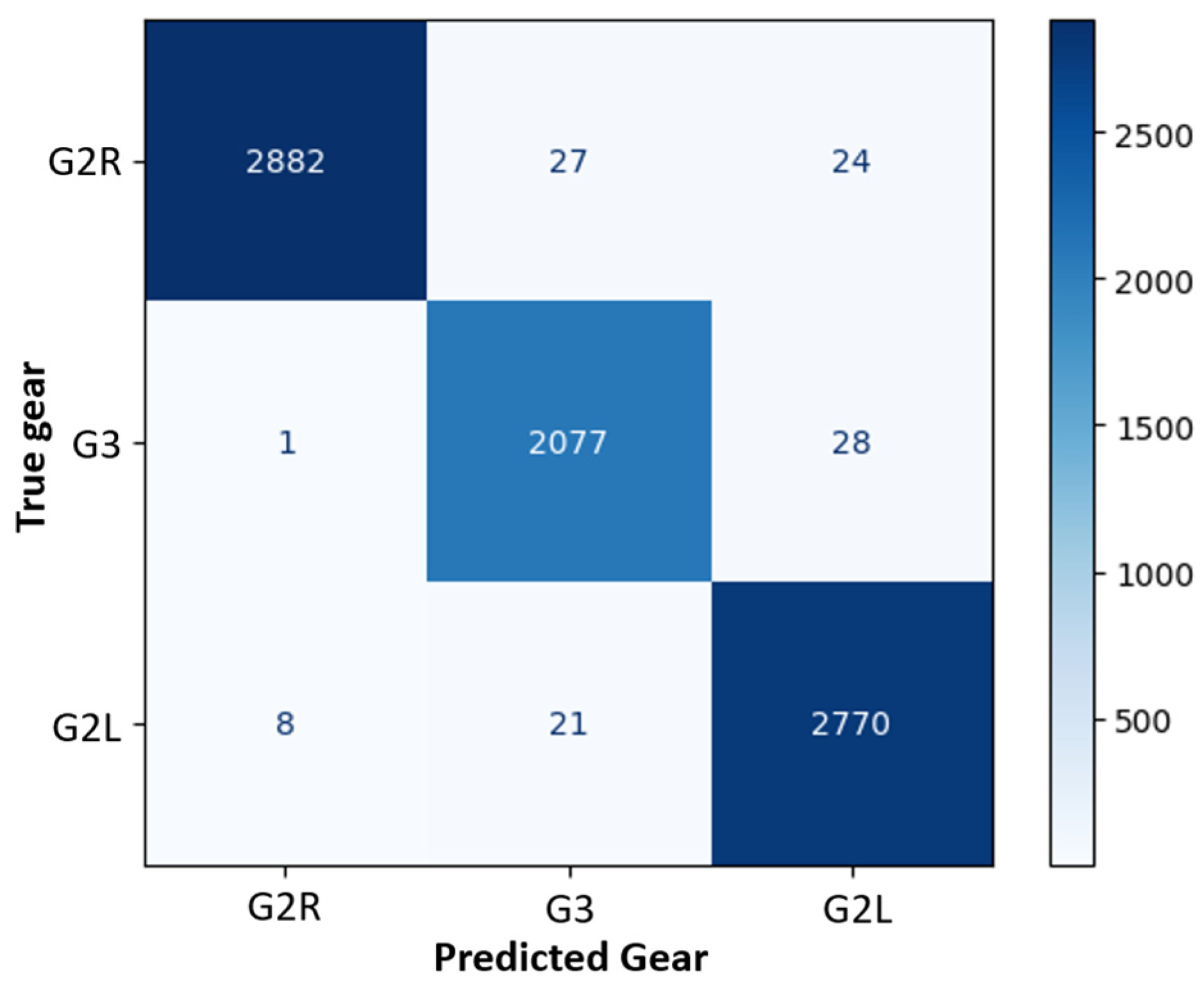
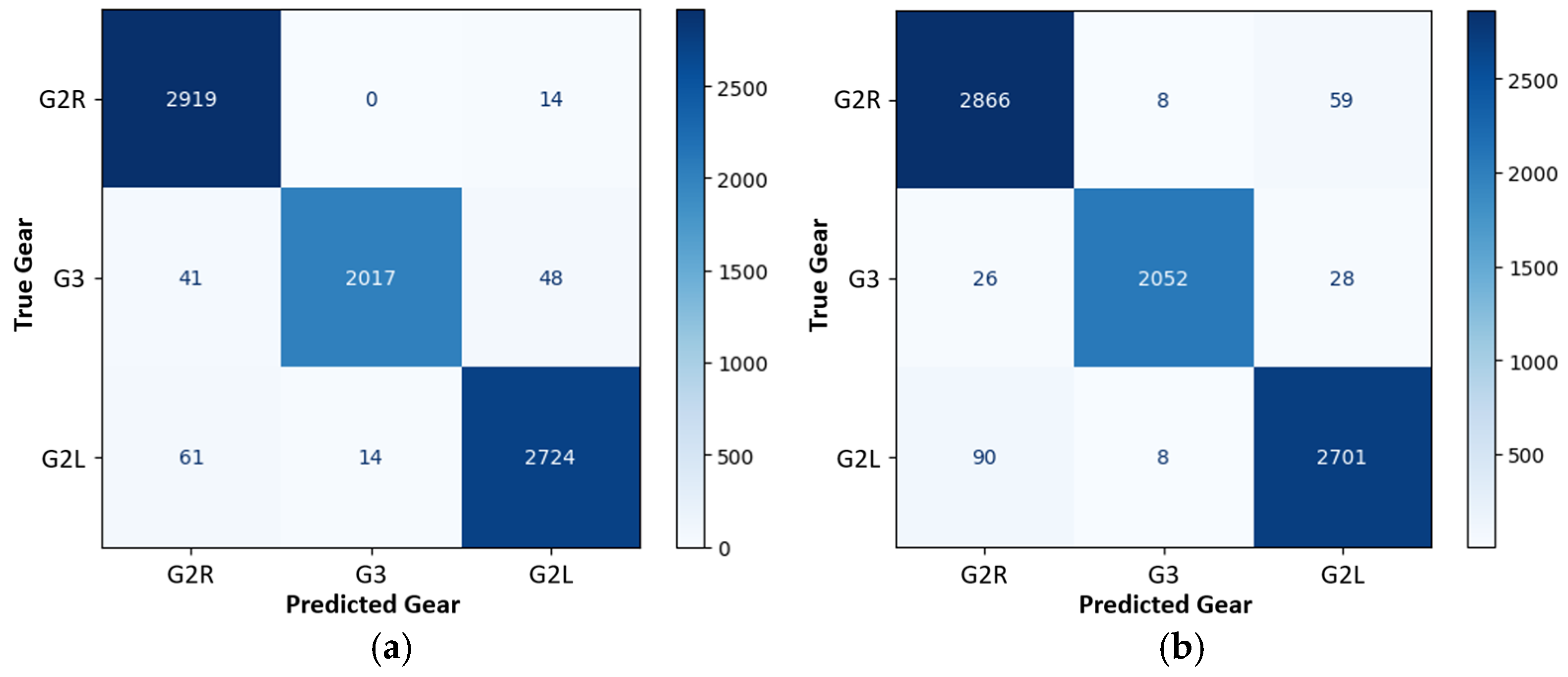
3.1. Classification Using Pressure Sensors
3.2. Classification Using Inertial Sensors
3.3. Classification with Combined Pressure and Inertial Sensors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdul Razak, A.H.; Zayegh, A.; Begg, R.K.; Wahab, Y. Foot Plantar Pressure Measurement System: A Review. Sensors 2012, 12, 9884–9912. [Google Scholar] [CrossRef]
- Seeberg, T.M.; Tjønnås, J.; Rindal, O.M.H.; Haugnes, P.; Dalgard, S.; Sandbakk, Ø. A Multi-Sensor System for Automatic Analysis of Classical Cross-Country Skiing Techniques. Sports Eng. 2017, 20, 313–327. [Google Scholar] [CrossRef]
- Howell, A.M.; Kobayashi, T.; Hayes, H.A.; Foreman, K.B.; Bamberg, S.J.M. Kinetic Gait Analysis Using a Low-Cost Insole. IEEE Trans. Biomed. Eng. 2013, 60, 3284–3290. [Google Scholar] [CrossRef]
- Wu, S.; Bin, G.; Shi, W.; Lin, L.; Xu, Y.; Zhao, D.; Morgan, S.P.; Sun, S. Empowering Diabetic Foot Ulcer Prevention: A Novel Cloud-Based Plantar Pressure Monitoring System for Enhanced Self-Care. Technol. Health Care 2024, 09287329241290943. [Google Scholar] [CrossRef]
- Cudejko, T.; Button, K.; Al-Amri, M. Wireless Pressure Insoles for Measuring Ground Reaction Forces and Trajectories of the Centre of Pressure during Functional Activities. Sci. Rep. 2023, 13, 14946. [Google Scholar] [CrossRef]
- Pousibet-Garrido, A.; Polo-Rodríguez, A.; Moreno-Pérez, J.A.; Ruiz-García, I.; Escobedo, P.; López-Ruiz, N.; Marcen-Cinca, N.; Medina-Quero, J.; Carvajal, M.Á. Gear Classification in Skating Cross-Country Skiing Using Inertial Sensors and Deep Learning. Sensors 2024, 24, 6422. [Google Scholar] [CrossRef]
- Nakazato, K.; Scheiber, P.; Müller, E. Comparison between the Force Application Point Determined by Portable Force Plate System and the Center of Pressure Determined by Pressure Insole System during Alpine Skiing. Sports Eng. 2013, 16, 297–307. [Google Scholar] [CrossRef]
- Pavailler, S.; Hintzy, F.; Millet, G.Y.; Horvais, N.; Samozino, P. Glide Time Relates to Mediolateral Plantar Pressure Distribution Rather Than Ski Edging in Ski Skating. Front. Sports Act. Living 2020, 2, 117. [Google Scholar] [CrossRef]
- Chen, J.-L.; Dai, Y.-N.; Grimaldi, N.S.; Lin, J.-J.; Hu, B.-Y.; Wu, Y.-F.; Gao, S. Plantar Pressure-Based Insole Gait Monitoring Techniques for Diseases Monitoring and Analysis: A Review. Adv. Mater. Technol. 2022, 7, 2100566. [Google Scholar] [CrossRef]
- Pineda-Lopez, F.; Guerra, A.; Montes, E.; Benitez, D.S. A Low Cost Baropodometric System for Children’s Postural and Gait Analysis. In Proceedings of the 2016 IEEE Colombian Conference on Communications and Computing (COLCOM), Cartagena, Colombia, 27–29 April 2016; pp. 1–4. [Google Scholar]
- Zhang, Z.; Xu, Z.; Chen, W.; Gao, S. Comparison between Piezoelectric and Piezoresistive Wearable Gait Monitoring Techniques. Materials 2022, 15, 4837. [Google Scholar] [CrossRef] [PubMed]
- Ayena, J.C.; Chapwouo T, L.D.; Otis, M.J.-D.; Menelas, B.-A.J. An Efficient Home-Based Risk of Falling Assessment Test Based on Smartphone and Instrumented Insole. In Proceedings of the 2015 IEEE International Symposium on Medical Measurements and Applications (MeMeA) Proceedings, Turin, Italy, 7–9 May 2015; pp. 416–421. [Google Scholar]
- Bamberg, S.J.M.; LaStayo, P.; Dibble, L.; Musselman, J.; Raghavendra, S.K.D. Development of a Quantitative In-Shoe Measurement System for Assessing Balance: Sixteen-Sensor Insoles. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 6041–6044. [Google Scholar]
- Biomechanics|Tekscan. Available online: https://www.tekscan.com/products-solutions/biomechanics (accessed on 10 January 2025).
- Paromed Australia—Home. Available online: https://www.paromed.com.au/ (accessed on 10 January 2025).
- Estimating CoP Trajectories and Kinematic Gait Parameters in Walking and Running Using Instrumented Insoles|IEEE Journals & Magazine|IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/7962151 (accessed on 10 January 2025).
- Mahalingam, S.; Mahendra, S.J.; Sanjay, H.S.; Hiremath, B. Integration of Gyroscopes and Force Sensitive Resistors for Gait Analysis of Lower Limb Injury Rehabilitation; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Pardoel, S.; Shalin, G.; Nantel, J.; Lemaire, E.D.; Kofman, J. Early Detection of Freezing of Gait during Walking Using Inertial Measurement Unit and Plantar Pressure Distribution Data. Sensors 2021, 21, 2246. [Google Scholar] [CrossRef]
- Matsumura, S.; Ohta, K.; Yamamoto, S.; Koike, Y.; Kimura, T. Comfortable and Convenient Turning Skill Assessment for Alpine Skiers Using IMU and Plantar Pressure Distribution Sensors. Sensors 2021, 21, 834. [Google Scholar] [CrossRef]
- Moticon. OpenGo Sensor Insoles—Wireless Pressure, Force & Motion Sensing. Available online: https://moticon.com/opengo/sensor-insoles (accessed on 26 January 2025).
- Stöggl, T.; Martiner, A. Validation of Moticon’s OpenGo Sensor Insoles during Gait, Jumps, Balance and Cross-Country Skiing Specific Imitation Movements. J. Sports Sci. 2017, 35, 196–206. [Google Scholar] [CrossRef]
- XON SKI-1|Cerevo. Available online: https://xon.cerevo.com/en/ski-1/ (accessed on 26 January 2025).
- Hua, R.; Wang, Y. A Customized Convolutional Neural Network Model Integrated With Acceleration-Based Smart Insole Toward Personalized Foot Gesture Recognition. IEEE Sens. Lett. 2020, 4, 5500704. [Google Scholar] [CrossRef]
- Agrawal, D.K.; Usaha, W.; Pojprapai, S.; Wattanapan, P. Fall Risk Prediction Using Wireless Sensor Insoles with Machine Learning. IEEE Access 2023, 11, 23119–23126. [Google Scholar] [CrossRef]
- Wang, C.; Evans, K.; Hartley, D.; Morrison, S.; Veidt, M.; Wang, G. A Systematic Review of Artificial Neural Network Techniques for Analysis of Foot Plantar Pressure. Biocybern. Biomed. Eng. 2024, 44, 197–208. [Google Scholar] [CrossRef]
- Zhang, Y.; Fei, Q.; Chen, Z.; Liu, X. Estimation of Normal Ground Reaction Forces in Multiple Treadmill Skiing Movements Using IMU Sensors With Optimized Locations. IEEE Sens. J. 2024, 24, 25972–25985. [Google Scholar] [CrossRef]
- Qi, J.; Li, D.; Zhang, C.; Wang, Y. Alpine Skiing Tracking Method Based on Deep Learning and Correlation Filter. IEEE Access 2022, 10, 39248–39260. [Google Scholar] [CrossRef]
- Dong, W.; Sheng, K.; Huang, B.; Xiong, K.; Liu, K.; Cheng, X. Stretchable Self-Powered TENG Sensor Array for Human-Robot Interaction Based on Conductive Ionic Gels and LSTM Neural Network. IEEE Sens. J. 2024, 24, 37962–37969. [Google Scholar] [CrossRef]
- Marsland, F.; Mackintosh, C.; Holmberg, H.-C.; Anson, J.; Waddington, G.; Lyons, K.; Chapman, D. Full Course Macro-Kinematic Analysis of a 10 Km Classical Cross-Country Skiing Competition. PLoS ONE 2017, 12, e0182262. [Google Scholar] [CrossRef]
- Johansson, M.; Korneliusson, M.; Lawrence, N.L. Identifying Cross Country Skiing Techniques Using Power Meters in Ski Poles. In Nordic Artificial Intelligence Research and Development; Bach, K., Ruocco, M., Eds.; Communications in Computer and Information Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 1056, pp. 52–57. ISBN 978-3-030-35663-7. [Google Scholar]
- Meyer, F.; Lund-Hansen, M.; Kocbach, J.; Seeberg, T.M.; Sandbakk, Ø.B.; Austeng, A. Inertial Sensor-Based Estimation of Temporal Events in Skating Sub-Techniques While In-Field Roller Skiing. J. Appl. Biomech. 2023, 39, 204–208. [Google Scholar] [CrossRef]
- Ohtonen, O.; Lindinger, S.; Lemmettylä, T.; Seppälä, S.; Linnamo, V. Validation of Portable 2D Force Binding Systems for Cross-Country Skiing. Sports Eng. 2013, 16, 281–296. [Google Scholar] [CrossRef]
- Nilsson, J.; Tveit, P.; Eikrehagen, O. Effects of Speed on Temporal Patterns in Classical Style and Freestyle Cross-Country Skiing. Sports Biomech. 2004, 3, 85–107. [Google Scholar] [CrossRef]
- Andersson, E.; Supej, M.; Sandbakk, Ø.; Sperlich, B.; Stöggl, T.; Holmberg, H.-C. Analysis of Sprint Cross-Country Skiing Using a Differential Global Navigation Satellite System. Eur. J. Appl. Physiol. 2010, 110, 585–595. [Google Scholar] [CrossRef]
- Torvik, P.-Ø.; von Heimburg, E.D.; Sende, T.; Welde, B. The Effect of Pole Length on Physiological and Perceptual Responses during G3 Roller Ski Skating on Uphill Terrain. PLoS ONE 2019, 14, e0211550. [Google Scholar] [CrossRef]
- Stöggl, T.; Holst, A.; Jonasson, A.; Andersson, E.; Wunsch, T.; Norström, C.; Holmberg, H.-C. Automatic Classification of the Sub-Techniques (Gears) Used in Cross-Country Ski Skating Employing a Mobile Phone. Sensors 2014, 14, 20589–20601. [Google Scholar] [CrossRef]
- Sakurai, Y.; Fujita, Z.; Ishige, Y. Automatic Identification of Subtechniques in Skating-Style Roller Skiing Using Inertial Sensors. Sensors 2016, 16, 473. [Google Scholar] [CrossRef]
- Rindal, O.M.H.; Seeberg, T.M.; Tjønnås, J.; Haugnes, P.; Sandbakk, Ø. Automatic Classification of Sub-Techniques in Classical Cross-Country Skiing Using a Machine Learning Algorithm on Micro-Sensor Data. Sensors 2018, 18, 75. [Google Scholar] [CrossRef]
- Polo-Rodríguez, A.; Martínez-Martí, F.; Marcen, N.; Carvajal, M.A.; Medina-Quero, J.; Martínez-García, M.S. Evaluation of Plantar Pressure Sensors for Classification of Ski Gear Using Deep Learning Models. In Proceedings of the International Conference on Ubiquitous Computing and Ambient Intelligence (UCAmI 2024), Northern Ireland, UK, 27–29 November 2024; Bravo, J., Nugent, C., Cleland, I., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 655–665. [Google Scholar]
- Martínez-Martí, F.; Latorre-Román, P.A.; Martínez-García, M.S.; Soto-Hermoso, V.M.; Carvajal, M.A.; López-Bedoya, J.; Palma, A.J. Acute Effects of Muscular Fatigue on Vertical Jump Performance in Acrobatic Gymnasts, Evaluated by Instrumented Insoles: A Pilot Study. J. Sens. 2021, 2021, 8849100. [Google Scholar] [CrossRef]
- Martínez-Martí, F.; González-Montesinos, J.L.; Morales, D.P.; Santos, J.R.F.; Castro-Piñero, J.; Carvajal, M.A.; Palma, A.J. Validation of Instrumented Insoles for Measuring Height in Vertical Jump. Int. J. Sports Med. 2016, 37, 374–381. [Google Scholar] [CrossRef]
- Martínez-Martí, F.; Martínez-García, M.S.; García-Díaz, S.G.; García-Jiménez, J.; Palma, A.J.; Carvajal, M.A. Embedded Sensor Insole for Wireless Measurement of Gait Parameters. Australas. Phys. Eng. Sci. Med. 2014, 37, 25–35. [Google Scholar] [CrossRef]
- Bötzel, K.; Marti, F.M.; Rodríguez, M.Á.C.; Plate, A.; Vicente, A.O. Gait Recording with Inertial Sensors—How to Determine Initial and Terminal Contact. J. Biomech. 2016, 49, 332–337. [Google Scholar] [CrossRef]
- Martínez-Martí, F.; Ocón-Hernández, O.; Martínez-García, M.S.; Torres-Ruiz, F.; Martínez-Olmos, A.; Carvajal, M.A.; Banqueri, J.; Palma, A.J. Plantar Pressure Changes and Their Relationships with Low Back Pain during Pregnancy Using Instrumented Insoles. J. Sens. 2019, 2019, 1567584. [Google Scholar] [CrossRef]

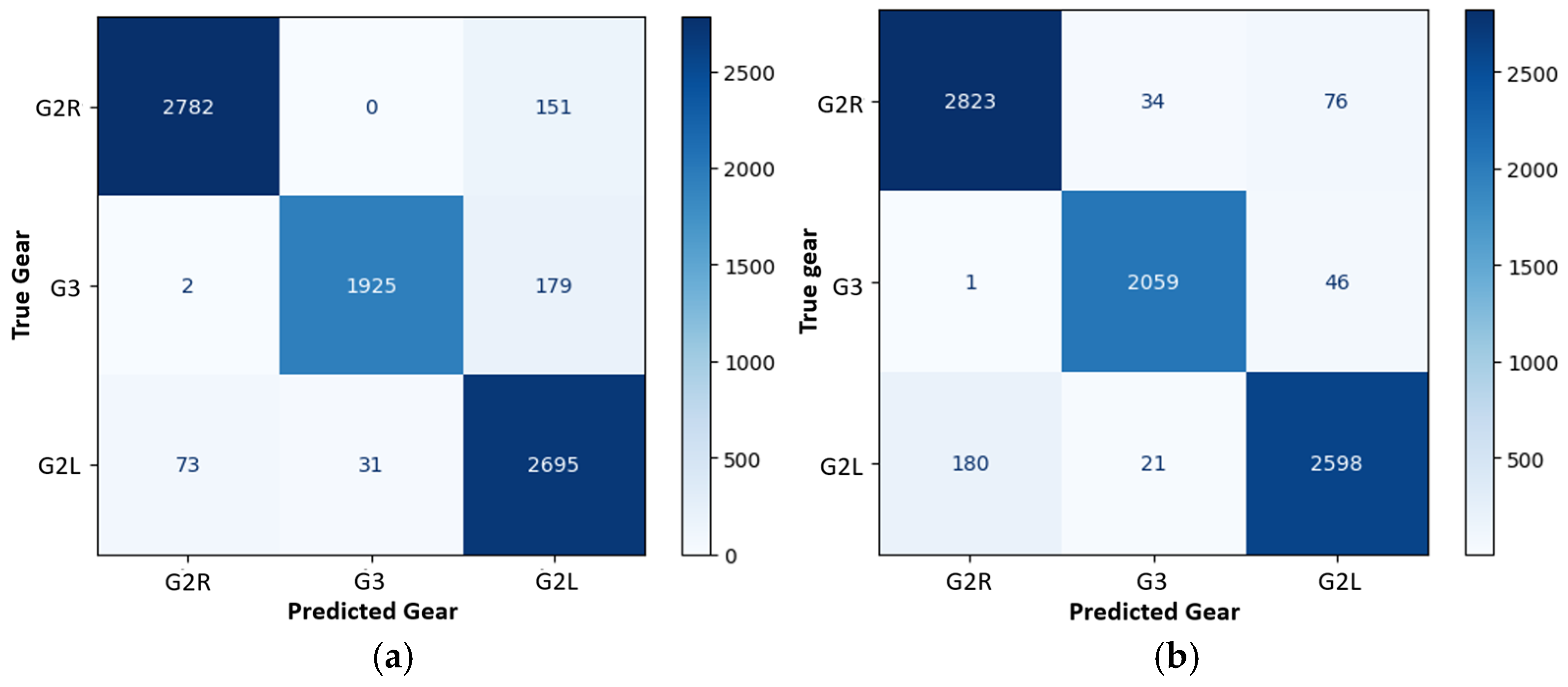
| Weighted Avg Accuracy | Avg (t/epoch) (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pressure Sensors | Inertial Sensors | Inertial Sensors | ||||||||||
| 1 m | 5 m | H | BT | None | A | AG | AGM | None | A | AG | AGM | |
| 0P | -- | 0.97 | 0.98 | 0.99 | 2 | 3 | 5 | |||||
| 2P | × | × | 0.95 | 0.97 | 0.98 | 0.98 | 1 | 2 | 6 | 8 | ||
| × | × | 0.94 | 0.96 | 0.98 | 0.97 | 1 | 2 | 5 | 11 | |||
| × | × | 0.95 | 0.96 | 0.98 | 0.98 | 1 | 3 | 4 | 11 | |||
| 3P | × | × | × | 0.94 | 0.97 | 0.97 | 0.97 | 2 | 3 | 7 | 14 | |
| 4P | × | × | × | × | 0.95 | 0.97 | 0.97 | 0.98 | 3 | 5 | 8 | 17 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| G2R | 0.97 | 0.95 | 0.96 | 2933 |
| G3 | 0.98 | 0.91 | 0.95 | 2106 |
| G2L | 0.89 | 0.96 | 0.93 | 2799 |
| WAA | 0.95 | 0.94 | 0.94 | 7838 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| G2R | 0.94 | 0.96 | 0.95 | 2933 |
| G3 | 0.97 | 0.98 | 0.98 | 2106 |
| G2L | 0.96 | 0.93 | 0.94 | 2799 |
| WAA | 0.95 | 0.95 | 0.95 | 7838 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| G2R | 1.00 | 0.98 | 0.99 | 2933 |
| G3 | 0.98 | 0.99 | 0.98 | 2106 |
| G2L | 0.98 | 0.99 | 0.99 | 2799 |
| WAA | 0.99 | 0.99 | 0.99 | 7838 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| G2R | 0.97 | 1.00 | 0.98 | 2933 |
| G3 | 0.99 | 0.96 | 0.98 | 2106 |
| G2L | 0.98 | 0.97 | 0.98 | 2799 |
| WAA | 0.98 | 0.98 | 0.98 | 7838 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| G2R | 0.96 | 0.98 | 0.97 | 2933 |
| G3 | 0.99 | 0.97 | 0.98 | 2106 |
| G2L | 0.97 | 0.96 | 0.97 | 2799 |
| WAA | 0.97 | 0.97 | 0.97 | 7838 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polo-Rodríguez, A.; Escobedo, P.; Martínez-Martí, F.; Marcen-Cinca, N.; Carvajal, M.A.; Medina-Quero, J.; Martínez-García, M.S. A Comparative Study of Plantar Pressure and Inertial Sensors for Cross-Country Ski Classification Using Deep Learning. Sensors 2025, 25, 1500. https://doi.org/10.3390/s25051500
Polo-Rodríguez A, Escobedo P, Martínez-Martí F, Marcen-Cinca N, Carvajal MA, Medina-Quero J, Martínez-García MS. A Comparative Study of Plantar Pressure and Inertial Sensors for Cross-Country Ski Classification Using Deep Learning. Sensors. 2025; 25(5):1500. https://doi.org/10.3390/s25051500
Chicago/Turabian StylePolo-Rodríguez, Aurora, Pablo Escobedo, Fernando Martínez-Martí, Noel Marcen-Cinca, Miguel A. Carvajal, Javier Medina-Quero, and María Sofía Martínez-García. 2025. "A Comparative Study of Plantar Pressure and Inertial Sensors for Cross-Country Ski Classification Using Deep Learning" Sensors 25, no. 5: 1500. https://doi.org/10.3390/s25051500
APA StylePolo-Rodríguez, A., Escobedo, P., Martínez-Martí, F., Marcen-Cinca, N., Carvajal, M. A., Medina-Quero, J., & Martínez-García, M. S. (2025). A Comparative Study of Plantar Pressure and Inertial Sensors for Cross-Country Ski Classification Using Deep Learning. Sensors, 25(5), 1500. https://doi.org/10.3390/s25051500










