Displacement-Sensing Method Based on Residual Scaling for One-Shot MMF Specklegram Prediction
Abstract
1. Introduction
2. Methods
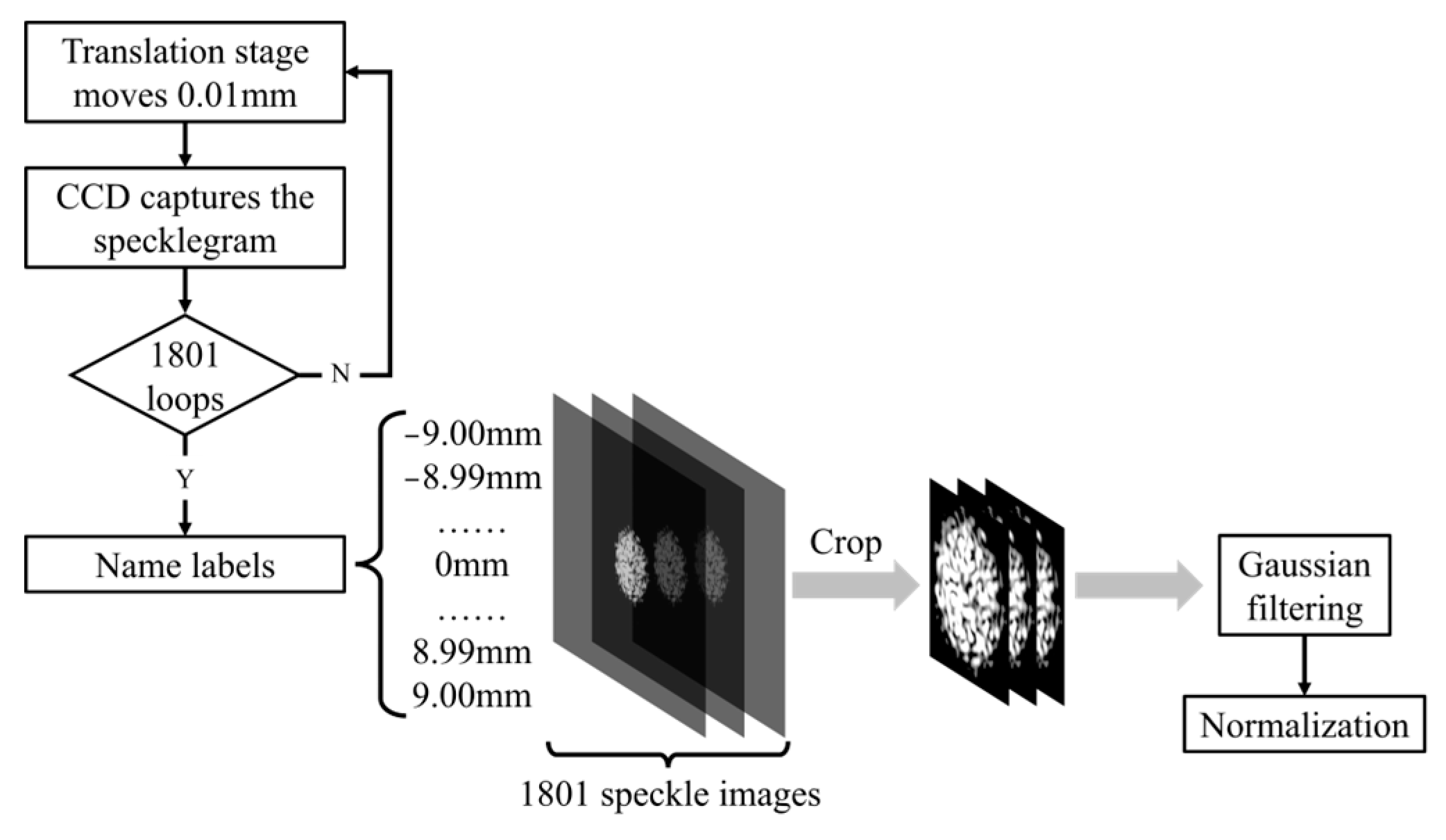
2.1. Experimental Setup and Data Processing
2.2. Model Architecture
3. Results and Analysis
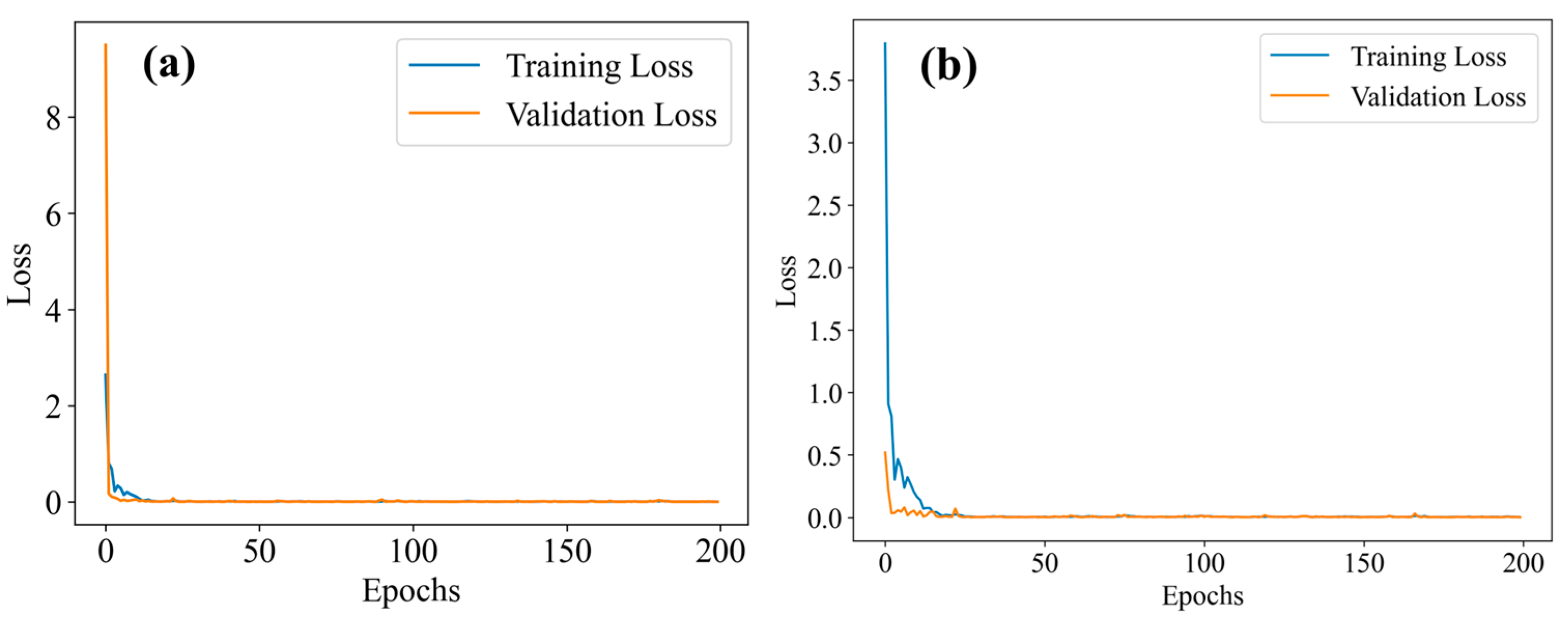
3.1. Experimental Results
3.2. Results
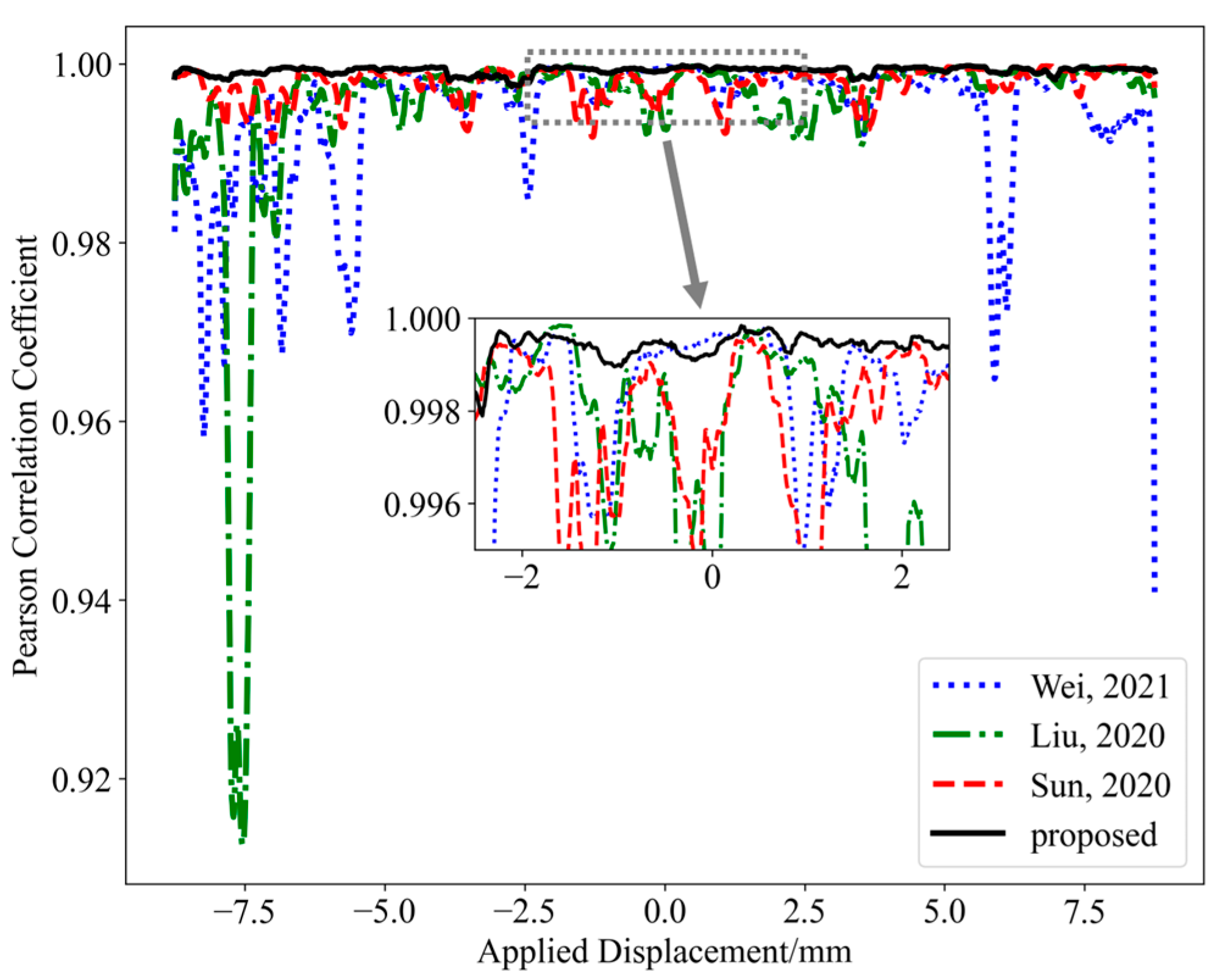
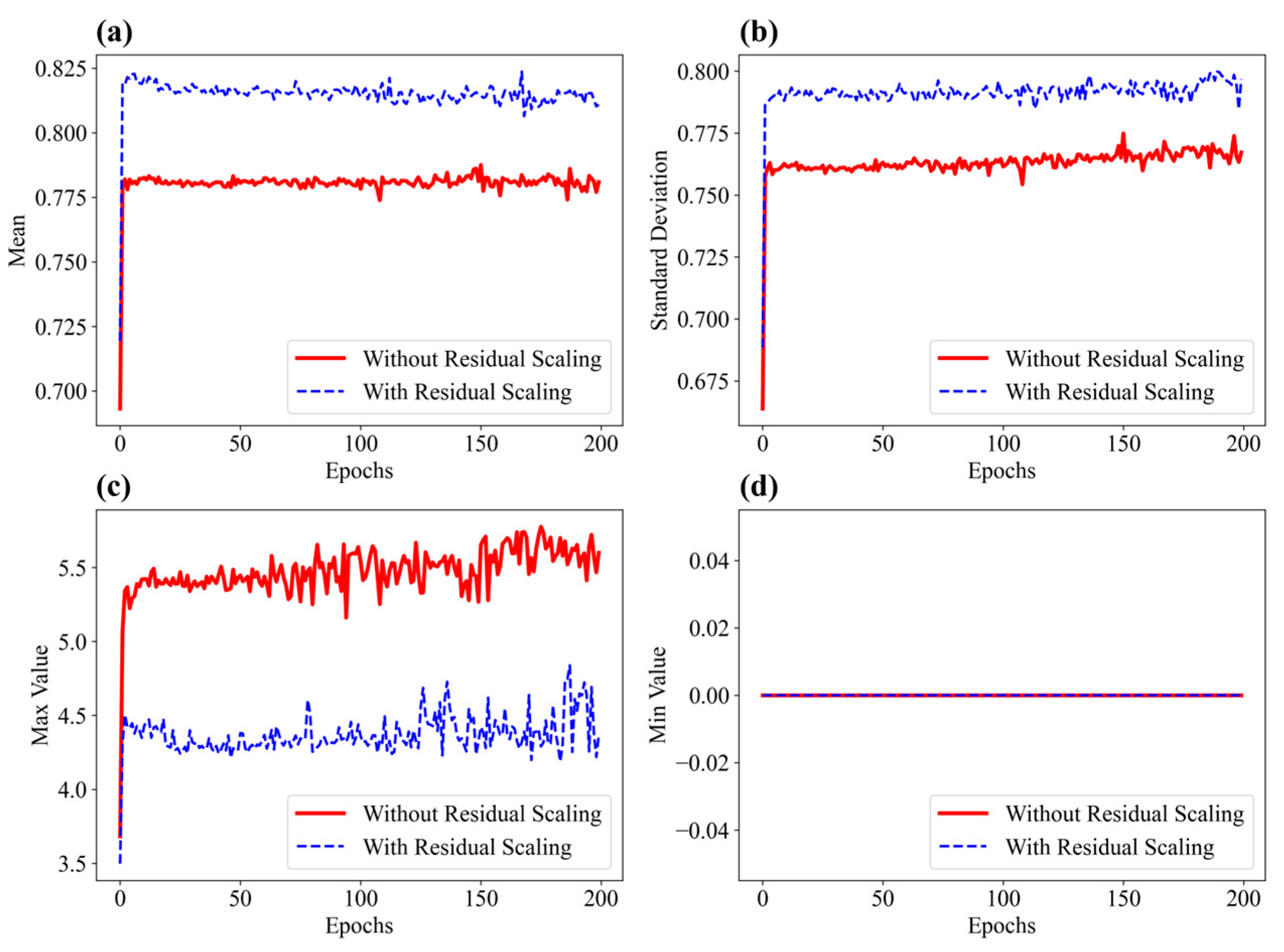
3.3. Analysis of Residual Scaling
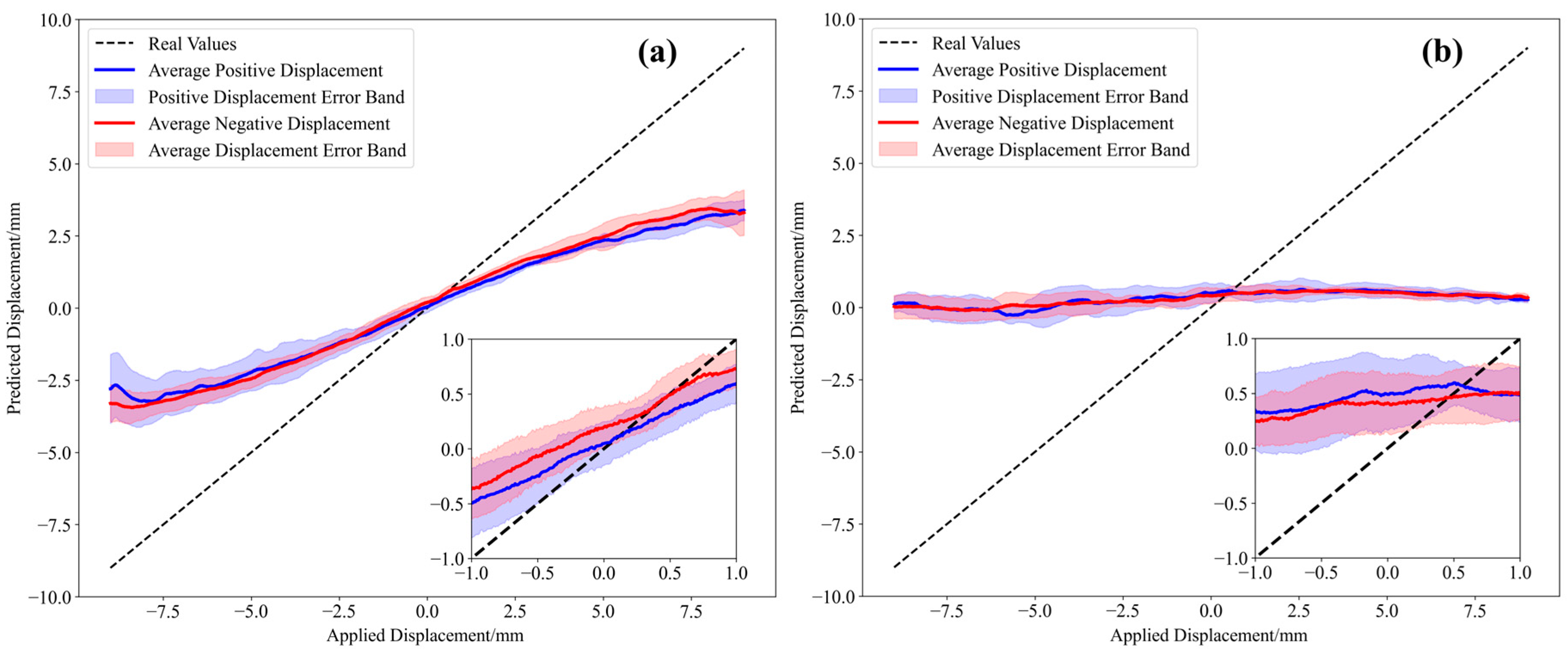
3.4. Generalization Validation
4. Temperature Noise and Immunity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chapalo, I.; Stylianou, A.; Mégret, P.; Theodosiou, A. Advances in Optical Fiber Speckle Sensing: A Comprehensive Review. Photonics 2024, 11, 299. [Google Scholar] [CrossRef]
- Yu, F.T.S.; Wen, M.; Yin, S.; Uang, C.-M. Submicrometer Displacement Sensing Using Inner-Product Multimode Fiber Speckle Fields. Appl. Opt. 1993, 32, 4685. [Google Scholar] [CrossRef] [PubMed]
- Rohollahnejad, J.; Xia, L.; Ran, Y.; Cheng, R. Deformation Independent FBG Strain Sensor Based on Speckle Pattern Processing. In Proceedings of the 2015 14th International Conference on Optical Communications and Networks (ICOCN), Nanjing, China, 3–5 July 2015; pp. 14–16. [Google Scholar] [CrossRef]
- Fujiwara, E.; Marques dos Santos, M.F.; Suzuki, C.K. Optical Fiber Specklegram Sensor Analysis by Speckle Pattern Division. Appl. Opt. 2017, 56, 1585. [Google Scholar] [CrossRef]
- Lomer, M.; Abascal, J.; Castrellon-Uribe, J.; Lopez-Higuera, J.M. Measurement of Displacement in the Micrometer Range Using Speckle Pattern Correlation in Multimode Fibers. In Proceedings of the Fifth European Workshop on Optical Fibre Sensors, Krakow, Poland, 19–22 May 2013; Volume 8794, p. 879445. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Q.; Liu, H.H.; Tan, Z.W.; Wang, M.G. Investigation of an Image Processing Method of Step-Index Multimode Fiber Specklegram and Its Application on Lateral Displacement Sensing. Opt. Fiber Technol. 2018, 46, 48–53. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Qin, Q.; Tan, Z.; Wang, M.; Yan, F. Bending Recognition Based on the Analysis of Fiber Specklegrams Using Deep Learning. Opt. Laser Technol. 2020, 131, 106424. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the ICLR 2015 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2014; pp. 1–14. [Google Scholar]
- Sun, K.; Ding, Z.; Zhang, Z. Fiber Directional Position Sensor Based on Multimode Interference Imaging and Machine Learning. Appl. Opt. 2020, 59, 5745. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Li, G.; Liu, Y.; Qin, Q.; Zou, X.; Wang, M.; Yan, F. Deep Learning Based Optical Curvature Sensor through Specklegram Detection of Multimode Fiber. Opt. Laser Technol. 2022, 149, 107873. [Google Scholar] [CrossRef]
- Li, G.; Liu, Y.; Qin, Q.; Zou, X.; Wang, M.; Ren, W. Feature Extraction Enabled Deep Learning From Specklegram for Optical Fiber Curvature Sensing. IEEE Sens. J. 2022, 22, 15974–15984. [Google Scholar] [CrossRef]
- Wei, M.; Tang, G.; Liu, J.; Zhu, L.; Liu, J.; Huang, C.; Zhang, J.; Shen, L.; Yu, S. Neural Network Based Perturbation-Location Fiber Specklegram Sensing System towards Applications with Limited Number of Training Samples. J. Lightware Technol. 2021, 39, 6315–6326. [Google Scholar] [CrossRef]
- Cuevas, A.R.; Fontana, M.; Rodriguez-Cobo, L.; Lomer, M.; Lopez-Higuera, J.M. Machine Learning for Turning Optical Fiber Specklegram Sensor into a Spatially-Resolved Sensing System. Proof of Concept. J. Lightware Technol. 2018, 36, 3733–3738. [Google Scholar] [CrossRef]
- Razmyar, S.; Mostafavi, M.T. Deep Learning for Estimating Deflection Direction of a Multimode Fiber from Specklegram. J. Lightware Technol. 2021, 39, 1850–1857. [Google Scholar] [CrossRef]
- Lu, S.; Tan, Z.; Li, G.; Jingya, Y. A Sensitized Plastic Fiber Sensor for Multi-Point Bending Measurement Based on Deep Learning. IEEE Photonics J. 2021, 13, 1. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, Z. 2D Tactile Sensor Based on Multimode Interference and Deep Learning. Opt. Laser Technol. 2021, 136, 106760. [Google Scholar] [CrossRef]
- Li, G.; Liu, Y.; Qin, Q.; Pang, L.; Ren, W.; Wei, J.; Wang, M. Fiber Specklegram Torsion Sensor Based on Residual Network. Opt. Fiber Technol. 2023, 80, 103446. [Google Scholar] [CrossRef]
- Li, F.-F.; Fergus, R.; Perona, P. One-Shot Learning of Object Categories. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 594–611. [Google Scholar] [CrossRef]
- Lake, B.M.; Salakhutdinov, R.; Gross, J.; Tenenbaum, J.B. One Shot Learning of Simple Visual Concepts. In Proceedings of the 33rd Annual Meeting of the Cognitive Science Society, CogSci 2011, Boston, MA, USA, 20–23 July 2011; pp. 2568–2573. [Google Scholar]
- Takai, N.; Asakura, T. Statistical Properties of Laser Speckles Produced under Illumination from a Multimode Optical Fiber. J. Opt. Soc. Am. A 1985, 2, 1282. [Google Scholar] [CrossRef]
- Spillman, W.B.; Kline, B.R.; Maurice, L.B.; Fuhr, P.L. Statistical-Mode Sensor for Fiber Optic Vibration Sensing Uses. Appl. Opt. 1989, 28, 3166. [Google Scholar] [CrossRef]
- Wu, S.; Yin, S.; Yu, F.T.S. Sensing with Fiber Specklegrams. Appl. Opt. 1991, 30, 4468. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, PR, USA, 2–4 May 2016; pp. 1–14. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Lecture Notes in Computer Science; Including its Subseries Lecture Notes in Artificial Intelligence (LNAI) and Lecture Notes in Bioinformatics; Springer: Cham, Switzerland, 2016; 9908 LNCS; pp. 630–645. [Google Scholar] [CrossRef]
- Rithwiq, M.A.; Abraham, P.A.; Nair, M.; Swapna, S.; Sankararaman, S.I. Quantifying Microplastic Leaching from Paper Cups: A Specklegram Image Analytical Approach. Photonics 2024, 11, 1121. [Google Scholar] [CrossRef]
- Yang, Z.; Gu, L.; Gao, H.; Hu, H. Demodulation of Fiber Specklegram Curvature Sensor Using Deep Learning. Photonics 2023, 10, 169. [Google Scholar] [CrossRef]
- Grebenyuk, A.A.; Ryabukho, V.P. How Nonlinear Processing of Digital Specklegrams Affects the Accuracy with Which Displacements Are Determined by Speckle Photography. J. Opt. Technol. 2011, 78, 680. [Google Scholar] [CrossRef]







| Horizon Fiber | S-Shaped Flexible Sensor | ||
|---|---|---|---|
| α | MAE/mm | α | MAE/mm |
| 0.1 | 0.0203 | 0.1 | 0.0228 |
| 0.2 | 0.0325 | 0.2 | 0.0168 |
| 0.3 | 0.0279 | 0.3 | 0.0127 |
| 0.4 | 0.0255 | 0.4 | 0.0240 |
| 0.5 | 0.0260 | 0.5 | 0.0459 |
| 0.6 | 0.0354 | 0.6 | 0.0483 |
| 0.7 | 0.0239 | 0.7 | 0.0274 |
| 0.8 | 0.0157 | 0.8 | 0.0220 |
| 0.9 | 0.0408 | 0.9 | 0.0237 |
| 1 | 0.0435 | 1 | 0.0268 |
| Reference | Backbone | MAE/mm | RMSE/mm | Max Error/mm | R2 |
|---|---|---|---|---|---|
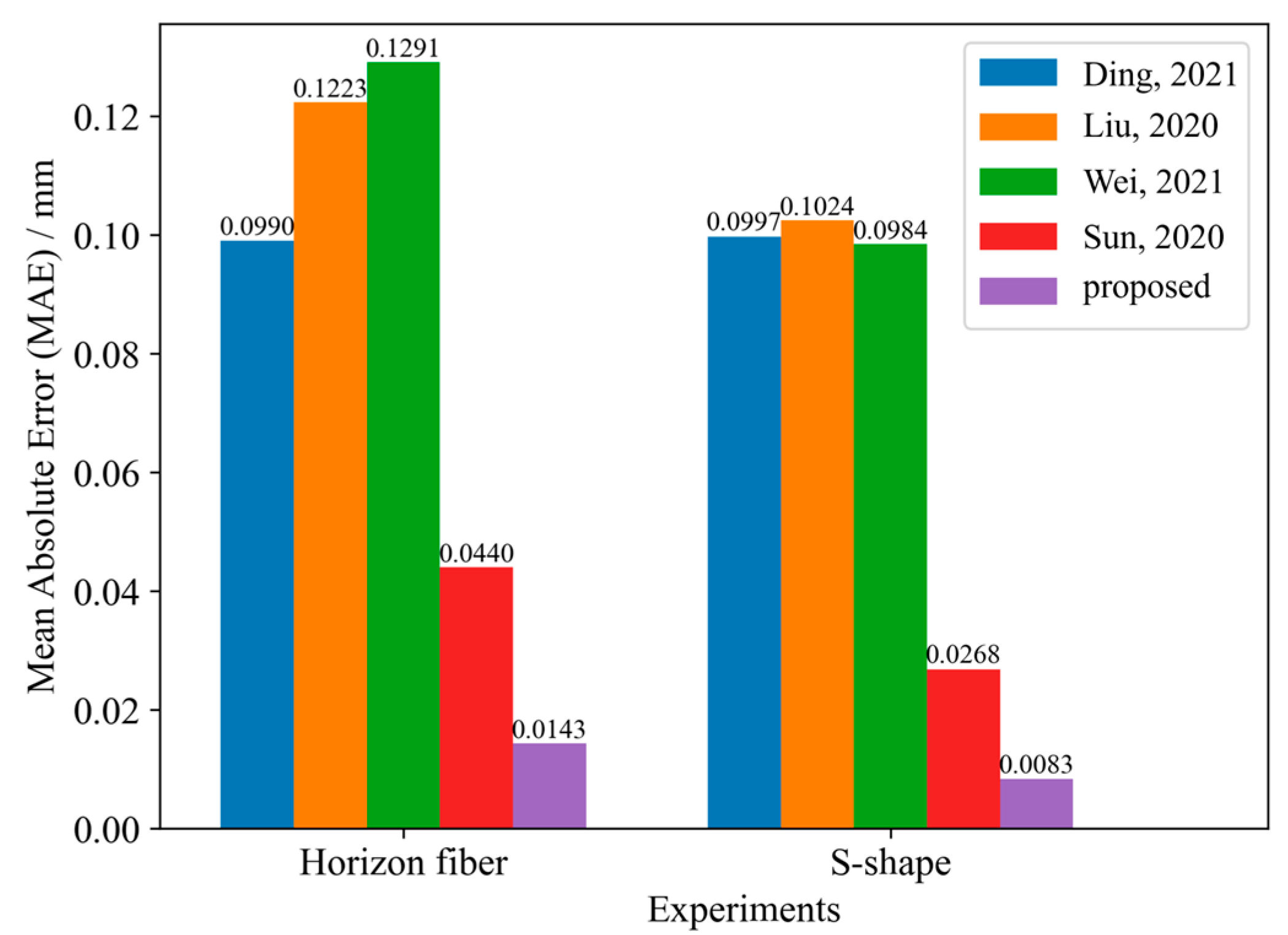
| Liu [7] | VGG | 0.0990 | 0.1262 | 0.4956 | 0.999425 |
| Li [11] | VGG | 0.1223 | 0.1623 | 0.4682 | 0.999048 |
| Wei [13] | CNN | 0.1291 | 0.1669 | 0.4850 | 0.998994 |
| Sun [9] | ResNet18 | 0.0440 | 0.0548 | 0.1612 | 0.999892 |
| Proposed | ResNet18 | 0.0143 | 0.0185 | 0.0612 | 0.999988 |
| Reference | Backbone | MAE/mm | RMSE/mm | Max Error/mm | R2 |
|---|---|---|---|---|---|
| Liu [7] | VGG | 0.0997 | 0.1322 | 0.5465 | 0.999465 |
| Li [11] | VGG | 0.1024 | 0.1177 | 0.2588 | 0.999500 |
| Wei [13] | CNN | 0.0984 | 0.1316 | 0.4696 | 0.999374 |
| Sun [9] | ResNet18 | 0.0268 | 0.0375 | 0.1229 | 0.999949 |
| Proposed | ResNet18 | 0.0083 | 0.0109 | 0.0397 | 0.999996 |
| Reference | Backbone | MAE/mm | RMSE/mm | Max Error/mm | R2 |
|---|---|---|---|---|---|
| Liu [7] | VGG | 0.2453 | 0.3115 | 1.5853 | 0.996496 |
| Li [11] | VGG | 0.0753 | 0.0936 | 0.2712 | 0.998710 |
| Wei [13] | CNN | 0.0754 | 0.1027 | 0.4651 | 0.999616 |
| Sun [9] | ResNet18 | 0.0266 | 0.0415 | 0.4056 | 0.999938 |
| Proposed | ResNet18 | 0.0138 | 0.0322 | 0.3960 | 0.999963 |
| Group | Temperature |
|---|---|
| 1 | 21.2 °C |
| 2 | 21.3 °C |
| 3 | 21.3 °C |
| 4 | 21.3 °C |
| 5 | 21.4 °C |
| 6 | 21.4 °C |
| 7 | 21.5 °C |
| 8 | 21.5 °C |
| 9 | 21.5 °C |
| 10 | 21.65 °C |
| 11 | 21.75 °C |
| 12 | 22.0 °C |
| 13 | 22.1 °C |
| 14 | 22.2 °C |
| 15 | 22.2 °C |
| 16 | 22.2 °C |
| 17 | 22.2 °C |
| 18 | 22.25 °C |
| 19 | 22.3 °C |
| 20 | 22.35 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, B.; Li, J. Displacement-Sensing Method Based on Residual Scaling for One-Shot MMF Specklegram Prediction. Sensors 2025, 25, 1434. https://doi.org/10.3390/s25051434
Shen B, Li J. Displacement-Sensing Method Based on Residual Scaling for One-Shot MMF Specklegram Prediction. Sensors. 2025; 25(5):1434. https://doi.org/10.3390/s25051434
Chicago/Turabian StyleShen, Bohao, and Jianzhi Li. 2025. "Displacement-Sensing Method Based on Residual Scaling for One-Shot MMF Specklegram Prediction" Sensors 25, no. 5: 1434. https://doi.org/10.3390/s25051434
APA StyleShen, B., & Li, J. (2025). Displacement-Sensing Method Based on Residual Scaling for One-Shot MMF Specklegram Prediction. Sensors, 25(5), 1434. https://doi.org/10.3390/s25051434





