Sea Surface Temperature Prediction Enhanced by Exploring Spatiotemporal Correlation Based on LSTM and Gaussian Process
Abstract
1. Introduction
- (1)
- The proposed LSTM-GPR framework effectively models the spatiotemporal patterns of SST, enabling accurate predictions. The Gaussian process models spatial correlations based on predicted SST values and their surrounding areas, while the LSTM captures temporal dynamics.
- (2)
- Our model provides valuable information on prediction uncertainties by leveraging the inherent advantages of Gaussian processes to estimate confidence intervals for SST forecasting.
- (3)
- The results of extensive experiments on the OISST dataset validate the superiority of our framework over existing methods.
2. Methodology
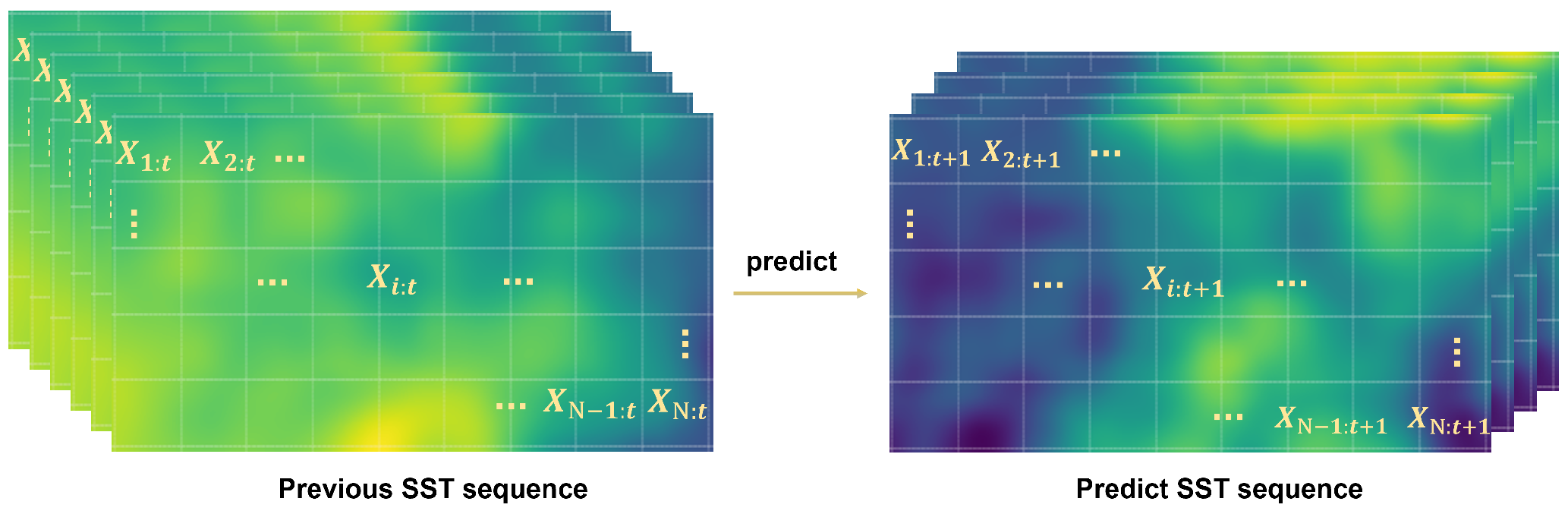
2.1. Problem Formulation
2.2. Overview of the LSTM-GPR SST Prediction Framework
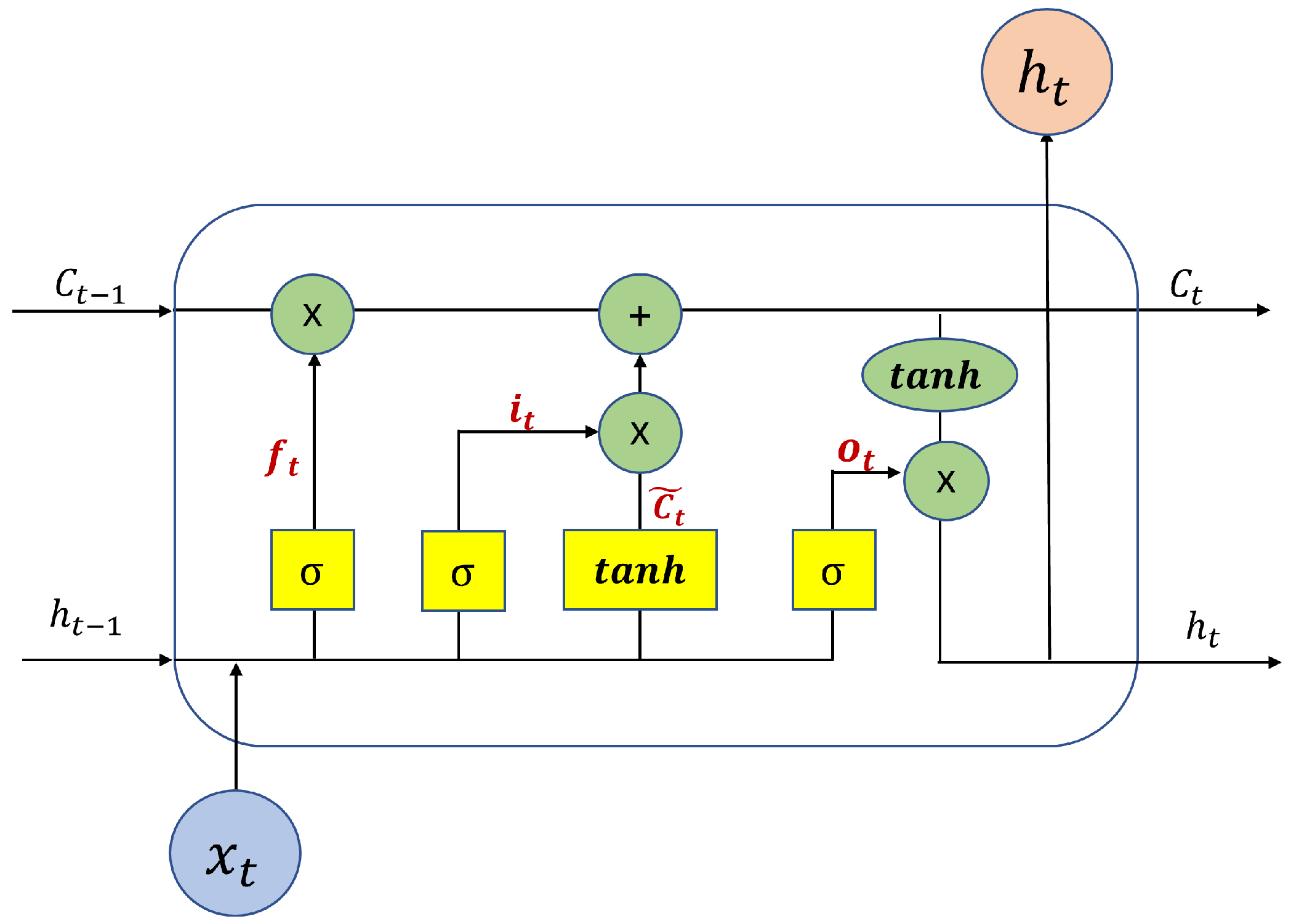
2.3. Temporal Dependency Extractor and LSTM Mechanism
2.4. Spatial Dependency Enhancement with GPR
3. Experiments
3.1. Datasets
3.2. Experiment Setup
3.3. Experiment Results and Discussion
3.3.1. Evaluation of the Model Performance
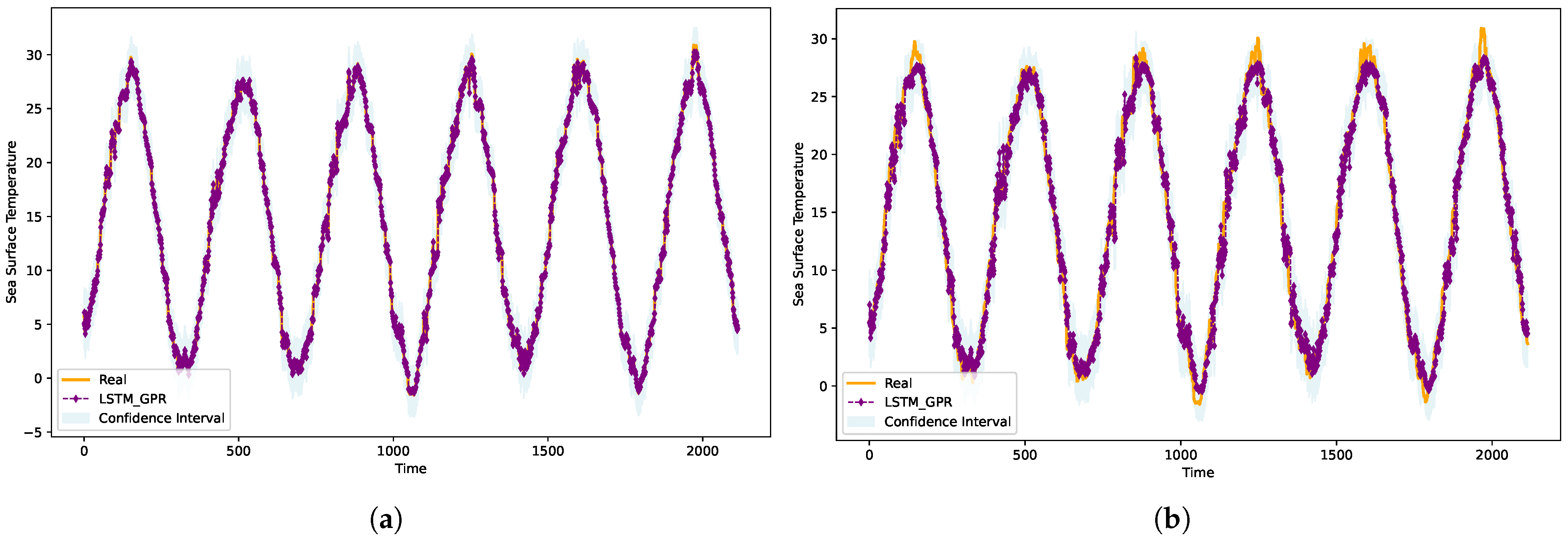
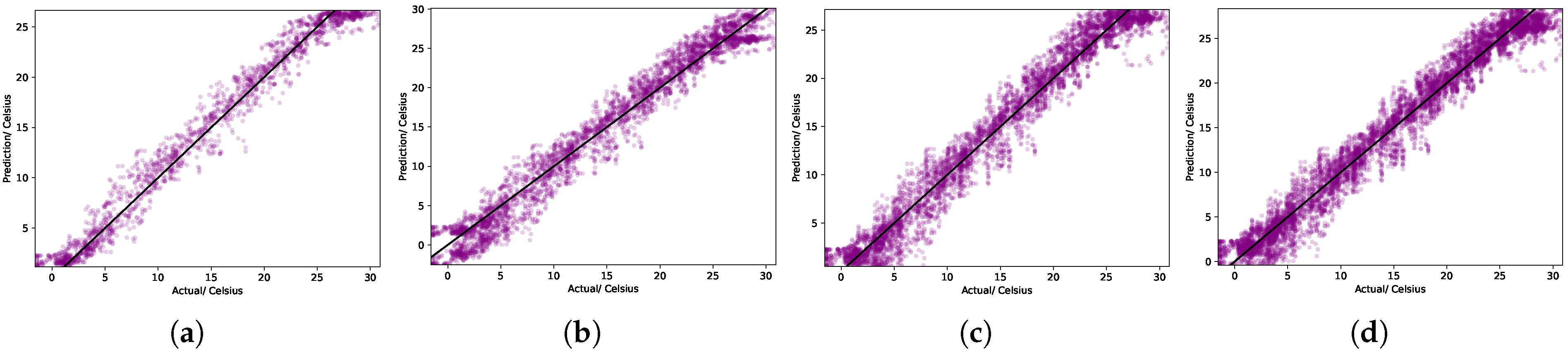
3.3.2. Visualization of Prediction Results
3.3.3. Other Experiments
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Garcia-Soto, C.; Cheng, L.; Caesar, L.; Schmidtko, S.; Jewett, E.B.; Cheripka, A.; Rigor, I.; Caballero, A.; Chiba, S.; Báez, J.C.; et al. An overview of ocean climate change indicators: Sea surface temperature, ocean heat content, ocean pH, dissolved oxygen concentration, arctic sea ice extent, thickness and volume, sea level and strength of the AMOC (Atlantic Meridional Overturning Circulation). Front. Mar. Sci. 2021, 8, 642372. [Google Scholar]
- de Mattos Neto, P.S.; Cavalcanti, G.D.; de O. Santos Júnior, D.S.; Silva, E.G. Hybrid systems using residual modeling for sea surface temperature forecasting. Sci. Rep. 2022, 12, 487. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.L.; Wu, H.; Duan, S.B.; Zhao, W.; Ren, H.; Liu, X.; Leng, P.; Tang, R.; Ye, X.; Zhu, J.; et al. Satellite remote sensing of global land surface temperature: Definition, methods, products, and applications. Rev. Geophys. 2023, 61, e2022RG000777. [Google Scholar] [CrossRef]
- Vance, T.C.; Huang, T.; Butler, K.A. Big data in Earth science: Emerging practice and promise. Science 2024, 383, eadh9607. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Wang, S.; Cao, J.; Philip, S.Y. Deep learning for spatio-temporal data mining: A survey. IEEE Trans. Knowl. Data Eng. 2020, 34, 3681–3700. [Google Scholar] [CrossRef]
- Jamshidi, E.J.; Yusup, Y.; Kayode, J.S.; Kamaruddin, M.A. Detecting outliers in a univariate time series dataset using unsupervised combined statistical methods: A case study on surface water temperature. Ecol. Inform. 2022, 69, 101672. [Google Scholar] [CrossRef]
- Goddard, L.; Gershunov, A. Impact of El Niño on weather and climate extremes. In El Niño Southern Oscillation in a Changing Climate; American Geophysical Union: Washington, DC, USA, 2020; pp. 361–375. [Google Scholar]
- Sun, T.; Feng, Y.; Li, C.; Zhang, X. High precision sea surface temperature prediction of long period and large area in the Indian ocean based on the temporal convolutional network and internet of things. Sensors 2022, 22, 1636. [Google Scholar] [CrossRef] [PubMed]
- Smale, D.A.; Wernberg, T.; Oliver, E.C.; Thomsen, M.; Harvey, B.P.; Straub, S.C.; Burrows, M.T.; Alexander, L.V.; Benthuysen, J.A.; Donat, M.G.; et al. Marine heatwaves threaten global biodiversity and the provision of ecosystem services. Nat. Clim. Chang. 2019, 9, 306–312. [Google Scholar] [CrossRef]
- Meng, Y.; Gao, F.; Rigall, E.; Dong, R.; Dong, J.; Du, Q. Physical Knowledge-Enhanced Deep Neural Network for Sea Surface Temperature Prediction. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Wilby, R.L.; Wigley, T.M. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Flemming, J.; Inness, A.; Flentje, H.; Huijnen, V.; Moinat, P.; Schultz, M.; Stein, O. Coupling global chemistry transport models to ECMWF’s integrated forecast system. Geosci. Model Dev. Discuss. 2009, 2, 763–795. [Google Scholar] [CrossRef]
- Durai, V.; Roy Bhowmik, S. Prediction of Indian summer monsoon in short to medium range time scale with high resolution global forecast system (GFS) T574 and T382. Clim. Dyn. 2014, 42, 1527–1551. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Shi, Z.; Zheng, H.; Dong, J. OceanVP: A HYCOM based benchmark dataset and a relational spatiotemporal predictive network for oceanic variable prediction. Ocean. Eng. 2024, 304, 117748. [Google Scholar] [CrossRef]
- Masini, R.P.; Medeiros, M.C.; Mendes, E.F. Machine learning advances for time series forecasting. J. Econ. Surv. 2023, 37, 76–111. [Google Scholar] [CrossRef]
- Shin, D.; Ha, E.; Kim, T.; Kim, C. Short-term photovoltaic power generation predicting by input/output structure of weather forecast using deep learning. Soft Comput. 2021, 25, 771–783. [Google Scholar] [CrossRef]
- Zivot, E.; Wang, J. Vector autoregressive models for multivariate time series. In Modeling Financial Time Series with S-PLUS®; Springer: New York, NY, USA, 2006; pp. 385–429. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Yang, H.; Li, W.; Hou, S.; Guan, J.; Zhou, S. HiGRN: A Hierarchical Graph Recurrent Network for Global Sea Surface Temperature Prediction. ACM Trans. Intell. Syst. Technol. 2023, 14, 1–19. [Google Scholar] [CrossRef]
- Lavine, M.; Lozier, S. A Markov random field spatio-temporal analysis of ocean temperature. Environ. Ecol. Stat. 1999, 6, 249–273. [Google Scholar] [CrossRef]
- Aguilar-Martinez, S.; Hsieh, W.W. Forecasts of tropical Pacific sea surface temperatures by neural networks and support vector regression. Int. J. Oceanogr. 2009, 2009, 167239. [Google Scholar] [CrossRef]
- Ahmed, N.K.; Atiya, A.F.; Gayar, N.E.; El-Shishiny, H. An empirical comparison of machine learning models for time series forecasting. Econom. Rev. 2010, 29, 594–621. [Google Scholar] [CrossRef]
- Xu, S.; Dai, D.; Cui, X.; Yin, X.; Jiang, S.; Pan, H.; Wang, G. A deep learning approach to predict sea surface temperature based on multiple modes. Ocean Model. 2023, 181, 102158. [Google Scholar] [CrossRef]
- Hao, P.; Li, S.; Song, J.; Gao, Y. Prediction of sea surface temperature in the South China Sea based on deep learning. Remote Sens. 2023, 15, 1656. [Google Scholar] [CrossRef]
- Shi, B.; Ge, C.; Lin, H.; Xu, Y.; Tan, Q.; Peng, Y.; He, H. Sea Surface Temperature Prediction Using ConvLSTM-Based Model with Deformable Attention. Remote Sens. 2024, 16, 4126. [Google Scholar] [CrossRef]
- Ren, J.; Wang, C.; Sun, L.; Huang, B.; Zhang, D.; Mu, J.; Wu, J. Prediction of Sea Surface Temperature Using U-Net Based Model. Remote Sens. 2024, 16, 1205. [Google Scholar] [CrossRef]
- Zhang, M.; Han, G.; Wu, X.; Li, C.; Shao, Q.; Li, W.; Cao, L.; Wang, X.; Dong, W.; Ji, Z. SST Forecast Skills Based on Hybrid Deep Learning Models: With Applications to the South China Sea. Remote Sens. 2024, 16, 1034. [Google Scholar] [CrossRef]
- Jia, X.; Ji, Q.; Han, L.; Liu, Y.; Han, G.; Lin, X. Prediction of Sea Surface Temperature in the East China Sea Based on LSTM Neural Network. Remote Sens. 2022, 14, 3300. [Google Scholar] [CrossRef]
- Wanigasekara, R.W.W.M.U.P.; Zhang, Z.; Wang, W.; Luo, Y.; Pan, G. Application of Fast MEEMD–ConvLSTM in Sea Surface Temperature Predictions. Remote Sens. 2024, 16, 2468. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of sea surface temperature using long short-term memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM model for sea surface temperature prediction. IEEE Geosci. Remote Sens. Lett. 2017, 15, 207–211. [Google Scholar] [CrossRef]
- Usharani, B. ILF-LSTM: Enhanced loss function in LSTM to predict the sea surface temperature. Soft Comput. 2022, 27, 13129–13141. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Gong, J.; Chen, Z. Short and mid-term sea surface temperature prediction using time-series satellite data and LSTM-AdaBoost combination approach. Remote Sens. Environ. 2019, 233, 111358. [Google Scholar] [CrossRef]
- Han, M.; Feng, Y.; Zhao, X.; Sun, C.; Hong, F.; Liu, C. A convolutional neural network using surface data to predict subsurface temperatures in the Pacific Ocean. IEEE Access 2019, 7, 172816–172829. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Xu, Z.; Cai, Y.; Xu, L.; Chen, Z.; Gong, J. A spatiotemporal deep learning model for sea surface temperature field prediction using time-series satellite data. Environ. Model. Softw. 2019, 120, 104502. [Google Scholar] [CrossRef]
- Araújo, R.d.A.; de Mattos Neto, P.S.; Nedjah, N.; Soares, S.C. On the Sea Surface Temperature Forecasting Problem with Deep Dilation-Erosion-Linear Models. Big Data Res. 2024, 36, 100455. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. arXiv 2022, arXiv:2210.02186. [Google Scholar]
- Juan, N.P.; Matutano, C.; Valdecantos, V.N. Uncertainties in the application of artificial neural networks in ocean engineering. Ocean Eng. 2023, 284, 115193. [Google Scholar] [CrossRef]
- Wang, T.; Li, Z.; Geng, X.; Jin, B.; Xu, L. Time series prediction of sea surface temperature based on an adaptive graph learning neural model. Future Internet 2022, 14, 171. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Frery, A.C.; Ren, P. Sea surface temperature prediction with memory graph convolutional networks. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, A.; Qin, M.; Hu, L.; Wu, S.; Du, Z.; Liu, R. A Graph Memory Neural Network for Sea Surface Temperature Prediction. Remote Sens. 2023, 15, 3539. [Google Scholar] [CrossRef]
- Lou, G.; Zhang, J.; Zhao, X.; Zhou, X.; Li, Q. A Non-Uniform Grid Graph Convolutional Network for Sea Surface Temperature Prediction. Remote Sens. 2024, 16, 3216. [Google Scholar] [CrossRef]
- Liu, M.; Meng, F.; Liang, Y. Generalized pose decoupled network for unsupervised 3d skeleton sequence-based action representation learning. Cyborg Bionic Syst. 2022, 2022, 0002. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.M. Improvements of the daily optimum interpolation sea surface temperature (DOISST) version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, L.; Qin, H.; Liu, Y.; Wang, C.; Yu, X.; Yin, X.; Li, J. Wind speed prediction method using shared weight long short-term memory network and Gaussian process regression. Appl. Energy 2019, 247, 270–284. [Google Scholar] [CrossRef]
- Hou, S.; Li, W.; Liu, T.; Zhou, S.; Guan, J.; Qin, R.; Wang, Z. MUST: A Multi-source Spatio-Temporal data fusion Model for short-term sea surface temperature prediction. Ocean Eng. 2022, 259, 111932. [Google Scholar] [CrossRef]
- Wentz, F.J.; Scott, J.; Hoffman, R.; Leidner, M.; Atlas, R.; Ardizzone, J. Cross-Calibrated Multi-Platform Ocean Surface Wind Vector Analysis Product V2, 1987-Ongoing; National Center for Atmospheric Research: Boulder, CO, USA, 2016. [Google Scholar]




| Study Area | Model Name | Metrics | Day = 1 | Day = 2 | Day = 3 | Day = 4 | Day = 5 | Day = 6 | Day = 7 |
|---|---|---|---|---|---|---|---|---|---|
| Bohai Sea | SVR | RMSE | 0.5041 | 0.7824 | 0.9587 | 1.0939 | 1.2164 | 1.3309 | 1.4439 |
| MAE | 0.3526 | 0.5789 | 0.7261 | 0.8391 | 0.9429 | 1.0409 | 1.1397 | ||
| 0.9964 | 0.9913 | 0.9869 | 0.9829 | 0.9789 | 0.9748 | 0.9703 | |||
| GPR | RMSE | 0.5163 | 0.7859 | 0.9565 | 1.0864 | 1.2040 | 1.3146 | 1.4221 | |
| MAE | 0.3443 | 0.5586 | 0.6987 | 0.8045 | 0.9005 | 0.9907 | 1.0798 | ||
| 0.9962 | 0.9911 | 0.9869 | 0.9831 | 0.9792 | 0.9753 | 0.9710 | |||
| LSTM | RMSE | 0.4679 | 0.7707 | 0.9963 | 1.1914 | 1.3832 | 1.5740 | 1.7632 | |
| MAE | 0.3239 | 0.5797 | 0.7739 | 0.9402 | 1.1014 | 1.2606 | 1.4186 | ||
| 0.9968 | 0.9914 | 0.9857 | 0.9794 | 0.9722 | 0.9639 | 0.9545 | |||
| LSTM-GPR | RMSE | 0.4384 | 0.6737 | 0.8171 | 0.9202 | 1.0117 | 1.0966 | 1.1710 | |
| MAE | 0.2954 | 0.4905 | 0.6105 | 0.6937 | 0.7666 | 0.8351 | 0.8967 | ||
| 0.9972 | 0.9935 | 0.9904 | 0.9879 | 0.9853 | 0.9828 | 0.9803 | |||
| South China Sea | SVR | RMSE | 0.2569 | 0.3902 | 0.4666 | 0.5191 | 0.5616 | 0.5993 | 0.6335 |
| MAE | 0.1763 | 0.2876 | 0.3537 | 0.3986 | 0.4346 | 0.4660 | 0.4945 | ||
| 0.9638 | 0.9183 | 0.8851 | 0.8593 | 0.8364 | 0.8142 | 0.7930 | |||
| GPR | RMSE | 0.2740 | 0.4095 | 0.4869 | 0.5403 | 0.5836 | 0.6223 | 0.6578 | |
| MAE | 0.1848 | 0.2991 | 0.3668 | 0.4131 | 0.4502 | 0.4827 | 0.5123 | ||
| 0.9574 | 0.9080 | 0.8725 | 0.8449 | 0.8207 | 0.7972 | 0.7745 | |||
| LSTM | RMSE | 0.2560 | 0.4030 | 0.4948 | 0.5605 | 0.6151 | 0.6641 | 0.7094 | |
| MAE | 0.1820 | 0.3057 | 0.3838 | 0.4390 | 0.4842 | 0.5247 | 0.5621 | ||
| 0.9647 | 0.9251 | 0.8948 | 0.8715 | 0.8512 | 0.8324 | 0.8149 | |||
| LSTM-GPR | RMSE | 0.2474 | 0.3792 | 0.4572 | 0.5117 | 0.5562 | 0.5950 | 0.6296 | |
| MAE | 0.1734 | 0.2838 | 0.3506 | 0.3965 | 0.4334 | 0.4651 | 0.4937 | ||
| 0.9669 | 0.9234 | 0.8902 | 0.8638 | 0.8401 | 0.8179 | 0.7970 |
| Method | SVR | GPR | LSTM | LSTM-GPR |
|---|---|---|---|---|
| MAE | 0.3637 | 0.3497 | 0.3168 | 0.2916 |
| RMSE | 0.5093 | 0.5175 | 0.4548 | 0.4293 |
| Study Area | Model Name | Metrics | Day = 1 | Day = 2 | Day = 3 | Day = 4 | Day = 5 | Day = 6 | Day = 7 |
|---|---|---|---|---|---|---|---|---|---|
| Bohai Sea | LSTM-GPR (SST) | RMSE | 0.4384 | 0.6737 | 0.8171 | 0.9202 | 1.0117 | 1.0966 | 1.1710 |
| MAE | 0.2954 | 0.4905 | 0.6105 | 0.6937 | 0.7666 | 0.8351 | 0.8967 | ||
| 0.9972 | 0.9935 | 0.9904 | 0.9879 | 0.9853 | 0.9828 | 0.9803 | |||
| LSTM-GPR (SST, USSW, VSSW) | RMSE | 0.4733 | 0.6595 | 0.7700 | 0.8487 | 0.9129 | 0.9669 | 1.0139 | |
| MAE | 0.3410 | 0.4885 | 0.5766 | 0.6383 | 0.6884 | 0.7321 | 0.7711 | ||
| 0.9968 | 0.9937 | 0.9915 | 0.9896 | 0.9880 | 0.9865 | 0.9852 | |||
| South China Sea | LSTM-GPR (SST) | RMSE | 0.2474 | 0.3792 | 0.4572 | 0.5117 | 0.5562 | 0.5950 | 0.6296 |
| MAE | 0.1734 | 0.2838 | 0.3506 | 0.3965 | 0.4334 | 0.4651 | 0.4937 | ||
| 0.9669 | 0.9234 | 0.8902 | 0.8638 | 0.8401 | 0.8179 | 0.7970 | |||
| LSTM-GPR (SST, USSW, VSSW) | RMSE | 0.2443 | 0.3643 | 0.4372 | 0.4879 | 0.5292 | 0.5655 | 0.5988 | |
| MAE | 0.1773 | 0.2770 | 0.3377 | 0.3794 | 0.4131 | 0.4427 | 0.4696 | ||
| 0.9673 | 0.9282 | 0.8983 | 0.8749 | 0.8538 | 0.8334 | 0.8132 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhu, Q.; Zhang, D.; Wu, H.; Peng, Y. Sea Surface Temperature Prediction Enhanced by Exploring Spatiotemporal Correlation Based on LSTM and Gaussian Process. Sensors 2025, 25, 1373. https://doi.org/10.3390/s25051373
Li Z, Zhu Q, Zhang D, Wu H, Peng Y. Sea Surface Temperature Prediction Enhanced by Exploring Spatiotemporal Correlation Based on LSTM and Gaussian Process. Sensors. 2025; 25(5):1373. https://doi.org/10.3390/s25051373
Chicago/Turabian StyleLi, Zhenglin, Qingxiong Zhu, Dan Zhang, Hao Wu, and Yan Peng. 2025. "Sea Surface Temperature Prediction Enhanced by Exploring Spatiotemporal Correlation Based on LSTM and Gaussian Process" Sensors 25, no. 5: 1373. https://doi.org/10.3390/s25051373
APA StyleLi, Z., Zhu, Q., Zhang, D., Wu, H., & Peng, Y. (2025). Sea Surface Temperature Prediction Enhanced by Exploring Spatiotemporal Correlation Based on LSTM and Gaussian Process. Sensors, 25(5), 1373. https://doi.org/10.3390/s25051373






