Design and Test of Adaptive Leveling System for Orchard Operation Platform
Abstract
1. Introduction
2. Materials and Methods
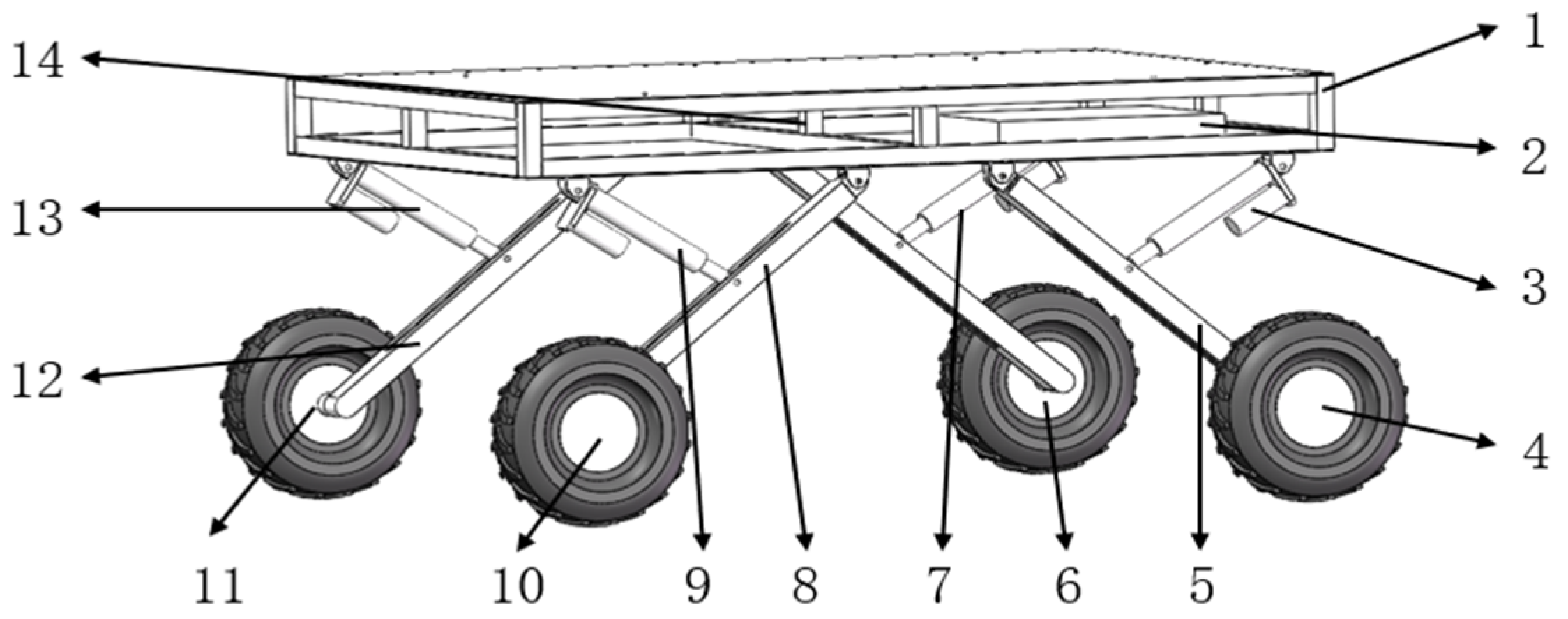
2.1. Structure of the Whole Machine
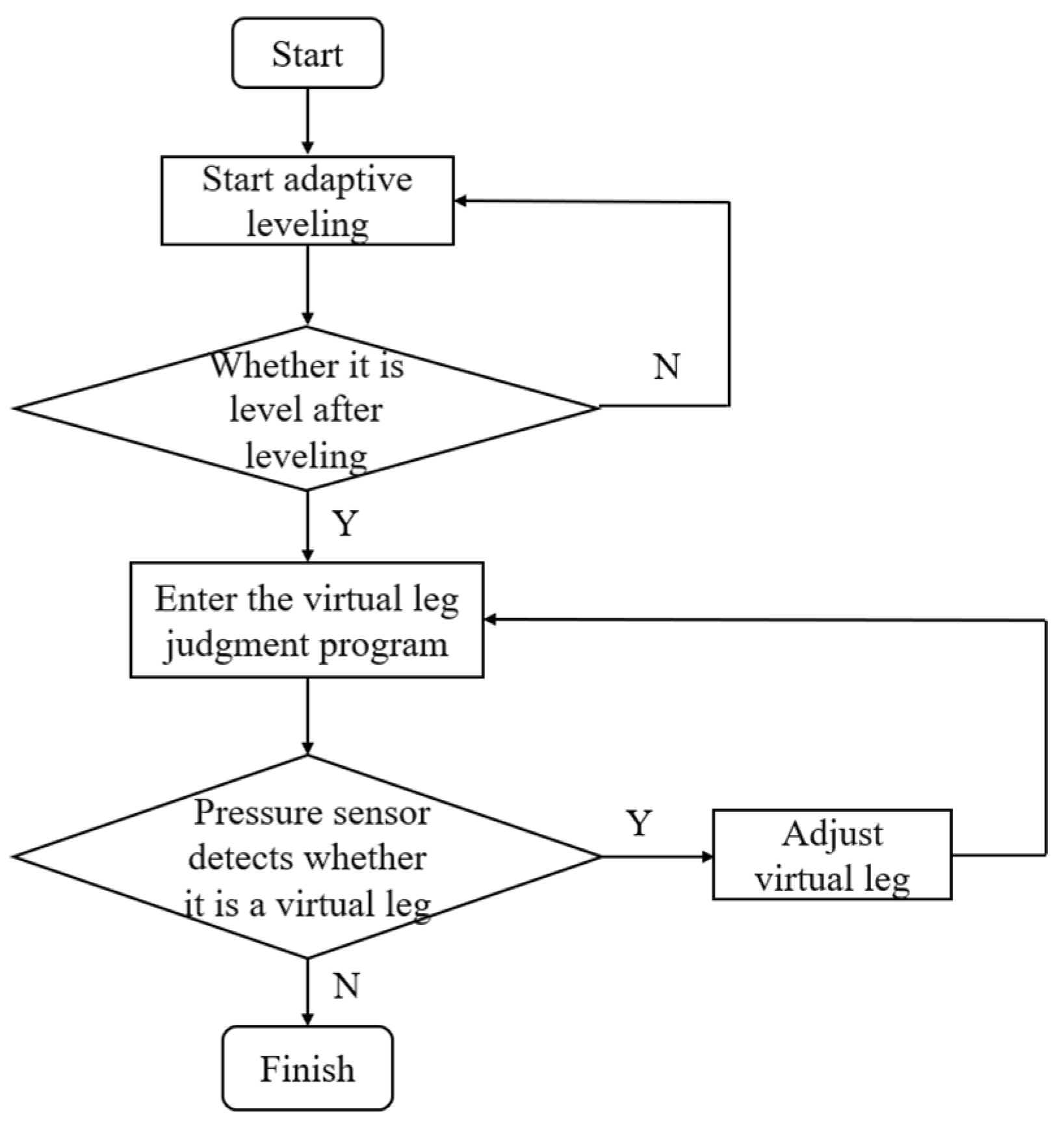
2.2. Leveling Principle of Operation
2.3. Leveling Strategy
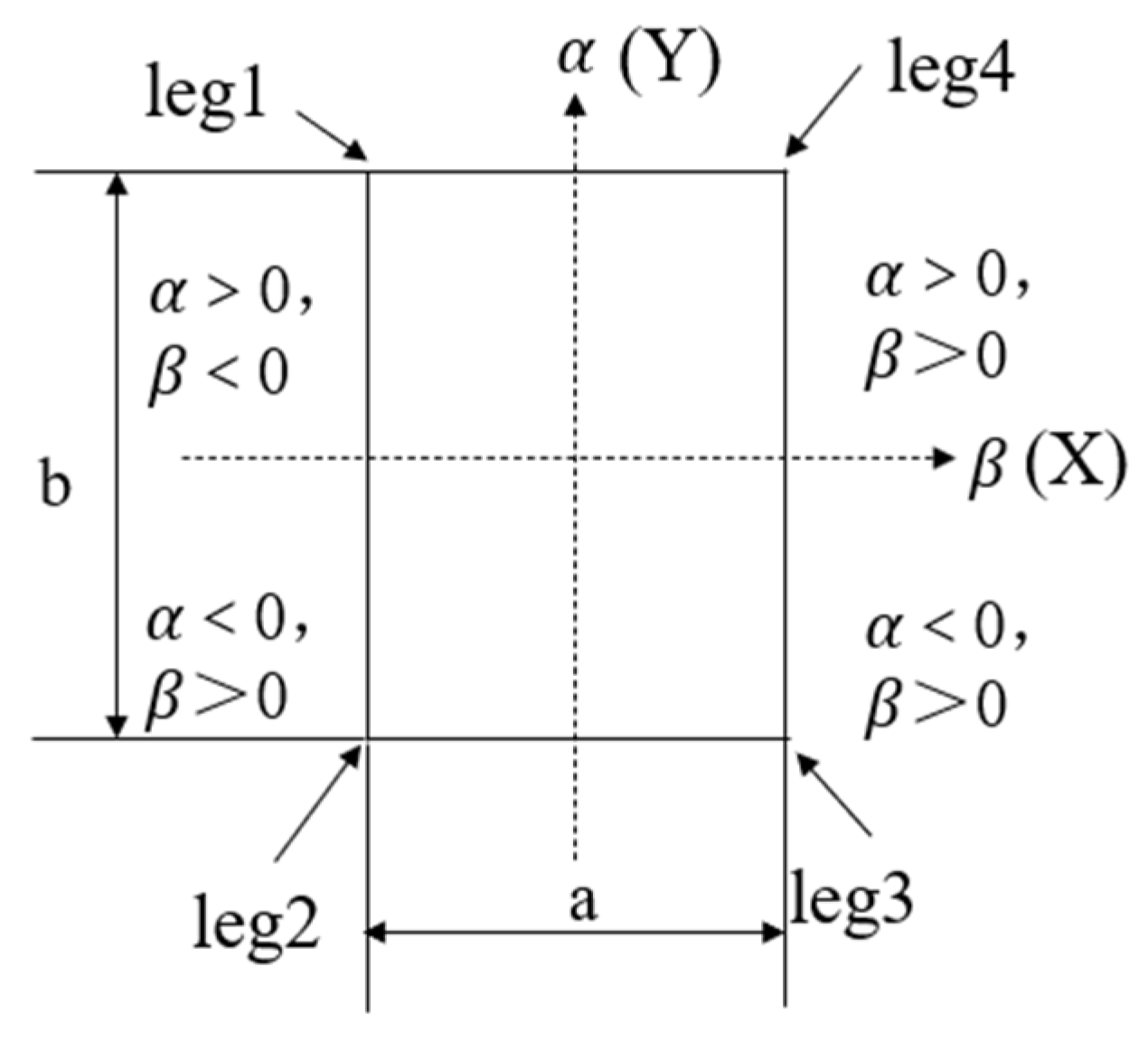
2.3.1. Platform Mathematical Modeling
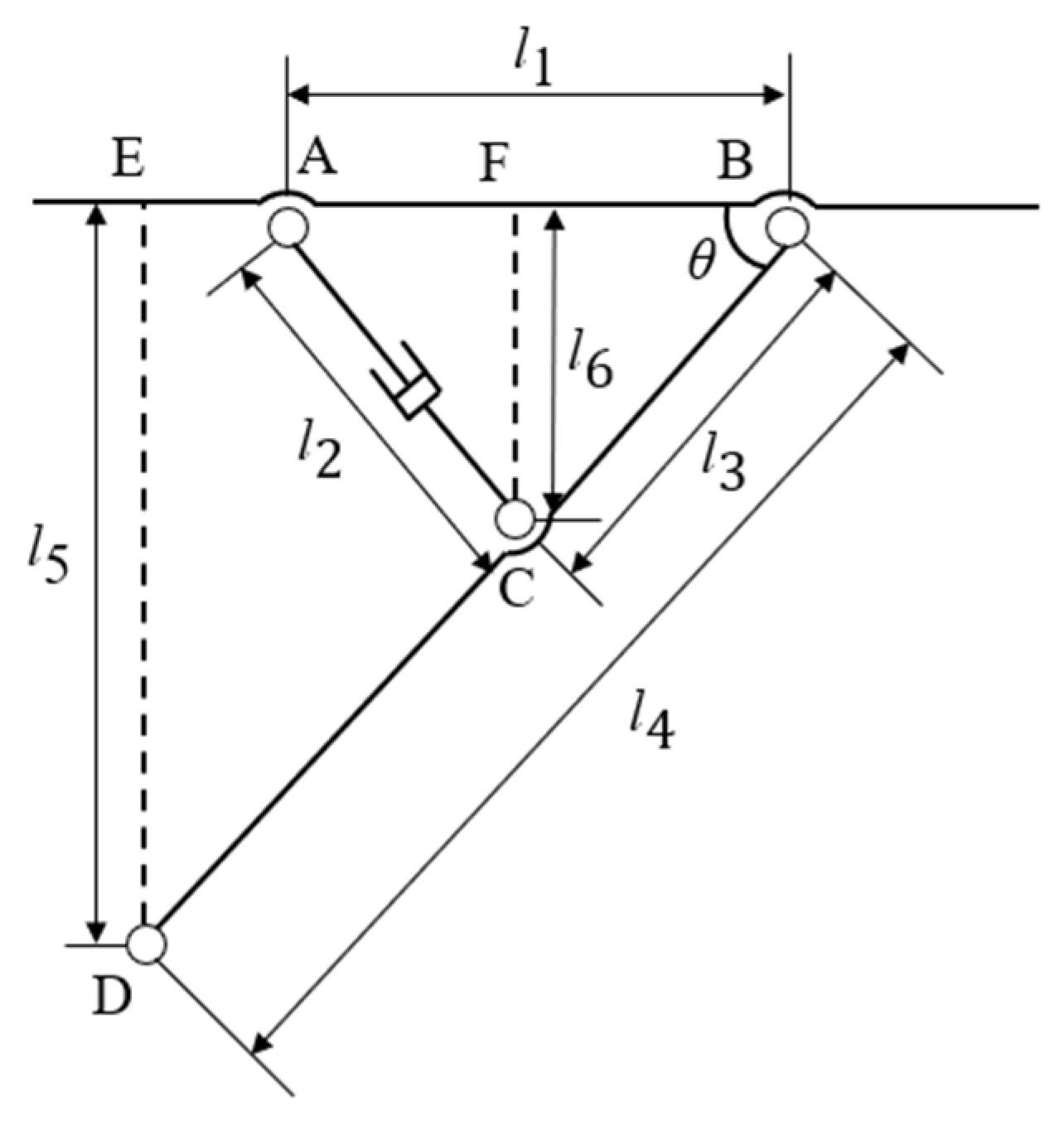
2.3.2. Analysis of Leveling Structure and Leveling Maximum Tilt Angle
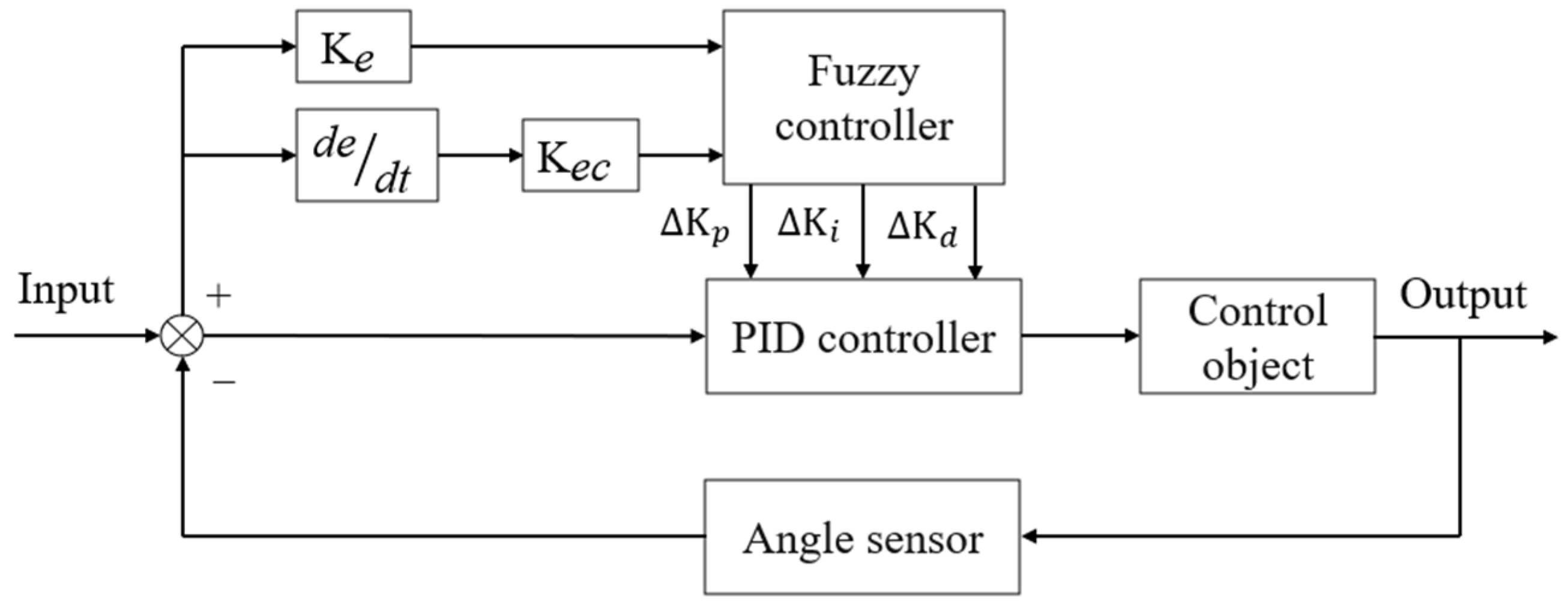
2.4. Control System Design
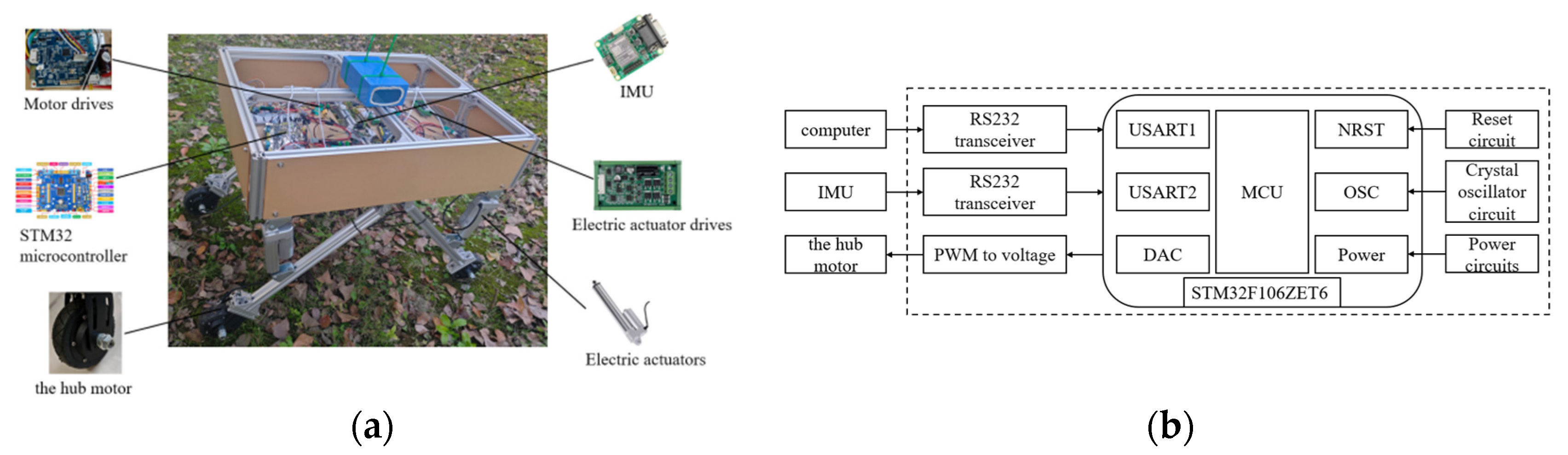
2.4.1. Hardware Design
2.4.2. Fuzzy PID Controller Design
- (1)
- When the deviation is large, to eliminate the deviation as quickly as possible and improve the response speed, should be increased. To prevent overshooting of the system, it is necessary to increase while reducing , and should be set to zero or a very small value.
- (2)
- When the deviation is small, to continue eliminating the deviation while simultaneously reducing oscillation and preventing overshooting, should be increased and should be appropriately decreased.
- (3)
- When the rate of change of the deviation is large, should be reduced, and should be increased.
- (4)
- The steady-state performance of the system can be adjusted through the differential component. When the error is very large, the value of should be set to zero or a very small value to reduce oscillation. Based on the above four rules, the fuzzy control rules for , , and are established.
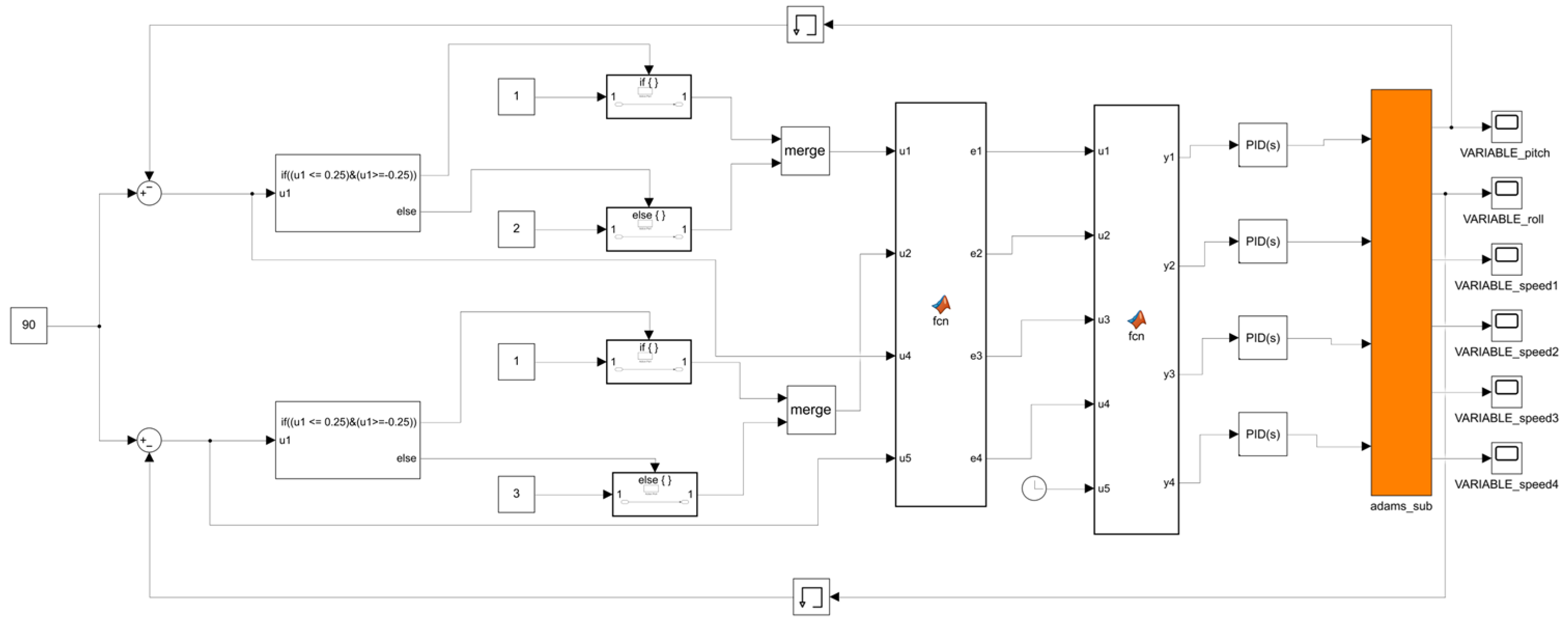
2.5. Co-Simulation Design Based on MATLAB-ADAMS
2.5.1. Co-Simulation Model Design
2.5.2. Co-Simulation System Construction
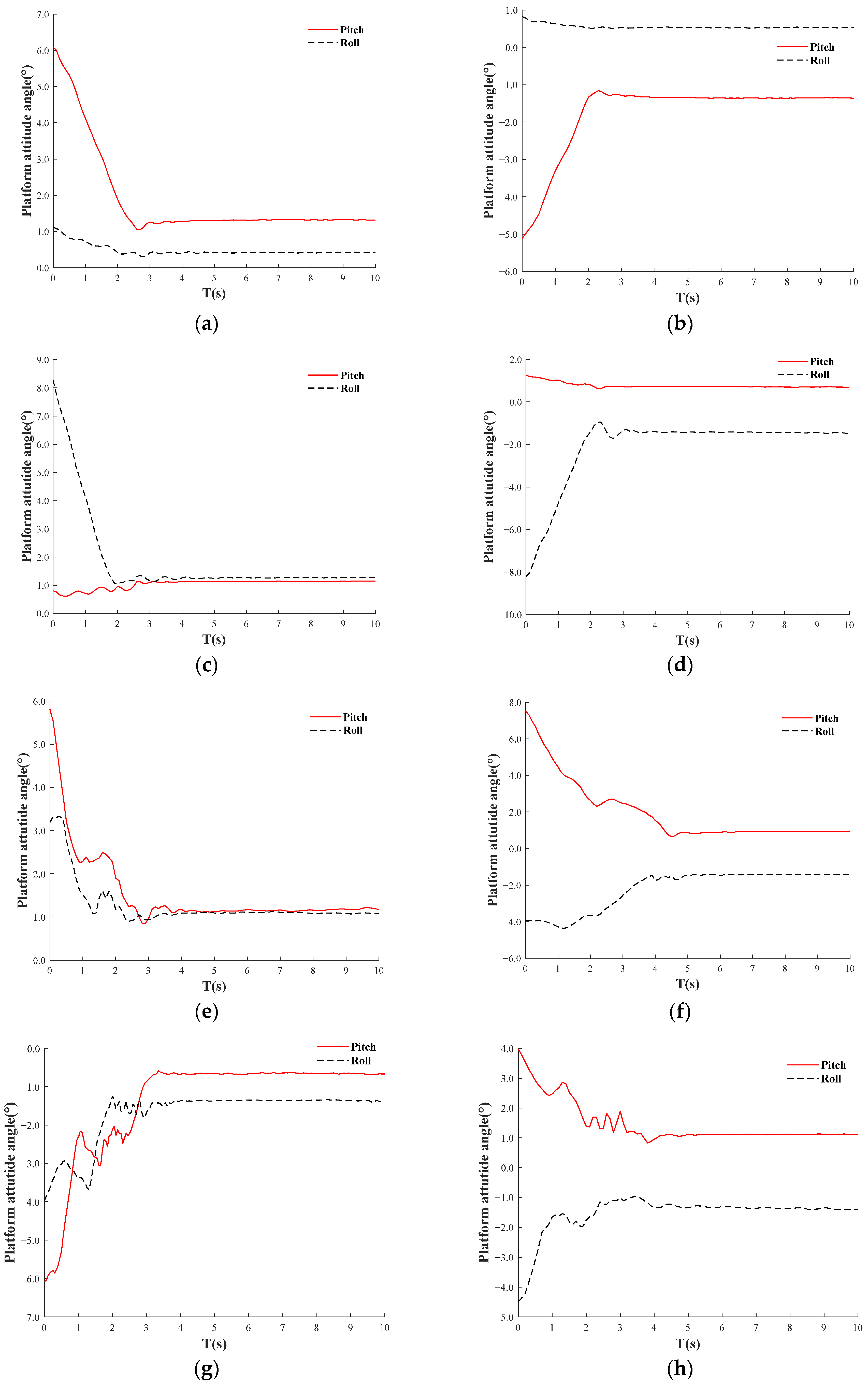
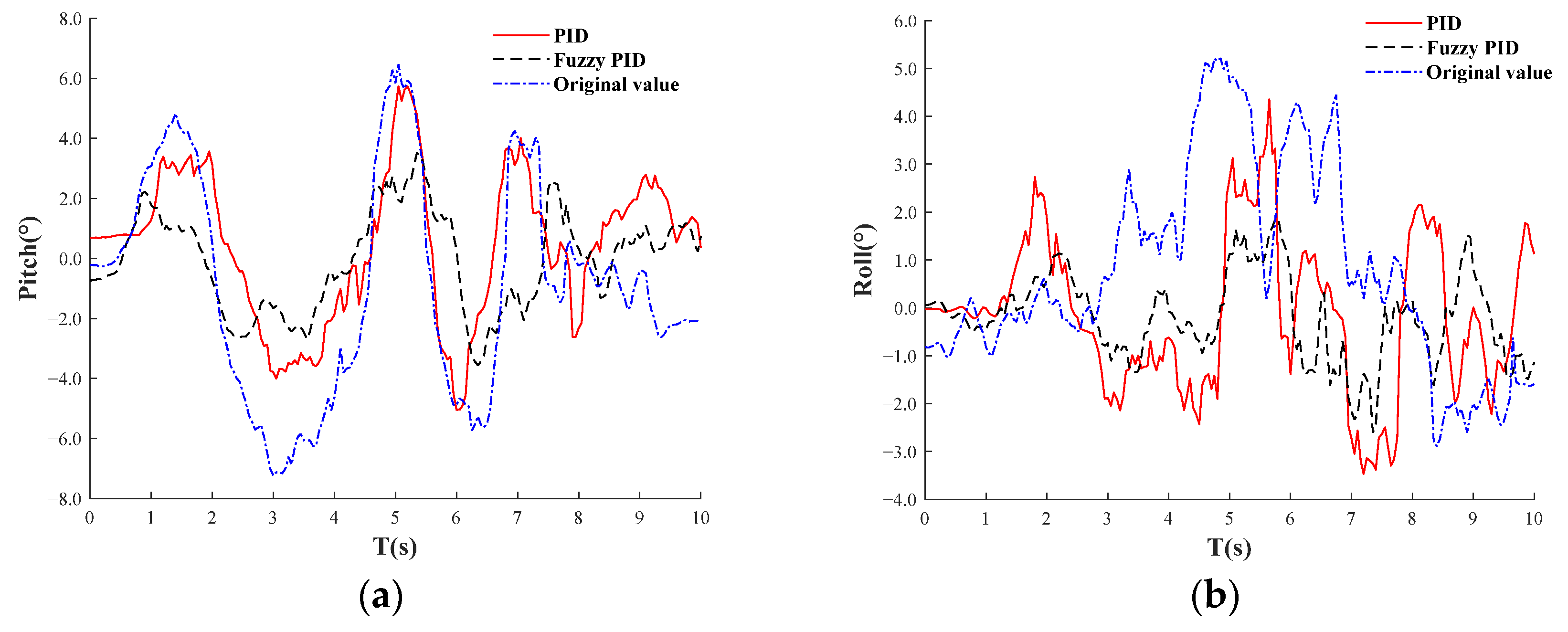
2.5.3. Co-Simulation Results Analysis
3. The Experimental Program and Analysis of Results
3.1. The Experimental Program
3.2. Analysis of Results
3.2.1. Analysis of Static Test Results
3.2.2. Analysis of Dynamic Test Results
3.3. Summary of Test Results
4. Conclusions
- (1)
- Theoretical analysis of the orchard operation platform’s leveling structural parameters led to the derivation of a mathematical relationship between the maximum adjustment angle and related parameters. Structural parameters were optimized, and a formula was developed to relate the platform’s attitude angle to the electric actuator’s displacement through coordinate transformation. Furthermore, a center-point leveling strategy was proposed, offering a solid theoretical foundation for leveling simulations and prototype development.
- (2)
- Using MATLAB, the PID algorithm parameters were fine-tuned, and a fuzzy PID algorithm was developed with well-defined fuzzy rules. After extensive testing, optimal parameters for the system were identified. Simulations of the orchard’s uneven terrain were conducted using MATLAB and ADAMS, applying both PID and fuzzy PID control strategies. Results showed that the fuzzy PID algorithm significantly outperformed the traditional PID, maintaining the platform’s attitude angle within the desired range. This finding lays a solid theoretical foundation for the development of the leveling system.
- (3)
- Static and dynamic tests on the prototype revealed an inclination adjustment error of 1.7° and an average leveling time of 3.6 s across eight inclination states. With fuzzy PID control, the prototype’s mean inclination values were 3.8°, 2.6°, and 1.6°, with standard deviations of 2.1°, 1.4°, and 0.8°, respectively. This adaptive leveling system exhibited superior performance, confirming the feasibility and accuracy of the proposed method. The leveling process activates when inclinations exceed ±1.5°, maintaining the platform’s attitude angle within ±3°, thus achieving stable dynamic leveling.
- (4)
- The research findings offer valuable insights for orchard operation platform studies and manufacturers. The theoretical analysis of leveling structural parameters aids in designing prototypes with enhanced leveling performance and understanding the influence of various structural parameters. By adjusting PID parameters and establishing fuzzy rules using MATLAB, followed by co-simulations with ADAMS, manufacturers can adopt the more effective fuzzy PID control algorithm for improved stability on uneven orchard terrain. Additionally, dynamic and static prototype tests provide concrete data on system performance, validating the practical application of the proposed leveling method and guiding the design of reliable and efficient leveling systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.J.; Chen, H.L.; Peng, J.B.; Meng, L.; Zhang, X.; Li, M.Z. Design and Test of Hydraulic Remote Control Crawler Power Chassis for Hilly and Mountainous Orchards. J. Agric. Mach. 2024, 55, 119–201, (In Chinese witch English abstract). [Google Scholar]
- Zheng, Y.J.; Jiang, S.; Chen, B.T.; Lu, H.T.; Wan, C.; Kang, F. Review on Technology and Equipment of Mechanization in Hilly Orchard. J. Agric. Mach. 2020, 51, 1–20, (In Chinese witch English abstract). [Google Scholar]
- Chen, Q.; Yin, C.K.; Guo, Z.L.; Wang, J.P.; Zhou, H.P.; Jiang, X.S. Current status and future development of the key technologies for apple picking robots. J. Trans. Chin. Soc. Agric. Eng. 2023, 38, 1–15, (In Chinese with English abstract). [Google Scholar]
- Li, H.B.; Chen, L.W.; Zhang, Z.Y. A Study on the Utilization Rate and Influencing Factors of Small Agricultural Machinery: Evidence from 10 Hilly and Mountainous Provinces in China. Agriculture 2023, 13, 51. [Google Scholar] [CrossRef]
- Yang, J.; Qin, X.; Lei, J.; Lu, L.; Zhang, J.; Wang, Z. Design and Experiment of a Crawler-Type Harvester for Red Cluster Peppers in Hilly and Mountainous Regions. Agriculture 2024, 14, 1742. [Google Scholar] [CrossRef]
- Mhamed, M.; Zhang, Z.; Yu, J.F.; Li, Y.F.; Zhang, M. Advances in apple’s automated orchard equipment: A comprehensive research. Comput. Electron. Agric. 2024, 221, 33. [Google Scholar] [CrossRef]
- Karl, A.; Knickerbocker, W.; Peck, G. Mechanically Harvesting Hard Cider Apples Is More Economically Favorable than Hand Harvesting, Regardless of Farm Scale. HortTechnology 2022, 32, 359–368. [Google Scholar] [CrossRef]
- Li, S.B.; Li, J.P.; Yu, S.M.; Wang, P.F.; Liu, H.J.; Yang, X. Anti-Drift Technology Progress of Plant Protection Applied to Orchards: A Review. Agronomy 2023, 13, 2679. [Google Scholar] [CrossRef]
- Almady, S.; Khelifi, M. Design and Preliminary Testing of a Pneumatic Prototype Machine to Control the Colorado Potato Beetle. Appl. Eng. Agric. 2021, 37, 645–651. [Google Scholar] [CrossRef]
- Bayat, A.; Itmeç, M.; Özlüoymak, Ö. Development and assessment of a novel servo-controlled spraying system for real time adjustment of the orientation angle of the nozzles of a boom sprayer. Pest Manag. Sci. 2023, 79, 4439–4450. [Google Scholar] [CrossRef] [PubMed]
- Dou, H.J.; Zhai, C.Y.; Chen, L.P.; Wang, X.; Zou, W. Comparison of Orchard Target-Oriented Spraying Systems Using Photoelectric or Ultrasonic Sensors. Agriculture 2021, 11, 753. [Google Scholar] [CrossRef]
- Khorsandi, F.; Ayers, P.D.; Fong, E.J. Evaluation of Crush Protection Devices for agricultural All-Terrain Vehicles. Biosyst. Eng. 2019, 185, 161–173. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Chen, W.; Hu, H.S.; Wu, X.F.; Xiao, C.S.; Song, X.Y. Multi-sensor based attitude prediction for agricultural vehicles. Comput. Electron. Agric. 2019, 156, 24–32. [Google Scholar] [CrossRef]
- Sun, J.; Meng, C.; Zhang, Y.; Chu, G.; Zhang, Y.; Yang, F.; Liu, Z. Design and physical model experiment of an attitude adjustment device for a crawler tractor in hilly and mountainous regions. Inf. Process. Agric. 2020, 7, 13. [Google Scholar] [CrossRef]
- van der Westhuizen, S.F.; Els, P.S. Slow active suspension control for rollover prevention. J. Terramech. 2013, 50, 29–36. [Google Scholar] [CrossRef]
- Hu, L.; Lin, C.X.; Luo, X.W.; Yang, W.W.; Xu, Y.; Zhou, H.; Zhang, Z.G. Design and experiment on auto leveling control system of agricultural implements. J. Trans. Chin. Soc. Agric. Eng. 2015, 31, 15–20, (In Chinese with English abstract). [Google Scholar]
- Jiang, Y.; Sun, Z.; Wang, R.; Xia, C.; Ye, Q.; Guo, Y. Design and performance test of the omnidirectional leveling system for crawler work machine in hilly areas. J. Trans. Chin. Soc. Agric. Eng. 2023, 39, 64–73, (In Chinese with English abstract). [Google Scholar]
- Guo, H.; Lu, H.; Gao, G.M.; Wu, T.L.; Chen, H.Y.; Qiu, Z.X. Design and Test of a Levelling System for a Mobile Safflower Picking Platform. Appl. Sci. 2023, 13, 18. [Google Scholar] [CrossRef]
- Jiang, Y.; Sun, Z.Y.; Wang, R.C.; Ding, R.K.; Ye, Q. Design and control of a new omnidirectional levelling system for hilly crawler work machines. Comput. Electron. Agric. 2024, 218, 15. [Google Scholar] [CrossRef]
- Chai, X.Y.; Hu, J.P.; Ma, T.L.; Liu, P.; Shi, M.L.; Zhu, L.J.; Zhang, M.; Xu, L.Z. Construction and Characteristic Analysis of Dynamic Stress Coupling Simulation Models for the Attitude-Adjustable Chassis of a Combine Harvester. Agronomy 2024, 14, 25. [Google Scholar] [CrossRef]
- Li, D.S.; Gao, F.; Li, Z.M.; Zhang, Y.T.; Gao, C.; Li, H.B. Design of a Leaf-Bottom Pest Control Robot with Adaptive Chassis and Adjustable Selective Nozzle. Agriculture 2024, 14, 23. [Google Scholar] [CrossRef]
- Sun, Y.X.; Xu, L.Z.; Jing, B.; Chai, X.Y.; Li, Y.M. Development of a four-point adjustable lifting crawler chassis and experiments in a combine harvester. Comput. Electron. Agric. 2020, 173, 12. [Google Scholar] [CrossRef]
- Yu, J.; Yan, Q.L.; Huang, G.Q.; Li, J.P. Simulation analysis on four corners leveling system of FRP products hydraulic press. In Proceedings of the 16th International Conference on Fluid Dynamic and Mechanical and Electrical Control Engineering (FDMECE 2012), Chinese Assoc Fluid Power Control Engn, Chongqing, China, 10–12 November 2012; pp. 146–149. [Google Scholar]
- Amertet, S.; Gebresenbet, G.; Alwan, H.M. Modeling of Unmanned Aerial Vehicles for Smart Agriculture Systems Using Hybrid Fuzzy PID Controllers. Appl. Sci. 2024, 14, 27. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, H. Control System Design of a DSP- based Real-time Leveling Platform. In Proceedings of the International Conference on Electronic, Information and Computer Engineering (ICEICE), Hong Kong, China, 26–27 April 2016. [Google Scholar]
- Liu, W.J.; Zeng, S.; Chen, X.G. Design and Experiment of Adaptive Profiling Heard Based on Multi-Body Dynamics-Discrete Element Method Coupling. Agriculture 2024, 14, 105. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Towards Type-3 Fuzzy Control Stability with a Fuzzy Lyapunov Approach: The Case of a Robotic Manipulator. In Proceedings of the International Conference on Intelligent and Fuzzy Systems (INFUS), Canakkale, Turkey, 16–18 July 2024; pp. 573–579. [Google Scholar]
- Chou, C.H.; Chen, P.T.; Yang, C.J.; Huang, K.D. Functionalization of Wireless Control and Fuzzy Systems to Hybrid Mini-Loaders. IEEE Access 2020, 8, 80914–80921. [Google Scholar] [CrossRef]
- Hu, J.P.; Pan, J.H.; Dai, B.W.; Chai, X.Y.; Sun, Y.X.; Xu, L.Z. Development of an Attitude Adjustment Crawler Chassis for Combine Harvester and Experiment of Adaptive Leveling System. Agronomy 2022, 12, 717. [Google Scholar] [CrossRef]
- Sun, X.Q.; Cai, Y.F.; Yuan, C.C.; Wang, S.H.; Chen, L. Fuzzy Sliding Mode Control for the Vehicle Height and Leveling Adjustment System of an Electronic Air Suspension. Chin. J. Mech. Eng. 2018, 31, 13. [Google Scholar] [CrossRef]
- Zuo, D.Q.; Qian, L.X.; Yang, T.E.; Cui, X.J.; Luo, Q. Coupling Leveling Control Based on Fuzzy PID for Synchronous Loading System of Load-Bearing Test Bed. Chin. J. Electron. 2017, 26, 1206–1212. [Google Scholar] [CrossRef]
- Chen, J.; Ning, X.; Li, Y.; Yang, G.; Wu, P.; Chen, S. A Fuzzy Control Strategy for The Forward Speed of a Combine Harvester Based on Kdd. Appl. Eng. Agric 2017, 33, 15–22. [Google Scholar]
- Zhu, Q.Z.; Zhu, Z.H.; Zhang, H.Y.; Gao, Y.Y.; Chen, L.P. Design of an Electronically Controlled Fertilization System for an Air-Assisted Side-Deep Fertilization Machine. Agriculture 2023, 13, 2210. [Google Scholar] [CrossRef]
- Ji, K.Z.; Li, Y.M.; Liang, Z.W.; Liu, Y.B.; Cheng, J.H.; Wang, H.H.; Zhu, R.H.; Xia, S.B.; Zheng, G.Q. Device and Method Suitable for Matching and Adjusting Reel Speed and Forward Speed of Multi-Crop Harvesting. Agriculture 2022, 12, 213. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Xia, C.G.; Jiang, Y.; Guo, Y.F.; Wang, R.C. Research on Omnidirectional Leveling Control of Crawler-type Work Machine Based on QBP-PID. J. Agric. Mach. 2023, 54, 397–406, (In Chinese witch English abstract). [Google Scholar]
- Huang, S.J.; Pan, K.X.; Wang, S.B.; Zhu, Y.; Zhang, Q.; Su, X.; Yu, H.J. Design and Test of an Automatic Navigation Fruit-Picking Platform. Agriculture 2023, 13, 25. [Google Scholar] [CrossRef]










| ∆Kp | e | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| ec | NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PS | PS | ZO | NS | |
| NS | PM | PM | PM | PS | ZO | NS | NS | |
| ZO | PM | PM | PS | ZO | NS | NM | NM | |
| PS | PS | PS | ZO | NS | NS | NM | NM | |
| PM | PS | ZO | NS | NM | NM | NM | NB | |
| PB | ZO | ZO | NM | NB | NB | NB | NB | |
| ΔKi | e | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| ec | NB | NB | NB | NM | NM | NS | ZO | ZO |
| NM | NB | NB | NM | NS | NS | ZO | ZO | |
| NS | NB | NM | NS | NS | ZO | PS | PS | |
| ZO | NM | NM | NS | ZO | PS | PM | PM | |
| PS | NM | NS | ZO | PS | PS | PM | PB | |
| PM | ZO | ZO | PS | PS | PM | PB | PB | |
| PB | ZO | ZO | PS | PM | PM | PB | PB | |
| ∆Kd | e | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | ||
| ec | NB | PS | NS | NB | NB | NB | NM | PS |
| NM | PS | NS | NB | NM | NM | NS | ZO | |
| NS | ZO | NS | NM | NM | NS | NS | ZO | |
| ZO | ZO | NS | NS | NS | NS | NM | ZO | |
| PS | ZO | ZO | ZO | ZO | ZO | ZO | ZO | |
| PM | PB | NS | PS | NS | PS | PS | PB | |
| PB | PB | PM | PM | PM | PS | PS | PB | |
| Group | Before Leveling | After Leveling | Leveling Time | ||
|---|---|---|---|---|---|
| α | β | α | β | ||
| Front highest | 6.1° | 1.1° | 1.3° | 0.4° | 3.0 s |
| Rear highest | −5.1° | 0.8° | −1.4° | 0.5° | 2.8 s |
| Left highest | 8.3° | 0.3° | 1.3° | 1.1° | 3.0 s |
| Right highest | −8.2° | 1.3° | −1.4° | 0.7° | 3.1 s |
| Left front highest | 5.8° | 3.1° | 1.1° | 1.0° | 3.8 s |
| Left front highest | 7.7° | −4.1° | 1.0° | −1.4° | 4.7 s |
| Right rear highest | −6.0° | −4.1° | −0.9° | −1.4° | 3.7 s |
| Right front highest | 4.1° | −4.1° | 1.2° | −1.4° | 4.5 s |
| Index | This Study | Ref [35] | Ref [36] | Improvement |
|---|---|---|---|---|
| Control method | Fuzzy PID | QBP-PID | No leveling | No training required |
| Drive mode | Electric drive | Hydraulic drive | Electric drive | Electronic control |
| Dynamic response | Quick response(±1.5°) | Quick response(<1.5°) | No leveling | No training required |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Lu, Z.; Cui, B.; Xie, Y. Design and Test of Adaptive Leveling System for Orchard Operation Platform. Sensors 2025, 25, 1319. https://doi.org/10.3390/s25051319
Guo J, Lu Z, Cui B, Xie Y. Design and Test of Adaptive Leveling System for Orchard Operation Platform. Sensors. 2025; 25(5):1319. https://doi.org/10.3390/s25051319
Chicago/Turabian StyleGuo, Jianpeng, Zemin Lu, Bingbo Cui, and Yuanzhen Xie. 2025. "Design and Test of Adaptive Leveling System for Orchard Operation Platform" Sensors 25, no. 5: 1319. https://doi.org/10.3390/s25051319
APA StyleGuo, J., Lu, Z., Cui, B., & Xie, Y. (2025). Design and Test of Adaptive Leveling System for Orchard Operation Platform. Sensors, 25(5), 1319. https://doi.org/10.3390/s25051319






