Sensitivity-Enhanced Temperature Sensor Based on PDMS-Coated Mach–Zehnder Interferometer
Abstract
1. Introduction
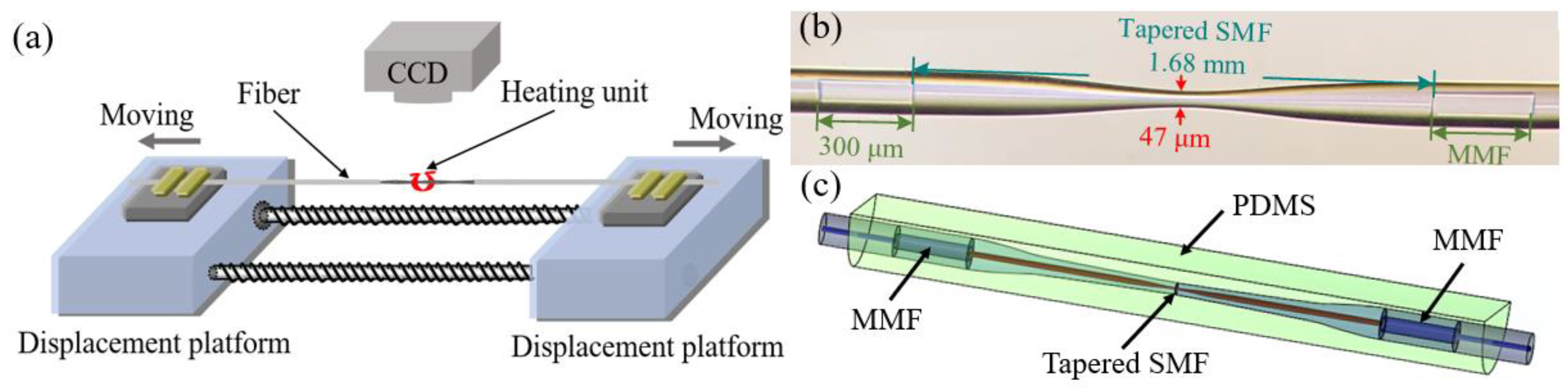
2. Fabrication and Principle
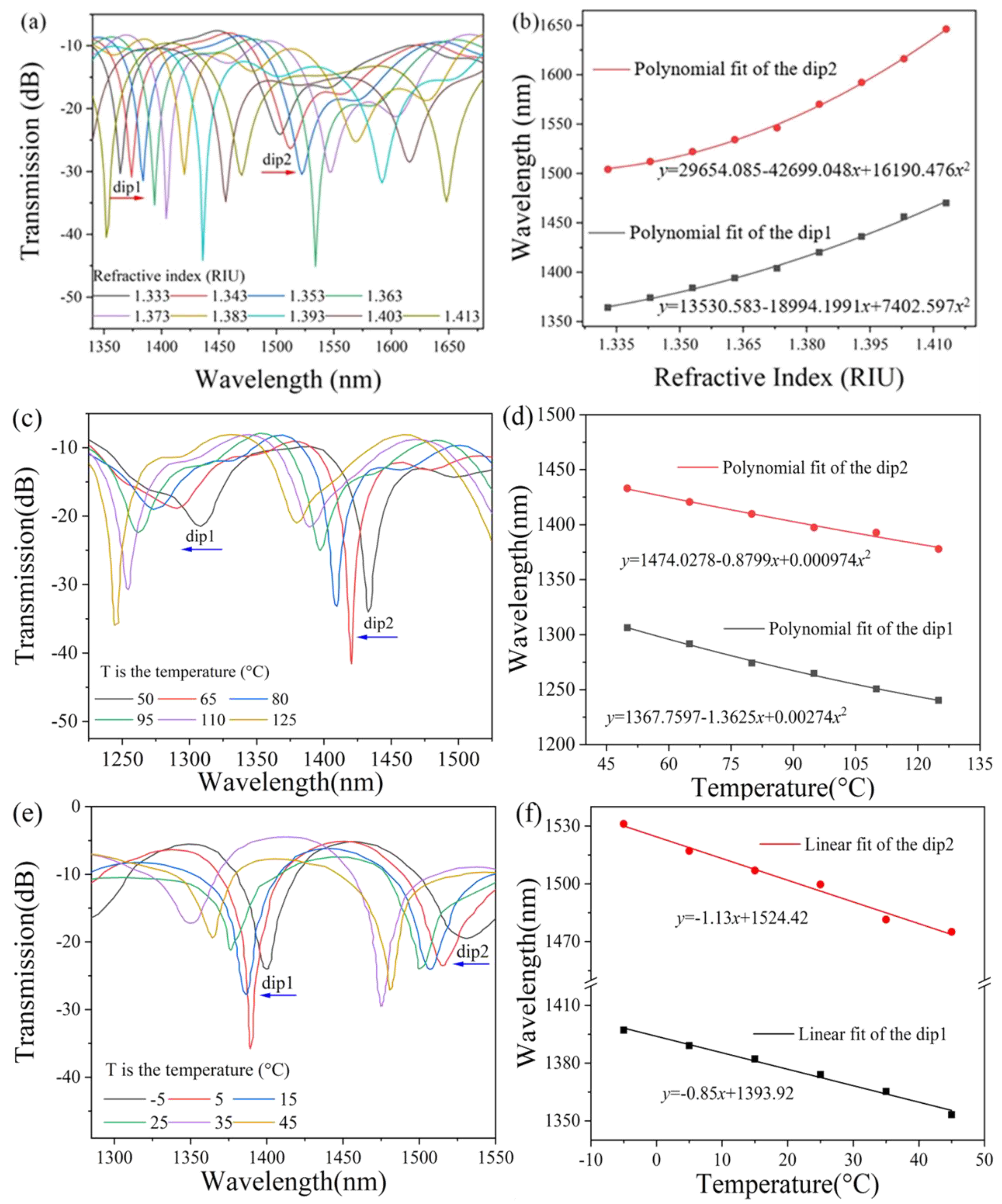
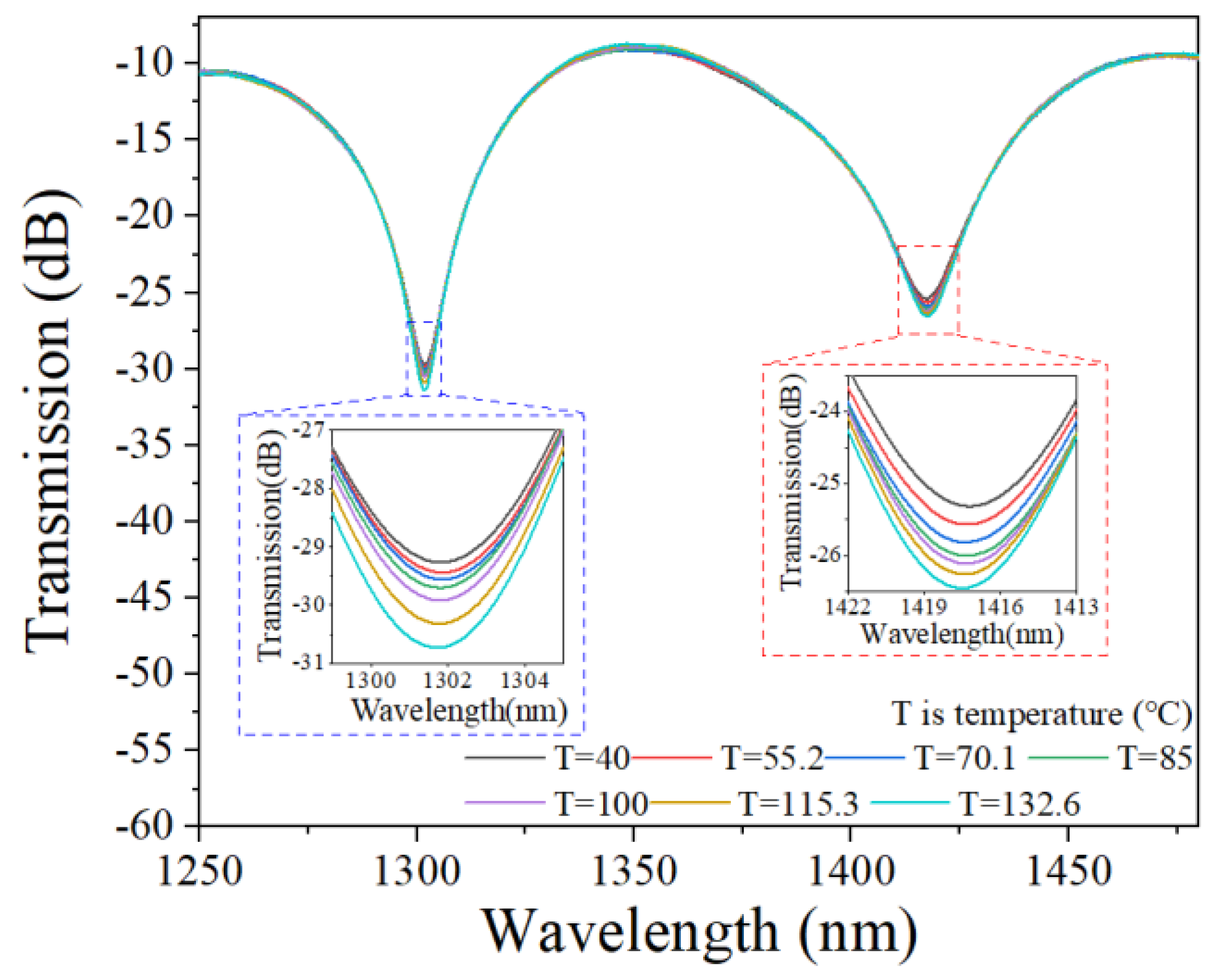
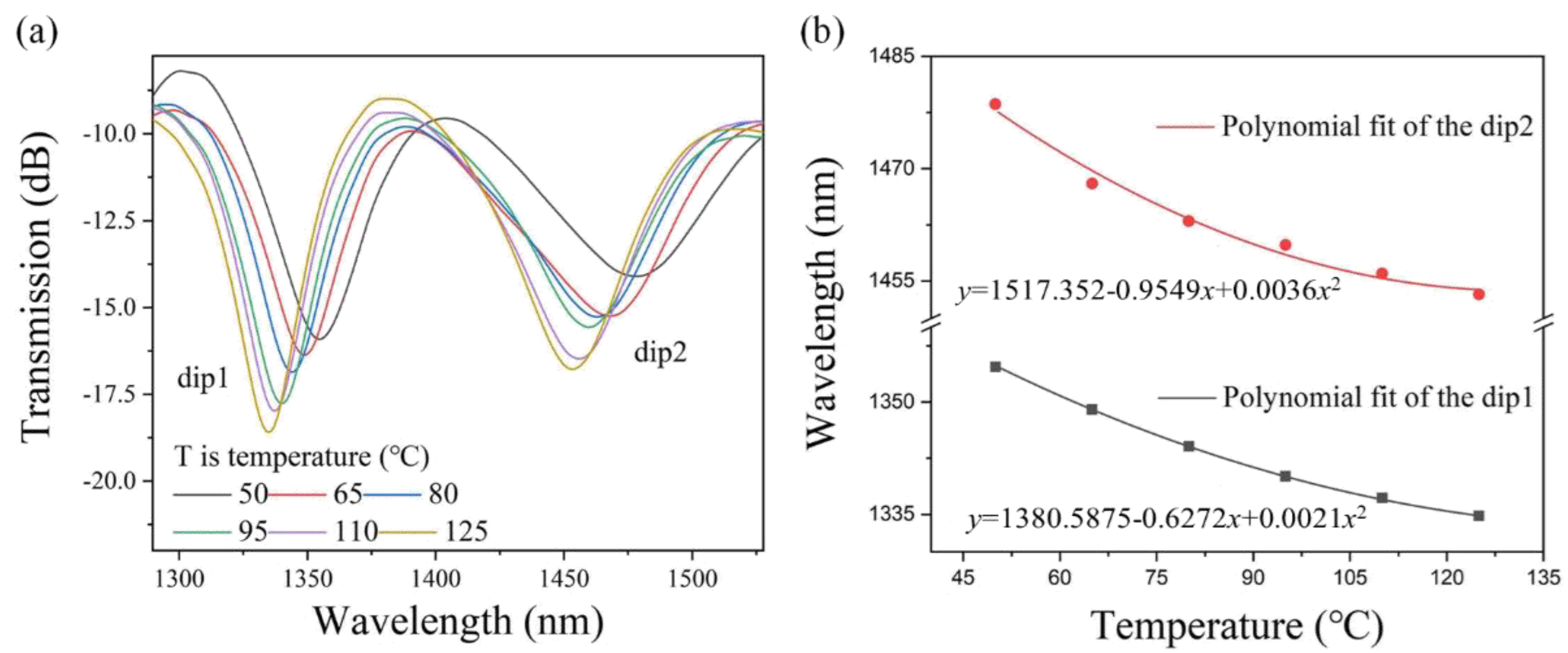
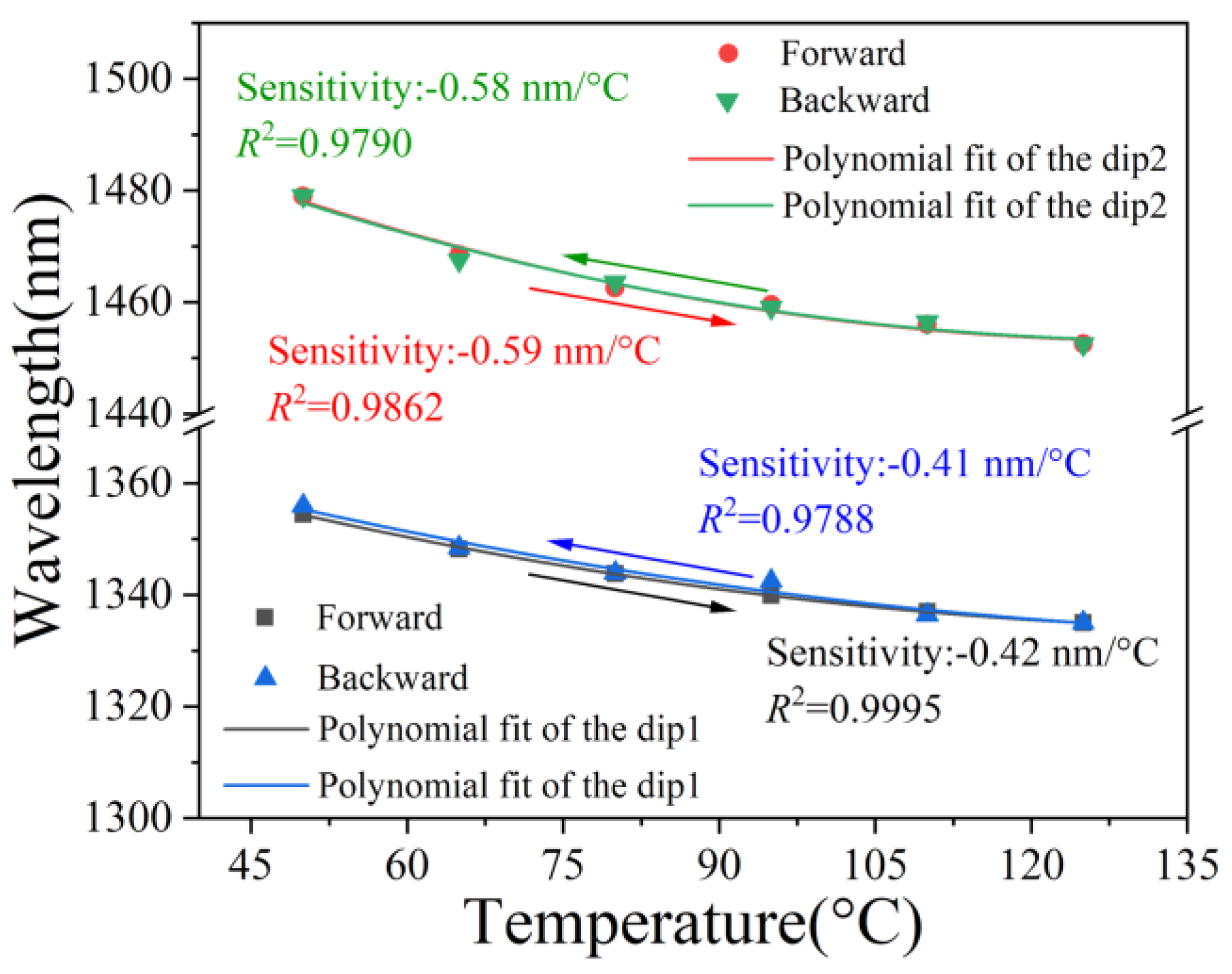
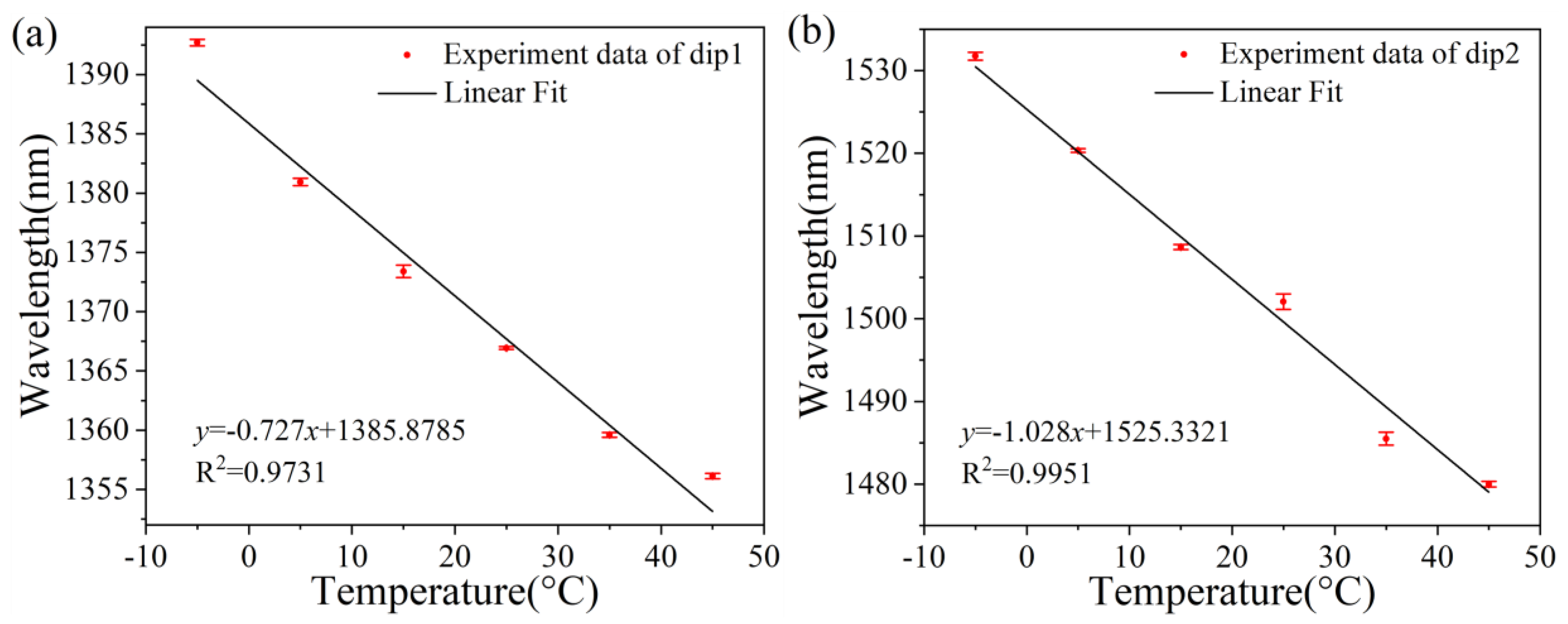
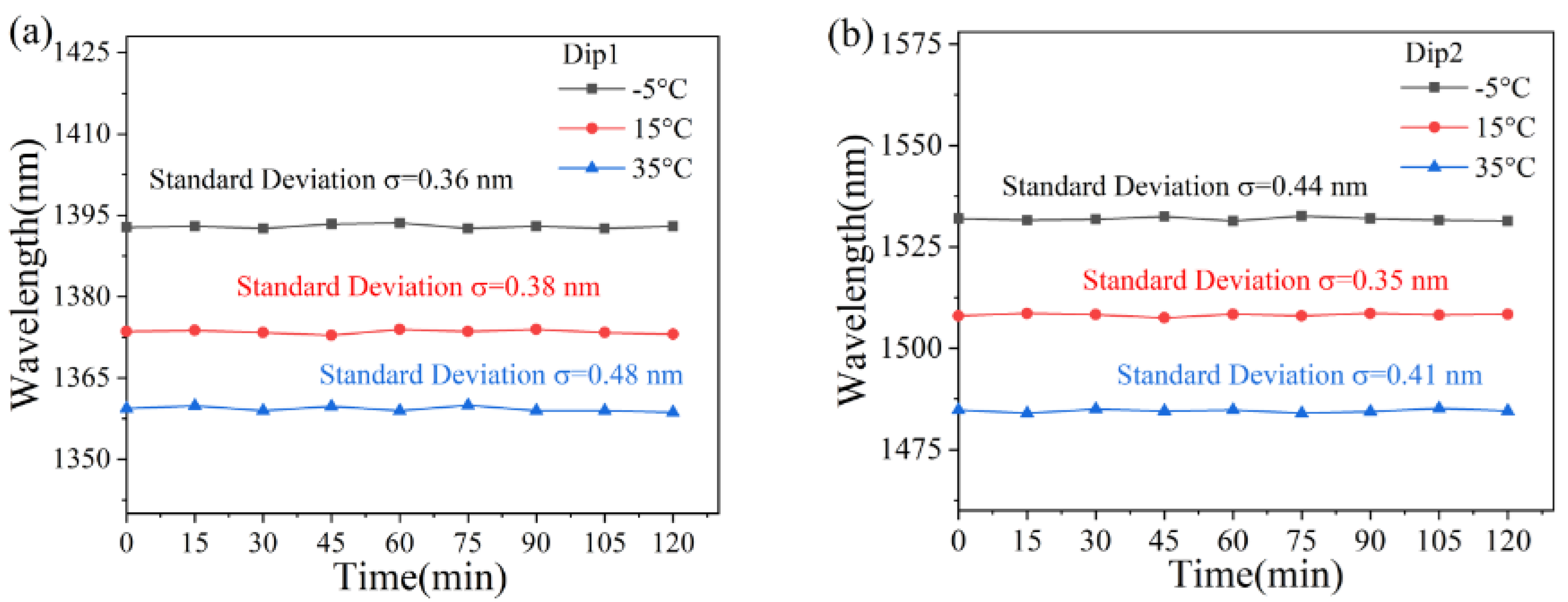
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schultze, S.R.; Campbell, M.N.; Walley, S.; Pfeiffer, K.; Wilkins, B. Exploration of sub-field microclimates and winter temperatures: Implications for precision agriculture. Int. J. Biometeorol. 2021, 65, 1043–1052. [Google Scholar] [CrossRef] [PubMed]
- Joe, H.-E.; Yun, H.; Jo, S.-H.; Jun, M.B.G.; Min, B.-K. A review on optical fiber sensors for environmental monitoring. Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 173–191. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Li, Z.; Hou, M.; Dong, G.; Liu, T.; Sun, T.; Grattan, K.T.V. Quasi-distributed fiber optic temperature and humidity sensor system for monitoring of grain storage in granaries. IEEE Sens. J. 2020, 20, 9226–9233. [Google Scholar] [CrossRef]
- Šopík, T.; Lazárková, Z.; Buňková, L.; Purevdorj, K.; Salek, R.N.; Talár, J.; Novotný, M.; Foltin, P.; Pachlová, V.; Buňka, F. Impact of long-term storage on the quality of selected sugar-based foods stored at different temperatures. LWT 2022, 157, 113095. [Google Scholar] [CrossRef]
- Zaman, N.I.D.; Hau, Y.W.; Leong, M.C.; Al-ashwal, R.H.A. A review on the significance of body temperature interpretation for early infectious disease diagnosis. Artif. Intell. Rev. 2023, 56, 15449–15494. [Google Scholar] [CrossRef]
- Huang, Y.; Zeng, X.; Wang, W.; Guo, X.; Hao, C.; Pan, W.; Liu, P.; Liu, C.; Ma, Y.; Zhang, Y.; et al. High-resolution flexible temperature sensor based graphite-filled polyethylene oxide and polyvinylidene fluoride composites for body temperature monitoring. Sens. Actuators A Phys. 2018, 278, 1–10. [Google Scholar] [CrossRef]
- Garavito, J.; Galvis, C.; López, A.M.; Franco, A.P.; Barreiro, F.; Tarazona, R.L.; Serpa-Imbett, C.M. Heating device based on modified microwave oven: Improved to measure liquid temperature by using FBG sensors. Photonics 2021, 8, 104. [Google Scholar] [CrossRef]
- Xu, W.; Bian, Q.; Liang, J.; Wang, Z.; Yu, Y.; Meng, Z. Recent advances in optical fiber high-temperature sensors and encapsulation technique. Chin. Opt. Lett. 2023, 21, 090007. [Google Scholar]
- Cong, X.; Wang, C.; Qin, Y.; Yu, R.; Ji, W.; Liu, A.; Shen, Y.; Xiao, L. 3D-printed ultracompact multicore fiber-tip probes for simultaneous measurement of nanoforce and temperature. ACS Appl. Mater. Interfaces 2024, 16, 30443–30452. [Google Scholar]
- Lv, R.-Q.; Li, S.-Q.; Wang, W.; Li, Z.-H.; Zhou, L.; Zang, Y.-M.; Zhang, M.-X.; Liu, J.-Y.; Liu, Y.-N. Temperature characterization of thin-walled-microsphere air-cavity fiber sensing structures. Sens. Actuators A Phys. 2023, 349, 114081. [Google Scholar] [CrossRef]
- Wu, C.; Fu, H.Y.; Qureshi, K.K.; Guan, B.-O.; Tam, H.Y. High-pressure and high-temperature characteristics of a Fabry-Perot interferometer based on photonic crystal fiber. Opt. Lett. 2011, 36, 412–414. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Wang, J.; Wang, Y.; Dai, X. A fast response temperature sensor based on fiber Bragg grating. Meas. Sci. Technol. 2014, 25, 075105. [Google Scholar] [CrossRef]
- Liu, J.; Luo, C.; Yang, H.; Yi, Z.; Liu, B.; He, X.; Wu, Q. Mach-Zehnder interferometer for high temperature (1000 °C) sensing based on a few-mode fiber. Photonic Sens. 2021, 11, 341–349. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, X.; Zhou, X.; Liu, W.; Song, D.; Yan, X.; Zhang, X.; Wang, F.; Suzuki, T.; Ohishi, Y.; et al. An antiinterference temperature sensor based on Mach-Zehnder interferometer using Kagome hollow-core photonic crystal fiber. IEEE Sens. J. 2023, 23, 8426–8434. [Google Scholar] [CrossRef]
- Deng, H.; Jiang, X.; Huang, X.; Chen, M.; Yang, H.; Cheng, Y.; Teng, C.; Xu, R.; Yuan, L. A temperature sensor based on composite optical waveguide. J. Light. Technol. 2022, 40, 2663–2669. [Google Scholar] [CrossRef]
- Li, X.; Gao, S.; Yang, J.; Ye, P.; Zhu, Z.; Li, P.; Shi, J.; Yuan, L.; Guan, C. High sensitivity temperature sensor based on directional coupler in a liquid-filled tapered hollow suspended dual-core fiber. J. Light. Technol. 2024, 42, 5048–5054. [Google Scholar] [CrossRef]
- Zhao, Y.; Dai, M.; Chen, Z.; Liu, X.; Gandhi, M.A.; Li, Q.; Fu, H. Ultrasensitive temperature sensor with Vernier-effect improved fiber Michelson interferometer. Opt. Express 2021, 29, 1090–1101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Wu, X.; Zhang, W.; Li, S.; Shi, J.; Zuo, C.; Fang, S.; Yu, B. High temperature Vernier probe utilizing photonic crystal fiber-based Fabry-Perot interferometers. Opt. Express 2019, 27, 37308–37317. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Pan, R.; Zhang, L.; Yang, Y.; Li, L.; Yu, S.; Sun, X.; Yu, X. Highly sensitive fiber-optic temperature sensor with compact hybrid interferometers enhanced by the harmonic Vernier effect. Opt. Express 2023, 31, 14570–14582. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, Q.; Xu, T.-S.; Wu, Q.; Fu, Y.; Ng, W.; Binns, R. Ultra-sensitive fiber optic temperature sensor based on Vernier effect in cascading Sagnac loops integrated with PMFs. Opt. Commun. 2024, 566, 130728. [Google Scholar] [CrossRef]
- Xin, Y.; Zhao, M.; Zhao, H.; Gong, H.; Shen, C.; Zhao, C.-L.; Dong, X. Alcohol-filled side-hole fiber based Mach-Zehnder interferometer for temperature measurement. Opt. Fiber Technol. 2018, 46, 72–76. [Google Scholar] [CrossRef]
- Yang, J.; Guan, C.; Tian, P.; Chu, R.; Ye, P.; Wang, K.; Shi, J.; Yang, J.; Yuan, L. High sensitivity temperature sensor based on liquid filled hole-assisted dual-core fiber. Sens. Actuators A Phys. 2020, 303, 111696. [Google Scholar] [CrossRef]
- Xue, Y.; Yu, Y.-S.; Yang, R.; Wang, C.; Chen, C.; Guo, J.-C.; Zhang, X.-Y.; Zhu, C.-C.; Sun, H.-B. Ultrasensitive temperature sensor based on an isopropanol-sealed optical microfiber taper. Opt. Lett. 2013, 38, 1209–1211. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Zhao, C.; Hu, X.; Chen, H.; Yu, Q.; Lian, Z.; Qu, H. Glycerol-water solution-assisted Mach-Zehnder temperature sensor in specialty fiber with two cores and one channel. Photonics 2021, 8, 103. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, W.; Zhang, L.; Li, C.; Guan, C.; Xiong, Y.; Yang, Y.; Li, L. The fiber temperature sensor with PDMS sensitization based on the T-MFM fiber structure. Opt. Fiber Technol. 2021, 67, 102701. [Google Scholar] [CrossRef]
- Chen, L.; Tian, J.; Wu, Q.; Wang, J.; Li, J.; Yao, Y. High-sensitivity temperature sensor based on PDMS-coated photonic crystal fiber interferometer. Opt. Fiber Technol. 2023, 80, 103409. [Google Scholar] [CrossRef]
- Zhang, S.; Deng, S.; Wang, Z.; Geng, T.; Yang, W.; Sun, C.; Yan, Q.; Li, Y.; Tong, C.; Dai, Q.; et al. A compact refractometer with high sensitivity based on multimode fiber embedded single mode-no core-single mode fiber structure. J. Light. Technol. 2020, 38, 1929–1935. [Google Scholar] [CrossRef]
- Song, Q.; Xiao, Y.; Huang, Z.; Sun, K.; Wu, Q. Investigation of temperature dependence of tapered optical fibers. Infrared Phys. Technol. 2025, 145, 105725. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, J.; Weng, Y.; Rong, Q.; Ma, Y.; Feng, Z.; Hu, M.; Qiao, X. Highly sensitive curvature sensor using an in-fiber Mach-Zehnder interferometer. IEEE Sens. J. 2013, 13, 1766–1770. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Hwang, D.; Moon, S.; Moon, D.S.; Chung, Y. High temperature fiber sensor with high sensitivity based on core diameter mismatch. Opt. Express 2008, 16, 11369–11375. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Lu, Y.; Wang, X.; Ma, T.; Li, L.; Yu, K.; Liu, Y.; Li, C.; Chen, Y. A highly sensitive temperature sensor with a PDMS-coated tapered dispersion compensation fiber structure. Opt. Commun. 2021, 497, 127183. [Google Scholar] [CrossRef]
- Biazoli, C.R.; Silva, S.; Franco, M.A.R.; Frazão, O.; Cordeiro, C.M.B. Multimode interference tapered fiber refractive index sensors. Appl. Opt. 2012, 51, 5941–5945. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, K.; Naveen, K. Comparative spectral tuning and fluctuation analysis of an all-fiber Mach Zehnder interferometer and micro Mach Zehnder interferometer. J. Opt. 2021, 23, 115702. [Google Scholar] [CrossRef]
- Fu, X.; Fu, Z.; Huang, Z.; Zhou, J.; Wang, J.; Jin, W.; Fu, G.; Bi, W. A directional curvature sensor using excentric heterogeneous fiber filled PDMS with spherical structure. IEEE Sens. J. 2023, 23, 22556–22563. [Google Scholar] [CrossRef]
- Khan, Y.; Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Thermal sensor based on polydimethylsiloxane polymer deposited on low-index-contrast dielectric photonic crystal structure. Photonics 2022, 9, 770. [Google Scholar] [CrossRef]
- Wu, H.; Song, Y.; Sun, M.; Wang, Q. Simulation of high-performance surface plasmon resonance sensor based on D-shaped dual channel photonic crystal fiber for temperature sensing. Materials 2023, 16, 37. [Google Scholar] [CrossRef]
- Lu, P.; Men, L.; Sooley, K.; Chen, Q. Tapered fiber Mach-Zehnder interferometer for simultaneous measurement of refractive index and temperature. Appl. Phys. Lett. 2009, 94, 131110. [Google Scholar] [CrossRef]
- Su, B.; Qi, B.; Zhang, F.; Zhong, L.; Xu, O.; Qin, Y. Hybrid fiber interferometer sensor for simultaneous measurement of strain and temperature with refractive index insensitivity. Opt. Commun. 2022, 522, 128637. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Tong, Z.; Wang, X.; Liu, D.; Wang, M.; Yu, H. Research on MZI sensor for refractive index and temperature based on D-shaped no core fiber. Opt. Mater. 2024, 148, 114933. [Google Scholar] [CrossRef]
- Gao, J.; Jiang, C.; Li, L.; Deng, L.; Hu, C.; Li, H.; Cao, T.; Sun, S. High sensitivity temperature and gas pressure sensor based on PDMS sealed tapered hollow-core fiber. Opt. Fiber Technol. 2024, 82, 103634. [Google Scholar] [CrossRef]
- Gong, J.; Shen, C.; Xiao, Y.; Liu, S.; Zhang, C.; Ding, Z.; Deng, H.; Fang, J.; Lang, T.; Zhao, C.; et al. High sensitivity fiber temperature sensor based PDMS film on Mach-Zehnder interferometer. Opt. Fiber Technol. 2019, 53, 102029. [Google Scholar] [CrossRef]
- Su, H.; Wang, Y.; Guan, C.; Yu, S.; Yu, X.; Yang, W. PDMS-sensitized MZI ffber optic temperature sensor based on TCF-NCF-TCF structure. Opt. Fiber Technol. 2022, 73, 103075. [Google Scholar] [CrossRef]
- Yi, D.; Liu, F.; Geng, Y.; Li, X.; Hong, X. High-sensitivity and large-range fiber optic temperature sensor based on PDMS-coated Mach-Zehnder interferometer combined with FBG. Opt. Express 2021, 29, 18624–18633. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Sun, S.; Jiang, C.; Chen, H.; Wang, S. Sensitivity-enhanced temperature sensor based on Mach–Zehnder interferometer coated with thermal-sensitive material. Rev. Sci. Instrum. 2021, 92, 125003. [Google Scholar] [CrossRef]





| Structure | Size (mm) | Range (°C) | Sensitivity (pm/°C) | Whether Temperature-Sensitive Materials Are Required | Ref. |
|---|---|---|---|---|---|
| Two-fiber taper | 54.5 | 20–60 | 77 | No | [37] |
| HCF and FMF | 50.037 | 0–120 | −38.8 | No | [38] |
| D-shaped no-core fiber | 40 | 25–80 | 86.1 | No | [39] |
| SHF | 80 | 23–90 | 105 | Yes (alcohol) | [21] |
| EHADCF | 10.5 | 10–100 | −562.4 | Yes (matching liquid) | [22] |
| Tapered HCF | 39 | 32–46 | −3232.1 | Yes (PDMS) | [40] |
| Mismatch structure of three SMFs | 40 | 20–100 | 101 | Yes (PDMS) | [41] |
| TCF–NCF–TCF | 30 | 45–80 | 130 | Yes (PDMS) | [42] |
| PDMS-coated MZI combined with an FBG | 2.34 | 30–60 | 11,190 | Yes (PDMS) | [43] |
| PCFI | 20 | 35–65 | −255 | Yes (PDMS) | [26] |
| TCF | 8 | 40–70 | 166.8 | Yes (PDMS) | [44] |
| STMS | 2.28 | −5–45 | −1060 | Yes (PDMS) | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Li, L.; Zhang, S.; Tian, K. Sensitivity-Enhanced Temperature Sensor Based on PDMS-Coated Mach–Zehnder Interferometer. Sensors 2025, 25, 1191. https://doi.org/10.3390/s25041191
Yang W, Li L, Zhang S, Tian K. Sensitivity-Enhanced Temperature Sensor Based on PDMS-Coated Mach–Zehnder Interferometer. Sensors. 2025; 25(4):1191. https://doi.org/10.3390/s25041191
Chicago/Turabian StyleYang, Wenlei, Le Li, Shuo Zhang, and Ke Tian. 2025. "Sensitivity-Enhanced Temperature Sensor Based on PDMS-Coated Mach–Zehnder Interferometer" Sensors 25, no. 4: 1191. https://doi.org/10.3390/s25041191
APA StyleYang, W., Li, L., Zhang, S., & Tian, K. (2025). Sensitivity-Enhanced Temperature Sensor Based on PDMS-Coated Mach–Zehnder Interferometer. Sensors, 25(4), 1191. https://doi.org/10.3390/s25041191






