Autonomous Mission Planning for Fixed-Wing Unmanned Aerial Vehicles in Multiscenario Reconnaissance
Abstract
1. Introduction
2. HTSP Path Planning
- Sequence Planning: This stage determines the order of visiting different scenarios. By optimizing the sequence, the UAV can minimize the overall flight range.
- Coverage Path Planning: The lower level addresses the coverage of area targets using BCD. This ensures that the UAV efficiently covers each area while adhering to constraints such as no-fly zones.
2.1. Sequence Planning
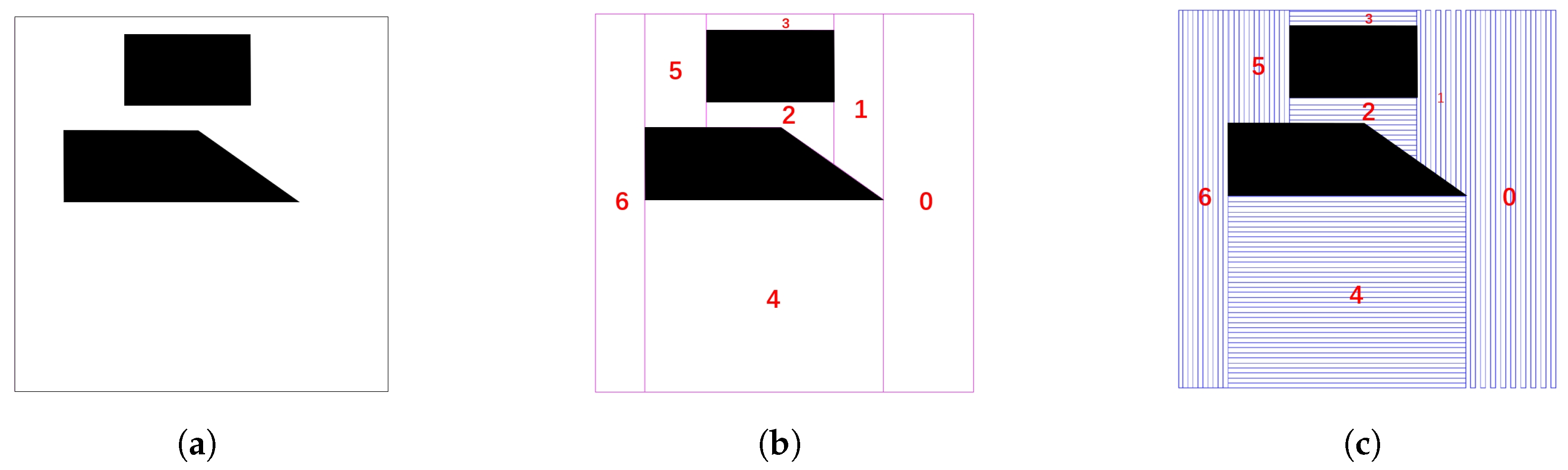
2.2. Coverage Path Planning with Area Target
- Binary decision variables:
- V is the set of cells except O.
- We ensure that each cell is entered and left at most once:
- Subtour elimination constraints (Miller–Tucker–Zemlin formulation):where is an auxiliary variable which keeps the number of visited cells until cell i in the solution. These constraints ensure that the solution forms a single continuous path.
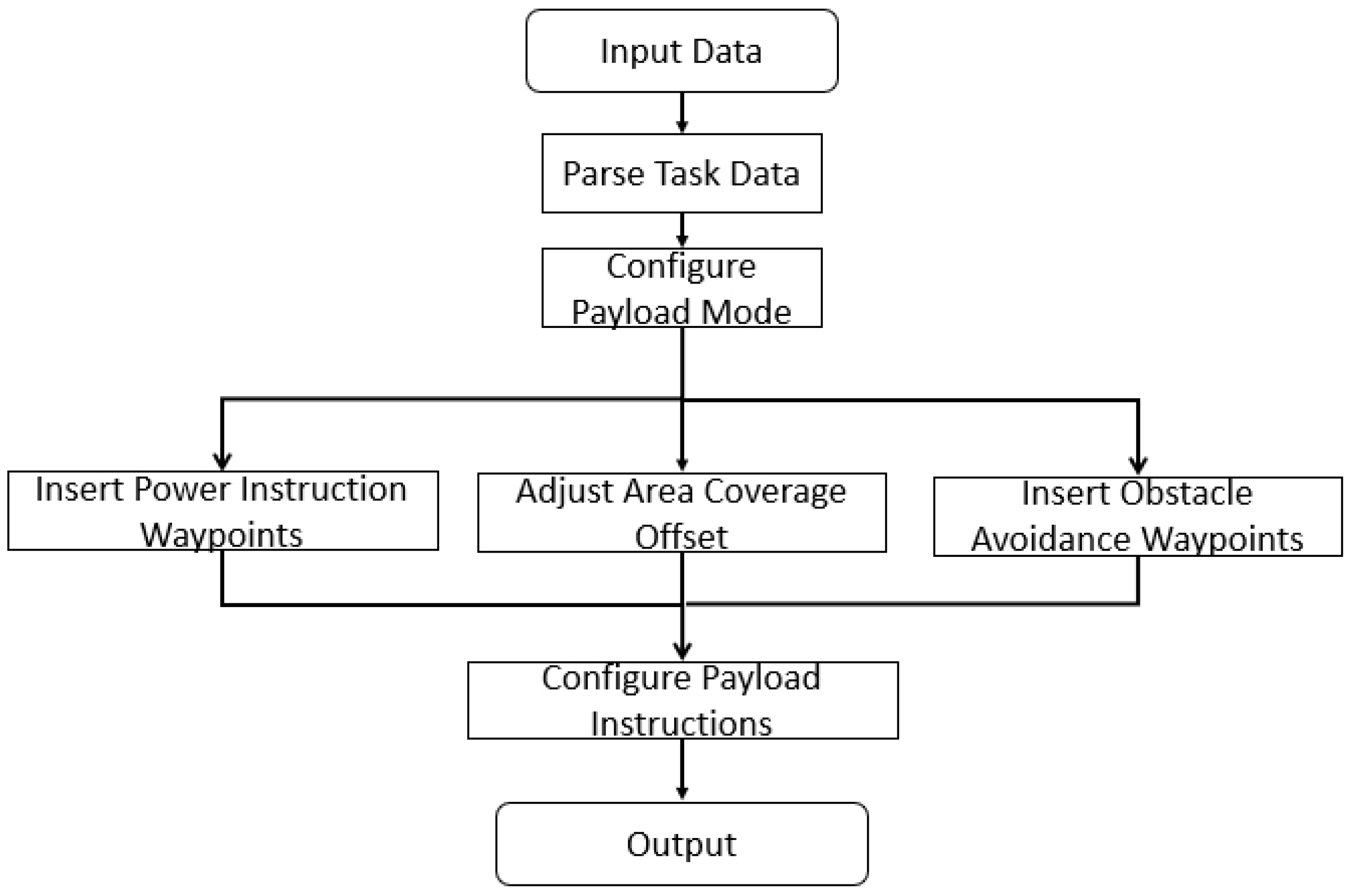
3. Payload Mission Planning
3.1. Power Instruction
3.2. Coverage Path Optimization with Payload
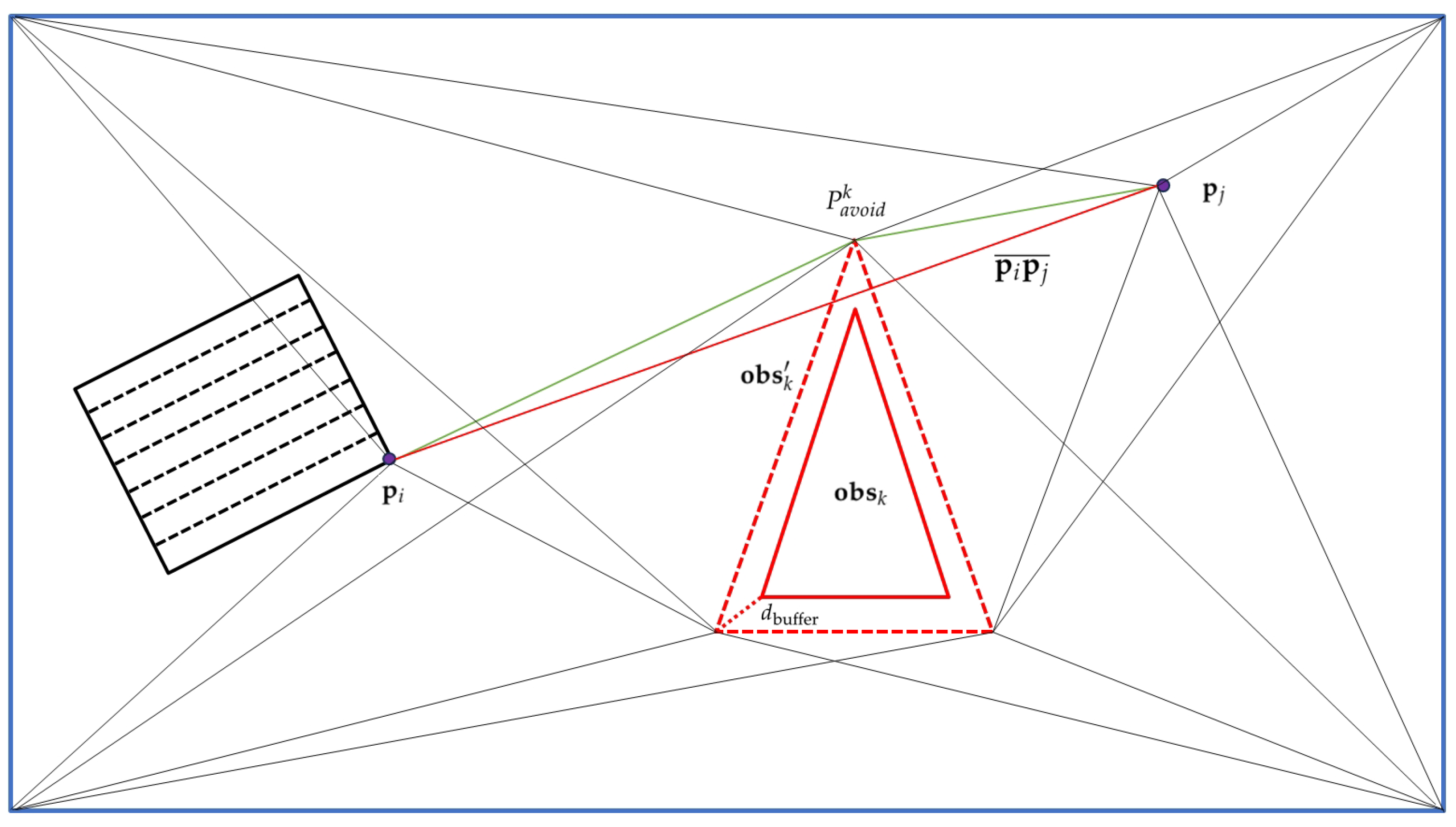
3.3. Obstacle Avoidance Based on Visibility Graph
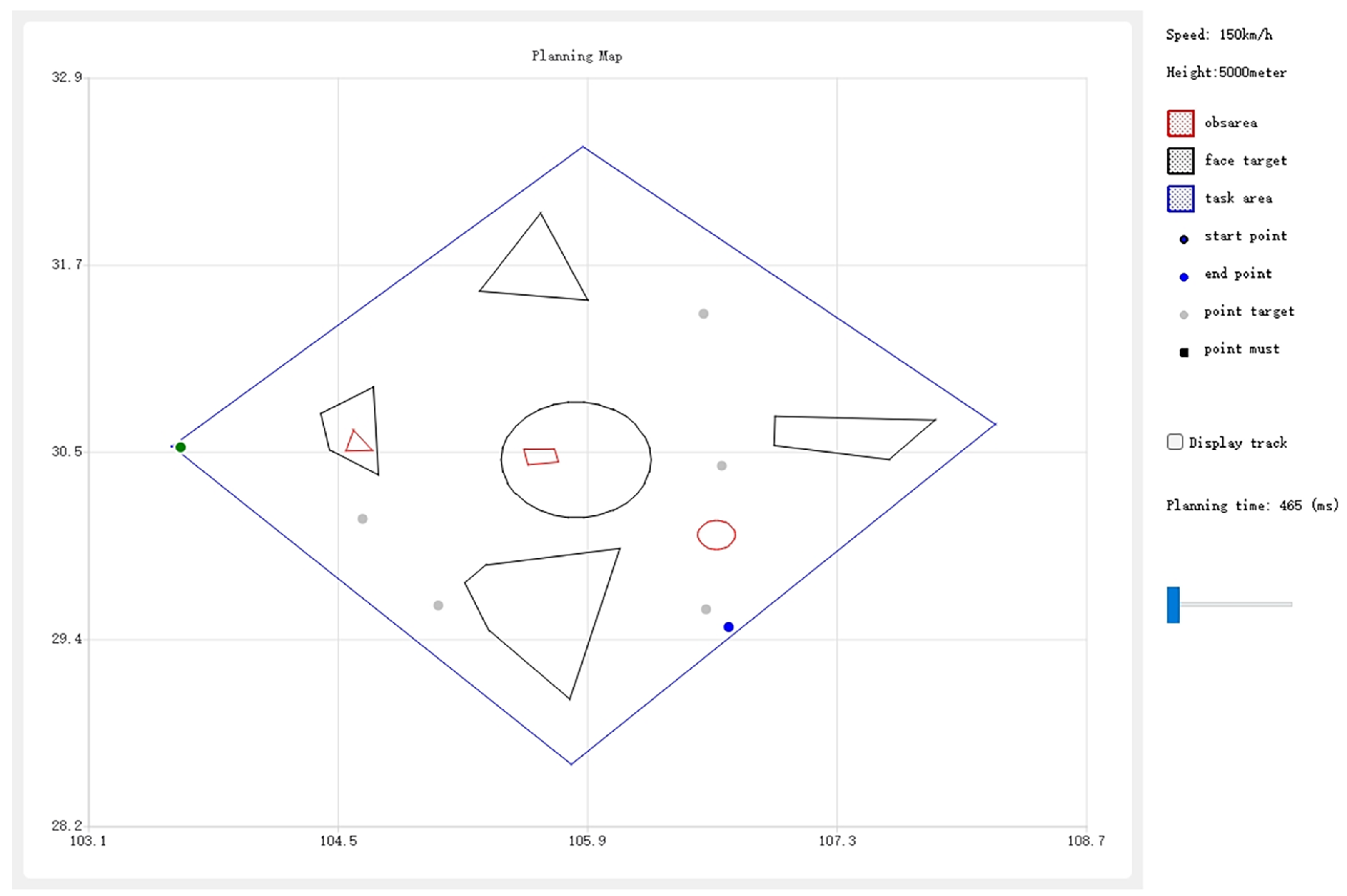
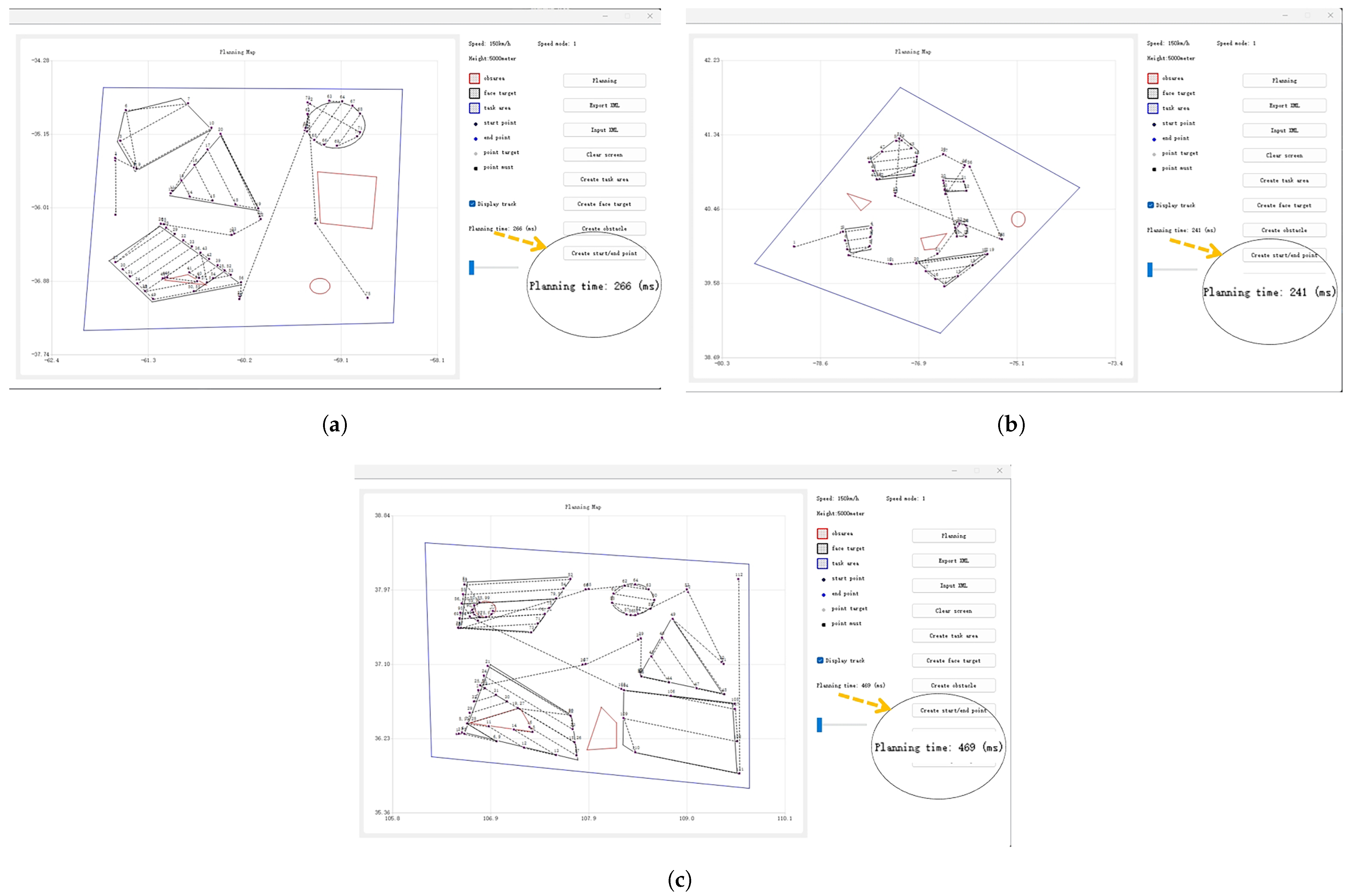
4. Experiments and Discussions
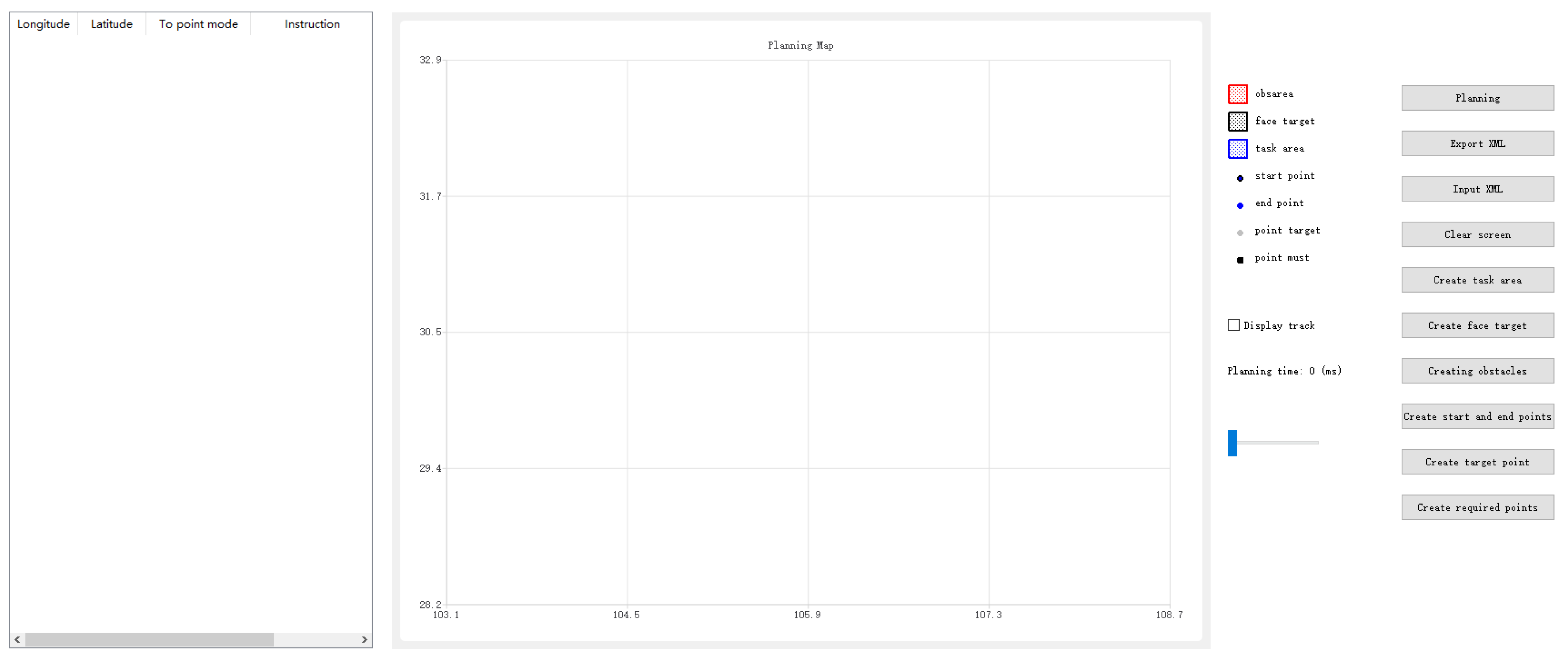
4.1. UI Design
4.2. Autonomous Mission Planning
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sonkar, S.; Kumar, P.; Philip, D.; Ghosh, A.K. Low-cost smart surveillance and reconnaissance using VTOL fixed wing UAV. In Proceedings of the 2020 IEEE Aerospace conference, Big Sky, MT, USA, 7 March 2020; pp. 1–7. [Google Scholar]
- Zhang, J.; Huang, H. Occlusion-aware UAV path planning for reconnaissance and surveillance. Drones 2021, 5, 98. [Google Scholar] [CrossRef]
- Ranasinghe, N.D.; Gunawardana, W.A.D.L. Development of gasoline-electric hybrid propulsion surveillance and reconnaissance VTOL UAV. In Proceedings of the 2021 IEEE International Conference on Robotics, Automation and Artificial Intelligence, Hong Kong, China, 21 April 2021; pp. 63–68. [Google Scholar]
- Liao, S.L.; Zhu, R.M.; Wu, N.Q.; Shaikh, T.A.; Sharaf, M.; Mostafa, A.M. Path planning for moving target tracking by fixed-wing UAV. Def. Technol. 2020, 16, 811–824. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Z.; Wang, X.; Yu, X.; Wang, G.; Shen, L. Image-based visual servo tracking control of a ground moving target for a fixed-wing unmanned aerial vehicle. J. Intell. Robot. Syst. 2021, 102, 1–20. [Google Scholar] [CrossRef]
- Sun, Z.; Garcia de Marina, H.; Anderson, B.D.; Yu, C. Collaborative target-tracking control using multiple fixed-wing unmanned aerial vehicles with constant speeds. J. Guid. Control. Dyn. 2021, 44, 238–250. [Google Scholar] [CrossRef]
- Yang, Y.; Leeghim, H.; Kim, D. Dubins Path-Oriented Rapidly Exploring Random Tree* for Three-Dimensional Path Planning of Unmanned Aerial Vehicles. Electronics 2022, 11, 2338. [Google Scholar] [CrossRef]
- Aiello, G.; Valavanis, K.P.; Rizzo, A. Fixed-wing uav energy efficient 3d path planning in cluttered environments. J. Intell. Robot. Syst. 2022, 105, 60. [Google Scholar] [CrossRef]
- Machmudah, A.; Shanmugavel, M.; Parman, S.; Manan, T.S.A.; Dutykh, D.; Beddu, S.; Rajabi, A. Flight trajectories optimization of fixed-wing UAV by bank-turn mechanism. Drones 2022, 6, 69. [Google Scholar] [CrossRef]
- Cui, Q. Multi-target points path planning for fixed-wing unmanned aerial vehicle performing reconnaissance missions. In Proceedings of the 5th International Conference on Information Science, Electrical, and Automation Engineering, Wuhan, China, 24 March 2023; Volume 12748, pp. 713–723. [Google Scholar]
- Ding, Z.; Huang, Y.; Yuan, H.; Dong, H. Introduction to reinforcement learning. In Deep Reinforcement Learning: Fundamentals, Research and Applications; Dong, H., Ding, Z., Zhang, S., Eds.; Springer: Singapore, 2020; pp. 47–123. [Google Scholar]
- Chen, J.; Ling, F.; Zhang, Y.; You, T.; Liu, Y.; Du, X. Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Theile, M.; Bayerlein, H.; Nai, R.; Gesbert, D.; Caccamo, M. UAV coverage path planning under varying power constraints using deep reinforcement learning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 24 October 2020; pp. 1444–1449. [Google Scholar]
- Jia, Y.; Zhou, S.; Zeng, Q.; Li, C.; Chen, D.; Zhang, K.; Liu, L.; Chen, Z. The UAV path coverage algorithm based on the greedy strategy and ant colony optimization. Electronics 2022, 17, 2667. [Google Scholar] [CrossRef]
- Majeed, A.; Hwang, S.O. A multi-objective coverage path planning algorithm for UAVs to cover spatially distributed regions in urban environments. Aerospace 2021, 11, 343. [Google Scholar] [CrossRef]
- Vazquez-Carmona, E.V.; Vasquez-Gomez, J.I.; Herrera-Lozada, J.C.; Antonio-Cruz, M. Coverage path planning for spraying drones. Comput. Ind. Eng. 2022, 168, 108125. [Google Scholar] [CrossRef] [PubMed]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Vasquez-Gomez, J.I.; Marciano-Melchor, M.; Valentin, L.; Herrera-Lozada, J.C. Coverage path planning for 2d convex regions. J. Intell. Robot. Syst. 2020, 97, 81–94. [Google Scholar] [CrossRef]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Barrientos, A.; Colorado, J.; Cerro, J.D.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial remote sensing in agriculture: A practical approach to area coverage and path planning for fleets of mini aerial robots. J. Field Robot. 2011, 28, 667–689. [Google Scholar] [CrossRef]
- Hasan, K.M.; Reza, K.J. Path planning algorithm development for autonomous vacuum cleaner robots. In Proceedings of the 2014 International Conference on Informatics, Electronics & Vision, Dhaka, Bangladesh, 23 May 2014; pp. 1–6. [Google Scholar]
- Bähnemann, R.; Lawrance, N.; Chung, J.J.; Pantic, M.; Siegwart, R.; Nieto, J. Revisiting boustrophedon coverage path planning as a generalized traveling salesman problem. In Proceedings of the Field and Service Robotics: Results of the 12th International Conference, Tokyo, Japan, 29 August 2019; pp. 277–290. [Google Scholar]
- Kumar, K.; Kumar, N. Region coverage-aware path planning for unmanned aerial vehicles: A systematic review. Phys. Commun. 2023, 59, 102073. [Google Scholar] [CrossRef]
- Choset, H.; Pignon, P. Coverage path planning: The boustrophedon cellular decomposition. In Proceedings of the Field and Service Robotics, Canberra, Australia, 8–10 December 1997; pp. 203–209. [Google Scholar]
- Choset, H. Coverage of known spaces: The boustrophedon cellular decomposition. Auton. Robot. 2000, 9, 247–253. [Google Scholar] [CrossRef]
- Apostolidis, S.D.; Kapoutsis, P.C.; Kapoutsis, A.C.; Kosmatopoulos, E.B. Cooperative multi-UAV coverage mission planning platform for remote sensing applications. Auton. Robot. 2022, 46, 373–400. [Google Scholar] [CrossRef]
- Stecz, W.; Gromada, K. UAV mission planning with SAR application. Sensors 2020, 4, 1080. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Yan, Y.; Jiang, F.; Gao, X. Research on single target cognitive electronic reconnaissance strategy for unmanned aerial vehicle. IET Radar Sonar Navig. 2023, 11, 1711–1727. [Google Scholar] [CrossRef]
- Stecz, W.; Gromada, K. Determining UAV flight trajectory for target recognition using EO/IR and SAR. Sensors 2020, 20, 5712. [Google Scholar] [CrossRef] [PubMed]
- Asiyabi, R.M.; Ghorbanian, A.; Tameh, S.N.; Amani, M.; Jin, S.; Mohammadzadeh, A. Synthetic aperture radar (SAR) for ocean: A review. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2023, 16, 9106–9138. [Google Scholar] [CrossRef]
- Luomei, Y.; Xu, F. Segmental aperture imaging algorithm for multirotor UAV-borne MiniSAR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–8. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, W.; Chen, Z.; Wang, P.; Zhang, H.; Qiu, J.; Zhao, Q.; Deng, Y.; Zhang, Z.; Yu, W.; et al. Digital beamforming synthetic aperture radar (DBSAR): Experiments and performance analysis in support of 16-channel airborne X-band SAR data. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6784–6798. [Google Scholar] [CrossRef]
- García-Fernández, M.; Álvarez-Narciandi, G.; López, Y.; Las-Heras, F. Array-based ground penetrating synthetic aperture radar on board an unmanned aerial vehicle for enhanced buried threats detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Yuan, Y.; Cattaruzza, D.; Ogier, M.; Semet, F. A branch-and-cut algorithm for the generalized traveling salesman problem with time windows. Eur. J. Oper. Res. 2020, 286, 849–866. [Google Scholar] [CrossRef]
- Nourmohammadzadeh, A.; Sarhani, M.; Voß, S. A matheuristic approach for the family traveling salesman problem. J. Heuristics 2023, 29, 435–460. [Google Scholar] [CrossRef]
- Helsgaun, K. Solving the equality generalized traveling salesman problem using the Lin–Kernighan–Helsgaun Algorithm. Math. Prog. Comp. 2015, 7, 269–287. [Google Scholar] [CrossRef]
- Fabri, A.; Pion, S. CGAL: The computational geometry algorithms library. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 538–539. [Google Scholar]


| Default Work Altitude | Imaging Resolution | Range | Imaging Width |
|---|---|---|---|
| 5000 m | 0.5 m | 16–80 km | 5 km × 5 km |
| 0.3 m | 12–60 km | 3 km × 3 km | |
| 0.1 m | 12–30 km | 1 km × 1 km |
| Default Work Altitude | Imaging Resolution | Range | Imaging Width |
|---|---|---|---|
| 5000 m | 5 m | 72–120 km | 405 km |
| 1 m | 60–100 km | 203 km | |
| 0.5 m | 48–80 km | 12 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Yan, J.; Zhou, Z.; Lai, R.; Lin, J. Autonomous Mission Planning for Fixed-Wing Unmanned Aerial Vehicles in Multiscenario Reconnaissance. Sensors 2025, 25, 1176. https://doi.org/10.3390/s25041176
Chen B, Yan J, Zhou Z, Lai R, Lin J. Autonomous Mission Planning for Fixed-Wing Unmanned Aerial Vehicles in Multiscenario Reconnaissance. Sensors. 2025; 25(4):1176. https://doi.org/10.3390/s25041176
Chicago/Turabian StyleChen, Bei, Jiaxin Yan, Zebo Zhou, Rui Lai, and Jiejian Lin. 2025. "Autonomous Mission Planning for Fixed-Wing Unmanned Aerial Vehicles in Multiscenario Reconnaissance" Sensors 25, no. 4: 1176. https://doi.org/10.3390/s25041176
APA StyleChen, B., Yan, J., Zhou, Z., Lai, R., & Lin, J. (2025). Autonomous Mission Planning for Fixed-Wing Unmanned Aerial Vehicles in Multiscenario Reconnaissance. Sensors, 25(4), 1176. https://doi.org/10.3390/s25041176






