A Novel Hybrid Approach for UT1-UTC Ultra-Short-Term Prediction Utilizing LOD Series and Sum Series of LOD and First-Order-Difference UT1-UTC
Abstract
1. Introduction
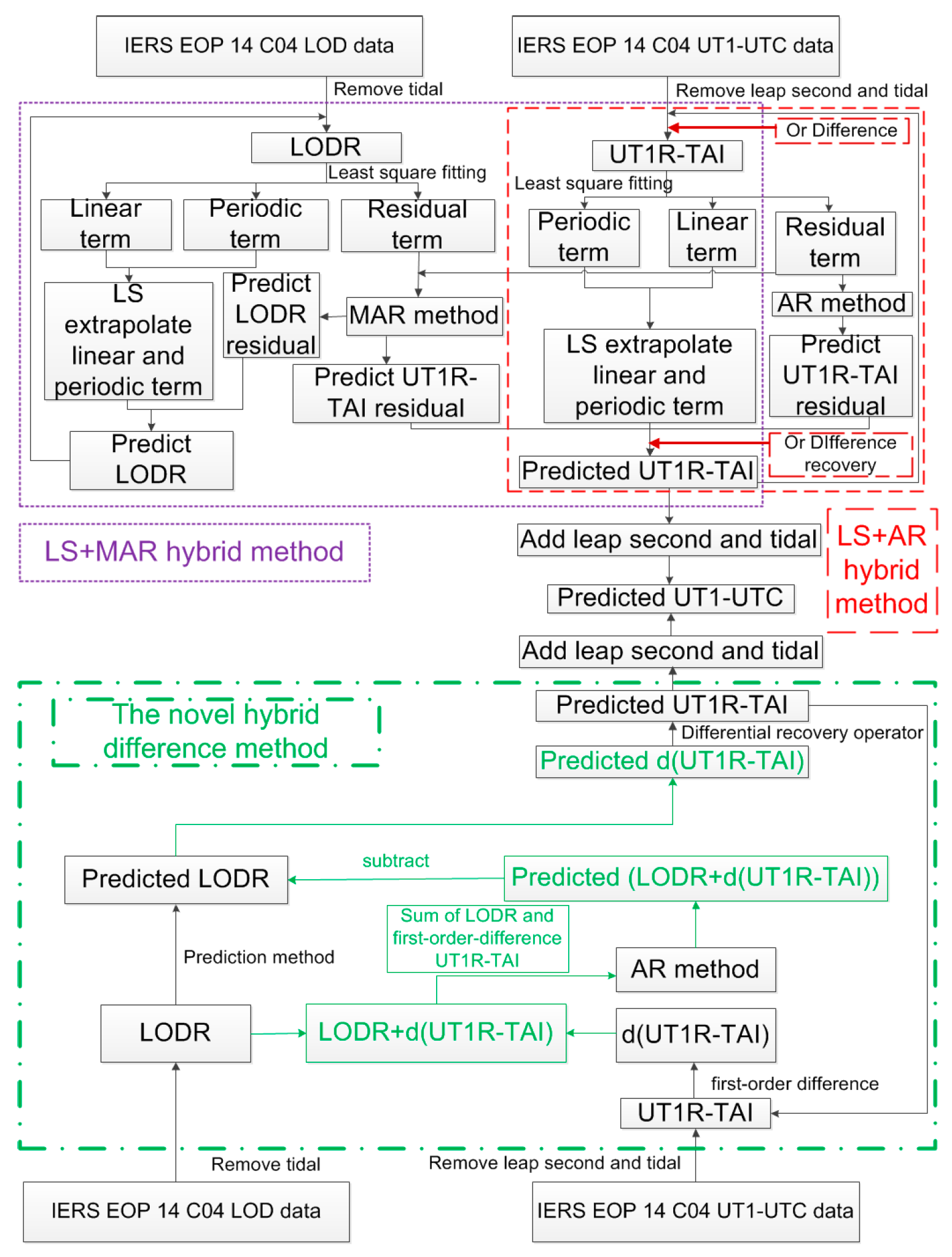
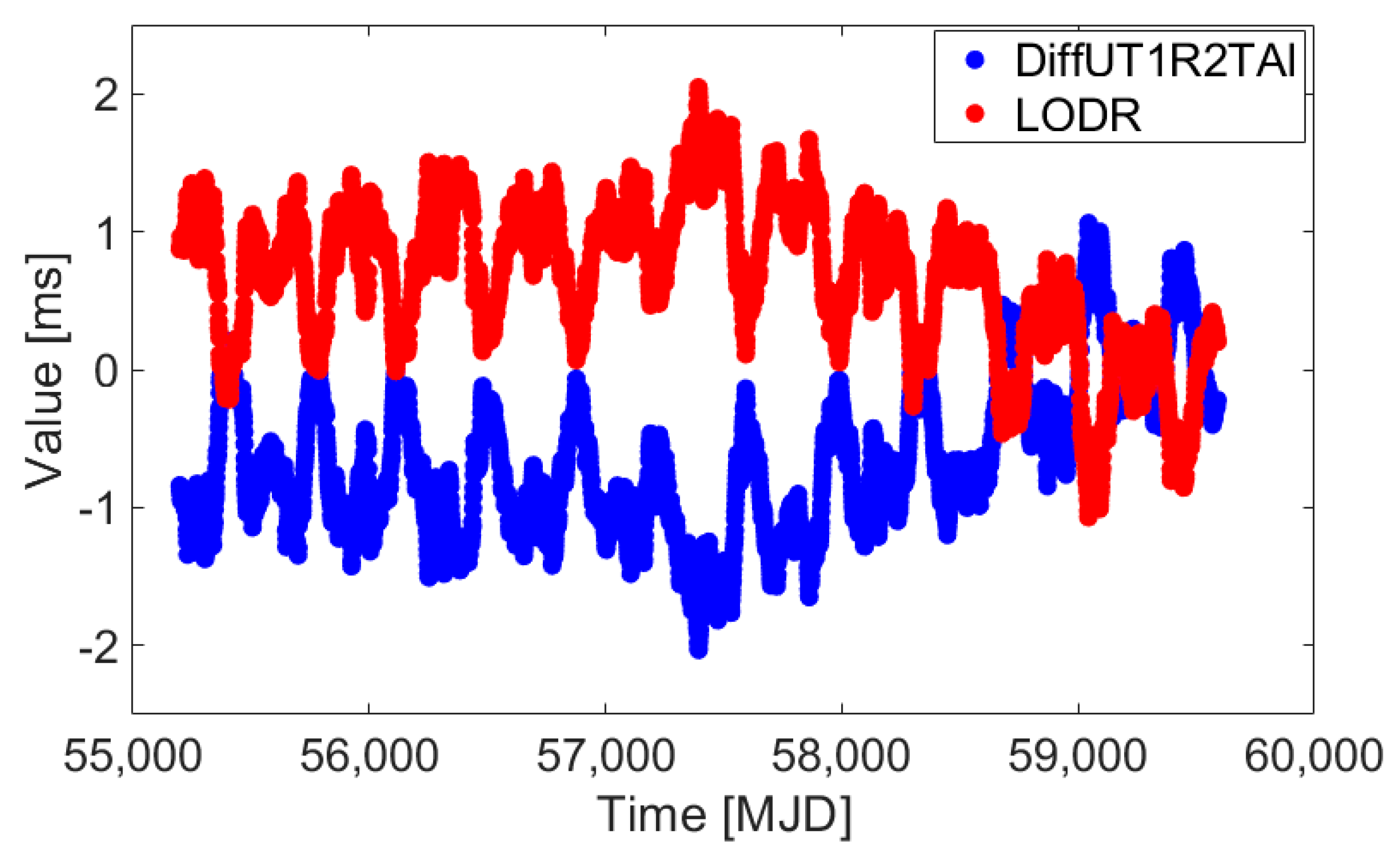
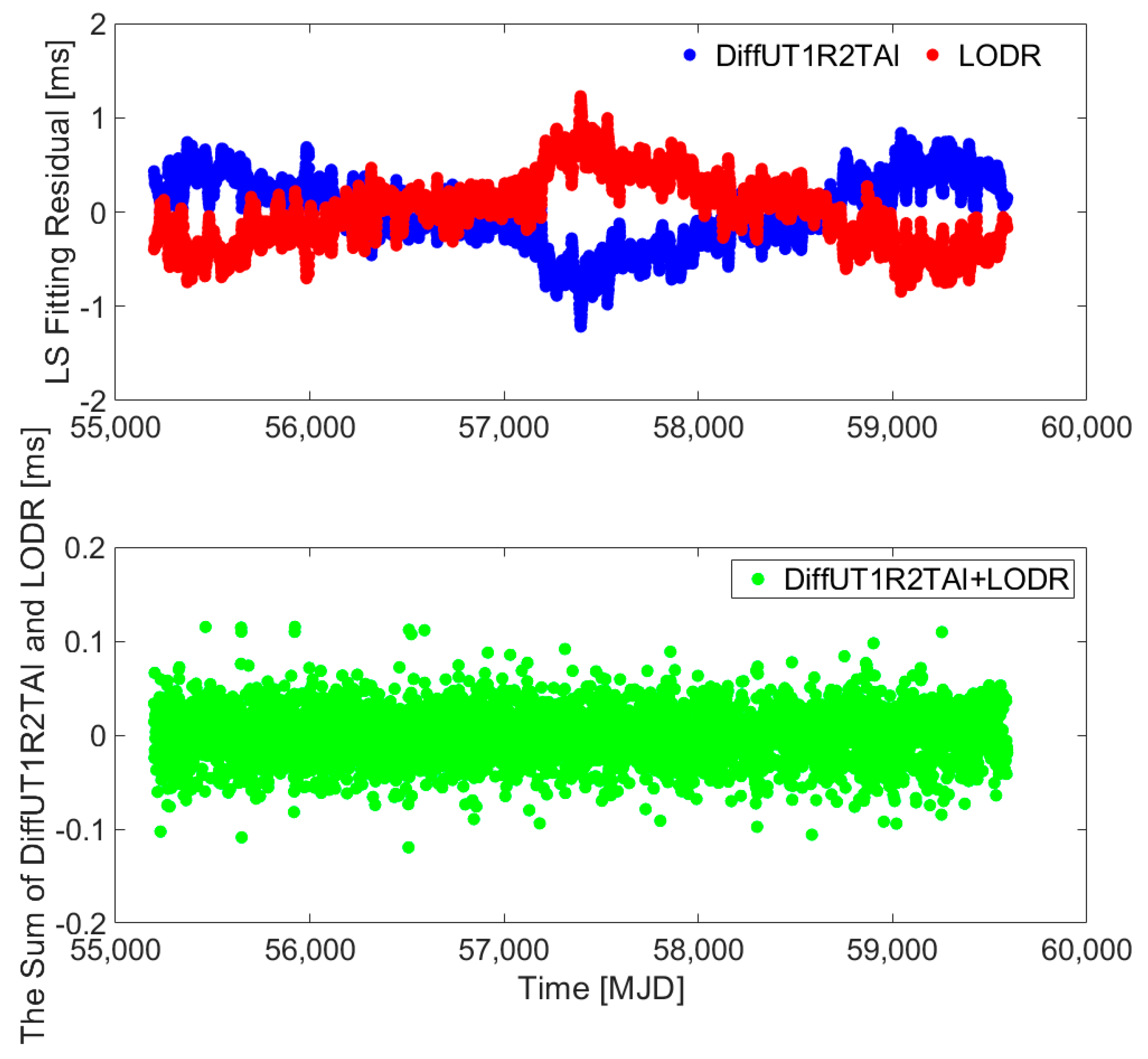
2. Novel Hybrid Difference Method for UT1-UTC Ultra-Short-Term Prediction
3. Results
- Case LS + AR: LS + AR hybrid method based on the UT1-UTC data series, namely the traditional LS + AR hybrid method [9];
- Case First-diff LS + AR: LS + AR hybrid method based on the first-order-difference UT1-UTC data series, namely the traditional first-order-difference LS + AR hybrid method [25];
- Case Second-diff LS + AR: LS + AR hybrid method based on the second-order-difference UT1-UTC data series, namely the traditional second-order-difference LS + AR hybrid method [35];
- Case First-diff LS + MAR: LS + MAR hybrid method based on the first-order-difference UT1-UTC and LOD data series, namely the traditional first-order-difference LS + MAR hybrid method [13];
- Case new method: The novel hybrid difference method based on the UT1-UTC and LOD data series.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bradley, B.K.; Sibois, A.; Axelrad, P. Influence of ITRS/GCRS implementation for astrodynamics: Coordinate transformations. Adv. Space Res. 2016, 57, 850–866. [Google Scholar] [CrossRef]
- Schartner, M.; Kern, L.; Nothnagel, A.; Böhm, J.; Soja, B. Optimal VLBI baseline geometry for UT1-UTC Intensive observations. J. Geod. 2021, 95, 75. [Google Scholar] [CrossRef]
- Krásná, H.; Malkin, Z.; Böhm, J. Non-linear VLBI station motions and their impact on the celestial reference frame and Earth orientation parameters. J. Geod. 2015, 89, 1019–1033. [Google Scholar] [CrossRef] [PubMed]
- Haas, R.; Varenius, E.; Matsumoto, S.; Schartner, M. Observing UT1-UTC with VGOS. Earth Planets Space 2021, 73, 78. [Google Scholar] [CrossRef]
- Lutz, S.; Beutler, G.; Schaer, S.; Dach, R.; Jäggi, A. CODE’s new ultra-rapid orbit and ERP products for the IGS. GPS Solut. 2016, 20, 239–250. [Google Scholar] [CrossRef]
- Kosek, W.; Mccarthy, D.D.; Luzum, B.J. Possible improvement of Earth orientation forecast using autocovariance prediction procedures. J. Geod. 1998, 72, 189–199. [Google Scholar] [CrossRef]
- Freedman, A.P.; Steppe, J.A.; Dickey, J.O.; Eubanks, T.M.; Sung, L.Y. The short-term prediction of universal time and length of day using atmospheric angular momentum. J. Geophys. Res. Solid Earth 1994, 99, 6981–6996. [Google Scholar] [CrossRef]
- Gross, R.S.; Eubanks, T.M.; Steppe, J.A.; Freedman, A.P.; Dickey, J.O.; Runge, T.F. A Kalman-filter-based approach to combining independent Earth-orientation series. J. Geod. 1998, 72, 215–235. [Google Scholar] [CrossRef]
- Kalarus, M.; Schuh, H.; Kosek, W.; Akyilmaz, O.; Bizouard, C.; Gambis, D.; Gross, R.; Jovanović, B.; Kumakshev, S.; Kutterer, H.; et al. Achievements of the Earth orientation parameters prediction comparison campaign. J. Geod. 2010, 84, 587–596. [Google Scholar] [CrossRef]
- Ye, F.; Yuan, Y. A modified stochastic model for LS+AR hybrid method and its application in polar motion short-term prediction. Geod. Geodyn. 2024, 15, 100–105. [Google Scholar] [CrossRef]
- Wang, L.; Miao, W.; Wu, F. A new polar motion prediction method combined with the difference between polar motion series. Geod. Geodyn. 2022, 13, 564–572. [Google Scholar] [CrossRef]
- Niedzielski, T.; Kosek, W. Prediction of UT1–UTC, LOD and AAM χ3 by combination of least-squares and multivariate stochastic methods. J. Geod. 2008, 82, 83–92. [Google Scholar] [CrossRef]
- Ye, F.; Yuan, Y. Improved LS+MAR hybrid method to UT1-UTC ultra-short-term prediction by using first-order-difference UT1-UTC. Geod. Geodyn. 2024, 15, 379–385. [Google Scholar] [CrossRef]
- Xu, X.Q.; Zhou, Y.H.; Liao, X.H. Short-term earth orientation parameters predictions by combination of the least-squares, AR model and Kalman filter. J. Geodyn. 2012, 62, 83–86. [Google Scholar] [CrossRef]
- Tan, Z.; Ye, F.; Hua, L. Polar Motion Ultra-Short-Term Prediction of Least-Squares+Multivariate Autoregressive Hybrid Method by Using the Kalman Filter. Sensors 2024, 24, 6260. [Google Scholar] [CrossRef] [PubMed]
- Schuh, H.; Ulrich, M.; Egger, D.; Müller, J.; Schwegmann, W. Prediction of Earth orientation parameters by artificial neural networks. J. Geod. 2002, 76, 247–258. [Google Scholar] [CrossRef]
- Akyilmaz, O.; Kutterer, H.; Shum, C.; Ayan, T. Fuzzy-wavelet based prediction of Earth rotation parameters. Appl. Soft Comput. 2011, 11, 837–841. [Google Scholar] [CrossRef]
- Modiri, S.; Belda, S.; Hoseini, M.; Heinkelmann, R.; Ferrándiz, J.M.; Schuh, H. A new hybrid method to improve the ultra-short-term prediction of LOD. J. Geod. 2020, 94, 23. [Google Scholar] [CrossRef]
- Jia, S.; Xu, T.-H.; Sun, Z.-Z.; Li, J.-J. Middle and long-term prediction of UT1-UTC based on combination of Gray Model and Autoregressive Integrated Moving Average. Adv. Space Res. 2017, 59, 888–894. [Google Scholar] [CrossRef]
- Yao, Y.; Yue, S.; Chen, P. A new LS+AR model with additional error correction for polar motion forecast. Sci. China Earth Sci. 2013, 56, 818–828. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Y. EOP prediction using least square fitting and autoregressive filter over optimized data intervals. Adv. Space Res. 2015, 56, 2248–2253. [Google Scholar] [CrossRef]
- Ye, F.; Yuan, Y.; Deng, Z. Improved Ultra-Rapid UT1-UTC Determination and Its Preliminary Impact on GNSS Satellite Ultra-Rapid Orbit Determination. Remote Sens. 2020, 12, 3584. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, T. Prediction of earth rotation parameters based on improved weighted least squares and autoregressive model. Geod. Geodyn. 2012, 3, 57–64. [Google Scholar] [CrossRef]
- Wu, F.; Chang, G.; Deng, K. One-step method for predicting LOD parameters based on LS+AR model. J. Spat. Sci. 2021, 66, 317–328. [Google Scholar] [CrossRef]
- Lei, Y.; Cai, H.; Zhao, D. A Simple Differencing Technology to Improve Prediction Accuracy of Earth Rotation Parameters. In China Satellite Navigation Conference (CSNC) 2016, Proceedings: Volume III, Changsha, China, 18–20 May 2016; Springer: Singapore, 2016; pp. 201–211. [Google Scholar]
- Dill, R.; Dobslaw, H.; Thomas, M. Improved 90-day Earth orientation predictions from angular momentum forecasts of atmosphere, ocean, and terrestrial hydrosphere. J. Geod. 2019, 93, 287–295. [Google Scholar] [CrossRef]
- Kosek, W. Future Improvements in EOP Prediction. In Geodesy for Planet Earth, Proceedings of the 2009 IAG Symposium, Buenos Aires, Argentina, 31 August–4 September 2009; Springer: Berlin/Heidelberg, Germany, 2012; pp. 513–520. [Google Scholar]
- Shumate, N.A.; Luzum, B.J.; Kosek, W. Earth Orientation Parameters Combination of Prediction Pilot Project. In Proceedings of the Agu Fall Meeting 2013, San Fransisco, CA, USA, 9–13 December 2013. [Google Scholar]
- Malkin, Z. Employing combination procedures to short-time EOP prediction. arXiv 2010, arXiv:1011.2581. [Google Scholar] [CrossRef]
- Malkin, Z. Improving short-term EOP prediction using combination procedures. In Proceedings of the Journees 2008: Astrometry, Geodynamics and Astronomical Reference Systems, Dresden, Germany, 22–24 September 2008; pp. 164–167. [Google Scholar]
- Malkin, Z.; Skurikhina, E. On Prediction of EOP. Communications of the Institute of Applied Astronomy RAS 93:1. 1996. Available online: https://arxiv.org/abs/0910.3336 (accessed on 17 October 2009).
- Hu, C.; Wang, Q.; Wang, Z.; Mao, Y. A Method for Improving the Short-Term Prediction Model for ERP Based on Long-Term Observations. In China Satellite Navigation Conference (CSNC) 2019, Proceedings: Volume II, Beijing, China, 22–25 May 2019; Springer: Singapore, 2019; pp. 24–38. [Google Scholar]
- Wang, Q.; Hu, C.; Xu, T.; Chang, G.; Hernández Moraleda, A. Impacts of Earth rotation parameters on GNSS ultra-rapid orbit prediction: Derivation and real-time correction. Adv. Space Res. 2017, 60, 2855–2870. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010) [R]. France. pp: 6-179: Bureau International des Poids et mesures sevres 2010: Technical Note: 6-179. Available online: https://iers-conventions.obspm.fr/content/tn36.pdf (accessed on 26 November 2024).
- Chen, L.; Tang, G.; Hu, S.; Ping, J.; Xu, X.; Xia, J. High Accuracy Differential Prediction of UT1-UTC. J. Deep. Space Explor. 2014, 1, 230–235. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, T.; Zhou, S.E.; Jiang, N.; Jiang, C.; Yang, Y. Analysis on the differences between EOP 08C04 and EOP 14C04 related to the Earth rotation characteristics. J. Spat. Sci. 2022, 67, 111–127. [Google Scholar] [CrossRef]
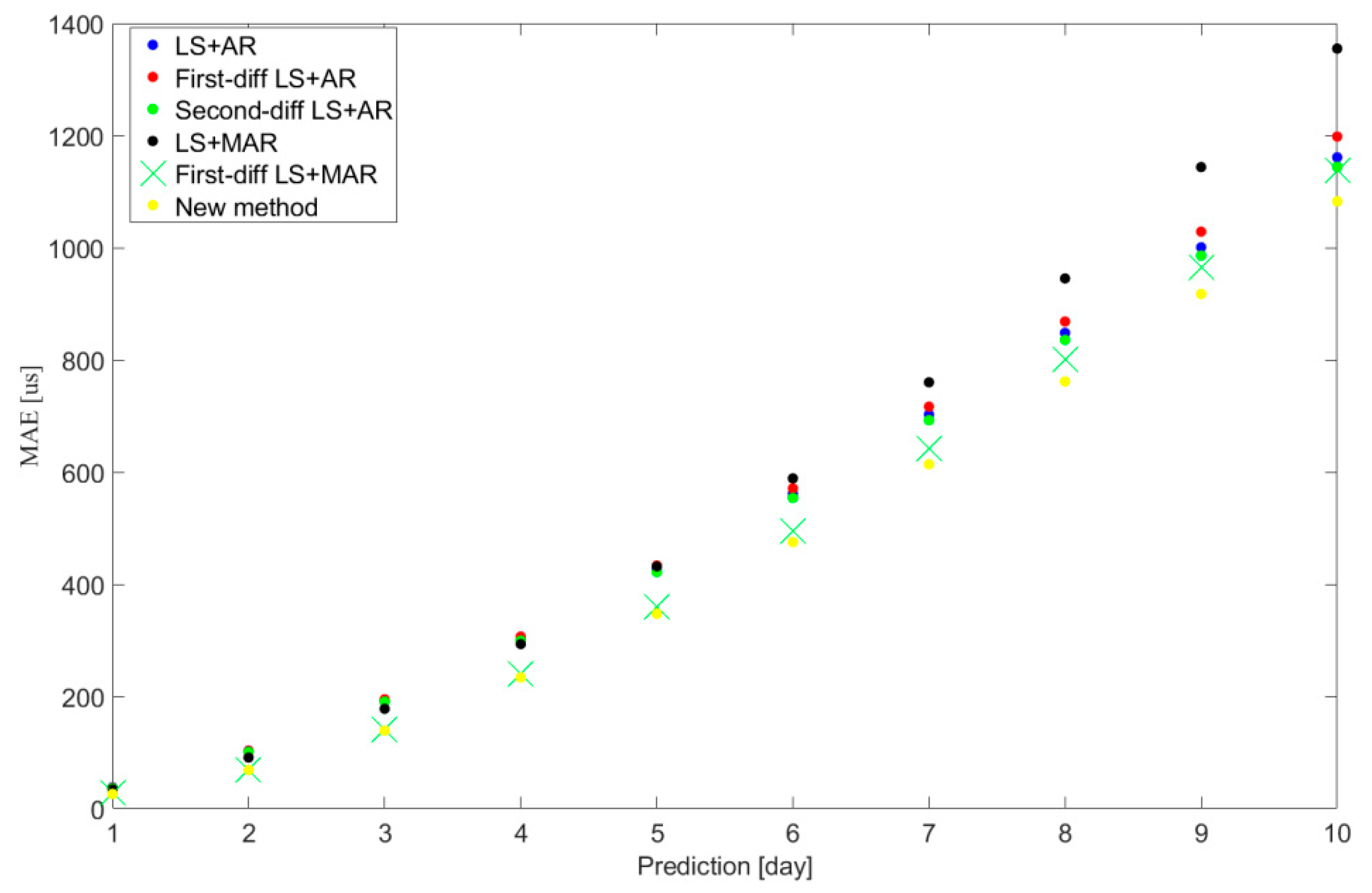
| Prediction Day/Cases | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| LS + AR | 28 | 78 | 150 | 242 | 344 | 456 | 576 | 694 | 817 | 942 |
| First-diff LS + AR | 27 | 78 | 152 | 245 | 349 | 462 | 583 | 709 | 840 | 978 |
| Second-diff LS + AR | 26 | 76 | 149 | 239 | 339 | 445 | 558 | 673 | 796 | 922 |
| LS + MAR | 26 | 70 | 134 | 218 | 320 | 434 | 558 | 692 | 831 | 976 |
| First-diff LS + MAR | 21 | 56 | 112 | 191 | 291 | 403 | 526 | 657 | 794 | 934 |
| New method | 21 | 56 | 111 | 191 | 286 | 390 | 502 | 619 | 741 | 869 |
| IMP1 (%) | 25 | 28 | 26 | 21 | 17 | 14 | 13 | 11 | 9 | 8 |
| IMP2 (%) | 22 | 28 | 27 | 22 | 18 | 16 | 14 | 13 | 12 | 11 |
| IMP3 (%) | 19 | 26 | 26 | 20 | 16 | 12 | 10 | 8 | 7 | 6 |
| IMP4 (%) | 19 | 20 | 17 | 12 | 11 | 10 | 10 | 11 | 11 | 11 |
| IMP5 (%) | 0 | 0 | 1 | 0 | 2 | 3 | 5 | 6 | 7 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, F.; Ao, M.; Li, N.; Zeng, R.; Zeng, X. A Novel Hybrid Approach for UT1-UTC Ultra-Short-Term Prediction Utilizing LOD Series and Sum Series of LOD and First-Order-Difference UT1-UTC. Sensors 2025, 25, 1087. https://doi.org/10.3390/s25041087
Ye F, Ao M, Li N, Zeng R, Zeng X. A Novel Hybrid Approach for UT1-UTC Ultra-Short-Term Prediction Utilizing LOD Series and Sum Series of LOD and First-Order-Difference UT1-UTC. Sensors. 2025; 25(4):1087. https://doi.org/10.3390/s25041087
Chicago/Turabian StyleYe, Fei, Minsi Ao, Ningbo Li, Rong Zeng, and Xiangqiang Zeng. 2025. "A Novel Hybrid Approach for UT1-UTC Ultra-Short-Term Prediction Utilizing LOD Series and Sum Series of LOD and First-Order-Difference UT1-UTC" Sensors 25, no. 4: 1087. https://doi.org/10.3390/s25041087
APA StyleYe, F., Ao, M., Li, N., Zeng, R., & Zeng, X. (2025). A Novel Hybrid Approach for UT1-UTC Ultra-Short-Term Prediction Utilizing LOD Series and Sum Series of LOD and First-Order-Difference UT1-UTC. Sensors, 25(4), 1087. https://doi.org/10.3390/s25041087




