Multi-Scale Analysis of Knee Joint Acoustic Signals for Cartilage Degeneration Assessment
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Participants
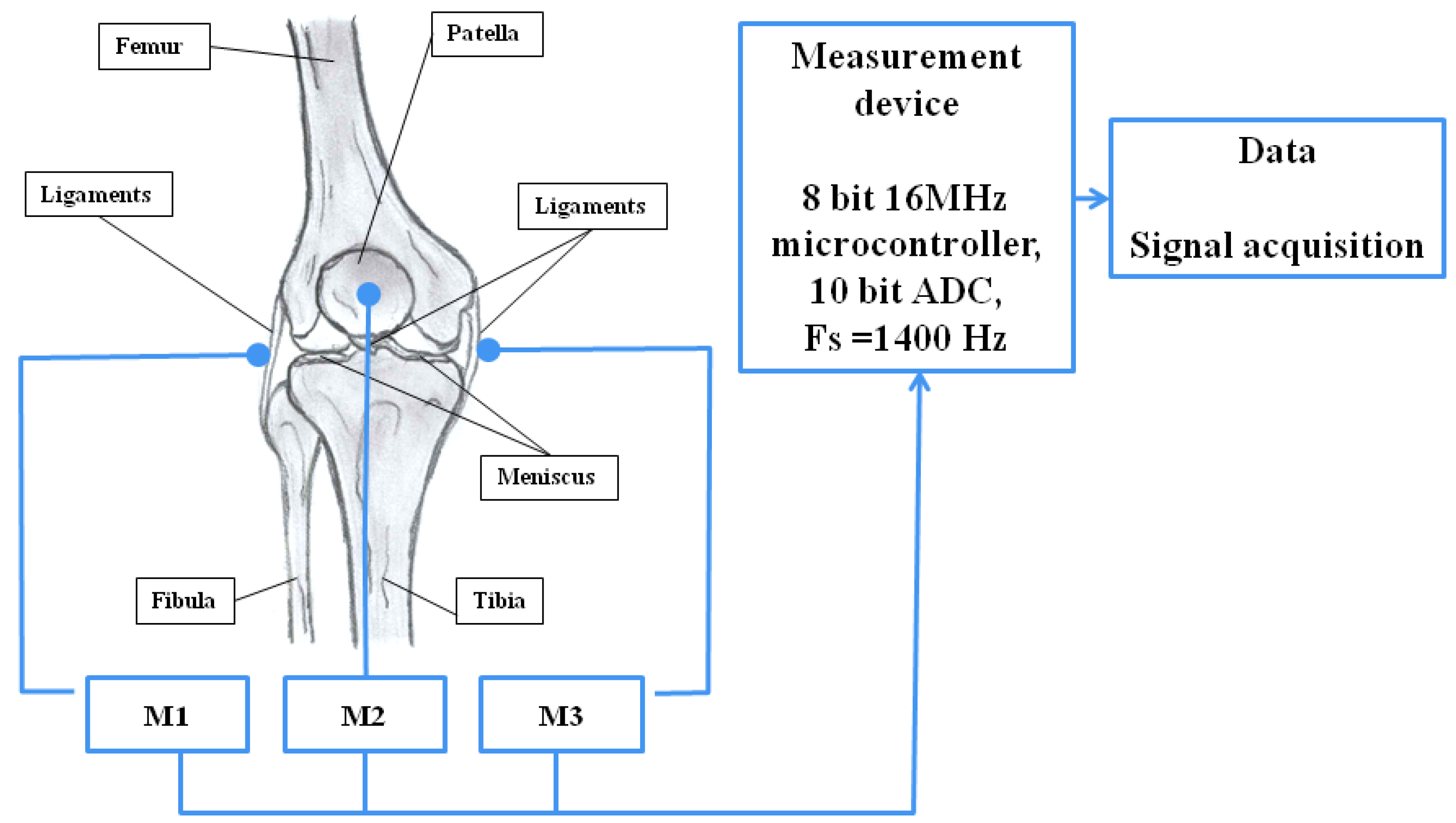
2.2. Measurement System and Procedure for Recording Vibroacoustic Signals
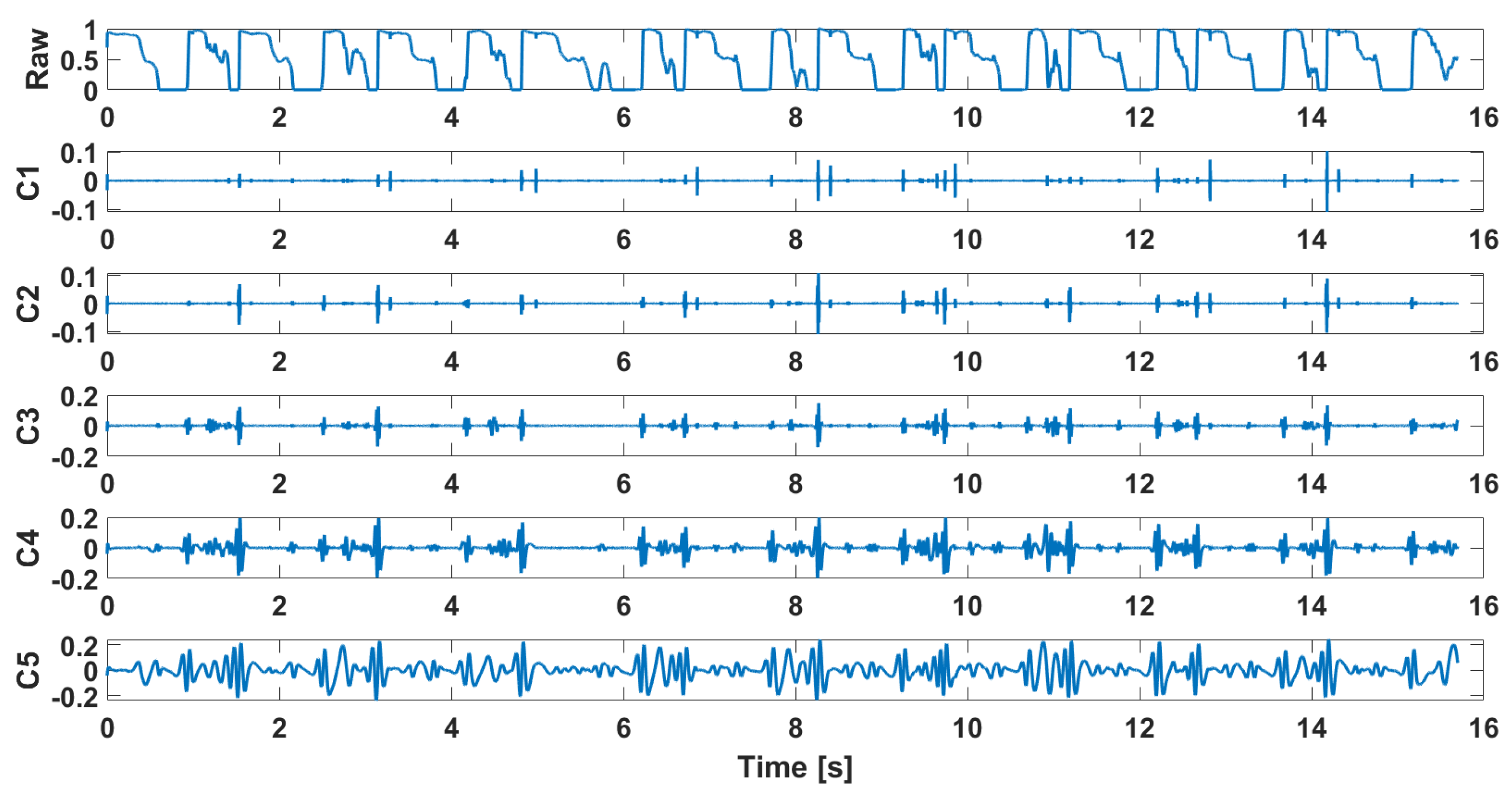
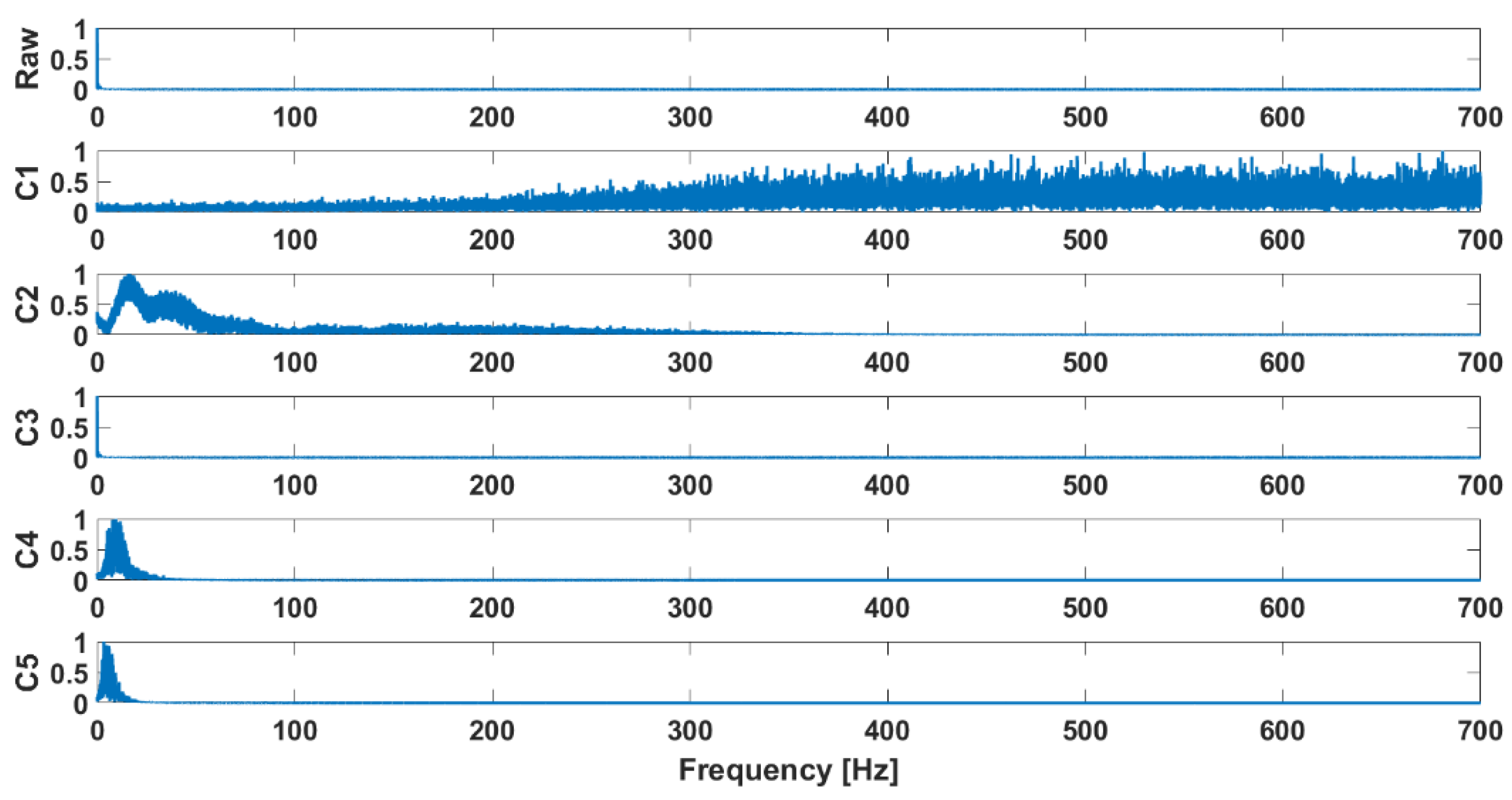
3. Preprocessing and Filtering of VAG Signals
- The number of extrema and the number of zero crossings must be equal or differ at most by one.
- The mean value of the local envelopes (upper and lower) is equal to zero.
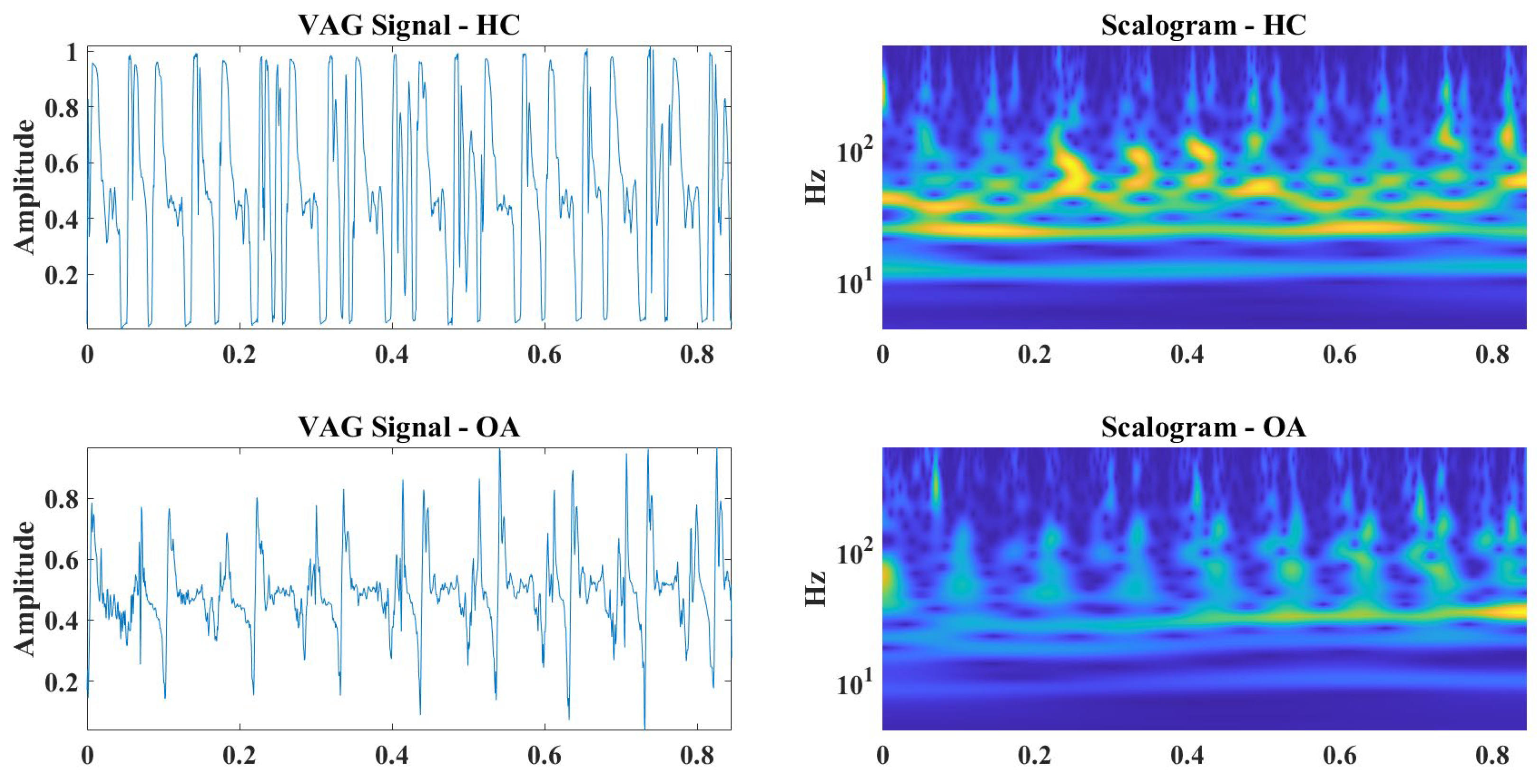
4. Analysis and Data Preparation for Classification
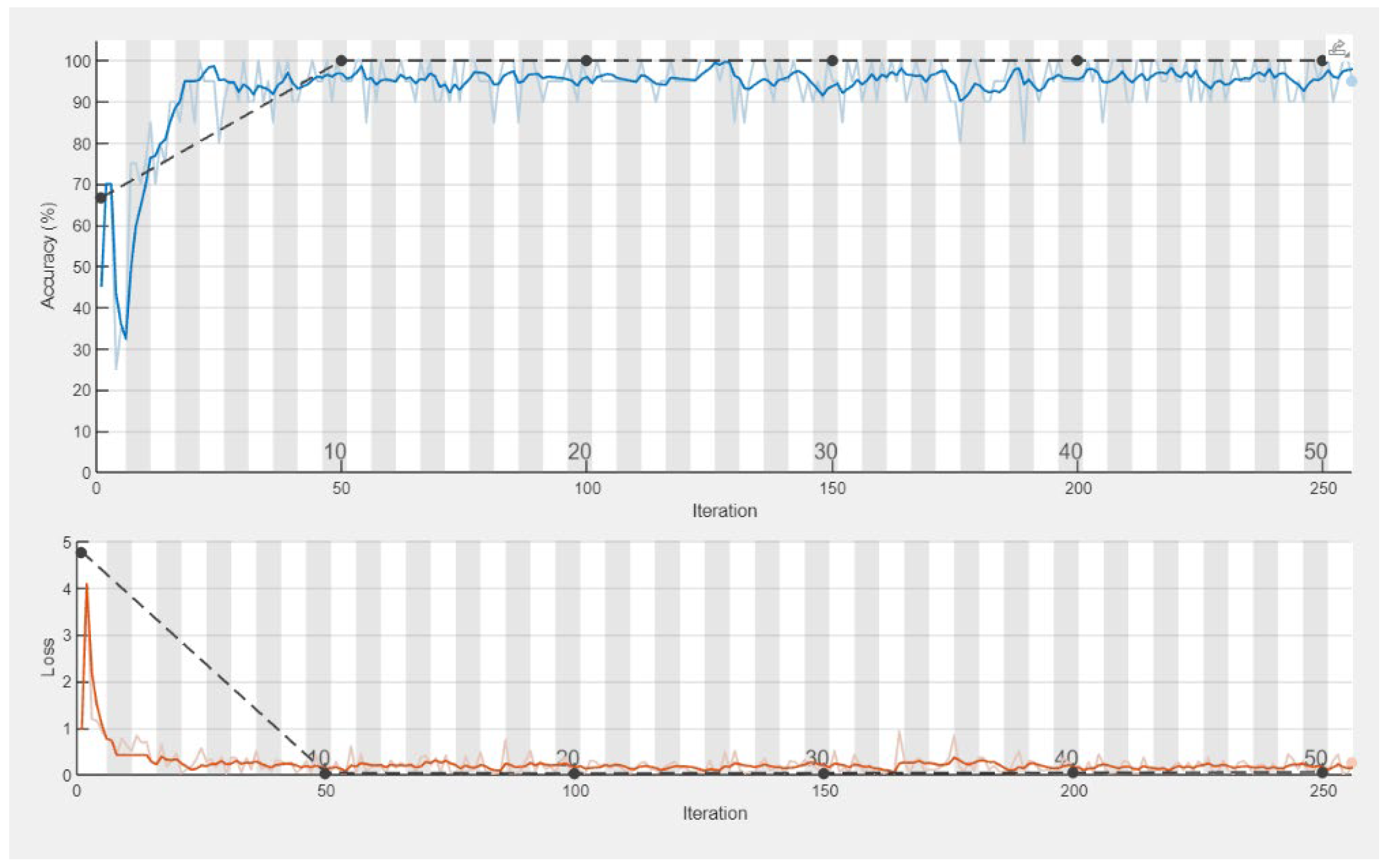
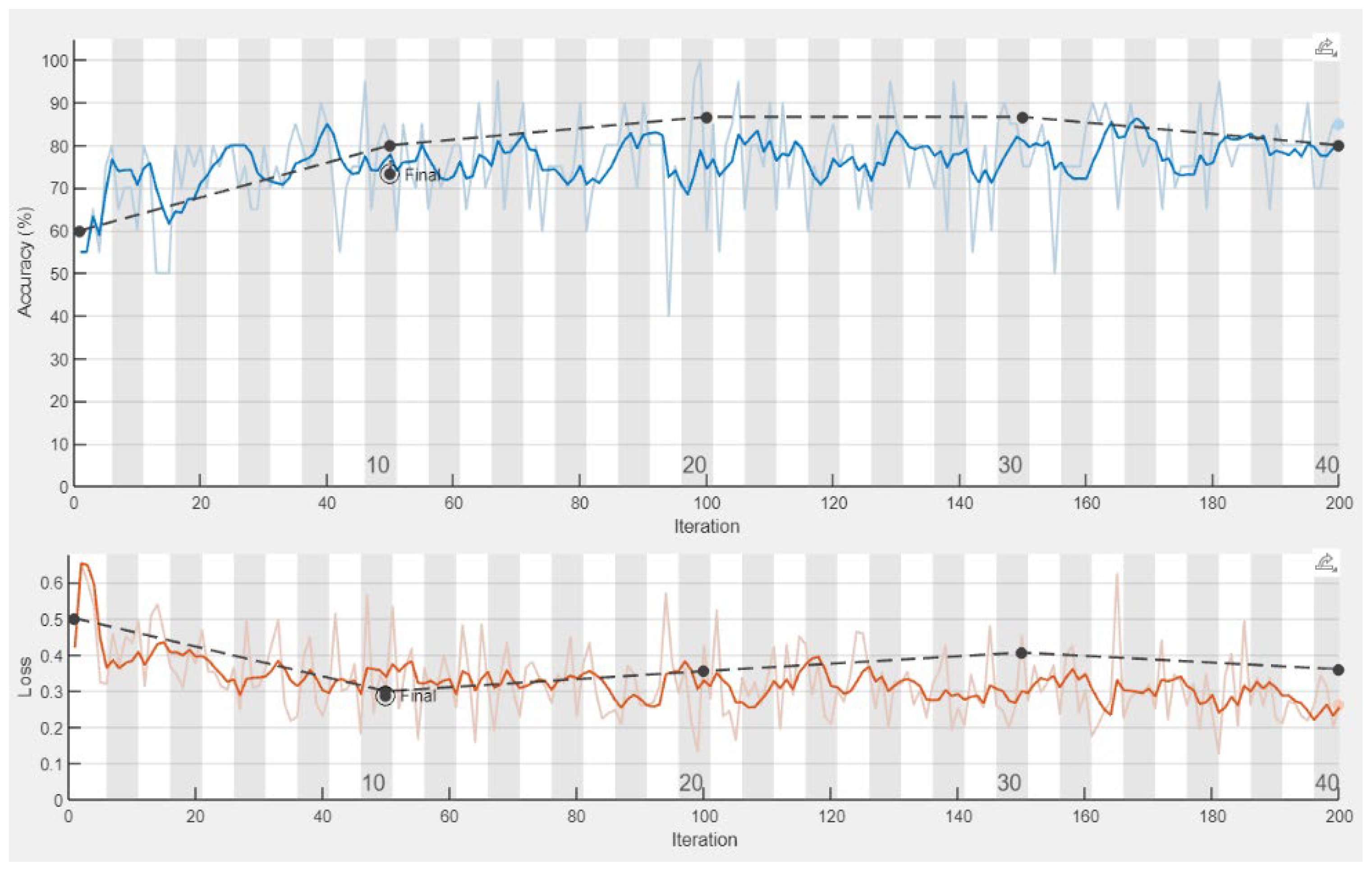
5. Convolutional Neural Networks and Classification
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krakowski, P.; Rejniak, A.; Sobczyk, J.; Karpiński, R. Cartilage Integrity: A Review of Mechanical and Frictional Properties and Repair Approaches in Osteoarthritis. Healthcare 2024, 12, 1648. [Google Scholar] [CrossRef] [PubMed]
- Link, J.M.; Salinas, E.Y.; Hu, J.C.; Athanasiou, K.A. The Tribology of Cartilage: Mechanisms, Experimental Techniques, and Relevance to Translational Tissue Engineering. Clin. Biomech. 2020, 79, 104880. [Google Scholar] [CrossRef] [PubMed]
- Moore, A.C.; Burris, D.L. Tribological and Material Properties for Cartilage of and throughout the Bovine Stifle: Support for the Altered Joint Kinematics Hypothesis of Osteoarthritis. Osteoarthr. Cartil. 2015, 23, 161–169. [Google Scholar] [CrossRef]
- Grushko, G.; Schneiderman, R.; Maroudas, A. Some Biochemical and Biophysical Parameters for the Study of the Pathogenesis of Osteoarthritis: A Comparison Between the Processes of Ageing and Degeneration in Human Hip Cartilage. Connect. Tissue Res. 1989, 19, 149–176. [Google Scholar] [CrossRef]
- Cibere, J.; Sayre, E.C.; Guermazi, A.; Nicolaou, S.; Kopec, J.A.; Esdaile, J.M.; Thorne, A.; Singer, J.; Wong, H. Natural History of Cartilage Damage and Osteoarthritis Progression on Magnetic Resonance Imaging in a Population-Based Cohort with Knee Pain. Osteoarthr. Cartil. 2011, 19, 683–688. [Google Scholar] [CrossRef]
- Herzog, W.; Federico, S. Considerations on Joint and Articular Cartilage Mechanics. Biomech. Model. Mechanobiol. 2006, 5, 64–81. [Google Scholar] [CrossRef]
- Mansour, J.M. Biomechanics of Cartilage. Kinesiol. Mech. Pathomech. Hum. Mov. 2003, 2, 66–79. [Google Scholar]
- Grodzinsky, A.J.; Levenston, M.E.; Jin, M.; Frank, E.H. Cartilage Tissue Remodeling in Response to Mechanical Forces. Annu. Rev. Biomed. Eng. 2000, 2, 691–713. [Google Scholar] [CrossRef]
- Castagnini, F.; Sudanese, A.; Bordini, B.; Tassinari, E.; Stea, S.; Toni, A. Total Knee Replacement in Young Patients: Survival and Causes of Revision in a Registry Population. J. Arthroplast. 2017, 32, 3368–3372. [Google Scholar] [CrossRef]
- Kellgren, J.H.; Lawrence, J.S. Radiological Assessment of Osteo-Arthrosis. Ann. Rheum. Dis. 1957, 16, 494–502. [Google Scholar] [CrossRef]
- Krakowski, P.; Karpiński, R.; Jojczuk, M.; Nogalska, A.; Jonak, J. Knee MRI Underestimates the Grade of Cartilage Lesions. Appl. Sci. 2021, 11, 1552. [Google Scholar] [CrossRef]
- Riecke, B.F.; Christensen, R.; Torp-Pedersen, S.; Boesen, M.; Gudbergsen, H.; Bliddal, H. An Ultrasound Score for Knee Osteoarthritis: A Cross-Sectional Validation Study. Osteoarthr. Cartil. 2014, 22, 1675–1691. [Google Scholar] [CrossRef] [PubMed]
- Karpiński, R.; Prus, A.; Jonak, K.; Krakowski, P. Vibroarthrography as a Noninvasive Screening Method for Early Diagnosis of Knee Osteoarthritis: A Review of Current Research. Appl. Sci. 2025, 15, 279. [Google Scholar] [CrossRef]
- Choi, S.; Seo, S.; Shin, B.; Byun, H.; Kersner, M.; Kim, B.; Kim, D.; Ha, S. Temporal Convolution for Real-Time Keyword Spotting on Mobile Devices. arXiv 2019, arXiv:1904.03814. [Google Scholar]
- Triki, N.; Karray, M.; Ksantini, M. A Real-Time Traffic Sign Recognition Method Using a New Attention-Based Deep Convolutional Neural Network for Smart Vehicles. Appl. Sci. 2023, 13, 4793. [Google Scholar] [CrossRef]
- Gupta, M.; Wadhvani, R.; Rasool, A. A Real-Time Adaptive Model for Bearing Fault Classification and Remaining Useful Life Estimation Using Deep Neural Network. Knowl. Based Syst. 2023, 259, 110070. [Google Scholar] [CrossRef]
- Hasan, M.D.A.; Balasubadra, K.; Vadivel, G.; Arunfred, N.; Ishwarya, M.V.; Murugan, S. IoT-Driven Image Recognition for Microplastic Analysis in Water Systems Using Convolutional Neural Networks. In Proceedings of the 2024 2nd International Conference on Computer, Communication and Control (IC4), Indore, India, 8–10 February 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Hangaragi, S.; Singh, T.; N, N. Face Detection and Recognition Using Face Mesh and Deep Neural Network. Procedia Comput. Sci. 2023, 218, 741–749. [Google Scholar] [CrossRef]
- Fayaz, J.; Galasso, C. A Deep Neural Network Framework for Real-time On-site Estimation of Acceleration Response Spectra of Seismic Ground Motions. Comput. Aided Civ. Infrastruct. Eng. 2023, 38, 87–103. [Google Scholar] [CrossRef]
- Machrowska, A.; Karpiński, R.; Krakowski, P.; Jonak, J. Diagnostic Factors for Opened and Closed Kinematic Chain of Vibroarthrography Signals. Appl. Comput. Sci. 2019, 15, 34–44. [Google Scholar] [CrossRef]
- Machrowska, A.; Karpiński, R.; Maciejewski, M.; Jonak, J.; Krakowski, P. Application of Eemd-Dfa Algorithms and Ann Classification for Detection of Knee Osteoarthritis Using Vibroarthrography. Appl. Comput. Sci. 2024, 20, 90–108. [Google Scholar] [CrossRef]
- Karpiński, R.; Krakowski, P.; Jonak, J.; Machrowska, A.; Maciejewski, M.; Nogalski, A. Diagnostics of Articular Cartilage Damage Based on Generated Acoustic Signals Using ANN—Part I: Femoral-Tibial Joint. Sensors 2022, 22, 2176. [Google Scholar] [CrossRef] [PubMed]
- Karpiński, R.; Krakowski, P.; Jonak, J.; Machrowska, A.; Maciejewski, M.; Nogalski, A. Diagnostics of Articular Cartilage Damage Based on Generated Acoustic Signals Using ANN—Part II: Patellofemoral Joint. Sensors 2022, 22, 3765. [Google Scholar] [CrossRef] [PubMed]
- Karpiński, R.; Krakowski, P.; Jonak, J.; Machrowska, A.; Maciejewski, M.; Nogalski, A. Estimation of Differences in Selected Indices of Vibroacoustic Signals between Healthy and Osteoarthritic Patellofemoral Joints as a Potential Non-Invasive Diagnostic Tool. J. Phys. Conf. Ser. 2021, 2130, 012009. [Google Scholar] [CrossRef]
- Karpiński, R.; Szabelski, J.; Maksymiuk, J. Effect of Physiological Fluids Contamination on Selected Mechanical Properties of Acrylate Bone Cement. Materials 2019, 12, 3963. [Google Scholar] [CrossRef]
- Karpiński, R.; Krakowski, P.; Jonak, J.; Machrowska, A.; Maciejewski, M. Comparison of Selected Classification Methods Based on Machine Learning as a Diagnostic Tool for Knee Joint Cartilage Damage Based on Generated Vibroacoustic Processes. Appl. Comput. Sci. 2023, 19, 136–150. [Google Scholar] [CrossRef]
- Petrillo, L.; Martinelli, F.; Santone, A.; Mercaldo, F. Explainable Security Requirements Classification Through Transformer Models. Future Internet 2025, 17, 15. [Google Scholar] [CrossRef]
- Huang, P.; Luo, X. FDTs: A Feature Disentangled Transformer for Interpretable Squamous Cell Carcinoma Grading. IEEE/CAA J. Autom. Sin. 2024, 12, 1. [Google Scholar]
- Huang, P.; Xiao, H.; He, P.; Li, C.; Guo, X.; Tian, S.; Feng, P.; Chen, H.; Sun, Y.; Mercaldo, F.; et al. LA-ViT: A Network With Transformers Constrained by Learned-Parameter-Free Attention for Interpretable Grading in a New Laryngeal Histopathology Image Dataset. IEEE J. Biomed. Health Inform. 2024, 28, 3557–3570. [Google Scholar] [CrossRef]
- Huang, P.; Li, C.; He, P.; Xiao, H.; Ping, Y.; Feng, P.; Tian, S.; Chen, H.; Mercaldo, F.; Santone, A.; et al. MamlFormer: Priori-Experience Guiding Transformer Network via Manifold Adversarial Multi-Modal Learning for Laryngeal Histopathological Grading. Inf. Fusion 2024, 108, 102333. [Google Scholar] [CrossRef]
- Karpiński, R.; Machrowska, A.; Maciejewski, M.; Jonak, J.; Krakowski, P. Concept and validation of a system for recording vibroacoustic signals of the knee joint. IAPGOS 2024, 14, 17–21. [Google Scholar] [CrossRef]
- Karpiński, R.; Machrowska, A.; Maciejewski, M. Application of acoustic signal processing methods in detecting differences between open and closed kinematic chain movement for the knee joint. Appl. Comput. Sci. 2019, 15, 36–48. [Google Scholar] [CrossRef]
- Jonak, J.; Karpinski, R.; Machrowska, A.; Krakowski, P.; Maciejewski, M. A Preliminary Study on the Use of EEMD-RQA Algorithms in the Detection of Degenerative Changes in Knee Joints. IOP Conf. Ser. Mater. Sci. Eng. 2019, 710, 012037. [Google Scholar] [CrossRef]
- Karpiński, R.; Krakowski, P.; Jonak, J.; Machrowska, A.; Maciejewski, M.; Nogalski, A. Analysis of Differences in Vibroacoustic Signals between Healthy and Osteoarthritic Knees Using EMD Algorithm and Statistical Analysis. J. Phys. Conf. Ser. 2021, 2130, 012010. [Google Scholar] [CrossRef]
- Teja, K.; Tiwari, R.; Mohanty, S. Adaptive Denoising of ECG Using EMD, EEMD and CEEMDAN Signal Processing Techniques. J. Phys. Conf. Ser. 2020, 1706, 012077. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Y. A Method to Denoise the Epileptic EEG by EEMD and TFPF. In Proceedings of the 2021 International Conference on Electronic Information Engineering and Computer Science (EIECS), Changchun, China, 23–26 September 2021; IEEE: New York, NY, USA, 2021; pp. 197–200. [Google Scholar]
- Amarouayache, I.I.E.; Saadi, M.N.; Guersi, N.; Boutasseta, N. Bearing Fault Diagnostics Using EEMD Processing and Convolutional Neural Network Methods. Int. J. Adv. Manuf. Technol. 2020, 107, 4077–4095. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, Y.; Li, H.; Gao, X. Rolling Bearing Composite Fault Diagnosis Method Based on EEMD Fusion Feature. J. Mech. Sci. Technol. 2022, 36, 4563–4570. [Google Scholar] [CrossRef]
- Litak, G.; Sen, A.K.; Syta, A. Intermittent and Chaotic Vibrations in a Regenerative Cutting Process. Chaos Solitons Fractals 2009, 41, 2115–2122. [Google Scholar] [CrossRef]
- Syta, A.; Czarnigowski, J.; Jakliński, P. Detection of Cylinder Misfire in an Aircraft Engine Using Linear and Non-Linear Signal Analysis. Measurement 2021, 174, 108982. [Google Scholar] [CrossRef]
- Syta, A.; Czarnigowski, J.; Jakliński, P.; Marwan, N. Detection and Identification of Cylinder Misfire in Small Aircraft Engine in Different Operating Conditions by Linear and Non-Linear Properties of Frequency Components. Measurement 2023, 223, 113763. [Google Scholar] [CrossRef]
- Sen, A.K.; Litak, G.; Syta, A.; Rusinek, R. Intermittency and Multiscale Dynamics in Milling of Fiber Reinforced Composites. Meccanica 2013, 48, 783–789. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Li, S. Multifractal Detrended Fluctuation Analysis of Congestive Heart Failure Disease Based on Constructed Heartbeat Sequence. IEEE Access 2020, 8, 205244–205249. [Google Scholar] [CrossRef]
- Auno, S.; Lauronen, L.; Wilenius, J.; Peltola, M.; Vanhatalo, S.; Palva, J.M. Detrended Fluctuation Analysis in the Presurgical Evaluation of Parietal Lobe Epilepsy Patients. Clin. Neurophysiol. 2021, 132, 1515–1525. [Google Scholar] [CrossRef]
- Mahananto, F.; Anggraeni, W.; Astuti, N.D. Classification of Congestive Heart Failure Using Artificial Neural Network Based on Higher-Order Moments Detrended Fluctuation Analysis of Heart Rate Variability. Procedia Comput. Sci. 2024, 234, 614–621. [Google Scholar] [CrossRef]
- Correa, F.V.; Meneses, A.M.D.; Carvalho, S.P.; Mendes, A.P.; Santos, L.D. Influence of Anxiety on the Heart Rate Variability of Patients in Preoperative Orthopedic Surgery. RSD 2021, 10, e14410817237. [Google Scholar] [CrossRef]
- Dingwell, J.B.; Cusumano, J.P. Re-Interpreting Detrended Fluctuation Analyses of Stride-to-Stride Variability in Human Walking. Gait Posture 2010, 32, 348–353. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, S.; Zheng, F.; Cai, S.; Lu, M.; Wu, M. Removal of Artifacts in Knee Joint Vibroarthrographic Signals Using Ensemble Empirical Mode Decomposition and Detrended Fluctuation Analysis. Physiol. Meas. 2014, 35, 429. [Google Scholar] [CrossRef]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of Trends on Detrended Fluctuation Analysis. Phys. Rev. E 2001, 64, 011114. [Google Scholar] [CrossRef]
- Kirchner, M.; Schubert, P.; Liebherr, M.; Haas, C.T. Detrended Fluctuation Analysis and Adaptive Fractal Analysis of Stride Time Data in Parkinson’s Disease: Stitching Together Short Gait Trials. PLoS ONE 2014, 9, e85787. [Google Scholar] [CrossRef]
- Hollman, J.H.; Lee, W.D.; Ringquist, D.C.; Taisey, C.; Ness, D.K. Comparing Adaptive Fractal and Detrended Fluctuation Analyses of Stride Time Variability: Tests of Equivalence. Gait Posture 2022, 94, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Ravi, D.K.; Marmelat, V.; Taylor, W.R.; Newell, K.M.; Stergiou, N.; Singh, N.B. Assessing the Temporal Organization of Walking Variability: A Systematic Review and Consensus Guidelines on Detrended Fluctuation Analysis. Front. Physiol. 2020, 11, 562. [Google Scholar] [CrossRef] [PubMed]
- Kshatri, S.S.; Singh, D. Convolutional Neural Network in Medical Image Analysis: A Review. Arch. Comput. Methods Eng. 2023, 30, 2793–2810. [Google Scholar] [CrossRef]
- Shen, M.; Wen, P.; Song, B.; Li, Y. Real-Time Epilepsy Seizure Detection Based on EEG Using Tunable-Q Wavelet Transform and Convolutional Neural Network. Biomed. Signal Process. Control. 2023, 82, 104566. [Google Scholar] [CrossRef]
- Chen, J.; Yu, K.; Wang, F.; Zhou, Z.; Bi, Y.; Zhuang, S.; Zhang, D. Temporal Convolutional Network-Enhanced Real-Time Implicit Emotion Recognition with an Innovative Wearable fNIRS-EEG Dual-Modal System. Electronics 2024, 13, 1310. [Google Scholar] [CrossRef]
- Cheng, E.; Zhang, X.; Wu, J.; Chen, H.; Liu, D.; Fan, Y.; Lian, M.; Guo, T.; Chen, H. Point Calculation Detection System Based on In Suit Convolution Transistor for Clinical Diagnosis of Heart Disease. Adv. Funct. Mater. 2024, 34, 2316673. [Google Scholar] [CrossRef]
- Borzì, L.; Sigcha, L.; Rodríguez-Martín, D.; Olmo, G. Real-Time Detection of Freezing of Gait in Parkinson’s Disease Using Multi-Head Convolutional Neural Networks and a Single Inertial Sensor. Artif. Intell. Med. 2023, 135, 102459. [Google Scholar] [CrossRef]
- Lou, A.; Guan, S.; Loew, M. CFPNet-M: A Light-Weight Encoder-Decoder Based Network for Multimodal Biomedical Image Real-Time Segmentation. Comput. Biol. Med. 2023, 154, 106579. [Google Scholar] [CrossRef]
- Wang, T.; Lu, C.; Sun, Y.; Yang, M.; Liu, C.; Ou, C. Automatic ECG Classification Using Continuous Wavelet Transform and Convolutional Neural Network. Entropy 2021, 23, 119. [Google Scholar] [CrossRef]
- Wang, C.; He, B.; Wei, W.; Yi, Z.; Li, P.; Duan, S.; Wu, X. Prediction of Contralateral Lower-Limb Joint Angles Using Vibroarthrography and Surface Electromyography Signals in Time-Series Network. IEEE Trans. Automat. Sci. Eng. 2023, 20, 901–908. [Google Scholar] [CrossRef]
- Befrui, N.; Elsner, J.; Flesser, A.; Huvanandana, J.; Jarrousse, O.; Le, T.N.; Müller, M.; Schulze, W.H.W.; Taing, S.; Weidert, S. Vibroarthrography for Early Detection of Knee Osteoarthritis Using Normalized Frequency Features. Med. Biol. Eng. Comput. 2018, 56, 1499–1514. [Google Scholar] [CrossRef]
- Bhat, B.; Nageshwaran, S. A Diagnostic Approach for Osteoarthritis Using Vibroarthrography. In Proceedings of the 10th International Conference on Application of Information and Communication Technology and Statistics in Economy and Education ICAICTSEE–2020, Sofia, Bulgaria, 27–28 November 2020. [Google Scholar]
- Balajee, A.; Mahesh, T.R.; Vinoth Kumar, V.; Kumar, V.D.; Bhat, C.R. VAG Signal Based Computational System for Consumer’s Utilization Devices in Osteoarthritis Data Extraction and Classification. IEEE Trans. Consumer Electron. 2024, 70, 7225–7232. [Google Scholar] [CrossRef]
- Kalo, K.; Niederer, D.; Sus, R.; Sohrabi, K.; Banzer, W.; Groß, V.; Vogt, L. The Detection of Knee Joint Sounds at Defined Loads by Means of Vibroarthrography. Clin. Biomech. 2020, 74, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Rangayyan, R.M.; Wu, Y.F. Screening of Knee-Joint Vibroarthrographic Signals Using Statistical Parameters and Radial Basis Functions. Med. Biol. Eng. Comput. 2008, 46, 223–232. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, S.; Rangayyan, R.M.; Bell, G.D.; Frank, C.B. Adaptive Time-Frequency Analysis of Knee Joint Vibroarthrographic Signals for Noninvasive Screening of Articular Cartilage Pathology. IEEE Trans. Biomed. Eng. 2000, 47, 773–783. [Google Scholar] [CrossRef]
- Rangayyan, R.M.; Krishnan, S.; Bell, G.D.; Frank, C.B.; Ladly, K.O. Parametric Representation and Screening of Knee Joint Vibroarthrographic Signals. IEEE Trans. Biomed. Eng. 1997, 44, 1068–1074. [Google Scholar] [CrossRef]
- Rangayyan, R.M.; Wu, Y. Analysis of Vibroarthrographic Signals with Features Related to Signal Variability and Radial-Basis Functions. Ann. Biomed. Eng. 2009, 37, 156–163. [Google Scholar] [CrossRef]
- Rangayyan, R.M.; Wu, Y. Screening of Knee-Joint Vibroarthrographic Signals Using Probability Density Functions Estimated with Parzen Windows. Biomed. Signal Process. Control. 2010, 5, 53–58. [Google Scholar] [CrossRef]
- Krishnan, S.; Rangayyan, R.M.; Bell, G.D.; Frank, C.B.; Ladly, K.O. Adaptive Filtering, Modelling and Classification of Knee Joint Vibroarthrographic Signals for Non-Invasive Diagnosis of Articular Cartilage Pathology. Med. Biol. Eng. Comput. 1997, 35, 677–684. [Google Scholar] [CrossRef]
- Wu, Y.; Krishnan, S. Combining Least-Squares Support Vector Machines for Classification of Biomedical Signals: A Case Study with Knee-Joint Vibroarthrographic Signals. J. Exp. Theor. Artif. Intell. 2011, 23, 63–77. [Google Scholar] [CrossRef]
- Kim, K.S.; Seo, J.H.; Kang, J.U.; Song, C.G. An Enhanced Algorithm for Knee Joint Sound Classification Using Feature Extraction Based on Time-Frequency Analysis. Comput. Methods Programs Biomed. 2009, 94, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Acharya, U.R. Analysis of Knee-Joint Vibroarthographic Signals Using Bandwidth-Duration Localized Three-Channel Filter Bank. Comput. Electr. Eng. 2018, 72, 191–202. [Google Scholar] [CrossRef]
- Yang, S.; Cai, S.; Zheng, F.; Wu, Y.; Liu, K.; Wu, M.; Zou, Q.; Chen, J. Representation of Fluctuation Features in Pathological Knee Joint Vibroarthrographic Signals Using Kernel Density Modeling Method. Med. Eng. Phys. 2014, 36, 1305–1311. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Chen, P.; Luo, X.; Huang, H.; Liao, L.; Yao, Y.; Wu, M.; Rangayyan, R.M. Quantification of Knee Vibroarthrographic Signal Irregularity Associated with Patellofemoral Joint Cartilage Pathology Based on Entropy and Envelope Amplitude Measures. Comput. Methods Programs Biomed. 2016, 130, 1–12. [Google Scholar] [CrossRef]
- Kręcisz, K.; Bączkowicz, D. Analysis and Multiclass Classification of Pathological Knee Joints Using Vibroarthrographic Signals. Comput. Methods Programs Biomed. 2018, 154, 37–44. [Google Scholar] [CrossRef]
- Athavale, Y.; Krishnan, S. A Telehealth System Framework for Assessing Knee-Joint Conditions Using Vibroarthrographic Signals. Biomed. Signal Process. Control. 2020, 55, 101580. [Google Scholar] [CrossRef]
- Shidore, M.M.; Athreya, S.S.; Deshpande, S.; Jalnekar, R. Screening of Knee-Joint Vibroarthrographic Signals Using Time and Spectral Domain Features. Biomed. Signal Process. Control. 2021, 68, 102808. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, T.; Song, J.; Gao, W. A Novel Automatic Knee Osteoarthritis Detection Method Based on Vibroarthrographic Signals. Biomed. Signal Process. Control. 2021, 68, 102796. [Google Scholar] [CrossRef]
- Mascarenhas, E.; Nalband, S.; Fredo, A.R.J.; Prince, A.A. Analysis and Classification of Vibroarthrographic Signals Using Tuneable ‘Q’ Wavelet Transform. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 27–28 February 2020; IEEE: New York, NY, USA, 2020; pp. 65–70. [Google Scholar]
- Moreira, D.; Silva, J.; Correia, M.V.; Massada, M. Classification of Knee Arthropathy with Accelerometer-Based Vibroarthrography. Stud. Health Technol. Inform. 2016, 224, 33–39. [Google Scholar]
- Machrowska, A.; Karpiński, R.; Maciejewski, M.; Jonak, J.; Krakowski, P.; Syta, A. Application of Recurrence Quantification Analysis in the Detection of Osteoarthritis of the Knee with the Use of Vibroarthrography. Adv. Sci. Technol. Res. J. 2024, 18, 19–31. [Google Scholar] [CrossRef]
- Karpiński, R. Knee joint osteoarthritis diagnosis based on selected acoustic signal discriminants using machine learning. ACS 2022, 18, 71–85. [Google Scholar] [CrossRef]
- Jeong, H.K.; An, S.; Herrin, K.; Scherpereel, K.; Young, A.; Inan, O.T. Quantifying Asymmetry Between Medial and Lateral Compartment Knee Loading Forces Using Acoustic Emissions. IEEE Trans. Biomed. Eng. 2022, 69, 1541–1551. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Pan, T.; Ye, Y.; Wan, Z.; Liu, B.; Ding, T. Multiscale-Temporal Feature Extraction and Boundary Confusion Alleviation for VAG-Based Fine-Grained Multi-Grade Osteoarthritis Deterioration Monitoring. Comput. Methods Programs Biomed. 2024, 255, 108286. [Google Scholar] [CrossRef] [PubMed]
- Nsugbe, E.; Olorunlambe, K.; Dearn, K. On the Early and Affordable Diagnosis of Joint Pathologies Using Acoustic Emissions, Deep Learning Decompositions and Prediction Machines. Sensors 2023, 23, 4449. [Google Scholar] [CrossRef]
- Gharehbaghi, S.; Jeong, H.K.; Safaei, M.; Inan, O.T. A Feasibility Study on Tribological Origins of Knee Acoustic Emissions. IEEE Trans. Biomed. Eng. 2022, 69, 1685–1695. [Google Scholar] [CrossRef]
- Semiz, B.; Hersek, S.; Whittingslow, D.C.; Ponder, L.A.; Prahalad, S.; Inan, O.T. Using Knee Acoustical Emissions for Sensing Joint Health in Patients with Juvenile Idiopathic Arthritis: A Pilot Study. IEEE Sens. J. 2018, 18, 9128–9136. [Google Scholar] [CrossRef]
- Olorunlambe, K.A.; Hua, Z.; Shepherd, D.E.T.; Dearn, K.D. Towards a Diagnostic Tool for Diagnosing Joint Pathologies: Supervised Learning of Acoustic Emission Signals. Sensors 2021, 21, 8091. [Google Scholar] [CrossRef]
- Hersek, S.; Baran Pouyan, M.; Teague, C.N.; Sawka, M.N.; Millard-Stafford, M.L.; Kogler, G.F.; Wolkoff, P.; Inan, O.T. Acoustical Emission Analysis by Unsupervised Graph Mining: A Novel Biomarker of Knee Health Status. IEEE Trans. Biomed. Eng. 2018, 65, 1291–1300. [Google Scholar] [CrossRef]
- Richardson, K.L.; Nichols, C.J.; Stegeman, R.G.; Zachs, D.P.; Tuma, A.; Heller, J.A.; Schnitzer, T.; Peterson, E.J.; Lim, H.H.; Etemadi, M.; et al. Validating Joint Acoustic Emissions Models as a Generalizable Predictor of Joint Health. IEEE Sens. J. 2024, 24, 17219–17230. [Google Scholar] [CrossRef]
- Kraft, D.; Bieber, G. Vibroarthrography Using Convolutional Neural Networks. In Proceedings of the 13th ACM International Conference on PErvasive Technologies Related to Assistive Environments, Corfu, Greece, 30 June–3 July 2020; ACM: New York, NY, USA; pp. 1–6. [Google Scholar]





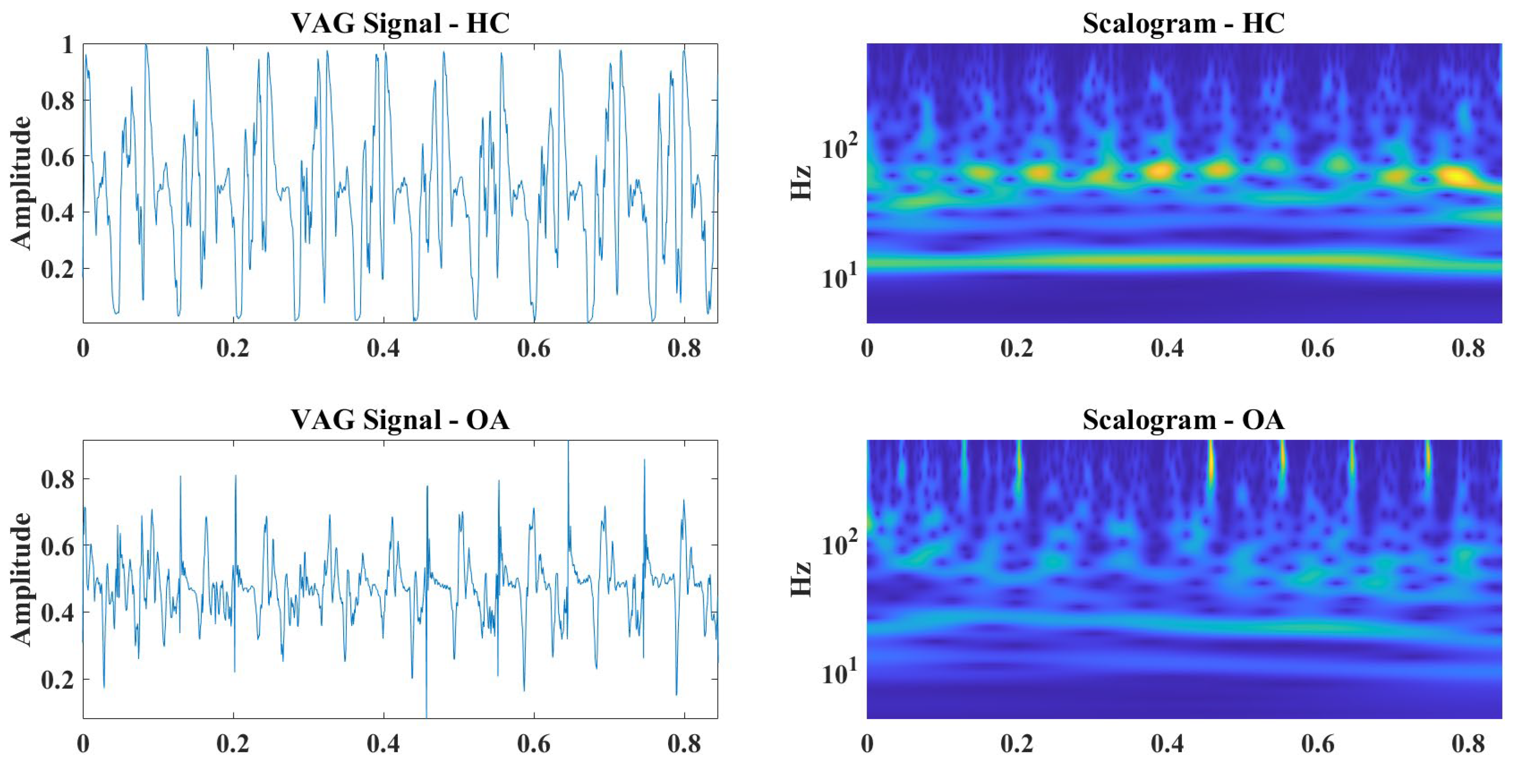

| Signal | Closed Kinematic Chain | Opened Kinematic Chain | ||||
|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | |
| IN | 0.121 | 0.268 | 0.112 | 0.088 | 0.046 | 0.026 |
| IMF 1 | 1.113 | 1.297 | 0.493 | 0.231 | 0.786 | 0.201 |
| IMF 2 | 4.977 | 1.811 | 2.202 | 1.612 | 0.085 | 0.030 |
| IMF 3 | 0.103 | 2.041 | 2.989 | 4.067 | 4.207 | 2.881 |
| IMF 4 | 0.052 | 4.438 | 0.204 | 0.452 | 4.168 | 0.769 |
| IMF 5 | 0.207 | 1.820 | 0.157 | 1.358 | 1.106 | 0.093 |
| IMF 6 | 0.179 | 0.543 | 0.233 | 0.266 | 0.781 | 0.028 |
| IMF 7 | 0.051 | 0.101 | 0.048 | 0.127 | 0.081 | 0.024 |
| IMF 8 | 0.011 | 0.080 | 0.023 | 0.045 | 0.004 | 0.010 |
| IMF 9 | 0.028 | 0.040 | 0.021 | 0.009 | 0.021 | 0.026 |
| IMF 10 | 0.030 | 0.041 | 0.025 | 0.021 | 0.036 | 0.005 |
| IMF 11 | 0.012 | 0.004 | 0.012 | 0.016 | 0.024 | 0.016 |
| IMF 12 | 0.010 | 0.003 | 0.005 | 0.012 | 0.010 | 0.011 |
| Accuracy [%] | Closed Kinematic Chain | Opened Kinematic Chain | |||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | ||
| Raw data | Learning | 74.6 | 77.3 | 73.7 | 73.2 | 75.8 | 65.7 |
| Validation | 71.3 | 73.3 | 69.7 | 72.1 | 67.3 | 63.4 | |
| Testing | 70.6 | 71.6 | 68.5 | 70.2 | 63.7 | 58.3 | |
| EEMD-DFA filtration | Learning | 99.1 | 100 | 98.7 | 99.4 | 100 | 98.5 |
| Validation | 98.7 | 99.3 | 98.5 | 99.2 | 98.6 | 98.3 | |
| Testing | 98.6 | 98.9 | 98.3 | 99.1 | 98.4 | 97.8 | |
| Authors and Sources | Features | Model | ACC |
|---|---|---|---|
| Rangayyan and Wu [67] | Statistical parameters in time domain | Neural network classifier based on radial basis functions | 0.82 |
| Krishnan et al. [68] | Statistical parameters in time and frequency domains | Logistic regression classifier | 0.77 |
| Rangayyan et al. [69] | Statistical parameters in time domain and a clinical features | Logistic regression classifier | 0.85 |
| Rangayyan and Wu [70] | Statistical parameters in time domain | Neural network classifier based on radial-basis functions | 0.91 |
| Rangayyan and Wu [71] | Statistical parameters in frequency domain | Neural network classifier based on radial-basis functions | 0.82 |
| Krishnan et al. [72] | Autoregression coefficients | Logistic regression classifier | 0.84 |
| Wu and Krishnan [73] | Statistical parameters in frequency domain | Recurrent neural network | 0.80 |
| Kim et al. [74] | Statistical parameters in frequency domain | Back-propagation neural network | 0.91 |
| Sharma and Acharya [75] | Statistical parameters in frequency domain | Least square support vector machine | 0.89 |
| Yang et al. [76] | Statistical parameters in frequency domain | Least square support vector machine | 0.88 |
| Wu et al. [77] | Statistical parameters in time and frequency domains | Support vector machine | 0.83 |
| Kręcisz and Bączkowicz [78] | Statistical parameters in time, nonlinear statistics | Logistic regression classifier with automatic attribute selection | 0.90 |
| Athavale and Krishnan [79] | Statistical parameters in time and frequency domains | Support vector machine | 0.84 |
| Shidore et al. [80] | Statistical parameters in time and frequency domains | Random forest classifier | 0.89 |
| Wang et al. [81] | Kernel-radius-based feature and statistic-based feature | Back-propagation neural network | 0.98 |
| Mascarenhas et al. [82] | Statistical parameters in time and frequency domains | Random forest classifier | 0.86 |
| Moreira et al. [83] | Statistical parameters in time and frequency domains | K-nearest neighbors classifier | 0.89 |
| Machrowska et al. [84] | Recurrence indicators | Multilayer perceptron, radial basis function | 0.91 |
| Karpiński [85] | Statistical parameters in time and frequency domains | Multilayer perceptron, radial basis function | 0.90 |
| Jeong et al. [86] | Time and frequency domains | Convolution neural network, support vector machine | 0.83 |
| Zhang et al. [87] | Frequency domain | Convolution neural network, confusion-free master–slave | 0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machrowska, A.; Karpiński, R.; Maciejewski, M.; Jonak, J.; Krakowski, P.; Syta, A. Multi-Scale Analysis of Knee Joint Acoustic Signals for Cartilage Degeneration Assessment. Sensors 2025, 25, 706. https://doi.org/10.3390/s25030706
Machrowska A, Karpiński R, Maciejewski M, Jonak J, Krakowski P, Syta A. Multi-Scale Analysis of Knee Joint Acoustic Signals for Cartilage Degeneration Assessment. Sensors. 2025; 25(3):706. https://doi.org/10.3390/s25030706
Chicago/Turabian StyleMachrowska, Anna, Robert Karpiński, Marcin Maciejewski, Józef Jonak, Przemysław Krakowski, and Arkadiusz Syta. 2025. "Multi-Scale Analysis of Knee Joint Acoustic Signals for Cartilage Degeneration Assessment" Sensors 25, no. 3: 706. https://doi.org/10.3390/s25030706
APA StyleMachrowska, A., Karpiński, R., Maciejewski, M., Jonak, J., Krakowski, P., & Syta, A. (2025). Multi-Scale Analysis of Knee Joint Acoustic Signals for Cartilage Degeneration Assessment. Sensors, 25(3), 706. https://doi.org/10.3390/s25030706






