Single Image Haze Removal via Multiple Variational Constraints for Vision Sensor Enhancement
Abstract
1. Introduction
- We propose a novel variational dehazing framework that incorporates multiple constraints: a flexible norm, an norm, and a weighted norm. The framework simultaneously estimates the accurate transmission map and produces high-quality clear results. Compared to previous methods based on integer-order norms, our embedded regularization offers a greater flexibility, making it more adaptable to a wide range of haze scenarios.
- We designed a weight function that incorporates both the local variances and the gradients of the clear image, which effectively controls the smoothness of the recovered image, helping to suppress noise and preserve important details.
- Experiments conducted on both synthetic and real hazy data demonstrated the competitive performance of our proposed algorithm in terms of the image quality and objective metrics.
2. Related Work
2.1. Prior-Based Dehazing Methods
2.2. Learning-Based Dehazing Methods
2.3. Variation-Based Dehazing Methods
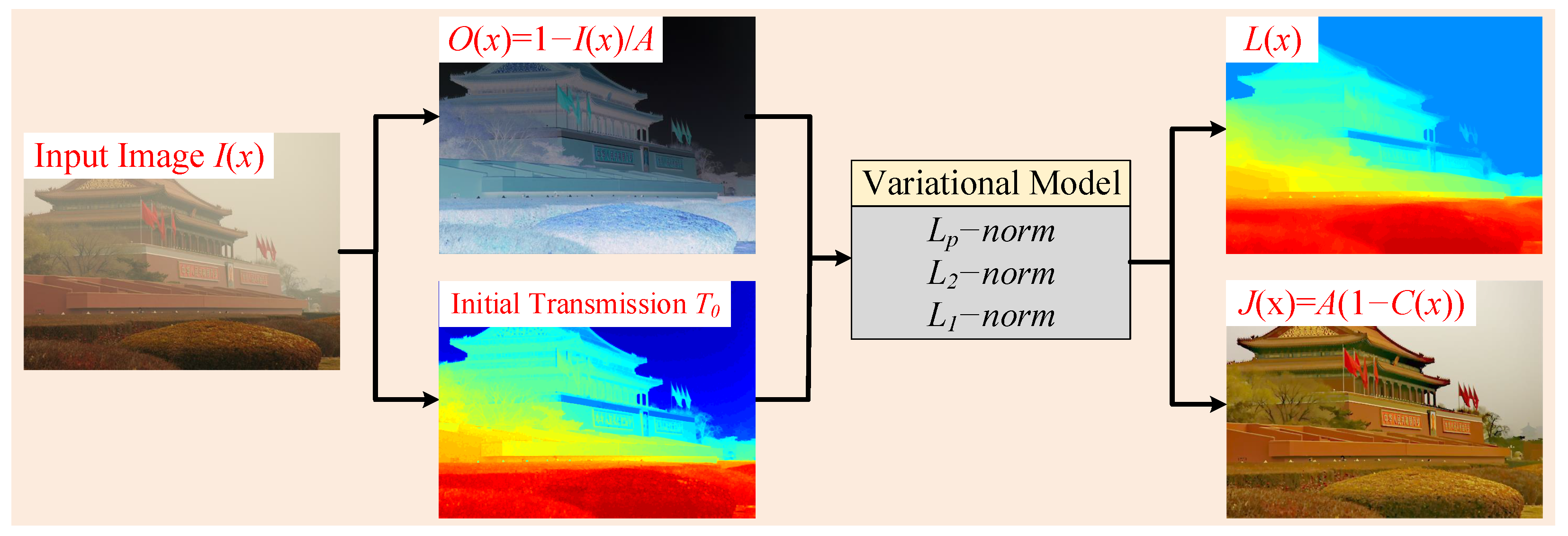
3. Methodology
3.1. Atmospheric Scattering Model (ASM)
3.2. Mixed Variational Model
| Algorithm 1 Solution of mixed variational model (4). |
| Input: O, parameters , , , and maximum number of iterations K. |
| Output: L and C |
| Initialization: , |
4. Experimental Results and Discussion
4.1. Experimental Settings
4.2. Comparisons on Real-World Hazy Images
4.3. Comparisons on Simulated Hazy Images
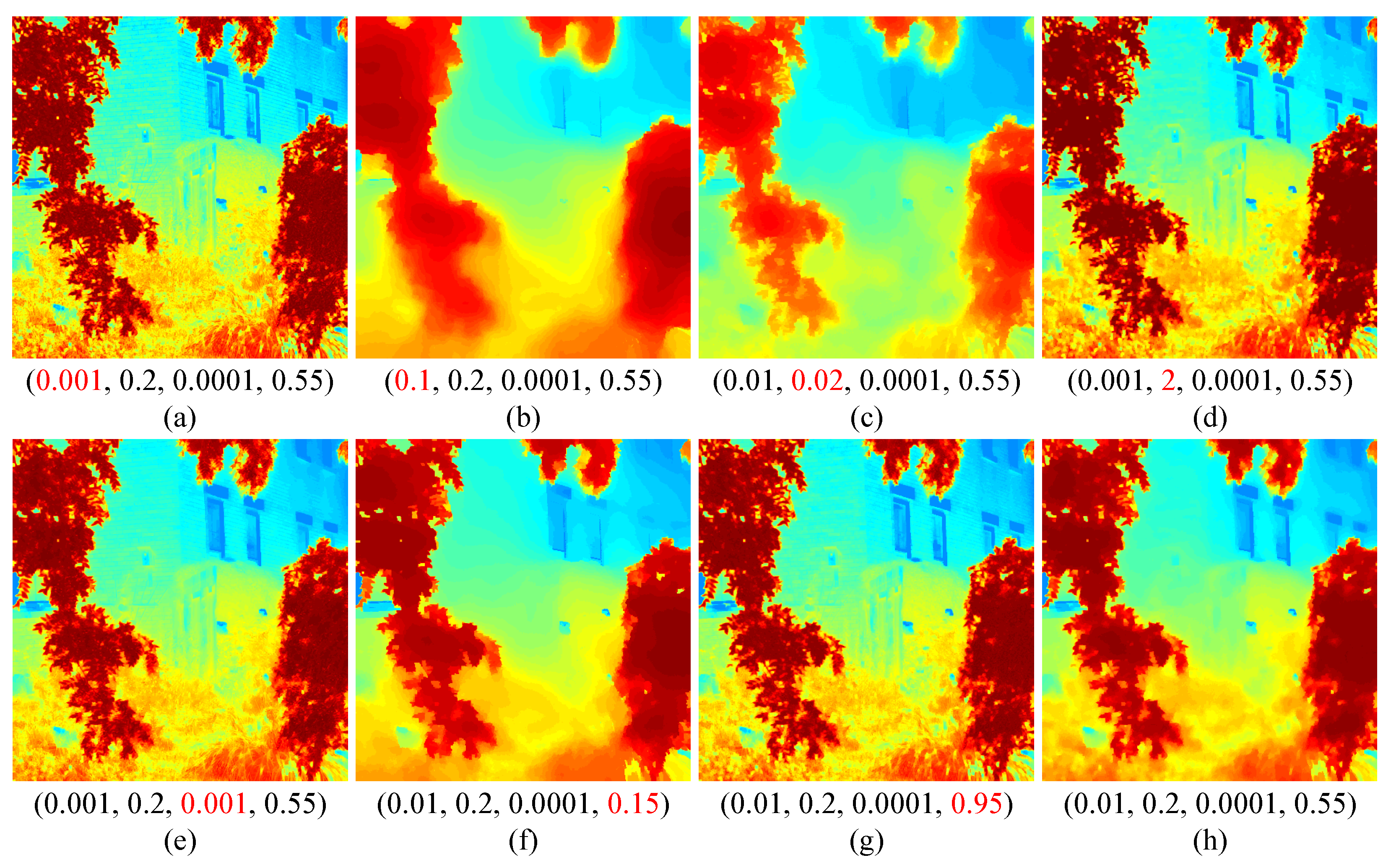
4.4. Parameter Study
4.5. Computational Complexity
4.6. High-Level Computer Vision Tasks
4.7. Generalization Applications
4.8. Limitations
4.9. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Crameri, F.; Hason, S. Navigating color integrity in data visualization. Patterns 2024, 5, 100792. [Google Scholar] [CrossRef]
- Yang, M. Investigating seasonal color change in the environment by color analysis and information visualization. Color Res. Appl. 2020, 45, 503–511. [Google Scholar] [CrossRef]
- Ancuti, C.O.; Ancuti, C. Single image dehazing by multi-scale fusion. IEEE Trans. Image Process. 2013, 22, 3271–3282. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Liu, Y.; Luo, S.; Ren, W.; Lin, W. Real-World Nighttime Dehazing via Score-Guided Multi-Scale Fusion and Dual-Channel Enhancement. IEEE Trans. Circuits Syst. Video Technol. 2025. early access. [Google Scholar] [CrossRef]
- Li, T.; Liu, Y.; Ren, W.; Shiri, B.; Lin, W. Single Image Dehazing Using Fuzzy Region Segmentation and Haze Density Decomposition. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 9964–9978. [Google Scholar] [CrossRef]
- McCartney, E. Optics of the Atmosphere: Scattering by Molecules and Particles; John Wiley and Sons, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Narasimhan, S.G.; Nayar, S.K. Chromatic framework for vision in bad weather. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2000, Hilton Head, SC, USA, 13–15 June 2000; Volume 1, pp. 598–605. [Google Scholar]
- Narasimhan, S.G.; Nayar, S.K. Vision and the atmosphere. Int. J. Comput. Vis. 2002, 48, 233–254. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar]
- Zhu, Q.; Mai, J.; Shao, L. A fast single image haze removal algorithm using color attenuation prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar] [CrossRef]
- Berman, D.; Treibitz, T.; Avidan, S. Single image dehazing using haze-lines. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 720–734. [Google Scholar] [CrossRef]
- Bui, T.M.; Kim, W. Single image dehazing using color ellipsoid prior. IEEE Trans. Image Process. 2018, 27, 999–1009. [Google Scholar] [CrossRef]
- Singh, D.; Kumar, V.; Kaur, M. Single image dehazing using gradient channel prior. Appl. Intell. 2019, 49, 4276–4293. [Google Scholar] [CrossRef]
- Ju, M.; Ding, C.; Guo, Y.J.; Zhang, D. IDGCP: Image dehazing based on gamma correction prior. IEEE Trans. Image Process. 2019, 29, 3104–3118. [Google Scholar] [CrossRef]
- Ju, M.; Ding, C.; Guo, C.A.; Ren, W.; Tao, D. IDRLP: Image dehazing using region line prior. IEEE Trans. Image Process. 2021, 30, 9043–9057. [Google Scholar] [CrossRef]
- Ling, P.; Chen, H.; Tan, X.; Jin, Y.; Chen, E. Single image dehazing using saturation line prior. IEEE Trans. Image Process. 2023, 32, 3238–3253. [Google Scholar] [CrossRef]
- Liang, S.; Gao, T.; Chen, T.; Cheng, P. A Remote Sensing Image Dehazing Method Based on Heterogeneous Priors. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- He, L.; Yi, Z.; Liu, J.; Chen, C.; Lu, M.; Chen, Z. ALSP+: Fast Scene Recovery via Ambient Light Similarity Prior. IEEE Trans. Image Process. 2025, 34, 4470–4484. [Google Scholar] [CrossRef]
- Cao, Z.H.; Liang, Y.J.; Deng, L.J.; Vivone, G. An efficient image fusion network exploiting unifying language and mask guidance. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 9845–9862. [Google Scholar] [CrossRef]
- Li, L.; Song, S.; Lv, M.; Jia, Z.; Ma, H. Multi-Focus Image Fusion Based on Fractal Dimension and Parameter Adaptive Unit-Linking Dual-Channel PCNN in Curvelet Transform Domain. Fractal Fract. 2025, 9, 157. [Google Scholar] [CrossRef]
- Krishnapriya, S.; Karuna, Y. Pre-trained deep learning models for brain MRI image classification. Front. Hum. Neurosci. 2023, 17, 1150120. [Google Scholar] [CrossRef] [PubMed]
- Nuanmeesri, S. Enhanced hybrid attention deep learning for avocado ripeness classification on resource constrained devices. Sci. Rep. 2025, 15, 3719. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. DehazeNet: An end-to-end system for single image haze removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef]
- Ren, W.; Liu, S.; Zhang, H.; Pan, J.; Cao, X.; Yang, M.H. Single image dehazing via multi-scale convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV) 2016, Amsterdam, The Netherlands, 11–14 October 2016; pp. 154–169. [Google Scholar]
- Ren, W.; Pan, J.; Zhang, H.; Cao, X.; Yang, M.H. Single image dehazing via multi-scale convolutional neural networks with holistic edges. Int. J. Comput. Vis. 2020, 128, 240–259. [Google Scholar] [CrossRef]
- Li, B.; Peng, X.; Wang, Z.; Xu, J.; Feng, D. Aod-net: All-in-one dehazing network. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) 2017, Venice, Italy, 22–29 October 2017; pp. 4770–4778. [Google Scholar]
- Deng, Q.; Huang, Z.; Tsai, C.C.; Lin, C.W. Hardgan: A haze-aware representation distillation gan for single image dehazing. In Proceedings of the European Conference on Computer Vision 2020, Glasgow, UK, 23–28 August 2020; pp. 722–738. [Google Scholar]
- Zheng, Y.; Su, J.; Zhang, S.; Tao, M.; Wang, L. Dehaze-AGGAN: Unpaired remote sensing image dehazing using enhanced attention-guide generative adversarial networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5630413. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Wan, S.; Ren, W.; Zhao, L.; Shen, L. Generative adversarial and self-supervised dehazing network. IEEE Trans Ind. Inform. 2024, 20, 4187–4197. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Shen, L.; Fan, E. GAN-based dehazing network with knowledge transferring. Multimed. Tools Appl. 2024, 83, 45095–45110. [Google Scholar] [CrossRef]
- Guo, C.L.; Yan, Q.; Anwar, S.; Cong, R.; Ren, W.; Li, C. Image dehazing transformer with transmission-aware 3d position embedding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 5812–5820. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2021, Montreal, QC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Liu, Y.; Yan, Z.; Chen, S.; Ye, T.; Ren, W.; Chen, E. Nighthazeformer: Single nighttime haze removal using prior query transformer. In Proceedings of the 31st ACM International Conference on Multimedia 2023, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 4119–4128. [Google Scholar]
- Wang, C.; Pan, J.; Lin, W.; Dong, J.; Wang, W.; Wu, X.M. Selfpromer: Self-prompt dehazing transformers with depth-consistency. In Proceedings of the AAAI Conference on Artificial Intelligence 2024, Vancouver, BC, Canada, 26–27 February 2024; pp. 5327–5335. [Google Scholar]
- Zhang, S.; Ren, W.; Tan, X.; Wang, Z.J.; Liu, Y.; Zhang, J.; Zhang, X.; Cao, X. Semantic-aware dehazing network with adaptive feature fusion. IEEE Trans. Cybern. 2023, 53, 454–467. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, X.; Ren, W.; Zhao, L.; Fan, E.; Huang, F. Exploring Fuzzy Priors From Multi-Mapping GAN for Robust Image Dehazing. IEEE Trans. Fuzzy Syst. 2025, 33, 3946–3958. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Shen, L.; Wan, S.; Ren, W. Wavelet-Based Physically Guided Normalization Network for Real-time Traffic Dehazing. Pattern Recognit. 2025, 172, 112451. [Google Scholar] [CrossRef]
- Wang, X.; Yang, G.; Ye, T.; Liu, Y. Dehaze-RetinexGAN: Real-World Image Dehazing via Retinex-based Generative Adversarial Network. In Proceedings of the AAAI Conference on Artificial Intelligence 2025, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 7997–8005. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, N.A.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Chen, Z.; Wang, Y.; Yang, Y.; Liu, D. PSD: Principled synthetic-to-real dehazing guided by physical priors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2021, Nashville, TN, USA, 19–25 June 2021; pp. 7180–7189. [Google Scholar]
- Meng, G.; Wang, Y.; Duan, J.; Xiang, S.; Pan, C. Efficient image dehazing with boundary constraint and contextual regularization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) 2013, Sydney, Australia, 1–8 December 2013; pp. 617–624. [Google Scholar]
- Galdran, A.; Vazquez-Corral, J.; Pardo, D.; Bertalmío, M. A variational framework for single image dehazing. In Proceedings of the Computer Vision-ECCV 2014 Workshops, Zurich, Switzerland, 6–12 September 2014; Part III 13. pp. 259–270. [Google Scholar]
- Wang, W.; He, C.; Xia, X.G. A constrained total variation model for single image dehazing. Pattern Recognit. 2018, 80, 196–209. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, X.; He, L.; Lu, W. Single image dehazing with depth-aware non-local total variation regularization. IEEE Trans. Image Process. 2018, 27, 5178–5191. [Google Scholar] [CrossRef]
- Liu, Y.; Shang, J.; Pan, L.; Wang, A.; Wang, M. A unified variational model for single image dehazing. IEEE Access 2019, 7, 15722–15736. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, Z.; Tan, J.; Li, Y. Multi-purpose oriented single nighttime image haze removal based on unified variational retinex model. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 1643–1657. [Google Scholar] [CrossRef]
- Jin, Z.; Ma, Y.; Min, L.; Zheng, M. Variational image dehazing with a novel underwater dark channel prior. Inverse Probl. Imaging 2024, 19, 334–354. [Google Scholar] [CrossRef]
- Li, C.; Hu, E.; Zhang, X.; Zhou, H.; Xiong, H.; Liu, Y. Visibility restoration for real-world hazy images via improved physical model and Gaussian total variation. Front. Comput. Sci. 2024, 18, 181708. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Hu, E.; Wang, A.; Shiri, B.; Lin, W. VNDHR: Variational Single Nighttime Image Dehazing for Enhancing Visibility in Intelligent Transportation Systems via Hybrid Regularization. IEEE Trans. Intell. Transp. Syst. 2025, 26, 10189–10203. [Google Scholar] [CrossRef]
- Dwivedi, P.; Chakraborty, S. Single image dehazing using extended local dark channel prior. Image Vis. Comput. 2023, 136, 104747. [Google Scholar] [CrossRef]
- Su, L.; Cui, S.; Zhang, W. An Algorithm for Enhancing Low-Light Images at Sea Based on Improved Dark Channel Priors. J. Nav. Aviat. Univ. 2024, 39, 576–586. [Google Scholar]
- Song, Y.; He, Z.; Qian, H.; Du, X. Vision transformers for single image dehazing. IEEE Trans. Image Process. 2023, 32, 1927–1941. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Ma, L.; Meng, X.; Zhou, F.; Liu, R.; Su, Z. Advancing real-world image dehazing: Perspective, modules, and training. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 9303–9320. [Google Scholar] [CrossRef]
- Liu, C.; Ng, M.K.P.; Zeng, T. Weighted variational model for selective image segmentation with application to medical images. Pattern Recognit. 2018, 76, 367–379. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, W.; Feng, X.; Han, Y. A new variational method for selective segmentation of medical images. Signal Process. 2022, 190, 108292. [Google Scholar] [CrossRef]
- Du, Y.; Xu, J.; Qiu, Q.; Zhen, X.; Zhang, L. Variational image deraining. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision 2020, Snowmass Village, CO, USA, 1–5 March 2020; pp. 2406–2415. [Google Scholar]
- Du, Y.; Xu, J.; Zhen, X.; Cheng, M.M.; Shao, L. Conditional variational image deraining. IEEE Trans. Image Process. 2020, 29, 6288–6301. [Google Scholar] [CrossRef]
- Hao, S.; Han, X.; Guo, Y.; Xu, X.; Wang, M. Low-light image enhancement with semi-decoupled decomposition. IEEE Trans. Multimed. 2020, 22, 3025–3038. [Google Scholar] [CrossRef]
- Fu, G.; Duan, L.; Xiao, C. A Hybrid L2-LP variational model for single low-light image enhancement with bright channel prior. In Proceedings of the 2019 IEEE International conference on image processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1925–1929. [Google Scholar]
- Hu, E.; Liu, Y.; Wang, A.; Shiri, B.; Ren, W.; Lin, W. Low-Light Image Enhancement Using a Retinex-based Variational Model with Weighted L p Norm Constraint. IEEE Trans. Multimed. 2025. early access. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, Z.; Xiong, H.; Liu, Y. A unified weighted variational model for simultaneously haze removal and noise suppression of hazy images. Displays 2022, 72, 102137. [Google Scholar] [CrossRef]
- Tseng, P. Convergence of a block coordinate descent method for nondifferentiable minimization. J. Optim. Theory Appl. 2001, 109, 475–494. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Barrett, R.; Berry, M.; Chan, T.F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; Van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Fattal, R. Single image dehazing. ACM Trans. Graph. 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Li, B.; Ren, W.; Fu, D.; Tao, D.; Feng, D.; Zeng, W.; Wang, Z. Benchmarking single-image dehazing and beyond. IEEE Trans. Image Process. 2019, 28, 492–505. [Google Scholar] [CrossRef]
- Kang, L.; Ye, P.; Li, Y.; Doermann, D. Convolutional neural networks for no-reference image quality assessment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2014, Columbus, OH, USA, 23–28 June 2014; pp. 1733–1740. [Google Scholar]
- Ke, J.; Wang, Q.; Wang, Y.; Milanfar, P.; Yang, F. Musiq: Multi-scale image quality transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2021, Montreal, QC, Canada, 11–17 October 2021; pp. 5148–5157. [Google Scholar]
- Talebi, H.; Milanfar, P. NIMA: Neural image assessment. IEEE Trans. Image Process. 2018, 27, 3998–4011. [Google Scholar] [CrossRef]
- Choi, L.K.; You, J.; Bovik, A.C. Referenceless prediction of perceptual fog density and perceptual image defogging. IEEE Trans. Image Process. 2015, 24, 3888–3901. [Google Scholar] [CrossRef]
- Ju, M.; Ding, C.; Ren, W.; Yang, Y.; Zhang, D.; Guo, Y.J. IDE: Image dehazing and exposure using an enhanced atmospheric scattering model. IEEE Trans. Image Process. 2021, 30, 2180–2192. [Google Scholar] [CrossRef]
- Ancuti, C.; Ancuti, C.O.; De Vleeschouwer, C. D-HAZY: A dataset to evaluate quantitatively dehazing algorithms. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2226–2230. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Ren, T.; Chen, Y.; Jiang, Q.; Zeng, Z.; Xiong, Y.; Liu, W.; Ma, Z.; Shen, J.; Gao, Y.; Jiang, X.; et al. Dino-x: A unified vision model for open-world object detection and understanding. arXiv 2024, arXiv:2411.14347. [Google Scholar]
- Fu, X.; Liao, Y.; Zeng, D.; Huang, Y.; Zhang, X.; Ding, X. A probabilistic method for image enhancement with simultaneous illumination and reflectance estimation. IEEE Trans. Image Process. 2015, 24, 4965–4977. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Ling, H. LIME: Low-light image enhancement via illumination map estimation. IEEE Trans. Image Process. 2017, 26, 982–993. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Zeng, D.; Huang, Y.; Zhang, X.; Ding, X. A weighted variational model for simultaneous reflectance and illumination estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 2782–2790. [Google Scholar]
- Huang, B.; Zhi, L.; Yang, C.; Sun, F.; Song, Y. Single satellite optical imagery dehazing using SAR image prior based on conditional generative adversarial networks. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision 2020, Snowmass Village, CO, USA, 1–5 March 2020; pp. 1806–1813. [Google Scholar]
- Ancuti, C.O.; Ancuti, C.; Sbert, M.; Timofte, R. Dense haze: A benchmark for image dehazing with dense-haze and haze-free images. In Proceedings of the IEEE International Conference on Image Processing (ICIP) 2019, Taipei, Taiwan, 22–25 September 2019. [Google Scholar]









| Methods | Venue | URHI Test Set | |||
|---|---|---|---|---|---|
| CNNIQA↑ | MUSIQ↑ | NIMA↑ | FADE↓ | ||
| CAP [10] | TIP2015 | 0.6164 | 58.5949 | 4.5574 | 1.9631 |
| DehazeNet [23] | TIP2016 | 0.6262 | 57.7627 | 4.7233 | 1.1125 |
| MSCNN [24] | ECCV2016 | 0.6394 | 59.0667 | 4.6235 | 1.5314 |
| RLP [15] | TIP2021 | 0.6682 | 59.2370 | 4.8978 | 0.7831 |
| SLP [16] | TIP2023 | 0.6452 | 58.5328 | 4.8271 | 0.9496 |
| ALSP [18] | TIP2025 | 0.6620 | 56.4242 | 4.9617 | 0.4091 |
| Our method | - | 0.6793 | 59.4488 | 4.9123 | 0.7583 |
| Methods | Venue | RTTS Test Set | |||
|---|---|---|---|---|---|
| CNNIQA↑ | MUSIQ↑ | NIMA↑ | FADE↓ | ||
| CAP [10] | TIP2015 | 0.5954 | 56.8876 | 4.6774 | 1.8792 |
| DehazeNet [23] | TIP2016 | 0.6039 | 56.4891 | 4.8311 | 1.1484 |
| MSCNN [24] | ECCV2016 | 0.6191 | 57.5146 | 4.7402 | 1.3640 |
| RLP [15] | TIP2021 | 0.6580 | 58.4325 | 4.9433 | 0.7502 |
| SLP [16] | TIP2023 | 0.6304 | 57.1622 | 4.8620 | 0.8420 |
| ALSP [18] | TIP2025 | 0.6405 | 55.9393 | 4.9329 | 0.3926 |
| Our method | - | 0.6714 | 58.0776 | 4.9121 | 0.7433 |
| Methods | Venue | PSNR↑ | SSIM ↑ | MUSIQ↑ | FADE↓ |
|---|---|---|---|---|---|
| CAP [10] | TIP2015 | 10.4343 | 0.5927 | 39.9742 | 1.2507 |
| DehazeNet [23] | TIP2016 | 12.2392 | 0.6111 | 41.7782 | 0.7251 |
| MSCNN [24] | ECCV2016 | 9.9641 | 0.5828 | 42.0376 | 1.2075 |
| IDE [72] | TIP2021 | 9.2873 | 0.5450 | 41.6226 | 0.9924 |
| RLP [15] | TIP2021 | 11.8260 | 0.6139 | 45.4642 | 0.7474 |
| SLP [16] | TIP2023 | 13.1661 | 0.7135 | 43.3794 | 0.5428 |
| ALSP [18] | TIP2025 | 12.2068 | 0.6605 | 43.0191 | 0.4892 |
| Our method | - | 13.7960 | 0.6920 | 44.6151 | 0.5040 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Zhao, W.; Wang, L.; Liu, H.; Li, Y.; Liu, Y. Single Image Haze Removal via Multiple Variational Constraints for Vision Sensor Enhancement. Sensors 2025, 25, 7198. https://doi.org/10.3390/s25237198
Feng Y, Zhao W, Wang L, Liu H, Li Y, Liu Y. Single Image Haze Removal via Multiple Variational Constraints for Vision Sensor Enhancement. Sensors. 2025; 25(23):7198. https://doi.org/10.3390/s25237198
Chicago/Turabian StyleFeng, Yuxue, Weijia Zhao, Luyao Wang, Hongyu Liu, Yuxiao Li, and Yun Liu. 2025. "Single Image Haze Removal via Multiple Variational Constraints for Vision Sensor Enhancement" Sensors 25, no. 23: 7198. https://doi.org/10.3390/s25237198
APA StyleFeng, Y., Zhao, W., Wang, L., Liu, H., Li, Y., & Liu, Y. (2025). Single Image Haze Removal via Multiple Variational Constraints for Vision Sensor Enhancement. Sensors, 25(23), 7198. https://doi.org/10.3390/s25237198






