Real-Time Subject-Specific Predictive Modeling of PPG Signals for Artifact-Resilient SpO2 Estimation Under Hypoxia
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Study
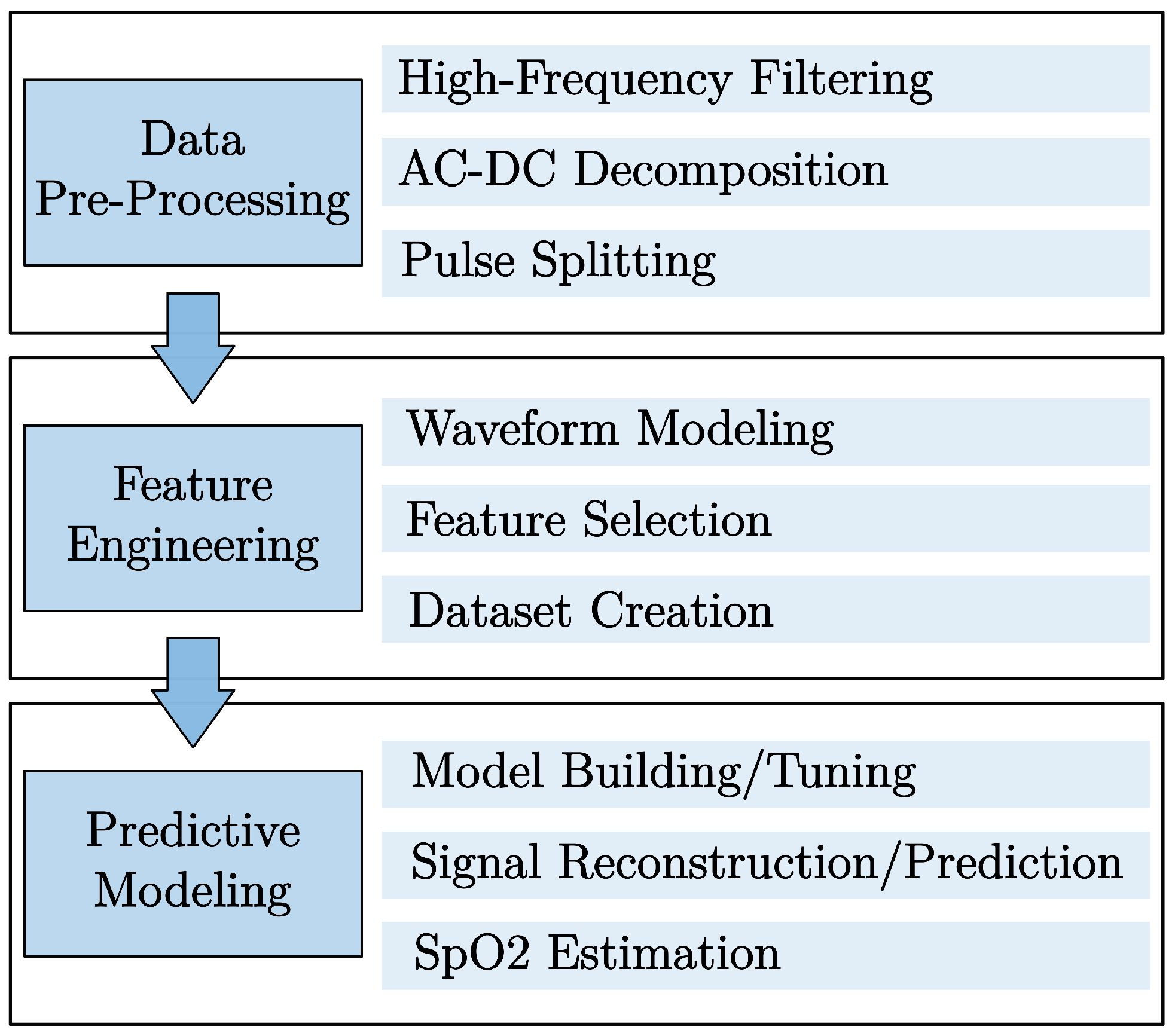
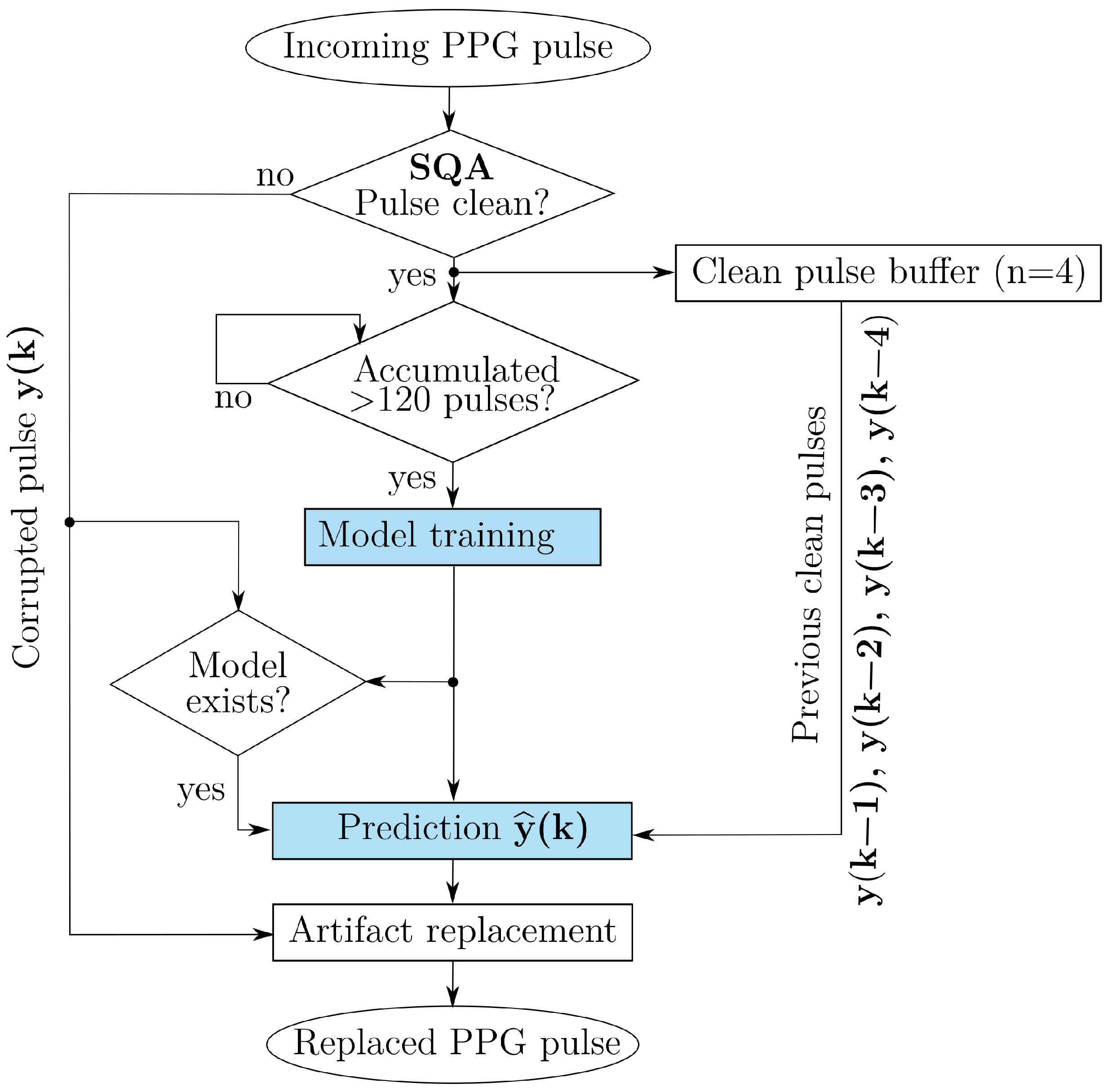
2.2. Methods Overview
2.3. Data Pre-Processing
2.4. Feature Engineering
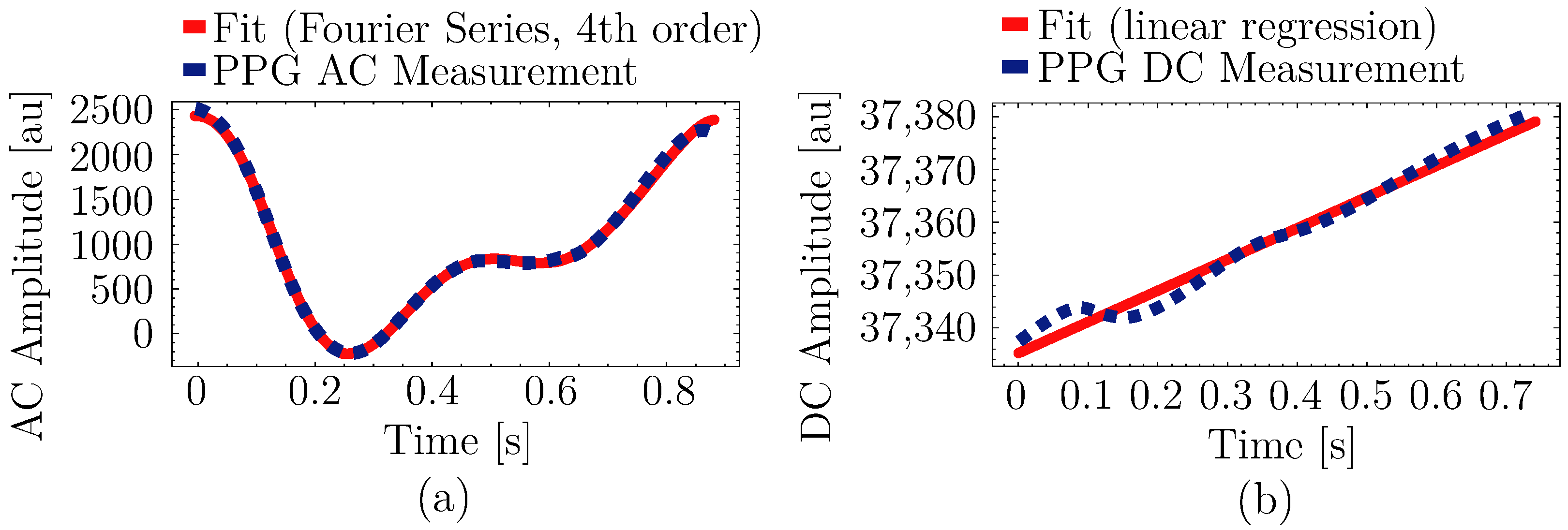
2.4.1. Waveform Modeling and Feature Selection
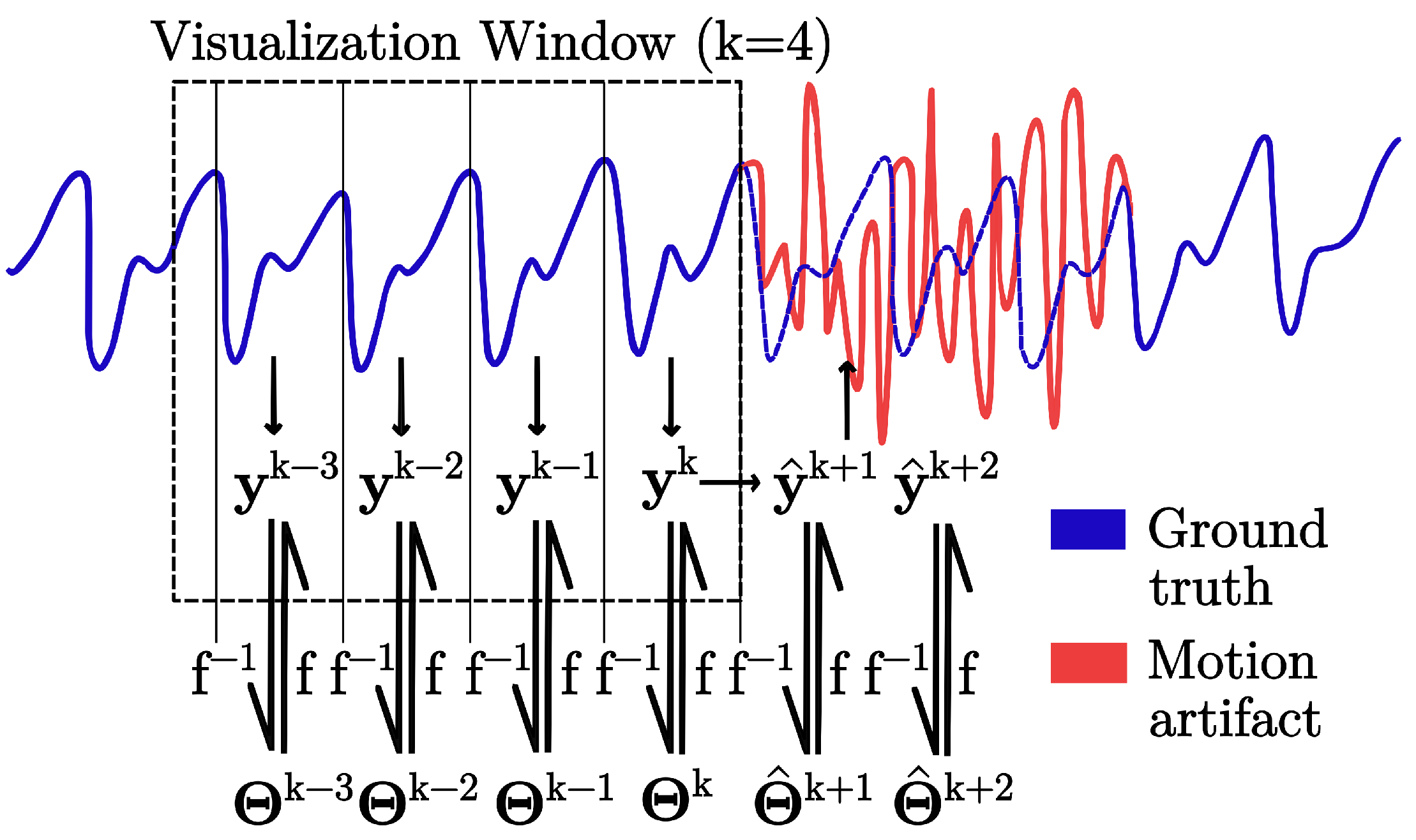
2.4.2. Dataset Preparation
2.5. Predictive Modeling
2.5.1. AC Component
2.5.2. DC Component
2.6. SpO2 Estimation
3. Results and Discussion
3.1. Feature Selection
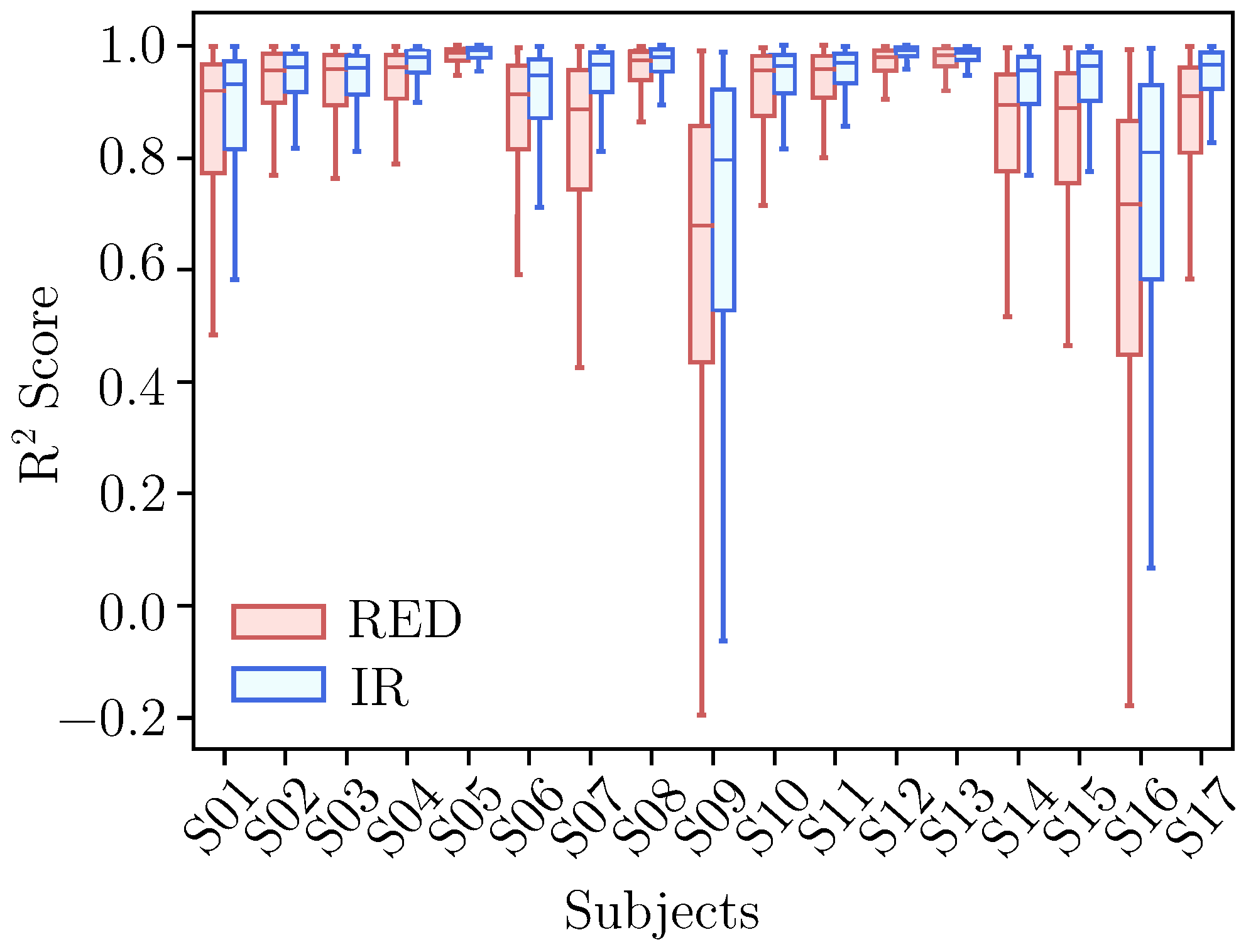
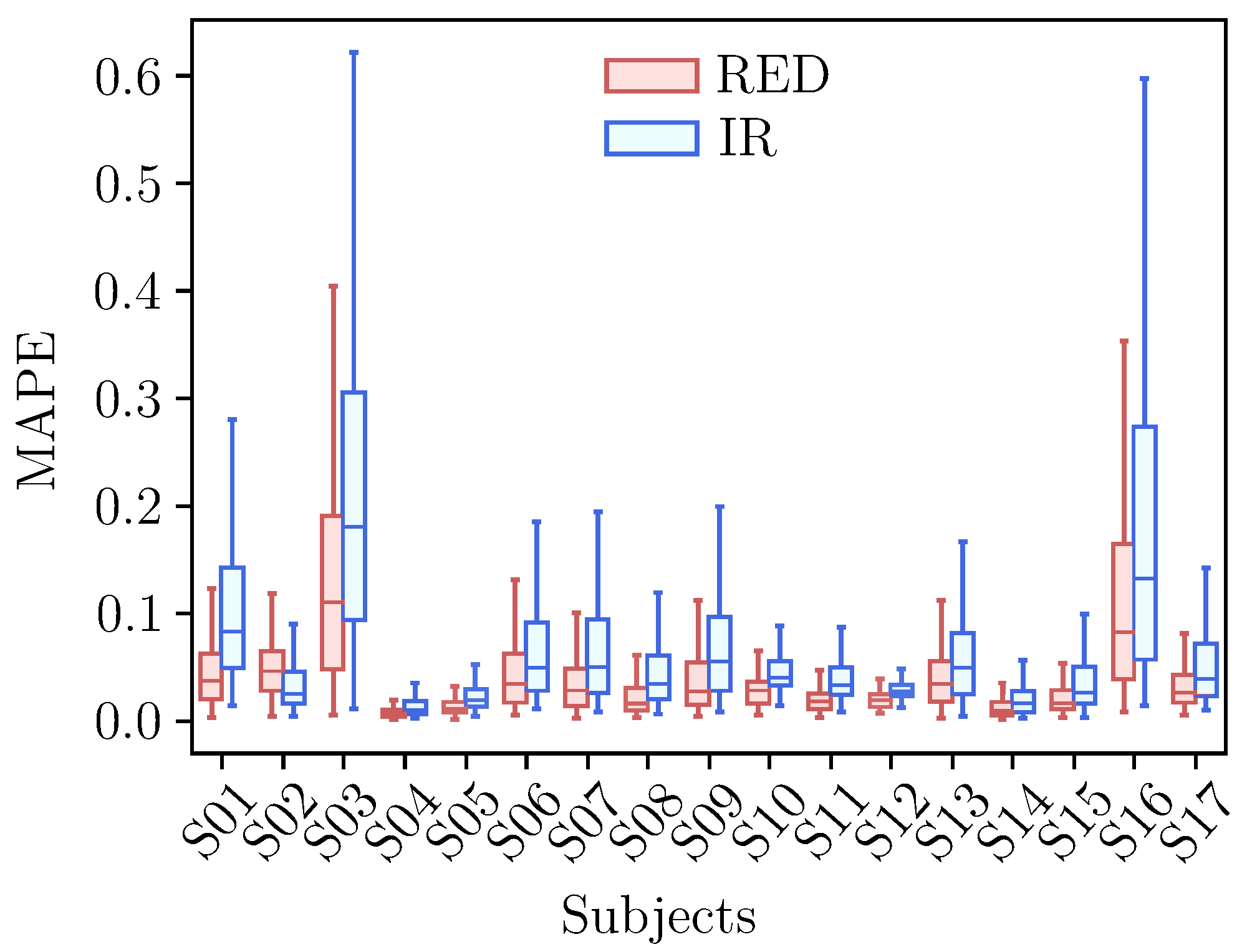
3.2. Forecasting Performance
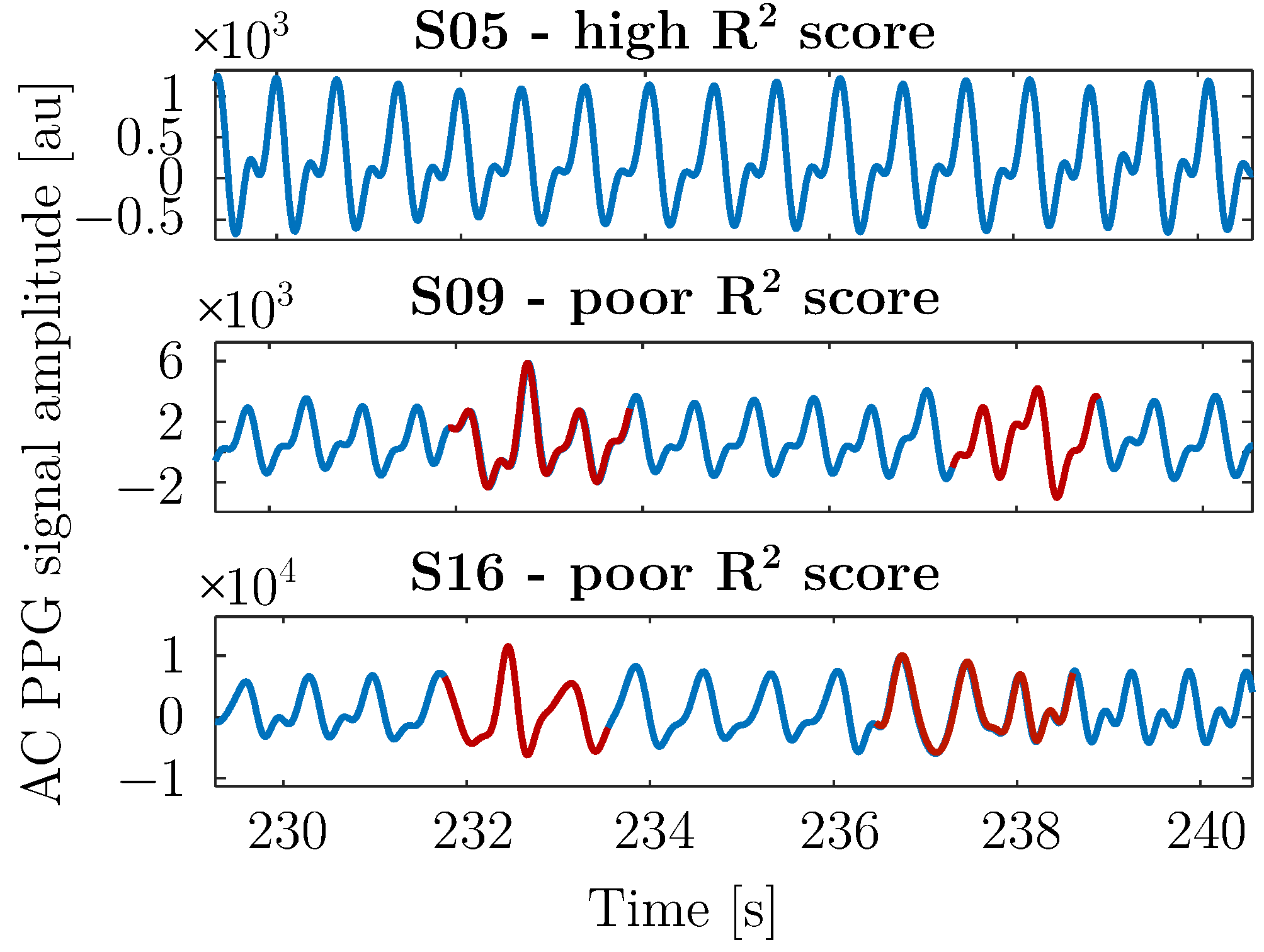
3.2.1. AC Forecasting
3.2.2. DC Forecasting
3.2.3. Optimal Training Size
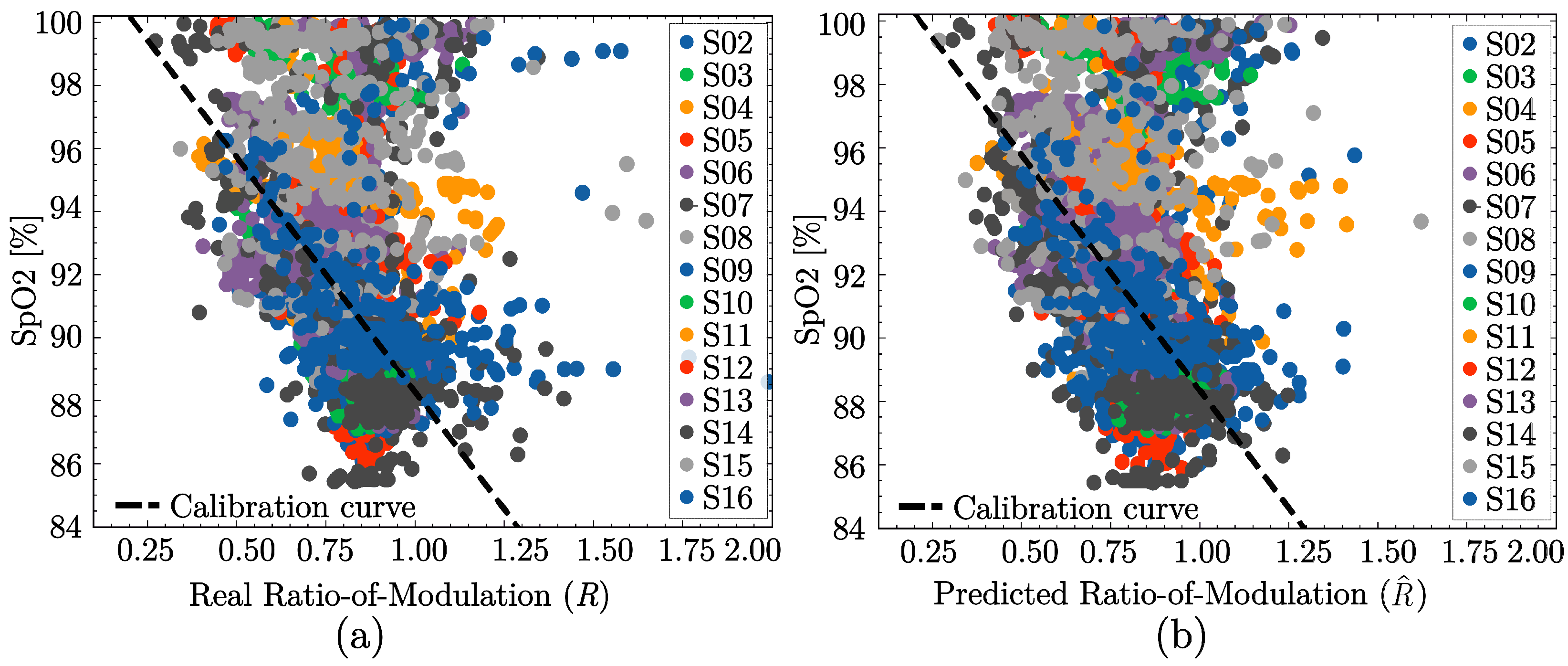
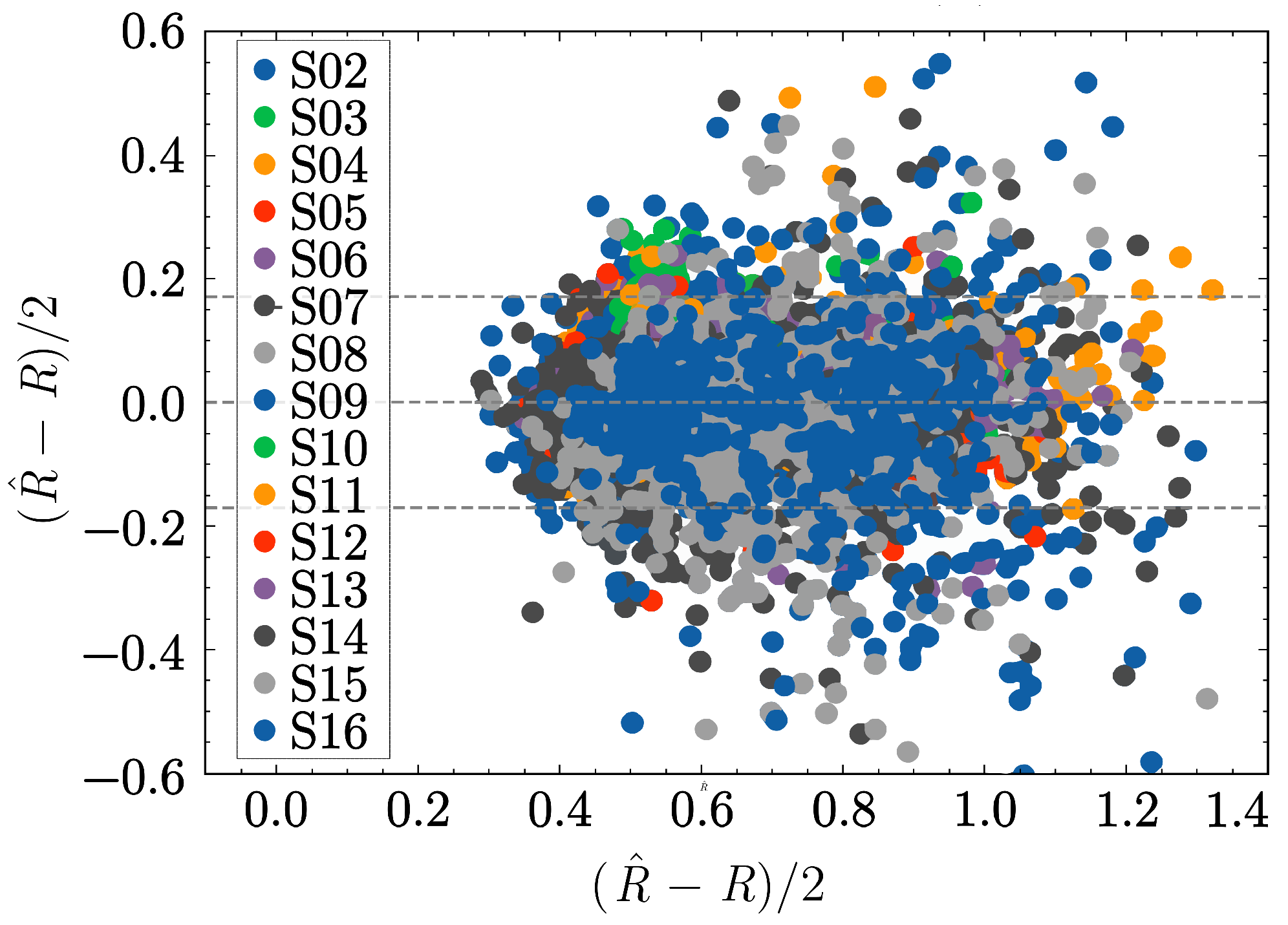
3.3. SpO2 Estimation Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| BGA | Blood Gas Analysis |
| BMI | Body Mass Index |
| CI | Confidence Intervals |
| CPU | Central Processing Unit |
| DC | Direct Current |
| FDA | U.S. Food and Drug Administration |
| FIR | Finite Impulse Response |
| FSPC | Fitzpatrick Skin Phototype Classification |
| GAN | Generative Adversarial Network |
| GPU | Graphics Processing Unit |
| HR | Heart Rate |
| HRV | Heart Rate Variability |
| ICA | Independent Component Analysis |
| IIR | Infinite Impulse Response |
| IR | Infrared |
| LoA | Limits-of-agreement |
| MA | Motion Artifacts |
| MAPE | Mean Absolute Percentage Error |
| MIMO | Multi-Input Multi-Output |
| PPG | Photoplethysmography |
| RMSE | Root Mean Squared Error |
| RR | Respiratory Rate |
| SaO2 | Arterial Oxygen Saturation |
| SpO2 | Peripheral arterial oxygen saturation |
| SQA | Signal Quality Assessment |
| XGBoost | Extreme Gradient Boost |
References
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1. [Google Scholar] [CrossRef]
- Kyriacou, P.A.; Chatterjee, S. The Origin of Photoplethysmography; Elsevier: Amsterdam, The Netherlands, 2021; pp. 17–43. [Google Scholar] [CrossRef]
- Mejia-Mejia, E.; Allen, J.; Budidha, K.; El-Hajj, C.; Kyriacou, P.A.; Charlton, P.H. Photoplethysmography signal processing and synthesis. In Photoplethysmography; Elsevier: Amsterdam, The Netherlands, 2022; pp. 69–146. [Google Scholar]
- Kyriacou, P.A. Pulse oximetry in the oesophagus. Physiol. Meas. 2006, 27, R1. [Google Scholar] [CrossRef] [PubMed]
- Badiola, I.; Blazek, V.; Kumar, V.J.; George, B.; Leonhardt, S.; Antink, C.H. Accuracy enhancement in reflective pulse oximetry by considering wavelength-dependent pathlengths. Physiol. Meas. 2022, 43, 095001. [Google Scholar] [CrossRef]
- U.S. Food and Drug Administration, Center for Devices and Radiological Health. Pulse Oximeters for Medical Purposes—Non-Clinical and Clinical Performance Testing, Labeling, and Premarket Submission Recommendations: Draft Guidance for Industry and Food and Drug Administration Staff; Draft Guidance Document; US Food and Drug Administration: Silver Spring, MD, USA, 2025; Docket Number: FDA-2023-N-4976. Draft—Not for implementation. Contains non-binding recommendations.
- Hess, D.R. Using SpO2: Not as Simple as It Seems. Respir. Care 2023, 68, 708–712. [Google Scholar] [CrossRef]
- Masimo Corporation. Pulse Oximetry Accuracy: Assessing the Accuracy of Pulse Oximetry in True Clinical Settings; Corporate Publication; Masimo Corporation: Irvine, CA, USA, 2007. [Google Scholar]
- Peng, F.; Zhang, Z.; Gou, X.; Liu, H.; Wang, W. Motion artifact removal from photoplethysmographic signals by combining temporally constrained independent component analysis and adaptive filter. Biomed. Eng. Online 2014, 13, 50. [Google Scholar] [CrossRef]
- Pollreisz, D.; TaheriNejad, N. Detection and Removal of Motion Artifacts in PPG Signals. Mob. Netw. Appl. 2022, 27, 728–738. [Google Scholar] [CrossRef]
- Wu, C.C.; Chen, I.W.; Fang, W.C. An implementation of motion artifacts elimination for PPG signal processing based on recursive least squares adaptive filter. In Proceedings of the 2017 IEEE Biomedical Circuits and Systems Conference (BioCAS), Turin, Italy, 19–21 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Kim, B.; Yoo, S. Motion artifact reduction in photoplethysmography using independent component analysis. IEEE Trans. Biomed. Eng. 2006, 53, 566–568. [Google Scholar] [CrossRef]
- Hanyu, S.; Xiaohui, C. Motion artifact detection and reduction in PPG signals based on statistics analysis. In Proceedings of the 29th Chinese Control and Decision Conference, CCDC 2017, Chongqing, China, 28–30 May 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2017; pp. 3114–3119. [Google Scholar] [CrossRef]
- Sadhukhan, D.; Pal, S.; Mitra, M. PPG Noise Reduction based on Adaptive Frequency Suppression using Discrete Fourier Transform for Portable Home Monitoring Applications. In Proceedings of the 2018 15th IEEE India Council International Conference (INDICON), Coimbatore, India, 16–18 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Reddy, K.; Kumar, J. Motion Artifact Reduction in Photoplethysmographic Signals using Singular Value Decomposition. In Proceedings of the 2007 IEEE Instrumentation & Measurement Technology Conference IMTC 2007, Warsaw, Poland, 1–3 May 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Raghuram, M.; Sivani, K.; Reddy, K.A. Use of complex EMD generated noise reference for adaptive reduction of motion artifacts from PPG signals. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 1816–1820. [Google Scholar] [CrossRef]
- Afandizadeh Zargari, A.H.; Aqajari, S.A.H.; Khodabandeh, H.; Rahmani, A.; Kurdahi, F. An accurate non-accelerometer-based ppg motion artifact removal technique using cyclegan. ACM Trans. Comput. Healthc. 2023, 1, 1–4. [Google Scholar] [CrossRef]
- Tarvirdizadeh, B.; Golgouneh, A.; Tajdari, F.; Khodabakhshi, E. A novel online method for identifying motion artifact and photoplethysmography signal reconstruction using artificial neural networks and adaptive neuro-fuzzy inference system. Neural Comput. Appl. 2020, 32, 3549–3566. [Google Scholar] [CrossRef]
- Shuzan, M.N.; Chowdhury, M.; Murugappan, P.; Bhuiyan, E.; Ayari, M.; Khandakar, A. Machine Learning-Based Respiration Rate and Blood Oxygen Saturation Estimation Using Photoplethysmogram Signals. Bioengineering 2023, 10, 167. [Google Scholar] [CrossRef]
- Sološenko, A.; Petrėnas, A.; Marozas, V.; Sörnmo, L. Modeling of the photoplethysmogram during atrial fibrillation. Comput. Biol. Med. 2017, 81, 130–138. [Google Scholar] [CrossRef]
- Martin-Martinez, D.; Casaseca-De-La-Higuera, P.; Martin-Fernandez, M.; Alberola-Lopez, C. Stochastic modeling of the PPG signal: A synthesis-by-analysis approach with applications. IEEE Trans. Biomed. Eng. 2013, 60, 2432–2441. [Google Scholar] [CrossRef]
- Reddy, K.; George, B.; Kumar, J. Use of Fourier Series Analysis for Motion Artifact Reduction and Data Compression of Photoplethysmographic Signals. IEEE Trans. Instrum. Meas. 2009, 58, 1706–1711. [Google Scholar] [CrossRef]
- den Brinker, A.C.; Sarkissian, H.H.D.; Wülbern, J.H.; Balmaekers, B.; Padalko, M.; Sénégas, J.; Springorum, R.; Possanzini, C. Camera PPG waveforms at the forehead. arXiv 2023, arXiv:2306.09879. [Google Scholar] [CrossRef]
- Maniezzo, M.; Sandoval, I.; Valencio, A.; Lima, R. Improving Photoplethysmographic Peak Detection through Higher-Order Interpolation Techniques. In Proceedings of the 52nd International Conference on Computing in Cardiology (CinC), São Paulo, Brazil, 14–17 September 2025. [Google Scholar]
- Ismail, S.; Akram, U.; Siddiqi, I. Heart rate tracking in photoplethysmography signals affected by motion artifacts: A review. EURASIP J. Adv. Signal Process. 2021, 2021, 5. [Google Scholar] [CrossRef]
- Mao, R.; Tweardy, M.; Wegerich, S.; Goergen, C.; Wodicka, G.; Zhu, F. Motion Artifact Reduction In Photoplethysmography For Reliable Signal Selection. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Virtual, 1–5 November 2021. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Hyder, R.; Hafiz, M.S.B.; Haque, M.A. Real-Time Robust Heart Rate Estimation From Wrist-Type PPG Signals Using Multiple Reference Adaptive Noise Cancellation. IEEE J. Biomed. Health Inform. 2018, 22, 450–459. [Google Scholar] [CrossRef]
- Venkat, S.; PS, M.; Alex, A.; Sp, P.; Balamugesh, T.; Christopher, D.; Joseph, J.; Sivaprakasam, M. Machine Learning based SpO2 Computation Using Reflectance Pulse Oximetry. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; Volume 2019, pp. 482–485. [Google Scholar] [CrossRef]
- Priem, G.; Martinez, C.; Bodinier, Q.; Carrault, G. Clinical grade SpO2 prediction through semi-supervised learning. In Proceedings of the 2020 IEEE 20th International Conference on Bioinformatics and Bioengineering (BIBE), Cincinnati, OH, USA, 26–28 October 2020; pp. 914–921. [Google Scholar] [CrossRef]
- Koteska, B.; Bodanova, A.M.; Mitrova, H.; Sidorenko, M.; Lehocki, F. A Deep Learning Approach to Estimate SpO2 from PPG Signals. In Proceedings of the ICBRA ’22: 9th International Conference on Bioinformatics Research and Applications, Berlin, Germany, 18–20 September 2022; pp. 142–148. [Google Scholar] [CrossRef]
- Pflugradt, M.; Orglmeister, R.; Gehring, H.; Osterhoff, G. A Novel Method for Motion Artifact Removal in Wearable PPG Sensors Based on Blind Source Separation. Biomed. Tech. Biomed. Eng. 2013, 58. [Google Scholar] [CrossRef]
- Bondala, V.R.; Komalla, A.R. An efficient model for extracting respiratory and blood oxygen saturation data from photoplethysmogram signals by removing motion artifacts using heuristic-aided ensemble learning model. Comput. Biol. Med. 2024, 180, 108911. [Google Scholar] [CrossRef]
- Yan, Y.s.; Poon, C.; Zhang, Y.T. Reduction of motion artifact in pulse oximetry by smoothed pseudo Wigner-Ville distribution. J. Neuroeng. Rehabil. 2005, 2, 3. [Google Scholar] [CrossRef]
- Zhang, Q.; Arney, D.; Goldman, J.M.; Isselbacher, E.M.; Armoundas, A.A. Design Implementation and Evaluation of a Mobile Continuous Blood Oxygen Saturation Monitoring System. Sensors 2020, 20, 6581. [Google Scholar] [CrossRef]
- Yousefi, R.; Nourani, M.; Ostadabbas, S.; Panahi, I. A Motion-Tolerant Adaptive Algorithm for Wearable Photoplethysmographic Biosensors. IEEE J. Biomed. Health Inform. 2014, 18, 670–681. [Google Scholar] [CrossRef]
- Ram, M.R.; Madhav, K.V.; Krishna, E.H.; Komalla, N.R.; Sivani, K.; Reddy, K.A. ICA-Based Improved DTCWT Technique for MA Reduction in PPG Signals With Restored Respiratory Information. IEEE Trans. Instrum. Meas. 2013, 62, 2639–2651. [Google Scholar] [CrossRef]
- Fan, F.; Yan, Y.; Tang, Y.; Zhang, H. A motion-tolerant approach for monitoring SpO2 and heart rate using photoplethysmography signal with dual frame length processing and multi-classifier fusion. Comput. Biol. Med. 2017, 91, 291–305. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Li, M.; Wei, Z. Continuous blood oxygen estimation using PPG based on VMD. J. Phys. Conf. Ser. 2022, 2246, 012086. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, Y.; Johnson, S.; Wiffen, R.; Yang, B. A comparative study of accuracy in major adaptive filters for motion artifact removal in sleep apnea tests. Med. Biol. Eng. Comput. 2023, 62, 829–842. [Google Scholar] [CrossRef] [PubMed]
- Nachman, D.; Eisenkraft, A.; Goldstein, N.; Ben-Ishay, A.; Fons, M.; Merin, R.; Gepner, Y. Influence of Sex, BMI, and Skin Color on the Accuracy of Non-Invasive Cuffless Photoplethysmography-Based Blood Pressure Measurements. Front. Physiol. 2022, 13, 911544. [Google Scholar] [CrossRef] [PubMed]
- Bickler, P.E.; Feiner, J.R.; Severinghaus, J.W. Effects of Skin Pigmentation on Pulse Oximeter Accuracy at Low Saturation. Anesthesiology 2005, 102, 715–719. [Google Scholar] [CrossRef]
- Feiner, J.R.; Severinghaus, J.W.; Bickler, P.E. Dark Skin Decreases the Accuracy of Pulse Oximeters at Low Oxygen Saturation: The Effects of Oximeter Probe Type and Gender. Anesth. Analg. 2007, 105, S18–S23. [Google Scholar] [CrossRef] [PubMed]
- Fallow, B.; Tanaka, H. Influence of skin type and wavelength on light wave reflectance. J. Clin. Monit. Comput. 2013, 27, 313–317. [Google Scholar] [CrossRef] [PubMed]
- Dehghanojamahalleh, S.; Kaya, M. Sex-Related Differences in Photoplethysmography Signals Measured From Finger and Toe. IEEE J. Transl. Eng. Health Med. 2019, 7, 1900607. [Google Scholar] [CrossRef]
- Nitzan, M.; Babchenko, A.; Khanokh, B.; Landau, D. The variability of the photoplethysmographic signal - A potential method for the evaluation of the autonomic nervous system. Physiol. Meas. 1998, 19, 93–102. [Google Scholar] [CrossRef]
- Shimojo, Y.; Nishimura, T.; Hazama, H.; Ozawa, T.; Awazu, K. Measurement of absorption and reduced scattering coefficients in Asian human epidermis, dermis, and subcutaneous fat tissues in the 400- to 1100-nm wavelength range for optical penetration depth and energy deposition analysis. J. Biomed. Opt. 2020, 25, 045002. [Google Scholar] [CrossRef]
- Poorzargar, K.; Pham, C.; Ariaratnam, J.; Lee, K.; Parotto, M.; Englesakis, M.; Chung, F.; Nagappa, M. Accuracy of pulse oximeters in measuring oxygen saturation in patients with poor peripheral perfusion: A systematic review. J. Clin. Monit. Comput. 2022, 36, 961–973. [Google Scholar] [CrossRef]
- Vijayarangan, S.; Suresh, P.; Joseph, J.; Sivaprakasam, M. Robust Modelling of Reflectance Pulse Oximetry for SpO2 Estimation. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 374–377. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, R.; Shao, W.; Karthik, K.; Kourkchi, E.; Rafatirad, S.; Homayoun, H. Rapid Adaptation of SpO2 Estimation to Wearable Devices via Transfer Learning on Low-Sampling-Rate PPG. arXiv 2025, arXiv:2509.12515. [Google Scholar]
- Ward, W.H.; Lambreton, F.; Goel, N.; Yu, J.Q.; Farma, J.M. Clinical Presentation and Staging of Melanoma. In Cutaneous Melanoma: Etiology and Therapy; Ward, W.H., Farma, J.M., Eds.; Codon Publications: Brisbane, Australian, 2017. [Google Scholar] [CrossRef]
- Liang, Y.; Elgendi, M.; Chen, Z.; Ward, R. Analysis: An optimal filter for short photoplethysmogram signals. Sci. Data 2018, 5, 180076. [Google Scholar] [CrossRef] [PubMed]
- Charlton, P.H.; Kotzen, K.; Mejía-Mejía, E.; Aston, P.J.; Budidha, K.; Mant, J.; Pettit, C.; Behar, J.A.; Kyriacou, P.A. Detecting beats in the photoplethysmogram: Benchmarking open-source algorithms. Physiol. Meas. 2022, 43, 085007. [Google Scholar] [CrossRef]
- van Gent, P.; Farah, H.; van Nes, N.; van Arem, B. Analysing noisy driver physiology real-time using off-the-shelf sensors: Heart rate analysis software from the taking the fast lane project. J. Open Res. Softw. 2019, 7, 32. [Google Scholar] [CrossRef]
- Raj, R.; Selvakumar, J.; Maik, V. Curve Approximation Models based on Statistical Distribution with Application to Photoplethysmography (PPG) Signal. J. Phys. Conf. Ser. 2021, 2007, 012056. [Google Scholar] [CrossRef]
- Walton, Z.; Silveman, D.; Shelley, K. Measuring venous oxygenation using the photoplethysmograph waveform. J. Clin. Monit. Comput. 2010, 24, 295–303. [Google Scholar] [CrossRef]
- Singstad, B.J.; Azulay, N.; Bjurstedt, A.; Bjorndal, S.; Drageseth, M.; Engeset, P.; Eriksen, K.; Gidey, M.; Granum, E.; Greaker, M.; et al. Estimation of Heart Rate Variability from Finger Photoplethysmography During Rest, Mild Exercise and Mild Mental Stress. J. Electr. Bioimpedance 2021, 12, 89–102. [Google Scholar] [CrossRef] [PubMed]
- Karlen, W.; Brouse, C.; Cooke, E.; Ansermino, M.; Dumont, G. Respiratory rate estimation using respiratory sinus arrhythmia from photoplethysmography. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; Volume 2011, pp. 1201–1204. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018; Available online: https://otexts.com/fpp2/ (accessed on 20 November 2025).
| Model | Order | Linear P () | Non-Linear P () |
|---|---|---|---|
| Sum of Gaussians | 2 | (3) | (4) |
| 3 | (4) | (6) | |
| 4 | (5) | (8) | |
| Polynomial Expansion | 6 | (7) | - |
| 7 | (8) | - | |
| 8 | (9) | - | |
| Fourier Series Expansion | 2 | (5) | (1) |
| 3 | (7) | (1) | |
| 4 | (9) | (1) |
| Signal Component | Model | Input | Output |
|---|---|---|---|
| AC | XGBoost | ||
| DC | Ridge |
| Model | Mean |
|---|---|
| Two Gaussians | 0.924 |
| Three Gaussians | 0.919 |
| Four Gaussians | 0.886 |
| 2nd order Fourier | 0.973 |
| 3rd order Fourier | 0.984 |
| 4th order Fourier | 0.993 |
| 6th degree Polynomial | 0.981 |
| 7th degree Polynomial | 0.985 |
| 8th degree Polynomial | 0.989 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badiola, I.; Balaji, S.; Silva, D.; Blazek, V.; Leonhardt, S.; Lüken, M. Real-Time Subject-Specific Predictive Modeling of PPG Signals for Artifact-Resilient SpO2 Estimation Under Hypoxia. Sensors 2025, 25, 7176. https://doi.org/10.3390/s25237176
Badiola I, Balaji S, Silva D, Blazek V, Leonhardt S, Lüken M. Real-Time Subject-Specific Predictive Modeling of PPG Signals for Artifact-Resilient SpO2 Estimation Under Hypoxia. Sensors. 2025; 25(23):7176. https://doi.org/10.3390/s25237176
Chicago/Turabian StyleBadiola, Idoia, Swati Balaji, Diogo Silva, Vladimir Blazek, Steffen Leonhardt, and Markus Lüken. 2025. "Real-Time Subject-Specific Predictive Modeling of PPG Signals for Artifact-Resilient SpO2 Estimation Under Hypoxia" Sensors 25, no. 23: 7176. https://doi.org/10.3390/s25237176
APA StyleBadiola, I., Balaji, S., Silva, D., Blazek, V., Leonhardt, S., & Lüken, M. (2025). Real-Time Subject-Specific Predictive Modeling of PPG Signals for Artifact-Resilient SpO2 Estimation Under Hypoxia. Sensors, 25(23), 7176. https://doi.org/10.3390/s25237176










