An Improved Variational Bayesian-Based Adaptive Federated Kalman Filter for Multi-Sensor Integrated Navigation Systems
Abstract
1. Introduction
2. Problem Formulation
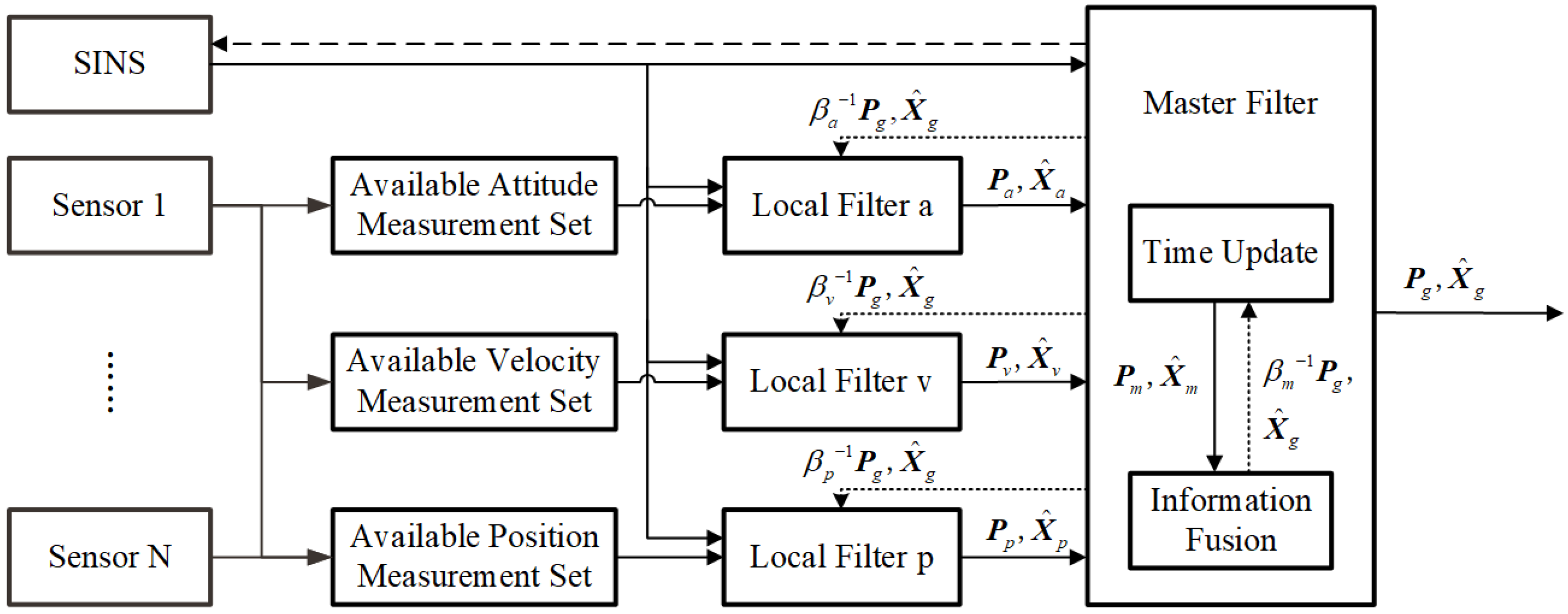
2.1. Information Fusion Structure of Multi-Sensor Integrated Navigation System
2.2. Sytem Model
- Attitude Measurement Model
- Velocity Measurement Model
- Position Measurement Model
- Vehicular Navigation System composed of Specific Sensors
3. Improved VBAKF-Based Federated Filter Algorithm
3.1. VBAKF Algorithm
- MNCM Update
- State Vector Update
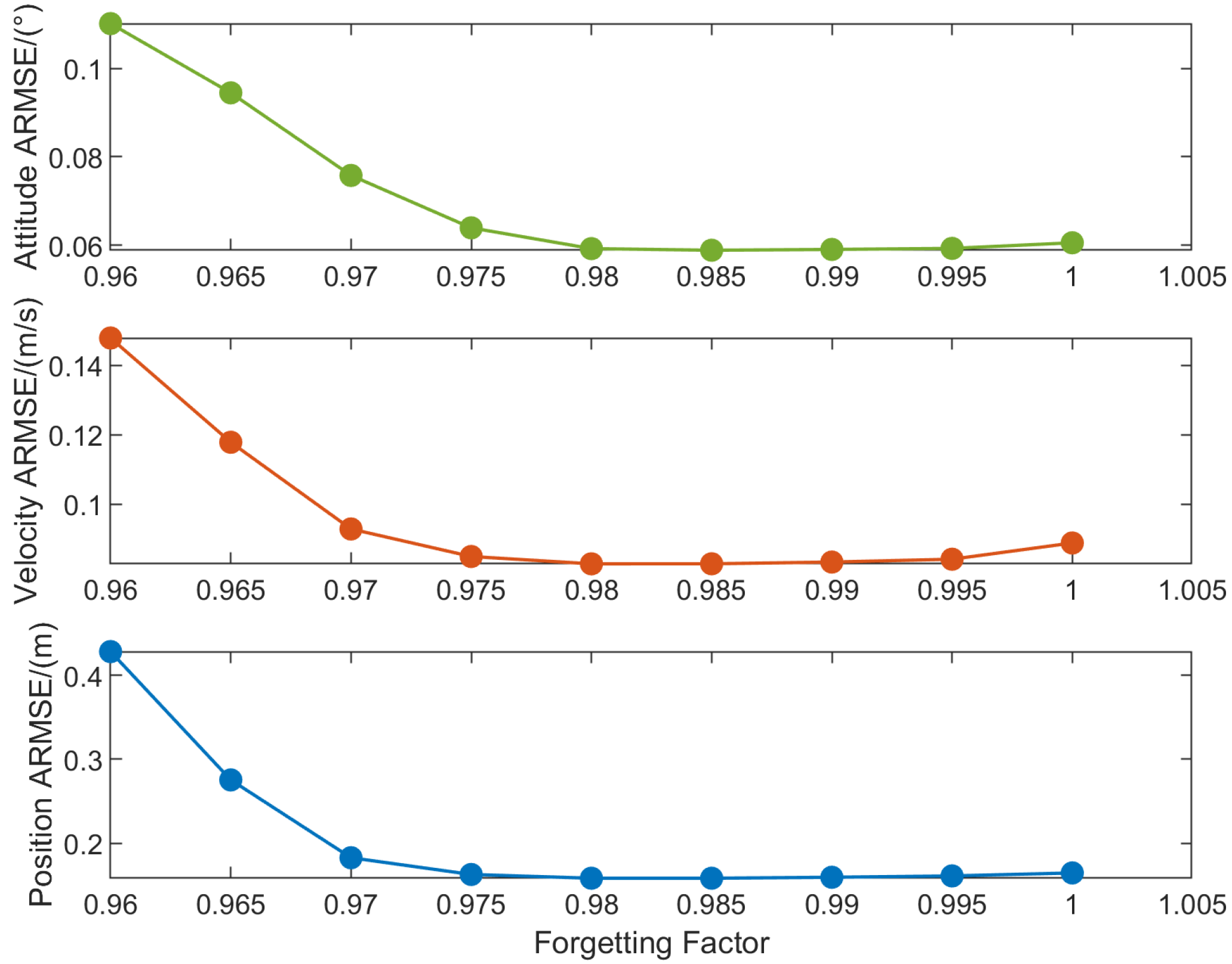
3.2. Adaptive Adjustment Strategy for the Forgetting Factor
| Algorithm 1: Flowchart of the IVBAFKF algorithm. |
Input: , , , , , , , , , , , , , m, , N Time Update: Measurement Update of Variational Bayesian: Initialize: , , for Update : , Update : end for , , , Update : Output: , , , , |
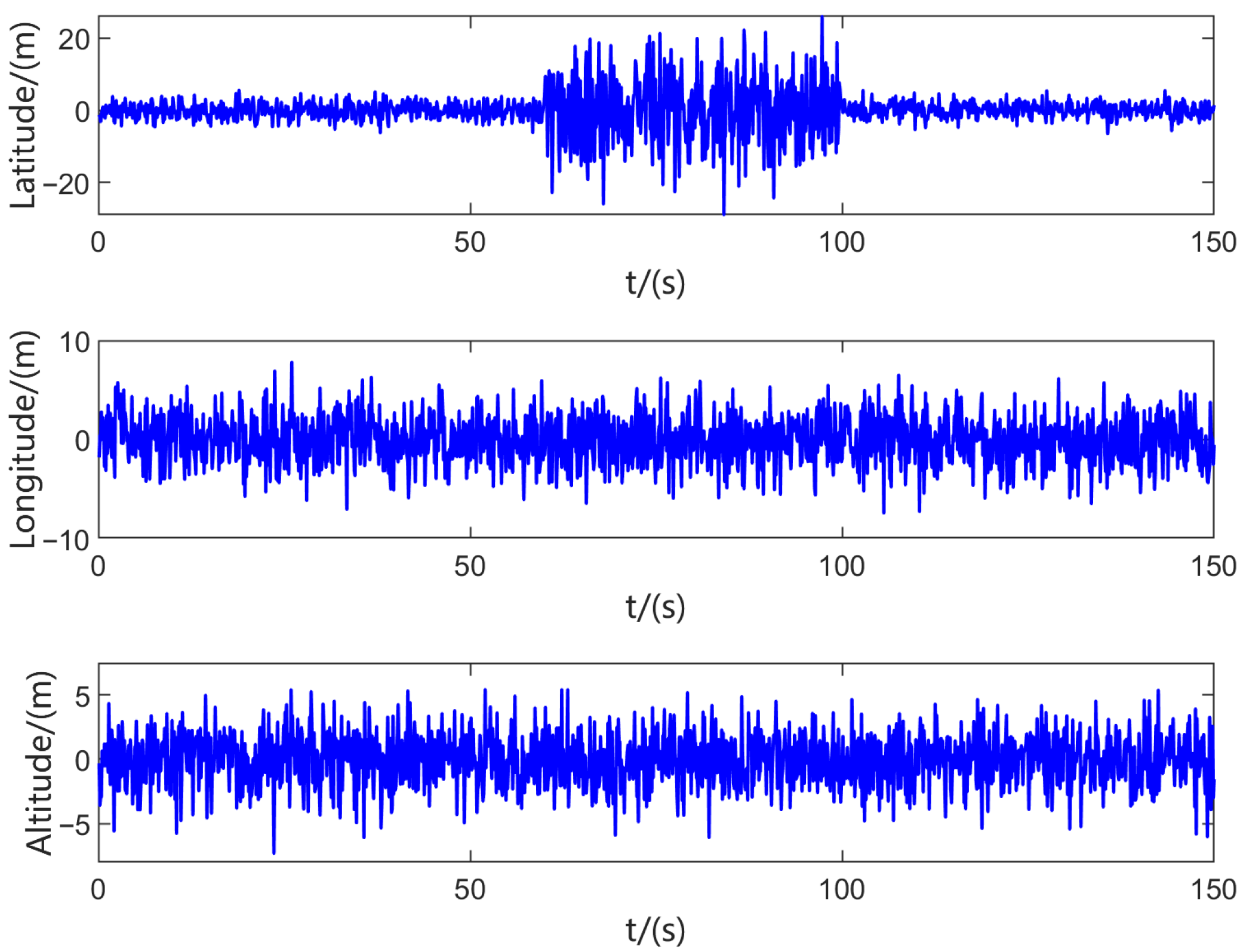
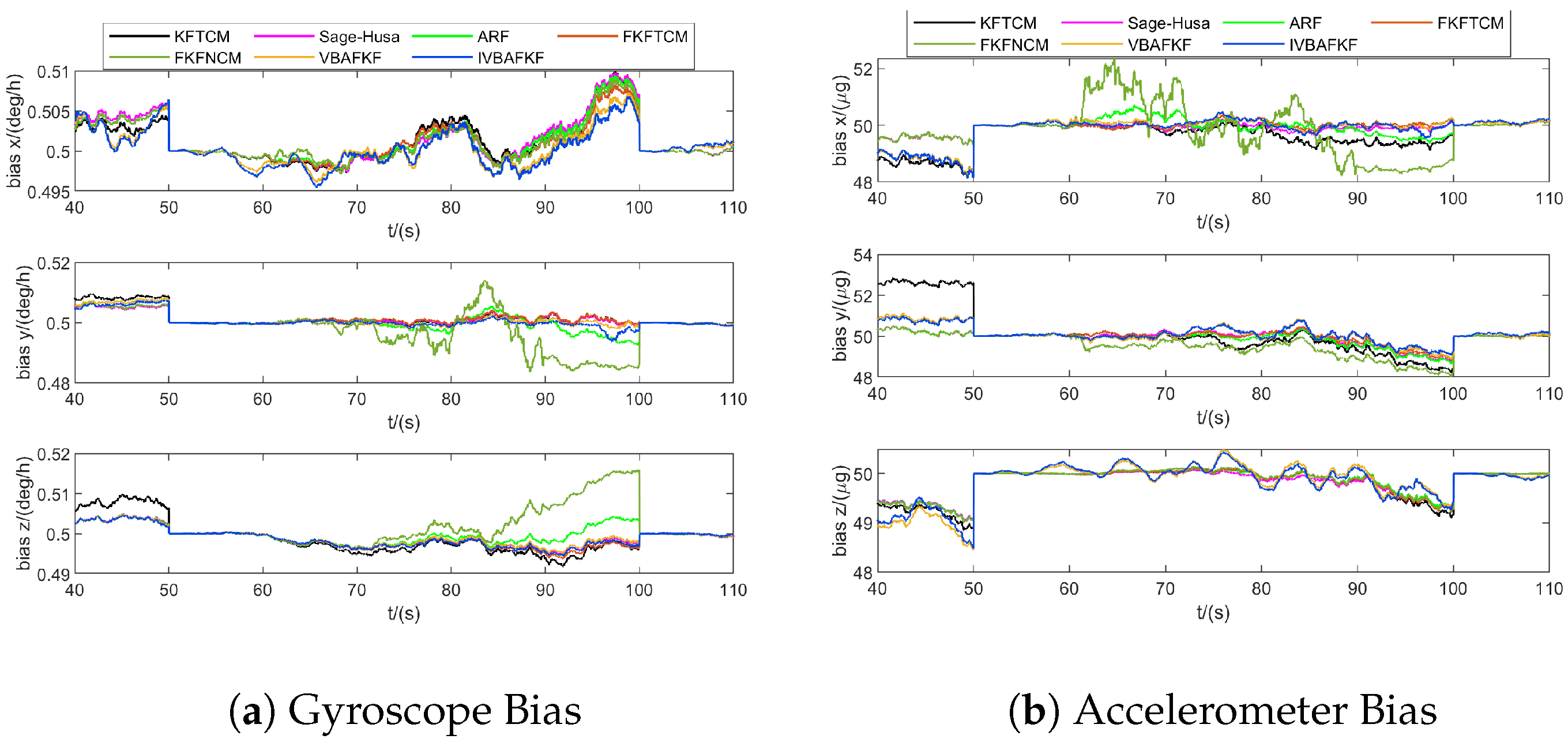
4. Simulations
- 1.
- The FKFNCM performs measurement updates based on a nominal MNCM. When the actual noise statistics change, these fixed parameters cannot accurately reflect the variations. Consequently, the ARMSE of the navigation state estimates increases significantly compared to FKFTCM. Under Noise ID 2, the position estimation error reaches 3.9634 m, exposing the inadequacy of the fixed noise model in adapting to dynamic environments.
- 2.
- Based on the IW distribution assumption, VBAFKF dynamically estimates the MNCM using a VBAKF as local filter with a constant forgetting factor. Experimental data show that this algorithm reduces the average ARMSE of navigation states by 41.99% across the four noise scenarios, effectively mitigating the impact of abnormal noise characteristics on filtering accuracy.
- 3.
- By adaptively adjusting the forgetting factor, IVBAFKF achieves higher accurate in tracking MNCM variations. Across all the current test scenarios, it demonstrates superior navigation state estimation accuracy over the VBAFKF, with an average improvement of 1.22%. IVBAFKF exhibits enhanced robustness in dynamic noise environments with time-varying statistical properties.
- 4.
- Compared to traditional adaptive filter algorithms such as Sage–Husa and ARF, IVBAFKF comprehensively outperforms them in the MRERP, achieving an average relative error reduction percentage of 43.21%, significantly higher than Sage–Husa (33.54%) and ARF (28.31%). This establishes its performance advantage in handling complex noise environments.
5. Conclusions
- 1.
- The proposed adaptive forgetting factor strategy significantly enhances tracking accuracy of the MNCM variations and maintains robustness under deteriorated measurement conditions induced by increased noise levels or undetectable minor sensor faults.
- 2.
- The navigation accuracy of the proposed algorithm is improved compared to baseline FKF algorithms (e.g., FKFTCM, FKFNCM, and VBAFKF), as demonstrated by performance metrics of ARMSE. The proposed algorithm achieves an average reduction of 43.21% in the ARMSEs of navigation states compared to FKFNCM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Wang, S.; Zhou, Y.; Shen, Z.; Li, X. Tightly coupled integration of GNSS, INS, and LiDAR for vehicle navigation in urban environments. IEEE Internet Things J. 2022, 9, 24721–24735. [Google Scholar] [CrossRef]
- Bai, S.; Lai, J.; Lyu, P.; Cen, Y.; Ji, B. Improved preintegration method for GNSS/IMU/In-vehicle sensors navigation using graph optimization. IEEE Trans. Veh. Technol. 2021, 70, 11446–11457. [Google Scholar] [CrossRef]
- Tang, C.; Wang, C.; Zhang, L.; Zhang, Y.; Song, H. Vehicle heterogeneous multi-source information fusion positioning method. IEEE Trans. Veh. Technol. 2024, 73, 12597–12613. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Gao, S.; Zhong, Y.; Gu, C. Multi-sensor optimal data fusion for INS/GNSS/CNS integration based on unscented Kalman filter. Int. J. Control. Autom. Syst. 2018, 16, 129–140. [Google Scholar] [CrossRef]
- Yue, Z.; Lian, B.; Tang, C.; Tong, K. A novel adaptive federated filter for GNSS/INS/VO integrated navigation system. Meas. Sci. Technol. 2020, 31, 085102. [Google Scholar] [CrossRef]
- Ben, Y.; Wang, K.; Li, Q. A robust factor graph optimization method for navigation in land vehicles based on dynamic kernel principal component analysis. IEEE Trans. Instrum. Meas. 2024, 73, 8503116. [Google Scholar] [CrossRef]
- Wei, X.; Li, J.; Zhang, D.; Feng, K. An improved integrated navigation method with enhanced robustness based on factor graph. Mech. Syst. Signal Process. 2021, 155, 107565. [Google Scholar] [CrossRef]
- Zhuang, Y.; Sun, X.; Li, Y.; Huai, J.; Hua, L.; Yang, X.; Cao, X.; Zhang, P.; Cao, Y.; Qi, L.; et al. Multi-sensor integrated navigation/positioning systems using data fusion: From analytics-based to learning-based approaches. Inf. Fusion 2023, 95, 62–90. [Google Scholar] [CrossRef]
- Gao, G.; Hu, G.; Zhong, Y.; Zhu, X. Distributed state fusion using sparse-grid quadrature filter with application to INS/CNS/GNSS integration. IEEE Sens. J. 2022, 22, 3430–3441. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhong, Y.; Zhu, X. Cubature rule-based distributed optimal fusion with identification and prediction of kinematic model error for integrated UAV navigation. Aerosp. Sci. Technol. 2021, 109, 106447. [Google Scholar] [CrossRef]
- Gao, S.; Zhong, Y.; Li, W. Random weighting method for multisensor data fusion. IEEE Sens. J. 2011, 11, 1955–1961. [Google Scholar] [CrossRef]
- Carlson, N.A. Federated filter for fault-tolerant integrated navigation systems. In Proceedings of the IEEE PLANS’88, Orlando, FL, USA, 29 November–2 December 1988; pp. 110–119. [Google Scholar]
- Carlson, N.A. Federated filter for computer-efficient, near-optimal GPS integration. In Proceedings of the Position, Location and Navigation Symposium—PLANS’96, Atlanta, GA, USA, 22–25 April 1996; pp. 306–314. [Google Scholar]
- Carlson, N.A.; Berarducci, M.P. Federated Kalman filter simulation results. Navigation 1994, 41, 297–322. [Google Scholar] [CrossRef]
- Xiong, Z.; Chen, J.; Wang, R.; Liu, J. A new dynamic vector formed information sharing algorithm in federated filter. Aerosp. Sci. Technol. 2013, 29, 37–46. [Google Scholar] [CrossRef]
- Wang, Q.; Cui, X.; Li, Y.; Ye, F. Performance enhancement of a USV INS/CNS/DVL integration navigation system based on an adaptive information sharing factor federated filter. Sensors 2017, 17, 239. [Google Scholar] [CrossRef] [PubMed]
- Lyu, X.; Hu, B.; Wang, Z.; Gao, D.; Li, K.; Chang, L. A SINS/GNSS/VDM integrated navigation fault-tolerant mechanism based on adaptive information sharing factor. IEEE Trans. Instrum. Meas. 2022, 71, 9506913. [Google Scholar] [CrossRef]
- Xiong, H.; Bian, R.; Li, Y.; Du, Z.; Mai, Z. Fault-tolerant GNSS/SINS/DVL/CNS integrated navigation and positioning mechanism based on adaptive information sharing factors. IEEE Syst. J. 2020, 14, 3744–3754. [Google Scholar] [CrossRef]
- Shen, K.; Wang, M.; Fu, M.; Yang, Y.; Yin, Z. Observability analysis and adaptive information fusion for integrated navigation of unmanned ground vehicles. IEEE Trans. Ind. Electron. 2019, 67, 7659–7668. [Google Scholar] [CrossRef]
- Xu, X.; Pang, F.; Ran, Y.; Bai, Y.; Zhang, L.; Tan, Z.; Wei, C.; Luo, M. An indoor mobile robot positioning algorithm based on adaptive federated Kalman filter. IEEE Sens. J. 2021, 21, 23098–23107. [Google Scholar] [CrossRef]
- Xiong, H.; Mai, Z.; Tang, J.; He, F. Robust GPS/INS/DVL navigation and positioning method using adaptive federated strong tracking filter based on weighted least square principle. IEEE Access 2019, 7, 26168–26178. [Google Scholar] [CrossRef]
- Liu, S.; Gao, M.; Huai, W.; Sheng, L. Federated strong tracking filtering for nonlinear systems with multiple sensors. Trans. Inst. Meas. Control 2022, 44, 3141–3153. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Gao, S.; Zhong, Y.; Gu, C. Multi-sensor optimal data fusion based on the adaptive fading unscented Kalman filter. Sensors 2018, 18, 488. [Google Scholar] [CrossRef]
- Hu, G.; Xu, L.; Gao, B.; Chang, L.; Zhong, Y. Robust unscented Kalman filter-Based decentralized multisensor information fusion for INS/GNSS/CNS integration in hypersonic vehicle navigation. IEEE Trans. Instrum. Meas. 2023, 72, 8504011. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, H.; Wang, J.; He, Z.; Wang, D. SINS/CNS/GNSS integrated navigation based on an improved federated Sage–Husa adaptive filter. Sensors 2019, 19, 3812. [Google Scholar] [CrossRef]
- Wang, L.; Li, S. Enhanced Multi-sensor data fusion methodology based on multiple model estimation for integrated navigation system. Int. J. Control Autom. Syst. 2018, 16, 295–305. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Zhang, W.; Liu, X.; Guo, Y. A nonlinear double model for multisensor-integrated navigation using the federated EKF algorithm for small UAVs. Sensors 2020, 20, 2974. [Google Scholar] [CrossRef] [PubMed]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans. Autom. Control 2017, 63, 594–601. [Google Scholar] [CrossRef]
- He, J.; Sun, C.; Zhang, B.; Wang, P. Variational Bayesian-based maximum correntropy cubature Kalman filter with both adaptivity and robustness. IEEE Sens. J. 2020, 21, 1982–1992. [Google Scholar] [CrossRef]
- Wang, B.; Wang, Z.; Yang, Y. A Variational Bayesian-based maximum correntropy adaptive Kalman filter for SINS/USBL Integrated Navigation System. IEEE Sens. J. 2025, 25, 20147–20157. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Chen, X.; Cao, H.; Wang, C.; Li, J.; Shen, C.; Tang, J. Information monitoring and adaptive information fusion of multi-source fusion navigation systems in complex environments. IEEE Internet Things J. 2024, 11, 25047–25056. [Google Scholar] [CrossRef]
- Wang, Z.; Li, N.; Wang, Z.; Zhu, F.; Du, X. An adaptive federated filter based on variational Bayes with application to multisource navigation. IEEE Sens. J. 2023, 23, 9859–9870. [Google Scholar] [CrossRef]
- Shi, W.; Xu, J.; He, H.; Li, D.; Tang, H.; Lin, E. Fault-tolerant SINS/HSB/DVL underwater integrated navigation system based on variational Bayesian robust adaptive Kalman filter and adaptive information sharing factor. Measurement 2022, 196, 111225. [Google Scholar] [CrossRef]
- Yan, G.; Weng, J. Strapdown Inertial Navigation Algorithm and Integrated Navigation Principle; Northwestern Polytechnical University Press: Xi’an, China, 2019; pp. 88–95. [Google Scholar]
- Qin, Y.; Zhang, H.; Wang, S. Kalman Filter and Principle of Integrated Navigation, 3rd ed.; Northwestern Polytechnical University Press: Xi’an, China, 2015; pp. 240–253. [Google Scholar]
- Wang, D.; Yang, J.; Xiong, K. Autonomous navigation method of satellite constellation based on adaptive forgetting factors. Chin. J. Aeronaut. 2024, 37, 317–332. [Google Scholar] [CrossRef]
- Matlab/PSINS Toolbox. Available online: https://psins.org.cn/kydm/ (accessed on 13 May 2024).
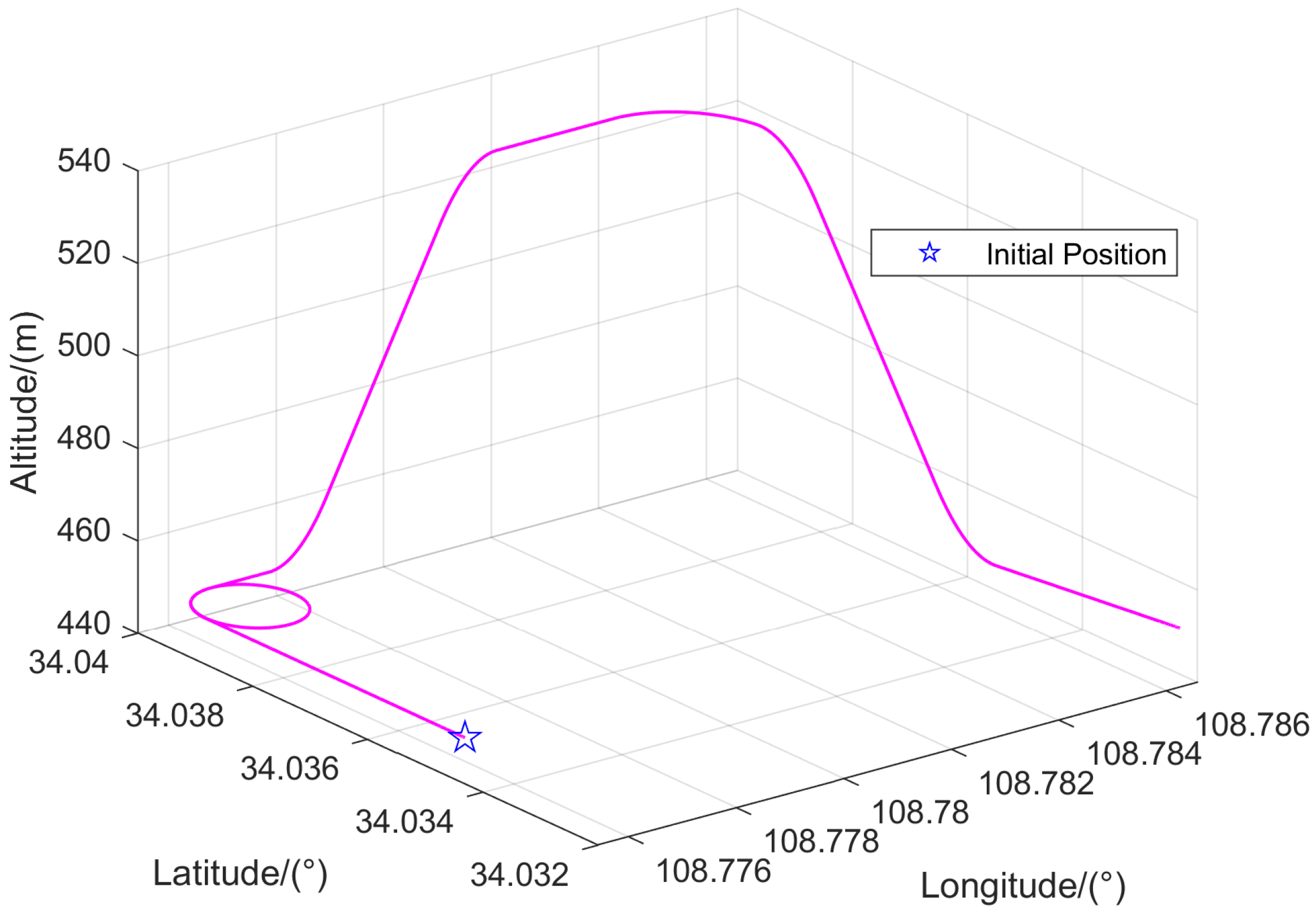
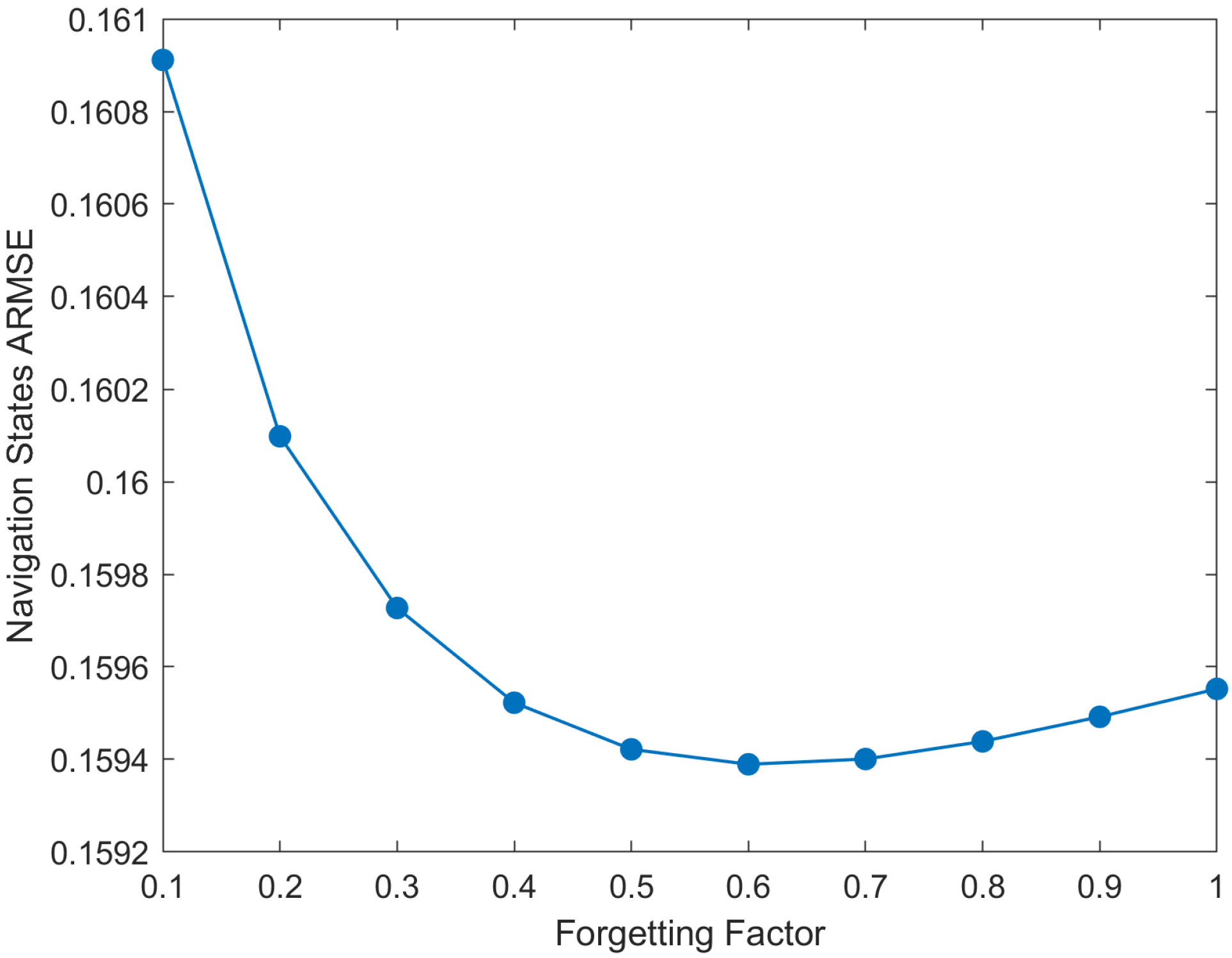
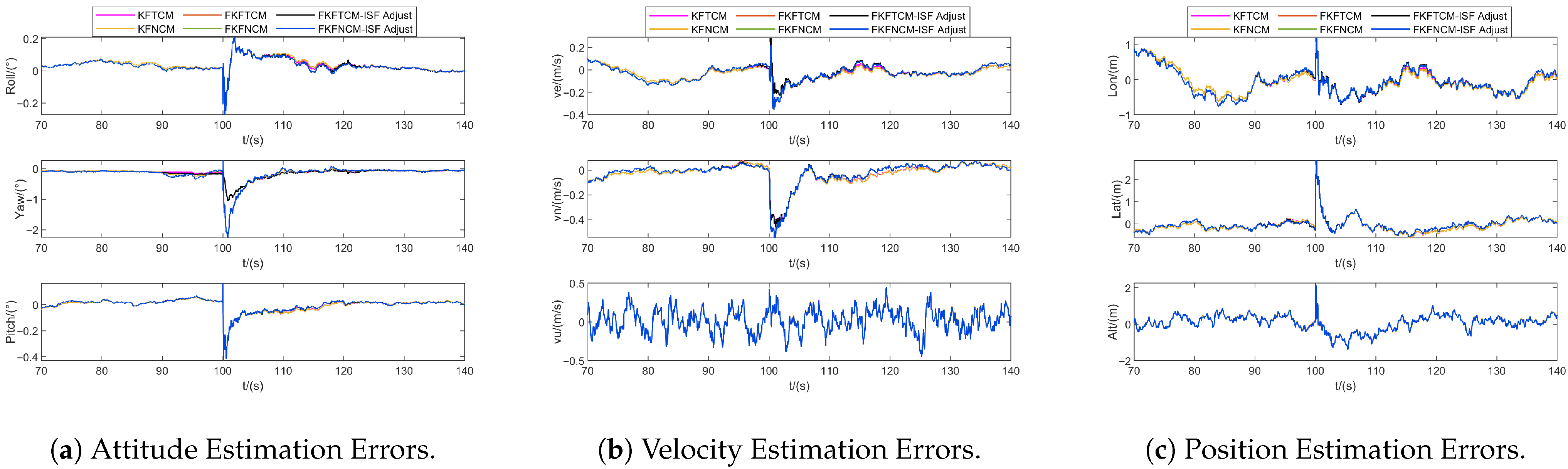
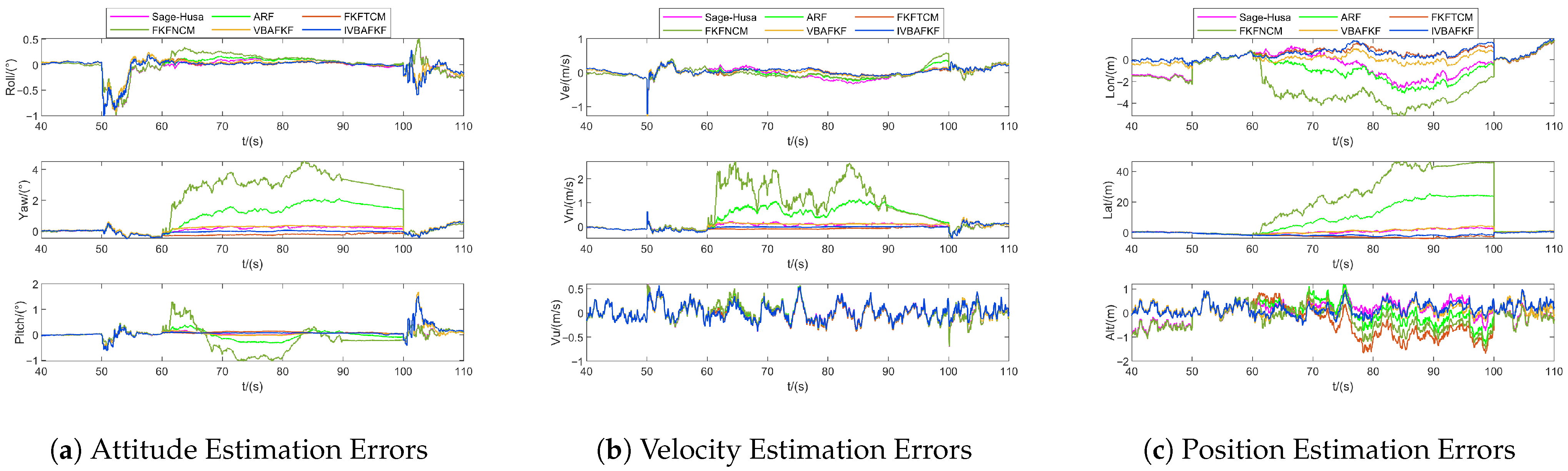
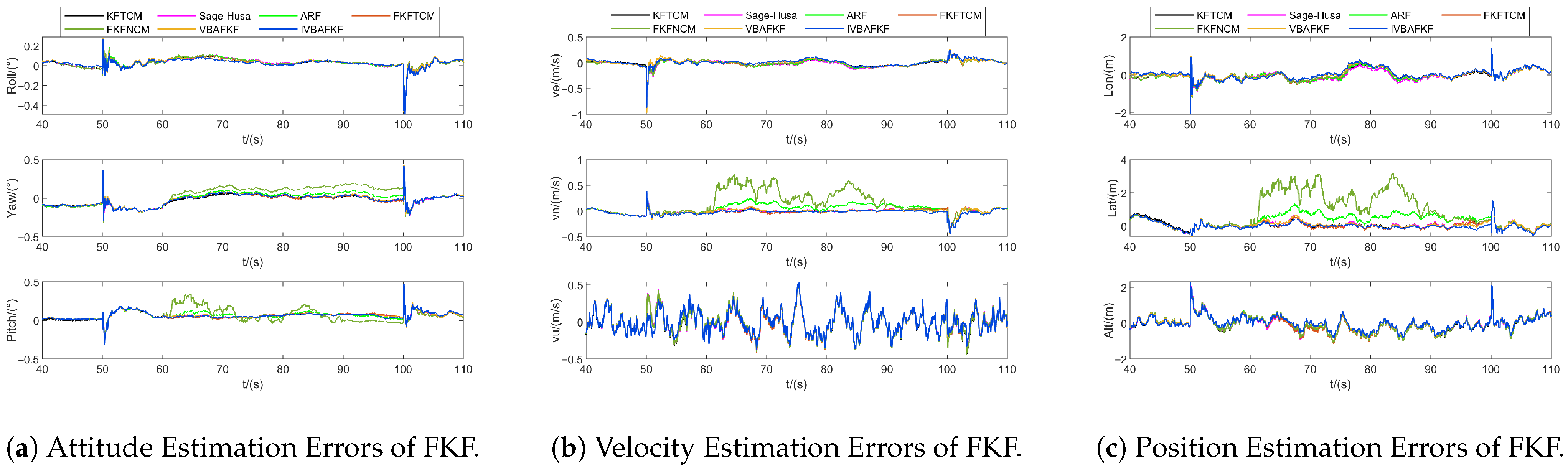
| Sensor | Parameter | Value | Sampling Rate |
|---|---|---|---|
| IMU | Gyro Constant Drift | 0.5°/h | 50 Hz |
| Gyro Angular Random Walk | 0.15° | ||
| Accelerometer Bias | 50 µg | ||
| Accelerometer Noise | 10 µg/ | ||
| GNSS | Position Noise | 2 m | 10 Hz |
| Velocity Noise | 1 m/s | ||
| Odometer | Velocity Noise | 1 m/s | 10 Hz |
| Magnetometer | Attitude Noise | 1° | 50 Hz |
| Noise ID | Sensor | Channel | Time Range |
|---|---|---|---|
| 1 | GNSS | North Velocity | 60–90 s |
| 2 | GNSS | Longitude | 120–150 s |
| 3 | Odometer | Forward Velocity | 80–110 s |
| 4 | Magnetometer | Yaw | 90–120 s |
| Noise ID | Algorithm | Attitude (°) | ARMSE Velocity (m/s) | Position (m) | Mean |
|---|---|---|---|---|---|
| 1 | KFTCM | 0.0998 | 0.1667 | 0.5337 | – |
| FKFTCM | 0.0998 | 0.1680 | 0.5396 | – | |
| FKFNCM | 0.1456 | 0.3466 | 1.5520 | – | |
| Sage–Husa | 0.0998 | 0.1705 | 0.5493 | – | |
| ARF | 0.1029 | 0.1867 | 0.6593 | – | |
| VBAFKF | 0.0995 | 0.1655 | 0.4906 | – | |
| IVBAFKF | 0.0991 | 0.1639 | 0.4826 | – | |
| 2 | KFTCM | 0.1043 | 0.1611 | 0.7280 | – |
| FKFTCM | 0.1063 | 0.1624 | 0.8434 | – | |
| FKFNCM | 0.1535 | 0.4441 | 3.9634 | – | |
| Sage–Husa | 0.1070 | 0.1950 | 2.5923 | – | |
| ARF | 0.1157 | 0.2685 | 3.1427 | – | |
| VBAFKF | 0.1060 | 0.1610 | 1.0996 | – | |
| IVBAFKF | 0.1045 | 0.1564 | 0.7590 | – | |
| 3 | KFTCM | 0.1622 | 0.5520 | 1.1926 | – |
| FKFTCM | 0.1666 | 0.5676 | 1.3010 | – | |
| FKFNCM | 0.1680 | 0.7760 | 1.5553 | – | |
| Sage–Husa | 0.1419 | 0.2220 | 0.6876 | – | |
| ARF | 0.1433 | 0.3214 | 0.7853 | – | |
| VBAFKF | 0.1410 | 0.2160 | 0.6645 | – | |
| IVBAFKF | 0.1411 | 0.2073 | 0.6559 | – | |
| 4 | KFTCM | 0.1898 | 0.1929 | 0.6769 | – |
| FKFTCM | 0.1911 | 0.1933 | 0.6774 | – | |
| FKFNCM | 0.2830 | 0.1943 | 0.6774 | – | |
| Sage–Husa | 0.3037 | 0.1953 | 0.6788 | – | |
| ARF | 0.2831 | 0.1954 | 0.6787 | – | |
| VBAFKF | 0.1959 | 0.1866 | 0.6477 | – | |
| IVBAFKF | 0.1935 | 0.1861 | 0.6470 | – | |
| MRERP | Sage–Husa | 17.48% | 44.44% | 38.69% | 33.54% |
| ARF | 17.14% | 35.92% | 31.89% | 28.31% | |
| VBAFKF | 27.36% | 48.03% | 50.58% | 41.99% | |
| IVBAFKF | 27.86% | 48.76% | 53.02% | 43.21% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Yang, J. An Improved Variational Bayesian-Based Adaptive Federated Kalman Filter for Multi-Sensor Integrated Navigation Systems. Sensors 2025, 25, 7173. https://doi.org/10.3390/s25237173
Yan Y, Yang J. An Improved Variational Bayesian-Based Adaptive Federated Kalman Filter for Multi-Sensor Integrated Navigation Systems. Sensors. 2025; 25(23):7173. https://doi.org/10.3390/s25237173
Chicago/Turabian StyleYan, Yuwei, and Jing Yang. 2025. "An Improved Variational Bayesian-Based Adaptive Federated Kalman Filter for Multi-Sensor Integrated Navigation Systems" Sensors 25, no. 23: 7173. https://doi.org/10.3390/s25237173
APA StyleYan, Y., & Yang, J. (2025). An Improved Variational Bayesian-Based Adaptive Federated Kalman Filter for Multi-Sensor Integrated Navigation Systems. Sensors, 25(23), 7173. https://doi.org/10.3390/s25237173







