Dual-Modality Ultrasound Imaging of SPIONs Distribution via Combined Magnetomotive and Passive Cavitation Imaging
Abstract
1. Introduction
2. Materials and Methods
2.1. Superparamagnetic Iron Oxide Nanoparticles
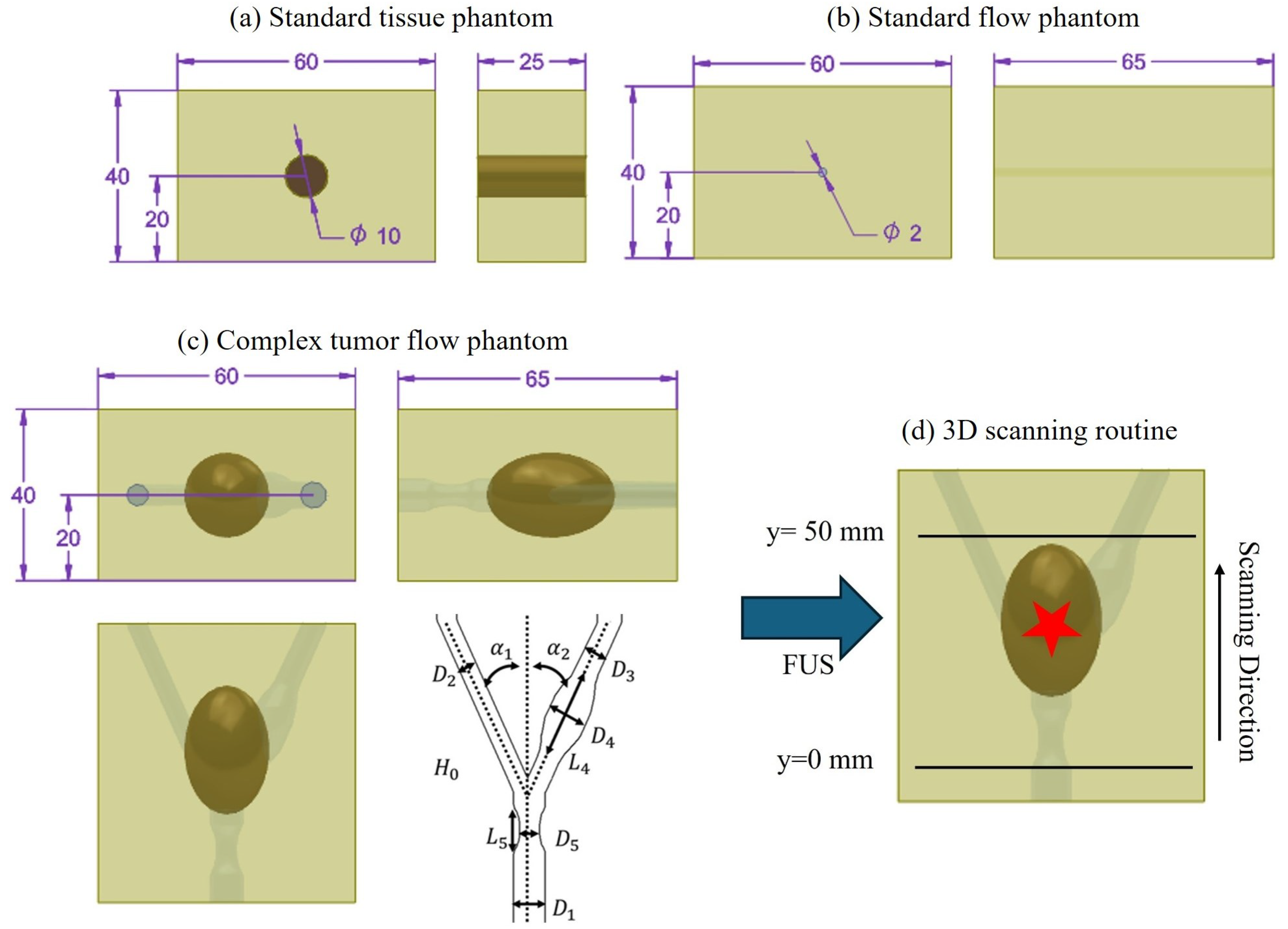
2.2. Ultrasound Phantom Fabrication
2.2.1. Standard Tissue Phantom
2.2.2. Standard Flow Phantom
2.2.3. Complex Flow Tumor Phantom
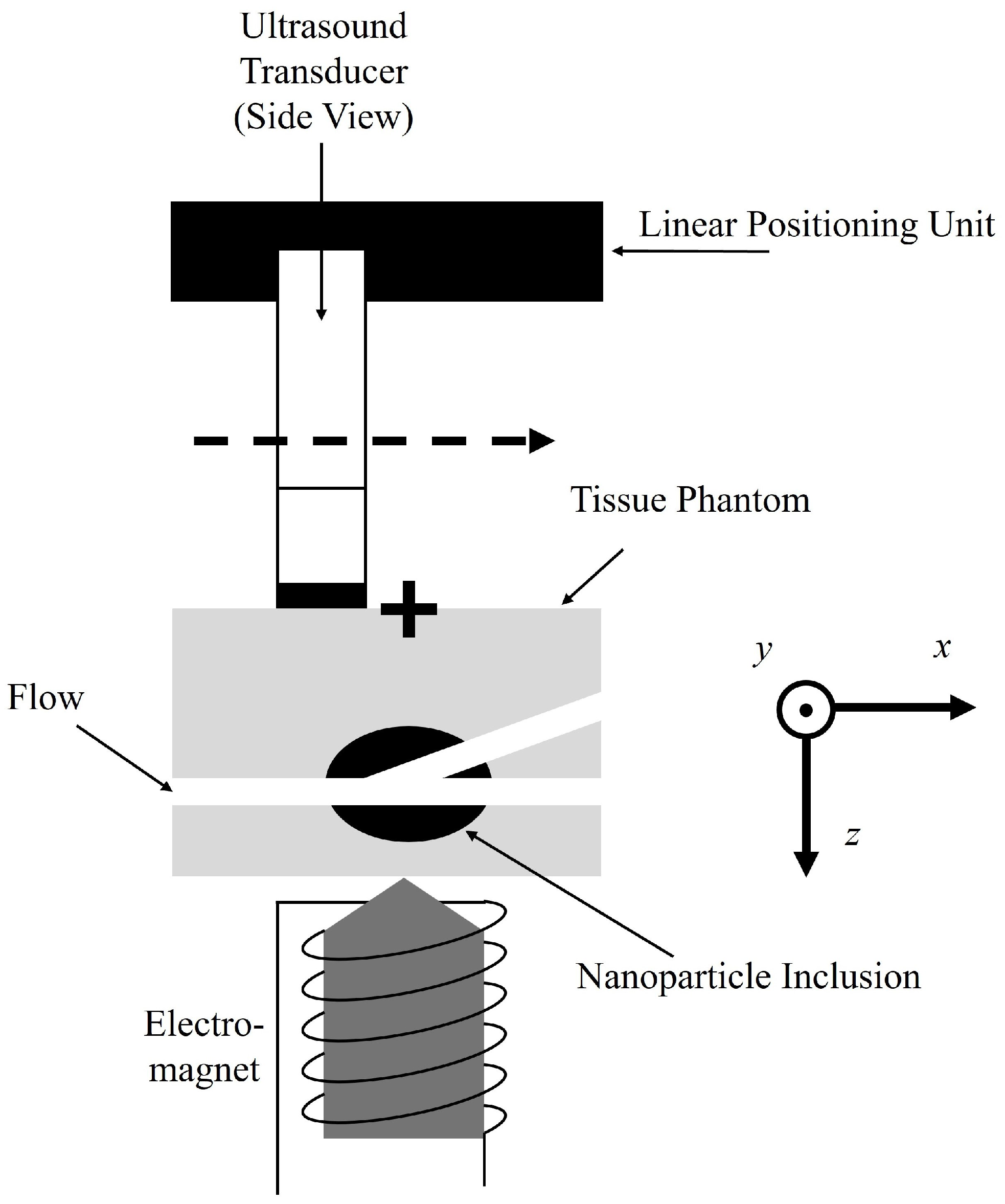
2.3. Magnetomotive Ultrasound
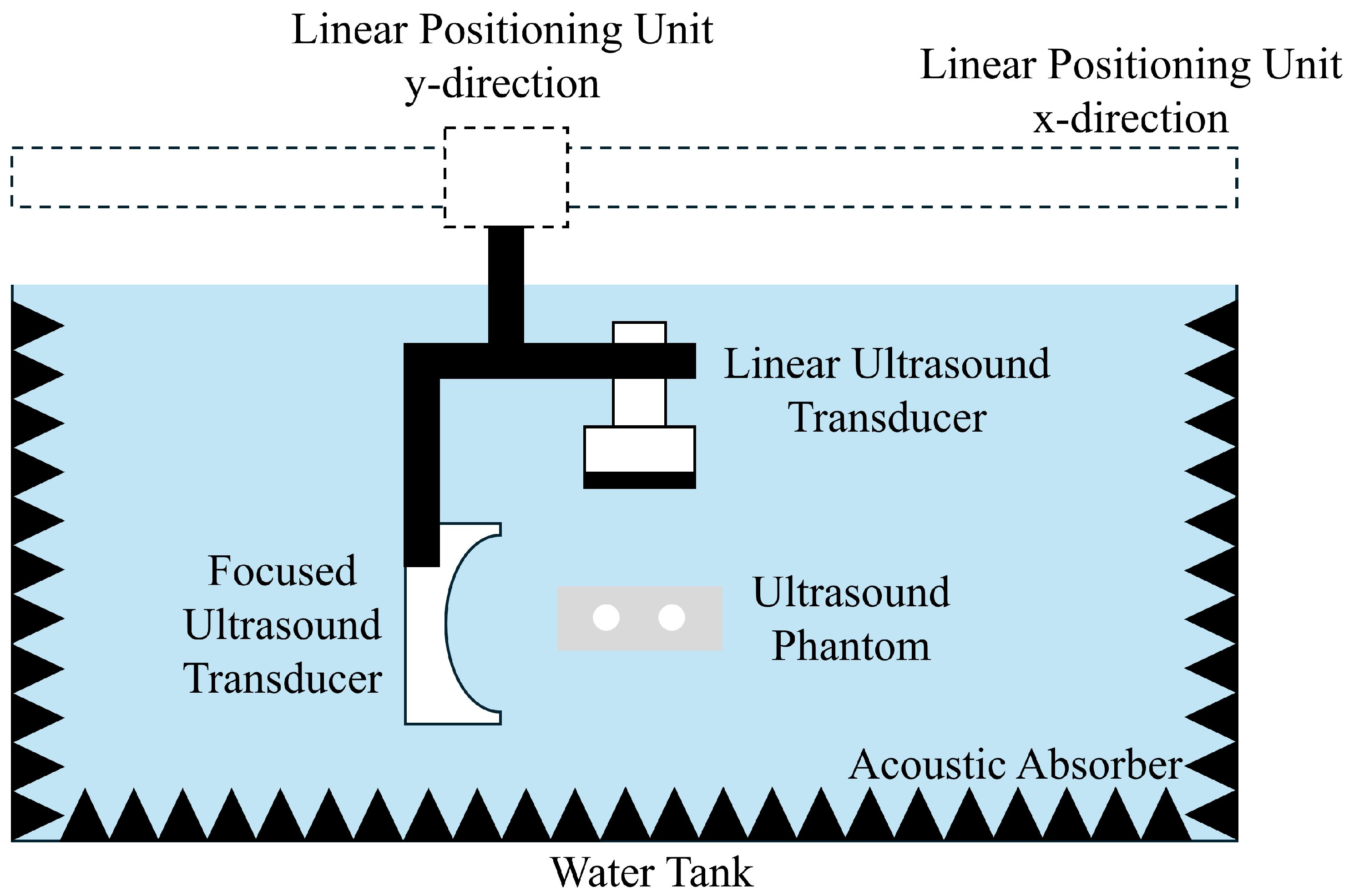
2.4. Passive Cavitation Mapping
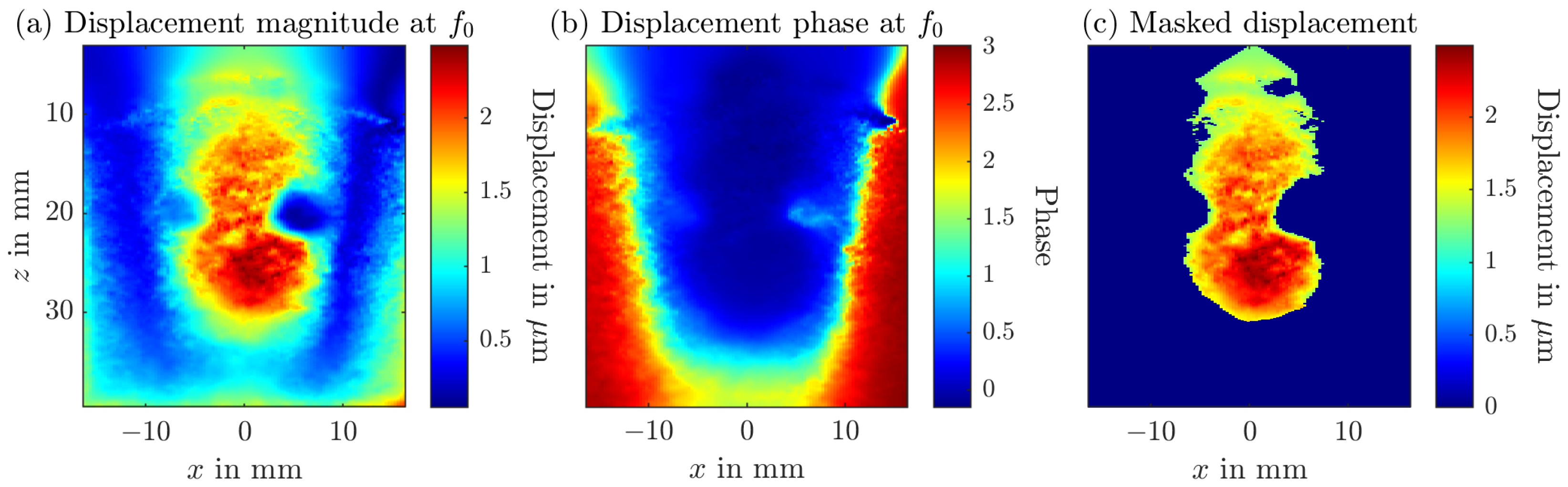
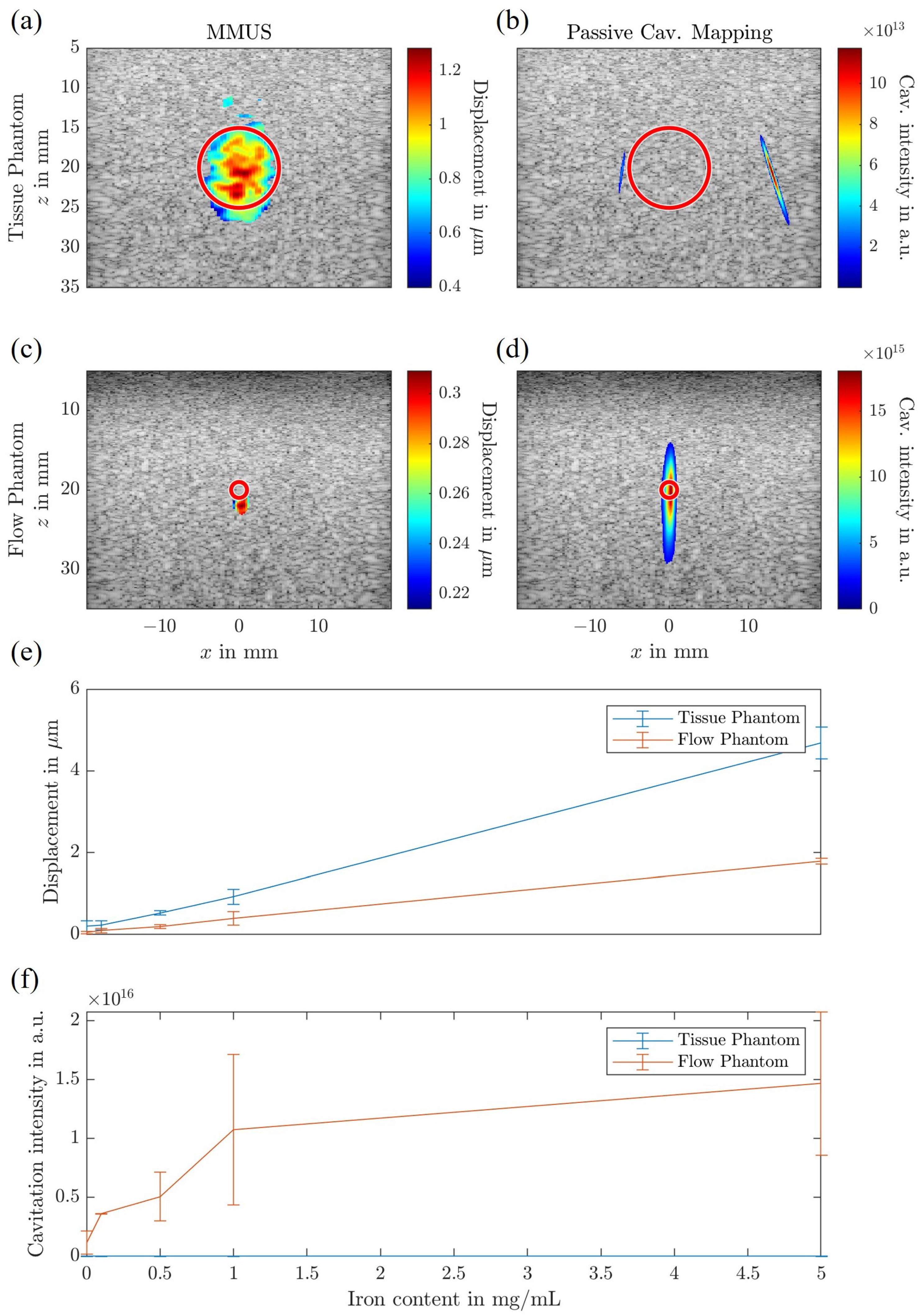
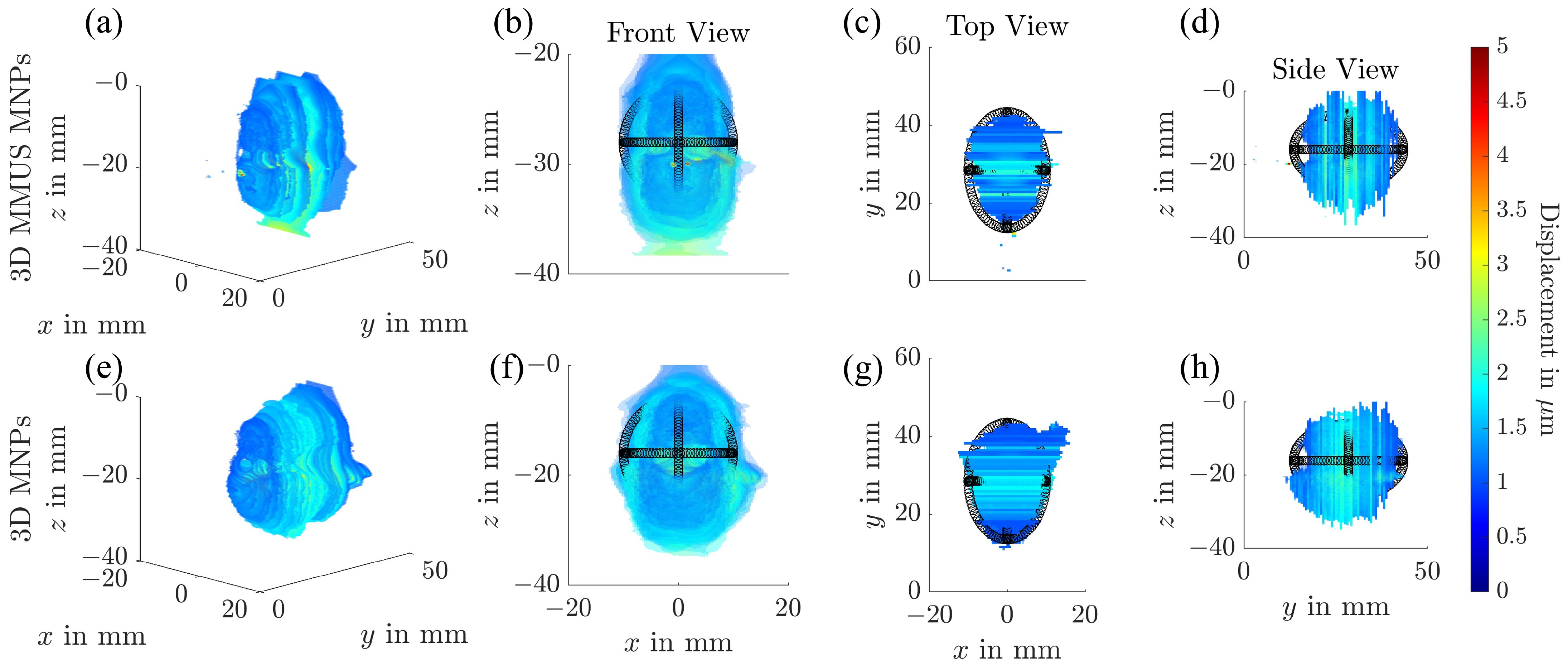
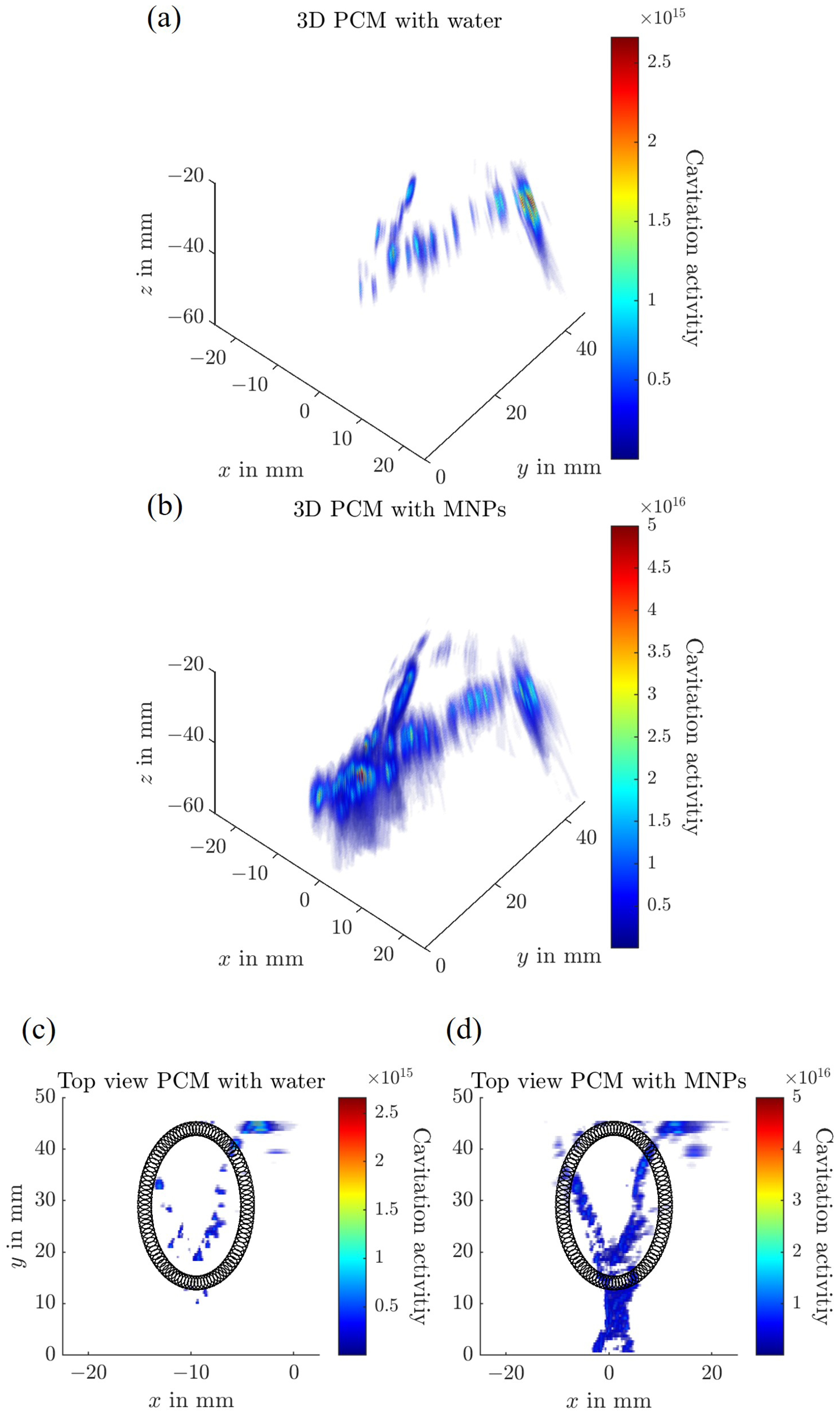
3. Results
4. Discussion
4.1. Ultrasound Phantom Fabrication
4.2. Magnetomotive Ultrasound
4.3. Passive Cavitation Mapping
4.4. Advantages, Limitations and Challenges of the Dual Modality Approach
4.5. Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABS | Acrylonitrile Butadiene Styrene |
| ACM | Active Cavitation Mapping |
| DAS | Delay and Sum Beamformer |
| DFT | Discrete Fourier Transform |
| DMAS | Delay Multiply and Sum |
| DMAS3 | Third order Delay Multiply and Sum |
| EPR | Enhanced Permeability and Retention |
| FTC | Freeze-Thaw Cycle |
| FUS | Focused Ultrasound |
| GLUE | Global Ultrasound Strain Elastography |
| HIPS | High-Impact Polystyrene |
| LA-SPIONs | Lauric Acid Superparamagnetic iron oxide nanoparticles |
| MDT | Magnetic Drug Targeting |
| MH | Magnetic Hyperthermia |
| MMUS | Magnetomotive Ultrasound |
| MPI | Magnetic Particle Imaging |
| MRI | Magnetic Resonance Imaging |
| PCM | Passive Cavitation Mapping |
| PVA | Polyvinyl Alcohol |
| RF | Radiofrequency |
| SPIONs | Superparamagnetic iron oxide nanoparticles |
| TEA | Time Exposure Acoustics |
| TMMs | Tissue-Mimicking Materials |
References
- Gaidai, O.; Cao, Y.; Loginov, S. Global Cardiovascular Diseases Death Rate Prediction. Curr. Probl. Cardiol. 2023, 48, 101622. [Google Scholar] [CrossRef]
- Ferlay, J.; Colombet, M.; Soerjomataram, I.; Parkin, D.M.; Piñeros, M.; Znaor, A.; Bray, F. Cancer statistics for the year 2020: An overview. Int. J. Cancer 2021, 149, 778–789. [Google Scholar] [CrossRef]
- Aghebati-Maleki, A.; Dolati, S.; Ahmadi, M.; Baghbanzhadeh, A.; Asadi, M.; Fotouhi, A.; Yousefi, M.; Aghebati-Maleki, L. Nanoparticles and cancer therapy: Perspectives for application of nanoparticles in the treatment of cancers. J. Cell. Physiol. 2020, 235, 1962–1972. [Google Scholar] [CrossRef]
- Chua, C.Y.X.; Ho, J.; Demaria, S.; Ferrari, M.; Grattoni, A. Emerging technologies for local cancer treatment. Adv. Ther. 2020, 3, 2000027. [Google Scholar] [CrossRef]
- Gavas, S.; Quazi, S.; Karpiński, T.M. Nanoparticles for Cancer Therapy: Current Progress and Challenges. Nanoscale Res. Lett. 2021, 16, 173. [Google Scholar] [CrossRef]
- Sun, L.; Liu, H.; Ye, Y.; Lei, Y.; Islam, R.; Tan, S.; Tong, R.; Miao, Y.B.; Cai, L. Smart nanoparticles for cancer therapy. Signal Transduct. Target. Ther. 2023, 8, 418. [Google Scholar] [CrossRef] [PubMed]
- Pfister, F.; Carnell, L.R.; Löffler, L.; Boosz, P.; Schaft, N.; Dörrie, J.; Stein, R.; Lenz, M.; Spiecker, E.; Huber, C.M.; et al. Loading of CAR-T cells with magnetic nanoparticles for controlled targeting suppresses inflammatory cytokine release and switches tumor cell death mechanism. MedComm 2025, 6, e70039. [Google Scholar] [CrossRef]
- Shinde, V.R.; Revi, N.; Murugappan, S.; Singh, S.P.; Rengan, A.K. Enhanced permeability and retention effect: A key facilitator for solid tumor targeting by nanoparticles. Photodiagnosis Photodyn. Ther. 2022, 39, 102915. [Google Scholar] [CrossRef] [PubMed]
- Kalyane, D.; Raval, N.; Maheshwari, R.; Tambe, V.; Kalia, K.; Tekade, R.K. Employment of enhanced permeability and retention effect (EPR): Nanoparticle-based precision tools for targeting of therapeutic and diagnostic agent in cancer. Mater. Sci. Eng. C Mater. Biol. Appl. 2019, 98, 1252–1276. [Google Scholar] [CrossRef]
- Metselaar, J.M.; Lammers, T. Challenges in nanomedicine clinical translation. Drug Deliv. Transl. Res. 2020, 10, 721–725. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Xiao, Y.; Sun, X.; Lin, X.; Koo, S.; Yaremenko, A.V.; Qin, D.; Kong, N.; Farokhzad, O.C.; Tao, W. Cancer nanomedicine toward clinical translation: Obstacles, opportunities, and future prospects. Med 2023, 4, 147–167. [Google Scholar] [CrossRef]
- Rümenapp, C.; Gleich, B.; Haase, A. Magnetic nanoparticles in magnetic resonance imaging and diagnostics. Pharm. Res. 2012, 29, 1165–1179. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.M.; Pavan, T.Z.; Ullmann, I.; Heim, C.; Rupitsch, S.J.; Vossiek, M.; Alexiou, C.; Ermert, H.; Lyer, S. A Review on Ultrasound-based Methods to Image the Distribution of Magnetic Nanoparticles in Biomedical Applications. Ultrasound Med. Biol. 2025, 51, 210–234. [Google Scholar] [CrossRef] [PubMed]
- Alphandéry, E. Nanomaterials as Ultrasound Theragnostic Tools for Heart Disease Treatment/Diagnosis. Int. J. Mol. Sci. 2022, 23, 1683. [Google Scholar] [CrossRef]
- Wong, X.Y.; Sena-Torralba, A.; Álvarez-Diduk, R.; Muthoosamy, K.; Merkoçi, A. Nanomaterials for Nanotheranostics: Tuning Their Properties According to Disease Needs. ACS Nano 2020, 14, 2585–2627. [Google Scholar] [CrossRef] [PubMed]
- Srinoi, P.; Chen, Y.T.; Vittur, V.; Marquez, M.D.; Lee, T.R. Bimetallic Nanoparticles: Enhanced Magnetic and Optical Properties for Emerging Biological Applications. Appl. Sci. 2018, 8, 1106. [Google Scholar] [CrossRef]
- Materón, E.M.; Miyazaki, C.M.; Carr, O.; Joshi, N.; Picciani, P.H.; Dalmaschio, C.J.; Davis, F.; Shimizu, F.M. Magnetic nanoparticles in biomedical applications: A review. Appl. Surf. Sci. Adv. 2021, 6, 100163. [Google Scholar] [CrossRef]
- Lübbe, A.S.; Alexiou, C.; Bergemann, C. Clinical applications of magnetic drug targeting. J. Surg. Res. 2001, 95, 200–206. [Google Scholar] [CrossRef]
- Agiotis, L.; Theodorakos, I.; Samothrakitis, S.; Papazoglou, S.; Zergioti, I.; Raptis, Y.S. Magnetic manipulation of superparamagnetic nanoparticles in a microfluidic system for drug delivery applications. J. Magn. Magn. Mater. 2016, 401, 956–964. [Google Scholar] [CrossRef]
- Tietze, R.; Lyer, S.; Dürr, S.; Struffert, T.; Engelhorn, T.; Schwarz, M.; Eckert, E.; Göen, T.; Vasylyev, S.; Peukert, W.; et al. Efficient drug-delivery using magnetic nanoparticles–biodistribution and therapeutic effects in tumour bearing rabbits. Nanomed. Nanotechnol. Biol. Med. 2013, 9, 961–971. [Google Scholar] [CrossRef]
- Rajan, A.; Sahu, N.K. Review on magnetic nanoparticle-mediated hyperthermia for cancer therapy. J. Nanoparticle Res. 2020, 22, 319. [Google Scholar] [CrossRef]
- Kita, E.; Oda, T.; Kayano, T.; Sato, S.; Minagawa, M.; Yanagihara, H.; Kishimoto, M.; Mitsumata, C.; Hashimoto, S.; Yamada, K.; et al. Ferromagnetic nanoparticles for magnetic hyperthermia and thermoablation therapy. J. Phys. D Appl. Phys. 2010, 43, 474011. [Google Scholar] [CrossRef]
- Bonini, M.; Berti, D.; Baglioni, P. Nanostructures for magnetically triggered release of drugs and biomolecules. Curr. Opin. Colloid Interface Sci. 2013, 18, 459–467. [Google Scholar] [CrossRef]
- Zhu, K.; Wang, J.; Wang, Z.; Chen, Q.; Song, J.; Chen, X. Ultrasound-Activated Theranostic Materials and Their Bioapplications. Angew. Chem. (Int. Ed. Engl.) 2025, 64, e202422278. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.; Fan, C.H.; Yeh, C.K. Ultrasound-activated nanomaterials for sonodynamic cancer theranostics. Drug Discov. Today 2022, 27, 1590–1603. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; George, B.; Rupitsch, S.J.; Ermert, H.; Ullmann, I.; Vossiek, M.; Lyer, S. Ultrasound-Mediated Cavitation of Magnetic Nanoparticles for Drug Delivery Applications. Curr. Dir. Biomed. Eng. 2022, 8, 568–571. [Google Scholar] [CrossRef]
- Huber, C.M.; Hageroth, L.; Meyer, C.; Ermert, H.; Ullmann, I.; Vossiek, M.; Lyer, S. Ultrasound-Induced Stable and Inertial Cavitation of Magnetic Nanoparticles for Drug Delivery Applications. Curr. Dir. Biomed. Eng. 2024, 10, 328–331. [Google Scholar] [CrossRef]
- Thalmayer, A.S.; Fink, L.; Fischer, G. Experimental and Simulative Characterization of a Hybrid Magnetic Array for Steering Superparamagnetic Nanoparticles in Drug Targeting. IEEE Trans. Bio-Med. Eng. 2025, 72, 940–952. [Google Scholar] [CrossRef]
- Yu, E.Y.; Bishop, M.; Zheng, B.; Ferguson, R.M.; Khandhar, A.P.; Kemp, S.J.; Krishnan, K.M.; Goodwill, P.W.; Conolly, S.M. Magnetic Particle Imaging: A Novel in Vivo Imaging Platform for Cancer Detection. Nano Lett. 2017, 17, 1648–1654. [Google Scholar] [CrossRef]
- Blyakhman, F.A.; Sokolov, S.Y.; Safronov, A.P.; Dinislamova, O.A.; Shklyar, T.F.; Zubarev, A.Y.; Kurlyandskaya, G.V. Ferrogels Ultrasonography for Biomedical Applications. Sensors 2019, 19, 3959. [Google Scholar] [CrossRef]
- Józefczak, A.; Kaczmarek, K.; Kubovčíková, M.; Rozynek, Z.; Hornowski, T. The effect of magnetic nanoparticles on the acoustic properties of tissue-mimicking agar-gel phantoms. J. Magn. Magn. Mater. 2017, 431, 172–175. [Google Scholar] [CrossRef]
- Li, Q.; Yang, L.; Zhang, S.; Wang, F.; Gu, Y.; Deng, X.; Yang, Y. Organic–Inorganic Hybrid Perovskite Materials for Ultrasonic Transducer in Medical Diagnosis. Crystals 2022, 12, 1043. [Google Scholar] [CrossRef]
- Oh, J.; Feldman, M.D.; Kim, J.; Condit, C.; Emelianov, S.; Milner, T.E. Detection of magnetic nanoparticles in tissue using magneto-motive ultrasound. Nanotechnology 2006, 17, 4183–4190. [Google Scholar] [CrossRef]
- Sjöstrand, S.; Evertsson, M.; Jansson, T. Magnetomotive Ultrasound Imaging Systems: Basic Principles and First Applications. Ultrasound Med. Biol. 2020, 46, 2636–2650. [Google Scholar] [CrossRef] [PubMed]
- Fink, M.; Rupitsch, S.J.; Ermert, H.; Lyer, S. In Vivo Study on Magnetomotive Ultrasound Imaging in the Framework of Nanoparticle based Magnetic Drug Targeting. Curr. Dir. Biomed. Eng. 2020, 6, 543–546. [Google Scholar] [CrossRef]
- Fink, M.; Rupitsch, S.J.; Lyer, S.; Ermert, H. Quantitative Determination of Local Density of Iron Oxide Nanoparticles Used for Drug Targeting Employing Inverse Magnetomotive Ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 2482–2495. [Google Scholar] [CrossRef] [PubMed]
- Neppiras, E.A. Acoustic cavitation. Phys. Rep. 1980, 61, 159–251. [Google Scholar] [CrossRef]
- Liu, H.L.; Fan, C.H.; Ting, C.Y.; Yeh, C.K. Combining microbubbles and ultrasound for drug delivery to brain tumors: Current progress and overview. Theranostics 2014, 4, 432–444. [Google Scholar] [CrossRef] [PubMed]
- Rich, J.; Tian, Z.; Huang, T.J. Sonoporation: Past, Present, and Future. Adv. Mater. Technol. 2022, 7, 2100885. [Google Scholar] [CrossRef]
- McDannold, N.; Vykhodtseva, N.; Hynynen, K. Targeted disruption of the blood-brain barrier with focused ultrasound: Association with cavitation activity. Phys. Med. Biol. 2006, 51, 793–807. [Google Scholar] [CrossRef]
- Peruzzi, G.; Sinibaldi, G.; Silvani, G.; Ruocco, G.; Casciola, C.M. Perspectives on cavitation enhanced endothelial layer permeability. Colloids Surf. B Biointerfaces 2018, 168, 83–93. [Google Scholar] [CrossRef]
- Husseini, G.A.; La Diaz de Rosa, M.A.; Richardson, E.S.; Christensen, D.A.; Pitt, W.G. The role of cavitation in acoustically activated drug delivery. J. Control. Release 2005, 107, 253–261. [Google Scholar] [CrossRef]
- Stride, E.; Coussios, C. Nucleation, mapping and control of cavitation for drug delivery. Nat. Rev. Phys. 2019, 1, 495–509. [Google Scholar] [CrossRef]
- Vaezy, S.; Shi, X.; Martin, R.W.; Chi, E.; Nelson, P.I.; Bailey, M.R.; Crum, L.A. Real-time visualization of high-intensity focused ultrasound treatment using ultrasound imaging. Ultrasound Med. Biol. 2001, 27, 33–42. [Google Scholar] [CrossRef]
- Li, T.; Khokhlova, T.D.; Sapozhnikov, O.A.; O’Donnell, M.; Hwang, J.H. A new active cavitation mapping technique for pulsed HIFU applications–bubble Doppler. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1698–1708. [Google Scholar] [CrossRef] [PubMed]
- Salgaonkar, V.A.; Datta, S.; Holland, C.K.; Mast, T.D. Passive cavitation imaging with ultrasound arrays. J. Acoust. Soc. Am. 2009, 126, 3071–3083. [Google Scholar] [CrossRef] [PubMed]
- Gyöngy, M.; Coussios, C.C. Passive cavitation mapping for localization and tracking of bubble dynamics. J. Acoust. Soc. Am. 2010, 128, EL175–EL180. [Google Scholar] [CrossRef] [PubMed]
- Gyöngy, M.; Coussios, C.C. Passive spatial mapping of inertial cavitation during HIFU exposure. IEEE Trans.-Bio-Med. Eng. 2010, 57, 48–56. [Google Scholar] [CrossRef]
- Jensen, C.R.; Ritchie, R.W.; Gyöngy, M.; Collin, J.R.T.; Leslie, T.; Coussios, C.C. Spatiotemporal monitoring of high-intensity focused ultrasound therapy with passive acoustic mapping. Radiology 2012, 262, 252–261. [Google Scholar] [CrossRef]
- Hashemi, H.S.; Rivaz, H. Global Time-Delay Estimation in Ultrasound Elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1625–1636. [Google Scholar] [CrossRef]
- Zaloga, J.; Janko, C.; Nowak, J.; Matuszak, J.; Knaup, S.; Eberbeck, D.; Tietze, R.; Unterweger, H.; Friedrich, R.P.; Duerr, S.; et al. Development of a lauric acid/albumin hybrid iron oxide nanoparticle system with improved biocompatibility. Int. J. Nanomed. 2014, 9, 4847–4866. [Google Scholar] [CrossRef] [PubMed]
- Culjat, M.O.; Goldenberg, D.; Tewari, P.; Singh, R.S. A review of tissue substitutes for ultrasound imaging. Ultrasound Med. Biol. 2010, 36, 861–873. [Google Scholar] [CrossRef] [PubMed]
- Levy, B.E.; Oldenburg, A.L. Elastometry of clot phantoms via magnetomotive ultrasound-based resonant acoustic spectroscopy. Phys. Med. Biol. 2022, 67, 155010. [Google Scholar] [CrossRef]
- Edgar Mazon Valadez, E.; Henrique Uliana, J.; Tiburcio Vicente, T.; Adilton Oliveira Carneiro, A.; Zeferino Pavan, T. Fully-Automated Theranostic System Integrating Magnetomotive Ultrasound and Magnetic Hyperthermia. IEEE Trans. Instrum. Meas. 2025, 74, 1–11. [Google Scholar] [CrossRef]
- Collazos-Burbano, D.A.; Freire, J.E.; Sanches, A.F.; Zufelato, N.; Uliana, J.H.; Brassesco, M.S.; Carneiro, A.A.O.; Pavan, T.Z. Beyond Axial Symmetry: Tracking Vectorial Motion Enhances Nanoparticles Mapping with Magnetomotive Ultrasound. IEEE Access 2025, 13, 62704–62716. [Google Scholar] [CrossRef]
- Mousavi, A.; Reniaud, J.; Santesson, M.; Persson, L.; Jansson, T. Design of a Phantom Mimicking Rectal Lymph Nodes for Magnetomotive Ultrasound. Ultrasound Med. Biol. 2025, 51, 77–84. [Google Scholar] [CrossRef]
- Evertsson, M.; Cinthio, M.; Fredriksson, S.; Olsson, F.; Persson, H.; Jansson, T. Frequency- and phase-sensitive magnetomotive ultrasound imaging of superparamagnetic iron oxide nanoparticles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 481–491. [Google Scholar] [CrossRef]
- Heim, C.; Saleem, T.; Rupitsch, S.J.; Huber, C.M.; Lyer, S.; Ermert, H.; Ullmann, I. D1.4—Modelling and Construction of Complex Shaped Polyvinyl Alcohol based Ultrasound Phantoms for Inverse Magnetomotive Ultrasound Imaging. In Proceedings of the 22. GMA/ITG-Fachtagung Sensoren und Messsysteme, Nürnberg, Germany, 11–12 June 2024; pp. 313–318. [Google Scholar] [CrossRef]
- Huber, C.M.; Heim, C.; Li, J.; Ermert, H.; Rupitsch, S.J.; Ullmann, I.; Lyer, S. Magnetomotive Displacement of Magnetic Nanoparticles in Different Tissue Phantoms. Curr. Dir. Biomed. Eng. 2024, 10, 324–327. [Google Scholar] [CrossRef]
- Fromageau, J.; Gennisson, J.L.; Schmitt, C.; Maurice, R.L.; Mongrain, R.; Cloutier, G. Estimation of polyvinyl alcohol cryogel mechanical properties with four ultrasound elastography methods and comparison with gold standard testings. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 498–509. [Google Scholar] [CrossRef]
- Huber, C.M.; Heim, C.; Ermert, H.; Rupitsch, S.J.; Ullmann, I.; Lyer, S. Wall-less Flow Phantoms with 3D printed Soluble Filament for Ultrasonic Experiments. Curr. Dir. Biomed. Eng. 2023, 9, 97–100. [Google Scholar] [CrossRef]
- Huber, C.M.; Heim, C.; Ermert, H.; Rupitsch, S.J.; Ullmann, I.; Vossiek, M.; Lyer, S. Ultrasound Phantom of a Carotid Bifurcation Tumor Using Multiple 3D Printed Soluble Filaments. In Proceedings of the 2024 IEEE International Symposium on Biomedical Imaging (ISBI), Athens, Greece, 27–30 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Huber, C.M.; Lahmadi, W.; Alballa, A.; Heim, C.; Rupitsch, S.J.; Ermert, H.; Ullmann, I.; Lyer, S. Water-soluble filament in multifilament approach for ultrasound phantom fabrication. Trans. Addit. Manuf. Meets Med. 2024, 6, 1793. [Google Scholar] [CrossRef]
- Kim, G.B.; Lee, S.J. X-ray PIV measurements of blood flows without tracer particles. Exp. Fluids 2006, 41, 195–200. [Google Scholar] [CrossRef]
- Park, H.; Yeom, E.; Lee, S.J. X-ray PIV measurement of blood flow in deep vessels of a rat: An in vivo feasibility study. Sci. Rep. 2016, 6, 19194. [Google Scholar] [CrossRef]
- Mallidi, S.; Wang, B.; Mehrmohammadi, M.; Qu, M.; Chen, Y.S.; Joshi, P.; Kim, S.; Homan, K.A.; Karpiouk, A.B.; Smalling, R.W.; et al. Ultrasound-based imaging of nanoparticles: From molecular and cellular imaging to therapy guidance. In Proceedings of the 2009 IEEE International Ultrasonics Symposium, Roma, Italy, 20–23 September 2009; pp. 27–36. [Google Scholar] [CrossRef]
- Ersepke, T.; Kranemann, T.C.; Schmitz, G. On the Performance of Time Domain Displacement Estimators for Magnetomotive Ultrasound Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 911–921. [Google Scholar] [CrossRef]
- Fink, M.; Ermert, H.; Alexiou, C.; Lyer, S. C2.2-Detection of Iron Oxide Nanoparticles for Local Chemotherapeutic Treatment Employing Coded Magnetomotive Ultrasound. In Proceedings of the Proceedings Sensor 2017, Wunstorf, Germany, 30 May–1 June 2017; pp. 323–328. [Google Scholar] [CrossRef]
- Fink, M.; Ermert, H.; Lyer, S.; Alexiou, C. Sonographic detection of magnetic nanoparticles for Magnetic Drug Targeting using coded magnetic fields. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Rivaz, H.; Boctor, E.M.; Choti, M.A.; Hager, G.D. Real-time regularized ultrasound elastography. IEEE Trans. Med. Imaging 2011, 30, 928–945. [Google Scholar] [CrossRef] [PubMed]
- Alexiou, C.; Diehl, D.; Henninger, P.; Iro, H.; Rockelein, R.; Schmidt, W.; Weber, H. A High Field Gradient Magnet for Magnetic Drug Targeting. IEEE Trans. Appl. Supercond. 2006, 16, 1527–1530. [Google Scholar] [CrossRef]
- Coviello, C.; Kozick, R.; Choi, J.; Gyöngy, M.; Jensen, C.; Smith, P.P.; Coussios, C.C. Passive acoustic mapping utilizing optimal beamforming in ultrasound therapy monitoring. J. Acoust. Soc. Am. 2015, 137, 2573–2585. [Google Scholar] [CrossRef]
- Lu, S.; Li, R.; Yu, X.; Wang, D.; Wan, M. Delay multiply and sum beamforming method applied to enhance linear-array passive acoustic mapping of ultrasound cavitation. Med. Phys. 2019, 46, 4441–4454. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.M.; Dorsch, N.; Ermert, H.; Vossiek, M.; Ullmann, I.; Lyer, S. Passive cavitation mapping for biomedical applications using higher order delay multiply and sum beamformer with linear complexity. Ultrasonics 2025, 153, 107653. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.; Liu, K.; Pouliopoulos, A.N.; Ji, R.; Konofagou, E.E. Real-Time Passive Acoustic Mapping with Enhanced Spatial Resolution in Neuronavigation-Guided Focused Ultrasound for Blood-Brain Barrier Opening. IEEE Trans. Bio-Med. Eng. 2023, 70, 2874–2885. [Google Scholar] [CrossRef]
- Haworth, K.J.; Mast, T.D.; Radhakrishnan, K.; Burgess, M.T.; Kopechek, J.A.; Huang, S.L.; McPherson, D.D.; Holland, C.K. Passive imaging with pulsed ultrasound insonations. J. Acoust. Soc. Am. 2012, 132, 544–553. [Google Scholar] [CrossRef] [PubMed]
- Su, C.C.; Wang, R.; Lin, H.J.; Liu, Y.L.; Chen, C.P.; Chang, Y.L.; Pei, S.C. Explorable Tone Mapping Operators. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2020; pp. 10320–10326. [Google Scholar]
- George, B.; Rupitsch, S.J. Assessing Ultrasound Safety: A Method for Correlating Stimulus Parameters with MI and TI. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2025, 72, 932–944. [Google Scholar] [CrossRef] [PubMed]
- Belova, V.; Gorin, D.A.; Shchukin, D.G.; Möhwald, H. Controlled effect of ultrasonic cavitation on hydrophobic/hydrophilic surfaces. ACS Appl. Mater. Interfaces 2011, 3, 417–425. [Google Scholar] [CrossRef] [PubMed]
- Blum, N.T.; Yildirim, A.; Gyorkos, C.; Shi, D.; Cai, A.; Chattaraj, R.; Goodwin, A.P. Temperature-Responsive Hydrophobic Silica Nanoparticle Ultrasound Contrast Agents Directed by Phospholipid Phase Behavior. ACS Appl. Mater. Interfaces 2019, 11, 15233–15240. [Google Scholar] [CrossRef]
- Montoya Mira, J.; Wu, L.; Sabuncu, S.; Sapre, A.; Civitci, F.; Ibsen, S.; Esener, S.; Yildirim, A. Gas-Stabilizing Sub-100 nm Mesoporous Silica Nanoparticles for Ultrasound Theranostics. ACS Omega 2020, 5, 24762–24772. [Google Scholar] [CrossRef]
- Kwan, J.J.; Lajoinie, G.; de Jong, N.; Stride, E.; Versluis, M.; Coussios, C.C. Ultrahigh-Speed Dynamics of Micrometer-Scale Inertial Cavitation from Nanoparticles. Phys. Rev. Appl. 2016, 6, 044004. [Google Scholar] [CrossRef]
- Keller, S.; Bruce, M.; Averkiou, M.A. Ultrasound Imaging of Microbubble Activity during Sonoporation Pulse Sequences. Ultrasound Med. Biol. 2019, 45, 833–845. [Google Scholar] [CrossRef]
- Martinez, P.; Bottenus, N.; Borden, M. Cavitation Characterization of Size-Isolated Microbubbles in a Vessel Phantom Using Focused Ultrasound. Pharmaceutics 2022, 14, 1925. [Google Scholar] [CrossRef]
- Yamamoto, T.; Komarov, S.V. Enhancement of oscillation amplitude of cavitation bubble due to acoustic wake effect in multibubble environment. Ultrason. Sonochemistry 2021, 78, 105734. [Google Scholar] [CrossRef]
- Maeda, K.; Maxwell, A.D.; Colonius, T.; Kreider, W.; Bailey, M.R. Energy shielding by cavitation bubble clouds in burst wave lithotripsy. J. Acoust. Soc. Am. 2018, 144, 2952. [Google Scholar] [CrossRef]
- Mondou, P.; Mériaux, S.; Nageotte, F.; Vappou, J.; Novell, A.; Larrat, B. State of the art on microbubble cavitation monitoring and feedback control for blood-brain-barrier opening using focused ultrasound. Phys. Med. Biol. 2023, 68, 18TR03. [Google Scholar] [CrossRef] [PubMed]
- Jagalingam, P.; Hegde, A.V. A Review of Quality Metrics for Fused Image. Aquat. Procedia 2015, 4, 133–142. [Google Scholar] [CrossRef]
- Zhang, L.; Dudley, N.J.; Lambrou, T.; Allinson, N.; Ye, X. Automatic image quality assessment and measurement of fetal head in two-dimensional ultrasound image. J. Med. Imaging 2017, 4, 024001. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, C.M.; Hageroth, L.; Dorsch, N.; Ringel, J.; Ermert, H.; Vossiek, M.; Rupitsch, S.J.; Ullmann, I.; Lyer, S. Dual-Modality Ultrasound Imaging of SPIONs Distribution via Combined Magnetomotive and Passive Cavitation Imaging. Sensors 2025, 25, 7171. https://doi.org/10.3390/s25237171
Huber CM, Hageroth L, Dorsch N, Ringel J, Ermert H, Vossiek M, Rupitsch SJ, Ullmann I, Lyer S. Dual-Modality Ultrasound Imaging of SPIONs Distribution via Combined Magnetomotive and Passive Cavitation Imaging. Sensors. 2025; 25(23):7171. https://doi.org/10.3390/s25237171
Chicago/Turabian StyleHuber, Christian Marinus, Lars Hageroth, Nicole Dorsch, Johannes Ringel, Helmut Ermert, Martin Vossiek, Stefan J. Rupitsch, Ingrid Ullmann, and Stefan Lyer. 2025. "Dual-Modality Ultrasound Imaging of SPIONs Distribution via Combined Magnetomotive and Passive Cavitation Imaging" Sensors 25, no. 23: 7171. https://doi.org/10.3390/s25237171
APA StyleHuber, C. M., Hageroth, L., Dorsch, N., Ringel, J., Ermert, H., Vossiek, M., Rupitsch, S. J., Ullmann, I., & Lyer, S. (2025). Dual-Modality Ultrasound Imaging of SPIONs Distribution via Combined Magnetomotive and Passive Cavitation Imaging. Sensors, 25(23), 7171. https://doi.org/10.3390/s25237171





