Reconstruction of Respiratory Flow from an Impedance-Based Contactless Sensor System
Abstract
1. Introduction
2. Materials and Methods
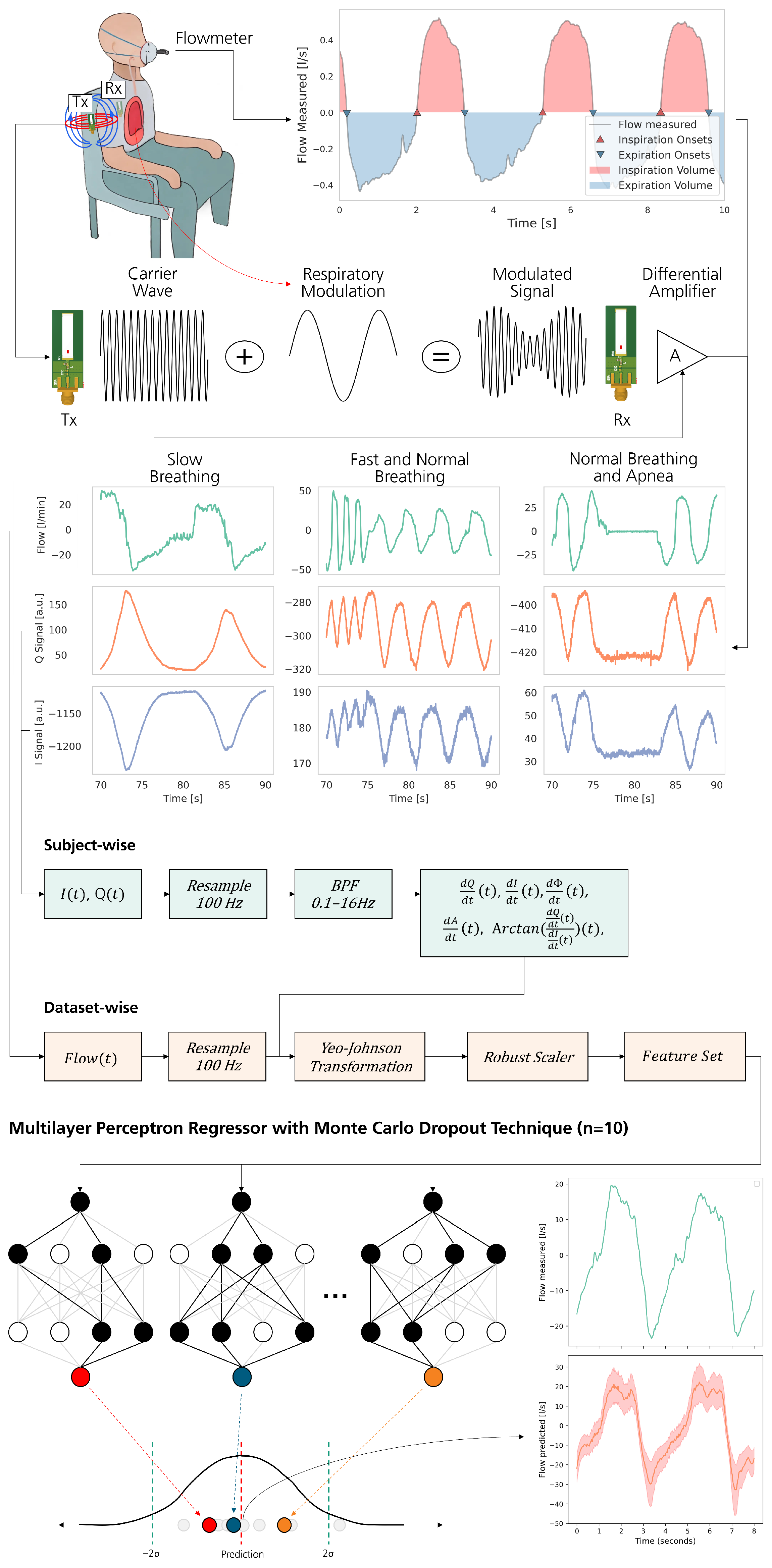
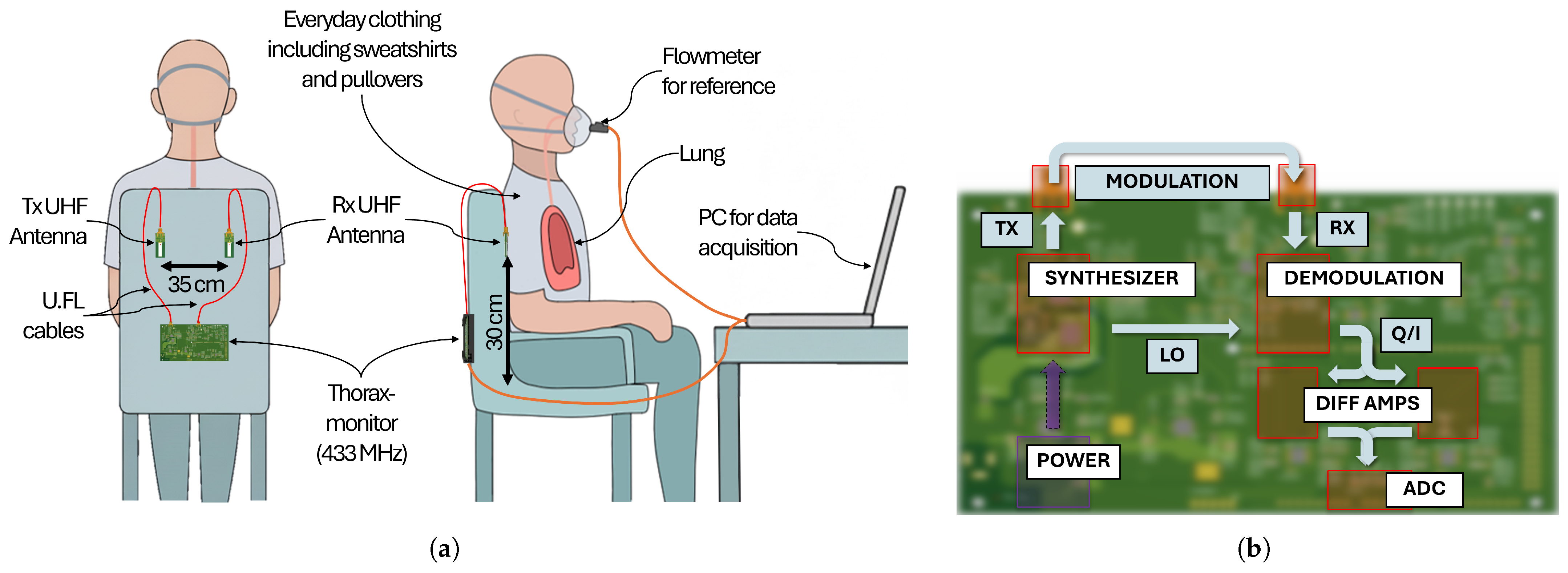
2.1. Thoraxmonitor
2.1.1. Data Acquisition
2.1.2. Data Wrangling
- Time derivatives of Q and I signals;
- Time derivative of amplitude and phase;
- A phase-related feature calculated from the derivatives of Q and I;
- The target respiratory signal.
2.1.3. Model Selection
2.1.4. Performance Evaluation
- Count of respiratory cycles;
- Duration of each respiratory cycle;
- Tidal volume of each respiratory cycle.
3. Results and Discussion
3.1. Dataset Overview
3.1.1. Data Selection and Quality Assessment
3.1.2. Classification of Respiratory Patterns
- Fast Breathing (≥20 breaths per minute; cycle duration of ≤ 3 ): ≈20% of cycles.
- Normal Breathing (10–20 breaths per minute; cycle duration between 3 to 6 ): ≈48% of cycles.
- Slow Breathing (≤10 breaths per minute; cycle duration ≥ 6 ): ≈20% of cycles.
- Apnea (absence of breathing): ≈12% of cycles.
3.1.3. Feature Extraction and Signal Analysis
3.1.4. Signal Integrity and Correlation Analysis
3.2. Automated Machine Learning
- Neuron configuration: [150, 550, 800, 200, 550];
- Learning rate: 0.00015;
- Dropout rate: 0.3 for regularization;
- Optimizer: AdamW;
- Loss function: HuberLoss.
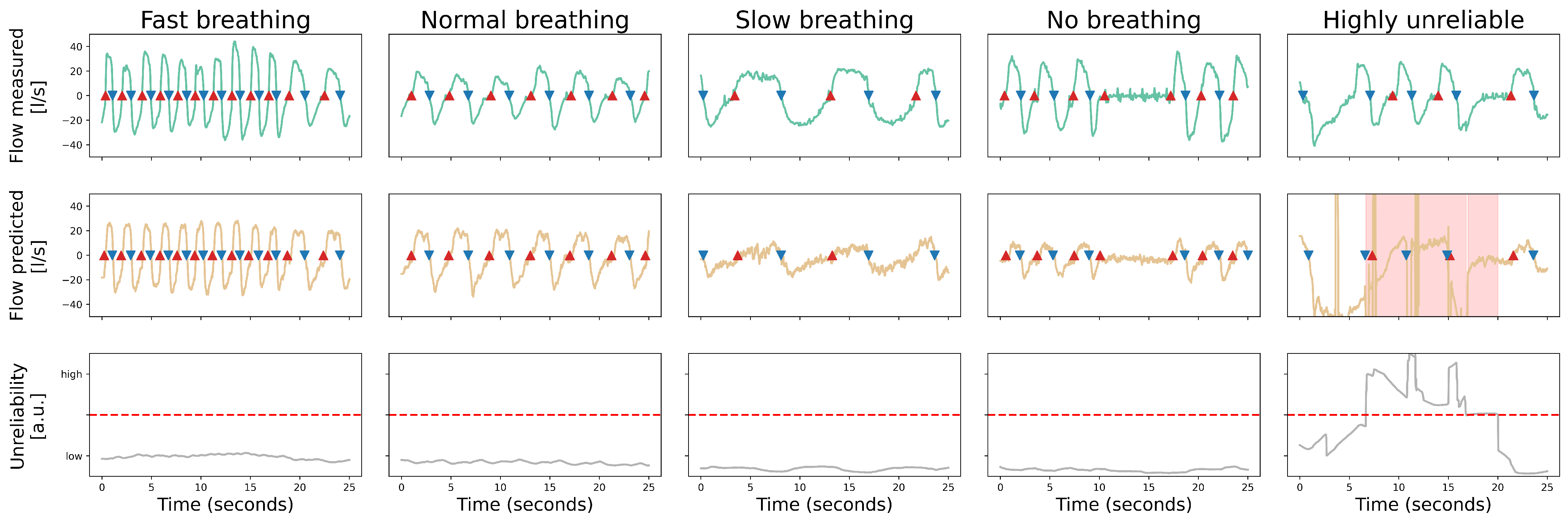
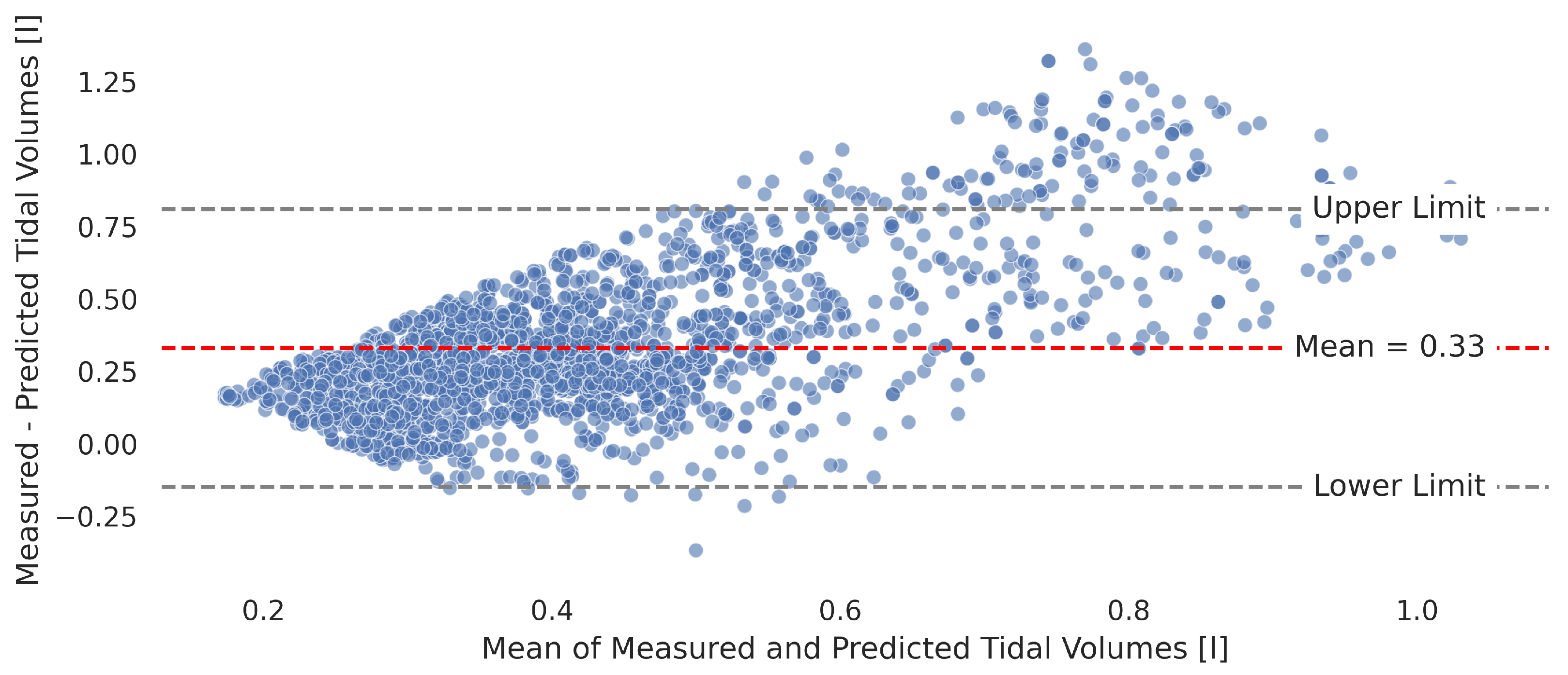
3.3. Accuracy of Signal Reconstruction
- The upper diagram shows a quantification of the observed respiratory signal (in ) via the reference flow meter.
- The middle diagram shows the reconstructed respiratory signal for the corresponding duration. An area is marked in red to indicate the increased unreliability.
- The lower diagram illustrates the reliability score over time, with a dashed line indicating the threshold value above which the outcome is considered unreliable.
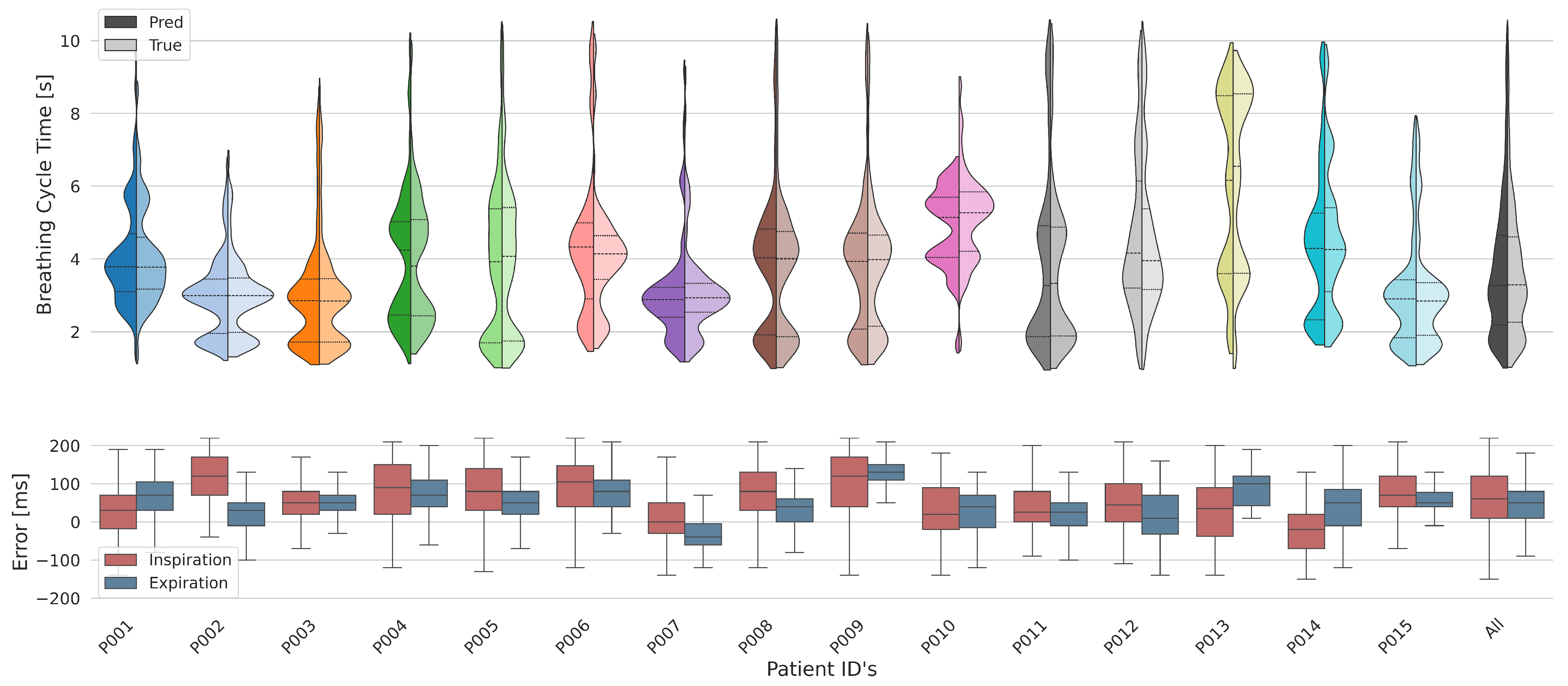
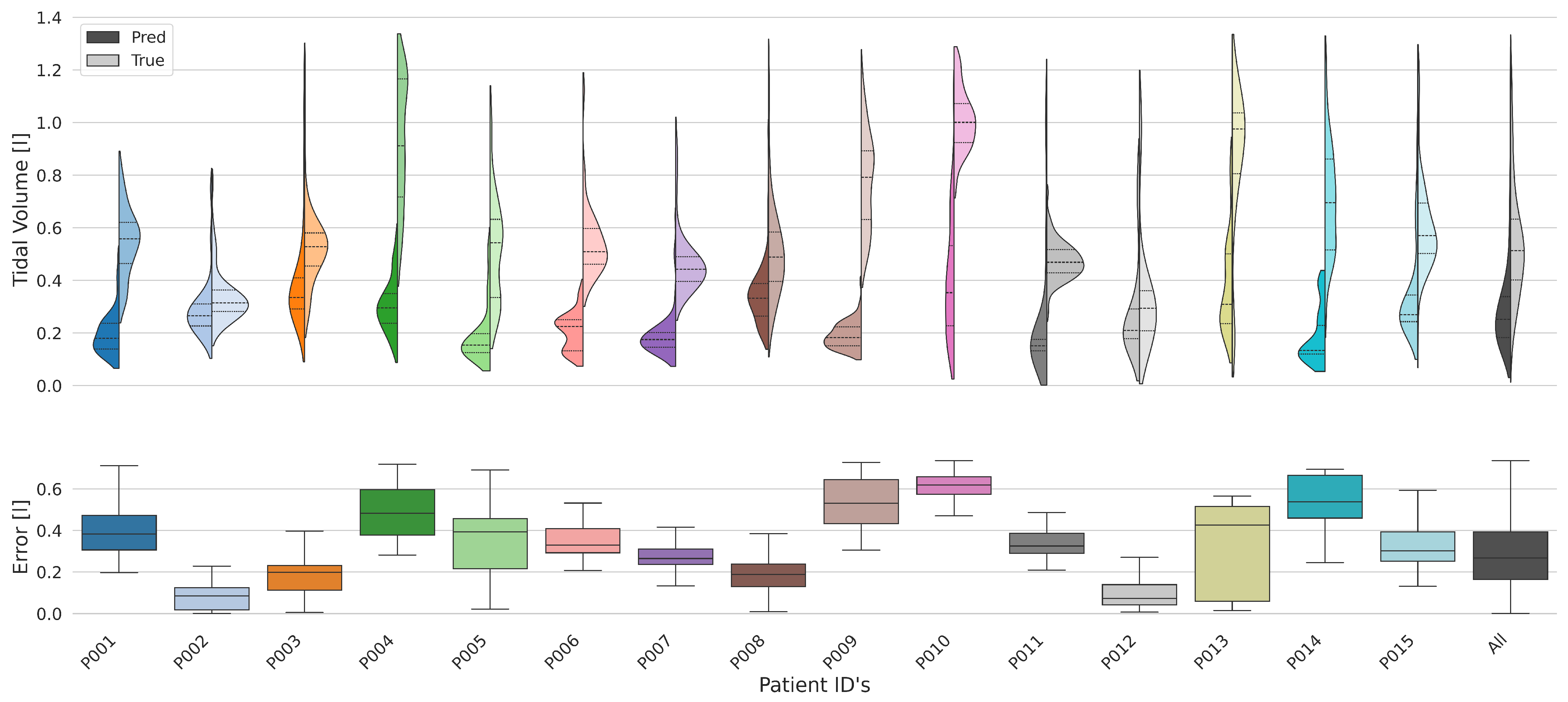
3.4. Results Across Subjects
3.4.1. Breathing Cycles
3.4.2. Tidal Volume
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADC | analog-to-digital converter |
| BCG | ballistocardiography |
| CW | continuous wave |
| FMCW | frequency-modulated continuous wave |
| IQ | in-phase and quadrature |
| iPPG | imaging photoplethysmography |
| LDV | laser Doppler vibrometry |
| MLP | multi-layer perceptron |
| PCB | printed circuit board |
| PPG | photoplethysmography |
| RX | receive |
| SNR | signal-to-noise ratio |
| TX | transmit |
| UHF | ultra-high frequency |
References
- Ringkamp, J.; Radler, P.; Lebhardt, P.; Langejürgen, J. A novel non-invasive, non-conductive method for measuring respiration. J. Sens. Sens. Syst. 2020, 9, 27–32. [Google Scholar] [CrossRef]
- Hahn, G.M.; Kernahan, P.; Martinez, A.; Pounds, D.; Prionas, S.; Anderson, T.; Justice, G. Some heat transfer problems associated with heating by ultrasound, microwaves, or radio frequency. Ann. N. Y. Acad. Sci. 1980, 335, 327–346. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, C.; Gabriel, S.; Corthout, Y. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 2231. [Google Scholar] [CrossRef] [PubMed]
- Caro, C.; Bloice, J. Contactless apnoea detector based on radar. Lancet 1971, 298, 959–961. [Google Scholar] [CrossRef] [PubMed]
- Saluja, J.; Casanova, J.; Lin, J. A supervised machine learning algorithm for heart-rate detection using Doppler motion-sensing radar. IEEE J. Electromagn. Rf Microwaves Med. Biol. 2019, 4, 45–51. [Google Scholar] [CrossRef]
- Janssen, R.; Wang, W.; Moço, A.; De Haan, G. Video-based respiration monitoring with automatic region of interest detection. Physiol. Meas. 2015, 37, 100. [Google Scholar] [CrossRef] [PubMed]
- Massaroni, C.; Lo Presti, D.; Formica, D.; Silvestri, S.; Schena, E. Non-contact monitoring of breathing pattern and respiratory rate via RGB signal measurement. Sensors 2019, 19, 2758. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Thakor, N. Photoplethysmography revisited: From contact to noncontact, from point to imaging. IEEE Trans. Biomed. Eng. 2015, 63, 463–477. [Google Scholar] [CrossRef] [PubMed]
- Teichmann, D.; Foussier, J.; Jia, J.; Leonhardt, S.; Walter, M. Noncontact monitoring of cardiorespiratory activity by electromagnetic coupling. IEEE Trans. Biomed. Eng. 2013, 60, 2142–2152. [Google Scholar] [CrossRef] [PubMed]
- Arlotto, P.; Grimaldi, M.; Naeck, R.; Ginoux, J.M. An ultrasonic contactless sensor for breathing monitoring. Sensors 2014, 14, 15371–15386. [Google Scholar] [CrossRef] [PubMed]
- Sirevaag, E.J.; Casaccia, S.; Richter, E.A.; O’Sullivan, J.A.; Scalise, L.; Rohrbaugh, J.W. Cardiorespiratory interactions: Noncontact assessment using laser Doppler vibrometry. Psychophysiology 2016, 53, 847–867. [Google Scholar] [CrossRef] [PubMed]
- Scalise, L.; Ercoli, I.; Marchionni, P.; Tomasini, E.P. Measurement of respiration rate in preterm infants by laser Doppler vibrometry. In Proceedings of the 2011 IEEE International Symposium on Medical Measurements and Applications, Bari, Italy, 30–31 May 2011; pp. 657–661. [Google Scholar]
- Marchionni, P.; Scalise, L.; Ercoli, I.; Tomasini, E.P. An optical measurement method for the simultaneous assessment of respiration and heart rates in preterm infants. Rev. Sci. Instrum. 2013, 84, 121705. [Google Scholar] [CrossRef] [PubMed]
- Inan, O.T.; Migeotte, P.F.; Park, K.S.; Etemadi, M.; Tavakolian, K.; Casanella, R.; Zanetti, J.; Tank, J.; Funtova, I.; Prisk, G.K.; et al. Ballistocardiography and seismocardiography: A review of recent advances. IEEE J. Biomed. Health Inform. 2014, 19, 1414–1427. [Google Scholar] [CrossRef] [PubMed]
- Uysal, C.; Filik, T. RF-based noncontact respiratory rate monitoring with parametric spectral estimation. IEEE Sens. J. 2019, 19, 9841–9849. [Google Scholar] [CrossRef]
- Wheeler, H.A. The radiansphere around a small antenna. Proc. IRE 1959, 47, 1325–1331. [Google Scholar] [CrossRef]
- Timmermann, C.C. Einführung in Leitungen, Vierpole, Transistormodelle und Simulation mit numerischen und symbolischen CAD/CAE-Systemen; PROFUND Verlag: Plankstadt, Germany, 1996. [Google Scholar]
- Wu, Y.; Ni, H.; Mao, C.; Han, J. Contactless Reconstruction of ECG and Respiration Signals with mmWave Radar based on RSSRnet. IEEE Sens. J. 2023, 24, 6358–6368. [Google Scholar] [CrossRef]
- Adam, S.P.; Alexandropoulos, S.A.N.; Pardalos, P.M.; Vrahatis, M.N. No free lunch theorem: A review. In Approximation and Optimization: Algorithms, Complexity and Applications; Springer: Cham, Switzerland, 2019; pp. 57–82. [Google Scholar]
- Russo, M.A.; Santarelli, D.M.; O’Rourke, D. The physiological effects of slow breathing in the healthy human. Breathe 2017, 13, 298–309. [Google Scholar] [CrossRef] [PubMed]
- Mouloudi, E.; Katsanoulas, K.; Anastasaki, M.; Hoing, S.; Georgopoulos, D. Bronchodilator delivery by metered-dose inhaler in mechanically ventilated COPD patients: Influence of tidal volume. Intensive Care Med. 1999, 25, 1215–1221. [Google Scholar] [CrossRef] [PubMed]
- Matteo, V.; Marina, A.; Giuseppina, B.; Ernesto, C.; Alfredo, C. Flow and volume response to bronchodilator in patients with COPD. Acta Bio Medica Atenei Parm. 2018, 89, 332. [Google Scholar]
| Technology | Measurement Principle | Primary Output | Advantages | Limitations |
|---|---|---|---|---|
| Radar [4,5] | Doppler shift in reflected radio waves from chest wall movement | Chest displacement, Rate | High sensitivity, Robust to lighting conditions, Can work through clothing | Susceptible to motion artifacts, Indirect flow measure, Complex signal processing for harmonics |
| Optical [6,7,8] | Image motion analysis (Optical Flow)/Light absorption changes (Imaging PPG) | Chest displacement, Rate, Blood volume pulse | Low cost, Widely available cameras, Can monitor multiple subjects | Line-of-sight required, Sensitive to lighting changes and shadows, Motion artifacts |
| Thermal Imaging [7] | Temperature difference between inhaled/exhaled air and ambient air | Airflow detection, Rate | Direct visualization of airflow at nostrils/mouth | Low signal-to-noise ratio, Highly sensitive to ambient temperature and air currents |
| Capacitive/Inductive [9] | Changes in electric field (capacitive) or magnetic field (inductive) due to thoracic impedance changes | Chest circumference/ volume change | Can be integrated into furniture (chairs, beds) or textiles | Requires close proximity, Signal quality depends on posture and position, Calibration needed |
| Ultrasound [10] | Doppler shift in ultrasonic waves reflected by exhaled air particles | Airflow detection, Rate | Non-ionizing, Direct airflow measure | Sensitive to ambient air currents, Limited range, Perturbed by ambient noise |
| Laser Doppler Vibrometry [11,12,13] | Doppler shift in laser light scattered from the skin surface | Skin surface velocity/ displacement, Rate | High precision and metrological quality, Can capture fine cardiorespiratory movements | Requires line-of-sight, Can be expensive, Sensitive to gross body movements |
| Ballisto-cardiography [14] | Measurement of body micromovements and recoil forces from cardiac blood ejection | Body acceleration/ displacement, Rate | Unobtrusive, Can be integrated into beds, chairs, or scales | Highly susceptible to motion artifacts, Indirect measure of respiration (often coupled with cardiac signal) |
| RF Sensing [15] | Modulation of the line-of-sight signal path by external thoracic movement | Chest displacement, Rate | Simple architecture (Tx/Rx), Can distinguish multiple subjects | Highly sensitive to any motion in the signal path, Environment-dependent |
| This Work | Transmission through the thorax to measure internal dielectric properties | Intrathoracic Air Volume Waveform | Direct volumetric signal for flow reconstruction | Subject position bias |
| Subject ID | Inspiration Error (ms) | Expiration Error (ms) | ||
|---|---|---|---|---|
| median | std | median | std | |
| All | 60.0 | ±79.4 | 50.0 | ±62.6 |
| P001 | 30.0 | ±80.5 | 70.0 | ±62.6 |
| P002 | 120.0 | ±63.1 | 30.0 | ±49.0 |
| P003 | 50.0 | ±57.0 | 50.0 | ±37.3 |
| P004 | 90.0 | ±90.7 | 70.0 | ±76.7 |
| P005 | 80.0 | ±85.6 | 50.0 | ±59.7 |
| P006 | 105.0 | ±83.5 | 80.0 | ±48.8 |
| P007 | 0.0 | ±67.5 | −40.0 | ±50.2 |
| P008 | 80.0 | ±76.2 | 40.0 | ±48.6 |
| P009 | 120.0 | ±87.8 | 130.0 | ±46.0 |
| P010 | 20.0 | ±80.3 | 40.0 | ±64.1 |
| P011 | 25.0 | ±77.7 | 25.0 | ±54.5 |
| P012 | 45.0 | ±78.4 | 10.0 | ±70.0 |
| P013 | 35.0 | ±99.1 | 100.0 | ±73.1 |
| P014 | -20.0 | ±83.9 | 50.0 | ±75.6 |
| P015 | 70.0 | ±63.5 | 50.0 | ±40.6 |
| Subject ID | Tidal Volume Error [l] | |
|---|---|---|
| median | std | |
| All | 0.287 | ±0.202 |
| P001 | 0.383 | ±0.124 |
| P002 | 0.119 | ±0.044 |
| P003 | 0.197 | ±0.107 |
| P004 | 0.663 | ±0.225 |
| P005 | 0.398 | ±0.171 |
| P006 | 0.332 | ±0.126 |
| P007 | 0.265 | ±0.074 |
| P008 | 0.192 | ±0.099 |
| P009 | 0.597 | ±0.154 |
| P010 | 0.646 | ±0.115 |
| P011 | 0.334 | ±0.160 |
| P012 | 0.086 | ±0.129 |
| P013 | 0.520 | ±0.259 |
| P014 | 0.632 | ±0.161 |
| P015 | 0.314 | ±0.155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bednorz, M.; Ringkamp, J.; Behrend, L.-J.; Lebhardt, P.; Langejürgen, J. Reconstruction of Respiratory Flow from an Impedance-Based Contactless Sensor System. Sensors 2025, 25, 7114. https://doi.org/10.3390/s25237114
Bednorz M, Ringkamp J, Behrend L-J, Lebhardt P, Langejürgen J. Reconstruction of Respiratory Flow from an Impedance-Based Contactless Sensor System. Sensors. 2025; 25(23):7114. https://doi.org/10.3390/s25237114
Chicago/Turabian StyleBednorz, Moritz, Jan Ringkamp, Lara-Jasmin Behrend, Philipp Lebhardt, and Jens Langejürgen. 2025. "Reconstruction of Respiratory Flow from an Impedance-Based Contactless Sensor System" Sensors 25, no. 23: 7114. https://doi.org/10.3390/s25237114
APA StyleBednorz, M., Ringkamp, J., Behrend, L.-J., Lebhardt, P., & Langejürgen, J. (2025). Reconstruction of Respiratory Flow from an Impedance-Based Contactless Sensor System. Sensors, 25(23), 7114. https://doi.org/10.3390/s25237114






