Low-Cost Eye-Tracking Fixation Analysis for Driver Monitoring Systems Using Kalman Filtering and OPTICS Clustering
Abstract
1. Introduction
2. Eye Fixation: A Window into Visual and Cognitive Processes
2.1. Cognitive and Perceptual Load
2.2. Emotional States
2.3. Attention, Distraction, and Decision-Making
3. Existing Techniques for Eye-Tracking Data Analysis and Processing
4. Proposed Feature Extraction Method for Eye-Tracking Data
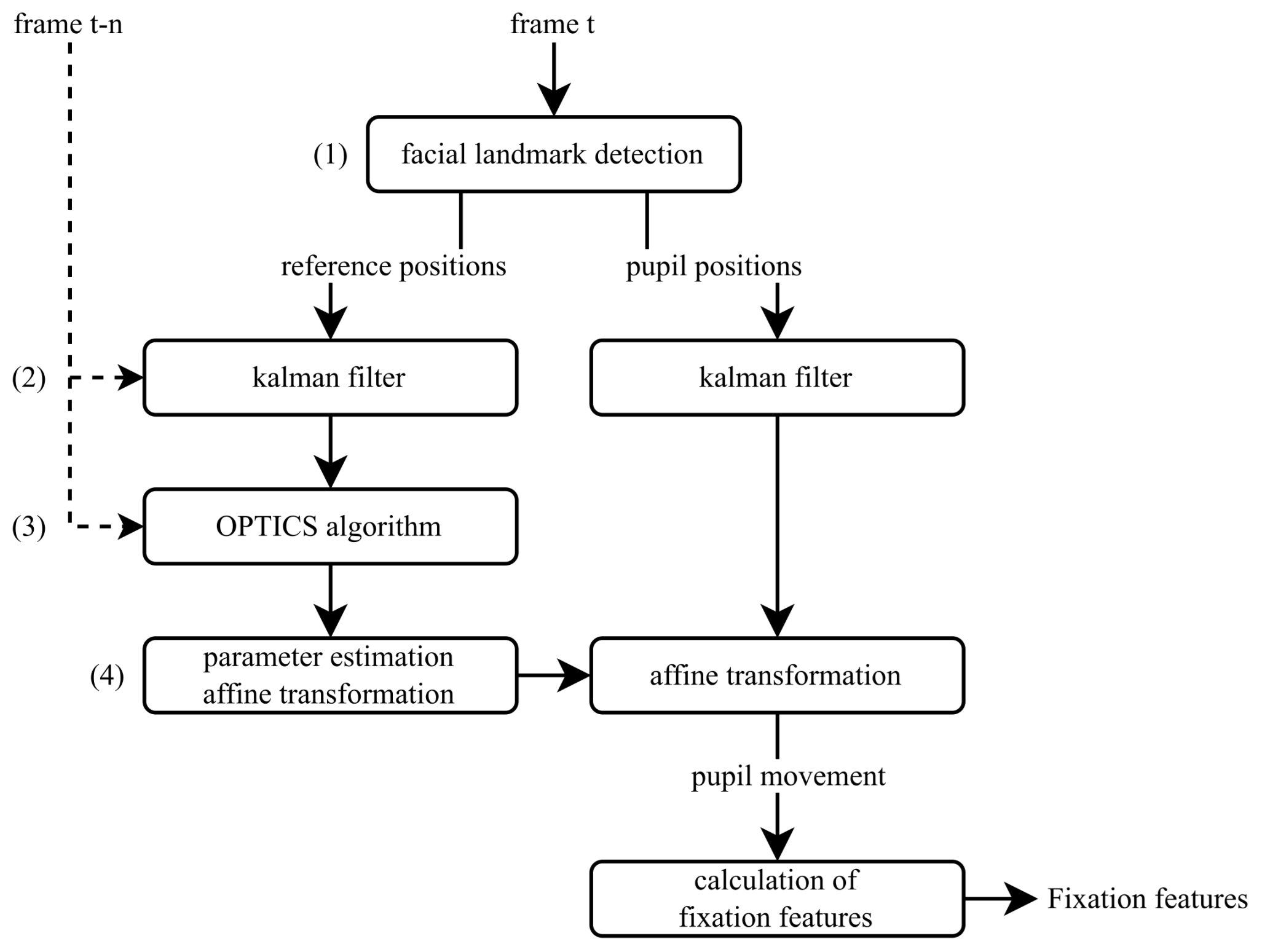
4.1. Data Preprocessing: Extraction and Noise Reduction
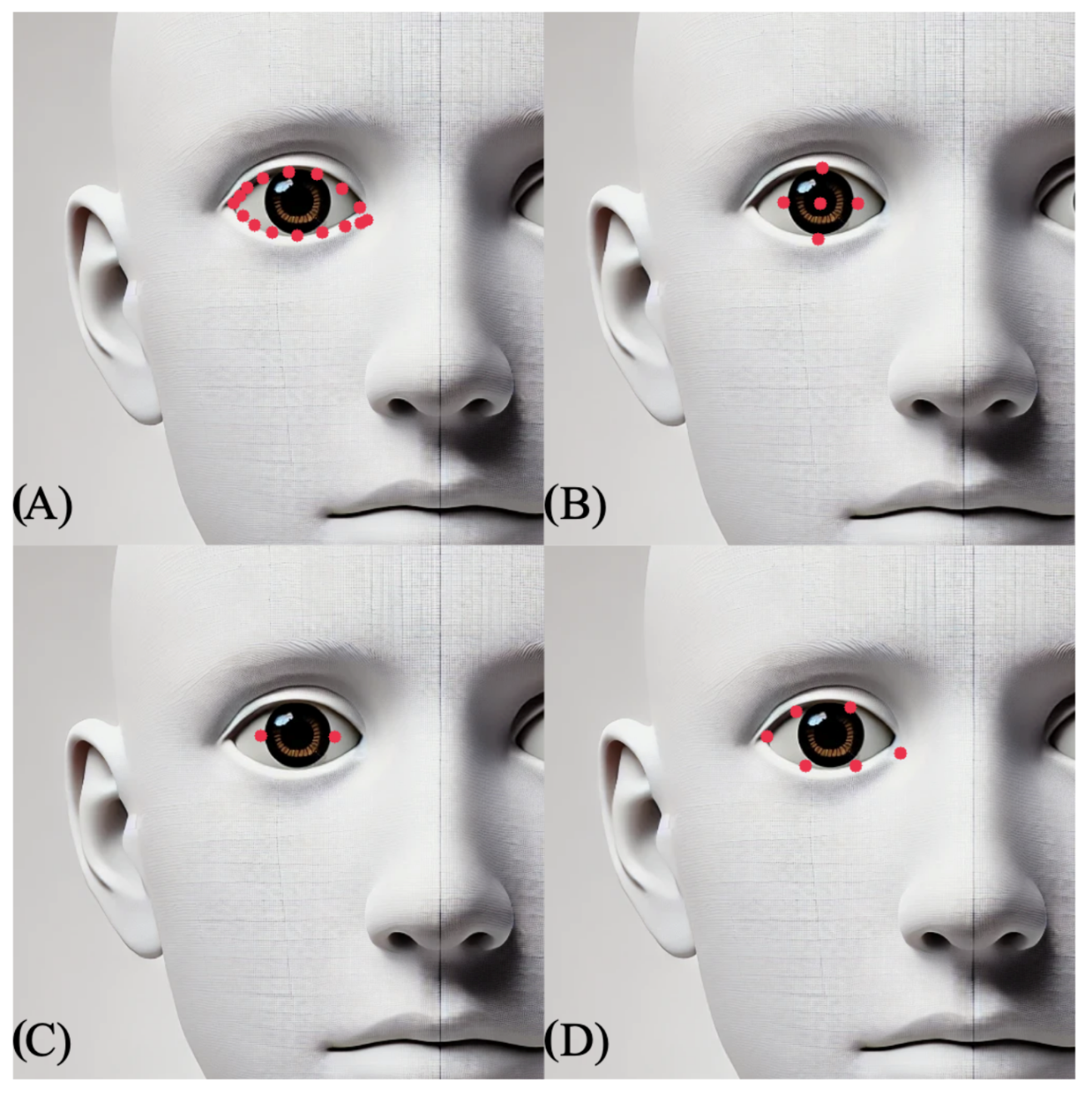
4.1.1. Facial Landmark Detection
- The algorithm must detect the center of the pupil and return the coordinates of this position.
- The algorithm must identify the outline of the eyes or points near the outline of the eyes, with at least four points per eye, and return the coordinates of these positions.
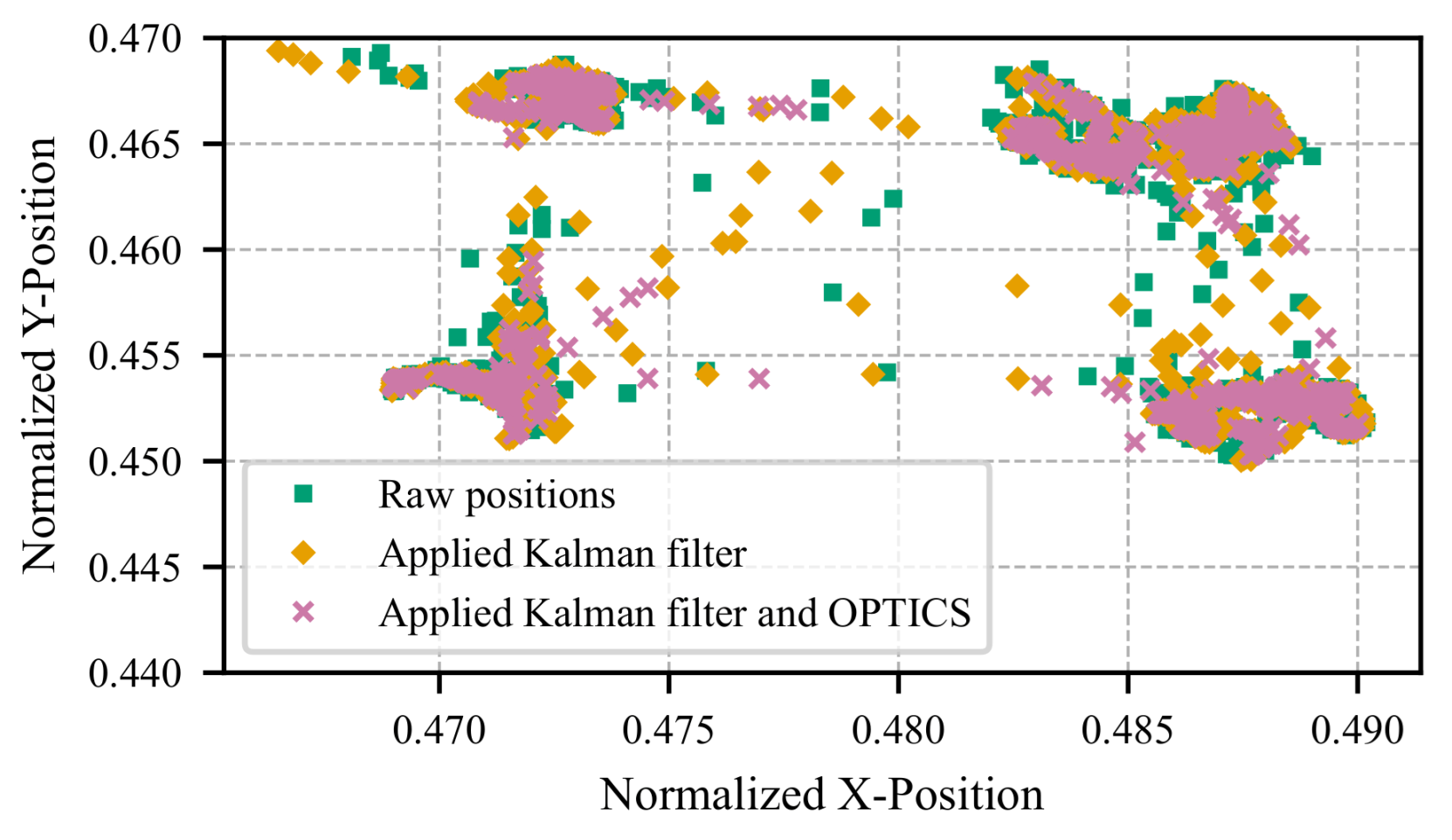
4.1.2. Kalman Filter
Initialization
Determine Initial State
Kalman Filter Loop
4.1.3. OPTICS Algorithm
4.1.4. Affine Transformation
Translation
Rotation
Scaling
4.2. Application of the Proposed Method
4.3. A Method for Approximating Fixation Feature Calculations
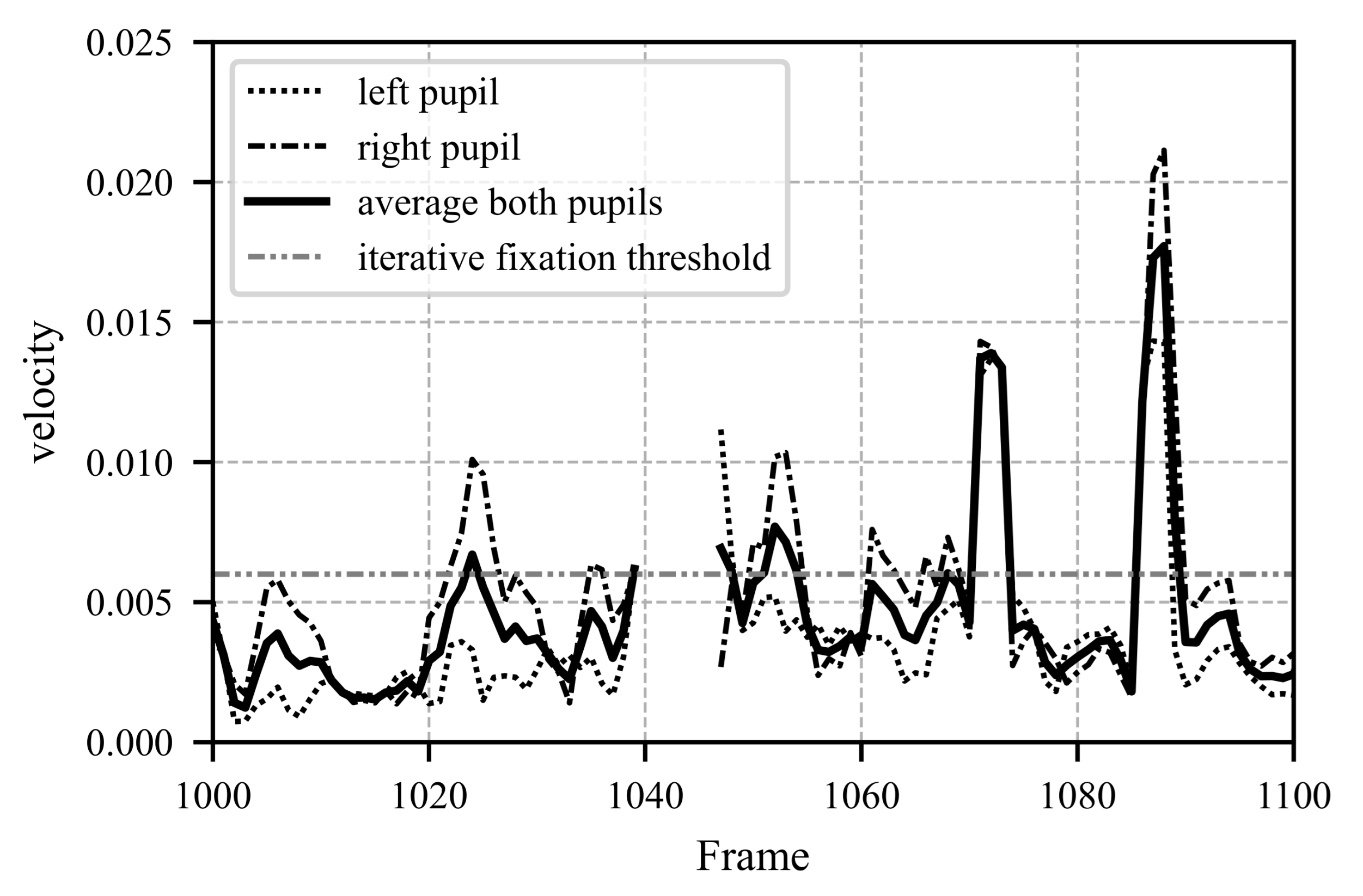
- The distance, and consequently the velocity, of pupil positions between consecutive frames is calculated using the Euclidean distance Formula (24).
- The average velocity is calculated using the velocities of the left and right pupil positions.
- An iterative process is used to approximate the fixation threshold, which represents the maximum pupil movement speed at which a fixation state can still be assumed. Details of this approach and its limitations are provided in Section 4.4. The threshold is iteratively adjusted until it satisfies the specified requirements for the defined time interval.
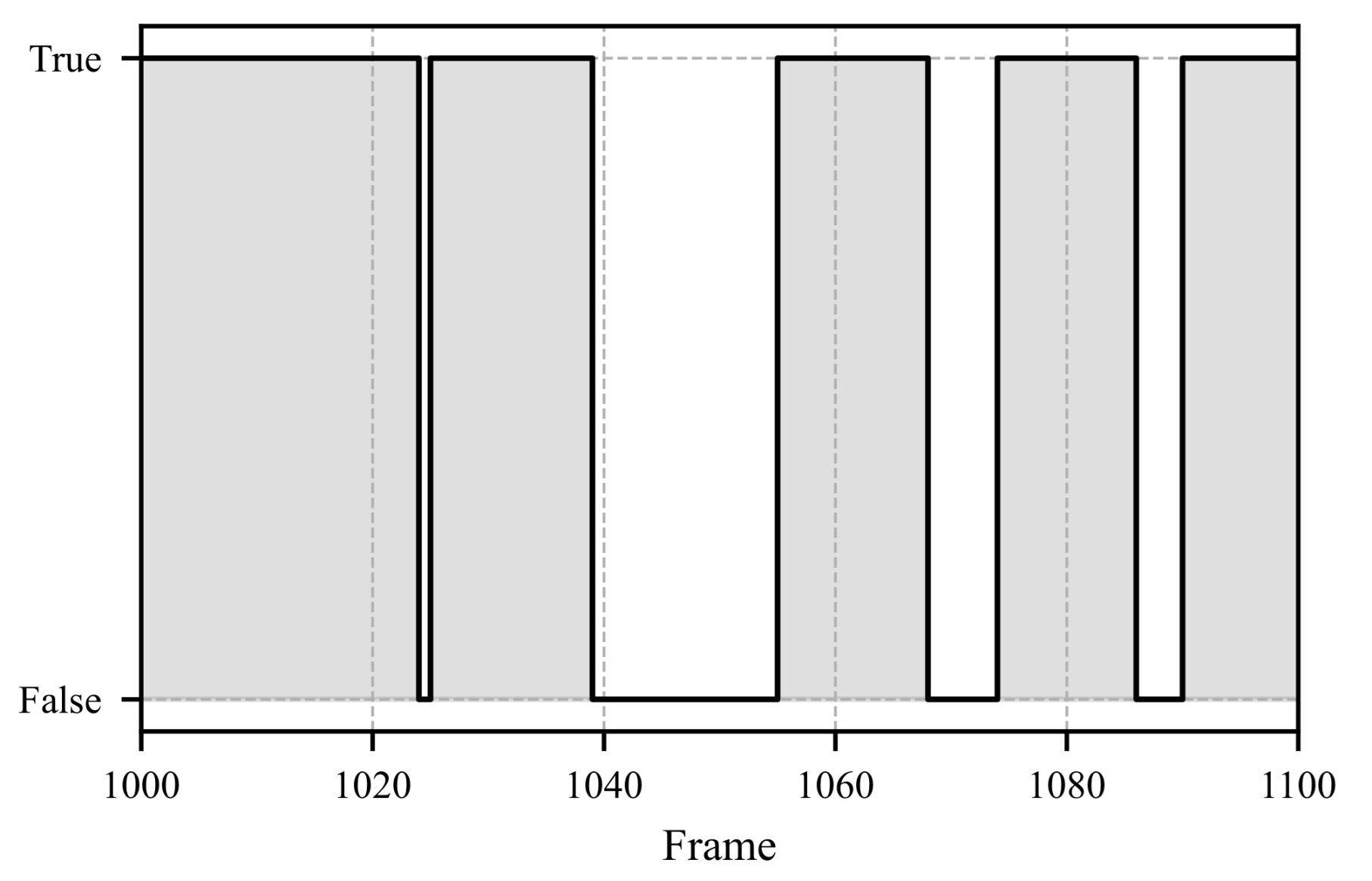
- A boolean vector is calculated based on the fixation threshold, marking instances where the velocity exceeds the defined value.
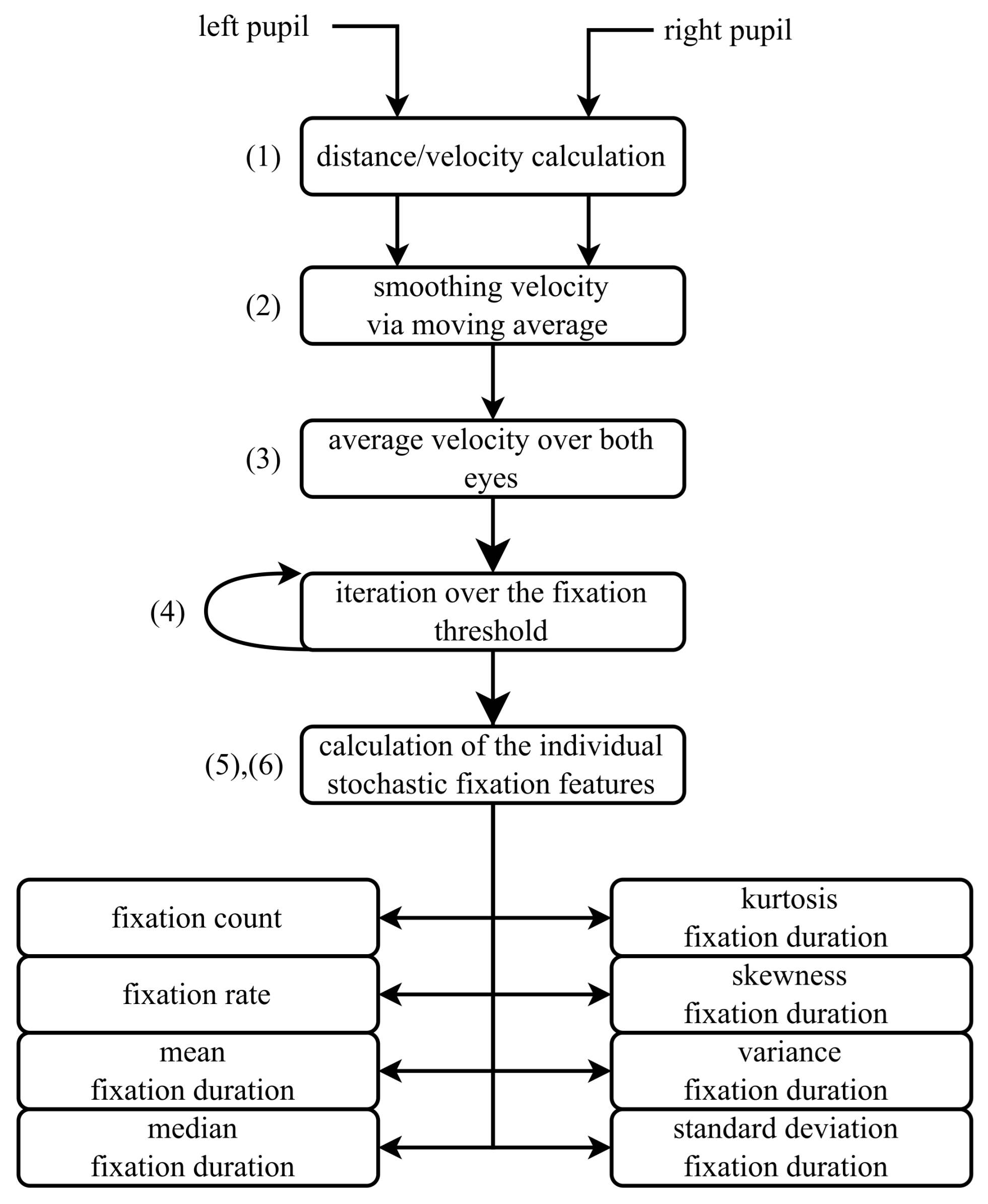
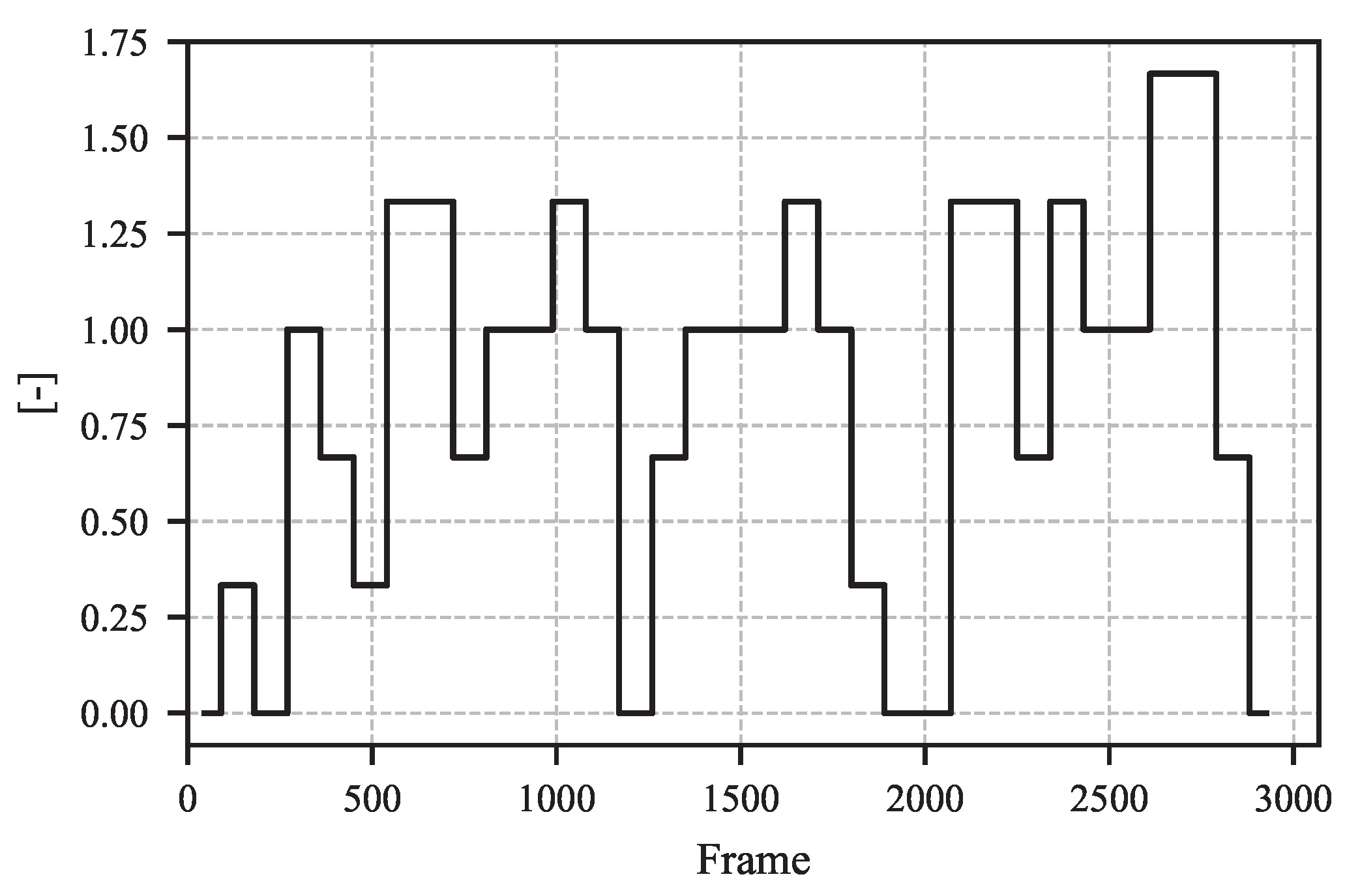
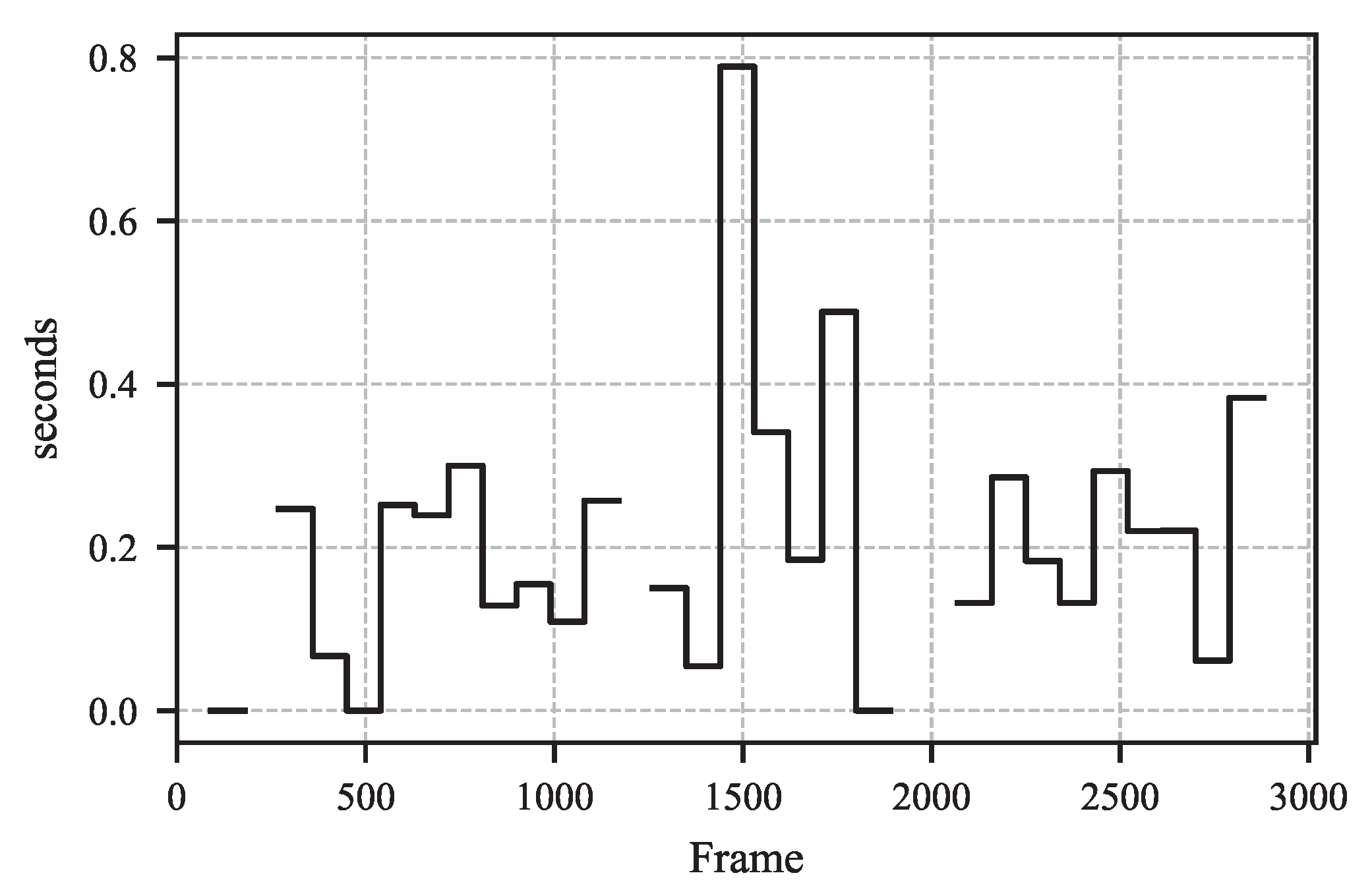
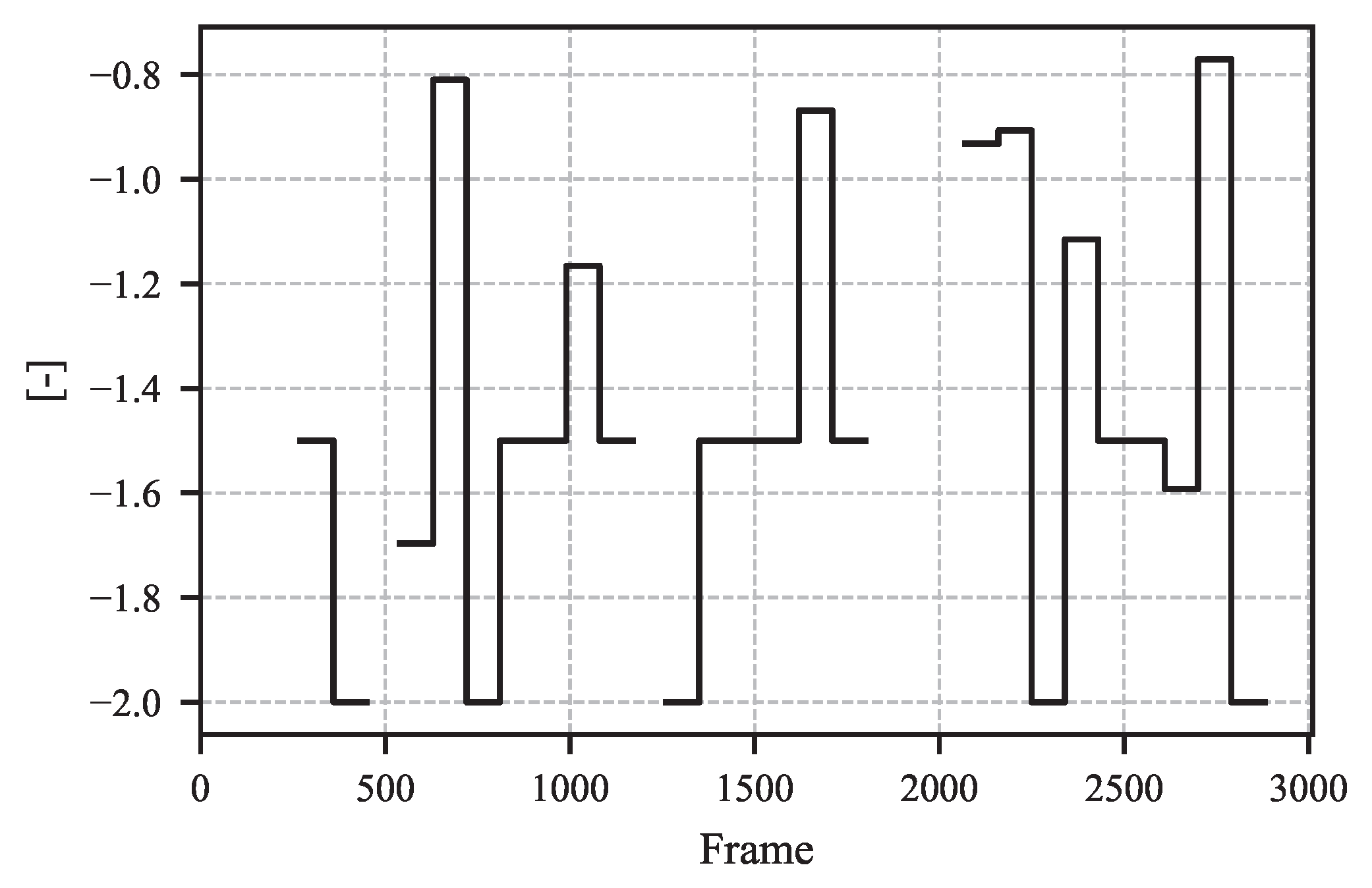
4.4. Iterative Fixation Threshold Estimation: Necessity and Implications
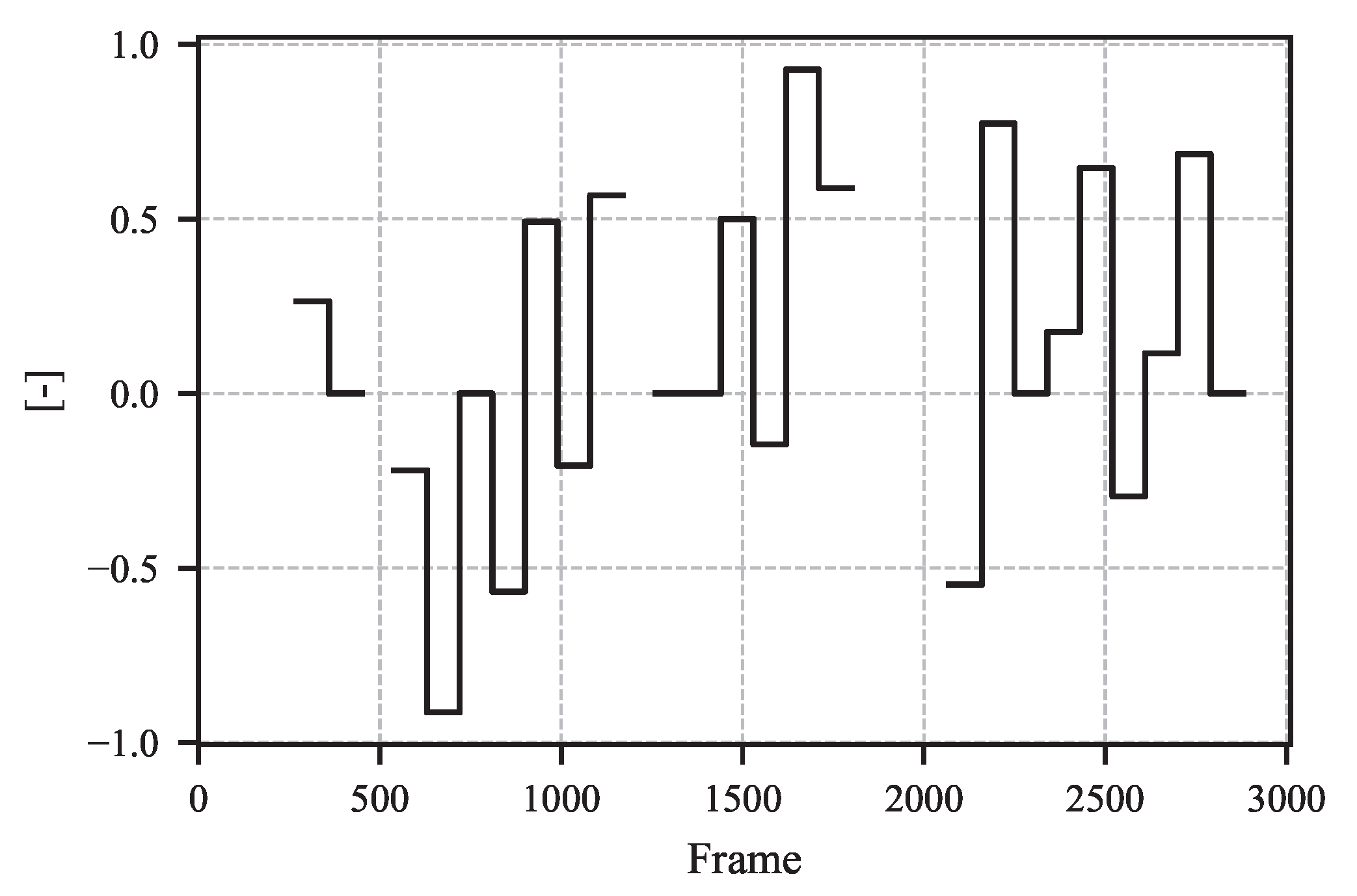
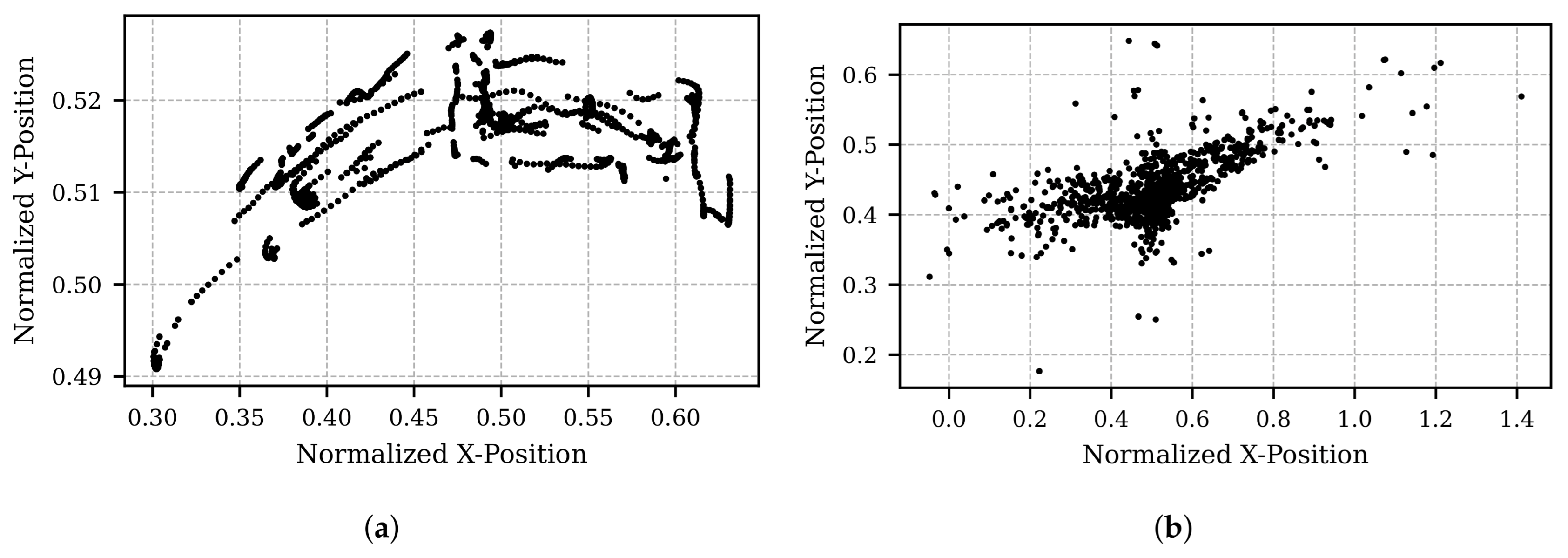
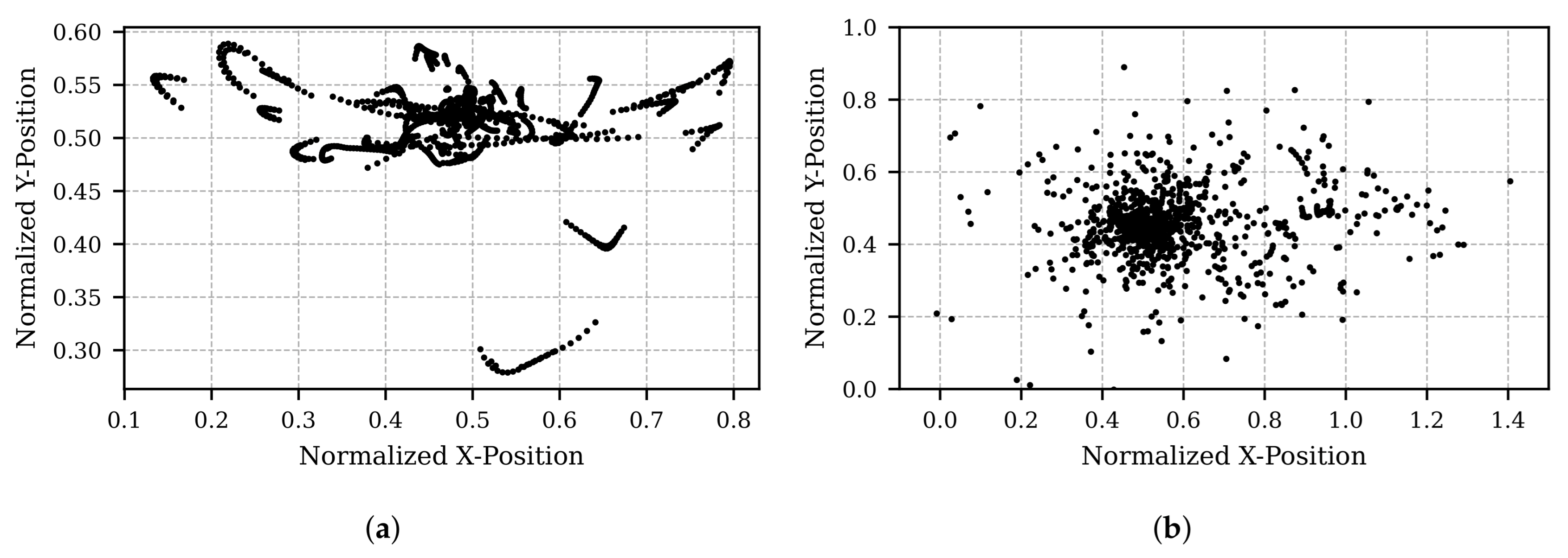
5. Example Results from Proposed Method
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2AFC | Two-Alternative Forced-Choice |
| ADAS | Advanced Driver Assistance Systems |
| AFD | Average Fixation Duration |
| AFKF | Attention Focus Kalman Filter |
| AI | Artificial Intelligence |
| BIRCH | Balanced Iterative Reducing and Clustering using Hierarchies |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| DMS | Driver Monitoring System |
| EAR | Eye Aspect Ratio |
| EEG | Electroencephalography |
| EU | European Union |
| FPS | Frames Per Second |
| HVAC | Heating, Ventilation, and Air Conditioning |
| NIR | Near-Infrared |
| OPTICS | Ordering Points To Identify the Clustering Structure |
| R-CNN | Regions with Convolutional Neural Networks |
| RGB | Red, Green, Blue |
| VR | Virtual Reality |
Appendix A

References
- Akbar, J.U.M.; Kamarulzaman, S.F.; Muzahid, A.J.M.; Rahman, M.A.; Uddin, M. A Comprehensive Review on Deep Learning Assisted Computer Vision Techniques for Smart Greenhouse Agriculture. IEEE Access 2024, 12, 4485–4522. [Google Scholar] [CrossRef]
- Europäisches Parlament und Rat der Europäischen Union. Verordnung (EU) 2019/2144 des Europäischen Parlaments und des Rates vom 27. 2019. Available online: https://eur-lex.europa.eu/legal-content/DE/TXT/?uri=CELEX:32019R2144 (accessed on 13 November 2025).
- Möller, T.; Schneiderbauer, T.; Garms, F.; Gläfke, A.; Köster, N.; Stegmüller, S.; Kern, M.; Werner, M.; Bobka, K. The Future of Interior in Automotive. McKinsey Center for Future Mobility. 2021. Available online: https://www.mckinsey.com/capabilities/mckinsey-center-for-future-mobility/our-insights/the-future-of-interior-in-automotive (accessed on 21 August 2025).
- Kumar, M. Reducing the Cost of Eye Tracking Systems; Technical Report; Stanford University: Stanford, CA, USA, 2006; Available online: https://purl.stanford.edu/gd382mg7248 (accessed on 17 October 2025).
- Nyström, M.; Hooge, I.T.; Hessels, R.S.; Andersson, R.; Hansen, D.W.; Johansson, R.; Niehorster, D.C. The Fundamentals of Eye Tracking Part 3: How to Choose an Eye Tracker. Behav. Res. Methods 2025, 57, 67. [Google Scholar] [CrossRef] [PubMed]
- Rakhmatulin, I. A Review of the Low-Cost Eye-Tracking Systems for 2010–2020. Zenodo 2020. [Google Scholar] [CrossRef]
- Iacobelli, E.; Ponzi, V.; Russo, S.; Napoli, C. Eye-Tracking System with Low-End Hardware: Development and Evaluation. Information 2023, 14, 644. [Google Scholar] [CrossRef]
- Fukuda, T.; Morimoto, K.; Yamana, H. Model-Based Eye-Tracking Method for Low-Resolution Eye-Images. In Proceedings of the 2nd Workshop on Eye Gaze in Intelligent Human–Machine Interaction (GAZEIN’11), Palo Alto, CA, USA, 13 February 2011; pp. 10–19. Available online: https://www.researchgate.net/publication/267366338_Model-Based_Eye-Tracking_Method_for_Low-Resolution_Eye-Images (accessed on 17 October 2025).
- Lemahieu, W.; Wyns, B. Low cost eye tracking for human-machine interfacing. J. Eye Track. Vis. Cogn. Emot. 2011. Available online: https://research.ulusofona.pt/pt/publications/low-cost-eye-tracking-for-human-machine-interfacing-8 (accessed on 17 October 2025).
- Huang, B.; Chen, R.; Zhou, Q.; Xu, W. Eye landmarks detection via weakly supervised learning. Pattern Recognit. 2020, 98, 107076. [Google Scholar] [CrossRef]
- Krafka, K.; Khosla, A.; Kellnhofer, P.; Kannan, H.; Bhandarkar, S.; Matusik, W.; Torralba, A. Eye Tracking for Everyone. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2176–2184. [Google Scholar] [CrossRef]
- Yan, C.; Pan, W.; Xu, C.; Dai, S.; Li, X. Gaze Estimation via Strip Pooling and Multi-Criss-Cross Attention Networks. Appl. Sci. 2023, 13, 5901. [Google Scholar] [CrossRef]
- Irwin, D.E. Visual MemoryWithin and Across Fixations. In Eye Movements and Visual Cognition: Scene Perception and Reading; Rayner, K., Ed.; Springer: New York, NY, USA, 1992; pp. 146–165. [Google Scholar] [CrossRef]
- Pannasch, S.; Helmert, J.; Roth, K.; Herbold, A.; Walter, H. Visual Fixation Durations and Saccade Amplitudes: Shifting Relationship in a Variety of Conditions. J. Eye Mov. Res. 2008, 2, 4. [Google Scholar] [CrossRef]
- Liu, J.C.; Li, K.A.; Yeh, S.L.; Chien, S.Y. Assessing Perceptual Load and Cognitive Load by Fixation-Related Information of Eye Movements. Sensors 2022, 22, 1187. [Google Scholar] [CrossRef]
- Herten, N.; Otto, T.; Wolf, O.T. The role of eye fixation in memory enhancement under stress—An eye tracking study. Neurobiol. Learn. Mem. 2017, 140, 134–144. [Google Scholar] [CrossRef]
- Fahrenberg, J. Psychophysiologie und Verhaltenstherapie. In Lehrbuch der Verhaltenstherapie: Band 1: Grundlagen—Diagnostik—Verfahren—Rahmenbedingungen; Margraf, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 107–124. [Google Scholar] [CrossRef]
- Mahanama, B.; Jayawardana, Y.; Rengarajan, S.; Jayawardena, G.; Chukoskie, L.; Snider, J.; Jayarathna, S. Eye Movement and Pupil Measures: A Review. Front. Comput. Sci. 2022, 3, 733531. [Google Scholar] [CrossRef]
- de Greef, T.; Lafeber, H.; van Oostendorp, H.; Lindenberg, J. Eye Movement as Indicators of Mental Workload to Trigger Adaptive Automation. In Proceedings of the Foundations of Augmented Cognition. Neuroergonomics and Operational Neuroscience, San Diego, CA, USA, 19–24 July 2009; Schmorrow, D.D., Estabrooke, I.V., Grootjen, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 219–228. [Google Scholar] [CrossRef]
- Mulckhuyse, M. The Influence of Emotional Stimuli on the Oculomotor System: A Review of the Literature. Cogn. Affect. Behav. Neurosci. 2018, 18, 411–425. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.Z.; Mountstephens, J.; Teo, J. Emotion Recognition Using Eye-Tracking: Taxonomy, Review and Current Challenges. Sensors 2020, 20, 2384. [Google Scholar] [CrossRef] [PubMed]
- López-Gil, J.M.; Virgili-Gomá, J.; Gil, R.; Guilera, T.; Batalla, I.; Soler-González, J.; García, R. Method for Improving EEG Based Emotion Recognition by Combining It with Synchronized Biometric and Eye Tracking Technologies in a Non-invasive and Low Cost Way. Front. Comput. Neurosci. 2016, 10, 85. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.J.; Zhou, R.; Zhao, L.M.; Lu, B.L. Multimodal Emotion Recognition from Eye Image, Eye Movement and EEG Using Deep Neural Networks. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 3071–3074. [Google Scholar] [CrossRef]
- Velichkovsky, B.M.; Rothert, A.; Kopf, M.; Dornhöfer, S.M.; Joos, M. Towards an express-diagnostics for level of processing and hazard perception. Transp. Res. Part F Traffic Psychol. Behav. 2002, 5, 145–156. [Google Scholar] [CrossRef]
- Glaholt, M.G.; Reingold, E.M. Eye Movement Monitoring as a Process Tracing Methodology in Decision Making Research. J. Neurosci. Psychol. Econ. 2011, 4, 125–146. [Google Scholar] [CrossRef]
- Jin, Y.; Guo, X.; Li, Y.; Xing, J.; Tian, H. Towards Stabilizing Facial Landmark Detection and Tracking via Hierarchical Filtering: A New Method. J. Frankl. Inst. 2020, 357, 3019–3037. [Google Scholar] [CrossRef]
- Nugroho, M.A.; Abdurohman, M.; Erfianto, B.; Sulistiyo, M.D.; Ahmad Kasim, A. Comparative Analysis of Filtering Techniques in Eye Landmark Tracking: Kalman, Savitzky-Golay, and Gaussian. In Proceedings of the 2023 International Conference on Electrical, Communication and Computer Engineering (ICECCE), Dubai, United Arab Emirates, 30–31 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Bagherzadeh, S.Z.; Toosizadeh, S. Eye Tracking Algorithm Based on Multi-Model Kalman Filter. HighTech Innov. J. 2022, 3, 15–27. [Google Scholar] [CrossRef]
- Komogortsev, O.V.; Khan, J.I. Kalman Filtering in the Design of Eye-Gaze-Guided Computer Interfaces. In Proceedings of the Human-Computer Interaction. HCI Intelligent Multimodal Interaction Environments, Beijing, China, 22–27 July 2007; Jacko, J.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 679–689. [Google Scholar] [CrossRef]
- Scott, J. Comparative Study of Clustering Techniques on Eye-Tracking in Dynamic 3D Virtual Environments. Master’s Thesis, Utah State University, Logan, UT, USA, 2023. [Google Scholar] [CrossRef]
- Naqshbandi, K.; Gedeon, T.; Abdulla, U.A. Automatic clustering of eye gaze data for machine learning. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 001239–001244. [Google Scholar] [CrossRef]
- Li, T. 3D Representation of Eye-Tracking Data: An Implementation in Automotive Perceived Quality Analysis. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2021. Available online: https://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-291222 (accessed on 17 October 2025).
- Narcizo, F.B.; dos Santos, F.E.D.; Hansen, D.W. High-Accuracy Gaze Estimation for Interpolation-Based Eye-Tracking Methods. Vision 2021, 5, 41. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Y.; Lv, C. Affine Layer-Enabled Transfer Learning for Eye Tracking with Facial Feature Detection in Human–Machine Interactions. Machines 2022, 10, 853. [Google Scholar] [CrossRef]
- Google. MediaPipe: A Cross-Platform Framework for Building Multimodal Applied Machine Learning Pipelines. 2020. Available online: https://github.com/google/mediapipe (accessed on 18 October 2025).
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Im, G. Notes on Kalman Filter (KF, EKF, ESKF, IEKF, IESKF). arXiv 2024, arXiv:2406.06427. [Google Scholar] [CrossRef]
- Marchthaler, R.; Dingler, S. Kalman-Filter; Springer: Wiesbaden, Germany, 2024. [Google Scholar] [CrossRef]
- Apple Inc. MacBook Pro (13-inch, M2, 2022)—Technical Specifications. 2022. Available online: https://support.apple.com/en-us/111869 (accessed on 18 October 2025).
- Python Software Foundation. Python 3.11.8 Documentation. 2024. Available online: https://docs.python.org/release/3.11.8/ (accessed on 18 October 2025).
- Fahrmeir, L.; Heumann, C.; Künstler, R.; Pigeot, I.; Tutz, G. Statistik: Der Weg zur Datenanalyse; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Holmqvist, K.; Nyström, M.; Andersson, R.; Dewhurst, R.; Jarodzka, H.; Van de Weijer, J. Eye Tracking: A Comprehensive Guide to Methods and Measures; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Martinez-Conde, S.; Macknik, S.L.; Hubel, D.H. The Role of Fixational Eye Movements in Visual Perception. Nat. Rev. Neurosci. 2004, 5, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Duchowski, A. Eye Tracking Methodology: Theory and Practice; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Rayner, K. The 35th Sir Frederick Bartlett Lecture: Eye movements and attention in reading, scene perception, and visual search. Q. J. Exp. Psychol. 2009, 62, 1457–1506. [Google Scholar] [CrossRef] [PubMed]
- Henderson, J.M. Human gaze control during real-world scene perception. Trends Cogn. Sci. 2003, 7, 498–504. [Google Scholar] [CrossRef]
- Rayner, K. Eye Movements in Reading and Information Processing: 20 Years of Research. Psychol. Bull. 1998, 124, 372–422. [Google Scholar] [CrossRef]
- Tatler, B.W.; Hayhoe, M.M.; Land, M.F.; Ballard, D.H. Eye guidance in natural vision: Reinterpreting salience. J. Vis. 2011, 11, 5. [Google Scholar] [CrossRef]
- Dewi, C.; Chen, R.C.; Jiang, X.; Yu, H. Adjusting Eye Aspect Ratio for Strong Eye Blink Detection Based on Facial Landmarks. PeerJ Comput. Sci. 2022, 8, e943. [Google Scholar] [CrossRef]
- Ayoub, M.; Abel, A.; Zhang, H. Optimization of Lacrimal Aspect Ratio for Explainable Eye Blinking. In Proceedings of the Intelligent Systems and Applications, Amsterdam, The Netherlands, 7–8 September 2023; Arai, K., Ed.; Springer: Cham, Switzerland, 2024; pp. 175–192. [Google Scholar] [CrossRef]


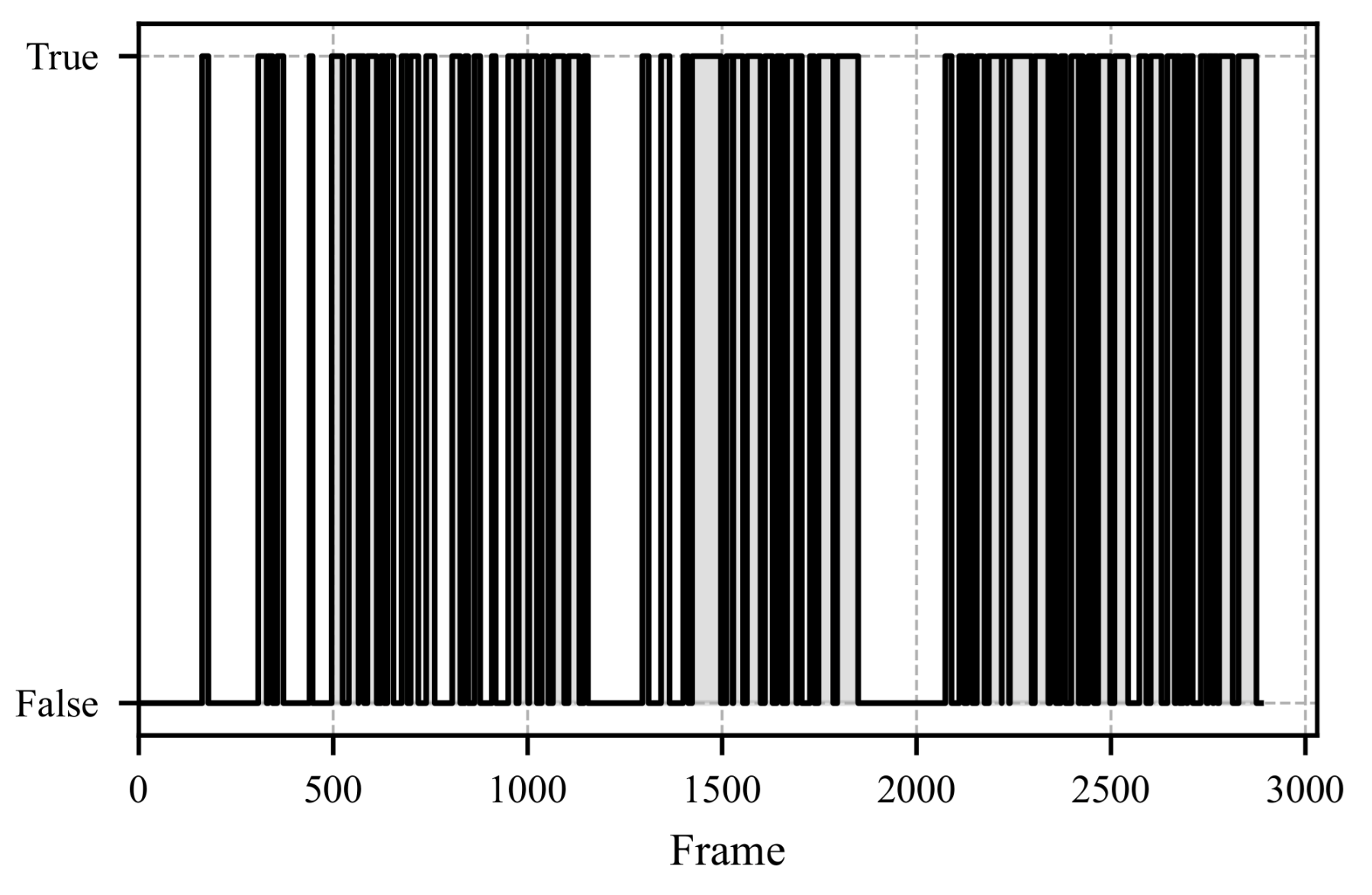
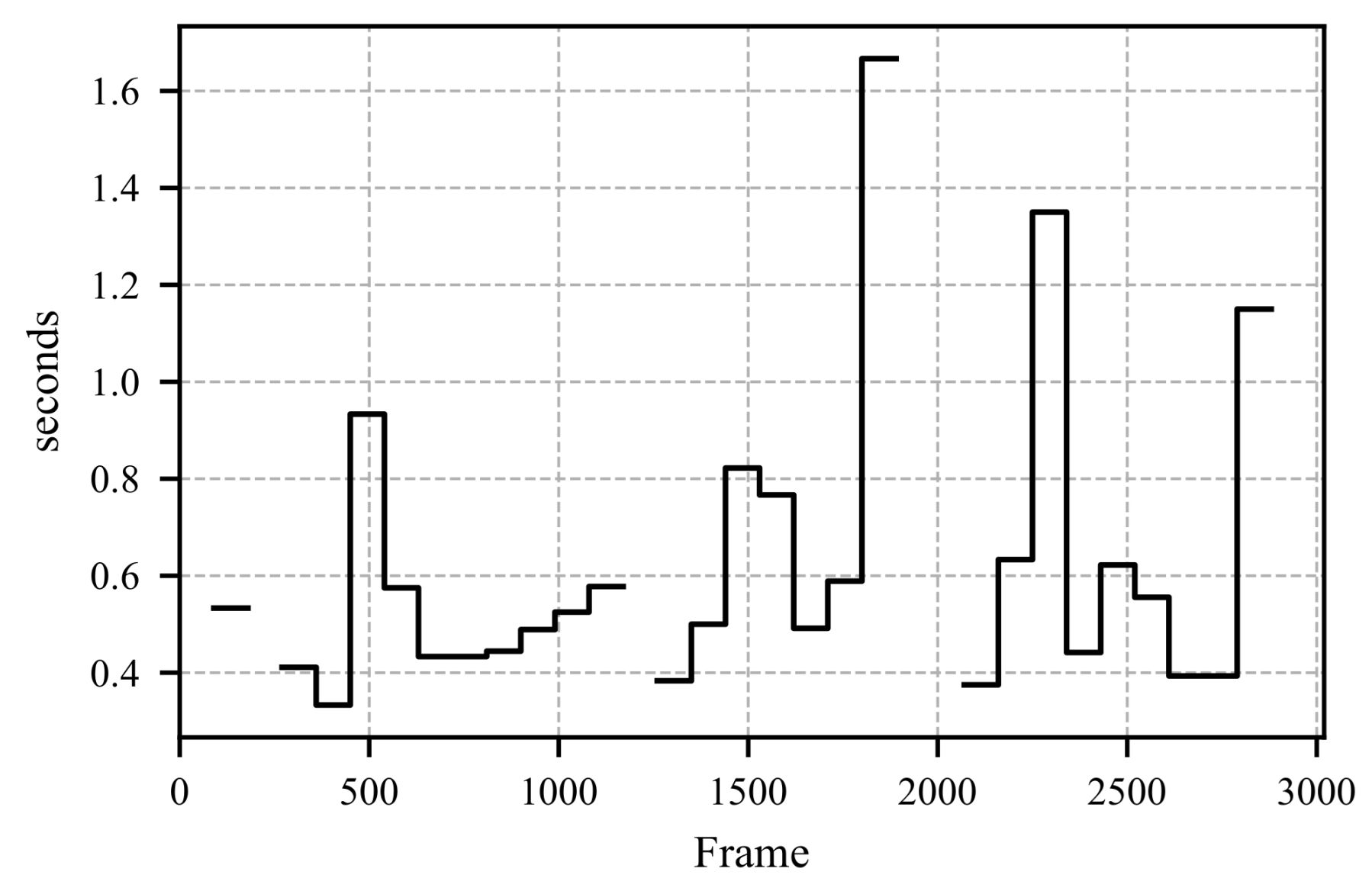
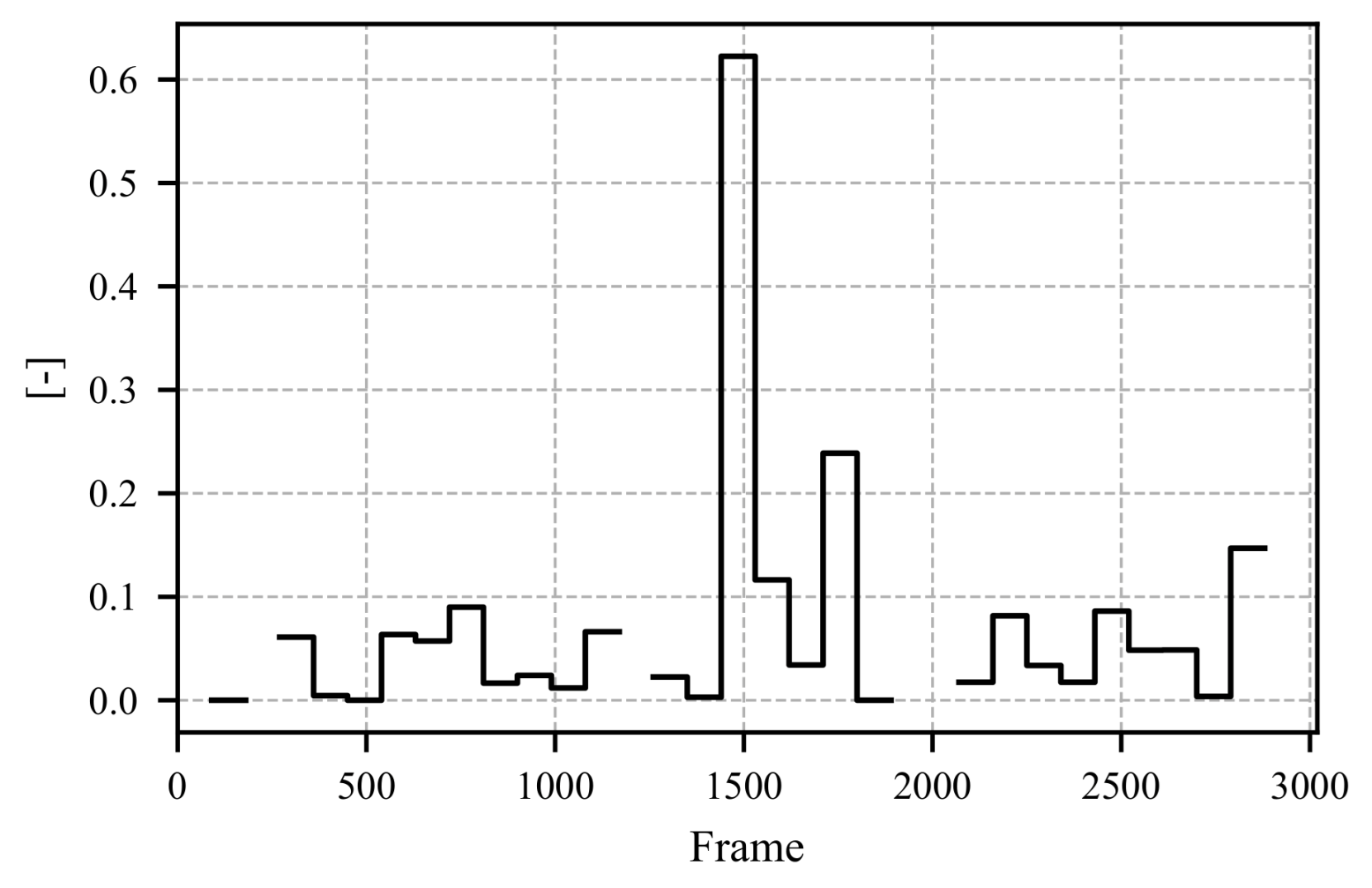
| Feature Name | Description |
|---|---|
| Fixation Count (FC) | Total number of fixations during the observation period. |
| Fixation Ratio (FR) | Proportion of fixation time relative to the total observation duration. |
| Mean Average Fixation Duration | Average length of individual fixations. |
| Median Average Fixation Duration | Representing the middle value when all durations are ordered. |
| Standard Deviation of Average Fixation Duration | Measure of variability in fixation durations. |
| Variance of Average Fixation Duration | Measure of the spread of fixation durations. |
| Skewness of Average Fixation Duration | A statistical metric assessing the asymmetry of the distribution of fixation durations. |
| Kurtosis of Average Fixation Duration | A statistical metric assessing the distribution’s peakedness or tail-heaviness. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandstetter, J.; Knoch, E.-M.; Gauterin, F. Low-Cost Eye-Tracking Fixation Analysis for Driver Monitoring Systems Using Kalman Filtering and OPTICS Clustering. Sensors 2025, 25, 7028. https://doi.org/10.3390/s25227028
Brandstetter J, Knoch E-M, Gauterin F. Low-Cost Eye-Tracking Fixation Analysis for Driver Monitoring Systems Using Kalman Filtering and OPTICS Clustering. Sensors. 2025; 25(22):7028. https://doi.org/10.3390/s25227028
Chicago/Turabian StyleBrandstetter, Jonas, Eva-Maria Knoch, and Frank Gauterin. 2025. "Low-Cost Eye-Tracking Fixation Analysis for Driver Monitoring Systems Using Kalman Filtering and OPTICS Clustering" Sensors 25, no. 22: 7028. https://doi.org/10.3390/s25227028
APA StyleBrandstetter, J., Knoch, E.-M., & Gauterin, F. (2025). Low-Cost Eye-Tracking Fixation Analysis for Driver Monitoring Systems Using Kalman Filtering and OPTICS Clustering. Sensors, 25(22), 7028. https://doi.org/10.3390/s25227028





