Advances in Flow of Water Through Variably Saturated Soils: A Review of Model Approaches and Experimental Investigations with Use of Sensors
Abstract
1. Introduction
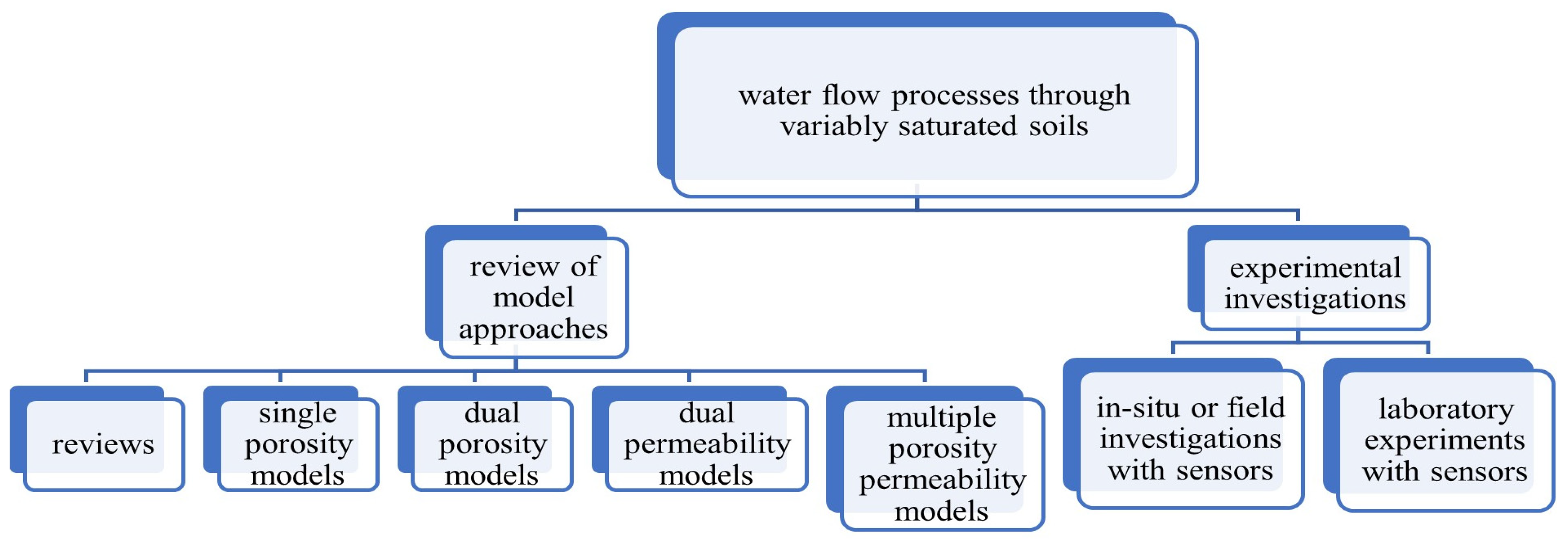
2. Research Methodology
- Water flow processes through variably saturated soil reviews—this section considers reviews on water flow processes through saturated and unsaturated soils for the purpose of the determination of the soil subsurface flow characteristics.
- Soil water flow models—this part discusses model approaches developed for different flow conditions.
- Experimental investigation of flow through variably saturated soils—this discussion is divided into in situ or field experiments and laboratory investigations of the flow of water through soil columns with the use of sensors.
3. Review of Model Approaches
3.1. Reviews
3.2. Single Porosity Models
3.3. Dual Porosity Models
3.4. Dual Permeability Models
3.5. Multiple Porosity/Permeability Models
4. Experimental Measurement of Soil Hydraulic Properties
4.1. Field Measurement of Soil Hydraulic Properties
4.2. Soil Column Laboratory Measurement of Soil Hydraulic Properties
5. The Future of Smart Sensors in Soil Column Water Flow Experiments
6. Conclusions
Funding
Conflicts of Interest
References
- Schoonover, J.E.; Crim, J.F. An Introduction to Soil Concepts and the Role of Soils in Watershed Management. J. Contemp. Water Res. Educ. 2015, 154, 21–47. [Google Scholar] [CrossRef]
- Arora, B.; Dwivedi, D.; Faybishenko, B.; Jana, R.B.; Wainwright, H.M. Understanding and Predicting Vadose Zone Processes. Rev. Miner. Geochem. 2019, 85, 303–328. [Google Scholar] [CrossRef]
- Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in Soil Evaporation Physics—A Review. Vadose Zone J. 2013, 12, vzj2012.0163. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Or, D. Effects of hydrophobic layers on evaporation from porous media. Geophys. Res. Lett. 2008, 35, 1–4. [Google Scholar] [CrossRef]
- Maskey, S. Chapter 4-Models of unsaturated (vadose) zone. In Catchment Hydrological Modelling; Maskey, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 59–79. [Google Scholar]
- Shokri, N.; Lehmann, P.; Or, D. Characteristics of evaporation from partially wettable porous media. Water Resour. Res. 2009, 45, 1–12. [Google Scholar] [CrossRef]
- Osame, P.U. Hydrodynamic Characterisation of Soil Subsurface Flows for Water Conservation Purposes. Ph.D. Thesis, Robert Gordon University, Aberdeen, UK, 2024. [Google Scholar] [CrossRef]
- Fredlund, D.; Xing, A. Equations for the Soil–Water Characteristic Curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Schwartz, R.C.; Juo, A.S.R.; McInnes, K.J. Estimating parameters for a dual-porosity model to describe non-equilibrium, reactive transport in a fine-textured soil. J. Hydrol. 2000, 229, 149–167. [Google Scholar] [CrossRef]
- Van Genuchten, M.; Simunek, J.J.; Leij, F.; Toride, N.; Šejna, M. STANMOD: Model Use, Calibration, and Validation. Trans. ASAE Am. Soc. Agric. Eng. 2012, 55, 1353–1366. [Google Scholar] [CrossRef]
- Leij, F.J.; Toride, N. Analytical Solutions for Solute Transport in Finite Soil Columns with Arbitrary Initial Distributions. Soil Sci. Soc. Am. J. 1998, 62, 855–864. [Google Scholar] [CrossRef]
- Zhou, W.; Yuen, K.; Tan, F. Estimation of soil–water characteristic curve and relative permeability for granular soils with different initial dry densities. Eng. Geol. 2014, 179, 1–9. [Google Scholar] [CrossRef]
- Lewandowska, J.; Szymkiewicz, A.; Gorczewska, W.; Vauclin, M. Infiltration in a double-porosity medium: Experiments and comparison with a theoretical model. Water Resour. Res. 2005, 41, w02022. [Google Scholar] [CrossRef]
- Mbonimpa, M.; Aubertin, M.; Bussière, B.; Chapuis, R. A model to predict the water retention curve from basic geotechnical properties. Can. Geotech. J. 2003, 40, 1104–1122. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Ehrhardt, A.; Berger, K.; Filipović, V.; Wöhling, T.; Vogel, H. ö; Gerke, H.H. Tracing lateral subsurface flow in layered soils by undisturbed monolith sampling, targeted laboratory experiments, and model-based analysis. Vadose Zone J. 2022, 21, e20206. [Google Scholar] [CrossRef]
- Rudiyanto; Minasny, B.; Chaney, N.W.; Maggi, F.; Goh Eng Giap, S.; Shah, R.M.; Fiantis, D.; Setiawan, B.I. Pedotransfer functions for estimating soil hydraulic properties from saturation to dryness. Geoderma 2021, 403, 115194. [Google Scholar] [CrossRef]
- Chaney, N.W.; Minasny, B.; Herman, J.D.; Nauman, T.W.; Brungard, C.W.; Morgan, C.L.S.; McBratney, A.B.; Wood, E.F.; Yimam, Y. POLARIS Soil Properties: 30-m Probabilistic Maps of Soil Properties Over the Contiguous United States. Water Resour. Res. 2019, 55, 2916–2938. [Google Scholar] [CrossRef]
- Hodnett, M.G.; Tomasella, J. Marked differences between van Genuchten soil water-retention parameters for temperate and tropical soils: A new water-retention pedo-transfer functions developed for tropical soils. Geoderma 2002, 108, 155–180. [Google Scholar] [CrossRef]
- Vereecken, H.; Maes, J.; Feyen, J.; Darius, P. Estimating the soil moisture retention characteristic from texture, bulk density, and carbon content. Soil Sci. 1989, 148, 389–403. [Google Scholar] [CrossRef]
- Morbidelli, R. On the determination of soil hydraulic properties. J. Hydrol. 2020, 580, 124362. [Google Scholar] [CrossRef]
- Lin, H. Earth’s Critical Zone and hydropedology: Concepts, characteristics, and advances. Hydrol. Earth Syst. Sci. Discuss. 2009, 14, 25–45. [Google Scholar] [CrossRef]
- Lai, J.; Ren, L. Assessing the Size Dependency of Measured Hydraulic Conductivity Using Double-Ring Infiltrometers and Numerical Simulation. Soil Sci. Soc. Am. J. 2007, 71, 1667–1675. [Google Scholar] [CrossRef]
- Ronayne, M.J.; Houghton, T.B.; Stednick, J.D. Field characterization of hydraulic conductivity in a heterogeneous alpine glacial till. J. Hydrol. 2012, 458–459, 103–109. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, Z.; Ding, H.; Li, W.; Wen, Y.; Zhang, J.; Dou, Y. Evaluation of suitable amount of water and fertilizer for mature grapes in drip irrigation in extreme arid regions. Sustainability 2019, 11, 2063. [Google Scholar] [CrossRef]
- El-Zehairy, A.; Nezhad, M.M.; Joekar-Niasar, V.; Guymer, I.; Kourra, N.; Williams, M. Pore-network modelling of non-Darcy flow through heterogeneous porous media. Adv. Water Resour. 2019, 131, 103378. [Google Scholar] [CrossRef]
- Atangana, A. Chapter 2-Principle of Groundwater Flow. In Fractional Operators with Constant and Variable Order with Application to Geo-Hydrology; Atangana, A., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 15–47. [Google Scholar]
- Dukhan, N.; Bağcı, Ö.; Özdemir, M. Experimental flow in various porous media and reconciliation of Forchheimer and Ergun relations. Exp. Therm. Fluid. Sci. 2014, 57, 425–433. [Google Scholar] [CrossRef]
- Hendrickx, J.M.H.; Dekker, L.W.; Boersma, O.H. Unstable Wetting Fronts in Water-Repellent Field Soils. J. Environ. Qual. 1993, 22, 109–118. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Pachepsky, Y.A.; Rawls, W.J. Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics. J. Hydrol. 2001, 251, 123–150. [Google Scholar] [CrossRef]
- Foundation, C.; Resources, B.; Studies, D.; Council, N. New Research Opportunities in the Earth Sciences; The National Academies Press: Washington, DC, USA, 2012; pp. 1–132. [Google Scholar]
- Heimovaara, T.J.; Freijer, J.I.; Bouten, W. The application of TDR in laboratory column experiments. Soil Technol. 1993, 6, 261–272. [Google Scholar] [CrossRef]
- Gerke, H.H.; Germann, P.; Nieber, J. Preferential and unstable flow; from the pore to the catchment scale. Vadose Zone J. 2010, 9, 207–212. [Google Scholar] [CrossRef]
- Köhne, J.M.; Mohanty, B.P. Water flow processes in a soil column with a cylindrical macropore: Experiment and hierarchical modeling. Water Resour. Res. 2005, 41, W03010. [Google Scholar] [CrossRef]
- Allaire, S.E.; Roulier, S.; Cessna, A.J. Quantifying preferential flow in soils: A review of different techniques. J. Hydrol. 2009, 378, 179–204. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids Through Porous Mediums. Ph.D. Thesis, Cornell University, New York, NY, USA, 1931. Available online: https://ui.adsabs.harvard.edu/abs/1931PhDT.........3R (accessed on 8 June 2023).
- Shao, L.; Wu, S.; Guo, X.; Wen, T. One−Dimensional Seepage of Unsaturated Soil Based on Soil−Water Characteristic Curve. Processes 2022, 10, 2564. [Google Scholar] [CrossRef]
- de Rooij, G.H. Modeling fingered flow of water in soils owing to wetting front instability: A review. J. Hydrol. 2000, 231–232, 277–294. [Google Scholar] [CrossRef]
- Nieber, J.L. Modeling finger development and persistence in initially dry porous media. Geoderma 1996, 70, 207–229. [Google Scholar] [CrossRef]
- Flury, M.; Leuenberger, J.; Studer, B.; Flühler, H. Transport of Anions and Herbicides in a Loamy and a Sandy Field Soil. Water Resour. Res. 1995, 31, 823–835. [Google Scholar] [CrossRef]
- Meakin, P. Fractal aggregates in geophysics. Rev. Geophys. 1991, 29, 317–354. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G. The Penetration of a Fluid into a Porous Medium or Hele-Shaw Cell Containing a More Viscous Liquid. Proc. R. Soc. Lond. Ser. A 1958, 245, 312–329. [Google Scholar] [CrossRef]
- Chuoke, R.; van Meurs, P.; van der Poel, C. The Instability of Slow, Immiscible, Viscous Liquid-Liquid Displacements in Permeable Media. Trans. AIME 1959, 216, 188–194. [Google Scholar] [CrossRef]
- Glass, R.J.; Parlange, J.-Y.; Steenhuis, T.S. Immiscible Displacement in Porous Media: Stability Analysis of Three-Dimensional, Axisymmetric Disturbances with Application to Gravity-Driven Wetting Front Instability. Water Resour. Res. 1991, 27, 1947–1956. [Google Scholar] [CrossRef]
- Philip, J.R. Stability Analysis of Infiltration. Soil Sci. Soc. Am. J. 1975, 39, 1042–1049. [Google Scholar] [CrossRef]
- White, I.; Colombera, P.M.; Philip, J.R. Experimental Study of Wetting Front Instability Induced by Sudden Change of Pressure Gradient. Soil Sci. Soc. Am. J. 1976, 40, 824–829. [Google Scholar] [CrossRef]
- Wang, Z.; Feyen, J.; Elrick, D.E. Prediction of fingering in porous media. Water Resour. Res. 1998, 34, 2183–2190. [Google Scholar] [CrossRef]
- Parlange, J.-Y.; Hill, D.E. Theorectical Analysis of Wetting Front Instability in Soils. Soil Sci. 1976, 122, 236–239. [Google Scholar] [CrossRef]
- Liu, Y.; Steenhuis, T.S.; Parlange, J.Y. Closed-form solution for finger width in sandy soils at different water contents. Water Resour. Res. 1994, 30, 949–952. [Google Scholar] [CrossRef]
- De Rooij, G.H.; Cho, H. Modelling solute leaching during fingered flow by integrating and expanding various theoretical and empirical concepts. Hydrol. Sci. J. 1999, 44, 447–465. [Google Scholar] [CrossRef]
- Glass, R.J.; Cann, S.; King, J.; Baily, N.; Parlange, J.; Steenhuis, T.S. Wetting front instability in unsaturated porous media: A three-dimensional study in initially dry sand. Transp. Porous Media 1990, 5, 247–268. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; van Genuchten, M.T.; Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Jarvis, N. The MACRO Model (Version 3.1): Technical Description and Sample Simulations; Swedish University of Agricultural Sciences, Department of Soil Sciences: Uppsala, Sweden, 1994. [Google Scholar]
- Durner, W.; Priesack, E.; Vogel, H.J.; Zurmühl, T. Determination of Parameters for Flexible Hydraulic Functions by Inverse Modeling. In Proceedings of the International Workshop on Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media, Riverside, CA, USA, 22–24 October 1997; University of California: Berkeley, CA, USA, 1999; pp. 817–829. [Google Scholar]
- Mohanty, B.P.; Bowman, R.S.; Hendrickx, J.M.H.; van Genuchten, M.T. New piecewise-continuous hydraulic functions for modeling preferential flow in an intermittent-flood-irrigated field. Water Resour. Res. 1997, 33, 2049–2063. [Google Scholar] [CrossRef]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]
- Othmer, H.; Diekkruger, B.; Kutilek, M. Bimodal Porosity and Unsaturated Hydraulic Conductivity. Soil Sci. 1991, 152, 139–150. [Google Scholar] [CrossRef]
- Gwo, J.P.; Jardine, P.M.; Wilson, G.V.; Yeh, G.T. A multiple-pore-region concept to modeling mass transfer in subsurface media. J. Hydrol. 1995, 164, 217–237. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Jaynes, D.B.; Logsdon, S.D.; Horton, R. Field Method for Measuring Mobile/Immobile Water Content and Solute Transfer Rate Coefficient. Soil Sci. Soc. Am. J. 1995, 59, 352–356. [Google Scholar] [CrossRef]
- Clothier, B.E.; Heng, L.; Magesan, G.N.; Vogeler, I. The measured mobile-water content of an unsaturated soil as a function of hydraulic regime. Soil Res. 1995, 33, 397–414. [Google Scholar] [CrossRef]
- Gerke, H.H. Preferential flow descriptions for structured soils. J. Plant Nutr. Soil Sci. 2006, 169, 382–400. [Google Scholar] [CrossRef]
- Hillel, D. Introduction to Environmental Soil Physics; Academic Press: Cambridge, MA, USA, 2004; Available online: https://search.worldcat.org/title/162572737 (accessed on 8 June 2023).
- Hendrickx, J.; Flury, M. Uniform and preferential flow mechanisms in the vadose zone. In Conceptual Models of Flow and Transport in the Fractured Vadose Zone; The National Academies Press: Washington, DC, USA, 2001; pp. 149–187. [Google Scholar]
- Heber Green, W.; Ampt, G.A. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Dekker, L.W.; Ritsema, C.J. Variation in water content and wetting patterns in Dutch water repellent peaty clay and clayey peat soils. Catena 1996, 28, 89–105. [Google Scholar] [CrossRef]
- Beven, K. On subsurface stormflow: Predictions with simple kinematic theory for saturated and unsaturated flows. Water Resour. Res. 1982, 18, 1627–1633. [Google Scholar] [CrossRef]
- Jarvis, N.; Jansson, P.; Dik, E.; Messing, I. Modelling water and solute transport in macroporous soil. I. Model description and sensitivity analysis. J. Soil Sci. 2006, 42, 59–70. [Google Scholar] [CrossRef]
- Molson, J.W.; Fala, O.; Aubertin, M.; Bussière, B. Numerical simulations of pyrite oxidation and acid mine drainage in unsaturated waste rock piles. J. Contam. Hydrol. 2005, 78, 343–371. [Google Scholar] [CrossRef]
- Valocchi, A.J. Use of temporal moment analysis to study reactive solute transport in aggregated porous media. Geoderma 1990, 46, 233–247. [Google Scholar] [CrossRef]
- Hornung, U.; Showalter, R.E. Diffusion models for fractured media. J. Math. Anal. Appl. 1990, 147, 69–80. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Dalton, F.N. Models for simulating salt movement in aggregated field soils. Geoderma 1986, 38, 165–183. [Google Scholar] [CrossRef]
- Bibby, R. Mass transport of solutes in dual-porosity media. Water Resour. Res. 1981, 17, 1075–1081. [Google Scholar] [CrossRef]
- Jarvis, N.J. A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality. Eur. J. Soil Sci. 2007, 58, 523–546. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and water flow in soils. Water Resour. Res. 1982, 18, 1311–1325. [Google Scholar] [CrossRef]
- Luxmoore, R.J. Micro-, Meso-, and Macroporosity of Soil. Soil Sci. Soc. Am. J. 1981, 45, 671–672. [Google Scholar] [CrossRef]
- Jarvis, N.J.; Leeds-Harrison, P.; Dosser, J.M. The use of tension infiltrometers to assess routes and rates of infiltration in a clay soil. J. Soil Sci. 1987, 38, 633–640. [Google Scholar] [CrossRef]
- Jardine, P.M.; Jacobs, G.K.; O’Dell, J.D. Unsaturated Transport Processes in Undisturbed Heterogeneous Porous Media: II. Co-Contaminants. Soil Sci. Soc. Am. J. 1993, 57, 954–962. [Google Scholar] [CrossRef]
- Wilson, G.V.; Yunsheng, L.; Essington, M.E.; Tyler, D.D.; Selim, H.M. Tillage and Cover Crop Effects on Saturated and Unsaturated Transport of Fluometuron. Soil Sci. Soc. Am. J. 1998, 62, 46–55. [Google Scholar] [CrossRef]
- Langner, H.W.; Gaber, H.M.; Wraith, J.M.; Huwe, B.; Inskeep, W.P. Preferential Flow through Intact Soil Cores Effects of Matric Head. Soil Sci. Soc. Am. J. 1999, 63, 1591–1598. [Google Scholar] [CrossRef]
- Shipitalo, M.; Butt, K. Occupancy and geometrical properties of Lumbricus terrestris L. burrows affecting infiltration. Pedobiologia 1999, 43, 782–794. [Google Scholar] [CrossRef]
- Zehe, E.; Flühler, H. Preferential transport of Isoproturon at a plot scale and a field scale tile-drained site. J. Hydrol. 2001, 247, 100–115. [Google Scholar] [CrossRef]
- Angers, D.; Caron, J. Plant-Induced Changes in Soil Structure: Processes and Feedbacks. Biogeochemistry 1998, 42, 55–72. [Google Scholar] [CrossRef]
- de Jonge, L.; Moldrup, P.; Rubaek, G.; Schelde, K.; Djurhuus, J. Particle Leaching and Particle-Facilitated Transport of Phosphorus at Field Scale. Vadose Zone J. 2004, 3, 462–470. [Google Scholar] [CrossRef]
- Kleinman, P.; Srinivasan, M.S.; Sharpley, A.; Gburek, W. Phosphorus leaching through intact soil columns before and after poultry manure application. Soil Sci. 2005, 170, 153–166. [Google Scholar] [CrossRef]
- Larsson, M.H.; Jarvis, N.J. A Dual-Porosity Model to Quantify Macropore Flow Effects on Nitrate Leaching. J. Environ. Qual. 1999, 28, 1298–1307. [Google Scholar] [CrossRef]
- Camobreco, V.; Richards, B.; Steenhuis, T.; Peverly, J.; Mcbride, M. Movement of Heavy Metals Through Undisturbed and Homogenized Soil Columns. Soil Sci. 1996, 161, 740–750. [Google Scholar] [CrossRef]
- Richards, B.K.; Steenhuis, T.S.; Peverly, J.H.; McBride, M.B. Metal mobility at an old, heavily loaded sludge application site. Environ. Pollut. 1998, 99, 365–377. [Google Scholar] [CrossRef]
- Haria, A.H.; Hodnett, M.G.; Johnson, A.C. Mechanisms of groundwater recharge and pesticide penetration to a chalk aquifer in southern England. J. Hydrol. 2003, 275, 122–137. [Google Scholar] [CrossRef]
- Roulier, S.; Baran, N.; Mouvet, C.; Stenemo, F.; Morvan, X.; Albrechtsen, H.; Clausen, L.; Jarvis, N. Controls on atrazine leaching through a soil-unsaturated fractured limestone sequence at Brévilles, France. J. Contam. Hydrol. 2006, 84, 81–105. [Google Scholar] [CrossRef]
- Gjettermann, B.; Nielsen, K.L.; Petersen, C.T.; Jensen, H.E.; Hansen, S. Preferential flow in sandy loam soils as affected by irrigation intensity. Soil Technol. 1997, 11, 139–152. [Google Scholar] [CrossRef]
- McLeod, M.; Schipper, L.A.; Taylor, M.D. Preferential flow in a well drained and a poorly drained soil under different overhead irrigation regimes. Soil Use Manag. 1998, 14, 96–100. [Google Scholar] [CrossRef]
- Williams, A.; Scholefield, D.; Dowd, J.; Holden, N.; Deeks, L. Investigating preferential flow in a large intact soil block under pasture. Soil Use Manag. 2000, 16, 264–269. [Google Scholar] [CrossRef]
- Gish, T.J.; Kung, K.-J.S.; Perry, D.C.; Posner, J.; Bubenzer, G.; Helling, C.S.; Kladivko, E.J.; Steenhuis, T.S. Impact of Preferential Flow at Varying Irrigation Rates by Quantifying Mass Fluxes. J. Environ. Qual. 2004, 33, 1033–1040. [Google Scholar] [CrossRef]
- Lewis, J.; Sjöstrom, J. Optimizing the experimental design of soil columns in saturated and unsaturated transport experiments. J. Contam. Hydrol. 2010, 115, 1–13. [Google Scholar] [CrossRef]
- Bromly, M.; Hinz, C.; Aylmore, L.A.G. Relation of dispersivity to properties of homogeneous saturated repacked soil columns. Eur. J. Soil Sci. 2007, 58, 293–301. [Google Scholar] [CrossRef]
- Ghodrati, M.; Chendorain, M.; Chang, Y.J. Characterization of Macropore Flow Mechanisms in Soil by Means of a Split Macropore Column. Soil Sci. Soc. Am. J. 1999, 63, 1093–1101. [Google Scholar] [CrossRef]
- Bégin, L.; Fortin, J.; Caron, J. Evaluation of the Fluoride Retardation Factor in Unsaturated and Undisturbed Soil Columns. Soil Sci. Soc. Am. J. 2003, 67, 1635–1646. [Google Scholar] [CrossRef]
- Hrapovic, L.; Sleep, B.; Major, D.; Hood, E. Laboratory Study of Treatment of Trichloroethene by Chemical Oxidation Followed by Bioremediation. Environ. Sci. Technol. 2005, 39, 2888–2897. [Google Scholar] [CrossRef]
- Communar, G.; Keren, R.; Li, F. Deriving Boron Adsorption Isotherms from Soil Column Displacement Experiments. Soil Sci. Soc. Am. J. 2004, 68, 481–488. [Google Scholar] [CrossRef]
- Sentenac, P.; Lynch, R.J.; Bolton, M. Measurement of a side-wall boundary effect in soil columns using fibre-optics sensing. Int. J. Phys. Model. Geotech. 2001, 1, 35–41. [Google Scholar] [CrossRef]
- Powelson, D.; Mills, A. Transport of Escherichia coli in sand columns with constant and changing water contents. J. Environ. Qual. 2001, 30, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Simon, R.; Colón, D.; Tebes-Stevens, C.; Weber, E.J. Effect of Redox Zonation on the Reductive Transformation of p-Cyanonitrobenzene in a Laboratory Sediment Column. Environ. Sci. Technol. 2000, 34, 3617–3622. [Google Scholar] [CrossRef]
- Corwin, D.L. Evaluation of a simple lysimeter-design modification to minimize sidewall flow. J. Contam. Hydrol. 2000, 42, 35–49. [Google Scholar] [CrossRef]
- Kanzari, S.; Šimůnek, J.; Daghari, I.; Younes, A.; Ali, K.B.; Mariem, S.B.; Ghannem, S. Modeling Irrigation of Tomatoes with Saline Water in Semi-Arid Conditions Using Hydrus-1D. Land 2024, 13, 739. [Google Scholar] [CrossRef]
- Ross, P.J.; Smettem, K.R.J. A Simple Treatment of Physical Nonequilibrium Water Flow in Soils. Soil Sci. Soc. Am. J. 2000, 64, 1926–1930. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, H.; Huang, X.; Liu, S. Modeling variably saturated flows in porous media using the numerical manifold method. Eng. Anal. Bound. Elem. 2024, 169, 106016. [Google Scholar] [CrossRef]
- Aharmouch, A.; Amaziane, B. Efficient mass conservative numerical model for solving variably saturated groundwater flow. J. Hydrol. 2021, 603, 126976. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Wierenga, P.J. Mass Transfer Studies in Sorbing Porous Media I. Analytical Solutions. Soil Sci. Soc. Am. J. 1976, 40, 473–480. [Google Scholar] [CrossRef]
- Vogel, T.; Gerke, H.H.; Zhang, R.; Van Genuchten, M.T. Modeling flow and transport in a two-dimensional dual-permeability system with spatially variable hydraulic properties. J. Hydrol. 2000, 238, 78–89. [Google Scholar] [CrossRef]
- Vogel, H.J.; Gerke, H.H.; Mietrach, R.; Zahl, R.; Wöhling, T. Soil hydraulic conductivity in the state of nonequilibrium. Vadose Zone J. 2023, 22, e20238. [Google Scholar] [CrossRef]
- Steenhuis, T.S.; Parlance, J.-Y.; Andreini, M.S. A numerical model for preferential solute movement in structured soils. Geoderma 1990, 46, 193–208. [Google Scholar] [CrossRef]
- Hutson, J.L.; Wagenet, R.J. A Multiregion Model Describing Water Flow and Solute Transport in Heterogeneous Soils. Soil Sci. Soc. Am. J. 1995, 59, 743–751. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Vandervaere, J.; Roulier, S.; Thony, J.; Gaudet, J.; Vauclin, M. Field measurement of soil surface hydraulic properties by disc and ring infiltrometers: A review and recent developments. Soil Tillage Res. 2000, 55, 1–29. [Google Scholar] [CrossRef]
- Voegelin, A.; Barmettler, K.; Kretzschmar, R. Heavy metal release from contaminated soils: Comparison of column leaching and batch extraction results. J. Environ. Qual. 2003, 32, 865–875. [Google Scholar] [CrossRef]
- Mali, N.; Urbanc, J.; Leis, A. Tracing of water movement through the unsaturated zone of a coarse gravel aquifer by means of dye and deuterated water. Environ. Geol. 2007, 51, 1401–1412. [Google Scholar] [CrossRef]
- Pütz, T.; Fank, J.; Flury, M. Lysimeters in Vadose Zone Research. Vadose Zone J. 2018, 17, 180035. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Govindaraju, R. In-Situ Measurements of Soil Saturated Hydraulic Conductivity: Assessment of Reliability Through Rainfall-Runoff Experiments: In-Situ Measurements of Soil Saturated Hydraulic Conductivity. Hydrol. Process. 2017, 31, 3084–3094. [Google Scholar] [CrossRef]
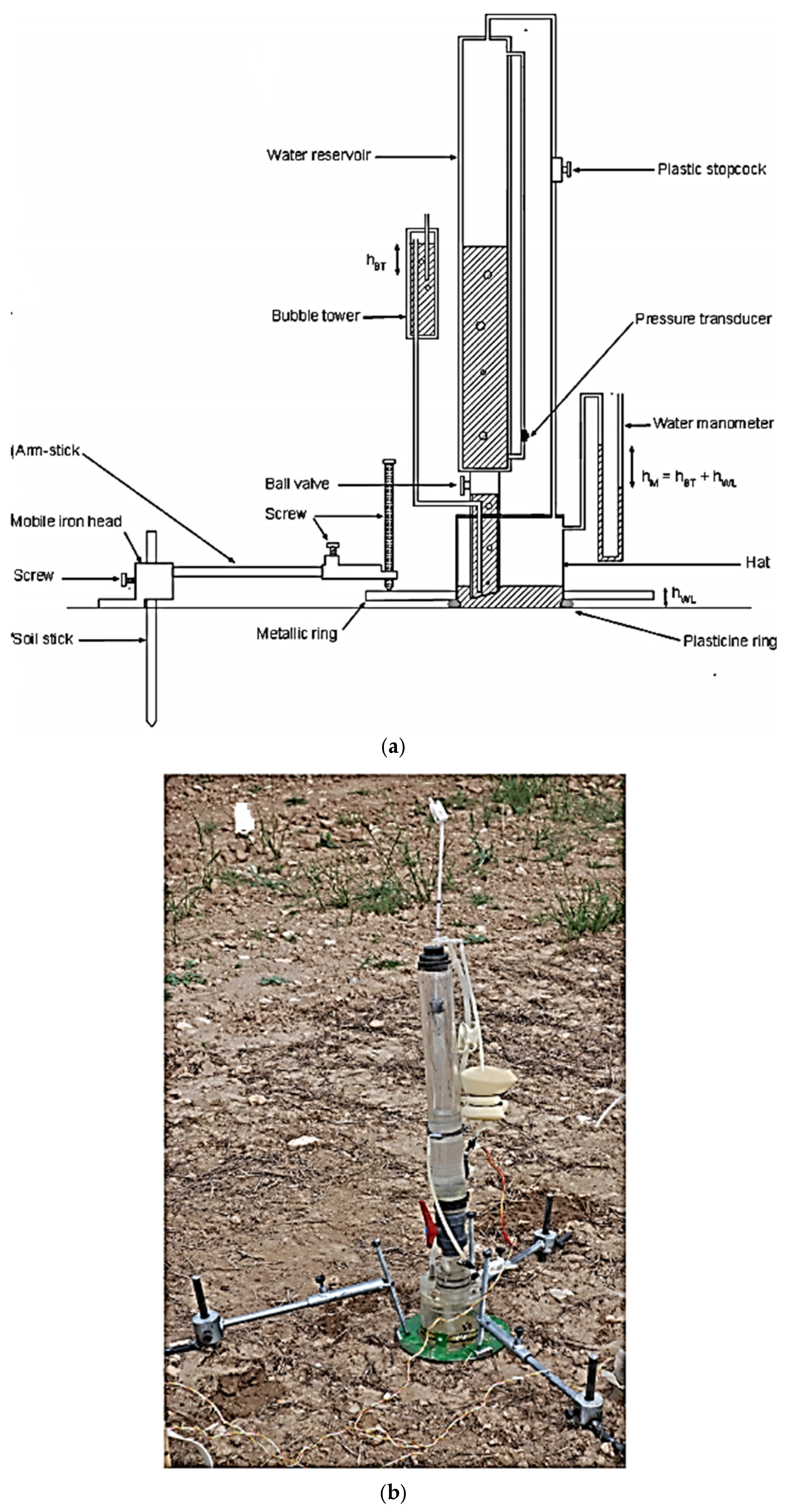
- Moret-Fernández, D.; González-Cebollada, C.; Latorre, B.; Pérez, V. A modified hood infiltrometer to estimate the soil hydraulic properties from the transient water flow measurements. J. Hydrol. 2015, 530, 554–560. [Google Scholar] [CrossRef]
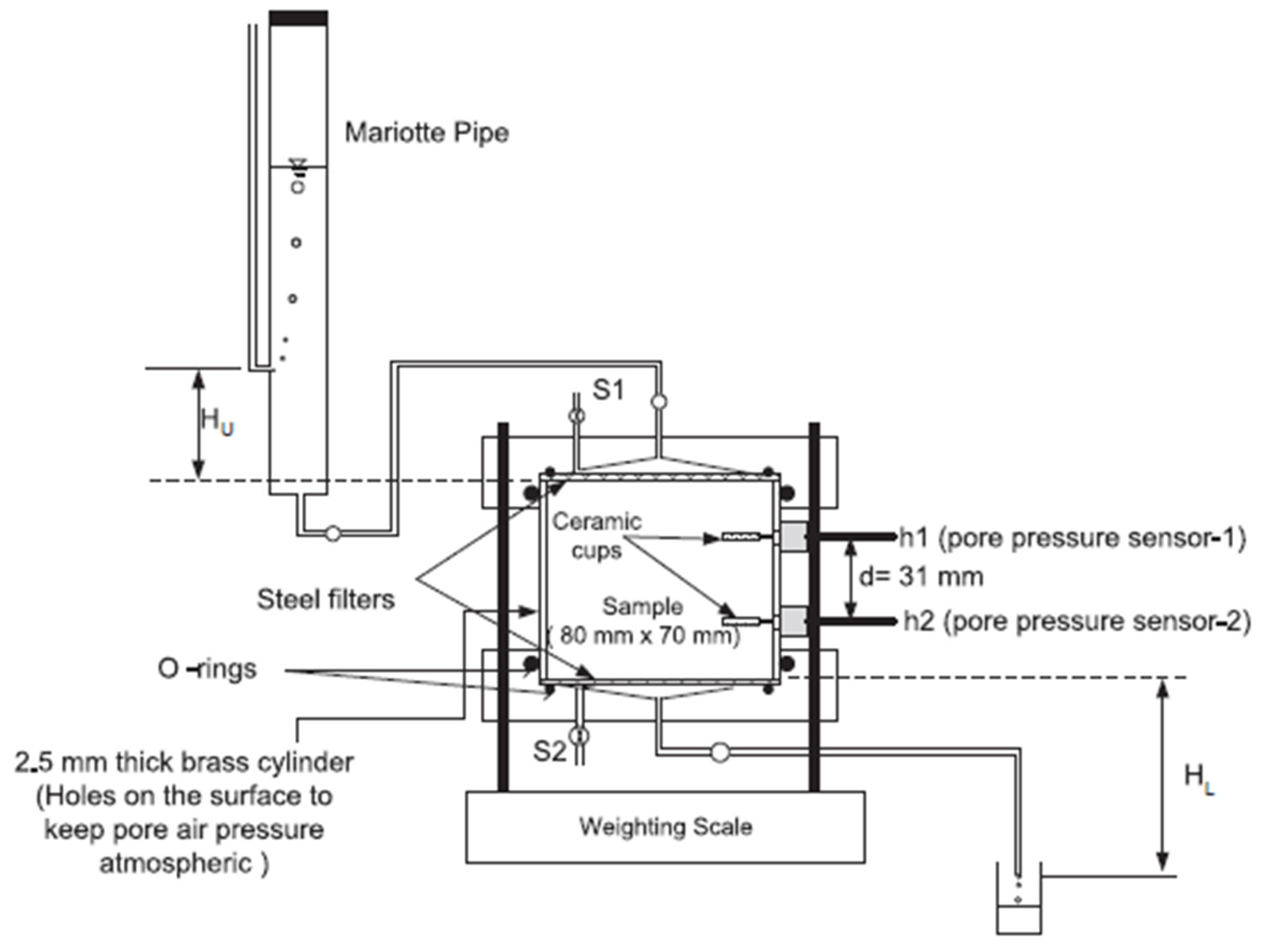
- Gallage, C.; Kodikara, J.; Uchimura, T. Laboratory measurement of hydraulic conductivity functions of two unsaturated sandy soils during drying and wetting processes. Soils Found. 2013, 53, 417–430. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Colorado State University Hydrology and Water, Resources Program. In Hydraulic Properties of Porous Media; Colorado State University Hydrology and Water Resources Program: Fort Collins, CO, USA, 1964. [Google Scholar]
- Bienvenue, T.; Xie, J.; Niu, Q. Developing a soil column system to measure hydrogeophysical properties of unconsolidated sediment. Vadose Zone J. 2022, 21, e20186. [Google Scholar] [CrossRef]
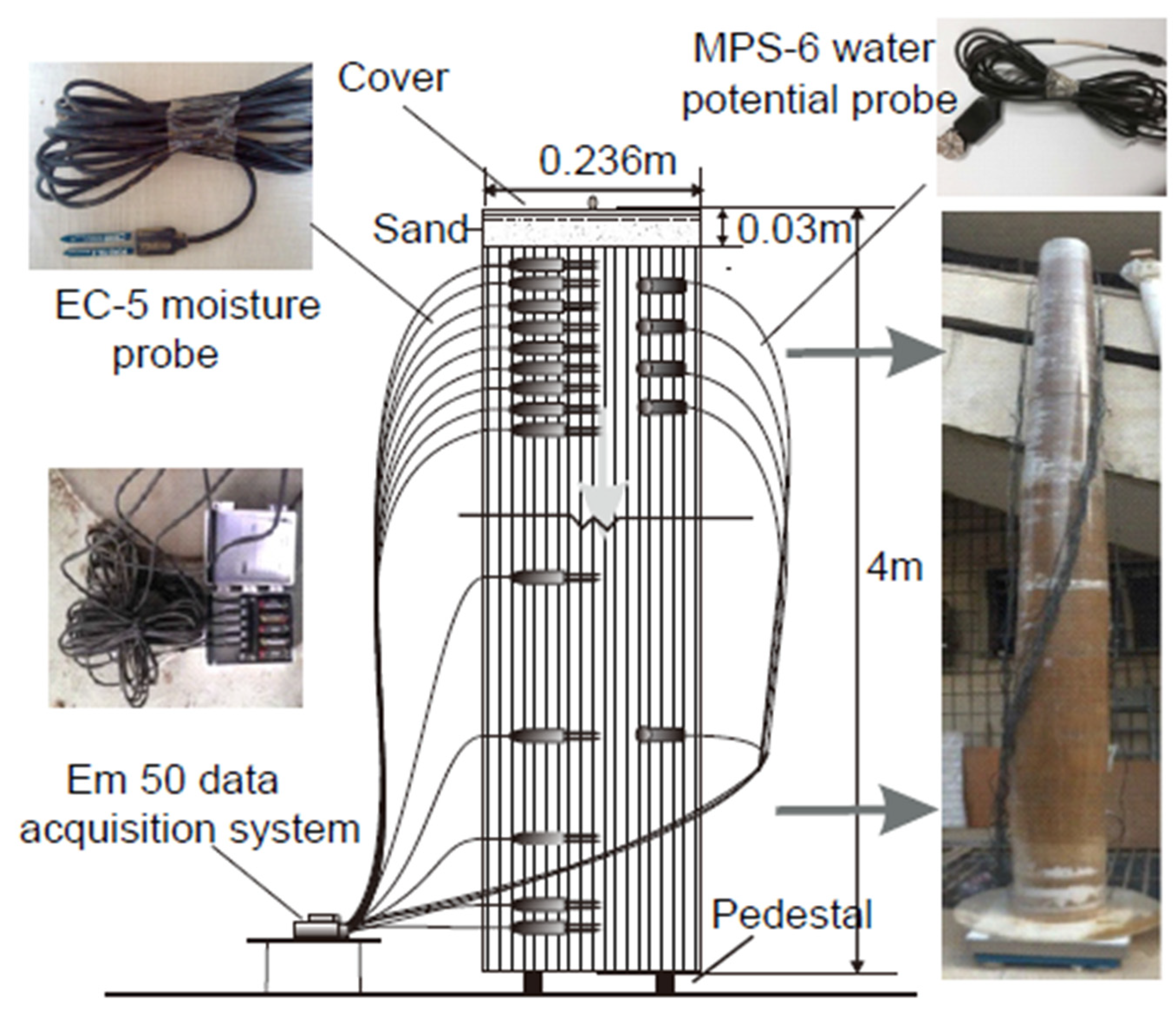
- Hou, X.; Vanapalli, S.; Li, T. Water flow in unsaturated soils subjected to multiple infiltration events. Can. Geotech. J. 2019, 57, 366–376. [Google Scholar] [CrossRef]
- Liu, Q.; Yasufuku, N.; Omine, K.; Hazarika, H. Automatic soil water retention test system with volume change measurement for sandy and silty soils. Soils Found. 2012, 52, 368–380. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R.; Regalado, C.M.; Vanclooster, M.; Lambot, S. Analysis of alternative measurement strategies for the inverse optimization of the hydraulic properties of a volcanic soil. J. Hydrol. 2004, 295, 124–139. [Google Scholar] [CrossRef]
- Aljoumani, B.; Sanchez-Espigares, J.; Wessolek, G. Estimating Pore Water Electrical Conductivity of Sandy Soil from Time Domain Reflectometry Records Using a Time-Varying Dynamic Linear Model. Sensors 2018, 18, 4403. [Google Scholar] [CrossRef] [PubMed]
- Osame, P.U.; Asim, T. Hydrodynamic Characterisation of the Inland Valley Soils of the Niger Delta Area for Sustainable Agricultural Water Management. Sensors 2025, 25, 4349. [Google Scholar] [CrossRef]
- Koorevaar, P.; Dirksen, C.; Menelik, G. Elements of Soil Physics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Dwevedi, A.; Kumar, P.; Kumar, P.; Kumar, Y.; Sharma, Y.K.; Kayastha, A.M. 15-Soil sensors: Detailed insight into research updates, significance, and future prospects. In New Pesticides and Soil Sensors; Grumezescu, A.M., Ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 561–594. [Google Scholar]
- Faqir, Y.; Qayoom, A.; Erasmus, E.; Schutte-Smith, M.; Visser, H.G. A review on the application of advanced soil and plant sensors in the agriculture sector. Comput. Electron. Agric. 2024, 226, 109385. [Google Scholar] [CrossRef]
- Uddin, M.J.; Sherrell, J.; Emami, A.; Khaleghian, M. Application of Artificial Intelligence and Sensor Fusion for Soil Organic Matter Prediction. Sensors 2024, 24, 2357. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, G.; Sun, X. Advanced technologies of soil moisture monitoring in precision agriculture: A Review. J. Agric. Food Res. 2024, 18, 101473. [Google Scholar] [CrossRef]





| No. | References | Expression for Rf [L] |
|---|---|---|
| 1 | [42,43,44] | |
| 2 | [45,46] | |
| 3 | [43,44,47] | |
| 4 | [44,48] | |
| 5 | [49] | |
| 6 | [44,50] | |
| 7 | [44,47,48] | |
| 8 | [51] |
| Psi | θ | SoilTemp | ECp |
|---|---|---|---|
| kPa | % | deg C | mS·m−1 |
| −436.5 | 2.3 | 19.8 | #-INF |
| −436.6 | 2.3 | 19.8 | #-INF |
| −439.9 | 2.3 | 19.8 | #-INF |
| −435.3 | 2.5 | 19.8 | #-INF |
| −423.1 | 2.2 | 19.8 | 0 |
| S/N | References | Year | Research Activity | Parameters | Sensors | Findings | Location |
|---|---|---|---|---|---|---|---|
| 1 | [38] | 2000 | Review of finger flow models | Finger radius, Rf | - | Eight expressions categorised into three groups | - |
| 2 | [52] | 2003 | Review of modelling preferential and non-equilibrium flow | - | - | Explanation of preferential flow in the structured media and prompting of development of Hydrus-1D and Hydrius-2D | - |
| 3 | [62] | 2006 | Review of model approaches to preferential flow | - | - | Flow through soil is uniform or nonuniform | - |
| 4 | [74] | 2007 | Review of non-equilibrium flow. | - | - | Mechanism of macropore water flow and solute transport is uncertain and the geometry is guessed | - |
| 5 | [95] | 2010 | Review of methods of conducting soil column experiments | - | - | Monolith and packed soil columns affect method of soil column construction | - |
| 6 | [96] | 2007 | Review of experimental methods | - | - | Packing of the soil column for lab exp. promotes homogeneity and reduces preferential flow | - |
| 7 | [63] | 2004 | Model description | C, K, D, h, θ, t, τ | - | Single-porosity, double-porosity models | - |
| 8 | [109] | 1976 | Model description | K, t, θ, θf, θm, Sf, Sm, , | - | Dual-porosity formulation for water flow | - |
| 9 | [111] | 2023 | Model description | K, t, θ, θf, θm, Sf, Sm, , | - | Dual permeability | - |
| 10 | [58] | 1995 | Model development | θ, S, D, | - | MURF and MURT models | - |
| 11 | [121] | 1980 | Model equation | θ, S, D, | - | SWCC, diffusivity, sorptivity | - |
| 12 | [8] | 1994 | Model equation | θ, S, D, | - | SWCC, diffusivity, sorptivity | - |
| 13 | [122] | 1964 | Model equation | θ, S, D, | - | SWCC, diffusivity, sorptivity | - |
| 14 | [129] | 1991 | Hydraulic properties description | θ, S, D, | - | SWCC, diffusivity, sorptivity | - |
| 15 | [118] | 2017 | Field Experiment | θs, θi, q, , Ks | DRI, GUELPH-CHP, CSIRO-TP | Devices’ estimates were not accurate | Perugia in Italy |
| 16 | [119] | 2015 | Field experiment | Ks, S | MHI | Accurate calculation of soil hydraulic properties | Zaragoza in Spain |
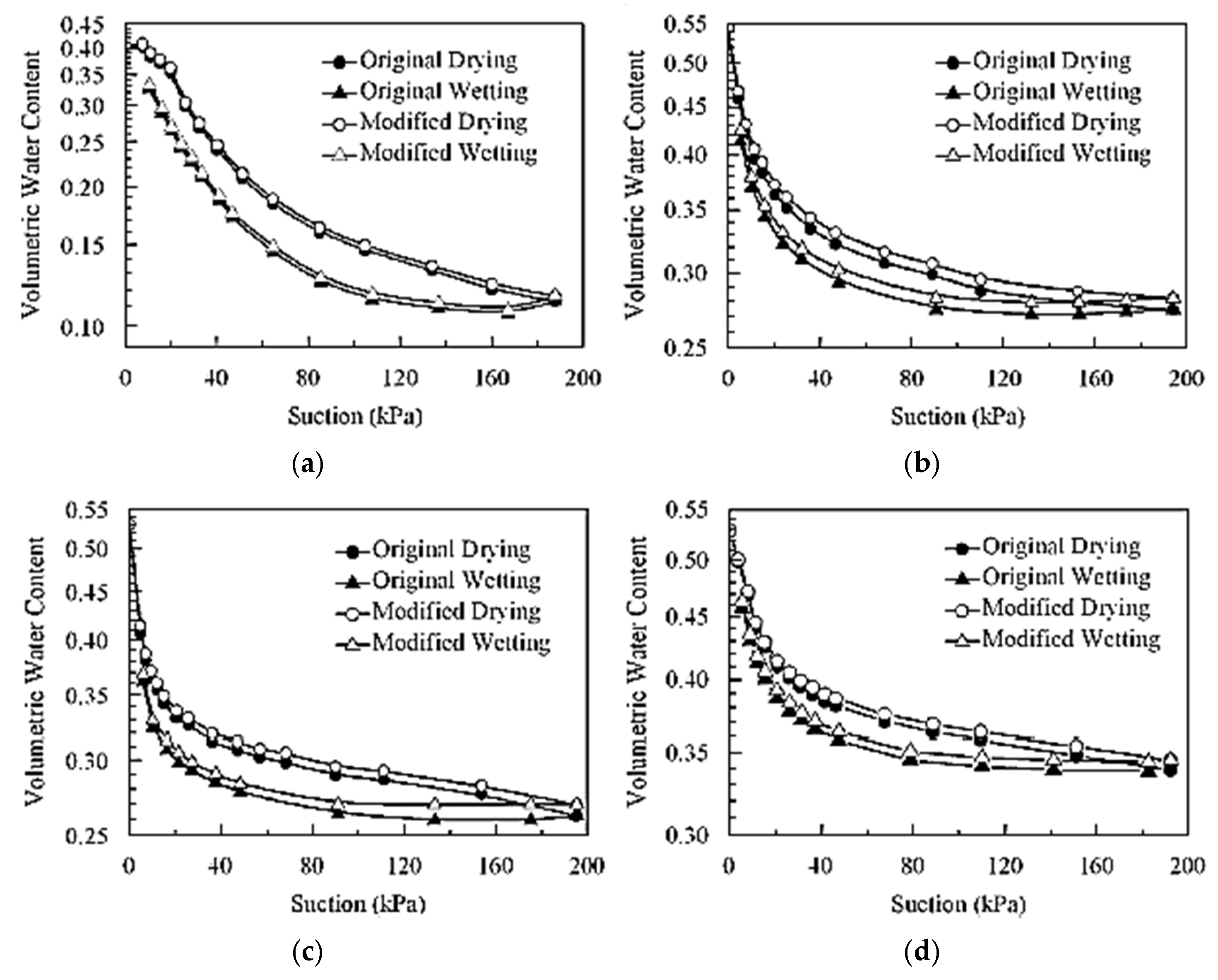
| 17 | [120] | 2013 | Laboratory experiment | Ks | Permeameter, Tensiometers | Fredlund forecast was more accurate | Specimen from Japan |
| 18 | [123] | 2022 | Laboratory experiment | Ks, σ*s, Cs | Hydrogeophysical probe | Direct measurement of hydraulic properties | Specimen from Mores Creek in USA |
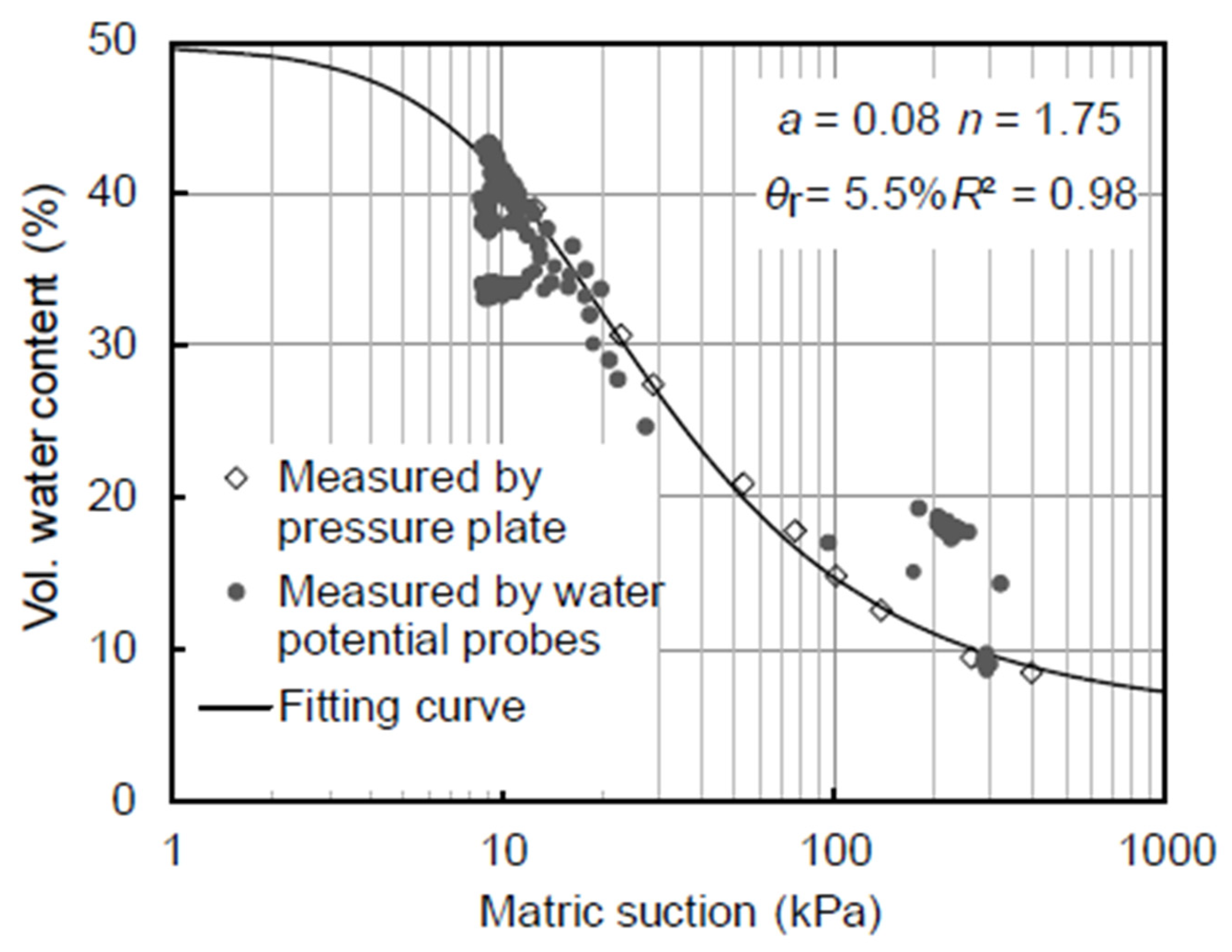
| 19 | [124] | 2019 | Laboratory experiment | θ, | Moisture probes, water potential probes | Wetting SWCC displayed. | Specimen from Gangsu Province in China. |
| 20 | [125] | 2012 | Laboratory experiment | θ, | Oedometer-type device, control software, water pressure transducer | As slope of soil water retention curve decreases, effect of volume change increases | Specimen from K-8, Sasaguri, Fukuchi, Takeda in Japan |
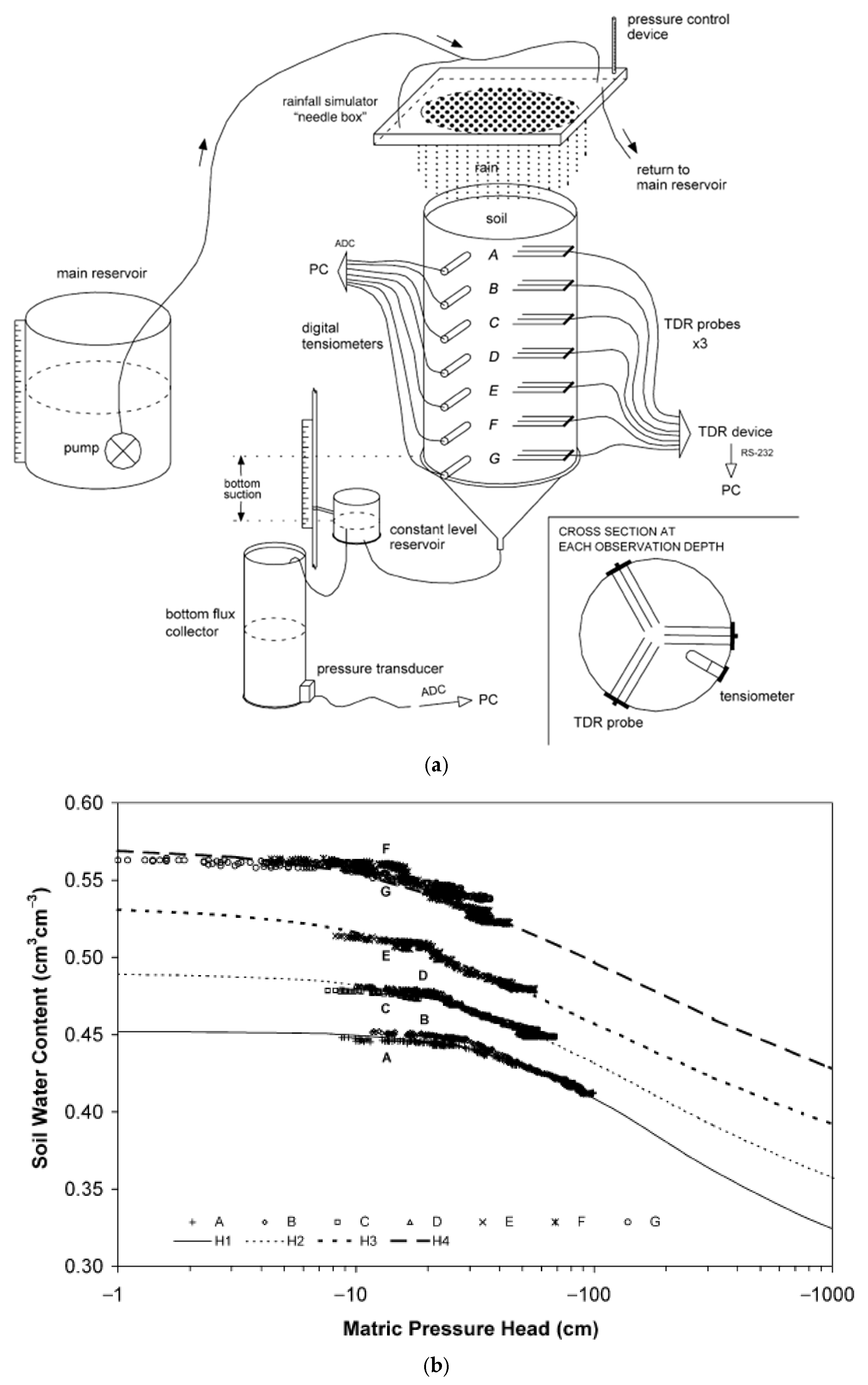
| 21 | [126] | 2004 | Laboratory experiment | θ, , q | Tensiometers, TDR probes | Water retention data from the first experiment were useful for selecting parameters for inverse modelling in the second experiment | Specimen from Tenerife in Spain |
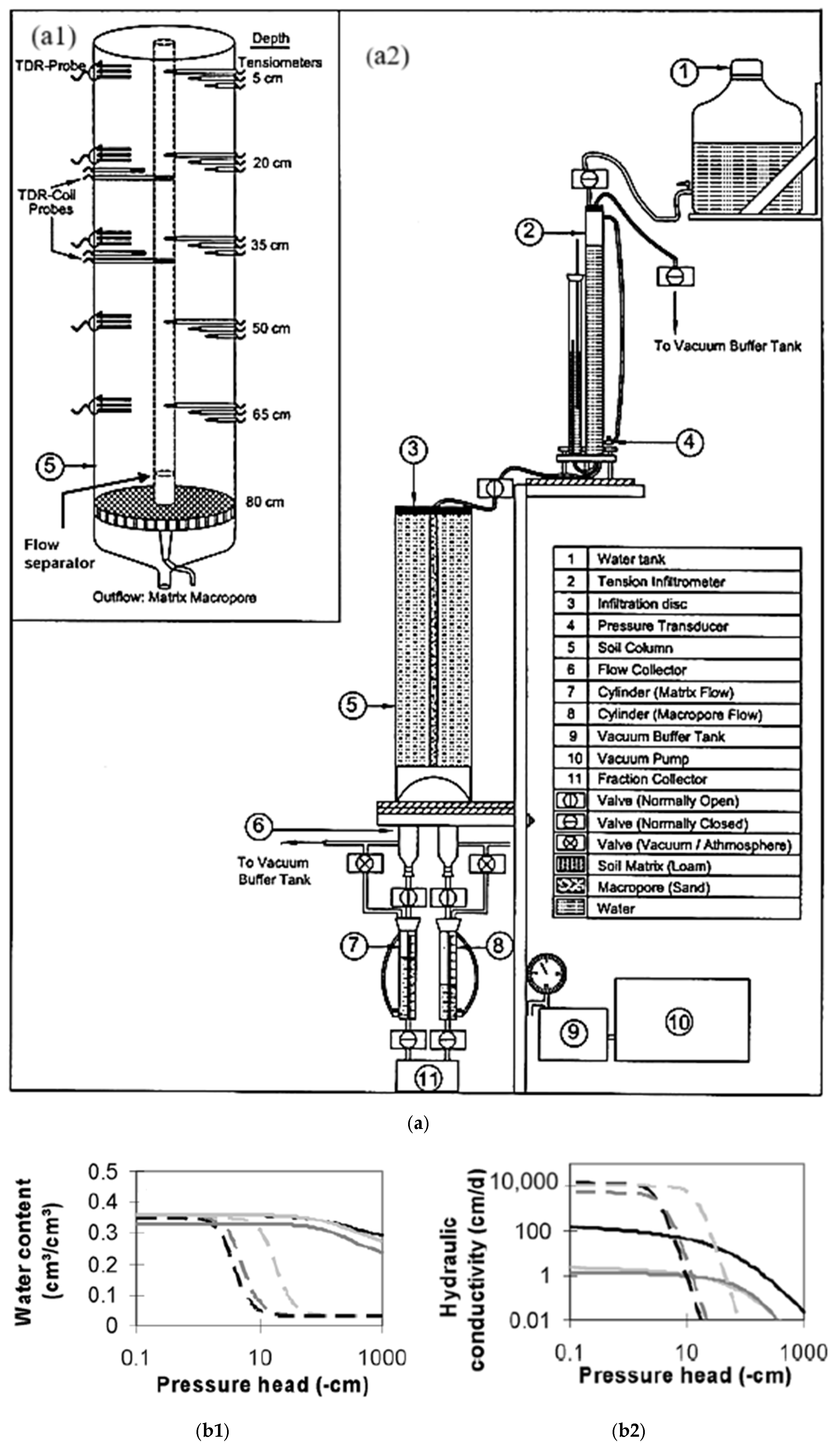
| 22 | [34] | 2005 | Laboratory experiment | θ, | Tensiometers, TDR probes | Hydraulic characteristics of macropore and matrix differ significantly | Specimen from College station in Texas. |
| 23 | [127] | 2018 | Laboratory experiment | σp, , | TDR probes, temperature probes | High positive autocorrelations between the residuals using the Hilhorst model. | Berlin, Germany |
| 24 | [128] | 2025 | Laboratory Experiment | θ, ψ, ECp | WET 150, EQ3 Equitensiomenter | Direct measurement of soil water content, soil matric potential, soil electrical conductivity | Specimen from Niger Delta area of Nigeria and Aberdeen in the UK. |
| Experimental Method | Measurable Parameter | Accuracy | Cost | Applicable Soil Type |
|---|---|---|---|---|
| Single-ring infiltrometer (SRI) | Ks | Limited. | USD 100–150 | Sandy and loamy soils |
| Double-ring infiltrometer (DRI) | θs, θi, q, , Ks | Limited by several factors. | USD 280–350 (lab) USD 1000–3000 (field) | Sandy, silty, loamy soils |
| Soil core method (SCM) | , θ, C, EC | Affected by discrepancies. | Variable, depends on project scope | Loam, silt, clay, not coarse soils |
| Rainfall simulator (RS) | θ, , | Generally accurate to 80%. | USD 120–150 educational models | Sand, loam, silt, clay |
| Tension permeameter (TP) | , q | Depends on soil properties. | USD 3000–10,000 | All soil types |
| Constant-head permeameter (CHP) | θs, Q, , Ks | Affected by soil type and permeability | USD 250–4000 | Sand and gravels |
| GUELPH-CHP | θs, Q, , Ks, S | Variable, though reliable for field estimate. | USD 5500–8600 full kit | Sand and gravels |
| CSIRO-TP | Ks, S | Variable accuracy | USD 800–3000 | From coarse-textured sand to fine-textured clay loams |
| Tensiometer | 1% for wider range | USD 50–150 (simple soil tensiometers) | Sandy soils and other light-textured soils | |
| TDR probes | T, θ, | 2–3% | USD 1900 (complete soil moisture unit) | All soil types |
| Temperature probes | T | 0.1–1.5% | USD 30–300 (for industrial applications) | All soil types |
| WET 150 | θ | 3% | USD 800 | Mineral soils, organic soils, peat |
| EQ3 equitensiometers | 10% | USD 900 | All non-saline soil types |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osame, P.U.; Peretomode, E.; Hawez, H.K. Advances in Flow of Water Through Variably Saturated Soils: A Review of Model Approaches and Experimental Investigations with Use of Sensors. Sensors 2025, 25, 7027. https://doi.org/10.3390/s25227027
Osame PU, Peretomode E, Hawez HK. Advances in Flow of Water Through Variably Saturated Soils: A Review of Model Approaches and Experimental Investigations with Use of Sensors. Sensors. 2025; 25(22):7027. https://doi.org/10.3390/s25227027
Chicago/Turabian StyleOsame, Peter Uloho, Ebikapaye Peretomode, and Haval Kukha Hawez. 2025. "Advances in Flow of Water Through Variably Saturated Soils: A Review of Model Approaches and Experimental Investigations with Use of Sensors" Sensors 25, no. 22: 7027. https://doi.org/10.3390/s25227027
APA StyleOsame, P. U., Peretomode, E., & Hawez, H. K. (2025). Advances in Flow of Water Through Variably Saturated Soils: A Review of Model Approaches and Experimental Investigations with Use of Sensors. Sensors, 25(22), 7027. https://doi.org/10.3390/s25227027








