High-Update-Rate (25 kHz) Laser Ranging with Random Noise Modulation for Fast and Precise Absolute Distance Measurement
Abstract
1. Introduction
2. Theoretical Analysis
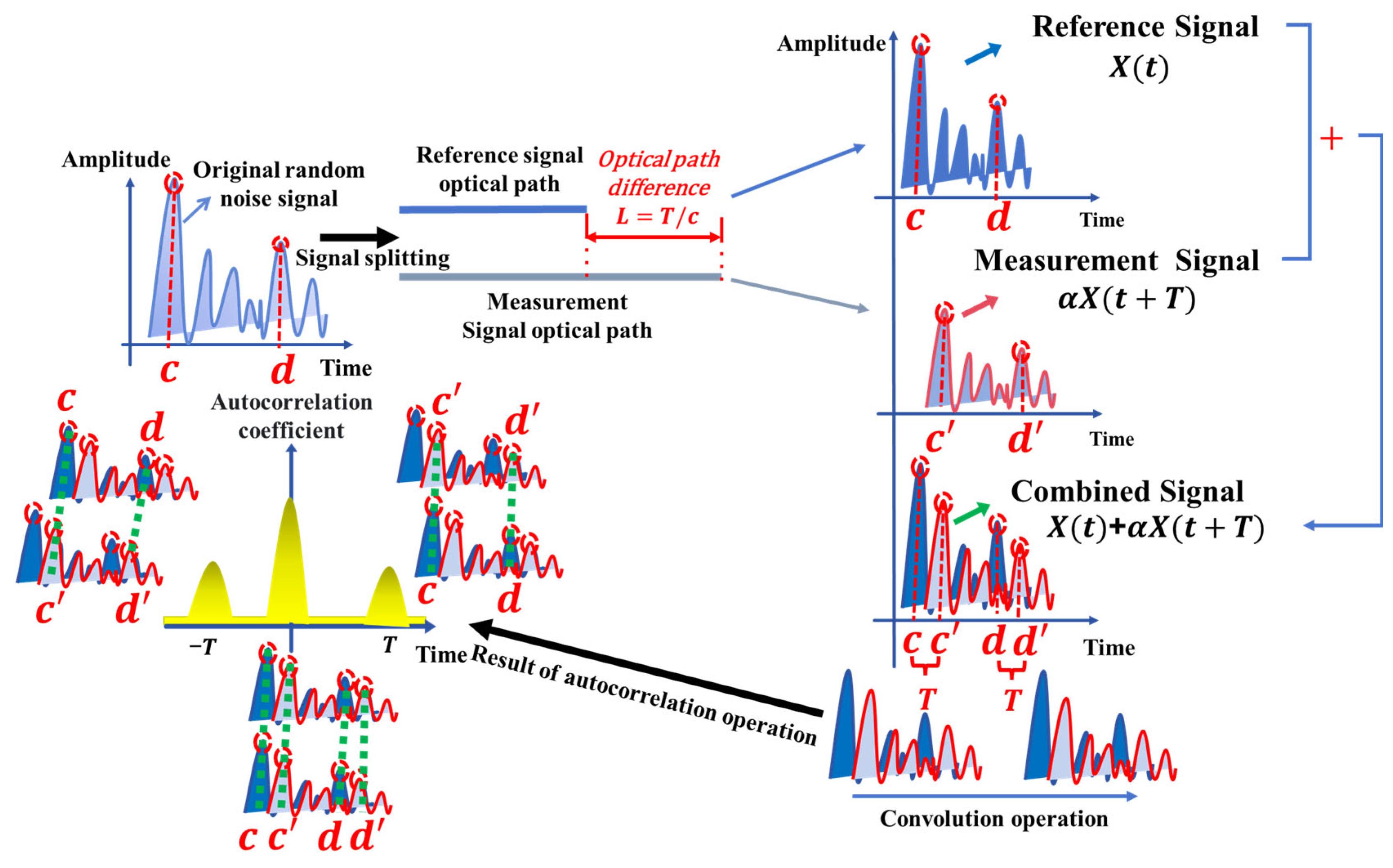
2.1. Ranging Principle of Ultra-Fast Random Noise
2.1.1. Mathematical Modeling of Signals
2.1.2. Signal-to-Noise Ratio Analysis
2.2. Simulation Analysis
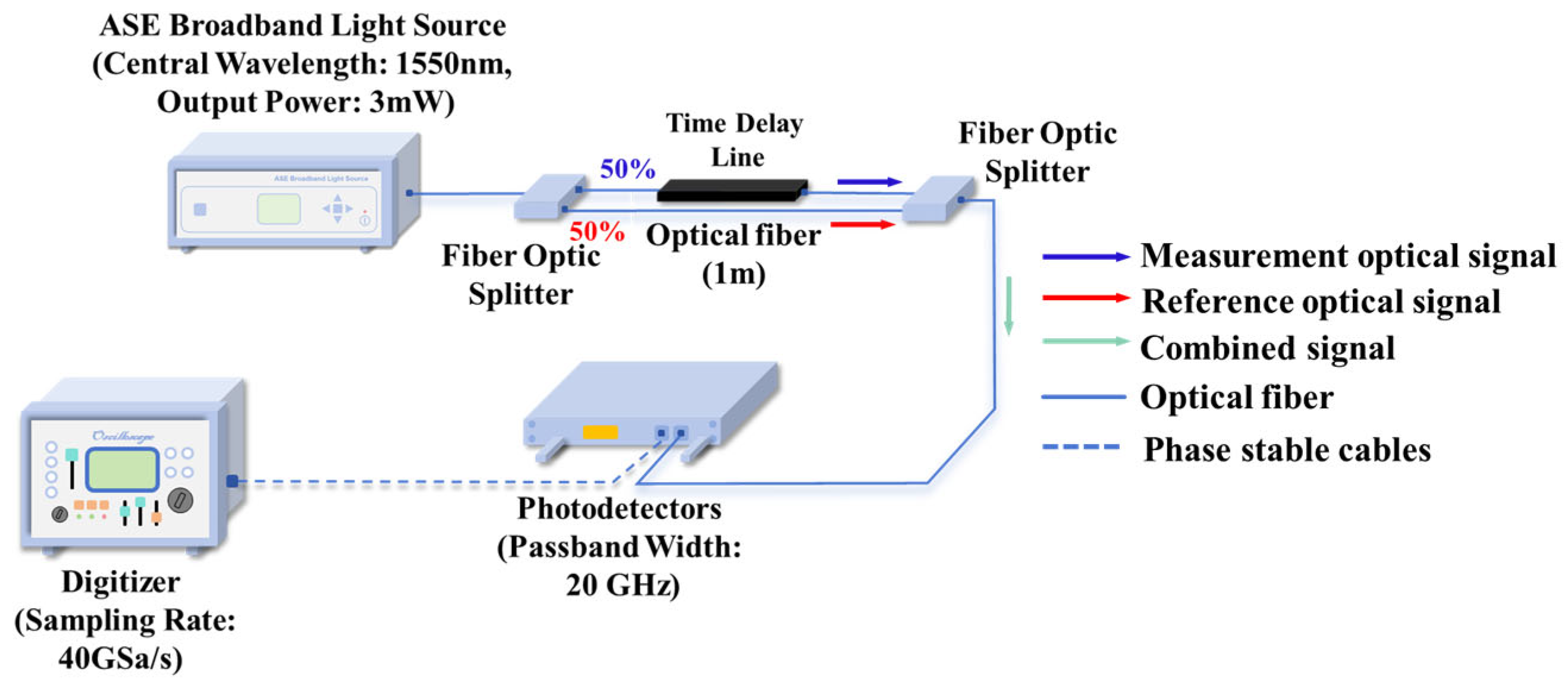
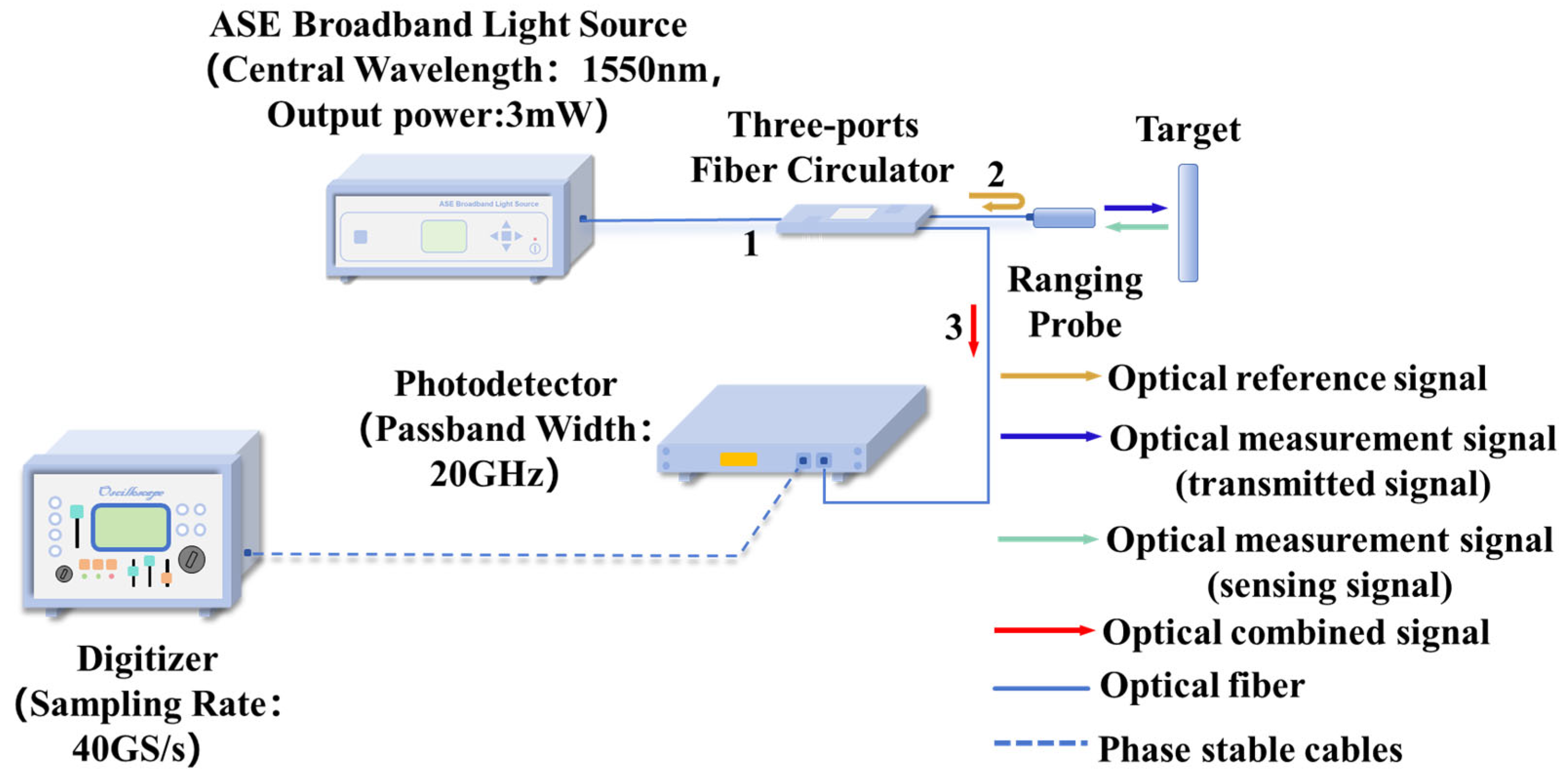
3. Experimental Setup
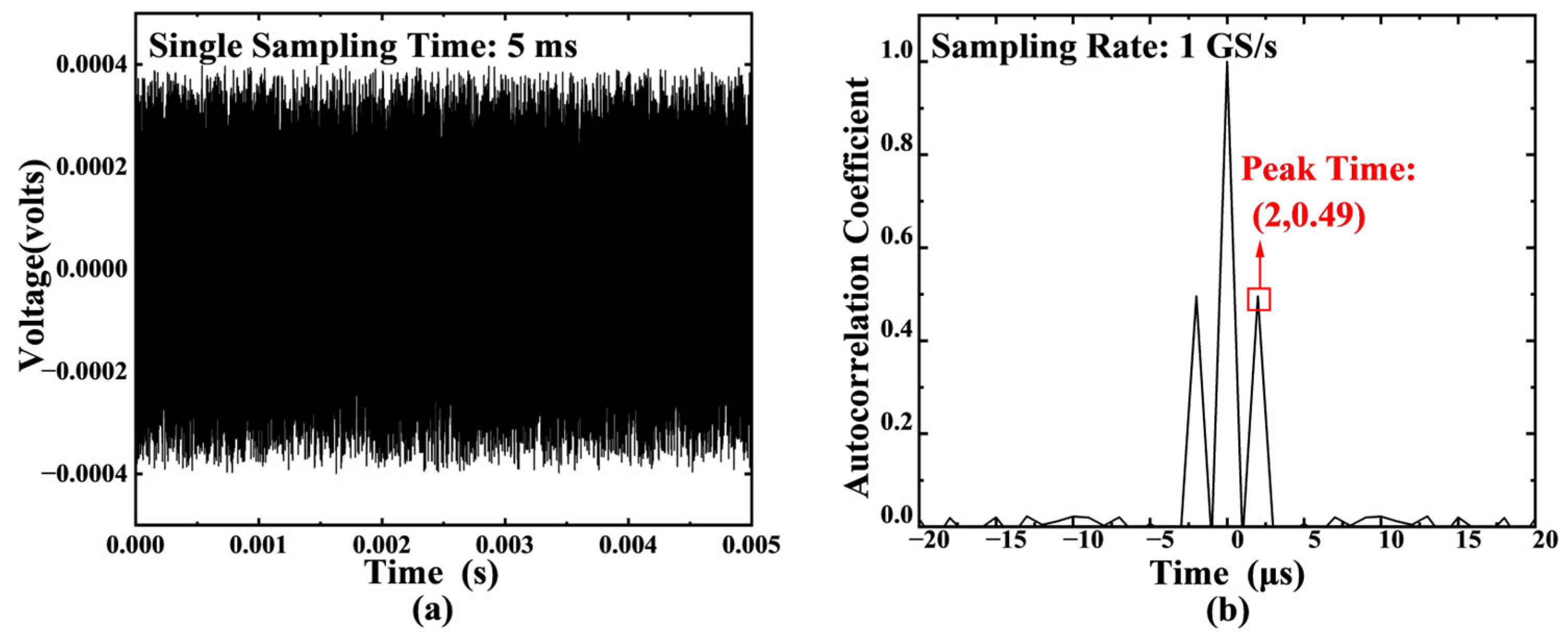
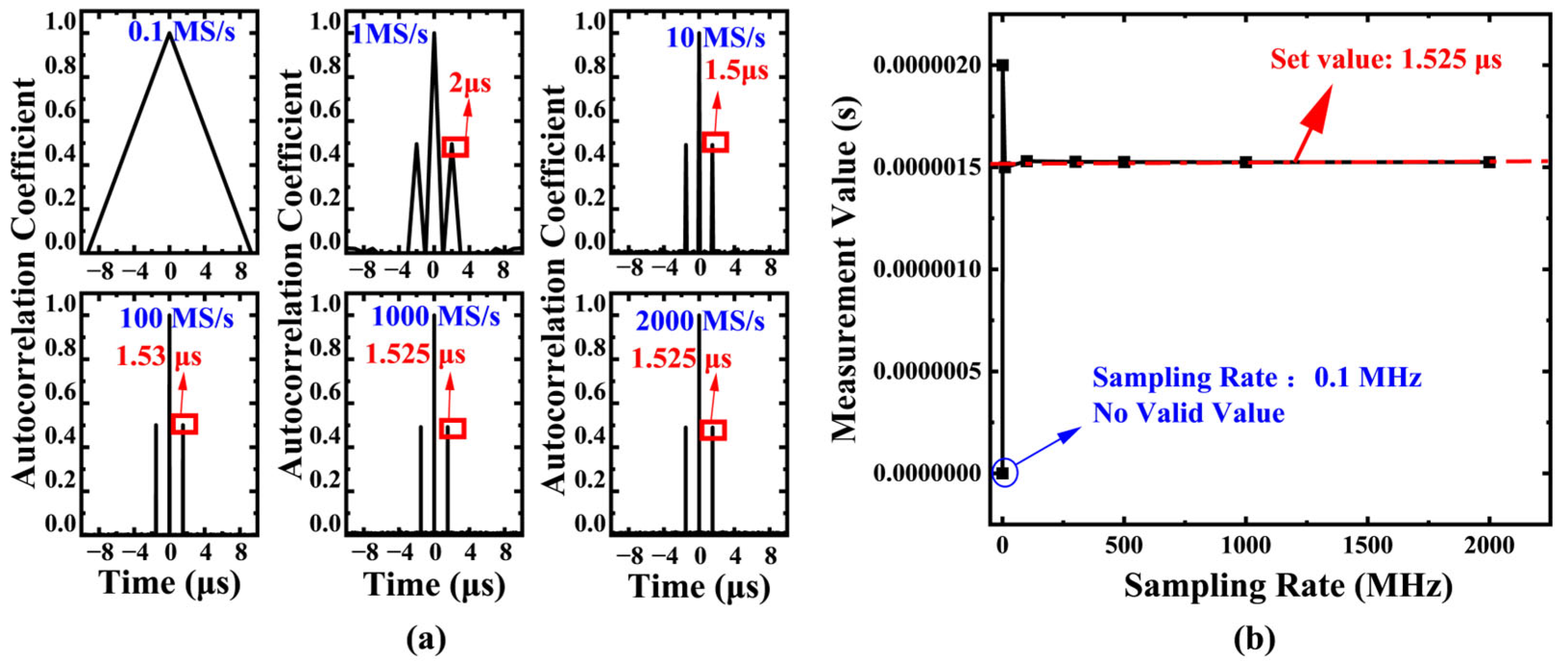
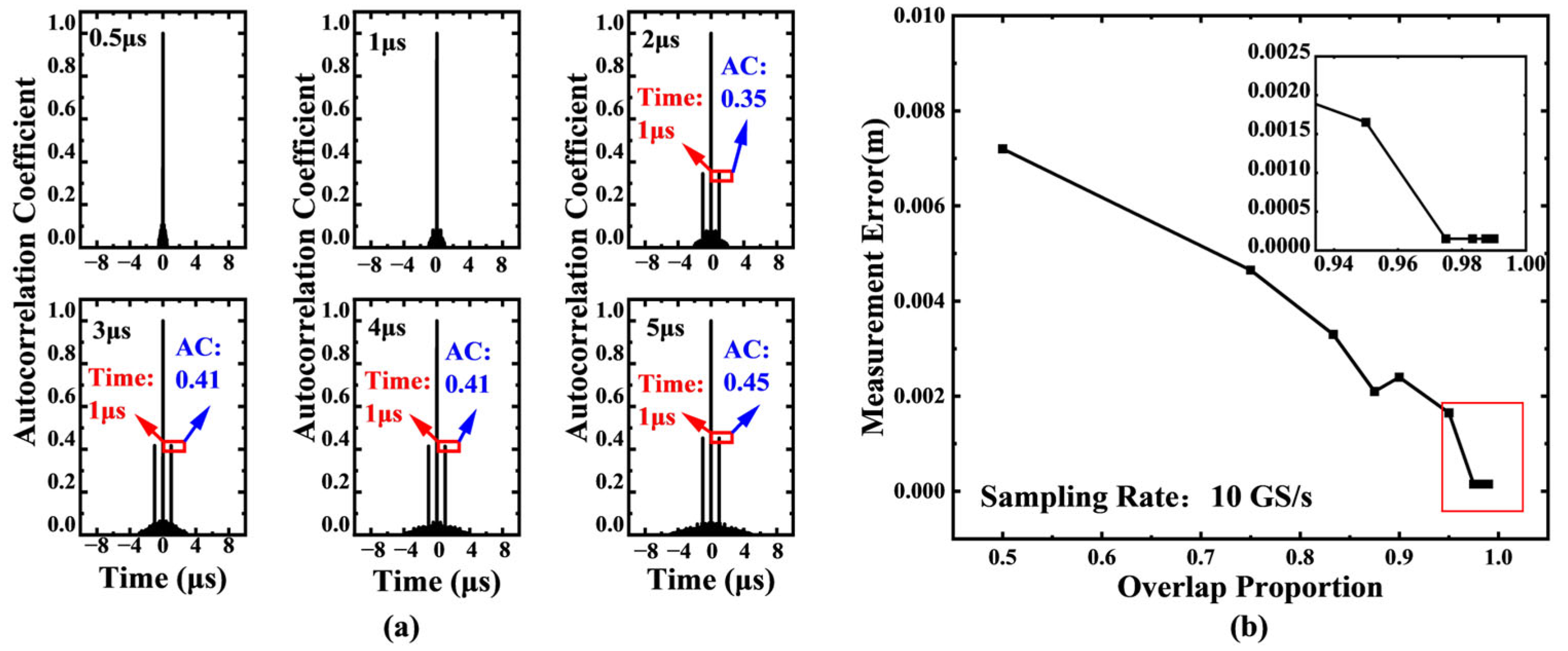
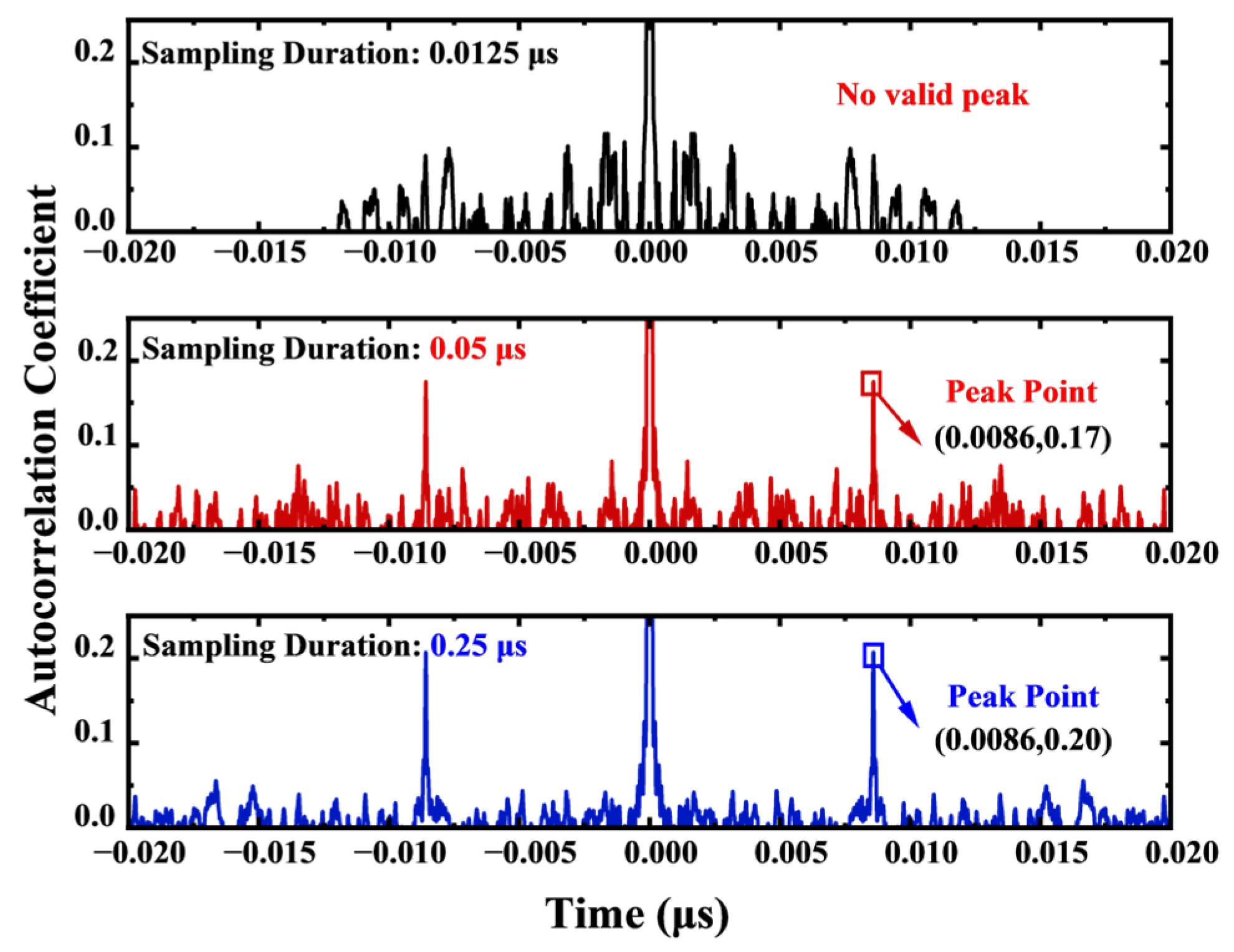
3.1. Time Delay Line Simulation Verification Experiment
3.2. Optical Probe Experiment
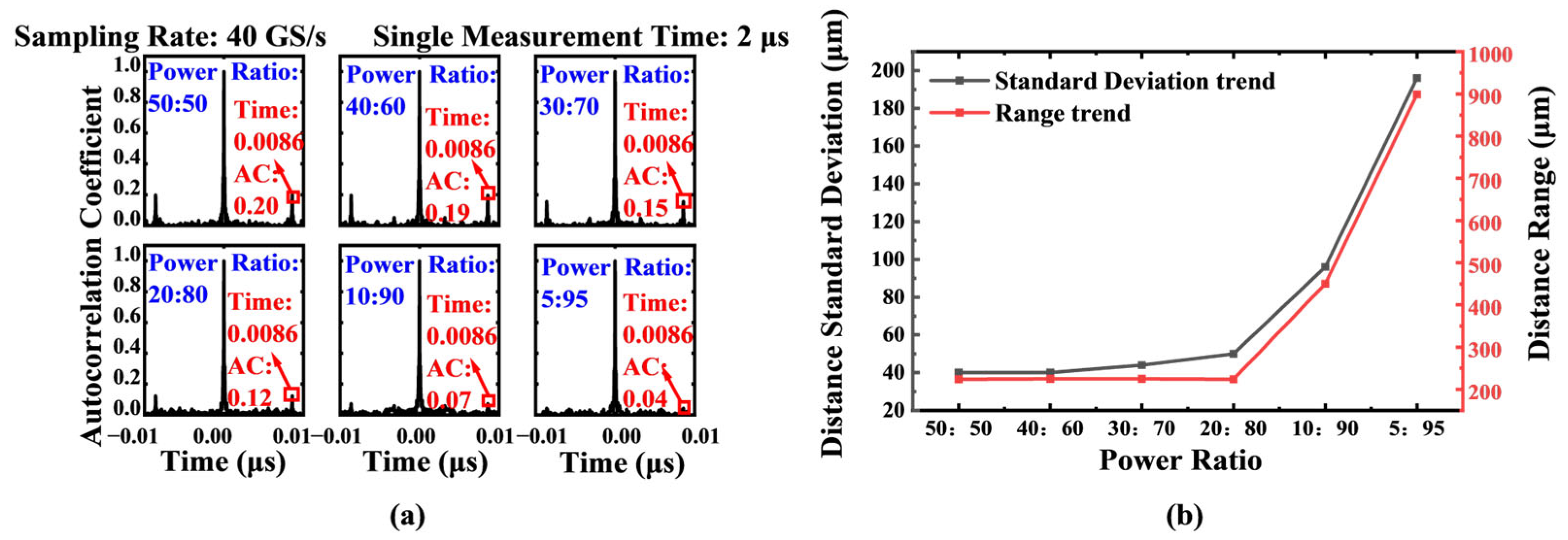
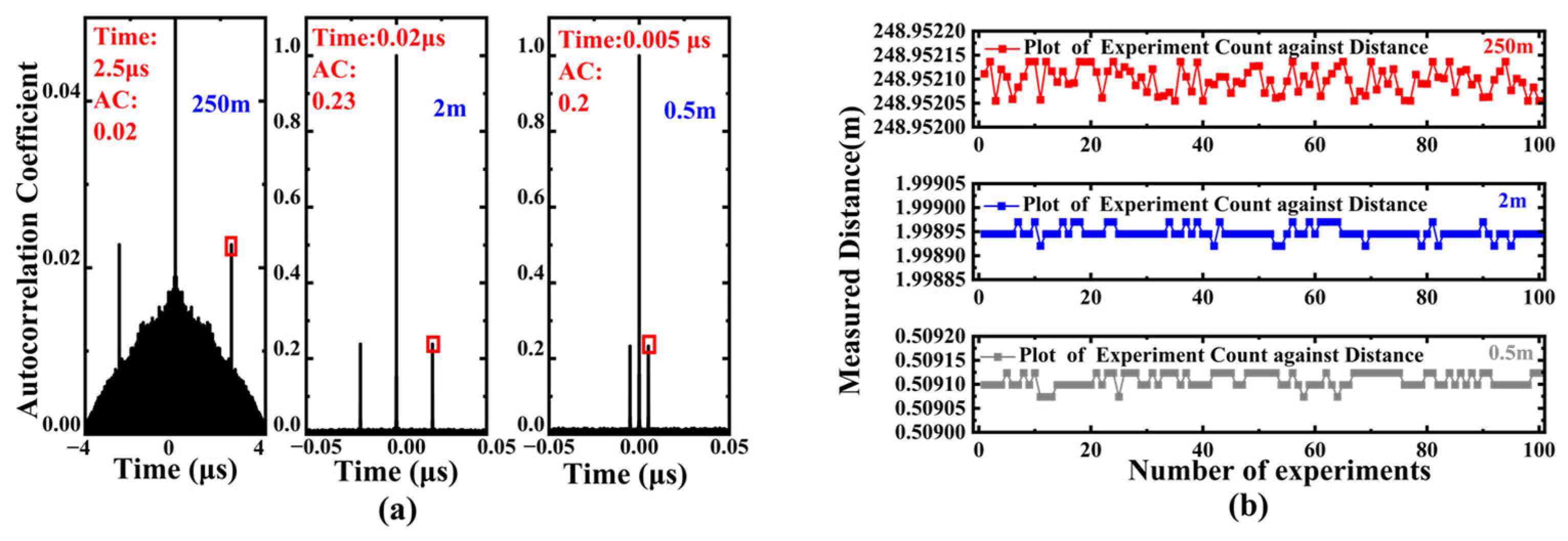
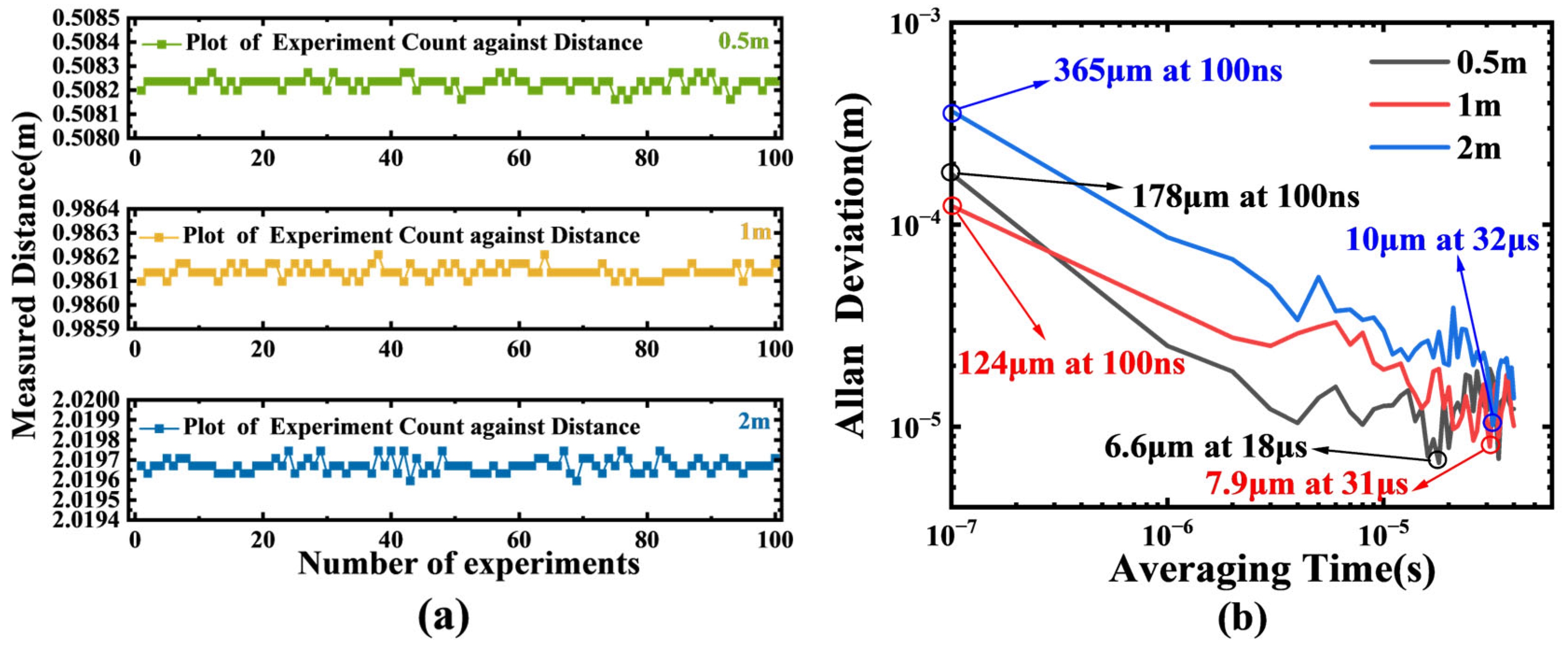
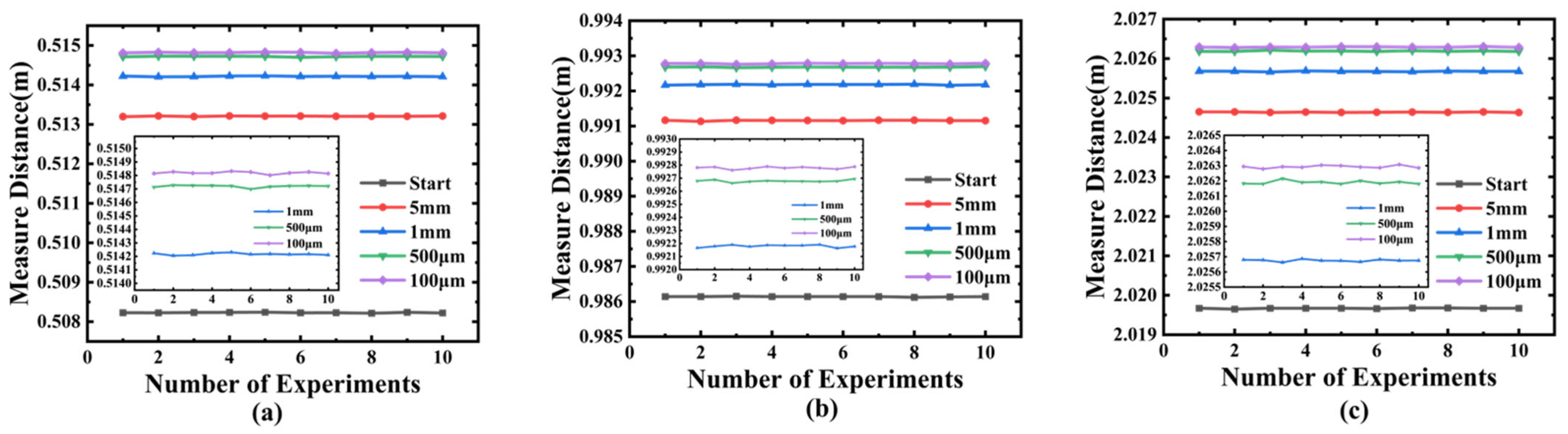
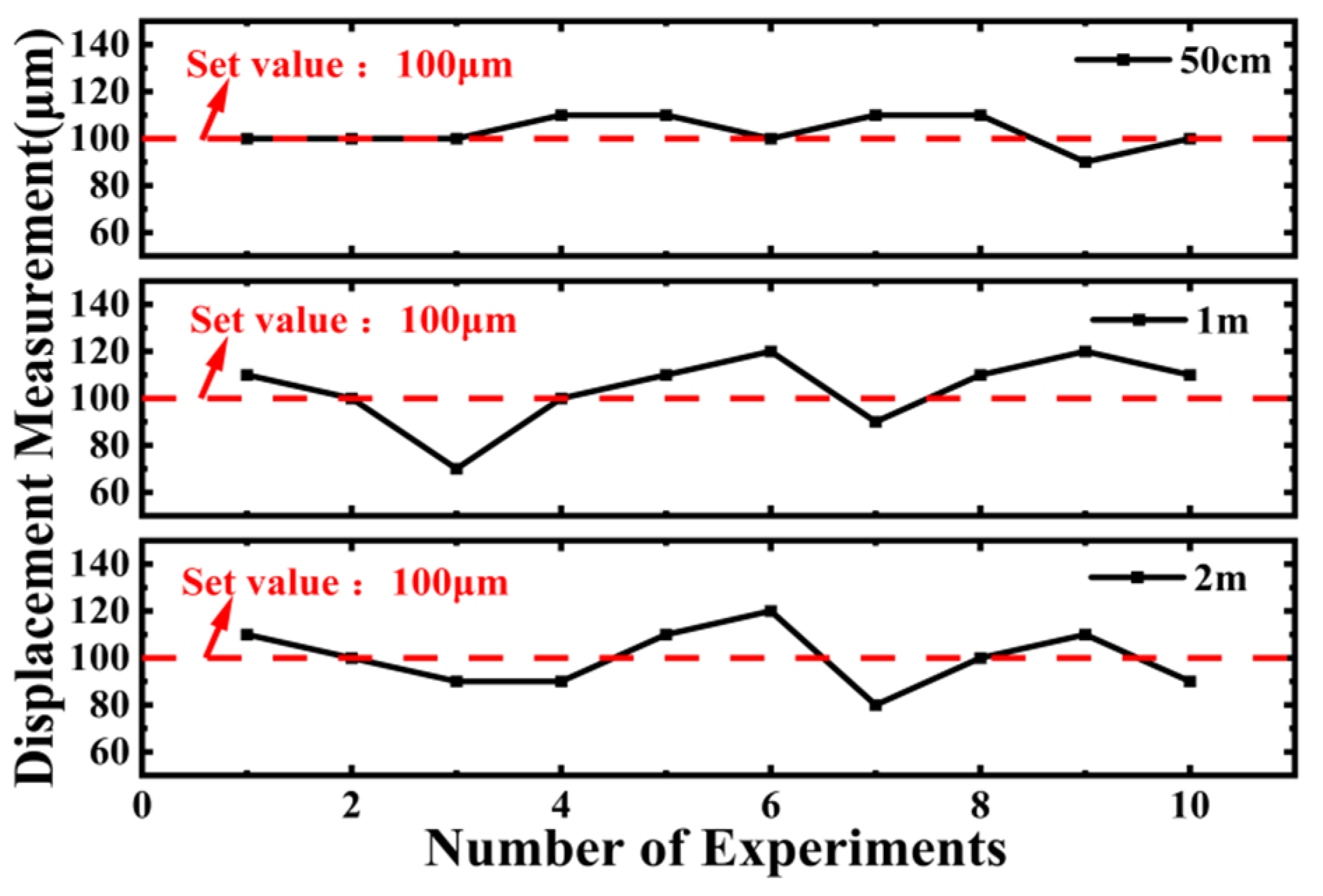
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berkovic, G.; Shafir, E. Optical methods for distance and displacement measurements. Adv. Opt. Photonics 2012, 4, 441–471. [Google Scholar] [CrossRef]
- Peng, Z.; Li, C. Portable microwave radar systems for short-range localization and life tracking: A review. Sensors 2019, 19, 1136. [Google Scholar] [CrossRef] [PubMed]
- Kim, I.; Martins, R.J.; Jang, J.; Badloe, T.; Khadir, S.; Jung, H.-Y.; Kim, H.; Kim, J.; Genevet, P.; Rho, J. Nanophotonics for light detection and ranging technology. Nat. Nanotechnol. 2021, 16, 508–524. [Google Scholar] [CrossRef]
- Lv, S.; Kemao, Q. Modeling the measurement precision of fringe projection profilometry. Light Sci. Appl. 2023, 12, 257. [Google Scholar] [CrossRef]
- Cheng, M.; Jiang, W.; Guo, L.; Li, J.; Forbes, A. Metrology with a twist: Probing and sensing with vortex light. Light Sci. Appl. 2025, 14, 4. [Google Scholar] [CrossRef]
- Zuo, C.; Qian, J.; Feng, S.; Yin, W.; Li, Y.; Fan, P.; Han, J.; Qian, K.; Chen, Q. Deep learning in optical metrology: A review. Light Sci. Appl. 2022, 11, 39. [Google Scholar] [CrossRef]
- Tang, J.; Emmanouilidis, C.; Salonitis, K. Reconfigurable manufacturing systems characteristics in digital twin context. IFAC-Pap. 2020, 53, 10585–10590. [Google Scholar] [CrossRef]
- Jardim-Goncalves, R.; Romero, D.; Grilo, A. Factories of the future: Challenges and leading innovations in intelligent manufacturing. Int. J. Comput. Integr. Manuf. 2017, 30, 4–14. [Google Scholar]
- Yan, L.; Xie, J.; Chen, B.; Lou, Y.; Zhang, S. Absolute distance measurement using laser interferometric wavelength leverage with a dynamic-sideband-locked synthetic wavelength generation. Opt. Express 2021, 29, 8344–8357. [Google Scholar] [CrossRef]
- Li, C.; Zhang, F.; Qu, X. High-resolution frequency-modulated continuous-wave LiDAR using multiple laser sources simultaneously scanning. J. Light. Technol. 2022, 41, 367–373. [Google Scholar] [CrossRef]
- Zehao, Y.; Cheng, L.; Guodong, L. FMCW LiDAR with an FM nonlinear kernel function for dynamic-distance measurement. Opt. Express 2022, 30, 19582–19596. [Google Scholar] [CrossRef]
- Weng, J.; Tao, T.; Liu, S.; Ma, H.; Wang, X.; Liu, C.; Tan, H. Optical-fiber frequency domain interferometer with nanometer resolution and centimeter measuring range. Rev. Sci. Instrum. 2013, 84, 113101. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Liu, S.; Tao, T.; Chen, L.; Tang, L.; Li, C.; Wu, J.; Jia, X.; Wang, X.; Weng, J. A high-performance ranging method with a long distance range and high accuracy. Optik 2022, 253, 168526. [Google Scholar] [CrossRef]
- Shi, G.; Wang, W.; Zhang, F. Precision improvement of frequency-modulated continuous-wave laser ranging system with two auxiliary interferometers. Opt. Commun. 2018, 411, 152–157. [Google Scholar] [CrossRef]
- Mohammadzadeh, S.; Keil, A.; Kocybik, M.; Schwenson, L.M.; Liebermeister, L.; Kohlhaas, R.; Globisch, B.; Von Freymann, G.; Seewig, J.; Friederich, F. Extreme Ultra-Wideband Optoelectronic Frequency-Modulated Continuous-Wave Terahertz Radar. Laser Photonics Rev. 2023, 17, 2300396. [Google Scholar] [CrossRef]
- Medhat, M.; Sobee, M.; Hussein, H.; Terra, O. Distance measurement using frequency scanning interferometry with mode-hoped laser. Opt. Laser Technol. 2016, 80, 209–213. [Google Scholar] [CrossRef]
- Zhou, Q.; Wu, T.; Long, X.; Zeng, Z.; Zhu, J. Frequency Scanning Interferometry Multi-Channel Synchronous Ranging Based on Rapid Suppression of Doppler Error. J. Light. Technol. 2024, 42, 6171–6181. [Google Scholar] [CrossRef]
- Li, H.; Feng, L.; Kang, J.; Yue, J.; Hou, Y.; Zhang, Z.; Xue, T.; Wu, B. Efficient phase demodulation of optical carrier-based microwave interferometry for high-precision dynamic distance measurement. J. Light. Technol. 2023, 42, 993–999. [Google Scholar] [CrossRef]
- Hussein, H.; Farid, N.; Terra, O. Absolute gauge block calibration using ultra-precise optical frequency synthesizer locked to a femtosecond comb. Appl. Opt. 2015, 54, 622–626. [Google Scholar] [CrossRef]
- Minoshima, K.; Matsumoto, H. High-accuracy measurement of 240-m distance in an optical tunnel by use of a compact femtosecond laser. Appl. Opt. 2000, 39, 5512–5517. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, F.; Meng, F.; Balling, P.; Li, J.; Pan, L.; Qu, X. Absolute distance measurement using frequency comb and a single-frequency laser. IEEE Photonics Technol. Lett. 2015, 27, 2587–2590. [Google Scholar] [CrossRef]
- Coddington, I.; Swann, W.C.; Nenadovic, L.; Newbury, N.R. Rapid and precise absolute distance measurements at long range. Nat. Photonics 2009, 3, 351–356. [Google Scholar] [CrossRef]
- Nanni, J.; Lenzi, E.; Perini, F.; Monari, J.; Mattana, A.; Caputo, F.; Maccaferri, G.; Orfei, A.; Kenney, D.; Wu, A. Accurate, cost-efficient microwave photonic fiber-transfer-delay measurement system. J. Light. Technol. 2024, 42, 7612–7618. [Google Scholar] [CrossRef]
- Donati, S. Photonic Instrumentation: Sensing and Measuring with Lasers; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Wu, H.; Zhang, F.; Liu, T.; Meng, F.; Li, J.; Qu, X. Absolute distance measurement using optical sampling by cavity tuning. IEEE Photonics Technol. Lett. 2016, 28, 1275–1278. [Google Scholar] [CrossRef]
- Xu, Z.; Yu, F.; Qiu, B.; Zhang, Y.; Xiang, Y.; Pan, S. Coherent Random-Modulated Continuous-Wave LiDAR Based on Phase-Coded Subcarrier Modulation. Photonics 2021, 8, 475. [Google Scholar] [CrossRef]
- Feng, W.; Jiang, N.; Jin, J.; Zhao, A.; Zhang, Y.; Liu, S.; Qiu, K. High-Resolution Chaos Lidar Using Self-Phase-Modulated Feedback External-Cavity Semiconductor Laser-based Chaos Source. In Proceedings of the 2021 19th International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 23–27 August 2021; pp. 1–3. [Google Scholar]
- Tseng, Y.-H.; Lin, Y.-C.; Lin, S.-C.; Hsieh, P.-H.; Lee, C.-T.; Chang, C.-H.; Lin, F.-Y. A Switched-Capacitor Cross-Correlation-Based Time-of-Flight Design for Pulsed Chaos Lidar Systems. In Proceedings of the 2024 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Taipei, Taiwan, 7–9 November 2024; pp. 335–338. [Google Scholar]
- Yang, J.; Fan, F.; Liu, J.; Su, Q.; Li, Y.; Huang, W.; Xu, B. Randomness quantification for quantum random number generation based on detection of amplified spontaneous emission noise. Quantum Sci. Technol. 2020, 6, 015002. [Google Scholar] [CrossRef]
- Cui, P.; Yang, L.; Guo, Y.; Lin, J.; Liu, Y.; Zhu, J. Absolute distance measurement using an optical comb and an optoelectronic oscillator. IEEE Photonics Technol. Lett. 2018, 30, 744–747. [Google Scholar] [CrossRef]
- Zhou, Y.; Yuan, Y.; Su, M. Research on Fiber-Optic Optical Coherence Ranging System Based on Laser Frequency Scanning Interferometry. Sensors 2024, 24, 1838. [Google Scholar] [CrossRef]
- Zhang, Z.; Kang, J.; Liu, R.; Cao, Y.; Hao, Y.; Sun, Z.; Feng, L.; Zhao, Z.; Wu, B.; Xue, T. Multi-Channel Absolute Distance Measurement Based on Optical Carrier-Based Microwave Scanning Interferometry. J. Light. Technol. 2024, 42, 5830–5838. [Google Scholar] [CrossRef]
- Niu, Q.; Zheng, J.; Cheng, X.; Liu, J.; Jia, L.; Ni, L.; Nian, J.; Zhang, F.; Qu, X. Arbitrary distance measurement without dead zone by chirped pulse spectrally interferometry using a femtosecond optical frequency comb. Opt. Express 2022, 30, 35029–35040. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Qu, X.; Zhang, F.; Zhao, X.; Peng, B. Absolute distance measurement based on spectral interferometry using femtosecond optical frequency comb. Opt. Lasers Eng. 2019, 120, 71–78. [Google Scholar] [CrossRef]
- Tomaru, T. Continuous-variable random-number generation from an amplified spontaneous emission light source. Appl. Opt. 2020, 59, 3109–3118. [Google Scholar] [CrossRef] [PubMed]
| Method | Measured Distance | Standard Deviation | Single Measurement Time |
|---|---|---|---|
| OSCAT [30] | 22 mm | 4 μm | 10 s |
| FSI [31] | 73.51 mm | 0.19 μm | 1 s |
| OCMSI [32] | 35 m | 60 μm | second level |
| CPSI [33] | 18 cm | 2.51 μm | 1.76 ms |
| SI [34] | 70 m | 30 μm | 100 ms |
| This work | 2 m | 8 μm | 40 μs |
| Sampling Rate (GS/s) | Measured Distance (m) | Standard Deviation (µm) | Distance Range (µm) |
|---|---|---|---|
| 1.25 GS/s | 1.3 m | 5268 µm | 25442 µm |
| 10 GS/s | 1.3 m | 255 µm | 1344 µm |
| 20 GS/s | 1.3 m | 80 µm | 384 µm |
| 40 GS/s | 1.3 m | 20 µm | 96 µm |
| Distance | Uncertainty | Standard Deviation | Single Measurement Time |
|---|---|---|---|
| 0.5 m | 4.84 μm | 7.65 μm | 40 μs |
| 1 m | 4.15 μm | 6.56 μm | 40 μs |
| 2 m | 5.17 μm | 8.17 μm | 40 μs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Liu, T.; Liu, S.; Tang, L.; Ma, H.; Tao, T.; Jia, X.; Wu, J.; Li, C.; Wang, X.; et al. High-Update-Rate (25 kHz) Laser Ranging with Random Noise Modulation for Fast and Precise Absolute Distance Measurement. Sensors 2025, 25, 6985. https://doi.org/10.3390/s25226985
Chen Y, Liu T, Liu S, Tang L, Ma H, Tao T, Jia X, Wu J, Li C, Wang X, et al. High-Update-Rate (25 kHz) Laser Ranging with Random Noise Modulation for Fast and Precise Absolute Distance Measurement. Sensors. 2025; 25(22):6985. https://doi.org/10.3390/s25226985
Chicago/Turabian StyleChen, Yongchao, Tianci Liu, Shenggang Liu, Longhuang Tang, Heli Ma, Tianjiong Tao, Xing Jia, Jian Wu, Chengjun Li, Xiang Wang, and et al. 2025. "High-Update-Rate (25 kHz) Laser Ranging with Random Noise Modulation for Fast and Precise Absolute Distance Measurement" Sensors 25, no. 22: 6985. https://doi.org/10.3390/s25226985
APA StyleChen, Y., Liu, T., Liu, S., Tang, L., Ma, H., Tao, T., Jia, X., Wu, J., Li, C., Wang, X., Wang, Z., Chen, W., Zhang, X., Li, E., Shi, J., & Weng, J. (2025). High-Update-Rate (25 kHz) Laser Ranging with Random Noise Modulation for Fast and Precise Absolute Distance Measurement. Sensors, 25(22), 6985. https://doi.org/10.3390/s25226985









