Robust Beamforming Design for Energy Efficiency and Spectral Efficiency Tradeoff in Multi-STAR-RIS-Aided C-HRSMA
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
- We propose a tradeoff scheme between EE and SE in a C-HRSMA system that incorporates common rate allocation, BS beamforming, and RIS beamforming. This approach exploits the spatial clustering characteristic of user distribution to enhance EE and SE.
- Given the uncertainties from ICSI and the non-convex fractional structure of the SE-EE maximization problem, we propose an iterative-based robust joint beamforming algorithm with the -procedure, the successive convex approximation (SCA) method and Dinkelbach’s approach.
- The simulation results validate that the integrated C-HRSMA algorithm exhibits superior performance in terms of both SE and EE.
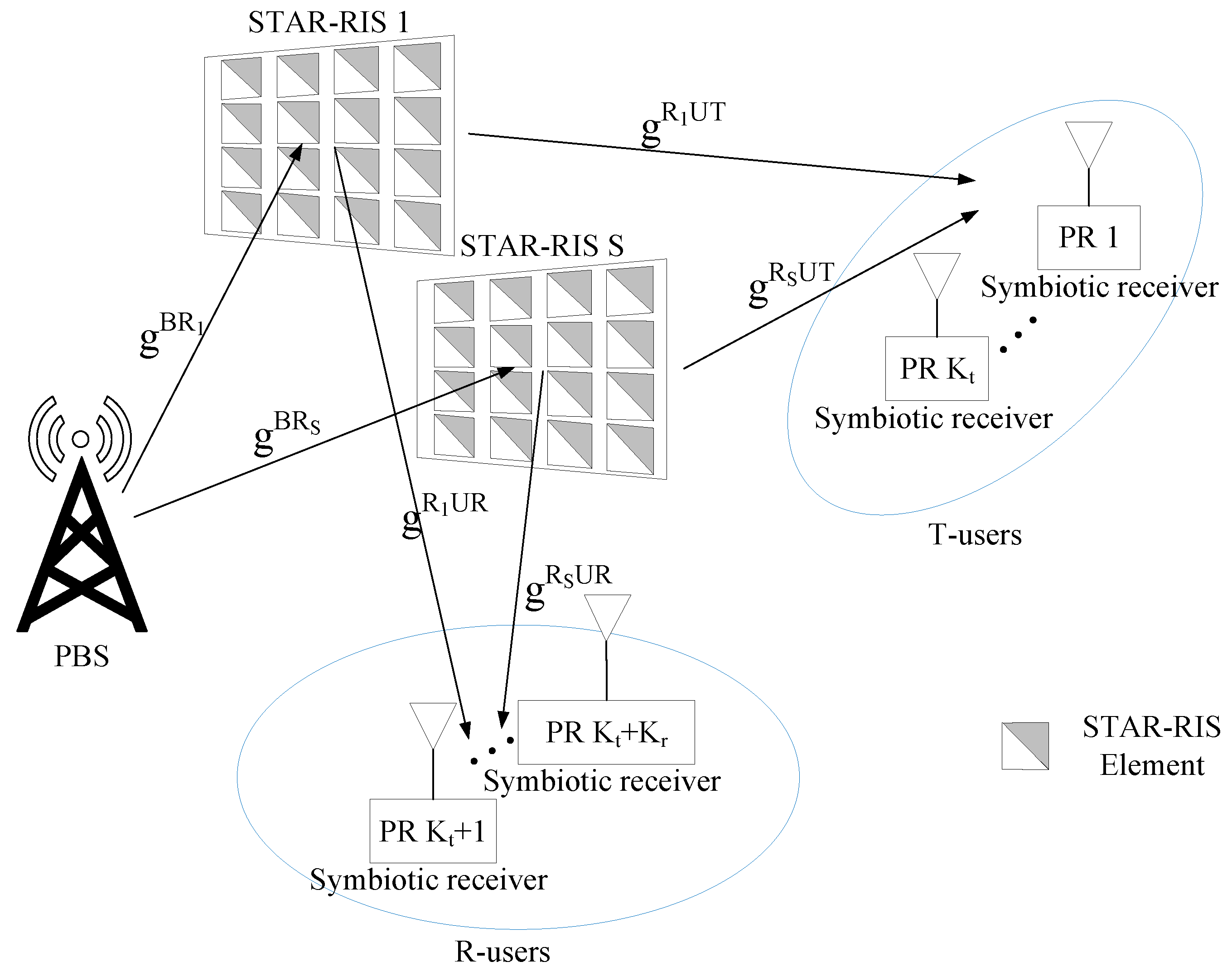
2. System Model
3. Problem Formulation
3.1. Precoder Design
3.2. Passive Beamforming Design
| Algorithm 1 AO-Based Joint Beamforming Design |
3.3. Computational Cost of Algorithm
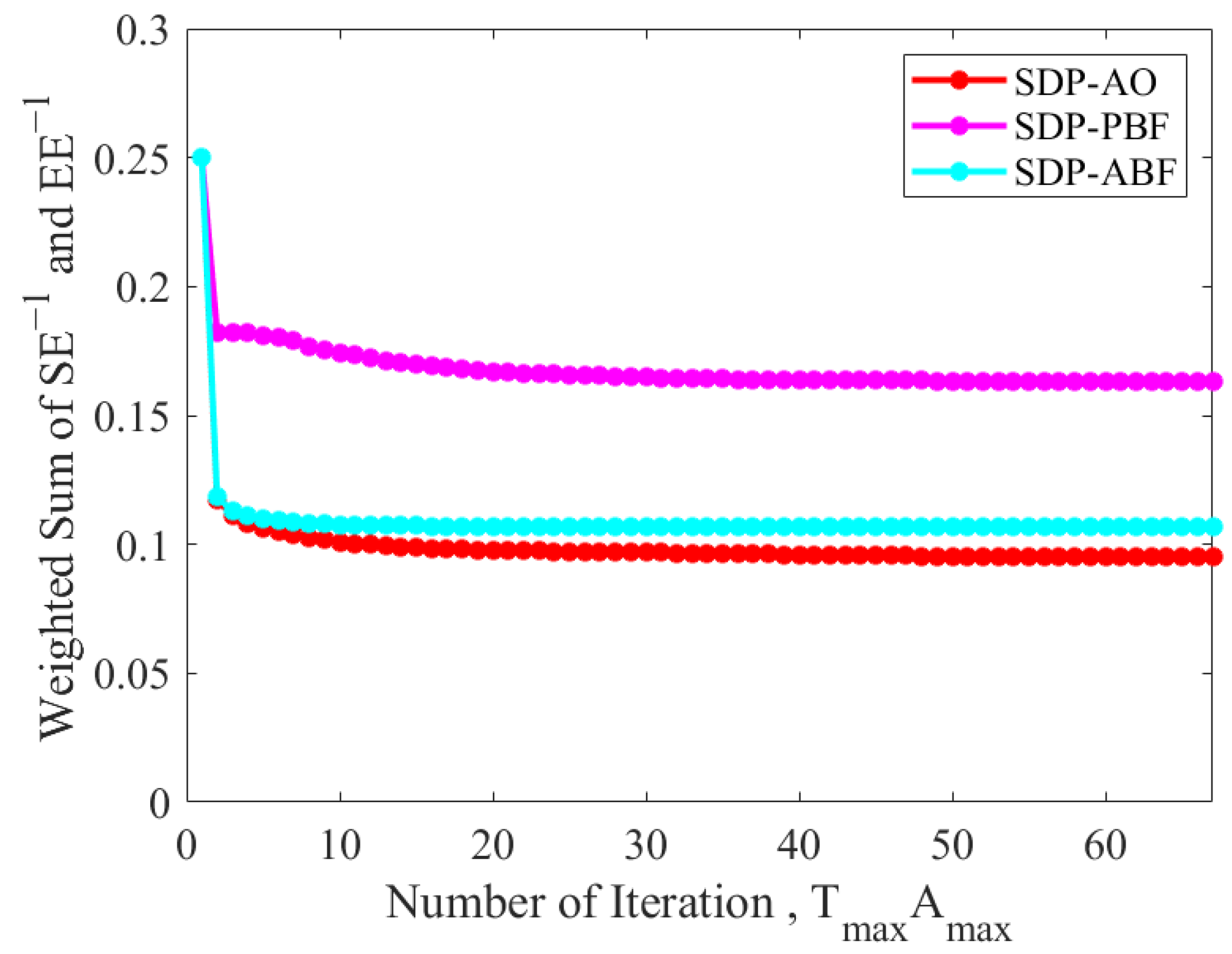
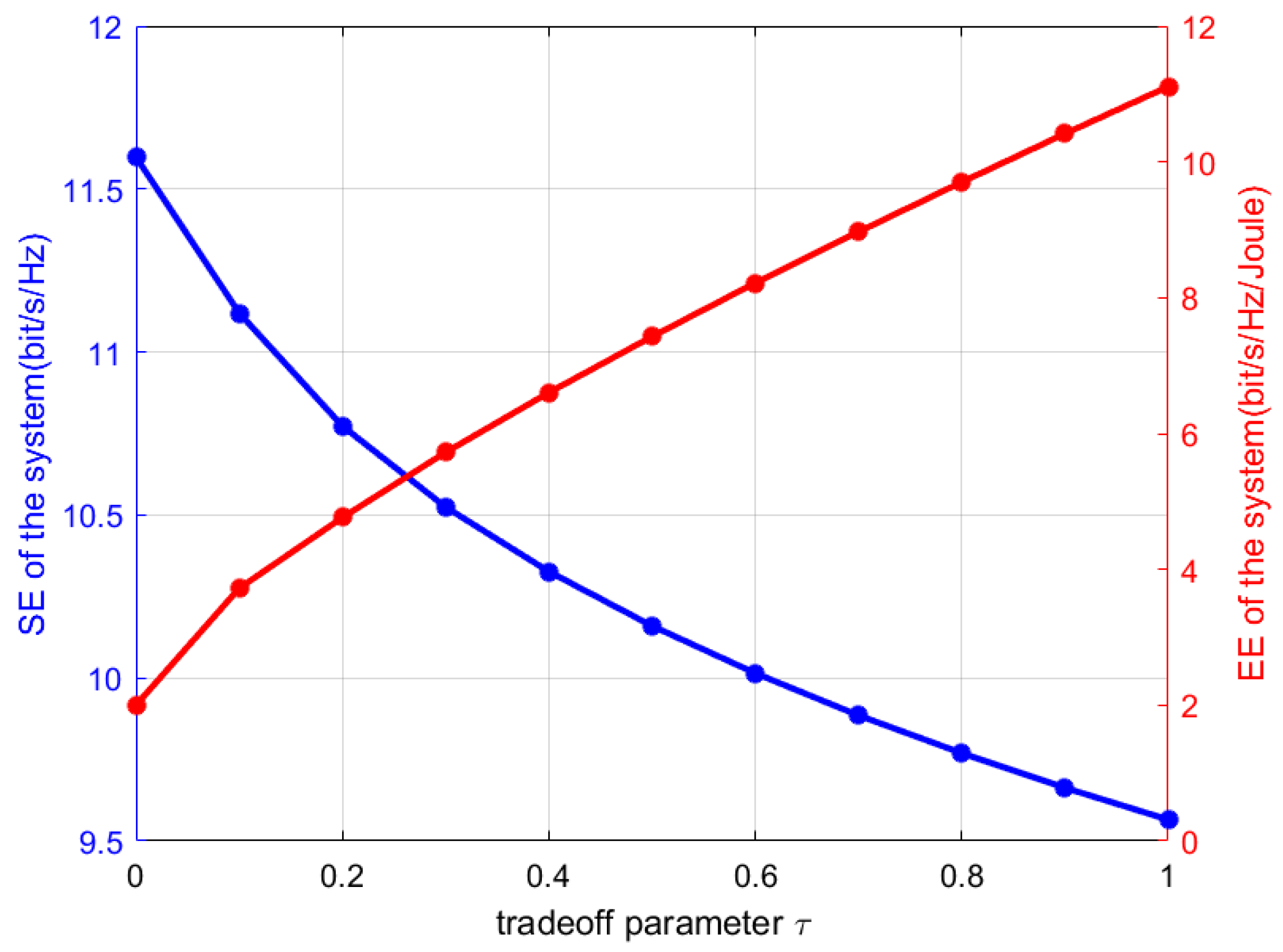
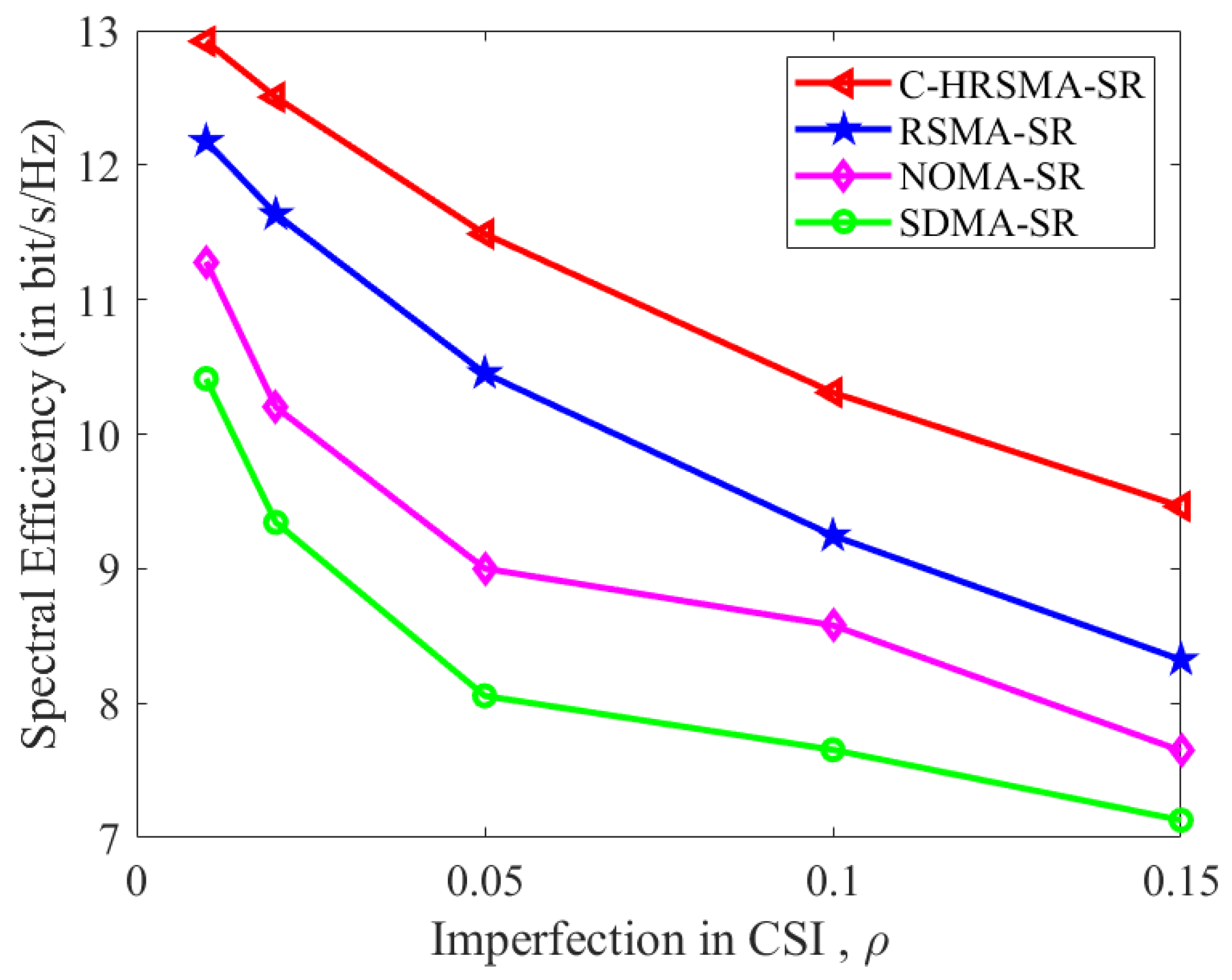
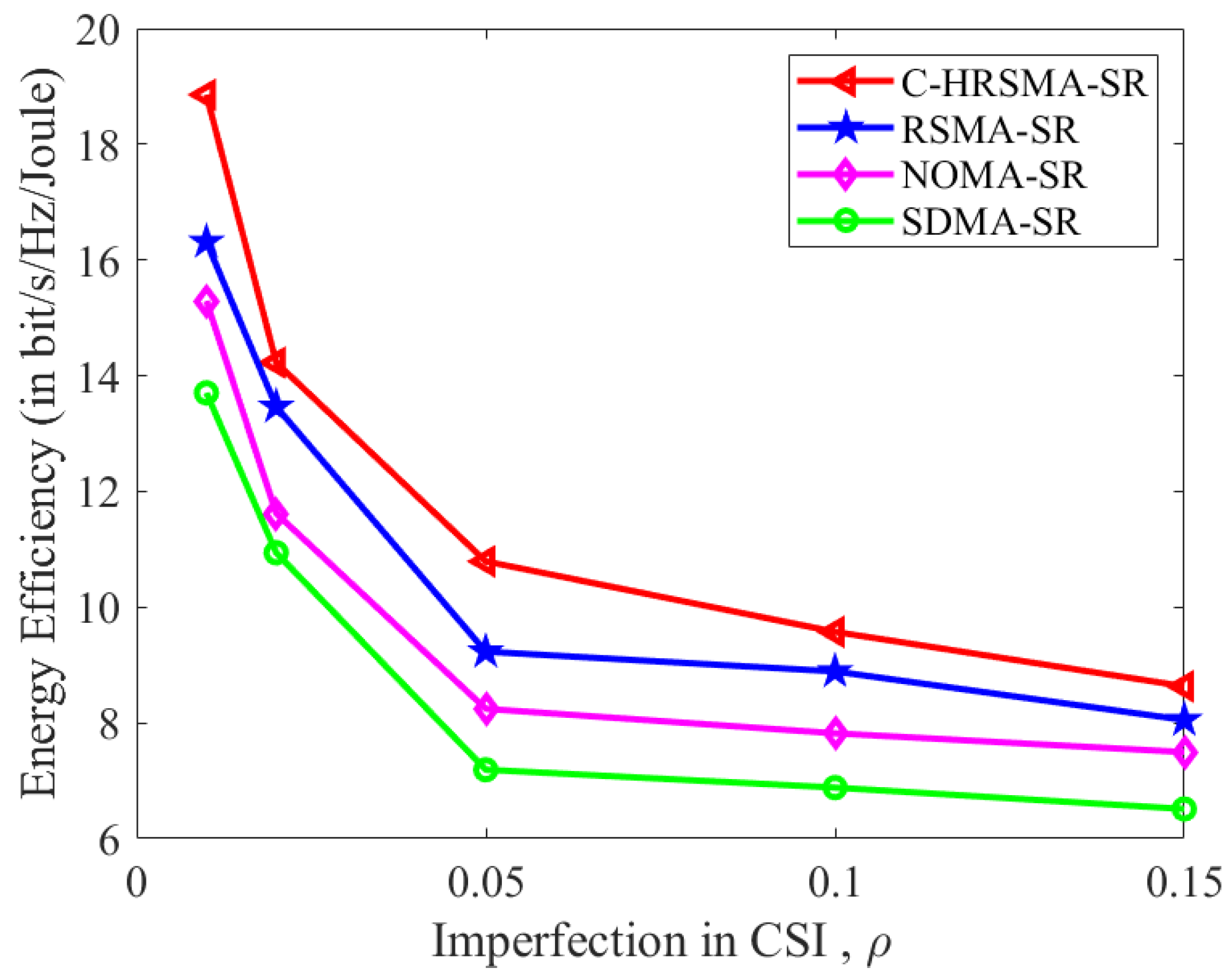
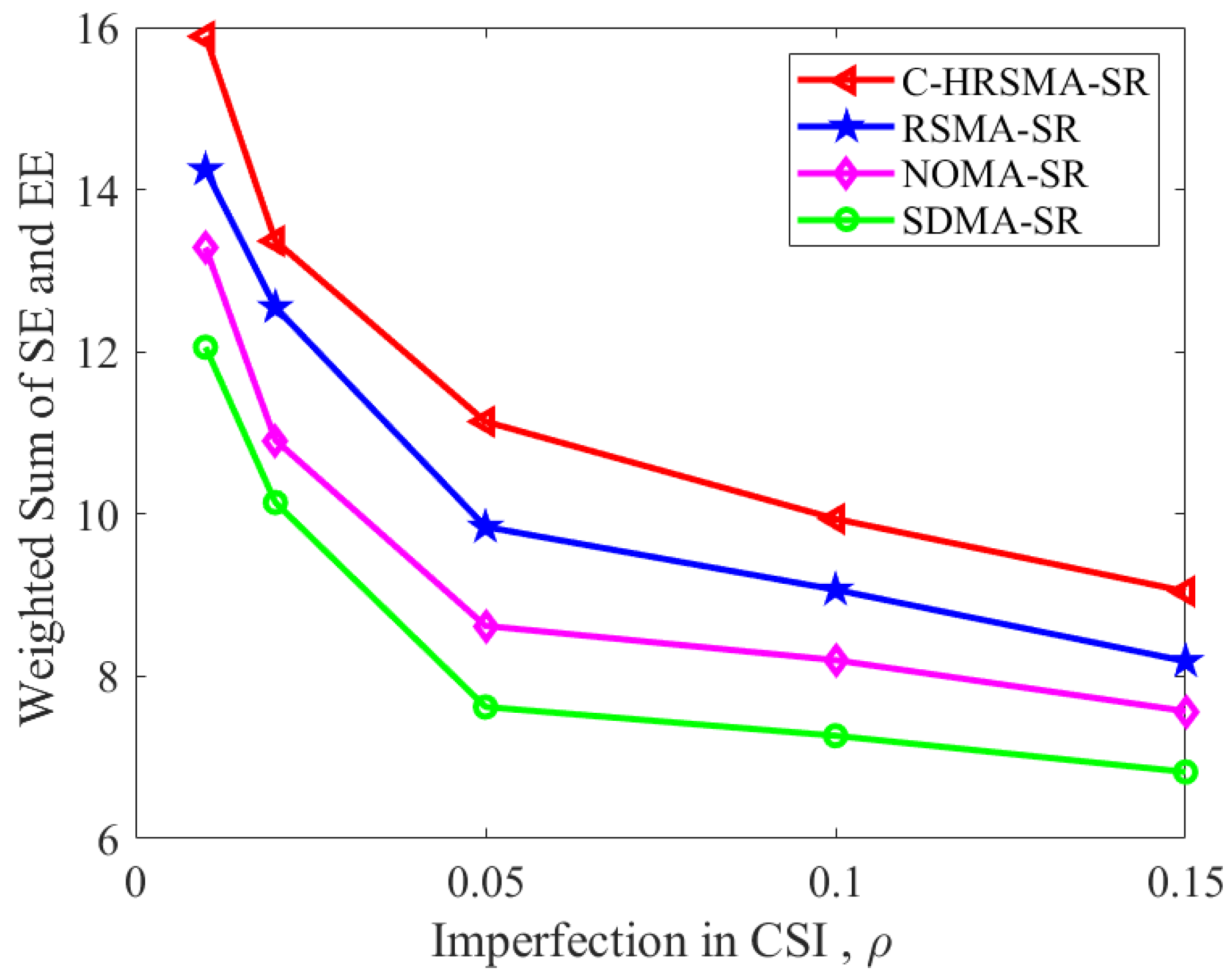
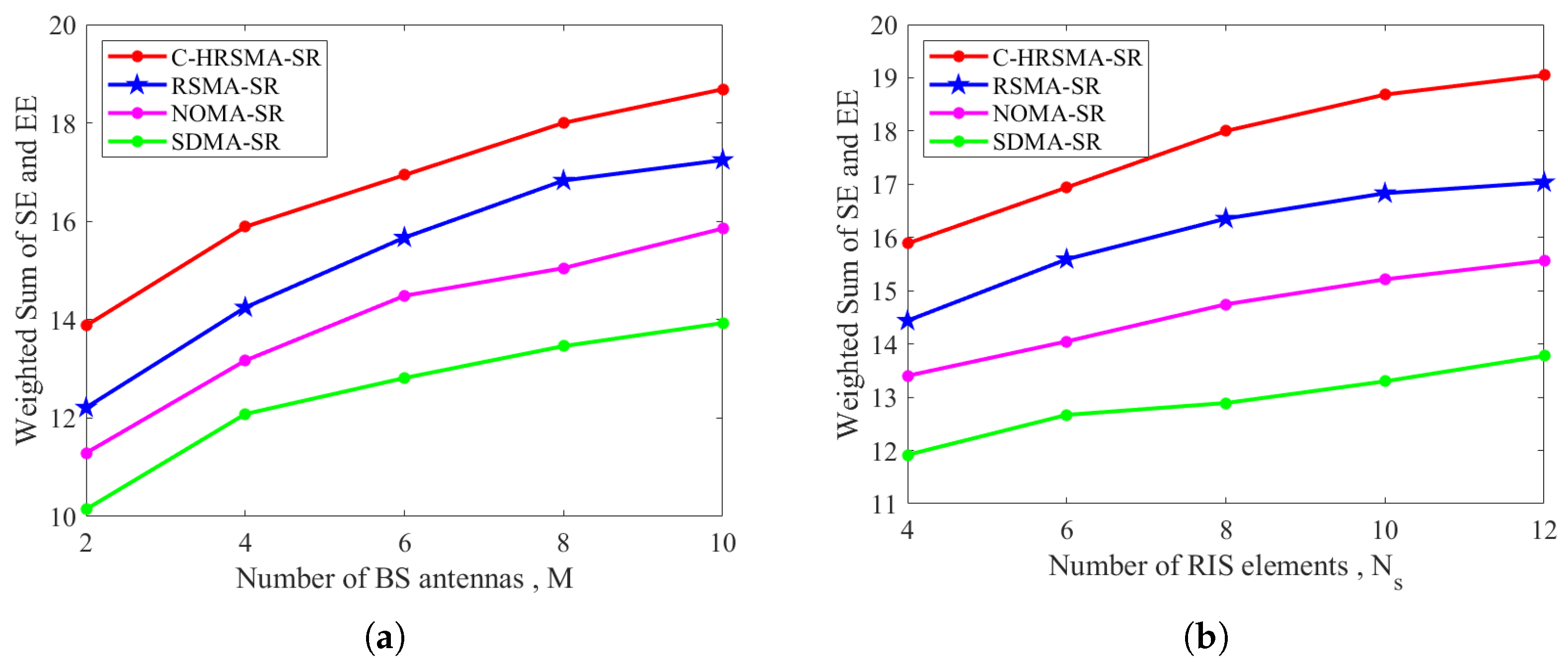
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Wang, M.; Jia, Y.; Jin, Y.; Ma, R.; Mao, Y.; Yuen, C. Robust Beamforming and Rate Optimization for RIS-Aided Symbiotic Radio Systems With RSMA. IEEE Commun. Lett. 2024, 28, 2328–2332. [Google Scholar] [CrossRef]
- Clerckx, B.; Mao, Y.; Jorswieck, E.; Yuan, J.; Love, D.J.; Erkip, E.; Niyato, D. A Primer on Rate-Splitting Multiple Access: Tutorial, Myths, and Frequently Asked Questions. IEEE J. Sel. Areas Commun. 2023, 41, 1265–1308. [Google Scholar] [CrossRef]
- Pala, S.; Katwe, M.; Singh, K.; Clerckx, B.; Li, C.-P. Spectral-efficient ris-aided rsma URLLC: Toward mobile broadband reliable low latency communication (mbrllc) system. IEEE Trans. Wirel. Commun. 2023, 23, 3507–3524. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, X.; Han, S.; Sun, M.; Liu, C.; Zhang, P. Energy efficiency aware computation offloading in RIS-enhanced symbiotic radio systems. IEEE Trans. Green Commun. Netw. 2023, 7, 1823–1835. [Google Scholar] [CrossRef]
- Singh, S.K.; Agrawal, K.; Singh, K.; Clerckx, B.; Li, C.-P. RSMA for Hybrid RIS-UAV-Aided Full-Duplex Communications with Finite Blocklength Codes Under Imperfect SIC. IEEE Trans. Wirel. Commun. 2023, 22, 5957–5975. [Google Scholar] [CrossRef]
- Bansal, A.; Singh, K.; Clerckx, B.; Li, C.-P.; Alouini, M.-S. Rate-splitting multiple access for intelligent reflecting surface aided multi-user communications. IEEE Trans. Veh. Technol. 2021, 70, 9217–9229. [Google Scholar] [CrossRef]
- Katwe, M.; Singh, K.; Clerckx, B.; Li, C.-P. Rate splitting multiple access for energy efficient RIS-aided multi-user short-packet communications. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 644–649. [Google Scholar]
- Chang, H.; Kang, X.; Lei, H.; Tsiftsis, T.A.; Pan, G.; Liu, H. STAR-RIS-Aided Covert Communications in MISO-RSMA Systems. IEEE Trans. Green Commun. Netw. 2024. early access. [Google Scholar] [CrossRef]
- Wang, B.; Tao, X.; Han, S.; Yang, K.; Wu, H. Secure Transmission Design for Rate-splitting Empowered STAR-RIS-Aided Networks. IEEE Wirel. Commun. Lett. 2024. early access. [Google Scholar] [CrossRef]
- Lyu, B.; Zhou, C.; Gong, S.; Wu, W.; Hoang, D.T.; Niyato, D. Energy-Efficiency Maximization for STAR-RIS Enabled Cell-Free Symbiotic Radio Communications. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 2209–2223. [Google Scholar] [CrossRef]
- Zhou, C.; Lyu, B.; Feng, Y.; Hoang, D.T. Transmit Power Minimization for STAR-RIS Empowered Symbiotic Radio Communications. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 1641–1656. [Google Scholar] [CrossRef]
- Zhou, C.; Lyu, B.; Gong, S.; You, C. Active STAR-RIS-Assisted Symbiotic Radio Communications Under Hardware Impairments. IEEE Commun. Lett. 2023, 27, 2797–2801. [Google Scholar] [CrossRef]
- Yeganeh, R.S.; Omidi, M.J.; Zeinali, F.; Mili, M.R.; Ghavami, M. QoS Improvement in Multi User Cellular-Symbiotic Radio Network Assisted by Active-Star-RIS. IEEE Trans. Cogn. Commun. Netw. 2025. early access. [Google Scholar] [CrossRef]
- Tao, Q.; Hu, X.; Zhang, S.; Zhong, C. Integrated Sensing and Communication for Symbiotic Radio Systems in Mobile Scenarios. IEEE Trans. Wirel. Commun. 2024, 23, 11213–11225. [Google Scholar] [CrossRef]
- Tao, Q.; Huang, C.; Chen, X. Integrated Sensing and Communication for Symbiotic Radio with Multiple IoT Devices. IEEE Commun. Lett. 2024, 28, 1820–1824. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Ouyang, J.; Zhu, W.-P.; Panagopoulos, A.D.; Alouini, M.-S. Robust Secure Beamforming for Multibeam Satellite Communication Systems. IEEE Trans. Veh. Technol. 2019, 68, 6202–6206. [Google Scholar] [CrossRef]
- Wang, W.; Gao, L.; Ding, R.; Lei, J.; You, L.; Chan, C.A.; Gao, X. Resource Efficiency Optimization for Robust Beamforming in Multi-Beam Satellite Communications. IEEE Trans. Veh. Technol. 2021, 70, 6958–6968. [Google Scholar] [CrossRef]
- Dai, M.; Clerckx, B.; Gesbert, D.; Caire, G. A Rate Splitting Strategy for Massive MIMO With Imperfect CSIT. IEEE Trans. Wirel. Commun. 2016, 15, 4611–4624. [Google Scholar] [CrossRef]
- Amin, O.; Bedeer, E.; Ahmed, M.H.; Dobre, O.A. Energy Efficiency–Spectral Efficiency Tradeoff: A Multiobjective Optimization Approach. IEEE Trans. Veh. Technol. 2016, 65, 1975–1981. [Google Scholar] [CrossRef]
- Dinkelbach, W. On nonlinear fractional programming. Manage. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Wan, J.; Guan, Y.; Song, J.; Song, Q.; Guo, L. Energy Efficiency and Spectral Efficiency Tradeoff in Multi-BD Symbiotic Radio Systems. In Proceedings of the 2023 IEEE/CIC International Conference on Communications in China (ICCC), Dalian, China, 10–12 August 2023. [Google Scholar]
- Katwe, M.V.; Deshpande, R.; Singh, K.; Pan, C.; Ghare, P.H.; Duong, T.Q. Spectrally-Efficient Beamforming Design for STAR-RIS-Aided URLLC NOMA Systems. IEEE Trans. Commun. 2024, 72, 4414–4431. [Google Scholar] [CrossRef]
| Symbols | Description | Symbols | Description |
|---|---|---|---|
| M | Number of BS antennas | K | Total number of users |
| S | Number of STAR-RISs | Set of STAR-RISs | |
| Number of elements per STAR-RIS | Set of STAR-RIS elements | ||
| Number of T-users | Set of T-users | ||
| Number of R-users | Set of R-users | ||
| Transmission coefficient matrix | Reflection coefficient matrix | ||
| Transmission coefficient vector | Reflection coefficient vector | ||
| Transmit amplitude coefficient | Reflect amplitude coefficient | ||
| Transmit phase-shift | Reflect phase-shift | ||
| BS-to-user k channel | BS-RIS s-user k channel | ||
| Estimated BS-to-user k channel | Estimated cascaded channel | ||
| Bounded error of | Bounded error of | ||
| Outer common stream | B | System bandwidth | |
| Inner common stream | Private stream (for user k) | ||
| Precoding matrix | Outer common precoder | ||
| Private precoder for user k | Maximum BS transmit power | ||
| Received signal at user k | Noise power at user | ||
| SINR for outer common stream | Total rate of user k | ||
| SINR for inner common stream | SINR for private stream | ||
| EE-SE tradeoff parameter | Minimum QoS rate for user k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, S.; Lin, X.; Wang, Y. Robust Beamforming Design for Energy Efficiency and Spectral Efficiency Tradeoff in Multi-STAR-RIS-Aided C-HRSMA. Sensors 2025, 25, 6917. https://doi.org/10.3390/s25226917
Teng S, Lin X, Wang Y. Robust Beamforming Design for Energy Efficiency and Spectral Efficiency Tradeoff in Multi-STAR-RIS-Aided C-HRSMA. Sensors. 2025; 25(22):6917. https://doi.org/10.3390/s25226917
Chicago/Turabian StyleTeng, Shiming, Xinwei Lin, and Yafeng Wang. 2025. "Robust Beamforming Design for Energy Efficiency and Spectral Efficiency Tradeoff in Multi-STAR-RIS-Aided C-HRSMA" Sensors 25, no. 22: 6917. https://doi.org/10.3390/s25226917
APA StyleTeng, S., Lin, X., & Wang, Y. (2025). Robust Beamforming Design for Energy Efficiency and Spectral Efficiency Tradeoff in Multi-STAR-RIS-Aided C-HRSMA. Sensors, 25(22), 6917. https://doi.org/10.3390/s25226917






