Stochastic Geometric-Based Modeling for Partial Offloading Task Computing in Edge-AI Systems
Abstract
1. Introduction
1.1. State-of-the-Art and Motivations
1.2. Contributions
- We propose a cooperative partial offloading model in MEC environments, where tasks can be processed either locally by neighboring users or centrally by a server, taking spatial and directional correlations into account where a closed-form upper bound for spatial correlation is derived to constrain offloading decisions based on user proximity and sensing overlap.
- To minimize learning loss under delay and resource constraints, a novel optimization problem is formulated that incorporates freshness-aware weighting, correlation modeling, and allocation decisions. Moreover, to improve robustness in non-i.i.d. settings, we integrate earth mover’s distance (EMD) into the loss function to capture distributional dissimilarity among users’ data.
- To ensure scalability, we develop a coordination-free solution method suitable for practical deployment in distributed MEC systems.
- Leveraging stochastic geometry, we provide tractable analytical characterizations of coverage probability and delay distribution, which not only enable probabilistic guarantees on task offloading but also ensure the generalizability of the proposed framework to large-scale and heterogeneous MEC networks.
- We show that using the proposed framework, we can significantly reduce the computation load on the central server compared to baseline schemes and for a given delay threshold, we can give service to considerably higher number of users.
2. Related Works
3. System Model and Parameters
4. The Proposed Problem
4.1. Constraints
4.2. Data Freshness and Distribution-Aware Loss Modeling
4.3. Problem Formulation
5. Feasibility Analysis
6. Solution Method
6.1. Dataset Description
6.2. Proposed Solution
6.2.1. Joint and Disjoint Optimization Protocols
6.2.2. Assignment Relaxation
6.2.3. Offloading Ratio Relaxation
6.2.4. Joint Optimization
6.2.5. PGD Mathematical Details
| Algorithm 1 Joint PGD-based offloading and assignment optimization |
|
6.2.6. Computational Complexity and Scalability Discussion
6.2.7. Implementation
6.2.8. Convergence and Penalty Analysis
7. Performance Evaluation
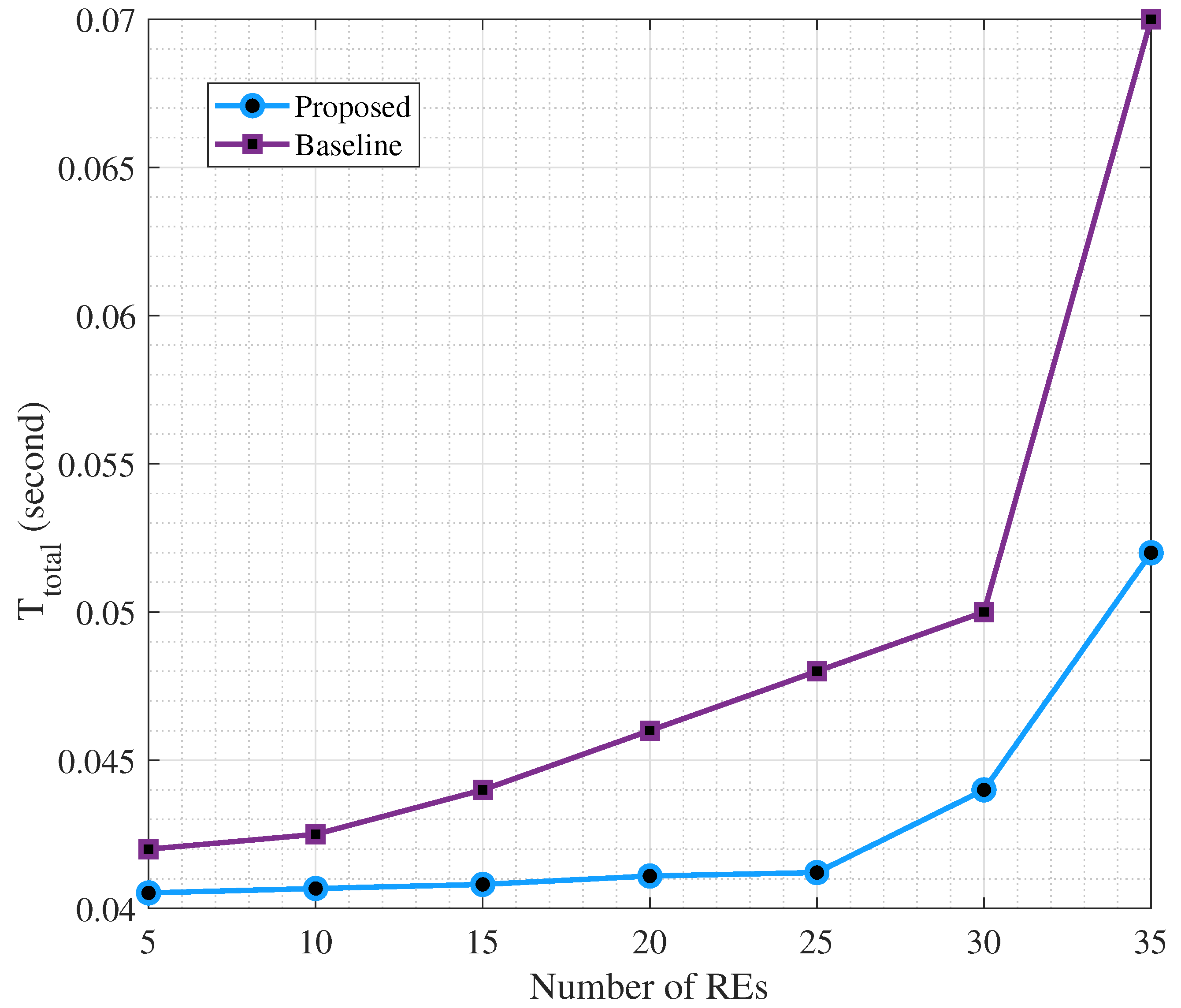
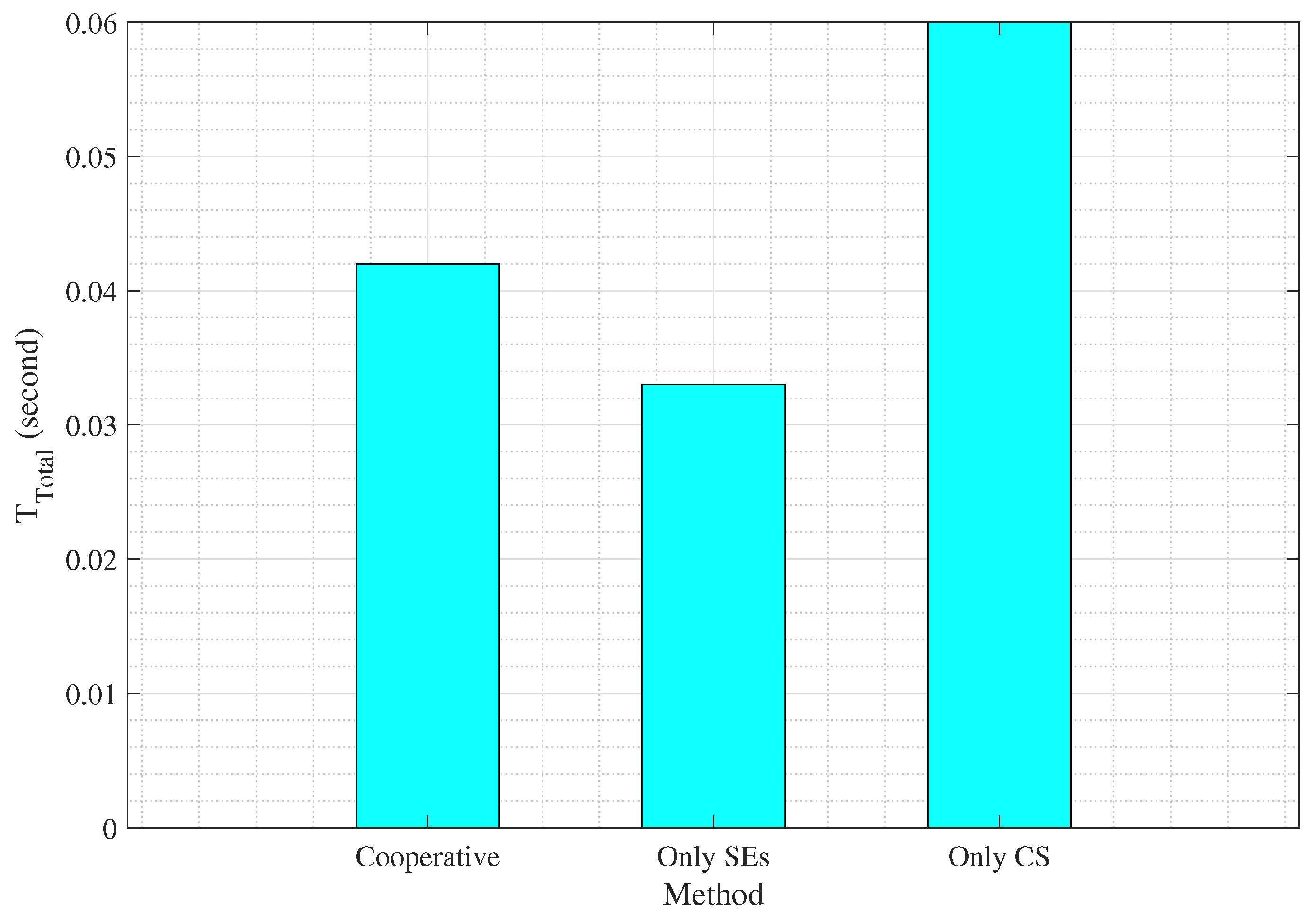
7.1. Task Offloading and Delay
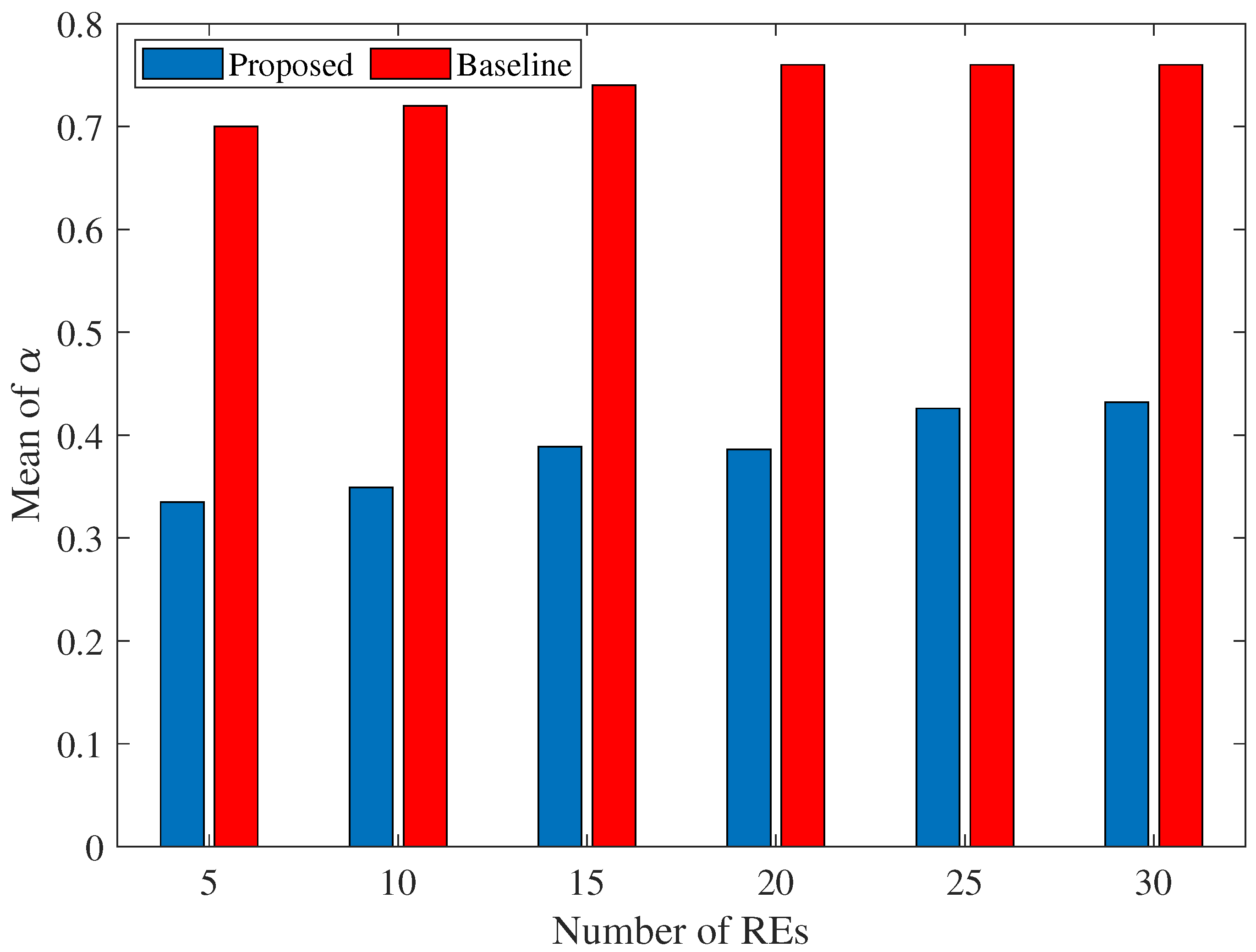
7.2. Comparison with the Baseline Scenario
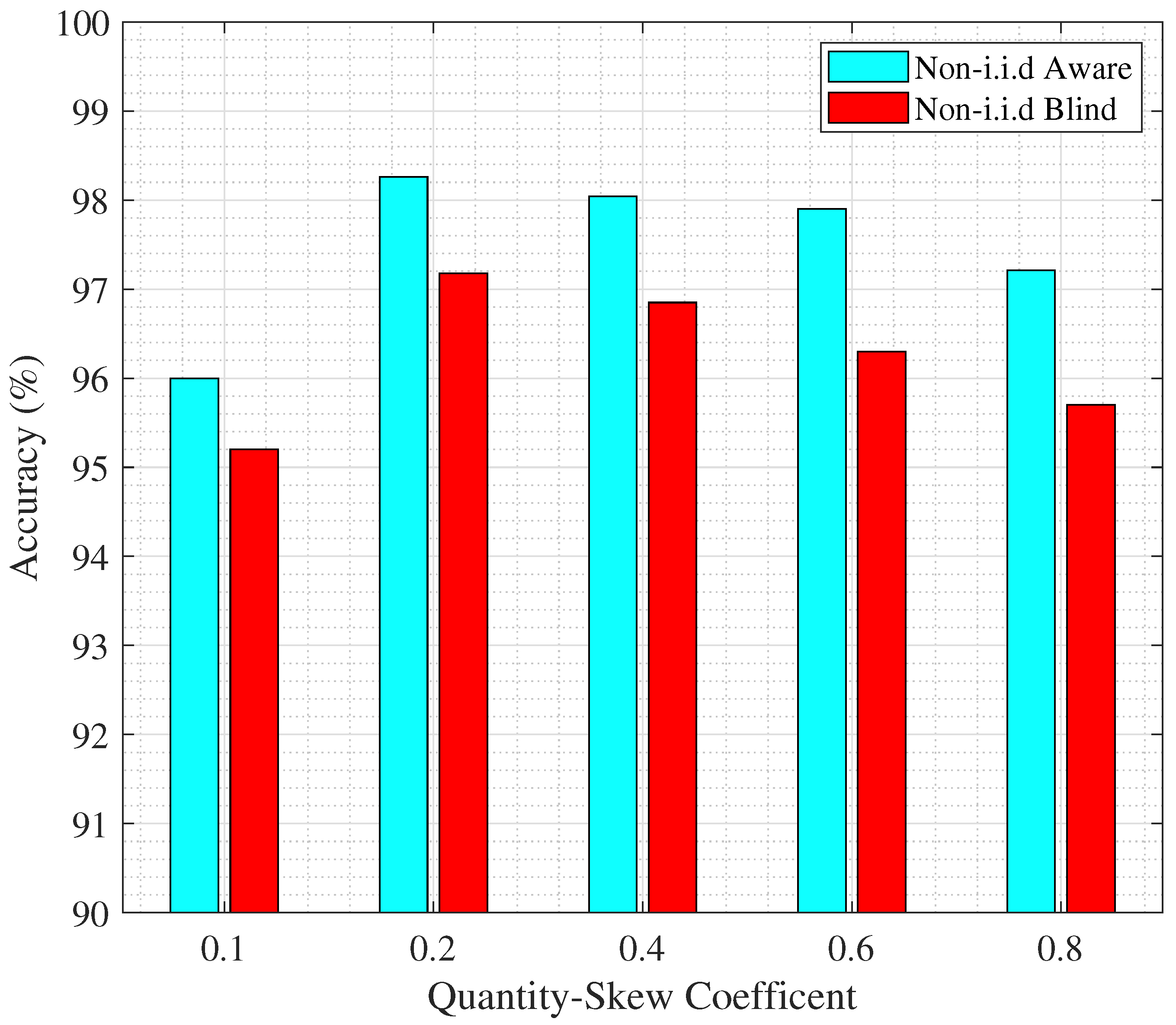
7.3. Comparing Non-i.i.d.-Blind and Non-i.i.d.-Aware Scenarios
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Ficili, I.; Giacobbe, M.; Tricomi, G.; Puliafito, A. From sensors to data intelligence: Leveraging IoT, cloud, and edge computing with AI. Sensors 2025, 25, 1763. [Google Scholar] [CrossRef] [PubMed]
- Bourechak, A.; Zedadra, O.; Kouahla, M.N.; Guerrieri, A.; Seridi, H.; Fortino, G. At the confluence of artificial intelligence and edge computing in IoT-based applications: A review and new perspectives. Sensors 2023, 23, 1639. [Google Scholar] [CrossRef] [PubMed]
- IEEE Future Networks. Edge Platforms and Services Evolving into 2030. 2021. Available online: https://futurenetworks.ieee.org/podcasts/edge-platforms-and-services-evolving-into-2030 (accessed on 23 July 2025).
- Grand View Research. Edge AI Market Size, Share & Growth|Industry Report, 2030. 2024. Available online: https://www.grandviewresearch.com/industry-analysis/edge-ai-market-report (accessed on 23 July 2025).
- MarketsandMarkets. Edge AI Hardware Industry Worth $58.90 Billion by 2030. 2025. Available online: https://www.marketsandmarkets.com/PressReleases/edge-ai-hardware.asp (accessed on 23 July 2025).
- Yang, J.; Chen, Y.; Lin, Z.; Tian, D.; Chen, P. Distributed Computation Offloading in Autonomous Driving Vehicular Networks: A Stochastic Geometry Approach. IEEE Trans. Intell. Veh. 2024, 9, 2701–2713. [Google Scholar] [CrossRef]
- Gu, Y.; Yao, Y.; Li, C.; Xia, B.; Xu, D.; Zhang, C. Modeling and Analysis of Stochastic Mobile-Edge Computing Wireless Networks. IEEE Internet Things J. 2021, 8, 14051–14065. [Google Scholar] [CrossRef]
- Tran, D.A.; Do, T.T.; Zhang, T. A stochastic geo-partitioning problem for mobile edge computing. IEEE Trans. Emerg. Top. Comput. 2020, 9, 2189–2200. [Google Scholar] [CrossRef]
- Hmamouche, Y.; Benjillali, M.; Saoudi, S.; Yanikomeroglu, H.; Renzo, M.D. New Trends in Stochastic Geometry for Wireless Networks: A Tutorial and Survey. Proc. IEEE 2021, 109, 1200–1252. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Du, H.; Yuan, X.; Kadoch, M.; Cheriet, M. Real-time remote health monitoring system driven by 5G MEC-IoT. Electronics 2020, 9, 1753. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Solans, D.; Heikkila, M.; Vitaletti, A.; Kourtellis, N.; Anagnostopoulos, A.; Chatzigiannakis, I. Non-i.i.d data in federated learning: A survey with taxonomy, metrics, methods, frameworks and future directions. arXiv 2024, arXiv:2411.12377. [Google Scholar]
- Lu, Z.; Pan, H.; Dai, Y.; Si, X.; Zhang, Y. Federated learning with non-iid data: A survey. IEEE Internet Things J. 2024, 11, 19188–19209. [Google Scholar] [CrossRef]
- Jimenez-Gutierrez, D.M.; Hassanzadeh, M.; Anagnostopoulos, A.; Chatzigiannakis, I.; Vitaletti, A. A thorough assessment of the non-iid data impact in federated learning. arXiv 2025, arXiv:2503.17070. [Google Scholar] [CrossRef]
- Su, W.; Li, L.; Liu, F.; He, M.; Liang, X. AI on the edge: A comprehensive review. Artif. Intell. Rev. 2022, 55, 6125–6183. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, K.; Jiang, T.; Zhang, J.; Letaief, K.B. Communication-efficient edge AI: Algorithms and systems. IEEE Commun. Surv. Tutor. 2020, 22, 2167–2191. [Google Scholar] [CrossRef]
- Letaief, K.B.; Shi, Y.; Lu, J.; Lu, J. Edge artificial intelligence for 6G: Vision, enabling technologies, and applications. IEEE J. Sel. Areas Commun. 2021, 40, 5–36. [Google Scholar] [CrossRef]
- Lin, F.P.C.; Hosseinalipour, S.; Michelusi, N.; Brinton, C.G. Delay-aware hierarchical federated learning. IEEE Trans. Cogn. Commun. Netw. 2023, 10, 674–688. [Google Scholar] [CrossRef]
- Wang, S.; Tuor, T.; Salonidis, T.; Leung, K.K.; Makaya, C.; He, T.; Chan, K. Adaptive federated learning in resource constrained edge computing systems. IEEE J. Sel. Areas Commun. 2019, 37, 1205–1221. [Google Scholar] [CrossRef]
- Xiao, H.; Xu, C.; Ma, Y.; Yang, S.; Zhong, L.; Muntean, G.M. Edge intelligence: A computational task offloading scheme for dependent IoT application. IEEE Trans. Wirel. Commun. 2022, 21, 7222–7237. [Google Scholar] [CrossRef]
- Qiao, D.; Guo, S.; Zhao, J.; Le, J.; Zhou, P.; Li, M.; Chen, X. ASMAFL: Adaptive staleness-aware momentum asynchronous federated learning in edge computing. IEEE Trans. Mob. Comput. 2024, 24, 3390–3406. [Google Scholar] [CrossRef]
- Fan, W.; Chen, Z.; Hao, Z.; Wu, F.; Liu, Y. Joint Task Offloading and Resource Allocation for Quality-Aware Edge-Assisted Machine Learning Task Inference. IEEE Trans. Veh. Technol. 2023, 72, 6739–6752. [Google Scholar] [CrossRef]
- Fan, W.; Li, S.; Liu, J.; Su, Y.; Wu, F.; Liu, Y. Joint Task Offloading and Resource Allocation for Accuracy-Aware Machine-Learning-Based IIoT Applications. IEEE Internet Things J. 2023, 10, 3305–3321. [Google Scholar] [CrossRef]
- Khalili, A.; Zarandi, S.; Rasti, M. Joint Resource Allocation and Offloading Decision in Mobile Edge Computing. IEEE Commun. Lett. 2019, 23, 684–687. [Google Scholar] [CrossRef]
- Kuang, Z.; Li, L.; Gao, J.; Zhao, L.; Liu, A. Partial Offloading Scheduling and Power Allocation for Mobile Edge Computing Systems. IEEE Internet Things J. 2019, 6, 6774–6785. [Google Scholar] [CrossRef]
- Zhang, S.; Gu, H.; Chi, K.; Huang, L.; Yu, K.; Mumtaz, S. DRL-Based Partial Offloading for Maximizing Sum Computation Rate of Wireless Powered Mobile Edge Computing Network. IEEE Trans. Wirel. Commun. 2022, 21, 10934–10948. [Google Scholar] [CrossRef]
- Malik, U.M.; Javed, M.A.; Frnda, J.; Rozhon, J.; Khan, W.U. Efficient matching-based parallel task offloading in iot networks. Sensors 2022, 22, 6906. [Google Scholar] [CrossRef]
- Bolat, Y.; Murray, I.; Ren, Y.; Ferdosian, N. Decentralized Distributed Sequential Neural Networks Inference on Low-Power Microcontrollers in Wireless Sensor Networks: A Predictive Maintenance Case Study. Sensors 2025, 25, 4595. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated learning with non-i.i.d data. arXiv 2018, arXiv:1806.00582. [Google Scholar]
- Lai, P.; He, Q.; Xia, X.; Chen, F.; Abdelrazek, M.; Grundy, J.; Hosking, J.; Yang, Y. Dynamic User Allocation in Stochastic Mobile Edge Computing Systems. IEEE Trans. Serv. Comput. 2022, 15, 2699–2712. [Google Scholar] [CrossRef]
- Lyu, Z.; Xiao, M.; Xu, J.; Skoglund, M.; Di Renzo, M. The larger the merrier? Efficient large AI model inference in wireless edge networks. arXiv 2025, arXiv:2505.09214. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, J. Modeling and Analysis of the Uplink Local Delay in MEC-Based VANETs. IEEE Trans. Veh. Technol. 2020, 69, 3538–3549. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, J. Modeling and Analysis of the Local Delay in an MEC-Based VANET for a Suburban Area. IEEE Internet Things J. 2022, 9, 7065–7079. [Google Scholar] [CrossRef]
- Cheng, Q.; Cai, G.; He, J.; Kaddoum, G. Design and Performance Analysis of MEC-Aided LoRa Networks with Power Control. IEEE Trans. Veh. Technol. 2025, 74, 1597–1609. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Ganti, R.K.; Baccelli, F.; Andrews, J.G. Modeling and Analysis of K-Tier Downlink Heterogeneous Cellular Networks. IEEE J. Sel. Areas Commun. 2012, 30, 550–560. [Google Scholar] [CrossRef]
- Andrews, J.G.; Baccelli, F.; Ganti, R.K. A Tractable Approach to Coverage and Rate in Cellular Networks. IEEE Trans. Commun. 2011, 59, 3122–3134. [Google Scholar] [CrossRef]
- Savi, M.; Tornatore, M.; Verticale, G. Impact of processing-resource sharing on the placement of chained virtual network functions. IEEE Trans. Cloud Comput. 2019, 9, 1479–1492. [Google Scholar] [CrossRef]
- Mu, Y.; Garg, N.; Ratnarajah, T. Federated learning in massive MIMO 6G networks: Convergence analysis and communication-efficient design. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4220–4234. [Google Scholar] [CrossRef]
- Wang, H.; Kaplan, Z.; Niu, D.; Li, B. Optimizing federated learning on non-i.i.d data with reinforcement learning. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 1698–1707. [Google Scholar]
- He, C.; Annavaram, M.; Avestimehr, S. Group knowledge transfer: Federated learning of large cnns at the edge. Adv. Neural Inf. Process. Syst. 2020, 33, 14068–14080. [Google Scholar]
- Deng, L. The MNIST database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- MNIST Dataset on Papers with Code. Available online: https://www.kaggle.com/datasets/hojjatk/mnist-dataset (accessed on 23 July 2025).
- Saeedi, H.; Nouruzi, A. Stochastic-Geometric-based Modeling for Partial Offloading Task Computing in Edge AI Systems. GitHub Repository. Available online: https://github.com/alinouruzi/Stochastic-Geometric-based-Modeling-for-Partial-Offloading-Task-Computing-in-Edge-AI-Systems (accessed on 21 September 2025).
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised deep embedding for clustering analysis. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 16–24 June 2016; pp. 478–487. [Google Scholar]
- 3GPP. 5G; Service Requirements for the 5G System (3GPP TS 22.261 Version 16.14.0 Release 16). Technical Specification ETSI TS 122 261 V16.14.0, ETSI. 2021. Available online: https://www.etsi.org/deliver/etsi_ts/122200_122299/122261/16.14.00_60/ts_122261v161400p.pdf (accessed on 29 July 2025).
- 5G Hub. 5G Ultra Reliable Low Latency Communication (URLLC). 2023. Available online: https://5ghub.us/5g-ultra-reliable-low-latency-communication-urllc/ (accessed on 29 July 2025).
- Wang, Q.; Haga, Y. Research on Structure Optimization and Accuracy Improvement of Key Components of Medical Device Robot. In Proceedings of the 2024 International Conference on Telecommunications and Power Electronics (TELEPE), Frankfurt, Germany, 29–31 May 2024; pp. 809–813. [Google Scholar] [CrossRef]
- Zrubka, Z.; Holgyesi, A.; Neshat, M.; Nezhad, H.M.; Mirjalili, S.; Kovács, L.; Péntek, M.; Gulácsi, L. Towards a single goodness metric of clinically relevant, accurate, fair and unbiased machine learning predictions of health-related quality of life. In Proceedings of the 2023 IEEE 27th International Conference on Intelligent Engineering Systems (INES), Nairobi, Kenya, 26–28 July 2023; pp. 000285–000290. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Dai, R.; Akyildiz, I.F. A spatial correlation model for visual information in wireless multimedia sensor networks. IEEE Trans. Multimed. 2009, 11, 1148–1159. [Google Scholar] [CrossRef]
- Haenggi, M. Stochastic Geometry for Wireless Networks; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
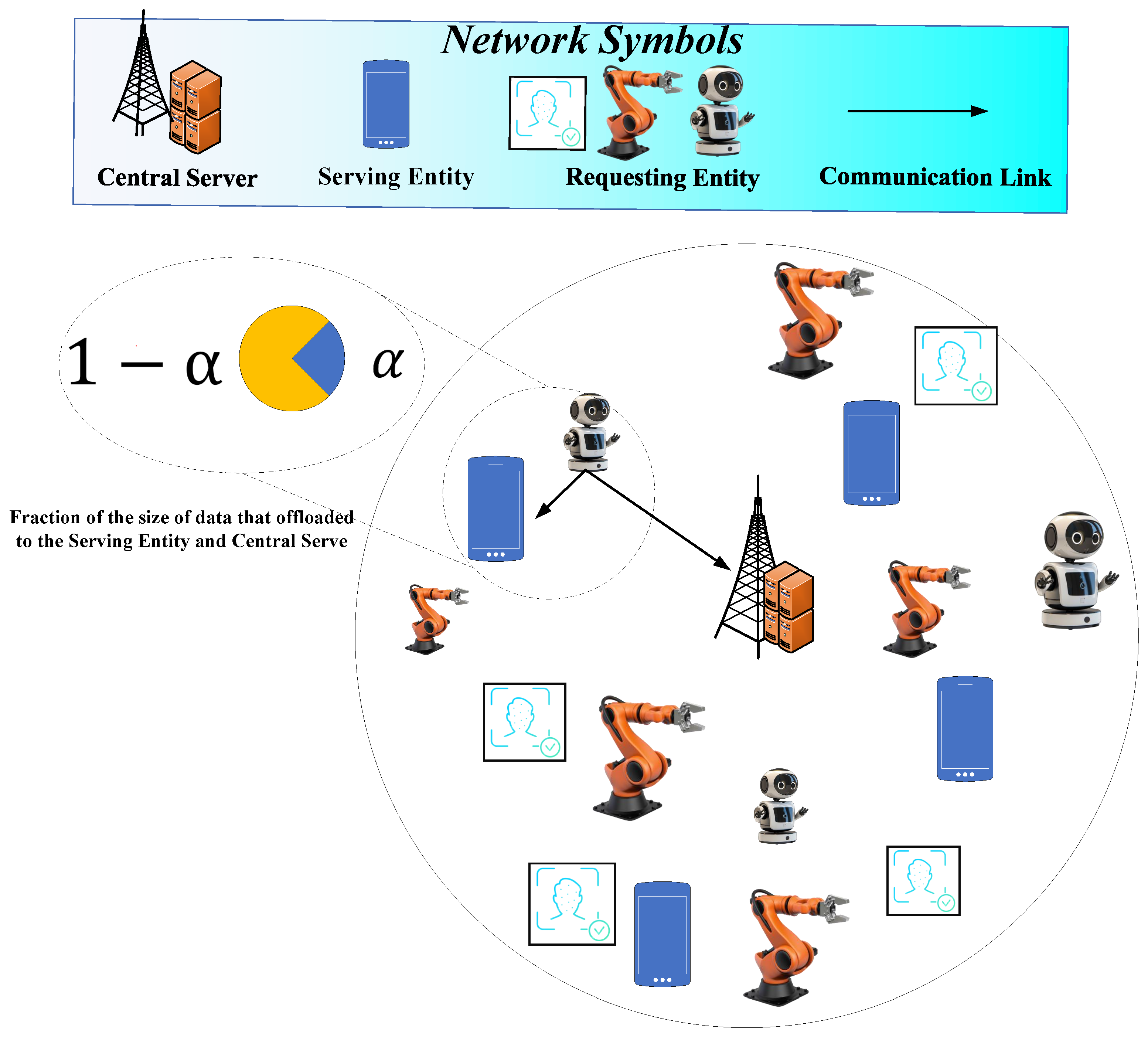
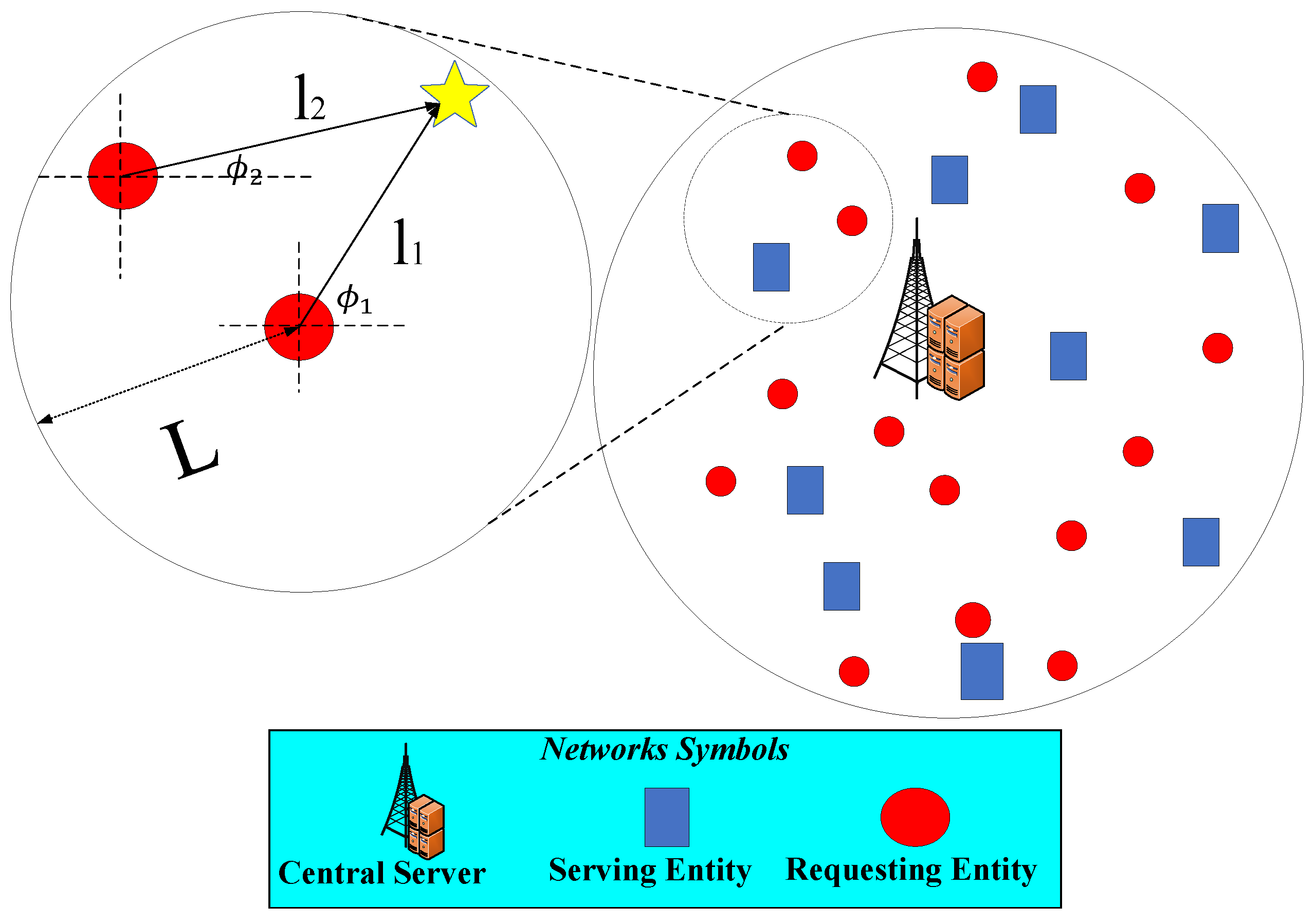

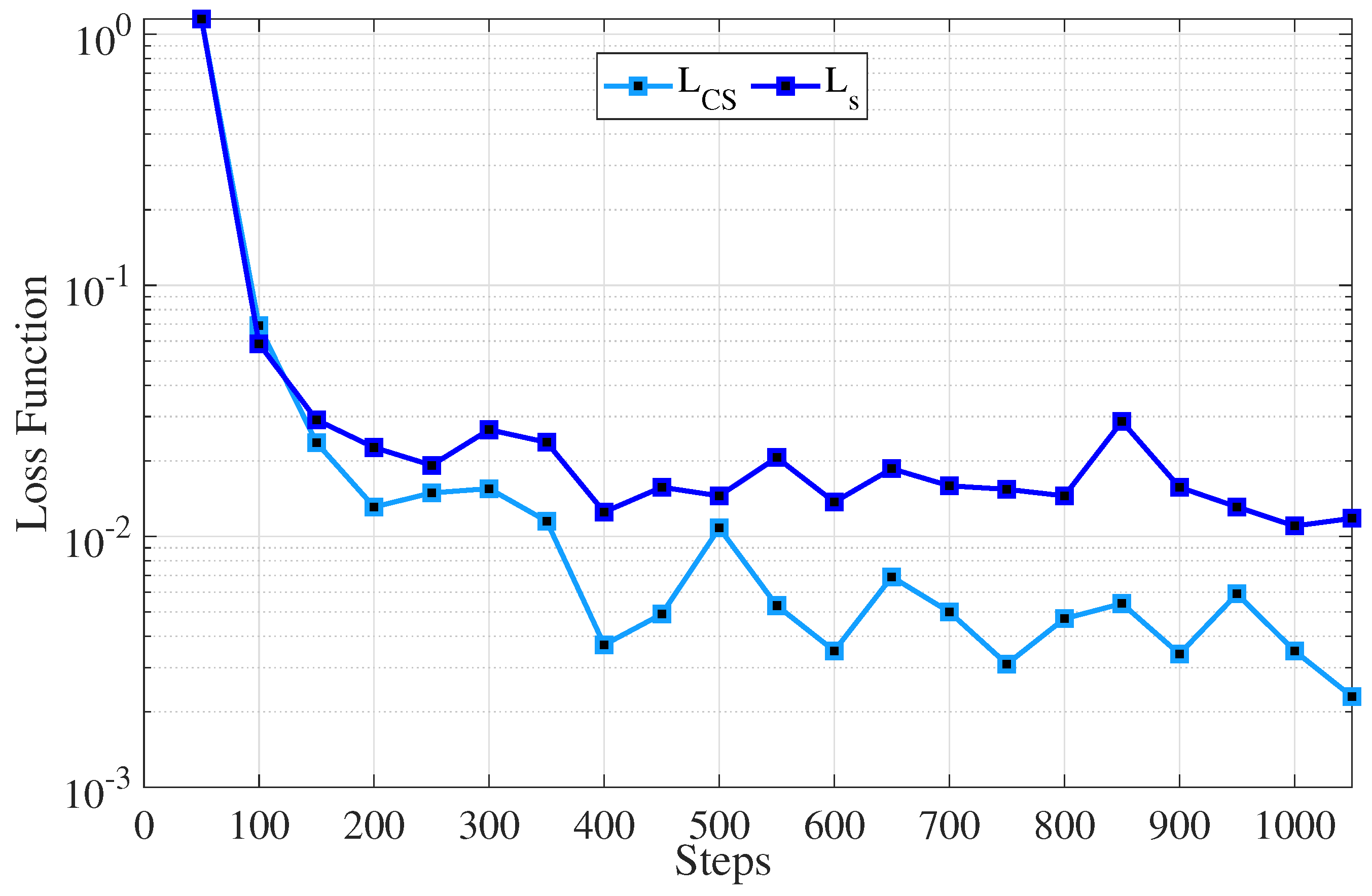
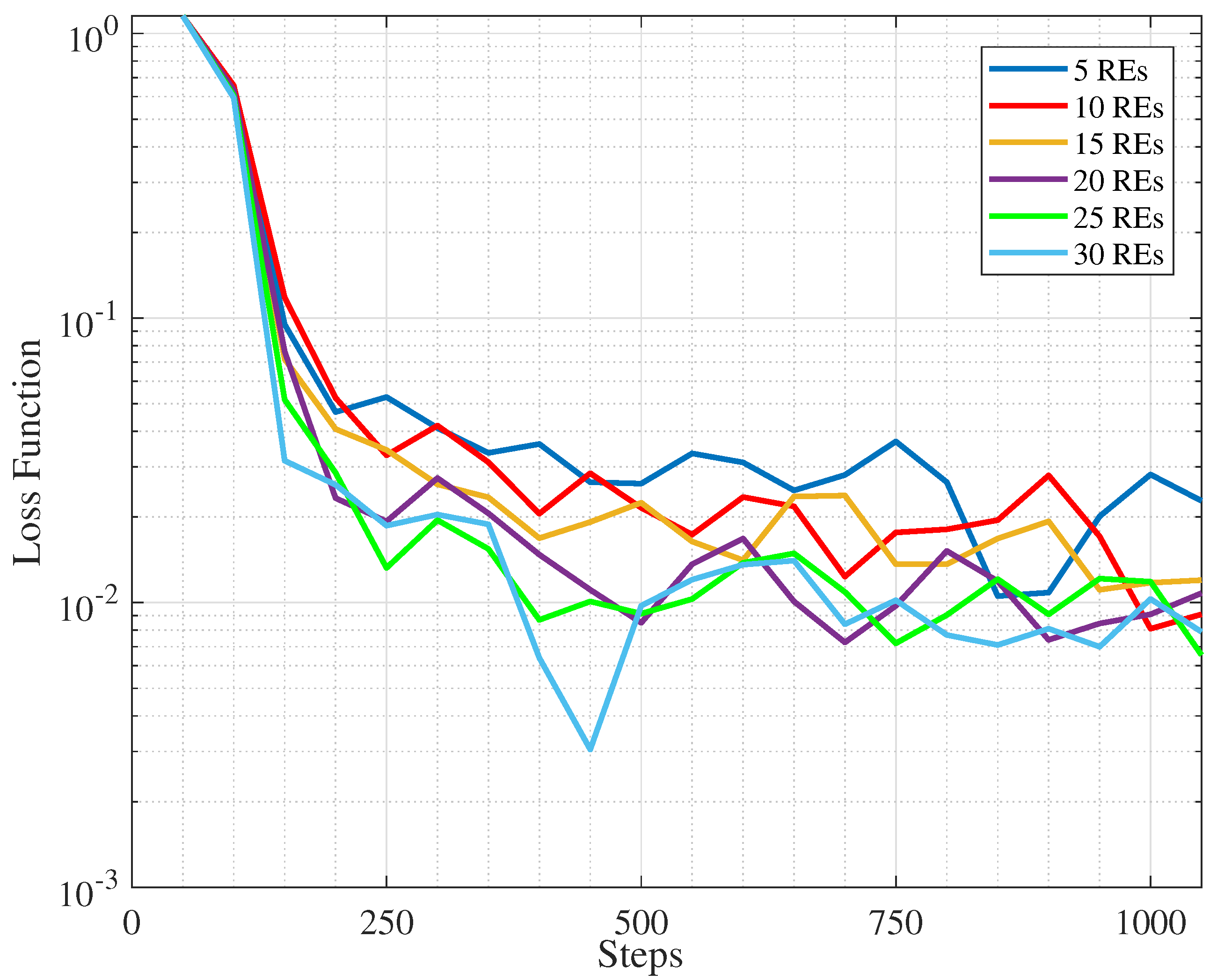



| Ref. | Method | Main Contribution | Comparison with Our Work |
|---|---|---|---|
| [27] | Matching-based allocation in fog IoT | Stable parallel sub-task execution, latency reduction | Focuses on fog parallelism, our work integrates spatial correlation and non-i.i.d. modeling in MEC |
| [20] | Multi-queue scheduling with Actor–Critic DRL | Dependent task completion, energy efficiency | Addresses task dependencies, our work emphasizes correlation-aware offloading and robustness to heterogeneous data |
| [22] | Lyapunov-based stochastic optimization | Joint offloading and resource allocation with latency/queue guarantees | Provides stability analysis, our framework couples delay guarantees with PGD-based optimization |
| [28] | Decentralized Sequential Neural Network (DDSNN) | Lightweight inference across low-power devices | Focuses on TinyML inference; our work targets MEC task offloading with stochastic geometry and learning integration |
| [21] | Adaptive local updates in heterogeneous FL | Handles device heterogeneity by adjusting update counts | Considers computational diversity, our approach also incorporates delay constraints and correlation-aware offloading |
| [18] | Client selection strategy for FL | Faster convergence, reduced communication overhead | Optimizes participant choice, our framework integrates delay guarantees and data heterogeneity in MEC |
| [29] | Adversarial FL with Earth Mover’s Distance | Improves global adaptation under non-i.i.d. data | Focuses on privacy-preserving FL, our work extends EMD to MEC with offloading and latency constraints |
| [30] | Label-invariant knowledge distillation in FL | Mitigates label skew via teacher-student framework | Addresses label heterogeneity, our framework also accounts for spatial correlation, partial offloading, and delay guarantees |
| Our Work | PGD-based joint optimization in MEC | Cooperative partial offloading, EMD-based robustness to non-i.i.d., stochastic geometry analysis, reduced CS load | Provides unified framework coupling task offloading, correlation modeling, and delay-aware learning optimization |
| Symbol | Description |
|---|---|
| Set of requesting entities (task generators) | |
| Set of serving entities (edge servers) | |
| Spatial density of REs (devices/m2) | |
| Spatial density of SEs (devices/m2) | |
| Total coverage area | |
| Task size of RE r (bytes) | |
| Computing capacity of SE s (CPU cycles/s) | |
| Computing capacity of central server (CS) | |
| L | Maximum sensing/coverage range of REs (m) |
| Viewing angle of RE r at time slot t | |
| Angular width of the field of view (FoV) | |
| Angular displacement between time slots | |
| Correlation threshold among REs’ FoVs | |
| PPP probability of observing k nodes in area |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeedi, H.; Nouruzi, A. Stochastic Geometric-Based Modeling for Partial Offloading Task Computing in Edge-AI Systems. Sensors 2025, 25, 6892. https://doi.org/10.3390/s25226892
Saeedi H, Nouruzi A. Stochastic Geometric-Based Modeling for Partial Offloading Task Computing in Edge-AI Systems. Sensors. 2025; 25(22):6892. https://doi.org/10.3390/s25226892
Chicago/Turabian StyleSaeedi, Hamid, and Ali Nouruzi. 2025. "Stochastic Geometric-Based Modeling for Partial Offloading Task Computing in Edge-AI Systems" Sensors 25, no. 22: 6892. https://doi.org/10.3390/s25226892
APA StyleSaeedi, H., & Nouruzi, A. (2025). Stochastic Geometric-Based Modeling for Partial Offloading Task Computing in Edge-AI Systems. Sensors, 25(22), 6892. https://doi.org/10.3390/s25226892




