Measurement of Form and Position Error of Small-Diameter Deep Holes Based on Collaboration Between a Lateral Confocal Displacement Sensor and Helical Scanning
Abstract
1. Introduction
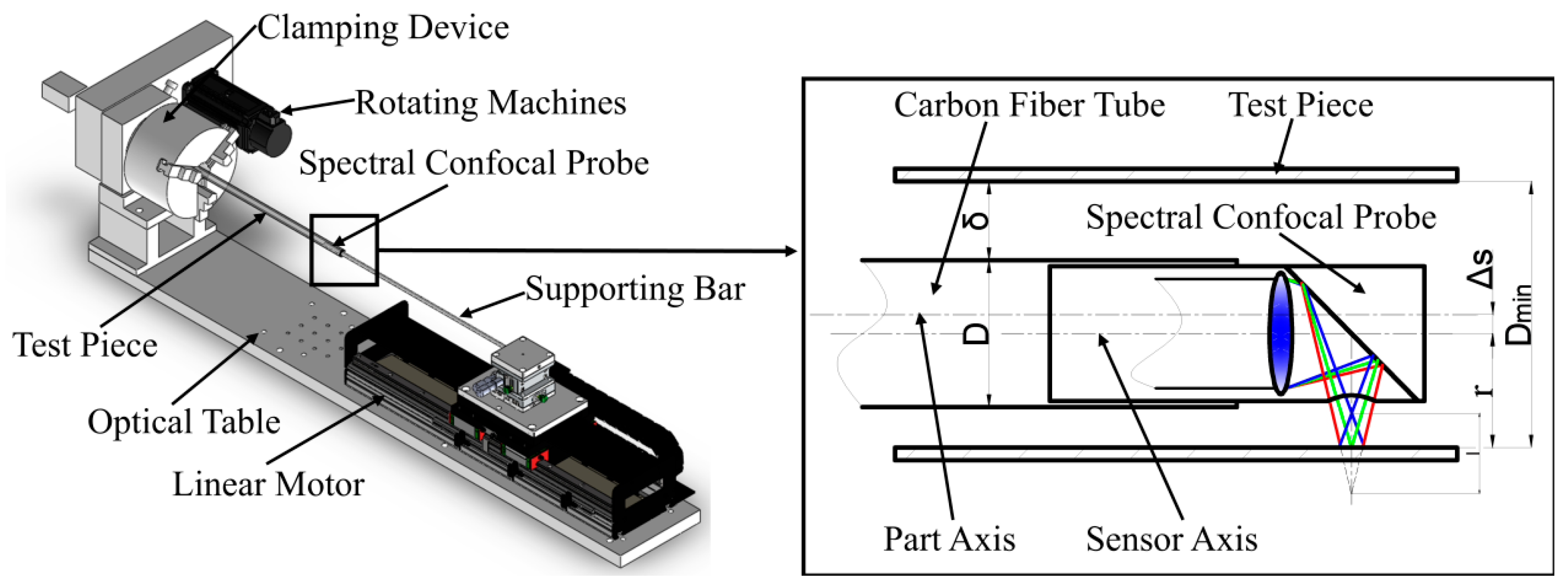
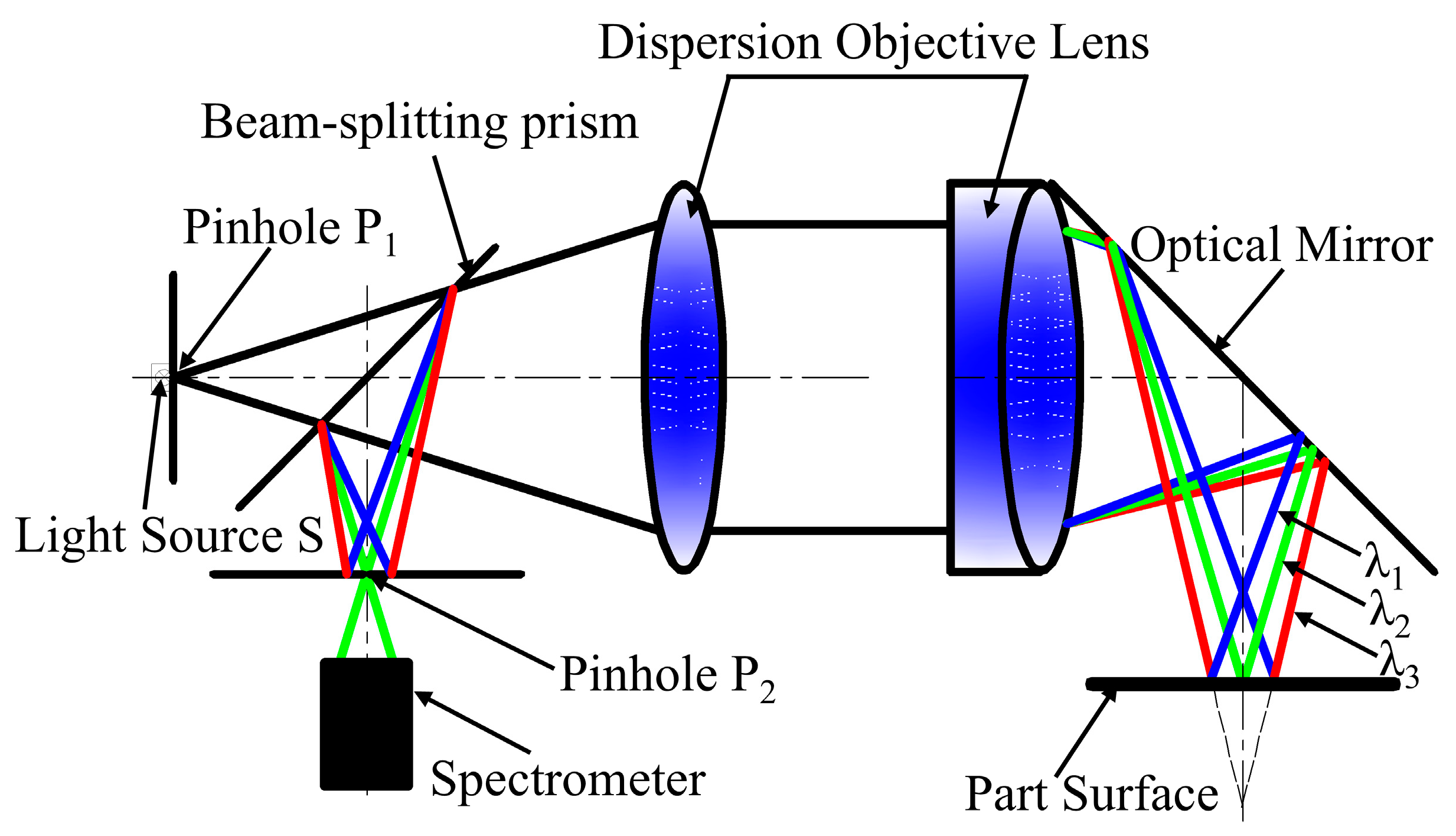
2. Measurement Principle
3. Compensation Methods
3.1. Data Preprocessing
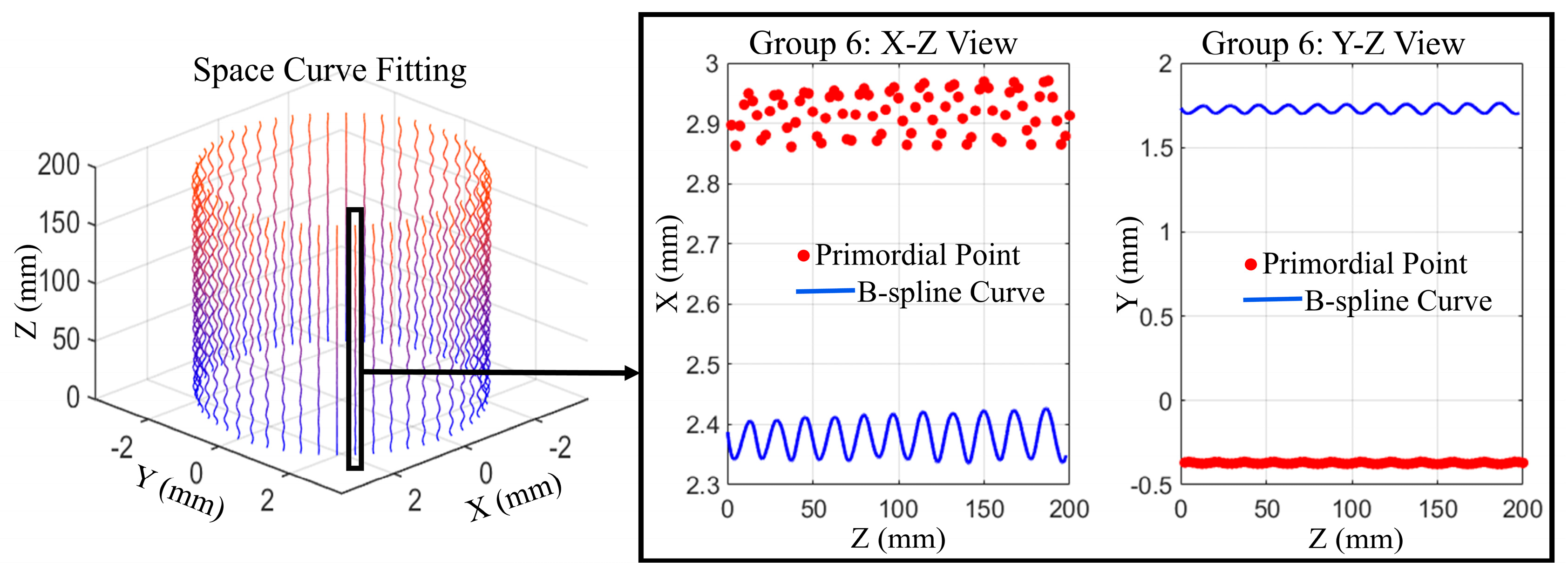
3.2. Virtual Slicing–B-Spline Reconstruction Method
4. Experimental Verification
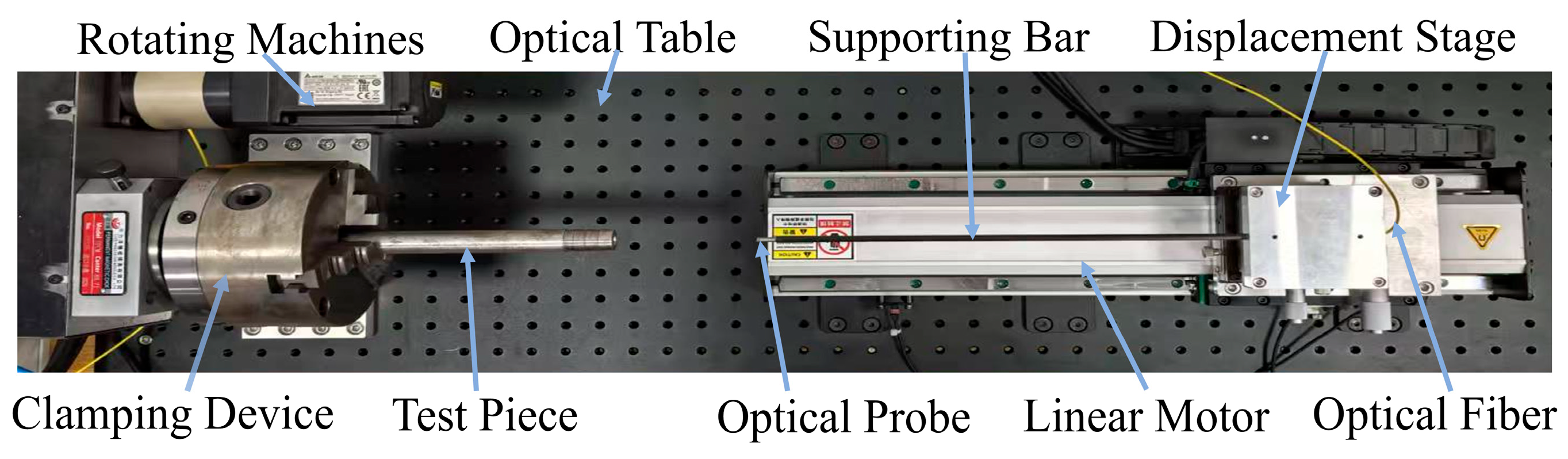
4.1. Lab Bench Construction
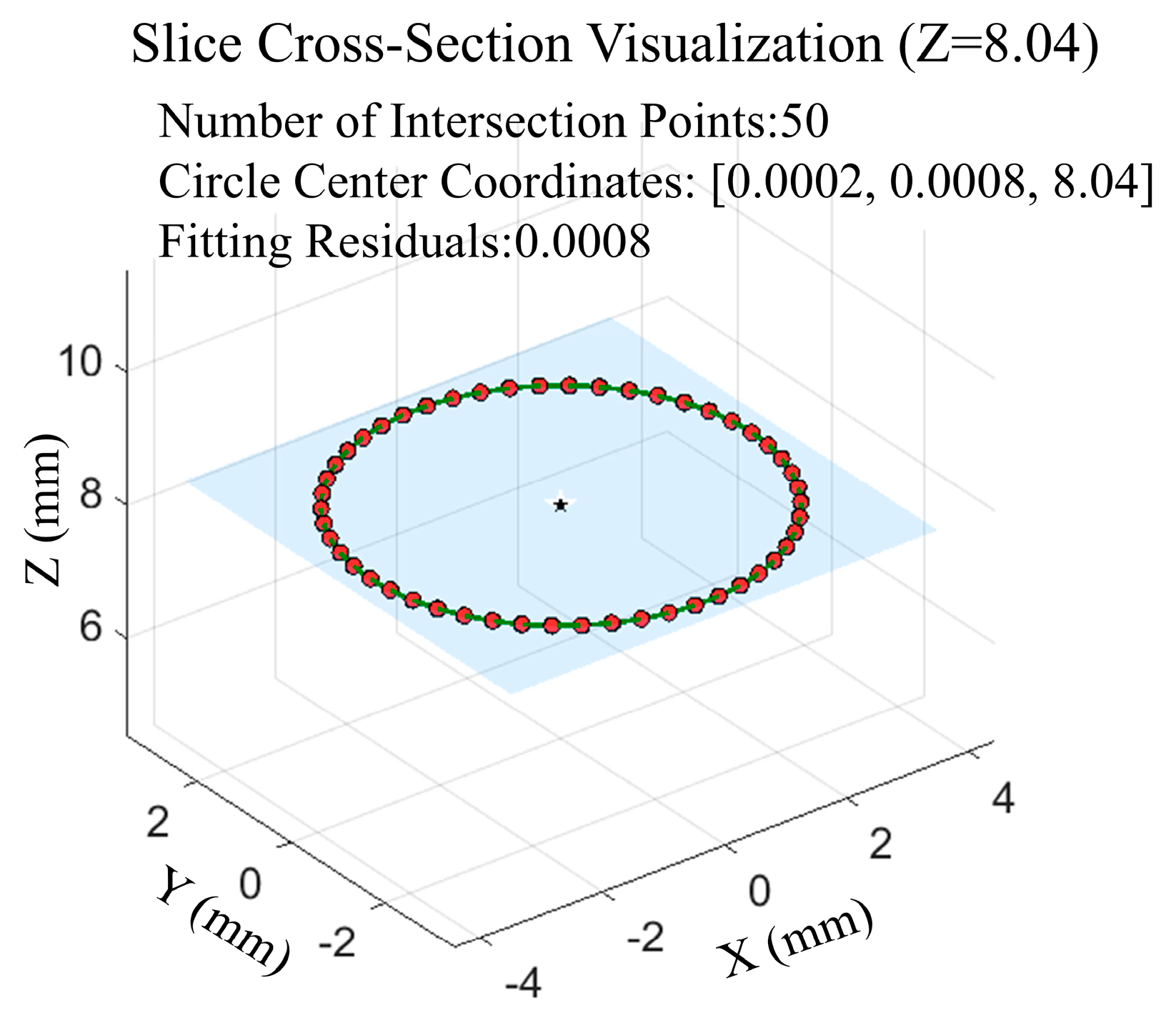
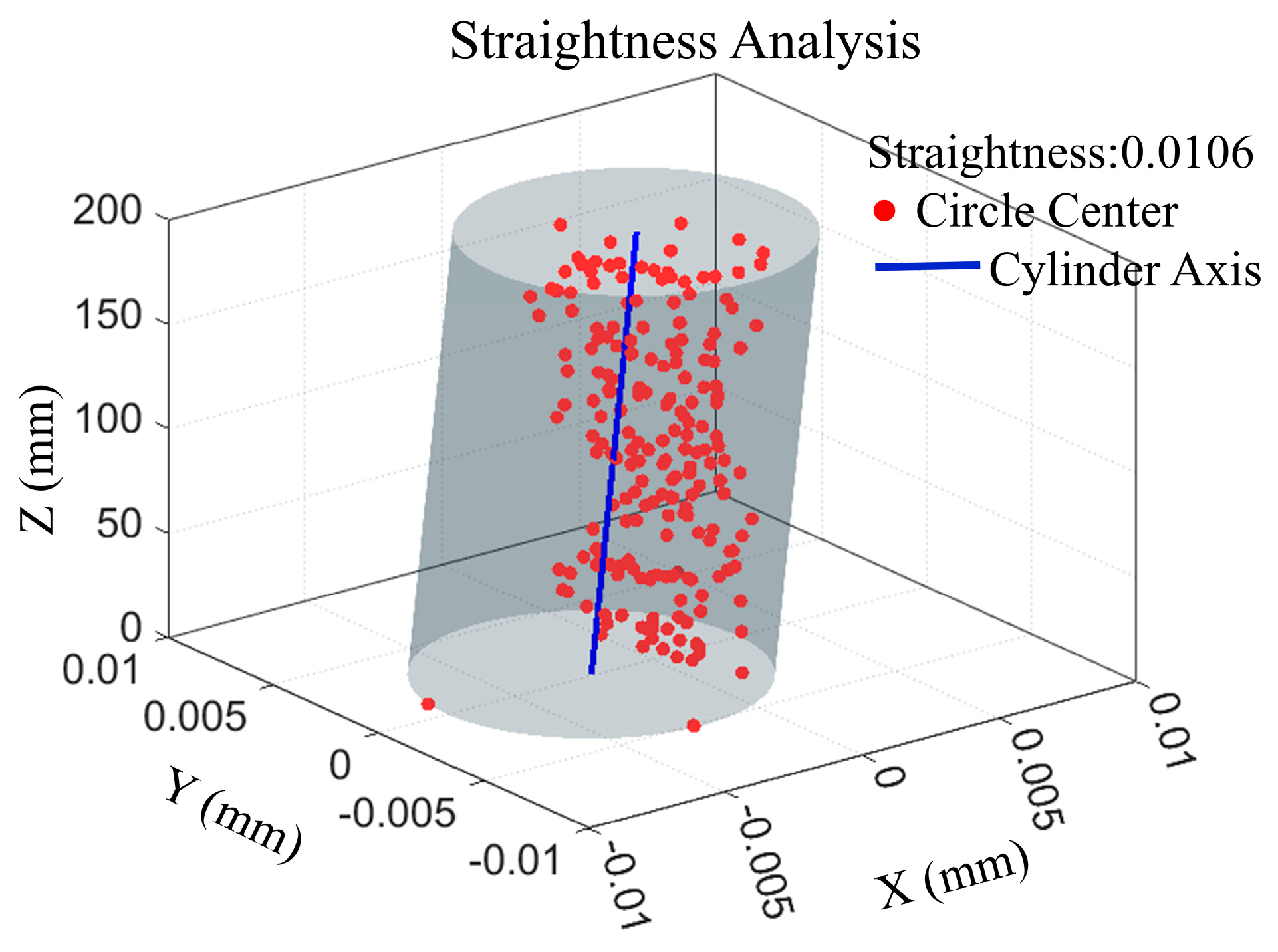
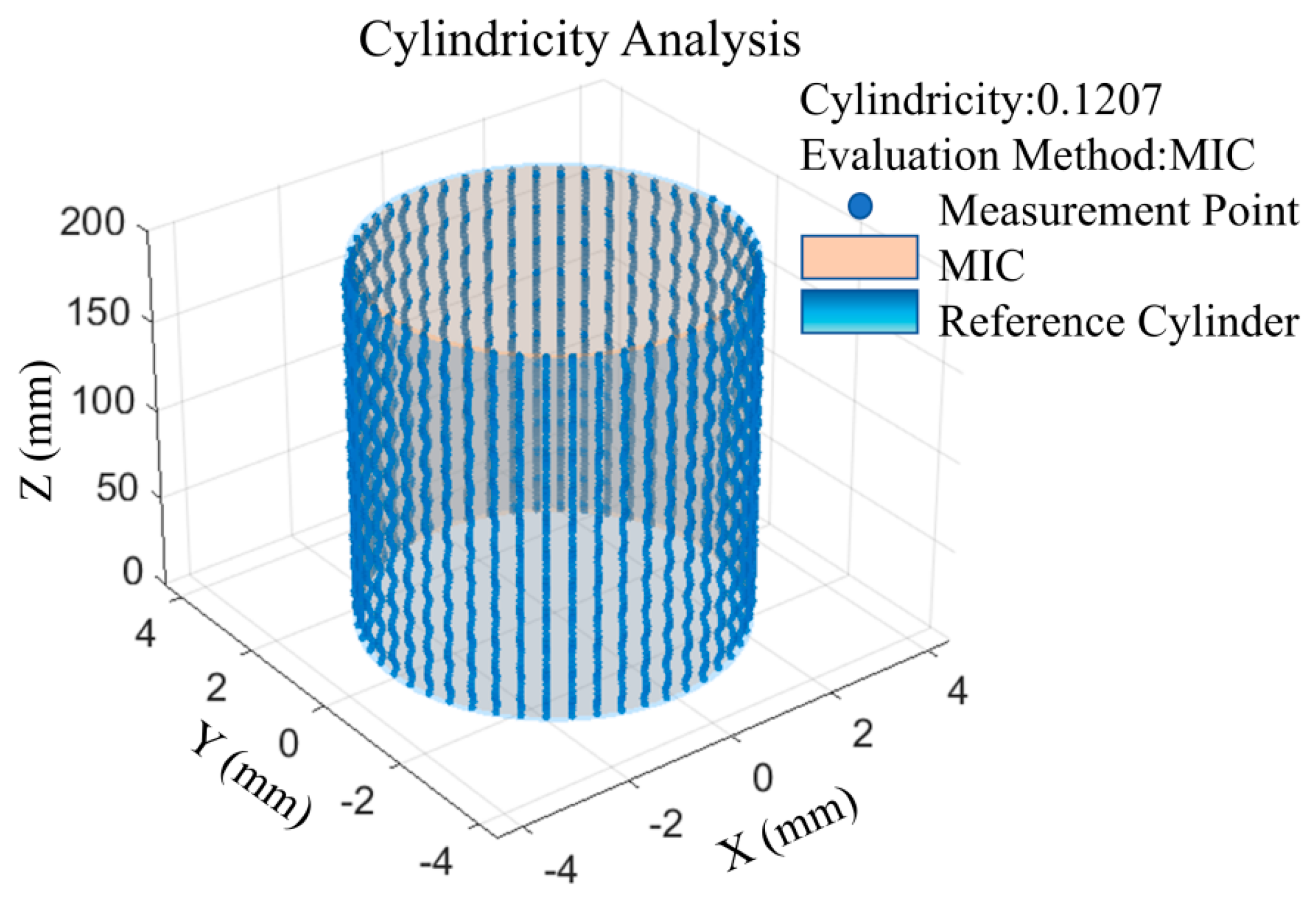
4.2. Measurement Results
4.2.1. Repeated Measurement Results
4.2.2. Measurement Result Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandar, J.B.; Nagarajan, L.; Kumar, M.S. Recent research progress in deep hole drilling process: A review. Surf. Rev. Lett. 2021, 28, 21300033. [Google Scholar] [CrossRef]
- Bhide, K.; Siddappaji, K.; Abdallah, S. Aspect Ratio Driven Relationship between Nozzle Internal Flow and Supersonic Jet Mixing. Aerospace 2021, 8, 78. [Google Scholar] [CrossRef]
- Natarajan, V.; Unnikrishnan, U.; Hwang, W.-S.; Choi, J.-Y.; Yang, V. Numerical study of two-phase flow dynamics and atomization in an open-type liquid swirl injector. Int. J. Multiph. Flow 2021, 143. [Google Scholar] [CrossRef]
- Xu, S.; Nixon, M.; Beall, J.; Wiklund, D.; Peluso, M. Process variability reduction in flow control and wedge flowmeter performance evaluation. Control. Eng. Pr. 2021, 110, 104780. [Google Scholar] [CrossRef]
- Dong, J.; Jing, C.; Peng, Y.; Liu, Y.; Ren, H.; Liu, X. Study on the measurement accuracy of an improved cemented carbide orifice flowmeter in natural gas pipeline. Flow Meas. Instrum. 2018, 59, 52–62. [Google Scholar] [CrossRef]
- Poljacek, S.M.; Risovic, D.; Furic, K.; Gojo, M. Comparison of fractal and profilometric methods for surface topography characterization. Appl. Surf. Sci. 2008, 254, 3449–3458. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, J.; Huang, N.; Zhang, Y.; Zhang, X.; Zhu, L. Surface form inspection with contact coordinate measurement: A review. Int. J. Extreme Manuf. 2023, 5, 022006. [Google Scholar] [CrossRef]
- Bian, X.; Cui, J.; Lu, Y.; Tan, J. Ultraprecision Diameter Measurement of Small Holes with Large Depth-To-Diameter Ratios Based on Spherical Scattering Electrical-Field Probing. Appl. Sci. 2019, 9, 242. [Google Scholar] [CrossRef]
- Fan, K.-C.; Cheng, F.; Pan, W.-T.; Li, R. Analysis of the contact probe mechanism for micro-coordinate measuring machines. Optoelectron. Instrum. Data Process. 2010, 46, 340–346. [Google Scholar] [CrossRef]
- Al-Musawi, R.S.J.; Brousseau, E.B.; Geng, Y.; Borodich, F.M. Insight into mechanics of AFM tip-based nanomachining: Bending of cantilevers and machined grooves. Nanotechnology 2016, 27, 385302. [Google Scholar] [CrossRef]
- Fu, S.; Cheng, F.; Tjahjowidodo, T.; Zhou, Y.; Butler, D. A Non-Contact Measuring System for In-Situ Surface Characterization Based on Laser Confocal Microscopy. Sensors 2018, 18, 2657. [Google Scholar] [CrossRef]
- Engel, T. 3D optical measurement techniques. Meas. Sci. Technol. 2022, 34, 032002. [Google Scholar] [CrossRef]
- Meng, F.; Yang, J.; Yang, G.; Lu, H.; Dong, Z.; Kang, R.; Guo, D.; Qin, Y. A Visual Measurement Method for Deep Holes in Composite Material Aerospace Components. Sensors 2024, 24, 3786. [Google Scholar] [CrossRef]
- Nguyen, A.; Le, B. 3D point cloud segmentation: A survey. In Proceedings of the 2013 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Phillippines, 12–15 November 2013; pp. 225–230. [Google Scholar] [CrossRef]
- ISO 12780-1:2011; Geometrical Product Specifications (GPS)—Straightness—Part 1: Vocabulary and Parameters of Straightness. International Organization for Standardization: Geneva, Switzerland, 2011.
- Minsky, M. Microscopy Apparatus. U.S. Patent 3,013,467, 19 December 1961. [Google Scholar]
- Bai, J.; Li, X.; Wang, X.; Wang, J.; Ni, K.; Zhou, Q. Self-reference dispersion correction for chromatic confocal displacement measurement. Opt. Lasers Eng. 2021, 140. [Google Scholar] [CrossRef]
- Bai, J.; Li, J.; Wang, X.; Zhou, Q.; Ni, K.; Li, X. A new method to measure spectral reflectance and film thickness using a modified chromatic confocal sensor. Opt. Lasers Eng. 2022, 154. [Google Scholar] [CrossRef]
- Yang, W.; Du, J.; Qi, M.; Yan, J.; Cheng, M.; Zhang, Z. Design of Optical System for Ultra-Large Range Line-Sweep Spectral Confocal Displacement Sensor. Sensors 2024, 24, 723. [Google Scholar] [CrossRef]
- Prause, K.; Herkommer, A.; Pinzer, B.R.; Layh, M. Single-shot high speed aerial chromatic confocal metrology sensor. Opt. Eng. 2021, 60, 124110. [Google Scholar] [CrossRef]
- Li, J.; Zhu, X.; Du, H.; Ji, Z.; Wang, K.; Zhao, M. Thickness measurement method for self-supporting film with double chromatic confocal probes. Appl. Opt. 2021, 60, 9447–9452. [Google Scholar] [CrossRef]
- Olsovsky, C.; Shelton, R.; Carrasco-Zevallos, O.; Applegate, B.E.; Maitland, K.C. Chromatic confocal microscopy for multi-depth imaging of epithelial tissue. Biomed. Opt. Express 2013, 4, 732–740. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T. Application of Wavelet and Wiener Filtering Algorithm in Image De-Noising. OALib 2016, 3, 1–7. [Google Scholar] [CrossRef]
- Al-Subaihi, I.A. Orthogonal least squares fitting with cylinders. Int. J. Comput. Math. 2016, 94, 841–851. [Google Scholar] [CrossRef]
- MacCallum, K.J.; Zhang, J.-M. Curve-smoothing Techniques Using B-splines. Comput. J. 1986, 29, 564–571. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.-H.; Su, Y.; Li, R.-C. Accurate polynomial fitting and evaluation via Arnoldi. Numer. Algebra Control. Optim. 2023, 14, 526–546. [Google Scholar] [CrossRef]
- Gill, P.E.; Wong, E. Sequential Quadratic Programming Methods. In Mixed Integer Nonlinear Programming; Springer: New York, NY, USA, 2012; pp. 147–224. [Google Scholar] [CrossRef]


| Feed Rate (mm/s) | Rotation Speed (rpm) | Sampling Period (s) | First | Second | Third | Fourth | Fifth | Average Value |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 4 | 0.05 | 0.0100 | 0.0096 | 0.0094 | 0.0104 | 0.0088 | 0.0096 |
| 0.5 | 8 | 0.05 | 0.0095 | 0.0099 | 0.0087 | 0.0106 | 0.0091 | 0.0096 |
| 0.5 | 12 | 0.1 | 0.0106 | 0.0107 | 0.0092 | 0.0091 | 0.0096 | 0.0098 |
| 0.5 | 24 | 0.1 | 0.0100 | 0.0098 | 0.0111 | 0.0108 | 0.0092 | 0.0102 |
| 1 | 24 | 0.1 | 0.0115 | 0.0117 | 0.0100 | 0.0110 | 0.0106 | 0.0110 |
| Feed Rate (mm/s) | Rotation Speed (rpm) | Sampling Period (s) | First | Second | Third | Fourth | Fifth | Average Value |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 4 | 0.05 | 0.1167 | 0.1211 | 0.1123 | 0.1189 | 0.1145 | 0.1167 |
| 0.5 | 8 | 0.05 | 0.1253 | 0.1338 | 0.1287 | 0.1361 | 0.1312 | 0.1310 |
| 0.5 | 12 | 0.1 | 0.1207 | 0.1166 | 0.1185 | 0.1085 | 0.1106 | 0.1150 |
| 0.5 | 24 | 0.1 | 0.1356 | 0.1309 | 0.1393 | 0.1387 | 0.1307 | 0.1350 |
| 1 | 24 | 0.1 | 0.1545 | 0.1552 | 0.1374 | 0.1495 | 0.1473 | 0.1488 |
| Parameter | Slicing Method | CMM | Absolute Deviation | Relative Deviation |
|---|---|---|---|---|
| Cylindricity | 0.1210 | 0.1269 | −0.0059 | −4.6% |
| Straightness | 0.0106 | 0.0111 | −0.0005 | −4.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yu, D.; Du, H.; Chen, T. Measurement of Form and Position Error of Small-Diameter Deep Holes Based on Collaboration Between a Lateral Confocal Displacement Sensor and Helical Scanning. Sensors 2025, 25, 6863. https://doi.org/10.3390/s25226863
Liu Y, Yu D, Du H, Chen T. Measurement of Form and Position Error of Small-Diameter Deep Holes Based on Collaboration Between a Lateral Confocal Displacement Sensor and Helical Scanning. Sensors. 2025; 25(22):6863. https://doi.org/10.3390/s25226863
Chicago/Turabian StyleLiu, Yao, Daguo Yu, Huifu Du, and Tong Chen. 2025. "Measurement of Form and Position Error of Small-Diameter Deep Holes Based on Collaboration Between a Lateral Confocal Displacement Sensor and Helical Scanning" Sensors 25, no. 22: 6863. https://doi.org/10.3390/s25226863
APA StyleLiu, Y., Yu, D., Du, H., & Chen, T. (2025). Measurement of Form and Position Error of Small-Diameter Deep Holes Based on Collaboration Between a Lateral Confocal Displacement Sensor and Helical Scanning. Sensors, 25(22), 6863. https://doi.org/10.3390/s25226863






