Research on Roll Attitude Estimation Algorithm for Precision Firefighting Extinguishing Projectiles Based on Single MEMS Gyroscope
Abstract
1. Introduction
- A roll attitude estimation framework is established based on a single MEMS gyroscope, incorporating installation error modeling that enables practical deployment on low-cost projectiles.
- A time–frequency adaptive IIR filtering algorithm is developed to track the time-varying roll angular rate and separate roll-related components from the measured signal.
- The proposed method is validated through both simulation and turntable experimentation, demonstrating its accuracy and robustness under dynamic motion conditions.
2. Methodology and Theoretical Analysis
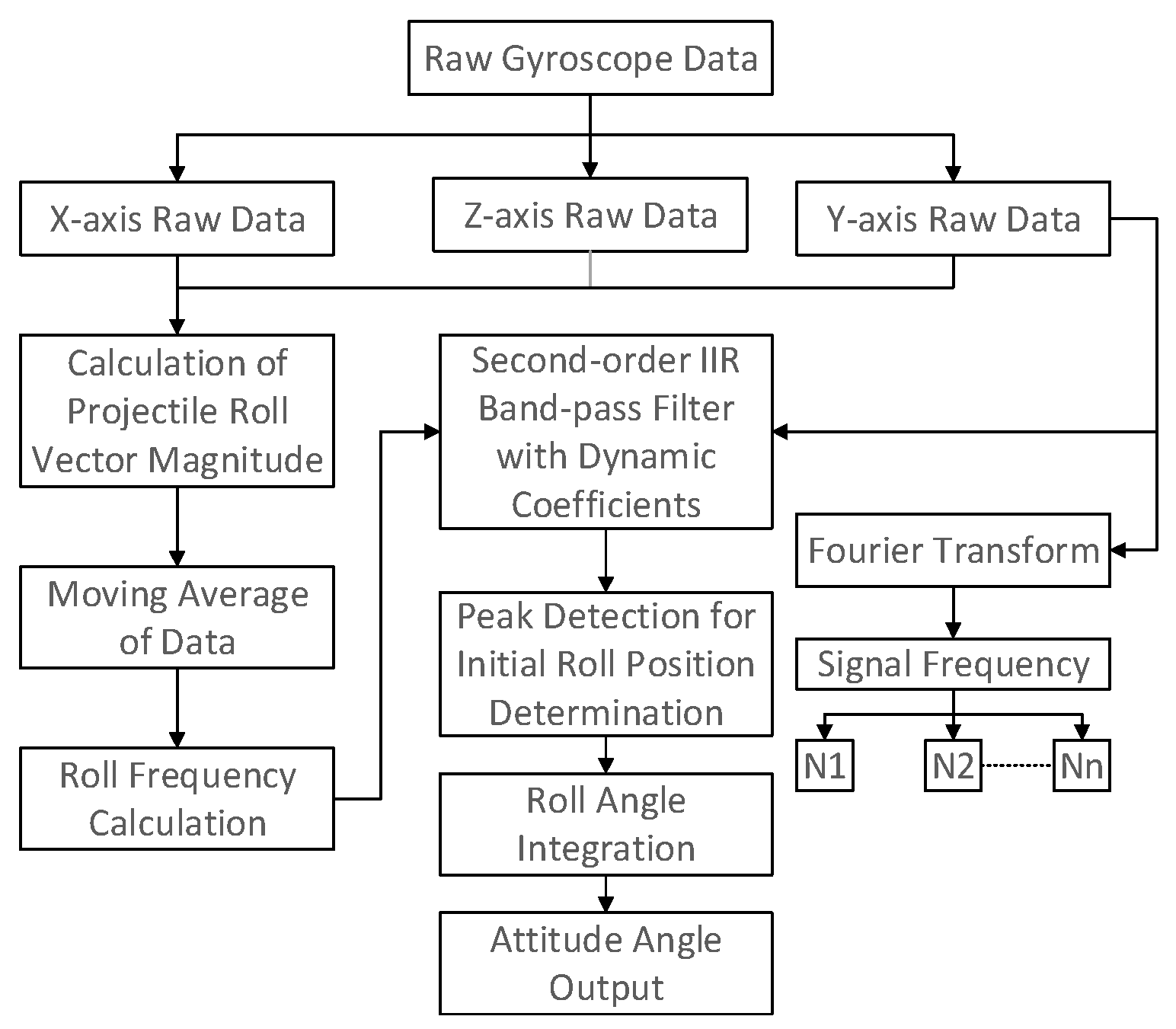
2.1. Overall Design Concept of the Method
- Data analysis and preprocessing: Calculate the modulus of the original gyroscope data to obtain the estimated value of the extinguishing projectile’s roll angular velocity, perform moving average calculation on the estimated value of the extinguishing projectile’s roll angular velocity, and solve the roll frequency to prepare for subsequent filtering processing.
- Data filtering: Perform filtering processing in the frequency domain. Considering that the change in roll angular velocity will cause frequency changes, this study combines angular velocity to perform dynamic coefficient second-order IIR band-pass filtering.
- Attitude angle calculation: Perform peak detection on the filtered data to determine the roll position of the extinguishing projectile. Calculate the roll attitude angle by combining the integral of the actual roll angular velocity of the extinguishing projectile, and output the roll attitude angle for the control of the extinguishing projectile.
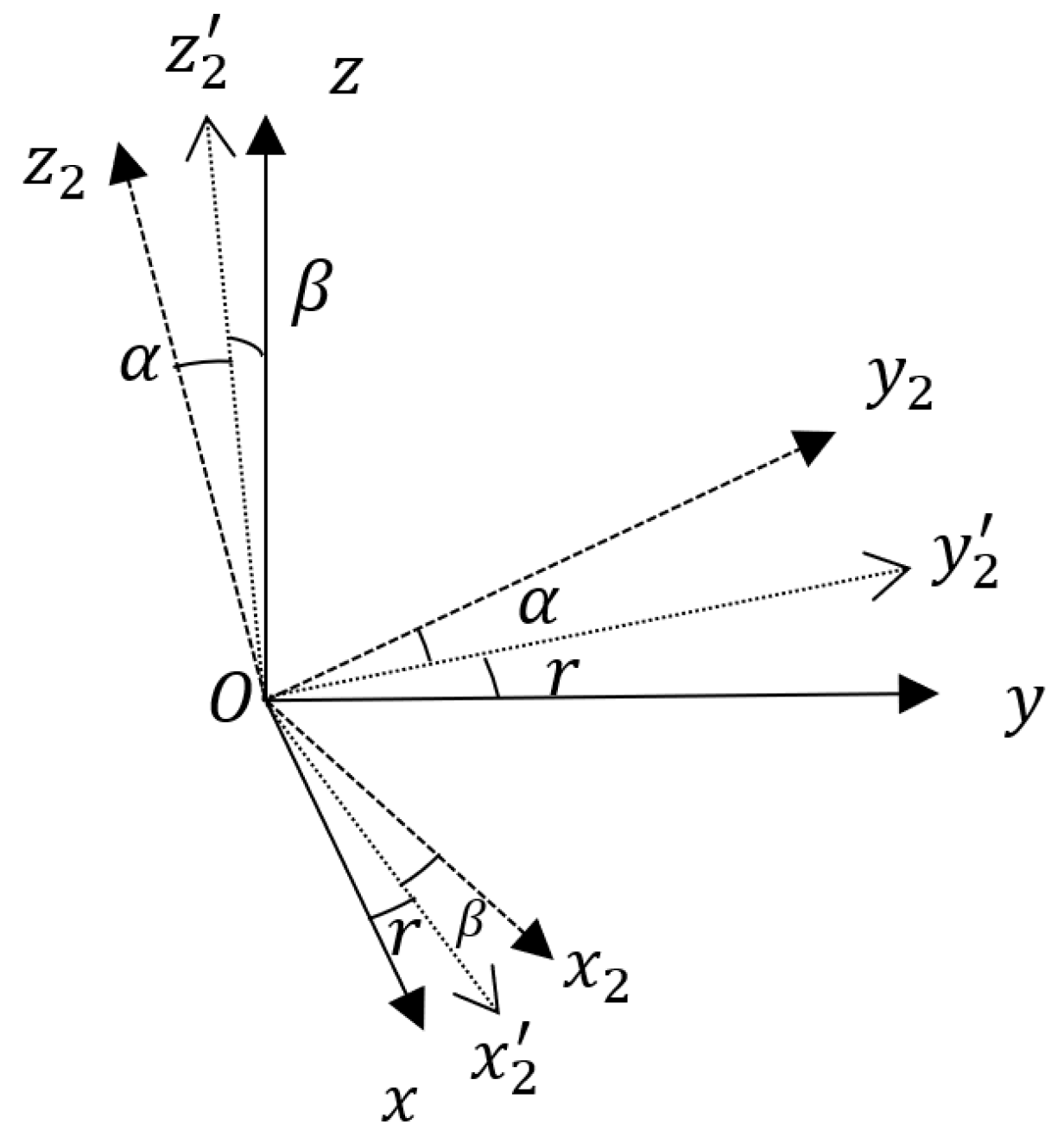
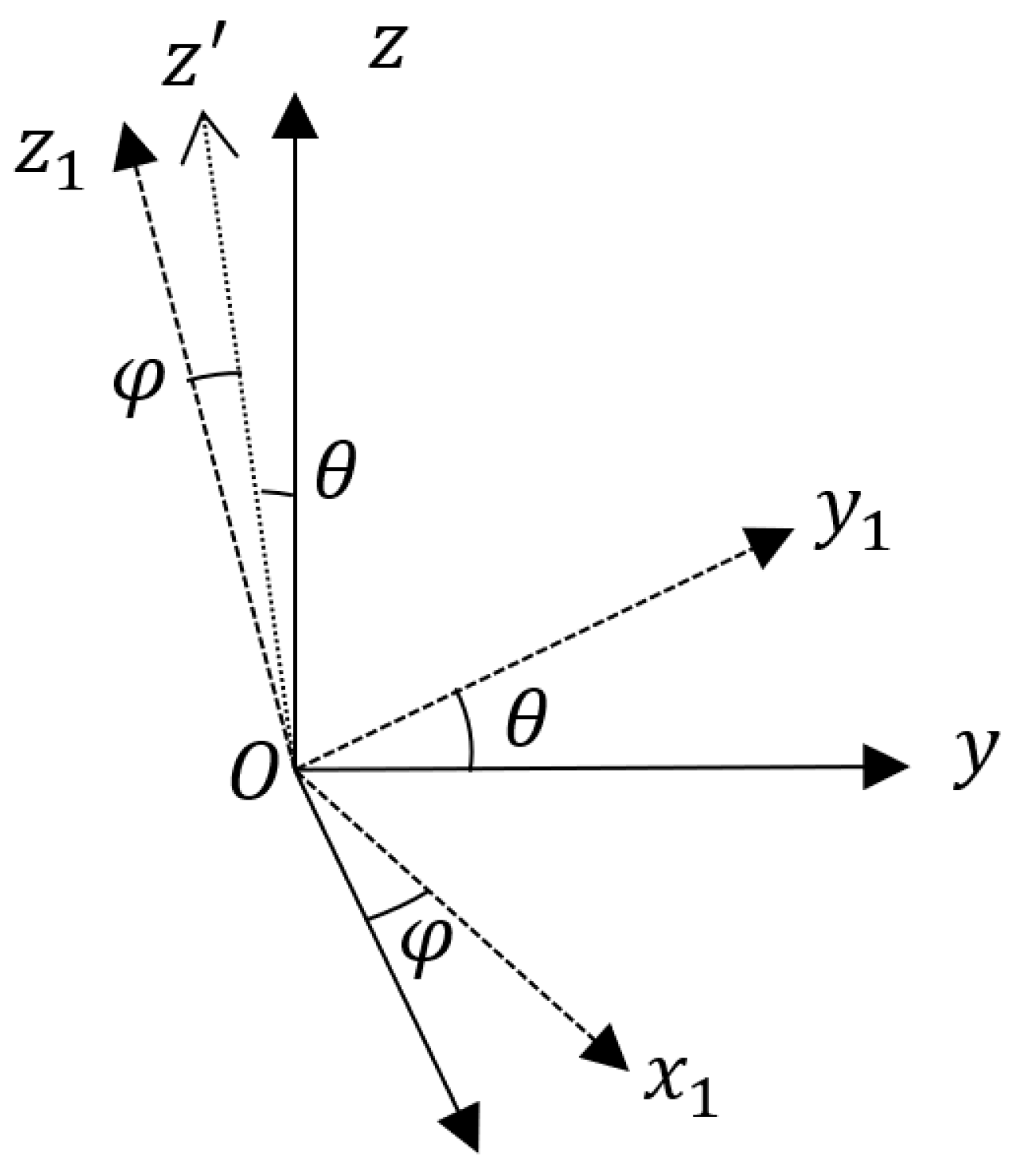
2.2. Principle Analysis of Single-Gyro Attitude Measurement
3. Data Filtering and Roll Attitude Calculation
3.1. Data Filtering
- α: Sensitivity coefficient (typical value: 0.1~0.3);
- fs: Sampling frequency (100–1000 Hz);
- ε: Minimum value (to avoid division by zero, 1 × 10−6).
3.2. Roll Attitude Calculation
4. Experimental Results and Analysis
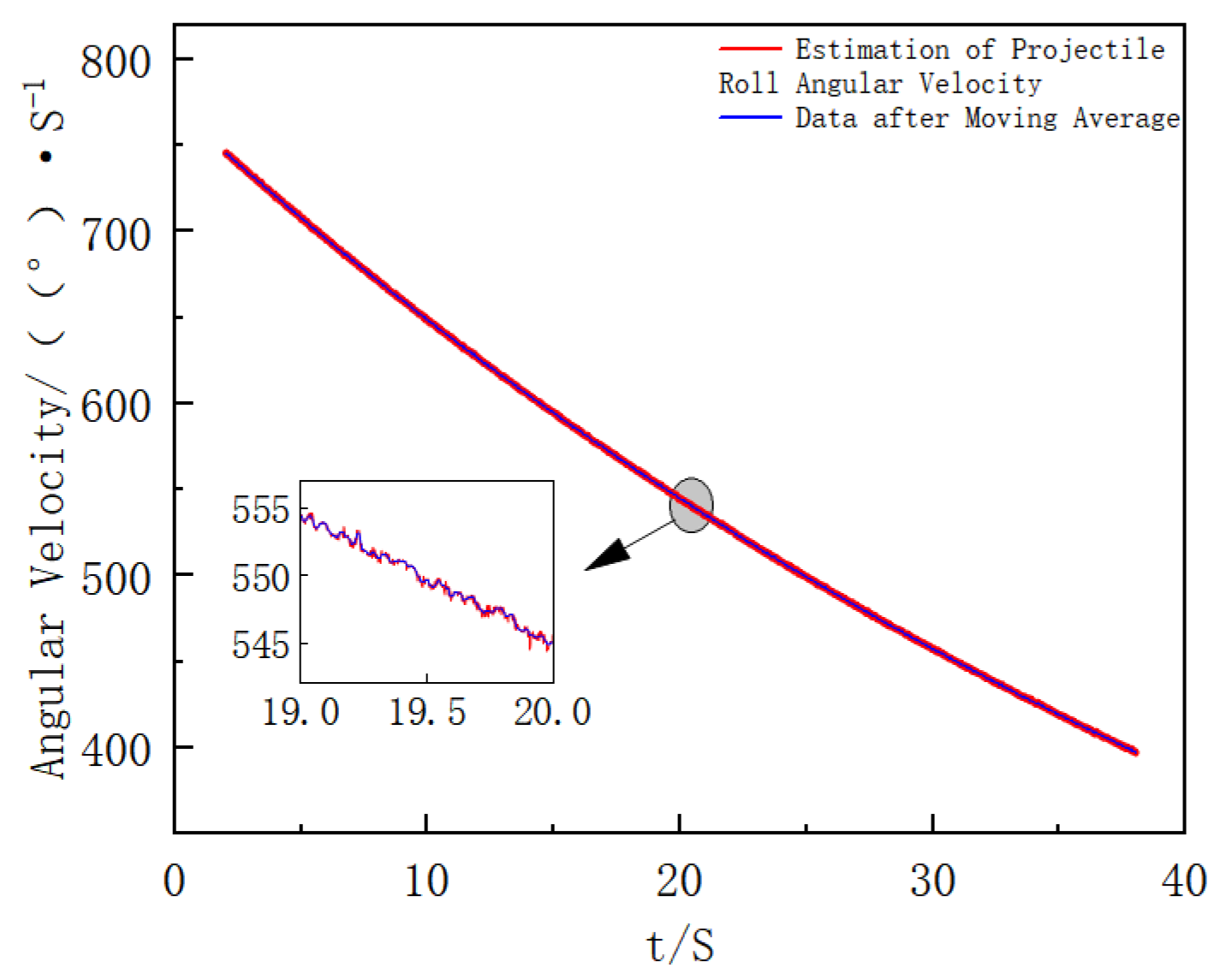
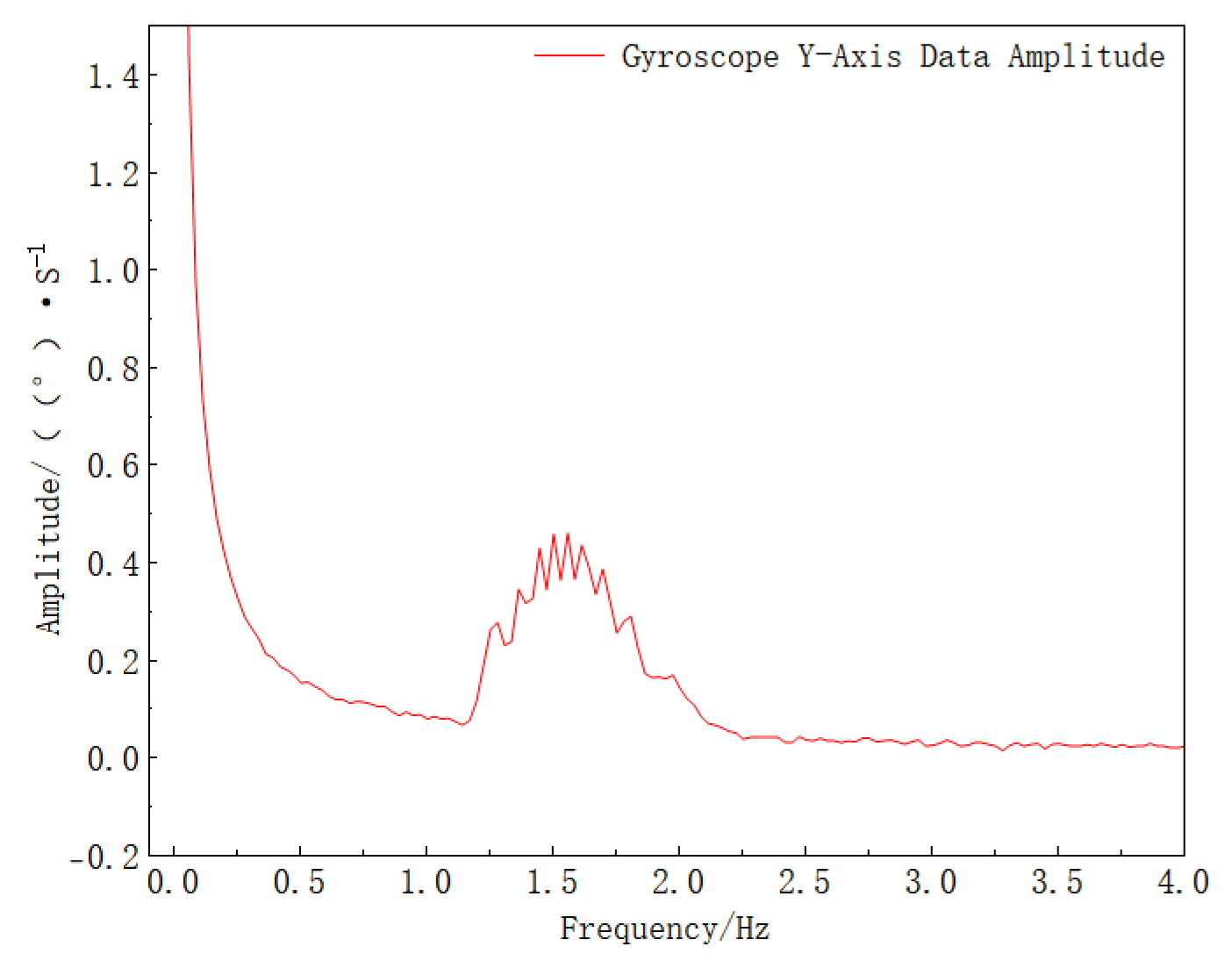
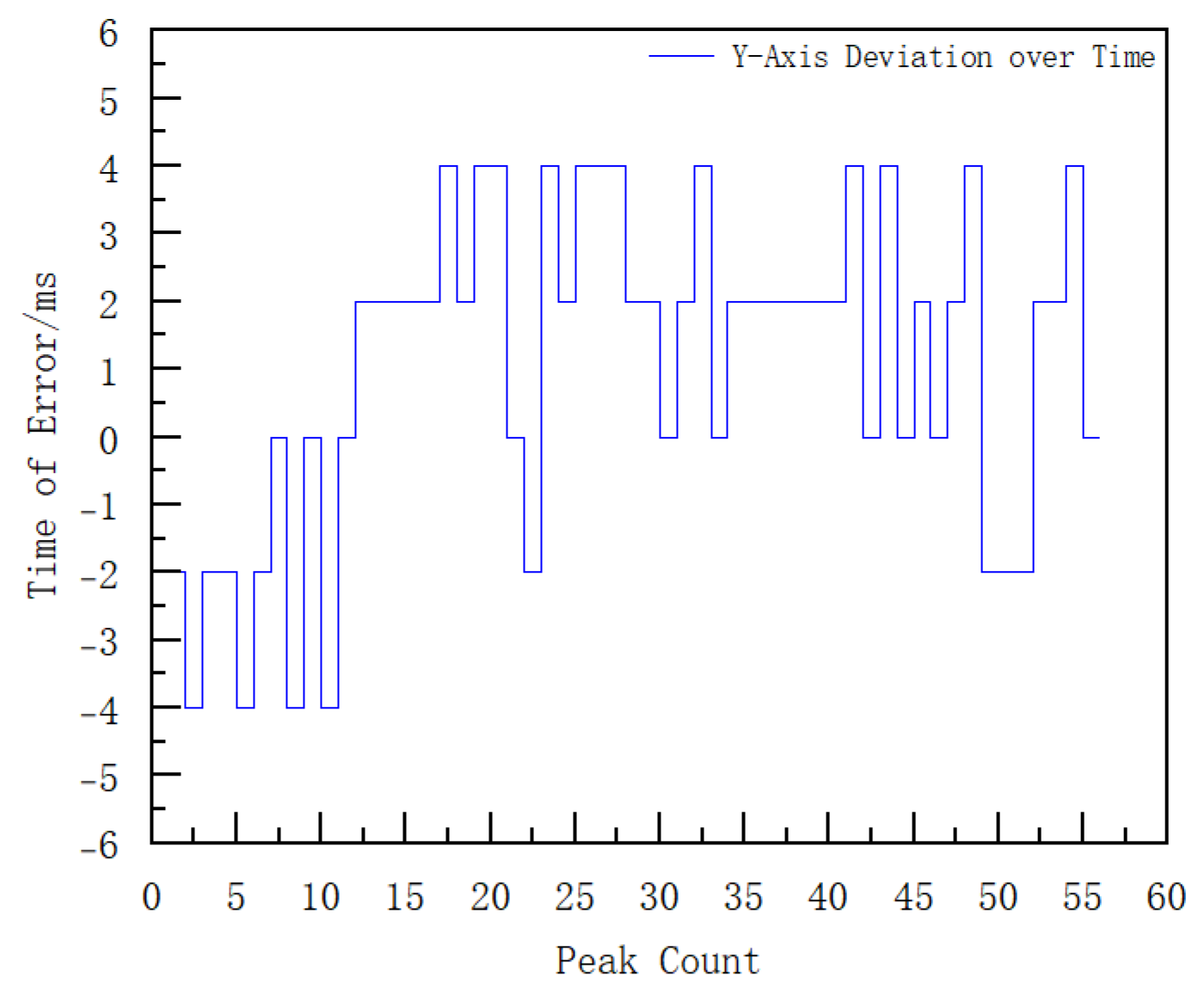
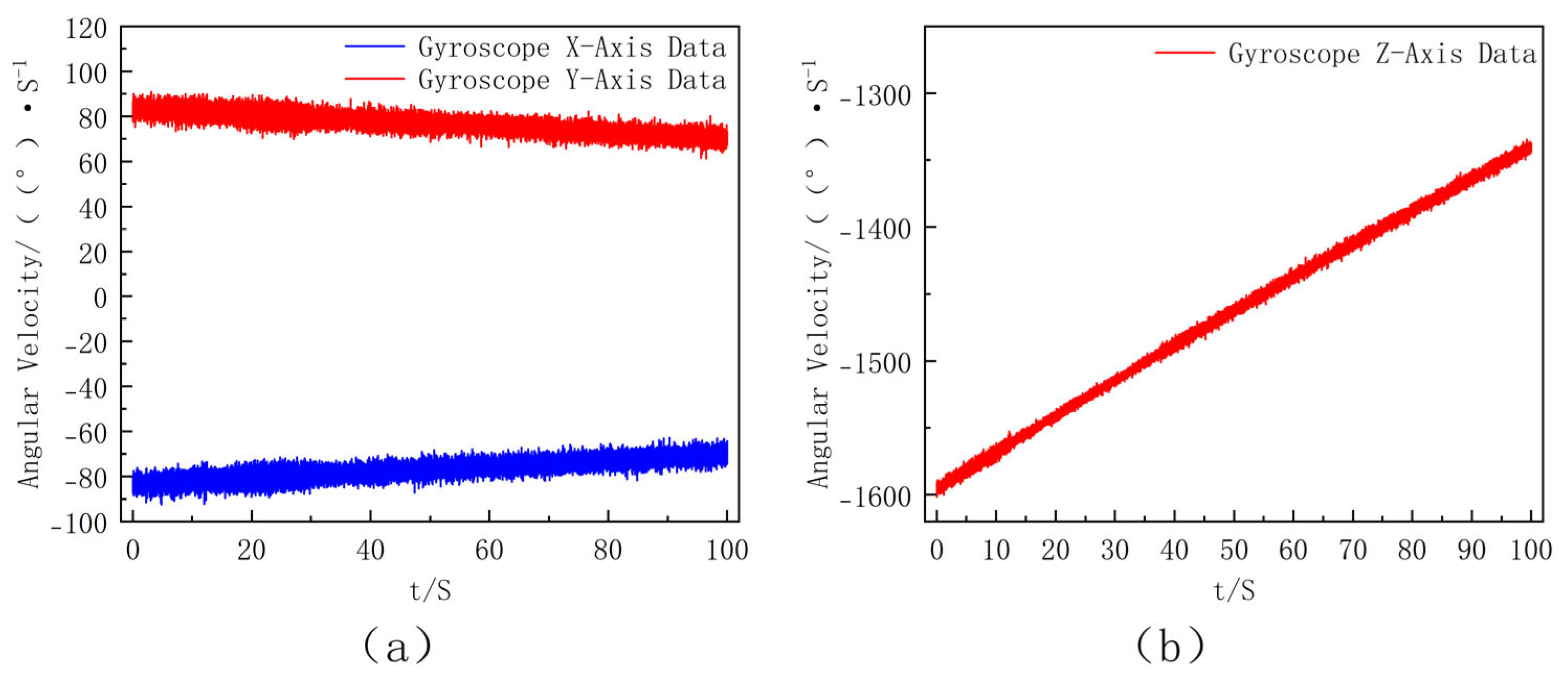
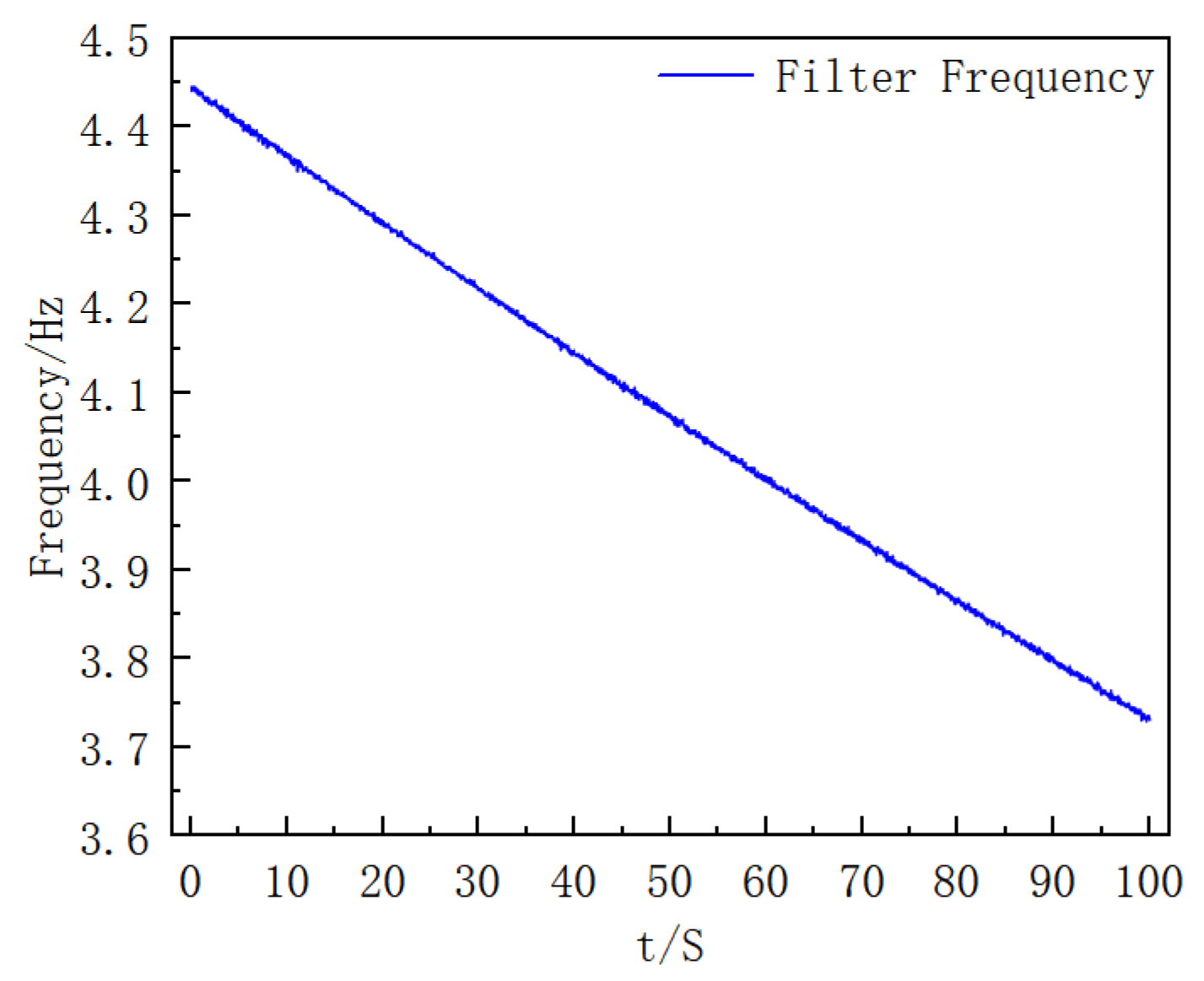
4.1. Modeling and Verification of Projectile External Ballistics Simulation Based on MATLAB
4.2. Turntable Experiment
4.3. Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, Y. Research on Inertial Navigation System Technologies Based on MIMU Array. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2025. [Google Scholar] [CrossRef]
- Chen, K.; Fang, Y.; Yang, R.; Li, X.; Song, J. Review of in-air alignment algorithms for guided projectiles. In Proceedings of the Seminar on the Development Trends of Inertial Technology—New Inertial Components and Advanced Navigation Technology, Harbin, China, 9 August 2023; Northwestern Polytechnical University: Xi’an, China, 2023; pp. 487–492. [Google Scholar] [CrossRef]
- Chen, S.; Yang, B.; Song, Y.; Zhang, Y. Overview on Guide Projectile Attitude Measurement Technology. J. Detect. Control 2021, 43, 9–13. [Google Scholar]
- Yang, W.; Yu, W.; Pei, D.; Zhang, Y.; Zu, J. Study on the Missile Projectile Parameter Test Technology. Electron. Devices 2016, 39, 667–670. [Google Scholar] [CrossRef]
- Shang, J.; Deng, Z.; Fu, M.; Wang, S.T. Advance and Perspective on Spin Rate Measurement Technology for Guided Projectile. Acta Autom. Sin. 2016, 42, 1620–1629. [Google Scholar] [CrossRef]
- She, H.; Yang, S.; Ni, H. New Algorithms to Estimate Initial Roll Angle for In-flight Alignment of GPS/INS Guided Munitions. Acta Armamentarii 2011, 32, 1265–1270. [Google Scholar]
- Zhang, Y.; Zhang, X.; Xue, Y. An estimation method of roll angle and rate of spinning projectile based on geomagnetic information. China Meas. 2021, 47, 38–43. [Google Scholar]
- Zhang, P.; Gao, M.; Wang, W.; Wang, Y.; Li, C. Projectile attitude measurement technology based on geomagnetism/gyroscope. J. Chin. Inert. Technol. 2024, 32, 874–881. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X.; Du, J.; Qiu, J. Fusion Algorithm for Geomagnetic and Gyroscope Attitudes Based on AEKF. Comput. Meas. Control 2025, 33, 271–279. [Google Scholar] [CrossRef]
- Yang, S.; Han, Y.; Jia, S. Research on Flight approach Landing based on GNSS/INS Navigation. Aviat. Comput. Technol. 2025, 55, 114–118. [Google Scholar]
- Zhang, B.; Zhang, P.; Cheng, C. Design and implementation of INS/GNSS integrated navigation system enhanced by 5G-enabled magnetic navigation. China Broadband 2025, 21, 115–117. [Google Scholar] [CrossRef]
- Cao, X.; Shi, Y.; Liu, Y.; Zhao, C.; Liu, T. Global positioning performance analysis of BDS-3/GPS integrated navigation system. Pearl River Shipp. 2024, 4, 24–29. [Google Scholar] [CrossRef]
- Gao, L. Attitude Estimation of Rotating Ammunition Based on Geomagnetic/MEMS Gyro Information Fusion. Master’s Thesis, North University of China, Taiyuan, China, 2021. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, J.; Fan, S.; Bai, C.; Zhou, Y.; Hu, S. In-flight Alignment Method of Guided Projectile Roll Angle Based on Trajectory Bending Angular Velocity Single Vector. Acta Armamentarii 2023, 44, 417–427. [Google Scholar] [CrossRef]
- Fukuda, G.; Kubo, N. Bias Estimation for Low-Cost IMU Including X- and Y-Axis Accelerometers in INS/GPS/Gyrocompass. Sensors 2025, 25, 1315. [Google Scholar] [CrossRef]
- Pang, S.; Zhang, B.; Lu, J.; Pan, R.; Wang, H.; Wang, Z.; Xu, S. Application of IMU/GPS Integrated Navigation System Based on Adaptive Unscented Kalman Filter Algorithm in 3D Positioning of Forest Rescue Personnel. Sensors 2024, 24, 5873. [Google Scholar] [CrossRef]
- Nagui, N.; Attallah, O.; Zaghloul, M.S.; Morsi, I. Improved GPS/IMU Loosely Coupled Integration Scheme Using Two Kalman Filter-based Cascaded Stages. Arab. J. Sci. Eng. 2020, 46, 1345–1367. [Google Scholar] [CrossRef]
- Ismail, M.; Abdelkawy, E. A hybrid error modeling for MEMS IMU in integrated GPS/INS navigation system. J. Glob. Position. Syst. 2018, 16, 6. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Shen, W.; Li, Y.; Chen, Q.; Zhang, H.; Niu, X. Evaluation on the impact of IMU grades on BDS + GPS PPP/INS tightly coupled integration. Adv. Space Res. 2017, 60, 1283–1299. [Google Scholar] [CrossRef]
- Deng, Z.; Qiang, S.; Zhao, D. Roll Angle Measurement for a Spinning Vehicle Based on GPS Signals Received by a Single-Patch Antenna. Sensors 2018, 18, 3479. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Tang, T.; Ding, W.; Meng, X.; Liu, J.; Jiang, J. A robust single-antenna GNSS/MEMS fusion structure for reliable attitude determination in challenged environments. Sci. Rep. 2025, 15, 24462. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Chen, L.; Sun, C.; Jia, W.; Yi, N.; Sun, W. Highly Accurate Attitude Estimation of Unmanned Aerial Vehicle Payloads Using Low-Cost MEMS. Micromachines 2025, 16, 632. [Google Scholar] [CrossRef]
- Dang, D.C.; Suh, Y.S. Improved Single Inertial-Sensor-Based Attitude Estimation during Walking Using Velocity-Aided Observation. Sensors 2021, 21, 3428. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, X.; Xu, H.; Jia, R. Estimation of IMU Misalignment and Gyro Drift in SINS. Fire Control. Command. Control. 2008, 33, 82–84. [Google Scholar]








| Parameter | Value/Setting |
|---|---|
| Initial velocity | 600 m/s |
| Initial pitch angle | 45° |
| Initial roll/yaw angle | 0°/0° |
| Initial roll angular rate | 800°/s |
| Damping coefficient | 1°/s |
| Simulation duration | 40 s |
| Time step | 0.01 s |
| (quality factor) | 4 |
| (Sensitivity coefficient) | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Liu, Z.; Liu, C. Research on Roll Attitude Estimation Algorithm for Precision Firefighting Extinguishing Projectiles Based on Single MEMS Gyroscope. Sensors 2025, 25, 6721. https://doi.org/10.3390/s25216721
Zeng J, Liu Z, Liu C. Research on Roll Attitude Estimation Algorithm for Precision Firefighting Extinguishing Projectiles Based on Single MEMS Gyroscope. Sensors. 2025; 25(21):6721. https://doi.org/10.3390/s25216721
Chicago/Turabian StyleZeng, Jinsong, Zeyuan Liu, and Chengyang Liu. 2025. "Research on Roll Attitude Estimation Algorithm for Precision Firefighting Extinguishing Projectiles Based on Single MEMS Gyroscope" Sensors 25, no. 21: 6721. https://doi.org/10.3390/s25216721
APA StyleZeng, J., Liu, Z., & Liu, C. (2025). Research on Roll Attitude Estimation Algorithm for Precision Firefighting Extinguishing Projectiles Based on Single MEMS Gyroscope. Sensors, 25(21), 6721. https://doi.org/10.3390/s25216721








