Super-Resolution Reconstruction of Sonograms Using Residual Dense Conditional Generative Adversarial Network
Abstract
1. Introduction
- (1)
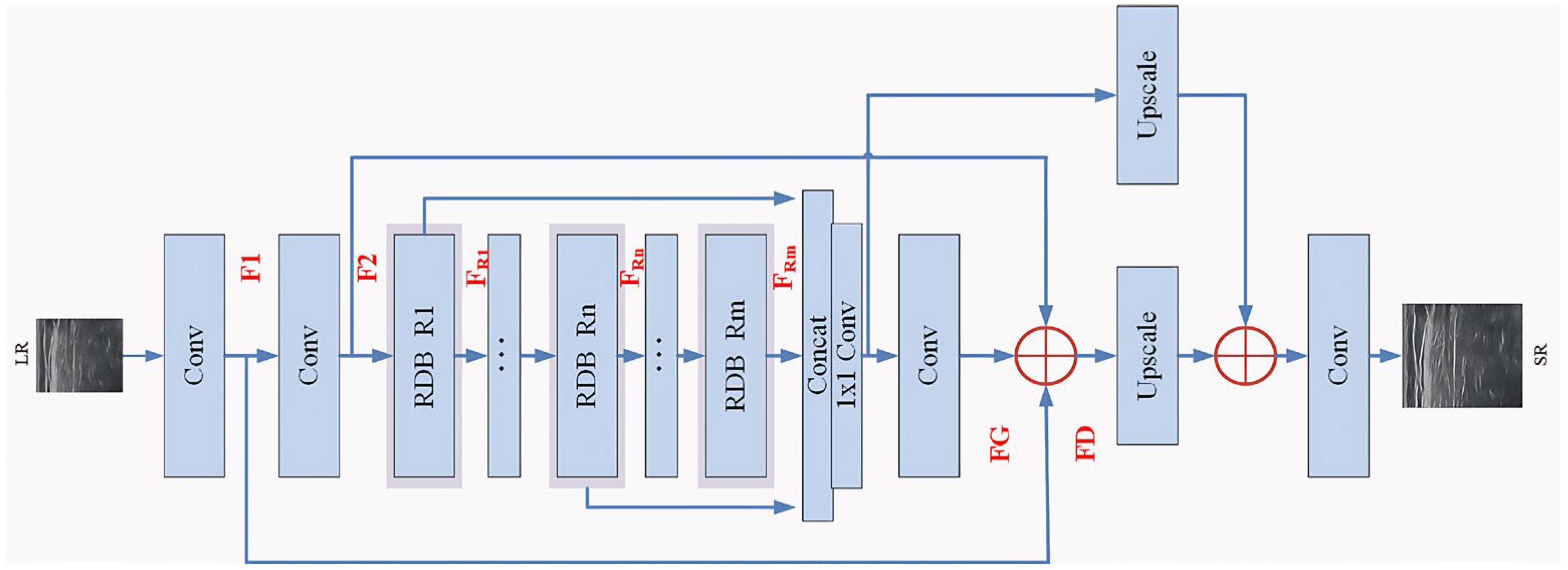
- In the generator, the features of different levels of the original LR image are fully learned and obtained through the cascading of multiple residual dense blocks (RDB), based on the works of SRGAN and Zhang [25]; through global feature fusion (GFF), the hierarchical structure features are adaptively retained in a global way to achieve the use of multi-level information.
- (2)
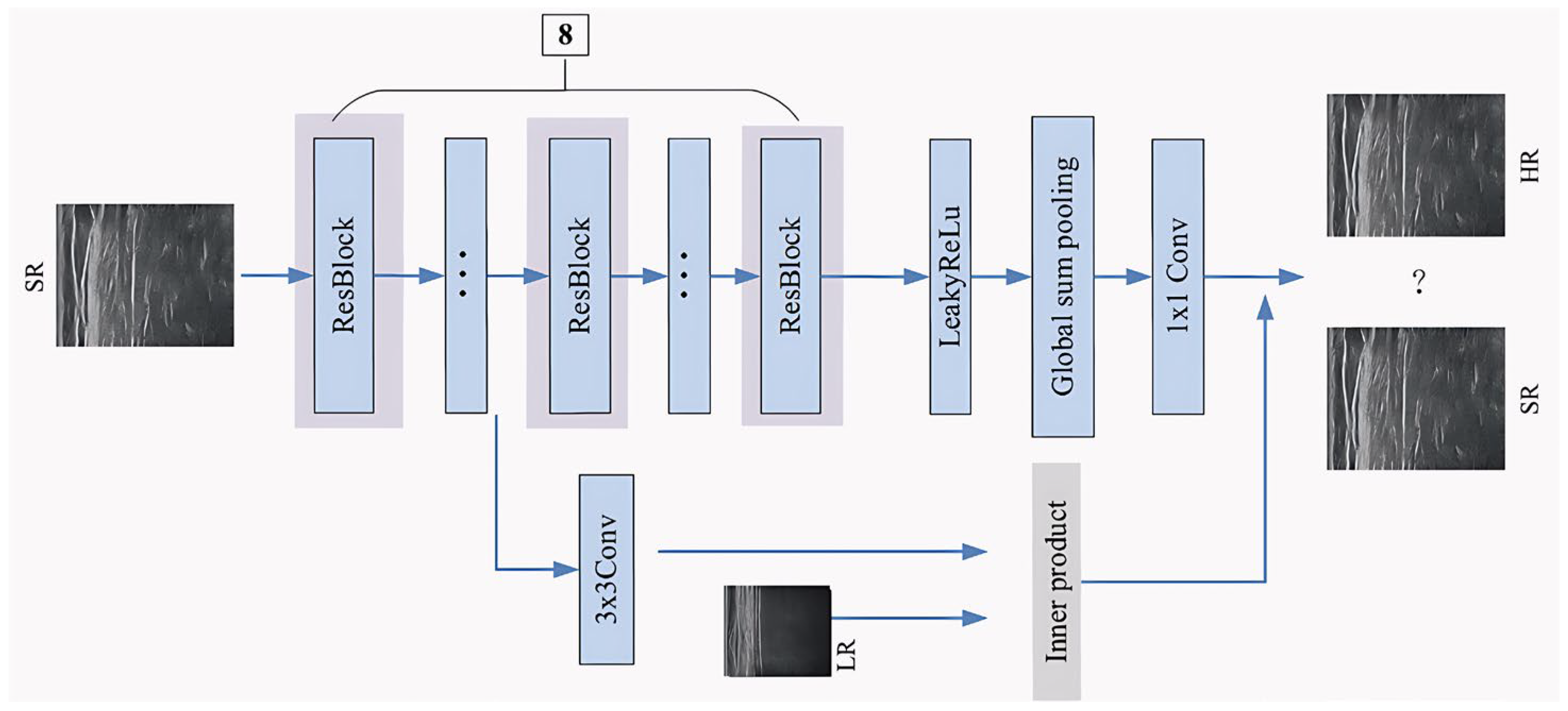
- In the discriminator, the low-resolution image is used as the condition variable to supervise the generation process of the generator; the feature dimension reduction adopts a 1 × 1 convolution layer instead of the full connection layer, which reduces the calculation amount and increases the nonlinear degree of the network, so as to improve the ability of accurate reconstruction of the network.
- (3)
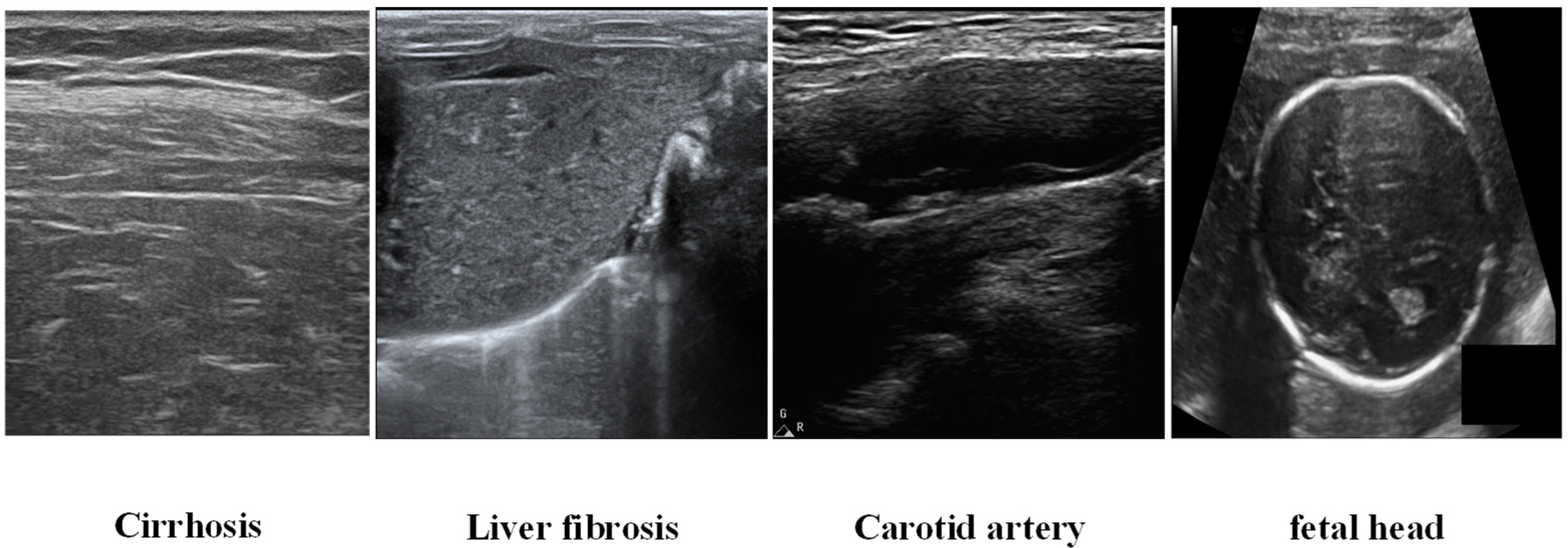
- A database of 5000 images was established based on some images from the International Symposium on Biomedical Imaging (ISBI) and some images of liver cirrhosis, liver fibrosis, and carotid artery directly provided by the cooperated hospitals. In comparison with some typical reconstruction super-resolution algorithms, our method improves in peak signal-to-noise ratio, structural similarity, and MOS score. In the stage diagnosis of liver cirrhosis, the accuracy and F1 score of mild and severe stages are improved by using reconstructed images.
2. Materials and Methods
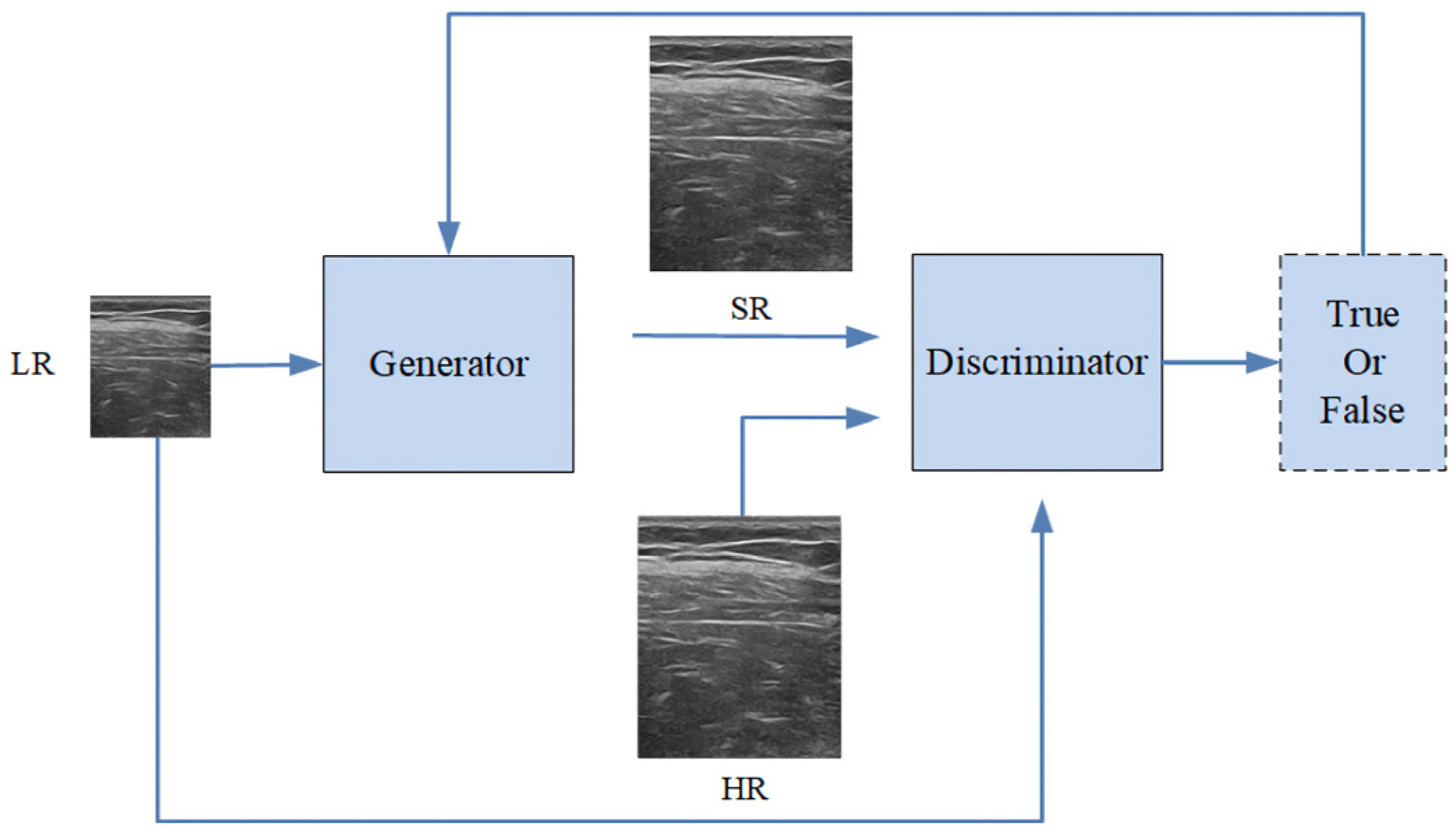
2.1. Designing Scheme
2.2. Generator
2.3. Discriminator
2.4. Loss Function
3. Results
3.1. Experimental Environment
3.2. Training Process
3.3. Evaluation Criterion
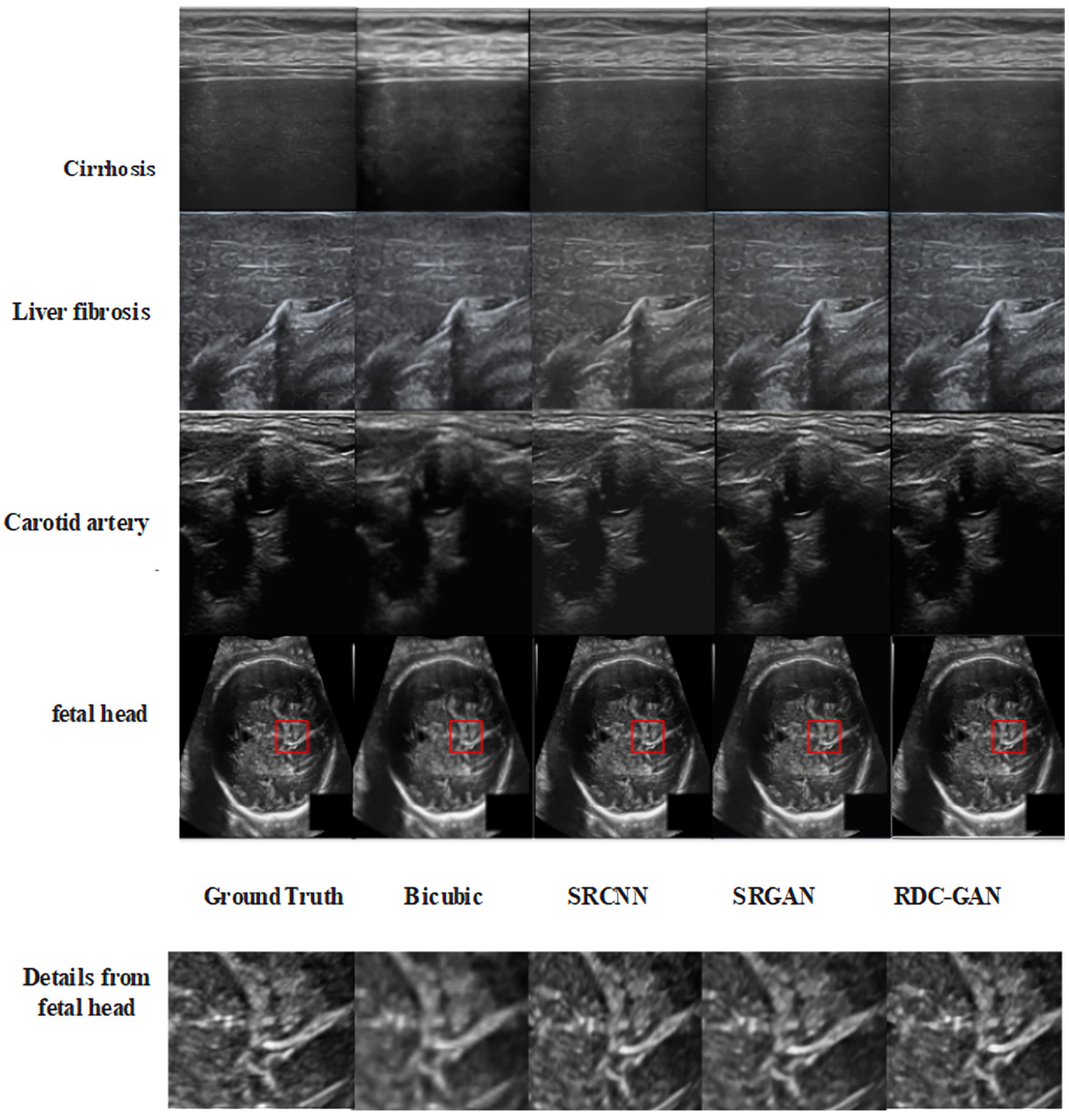
3.4. Experimental Results
4. Discussion
4.1. Quantitative Analysis
| Image | Algorithm | PSNR (dB) | SSIM (0–1) |
|---|---|---|---|
| Cirrhosis | Bicubic | 21.82 ± 0.06 | 0.75 ± 0.005 |
| SRCNN | 30.29 ± 0.08 | 0.84 ± 0.003 | |
| SRGAN | 25.66 ± 0.07 | 0.65 ± 0.004 | |
| RDC-GAN | 32.55 ± 0.06 | 0.88 ± 0.003 | |
| Liver fibrosis | Bicubic | 25.90 ± 0.09 | 0.80 ± 0.005 |
| SRCNN | 28.94 ± 0.06 | 0.83 ± 0.003 | |
| SRGAN | 26.09 ± 0.07 | 0.47 ± 0.004 | |
| RDC-GAN | 32.87 ± 0.06 | 0.88 ± 0.003 | |
| Carotid artery | Bicubic | 24.88 ± 0.07 | 0.83 ± 0.003 |
| SRCNN | 27.00 ± 0.08 | 0.79 ± 0.005 | |
| SRGAN | 24.57 ± 0.09 | 0.62 ± 0.003 | |
| RDC-GAN | 29.32 ± 0.06 | 0.88 ± 0.003 | |
| Fetal head | Bicubic | 25.57 ± 0.05 | 0.76 ± 0.004 |
| SRCNN | 30.86 ± 0.06 | 0.86 ± 0.004 | |
| SRGAN | 28.00 ± 0.07 | 0.58 ± 0.003 | |
| RDC-GAN | 34.11 ± 0.06 | 0.91 ± 0.003 |
| Stage | Algorithm | PSNR (dB) | SSIM (0–1) |
|---|---|---|---|
| Normal | Bicubic | 20.82 ± 0.07 | 0.74 ± 0.003 |
| SRCNN | 30.20 ± 0.08 | 0.85 ± 0.005 | |
| SRGAN | 24.97 ± 0.09 | 0.60 ± 0.004 | |
| RDC-GAN | 32.51 ± 0.07 | 0.89 ± 0.002 | |
| Mild | Bicubic | 24.31 ± 0.08 | 0.77 ± 0.003 |
| SRCNN | 31.30 ± 0.06 | 0.86 ± 0.005 | |
| SRGAN | 28.63 ± 0.05 | 0.78 ± 0.005 | |
| RDC-GAN | 32.21 ± 0.08 | 0.87 ± 0.003 | |
| Moderate | Bicubic | 21.61 ± 0.09 | 0.70 ± 0.004 |
| SRCNN | 29.48 ± 0.07 | 0.78 ± 0.002 | |
| SRGAN | 25.10 ± 0.06 | 0.59 ± 0.003 | |
| RDC-GAN | 32.04 ± 0.07 | 0.87 ± 0.003 | |
| Severe | Bicubic | 20.52 ± 0.05 | 0.79 ± 0.004 |
| SRCNN | 30.16 ± 0.06 | 0.85 ± 0.005 | |
| SRGAN | 23.95 ± 0.09 | 0.63 ± 0.003 | |
| RDC-GAN | 33.44 ± 0.06 | 0.87 ± 0.003 |
4.2. Qualitative Analysis
| Algorithm | Professional Doctors | Common People | MOS |
|---|---|---|---|
| Bicubic | 2.0 | 2.2 | 2.1 |
| SRCNN | 3.1 | 3.3 | 3.2 |
| SRGAN | 3.5 | 4.1 | 3.8 |
| RDC-GAN | 4.4 | 4.8 | 4.6 |
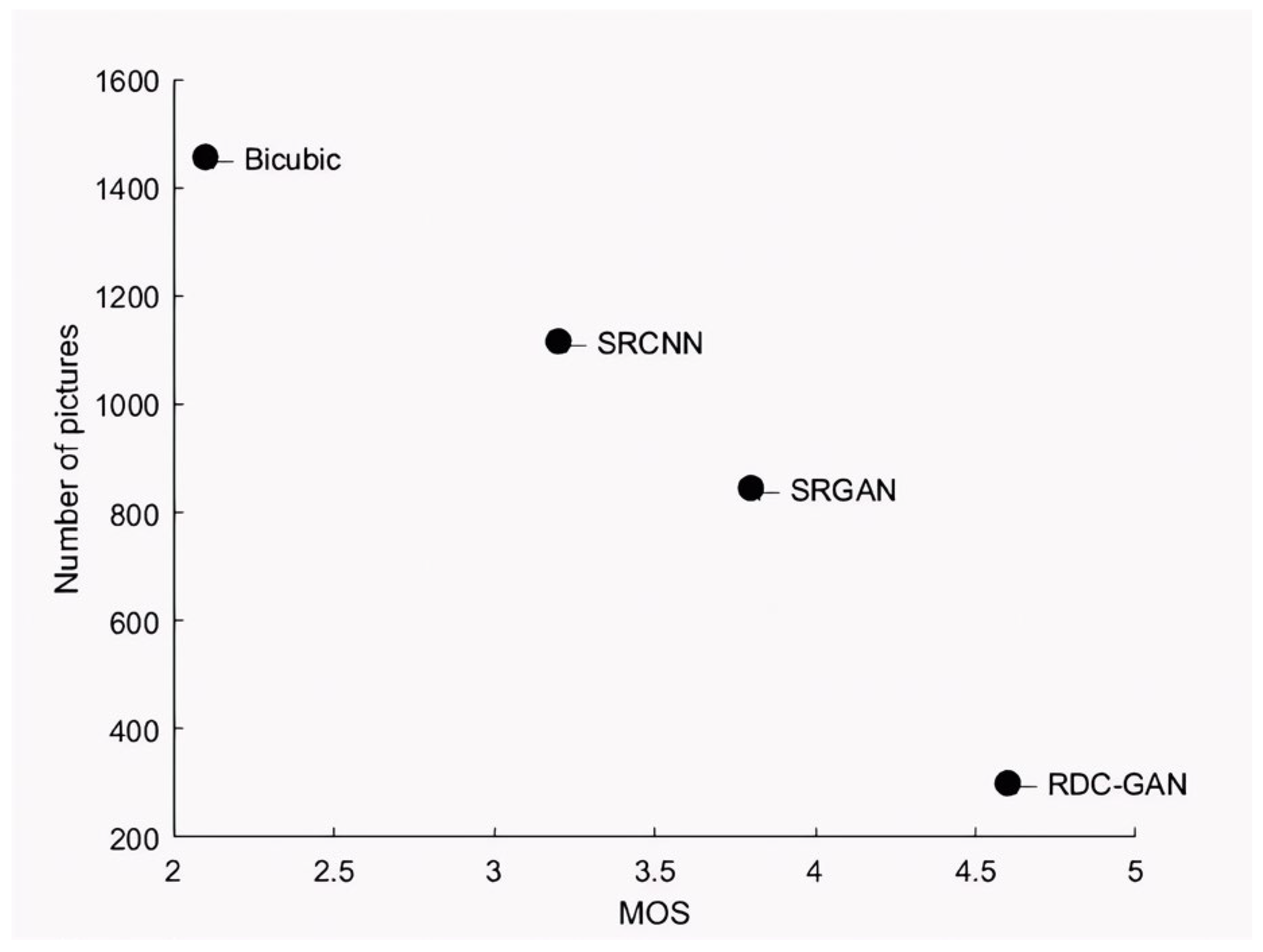
4.3. Ablation Experiments and Analysis
| Different Combination of RDB (with GFF), RDB (Without GFF), and Projection | ||||||
|---|---|---|---|---|---|---|
| RDB (with GFF) | × | √ | × | × | × | √ |
| RDB (without GFF) | × | × | √ | × | √ | × |
| projection | × | × | × | √ | √ | √ |
| PSNR (dB) | 27.93 ± 0.07 | 31.56 ± 0.08 | 28.79 ± 0.06 | 31.47 ± 0.05 | 31.64 ± 0.06 | 32.8 ± 0.07 |
4.4. Practical Application Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Jing, T.; Liu, C.; Chen, Y. A lightweight single-image super-resolution method based on the parallel connection of convolution and swin transformer blocks. Appl. Sci. 2025, 15, 1806. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, S.; Hu, Y.; Xie, C. Single-image super-resolution challenges: A brief review. Electronics 2023, 12, 2975. [Google Scholar] [CrossRef]
- Lv, J.; Wang, Z. Super-resolution image reconstruction based on double regression network model. Int. J. Adv. Netw. Monit. Control 2022, 7, 82–88. [Google Scholar] [CrossRef]
- Hwang, J.H.; Park, C.K.; Kang, S.B.; Choi, M.K.; Lee, W.H. Deep learning super-resolution technique based on magnetic resonance imaging for application of image-guided diagnosis and surgery of trigeminal neuralgia. Life 2024, 14, 355. [Google Scholar] [CrossRef]
- Ji, C.; Liu, J.; Liu, Z. An edge-oriented interpolation algorithm based on regularization. J. Electron. Inf. Technol. 2014, 36, 293–297. [Google Scholar] [CrossRef]
- Wei, D. Image super-resolution reconstruction using the high-order derivative interpolation associated with fractional filter functions. IET Signal Process. 2016, 10, 1052–1061. [Google Scholar] [CrossRef]
- Papyan, V.; Elad, M. Multi-scale patch-based image restoration. IEEE Trans. Image Process. 2016, 25, 249–261. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Sang, N.; Gao, C. Super-resolution reconstruction of license plate images with combined brightness-gradient constraints. J. Image Graph. 2018, 23, 802–813. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Gool, V.L.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar] [CrossRef]
- Chen, X.; Li, Z.; Pu, Y.; Liu, Y.; Zhou, J.; Qiao, Y.; Dong, C. A Comparative Study of Image Restoration Networks for General Backbone Network Design. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2024; pp. 74–91. [Google Scholar] [CrossRef]
- Hsu, C.; Lee, C.; Chou, Y. DRCT: Saving Image Super-resolution away from Information Bottleneck. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 6133–6142. [Google Scholar] [CrossRef]
- Chu, S.; Dou, Z.; Pan, J.; Weng, S.; Li, J. HMANet: Hybrid Multi-Axis Aggregation Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 6257–6266. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 391–407. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar] [CrossRef]
- Yang, W.; Liu, W.; Fan, F.L.; Lu, G.M. Deep Edge Guided Recurrent Residual Learning for Image Super-Resolution. IEEE Trans. Image Process. 2017, 26, 5895–5907. [Google Scholar] [CrossRef] [PubMed]
- Tai, Y.; Yang, J.; Liu, X. Image Super-Resolution via Deep Recursive Residual Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3147–3155. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, L.; Chen, Y.; Wang, D.; Yap, P.T. Super-resolution reconstruction of MR image with a novel residual learning network algorithm. Phys. Med. Biol. 2018, 63, 085011. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Li, Z.; Ying, S.; Wang, C.; Liu, Q.; Zhang, Q.; Yan, P. MR Image Super-Resolution Via Wide Residual Networks With Fixed Skip Connection. IEEE J. Biomed. Health Inform. 2019, 23, 1129–1140. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Yang, F.; Huang, J.; Liu, Y. Super-resolution construction of intravascular ultrasound images using generative adversarial networks. J. South. Med. Univ. 2019, 39, 82–87. [Google Scholar] [CrossRef]
- Choi, W.; Kim, M.; Lee, J.H.; Chang, J.H.; Song, T.K. Deep CNN-Based Ultrasound Super-Resolution for High-Speed High-Resolution B-Mode Imaging. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018. [Google Scholar] [CrossRef]
- Lu, J.; Liu, W. Unsupervised Super-Resolution Framework for Medical Ultrasound Images Using Dilated Convolutional Neural Networks. In Proceedings of the 2018 IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, 27–29 June 2018; pp. 329–333. [Google Scholar] [CrossRef]
- Temiz, H.; Bilge, H.S. Super Resolution of B-mode Ultrasound Images with Deep Learning. IEEE Access 2020, 8, 155163–155174. [Google Scholar] [CrossRef]
- Wang, R.; Fang, Z.; Gu, J.; Guo, Y.; Zhou, S.; Wang, Y.; Chang, C.; Yu, J. High-resolution image reconstruction for portable ultrasound imaging devices. EURASIP J. Adv. Signal Process. 2019, 2019, 1. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Tao, T.; Hou, S.; Han, J. Perception Consistency Ultrasound Image Super-resolution via Self-supervised CycleGAN. In Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1294–1298. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef]
- Timofte, R.; De Smet, V.; Van Gool, L. A+: Adjusted anchored neighborhood regression for fast super-resolution. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; pp. 111–126. [Google Scholar] [CrossRef]
- Xing, X.; Wei, M.; Fu, Y. Super-resolution reconstruction of medical images based on feature loss. Comput. Eng. Appl. 2018, 54, 202–207. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative Adversarial Networks: An Overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Shen, T.W.; Zheng, W.S. Image Super-Resolution Reconstruction Based on Disparity Map and CNN. IEEE Access 2018, 6, 53489–53498. [Google Scholar] [CrossRef]
- Miyato, T.; Koyama, M. cGANs with Projection Discriminator. arXiv 2018, arXiv:1802.05637. [Google Scholar] [CrossRef]
- Liu, X.; Ma, R.L.; Zhao, J.; Song, J.L.; Zhang, J.Q.; Wang, S.H. A clinical decision support system for predicting cirrhosis stages via high frequency ultrasound images. Expert Syst. Appl. 2021, 175, 114680. [Google Scholar] [CrossRef]

| Stage | Specificity/% | Recall/% | F1 score/% | |||
|---|---|---|---|---|---|---|
| OR | SR | OR | SR | OR | SR | |
| Normal | 100 | 100 | 95 | 95 | 97.44 | 97.44 |
| Mild | 94.12 | 100 | 88.89 | 94.44 | 91.43 | 97.14 |
| Moderate | 84.21 | 88.89 | 94.12 | 94.12 | 88.89 | 91.43 |
| Severe | 92.31 | 92.86 | 92.31 | 100 | 92.31 | 96.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Wei, Y. Super-Resolution Reconstruction of Sonograms Using Residual Dense Conditional Generative Adversarial Network. Sensors 2025, 25, 6694. https://doi.org/10.3390/s25216694
Xu Z, Wei Y. Super-Resolution Reconstruction of Sonograms Using Residual Dense Conditional Generative Adversarial Network. Sensors. 2025; 25(21):6694. https://doi.org/10.3390/s25216694
Chicago/Turabian StyleXu, Zengbo, and Yiheng Wei. 2025. "Super-Resolution Reconstruction of Sonograms Using Residual Dense Conditional Generative Adversarial Network" Sensors 25, no. 21: 6694. https://doi.org/10.3390/s25216694
APA StyleXu, Z., & Wei, Y. (2025). Super-Resolution Reconstruction of Sonograms Using Residual Dense Conditional Generative Adversarial Network. Sensors, 25(21), 6694. https://doi.org/10.3390/s25216694





