Evaluation Method for Resin Mold Using Reflective Wavefront Sensor
Abstract
1. Introduction
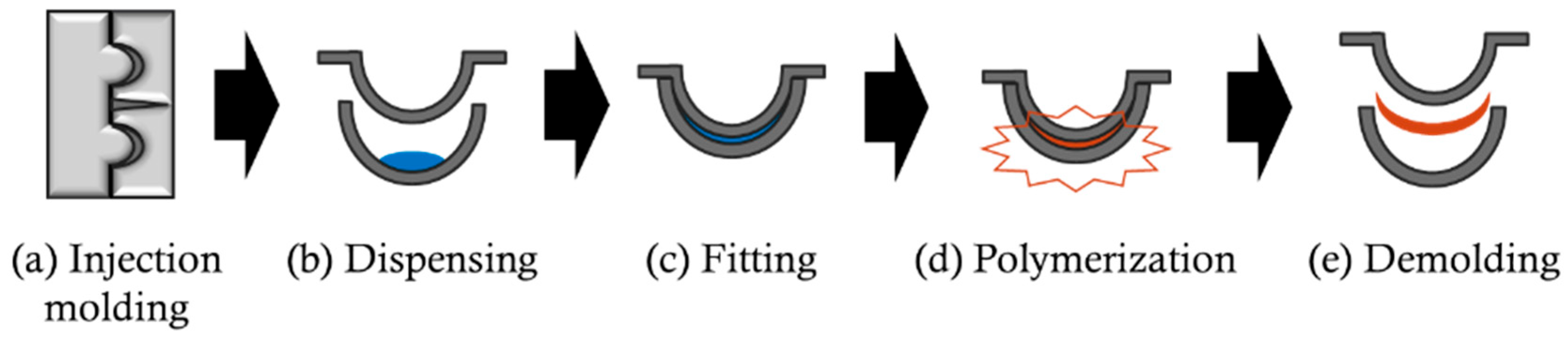
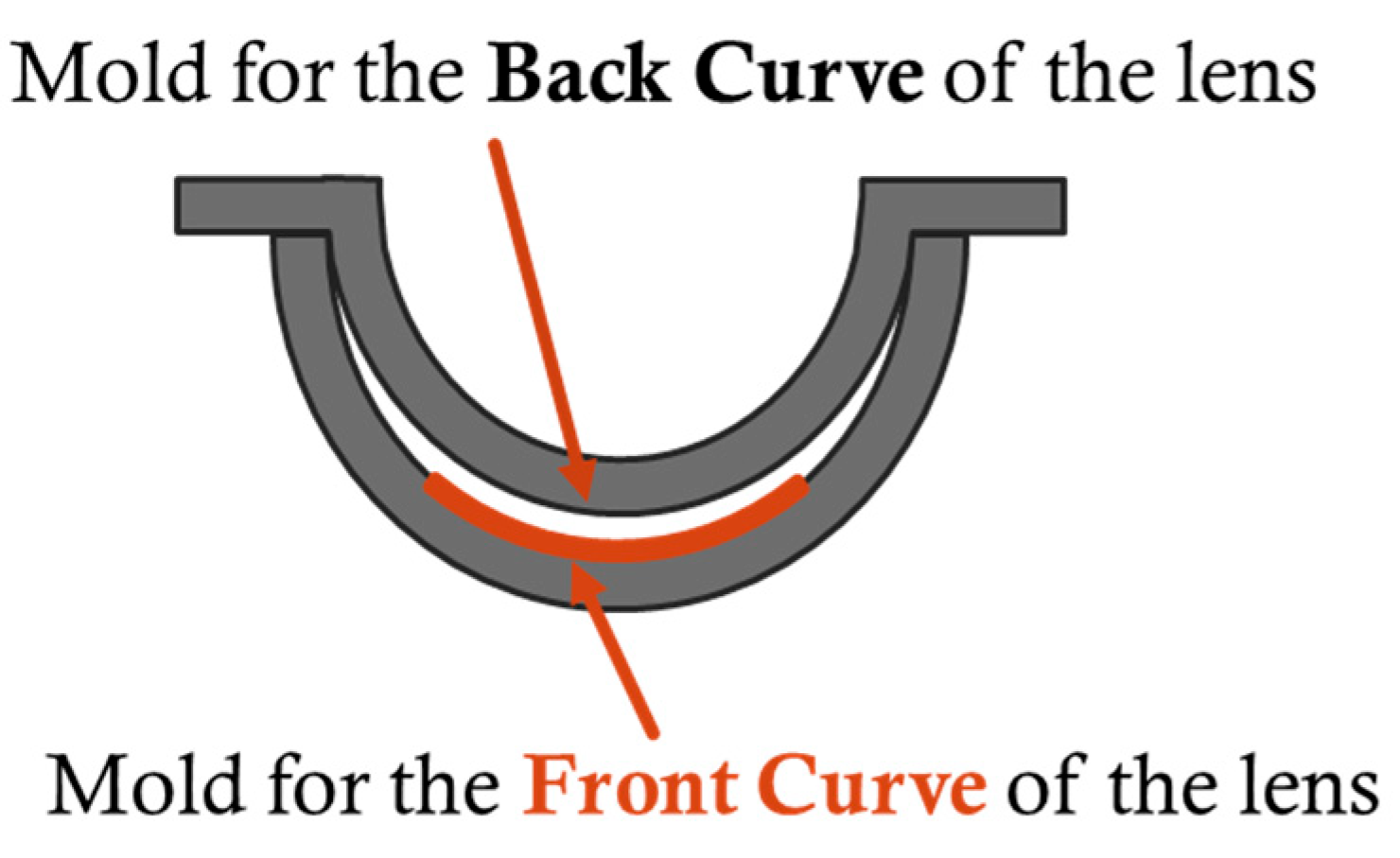
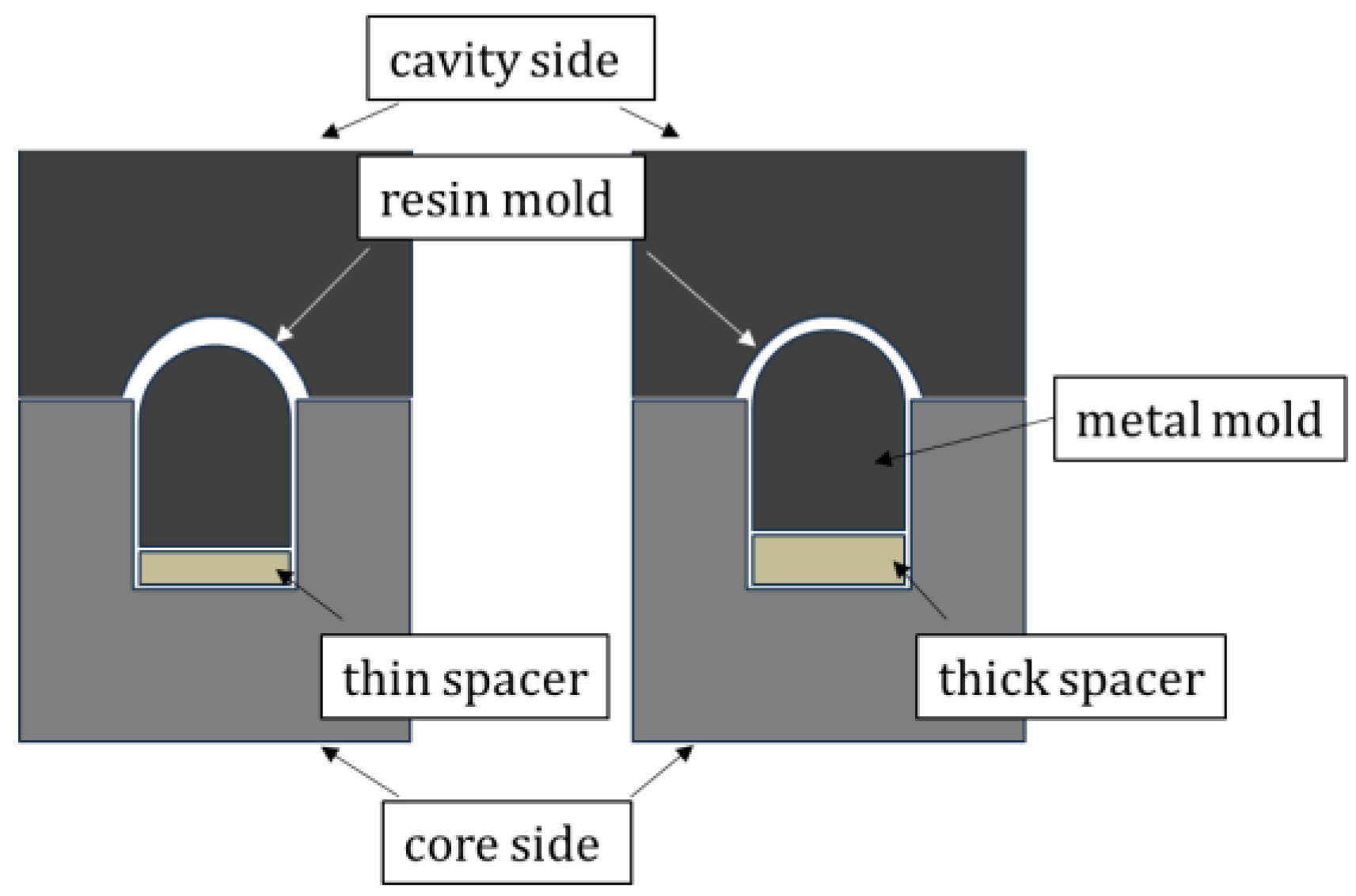
2. Injection Molding Technology and CL Manufacturing
3. Experimental Set-Up
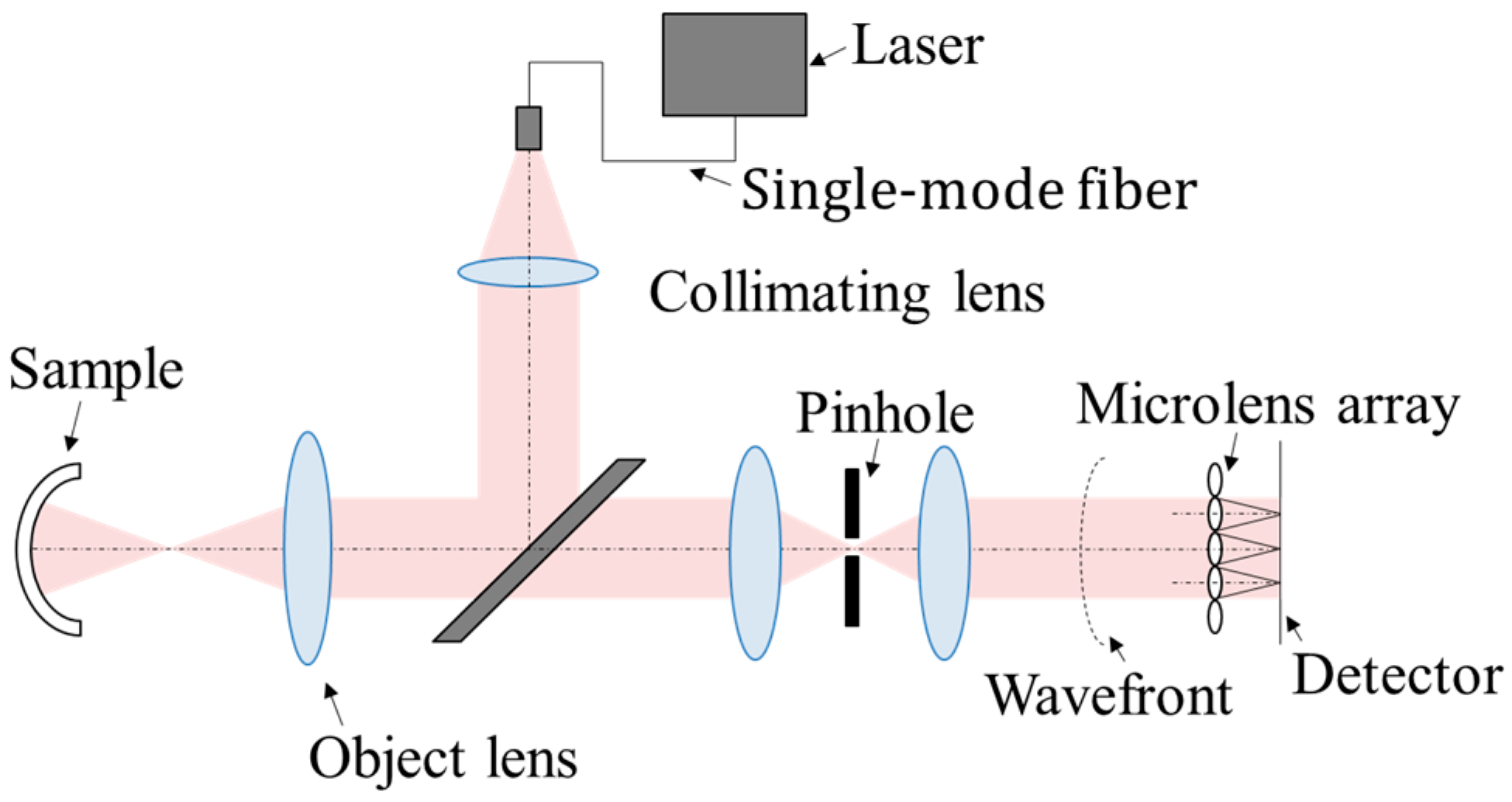
3.1. Wavefront Measurement
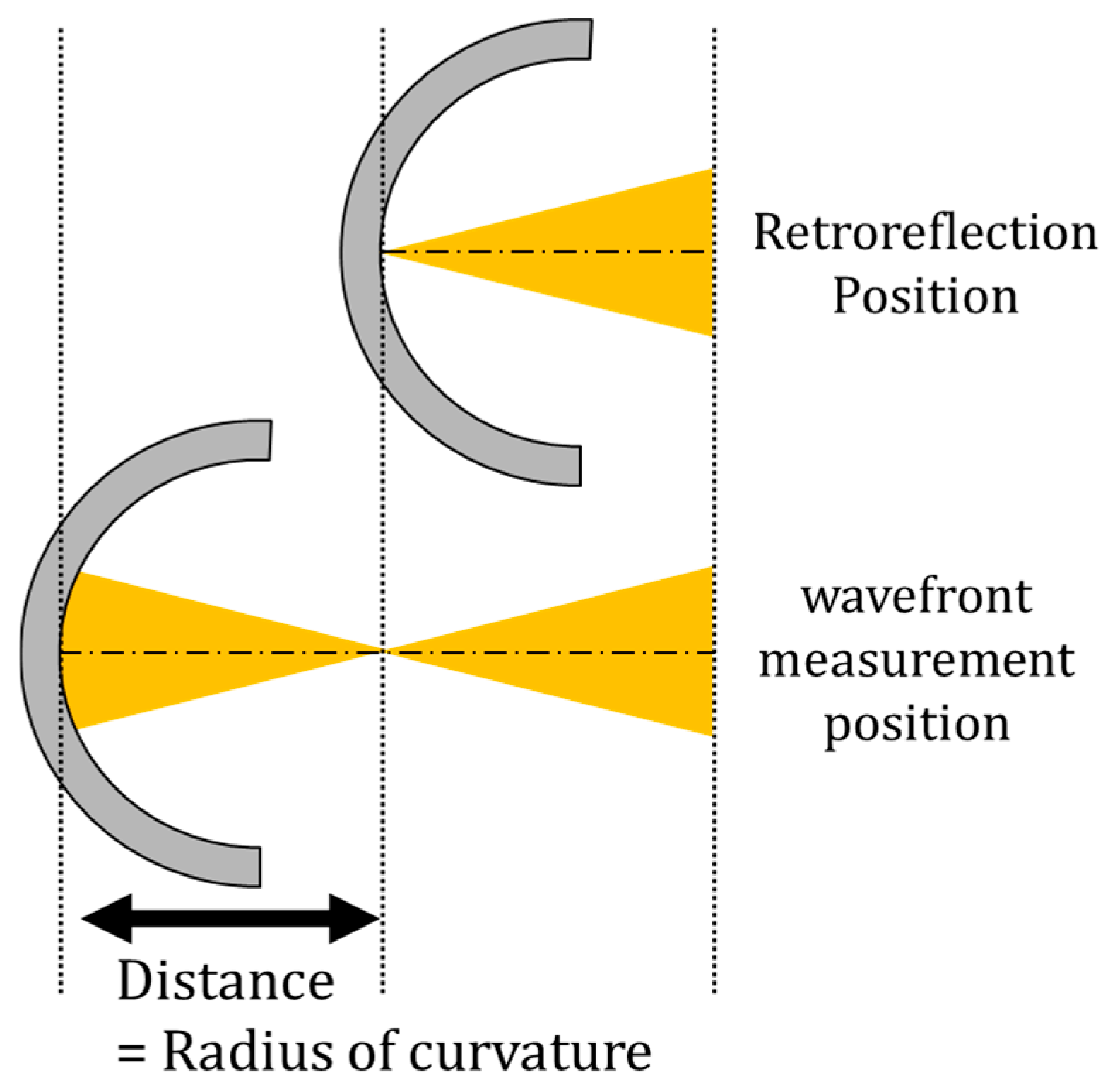
3.2. Radius of Curvature Measurement
3.3. Analysis Using Zernike Polynomials
4. Material and Method
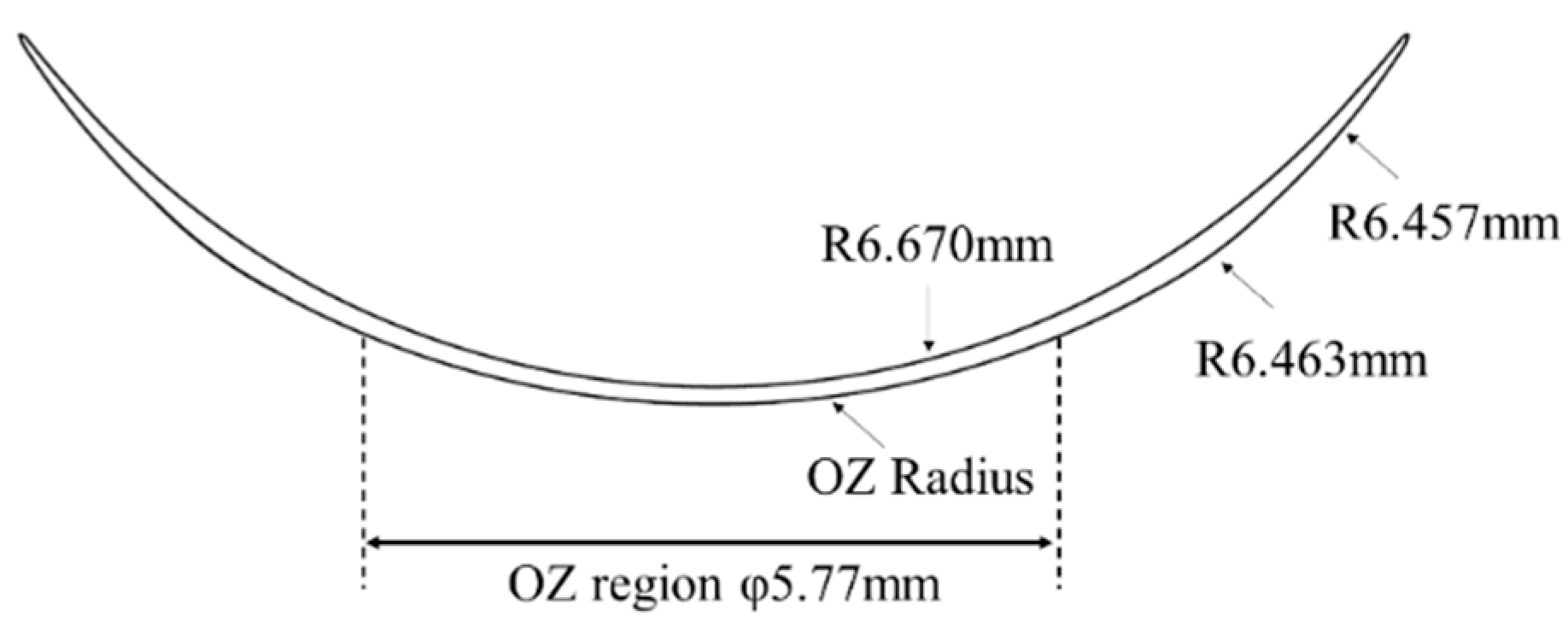
4.1. Measurement Sample
4.2. Method
5. Result
5.1. Variations in Zernike Coefficients
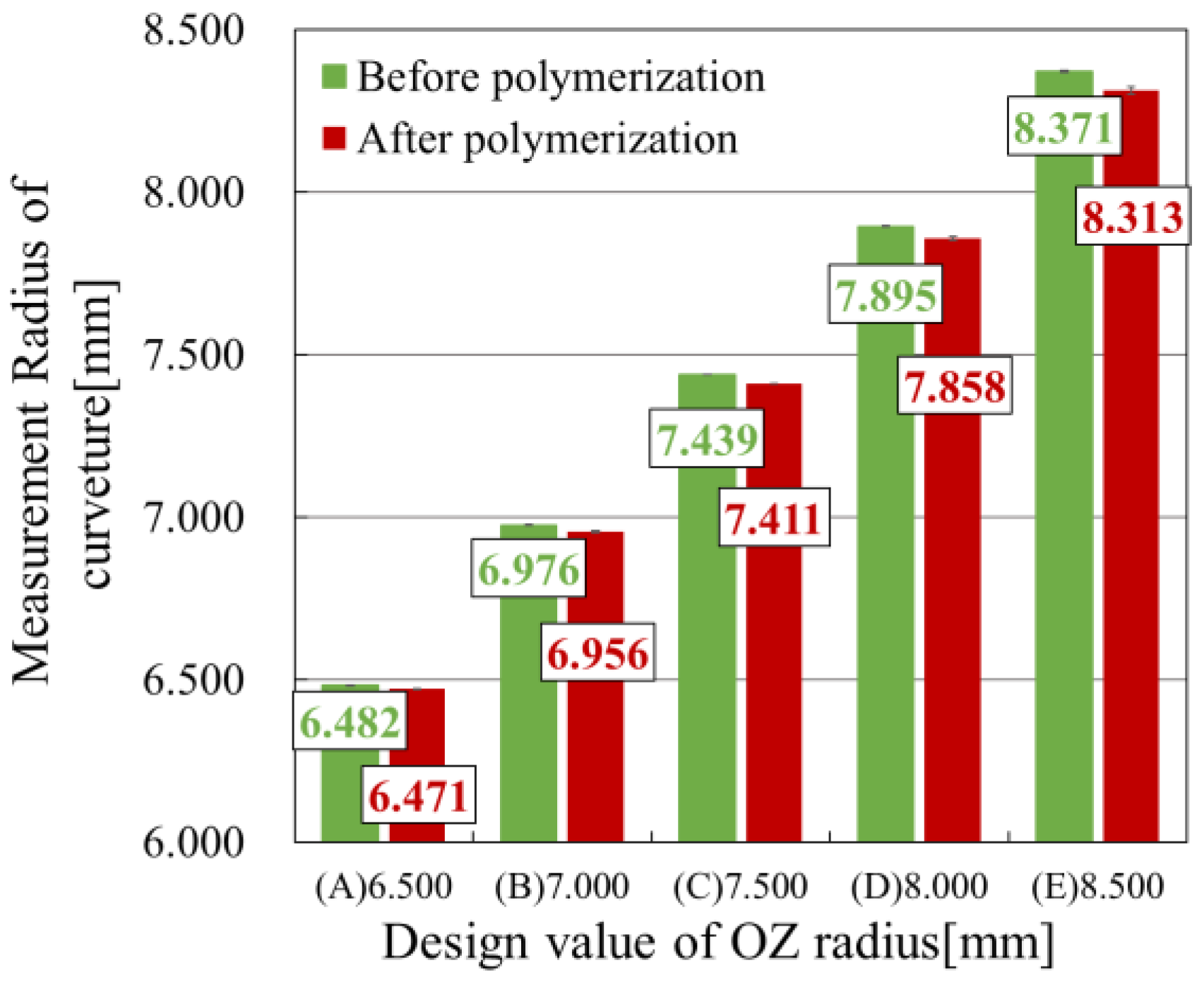
5.2. Radius of Curvature Measurements
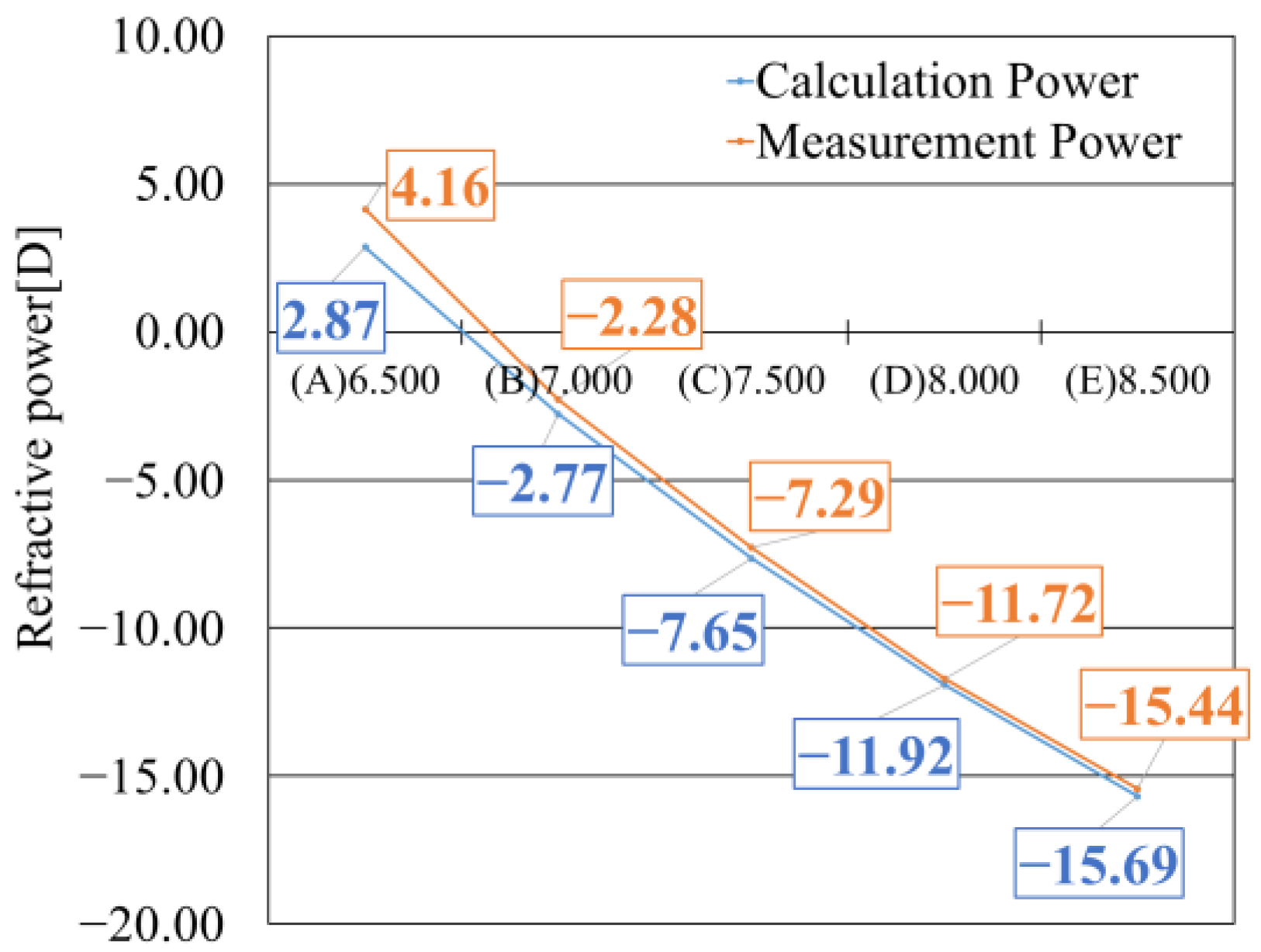
5.3. Results of CL Power Measurement
6. Discussion
6.1. Wavefront Measurement Results of Resin Molds Fabricated with Different Thicknesses
6.2. Relationship Between Resin Mold Thickness and Zernike Coefficients
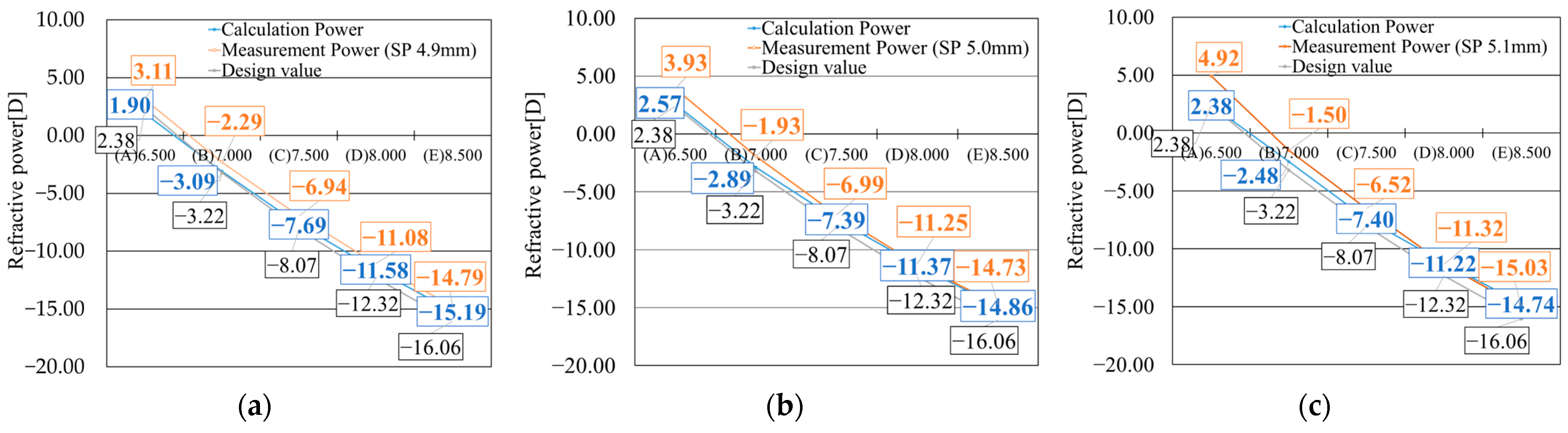
6.3. Relationship Between Resin Thickness and Lens Power
7. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rosato, D.V. Injection Molding Handbook, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Ciofu, C.; Mindru, D.T. Injection and micro injection of polymeric plastics materials: A review. Int. J. Mod. Manufact Technol. 2013, 1, 49–68. [Google Scholar]
- Holden, B.A.; Fricke, T.R.; Wilson, D.A.; Jong, M.; Naidoo, K.S.; Sankaridurg, P.; Wong, T.Y.; Naduvilath, T.; Resnikoff, S. Global prevalence of myopia and high myopia and temporal trends from 2000 through 2050. Ophthalmology 2016, 123, 1036–1042. [Google Scholar] [CrossRef] [PubMed]
- Morgan, P.B.; Efron, N.; Woods, C.A.; Jones, D.; Jones, L.; Nichols, J.J. International trends in daily disposable contact lens prescribing (2000–2023): An update. Contact Lens Anterior Eye 2024, 47, 102259. [Google Scholar] [CrossRef]
- Phillips, A.J.; Speedwell, L. Contact Lenses; Elsevier Health Sciences: Philadelphia, PA, USA, 2018. [Google Scholar] [CrossRef]
- Wichterle, O.; Lim, D. Hydrophilic gels for biological use. Nature 1960, 185, 117–118. [Google Scholar] [CrossRef]
- Shaker, L.M.; Al-Amiery, A.; Isahak, W.N.R.W. Revolutionizing contact lens manufacturing: Exploring cutting-edge techniques and innovations for enhanced vision and comfort. Int. J. Low-Carbon Technol. 2024, 19, 359–385. [Google Scholar] [CrossRef]
- Abdulamier, A.A.; Shaker, L.M.; Al-Amiery, A.A. Advancements in the chemistry of contact lenses: Innovations and applications. Sci. Prog. 2024, 107, 003685042311636. [Google Scholar] [CrossRef]
- Saeki, K.; Huyan, D.; Nakamura, A.; Kubota, S.; Uno, K.; Ohnuma, K.; Shiina, T. 2D and 3D measurement algorithms for real front and back curved surfaces of contact lenses. In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology, Vienna, Austria, 11–13 February 2021; pp. 73–80. [Google Scholar] [CrossRef]
- Saeki, K.; Huyan, D.; Sawada, M.; Nakamura, A.; Kubota, S.; Uno, K.; Ohnuma, K.; Shiina, T. Three-dimensional measurement for spherical and nonspherical shapes of contact lenses. Appl. Opt. 2021, 60, 3689–3698. [Google Scholar] [CrossRef]
- Musgrave, C.; O’Toole, L.; Mao, T.; Li, Q.; Lai, M.; Fang, F. Manufacturing of soft contact lenses using reusable and reliable cyclic olefin copolymer moulds. Polymers 2022, 14, 4681. [Google Scholar] [CrossRef]
- Lan, X.; Li, C.; Yang, C.; Xue, C. Optimization of injection molding process parameters and axial surface compensation for producing an aspheric plastic lens with large diameter and center thickness. Appl. Opt. 2019, 58, 927–934. [Google Scholar] [CrossRef]
- Ananthasayanam, B.; Joseph, P.F.; Joshi, D.; Gaylord, S.; Petit, L.; Blouin, V.Y.; Richardson, K.C.; Cler, D.L.; Stairiker, M.; Tardiff, M. Final shape of precision molded optics: Part I—Computational approach, material definitions and the effect of lens shape. J. Therm. Stress. 2012, 35, 550–578. [Google Scholar] [CrossRef]
- Torres, F.J. Application of digital holographic interferometry to pressure measurements of symmetric, supercritical, and circulation control airfoils in transonic flow fields. In High Speed Photography, Videography, and Photonics IV; SPIE: Philadelphia, PA, USA, 1986; Volume 693, pp. 199–216. [Google Scholar] [CrossRef]
- Abdelazeem, R.M.; Ahmed, M.M.; Agour, M. Characterization of thick and contact lenses using an adaptive Shack–Hartmann wavefront sensor: Limitations and solutions. Optik 2023, 283, 170922. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Wang, S.; Chen, Q. Optical wavefront aberration: Detection, recognition, and compensation techniques—A comprehensive review. Opt. Laser Technol. 2025, 183, 113342. [Google Scholar] [CrossRef]
- De Luca, A.; Bolognini, G.; Contestabile, G.; Di Pasquale, F. Wavefront control by an optical-feedback interferometer. Opt. Commun. 1989, 72, 15–20. [Google Scholar] [CrossRef]
- Go, G.-H.; Lee, D.; Oh, J.; Song, G.; Lee, D.; Jang, M. Meta Shack–Hartmann wavefront sensor with large sampling density and large angular field of view: Phase imaging of complex objects. Light: Sci. Appl. 2024, 13, 187. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, I.; Ragazzoni, R.; Julien, Y.; Artal, P. Extended source pyramid wavefront sensor for the human eye. Opt. Express 2002, 10, 419–428. [Google Scholar] [CrossRef]
- Chambouleyron, V.; Sengupta, A.; Salama, M.; van Kooten, M.; Gerard, B.L.; Haffert, S.Y.; Cetre, S.; Dillon, D.; Kupke, R.; Jensen-Clem, R.; et al. Using the Gerchberg–Saxton algorithm to reconstruct nonmodulated pyramid wavefront sensor measurements. Astron. Astrophys. 2024, 681, A48. [Google Scholar] [CrossRef]
- Atchison, D. Optics of the Human Eye; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar] [CrossRef]
- Hao, Q.; Liu, Y.; Hu, Y.; Tao, X. Measurement techniques for aspheric surface parameters. Light Adv. Manuf. 2023, 4, 292–310. [Google Scholar] [CrossRef]
- Moreddu, R.; Vigolo, D.; Yetisen, A.K. Contact lens technology: From fundamentals to applications. Adv Mater Technol. 2023, 8, e1900368. [Google Scholar] [CrossRef]
- Fink, J.K. Contact Lenses: Chemicals, Methods, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Wyant, J.C. Computerized interferometric surface measurements. Appl. Opt. 2013, 52, 1–8. [Google Scholar] [CrossRef]
- Plainis, S.; Atchison, D.A.; Charman, W.N. Power profiles of multifocal contact lenses and their interpretation. Optom. Vis. Sci. 2013, 90, 1066–1077. [Google Scholar] [CrossRef]
- Kinnstätter, A.; Lohmann, J.; Schwider, J.; Streibl, N. Accuracy of phase-shifting interferometry. Appl. Opt. 1988, 27, 5082–5089. [Google Scholar] [CrossRef]
- Schmit, J.; Creath, K. Extended averaging technique for derivation of error-compensating algorithms in phase-shifting interferometry. Appl. Opt. 1995, 34, 3610–3619. [Google Scholar] [CrossRef]
- Platt, B.C.; Shack, R. History and principles of Shack-Hartmann wavefront sensing. J. Refract. Surg. 2001, 17, S573–S577. [Google Scholar] [CrossRef]
- Li, P.; Tang, F.; Wang, X.; Li, J. High NA objective lens wavefront aberration measurement using a cat-eye retroreflector and Zernike polynomial. Opt. Express 2021, 29, 31812–31835. [Google Scholar] [CrossRef] [PubMed]
- Noll, R.J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Mahajan, V.N. Zernike circle polynomials and optical aberrations of systems with circular pupils. Appl. Opt. 1994, 33, 8121–8124. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Abass, A.; Stuart, S.; Lopes, B.T.; Zhou, D.; Geraghty, B.; Wu, R.; Jones, S.; Flux, I.; Stortelder, R.; Snepvangers, A.; et al. Simulated optical performance of soft contact lenses on the eye. PLoS ONE 2019, 14, e0216484. [Google Scholar] [CrossRef]
- Joannes, L.; Dubois, F.; Legros, J.C. Phase-shifting schlieren: High-resolution quantitative schlieren that uses the phase-shifting technique principle. Appl. Opt. 2003, 42, 5046–5053. [Google Scholar] [CrossRef]
- Kim, E.; Bakaraju, R.C.; Ehrmann, K. Reliability of power profiles measured on NIMO TR1504 (Lambda-X) and effects of lens decentration for single vision, bifocal and multifocal contact lenses. J. Optom. 2016, 9, 126–136. [Google Scholar] [CrossRef]
- Lin, C.M.; Miau, T.H. Optimization of injection-compression molding processing conditions for Fresnel lens based on optical performance and geometry deformation considerations. IEEE Access. 2022, 10, 65401–65413. [Google Scholar] [CrossRef]
- Vanek, J.; Ovsik, M.; Stanek, M.; Hanzlik, J.; Pata, V. Study of injection molding process to improve geometrical quality of thick-walled polycarbonate optical lenses by reducing sink marks. Polymers 2024, 16, 2318. [Google Scholar] [CrossRef]
- Kim, M.; Oh, E.S.; Kwak, M.K. Shrinkage-considered mold design for improvement of micro/nano-structured optical element performance. Micromachines 2020, 11, 941. [Google Scholar] [CrossRef]
- Jalie, M. The Principles of Ophthalmic Lenses, 4th ed.; Association of British Dispensing Opticians: Christchurch, New Zealand, 2015. [Google Scholar]
- Gambichler, T.; Moussa, M.; Sand, M.; Sand, D.; Altmeyer, P.; Hoffmann, K. Applications of optical coherence tomography in clinical dermatology. Appl. Opt. 2010, 49, D115–D124. [Google Scholar] [CrossRef]
- Shiina, T. Long path industrial OCT. In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology, Rome, Italy, 27–29 February 2016. [Google Scholar] [CrossRef]




| Index | Parameter |
|---|---|
| Manufacturer | Pulstec Industrial Co., Ltd. |
| Model | LUCUS |
| Measurement wavelength | 589 nm |
| Measurable radius of curvature for concave surfaces (measurement range) | 4.3 mm–46.5 mm (φ7.0 mm) |
| Measurable radius of curvature for convex surfaces (measurement range) | 5.7 mm–9.5 mm (φ9.0 mm) |
| Tolerance of wavefront incident angle | ±1.1 deg |
| Wavefront measurement accuracy | 1/100 λ |
| Repeatability | 1/200 λ |
| Radius measurement accuracy | ±10 μm |
| Number of microlens array | 108 × 80 |
| The focal length of the microlens array | 4 mm |
| Data update rate | 6 Hz |
| Focal lens | NA 0.81 |
| Term | Polynomial | Aberration |
|---|---|---|
| Z01 | x-Tilt | |
| Z02 | y-Tilt | |
| Z03 | Defocus | |
| Z04 | 0° Primary astigmatism | |
| Z05 | 45° Primary astigmatism | |
| Z06 | Primary x-coma | |
| Z07 | Primary y-coma | |
| Z08 | Primary spherical aberration | |
| Z09 | Secondary x-trefoil | |
| Z10 | Secondary y-trefoil |
| Sample No. | Designed Radius of Curvature in the OZ Region [mm] |
|---|---|
| (A) | 6.500 |
| (B) | 7.000 |
| (C) | 7.500 |
| (D) | 8.000 |
| (E) | 8.500 |
| Sample Data | Average Value | Standard Deviation | RMS | ||
|---|---|---|---|---|---|
| Z04 | Standard references | convex 6.200 mm | 0.023 | 0.004 | 0.003 |
| concave 9.500 mm | 0.014 | 0.005 | 0.004 | ||
| Resin mold | concave 6.500 mm | 0.729 | 0.018 | 0.015 | |
| Z07 | Standard references | convex 6.200 mm | −0.044 | 0.001 | 0.001 |
| concave 9.500 mm | −0.093 | 0.005 | 0.004 | ||
| Resin mold | concave 6.500 mm | 0.891 | 0.015 | 0.012 | |
| OZ radius | Standard references | convex 6.200 mm | 6.199 | 0.001 | 0.0005 |
| concave 9.500 mm | 9.499 | 0.001 | 0.0005 | ||
| Resin mold | concave 6.500 mm | 6.522 | 0.001 | 0.0005 | |
| Sample No. | Designed Radius of Curvature in the OZ Region [mm] | Measurement of OZ Radius [mm] | |
|---|---|---|---|
| Wavefront Sensor | Laser Interferometer | ||
| (A) | 6.500 | 6.482 | 6.476 |
| (B) | 7.000 | 6.976 | 6.975 |
| (C) | 7.500 | 7.439 | 7.441 |
| (D) | 8.000 | 7.895 | 7.899 |
| (E) | 8.500 | 8.371 | 8.378 |
| Sample No. | Designed Radius of Curvature in the OZ Region [mm] | Polymerization Shrinkage Rate |
|---|---|---|
| (A) | 6.500 | 0.17% |
| (B) | 7.000 | 0.29% |
| (C) | 7.500 | 0.38% |
| (D) | 8.000 | 0.47% |
| (E) | 8.500 | 0.69% |
| Sample Data | Average Value | Standard Deviation | RMS | ||
|---|---|---|---|---|---|
| Z04 | SP 4.9 mm | R6.500 | −0.873 | 0.511 | 0.417 |
| R8.500 | 1.939 | 0.080 | 0.065 | ||
| SP 5.1 mm | R6.500 | −1.740 | 0.432 | 0.353 | |
| R8.500 | 0.122 | 0.012 | 0.010 | ||
| Z07 | SP 4.9 mm | R6.500 | 0.997 | 0.262 | 0.214 |
| R8.500 | 0.647 | 0.006 | 0.005 | ||
| SP 5.1 mm | R6.500 | 1.197 | 0.413 | 0.337 | |
| R8.500 | 1.237 | 0.004 | 0.004 | ||
| OZ radius | SP 4.9 mm | R6.500 | 6.540 | 0.005 | 0.004 |
| R8.500 | 8.378 | 0.003 | 0.002 | ||
| SP 5.1 mm | R6.500 | 6.500 | 0.053 | 0.013 | |
| R8.500 | 8.314 | 0.002 | 0.001 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tatsumi, K.; Saeki, K.; Kubota, S.; Kaneda, Y.; Uno, K.; Ohnuma, K.; Shiina, T. Evaluation Method for Resin Mold Using Reflective Wavefront Sensor. Sensors 2025, 25, 6682. https://doi.org/10.3390/s25216682
Tatsumi K, Saeki K, Kubota S, Kaneda Y, Uno K, Ohnuma K, Shiina T. Evaluation Method for Resin Mold Using Reflective Wavefront Sensor. Sensors. 2025; 25(21):6682. https://doi.org/10.3390/s25216682
Chicago/Turabian StyleTatsumi, Kazumasa, Kentaro Saeki, Shin Kubota, Yoshikatsu Kaneda, Kenji Uno, Kazuhiko Ohnuma, and Tatsuo Shiina. 2025. "Evaluation Method for Resin Mold Using Reflective Wavefront Sensor" Sensors 25, no. 21: 6682. https://doi.org/10.3390/s25216682
APA StyleTatsumi, K., Saeki, K., Kubota, S., Kaneda, Y., Uno, K., Ohnuma, K., & Shiina, T. (2025). Evaluation Method for Resin Mold Using Reflective Wavefront Sensor. Sensors, 25(21), 6682. https://doi.org/10.3390/s25216682






