A Spatial Point Feature-Based Registration Method for Remote Sensing Images with Large Regional Variations
Abstract
1. Introduction
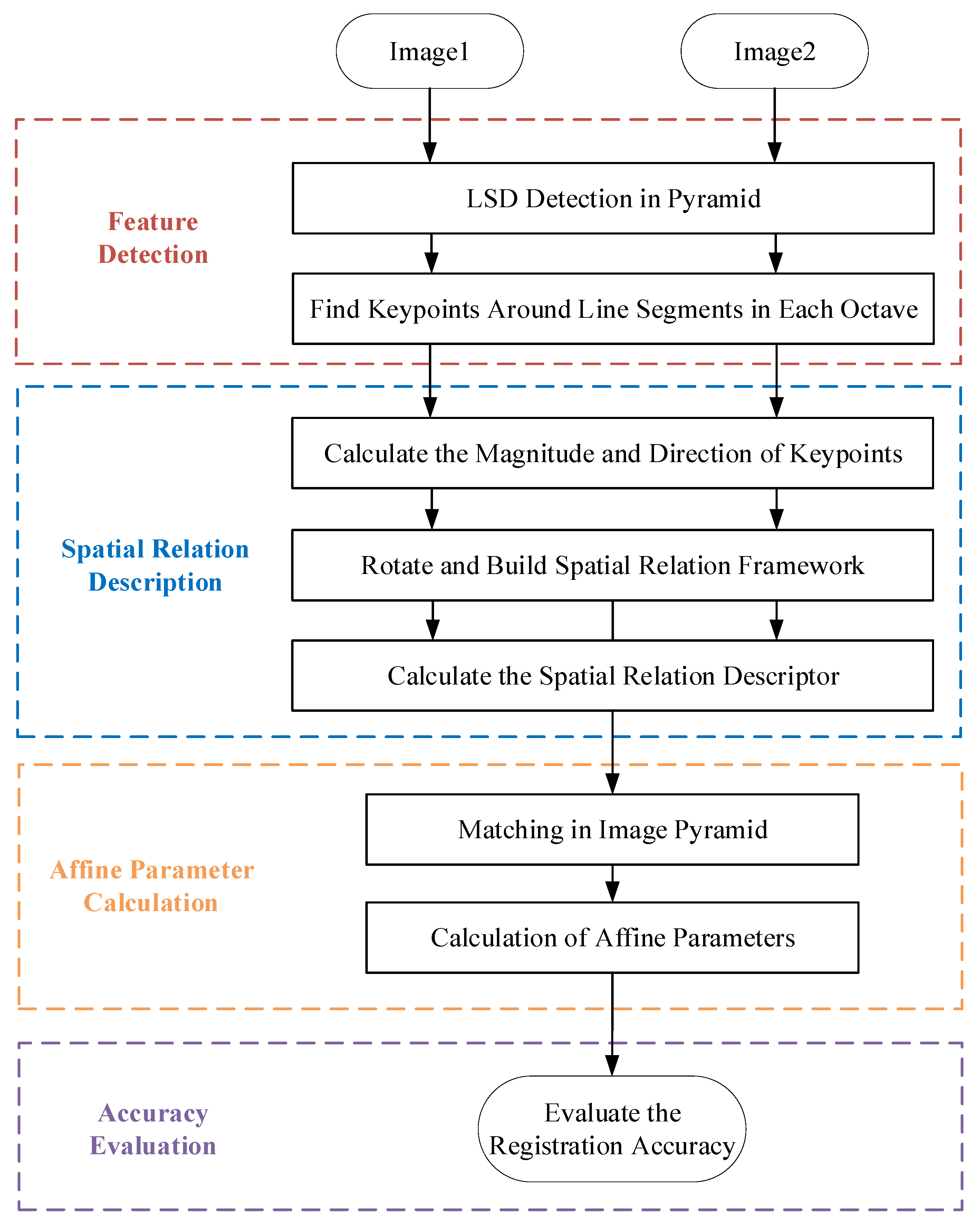
2. Methodology
2.1. Feature Extraction
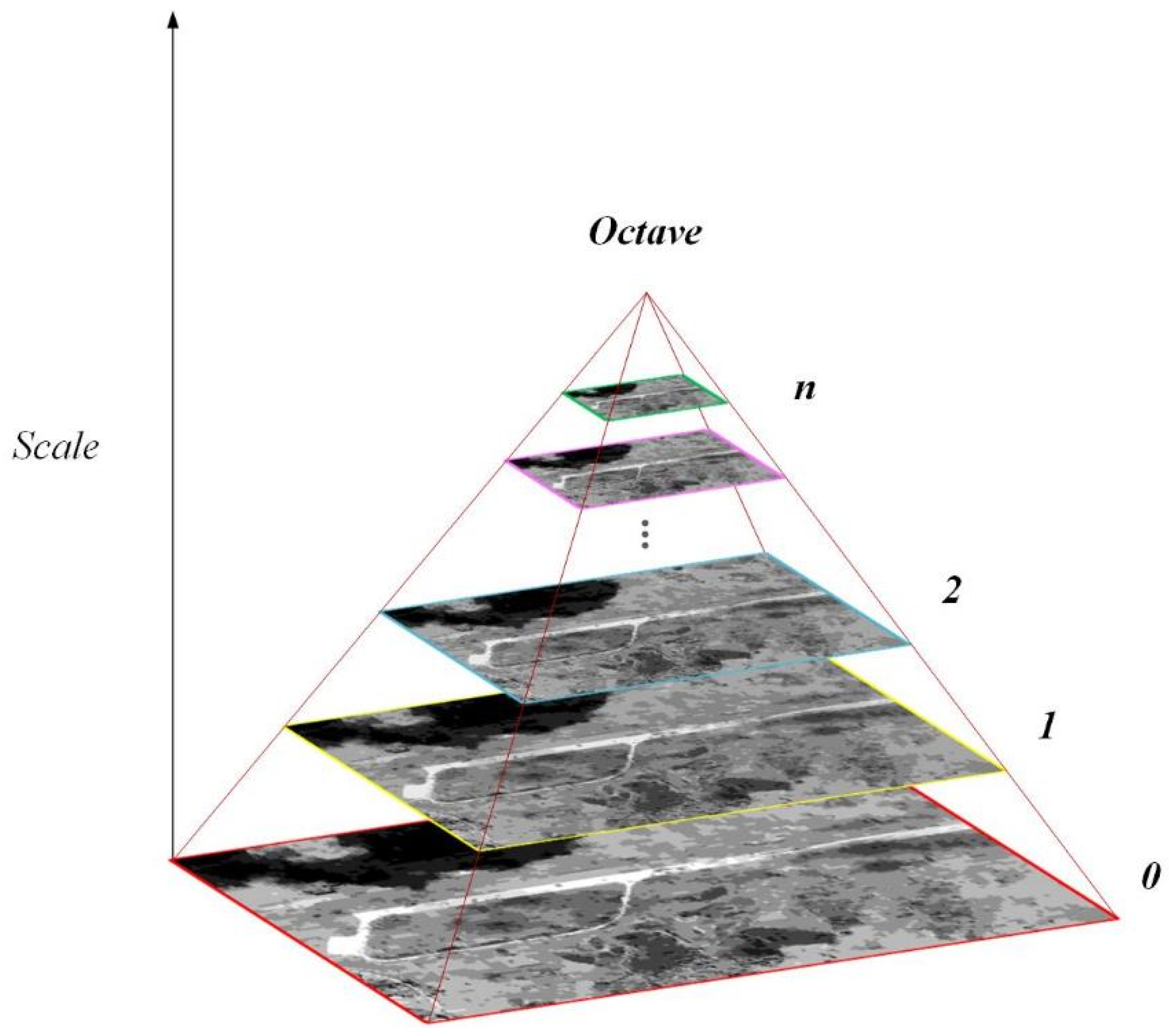
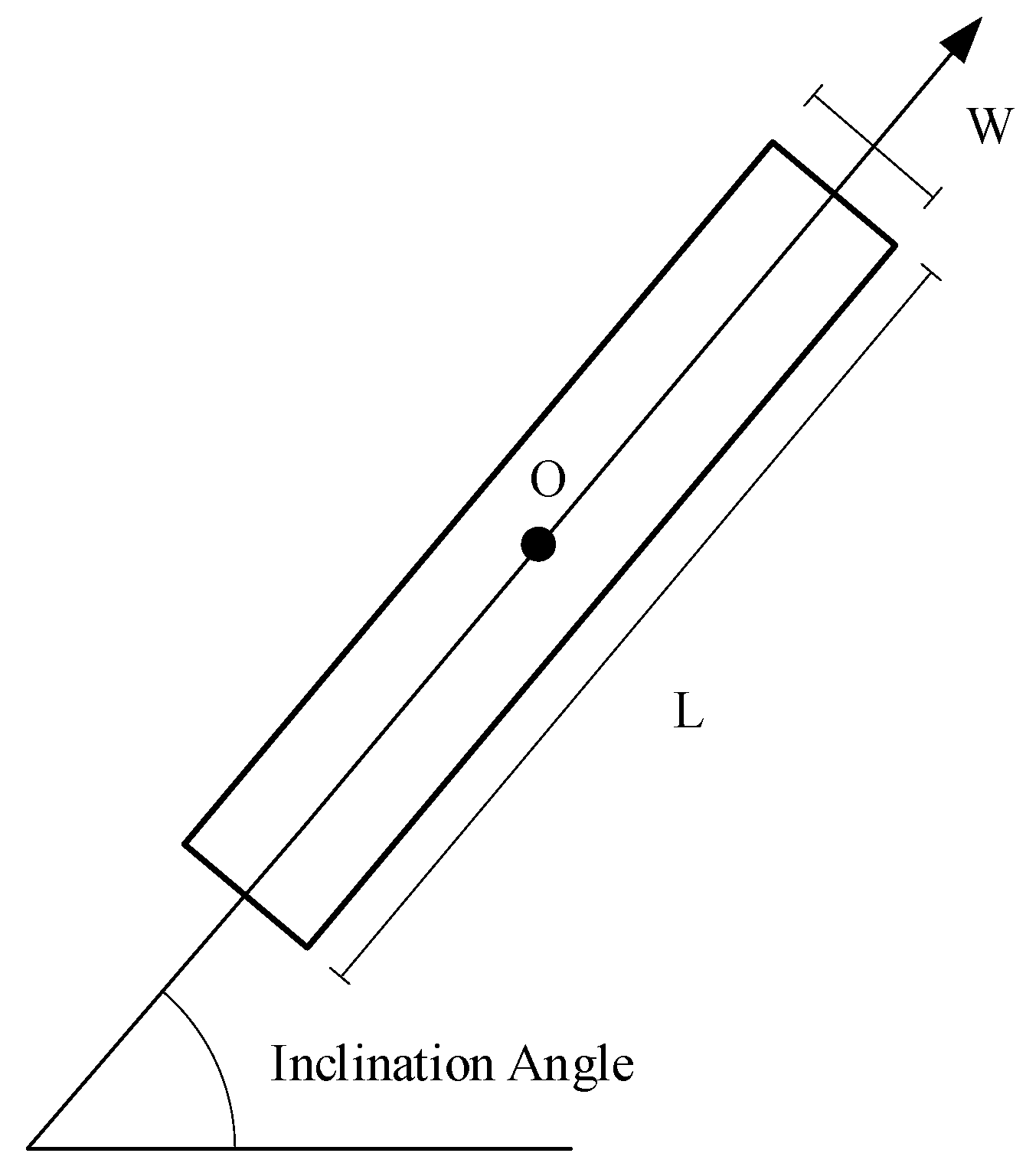
2.1.1. Line Segment Extraction
2.1.2. Keypoint Extraction
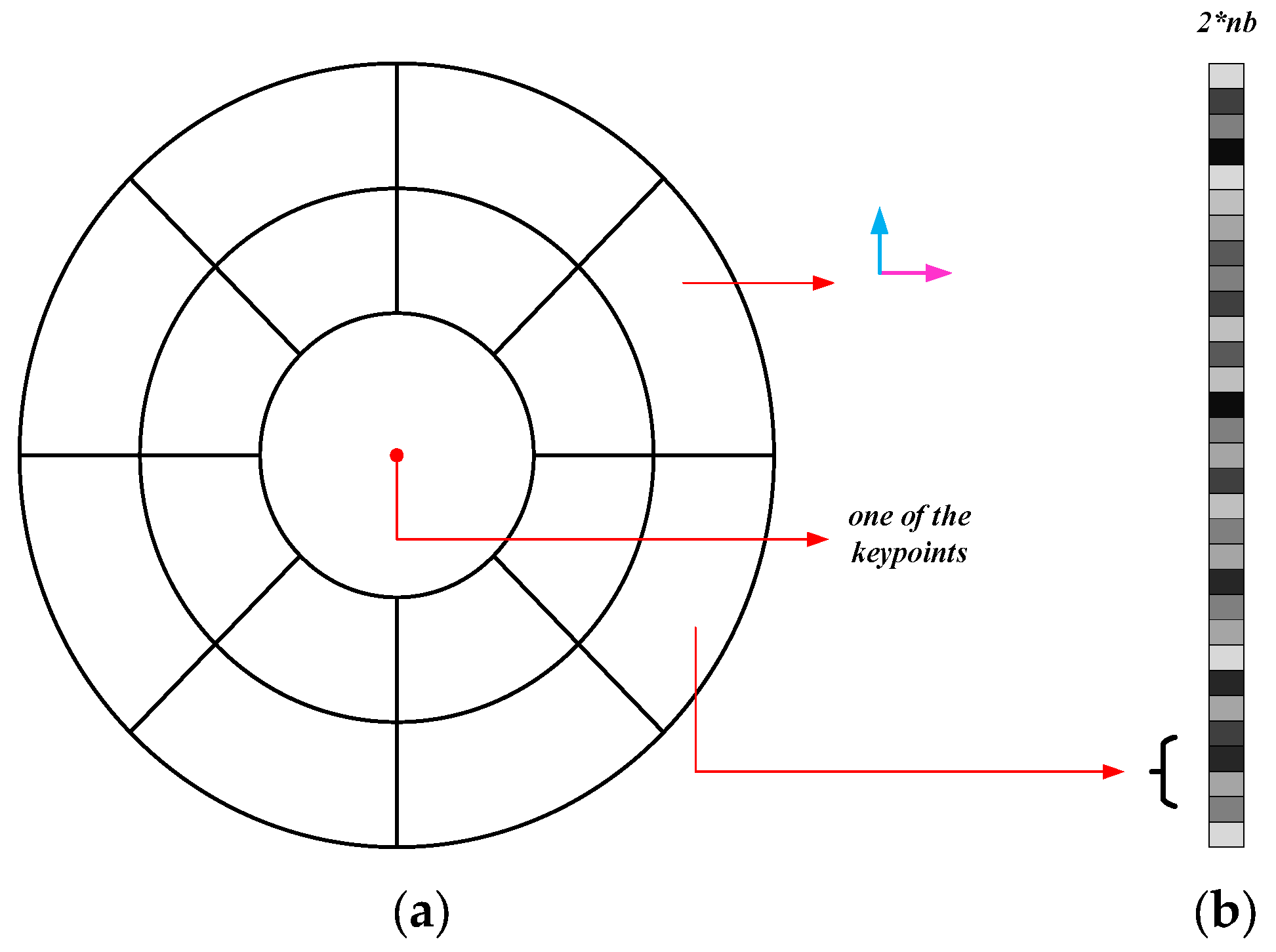
2.2. Descriptor Construction
2.3. Feature Matching
3. Results
3.1. Datasets
3.2. Evaluation Criterion
3.3. Experimental Results
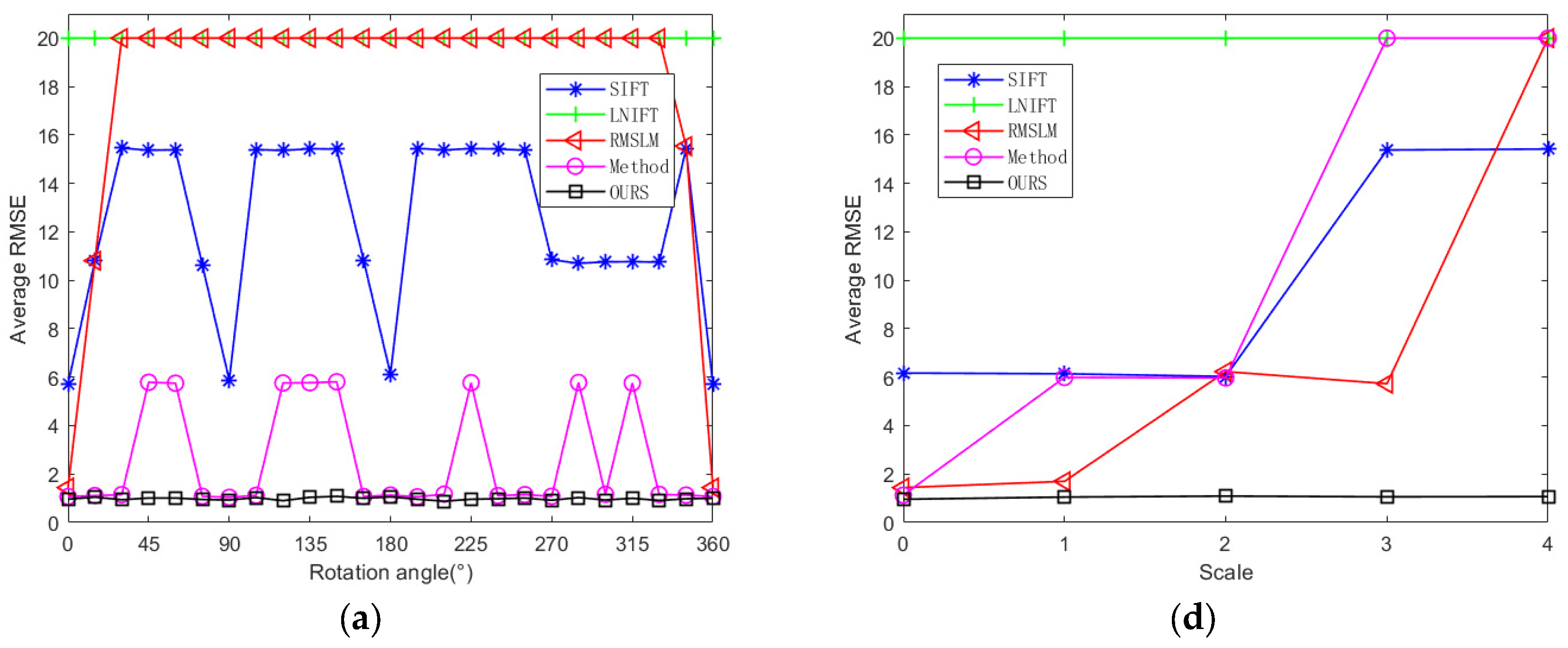
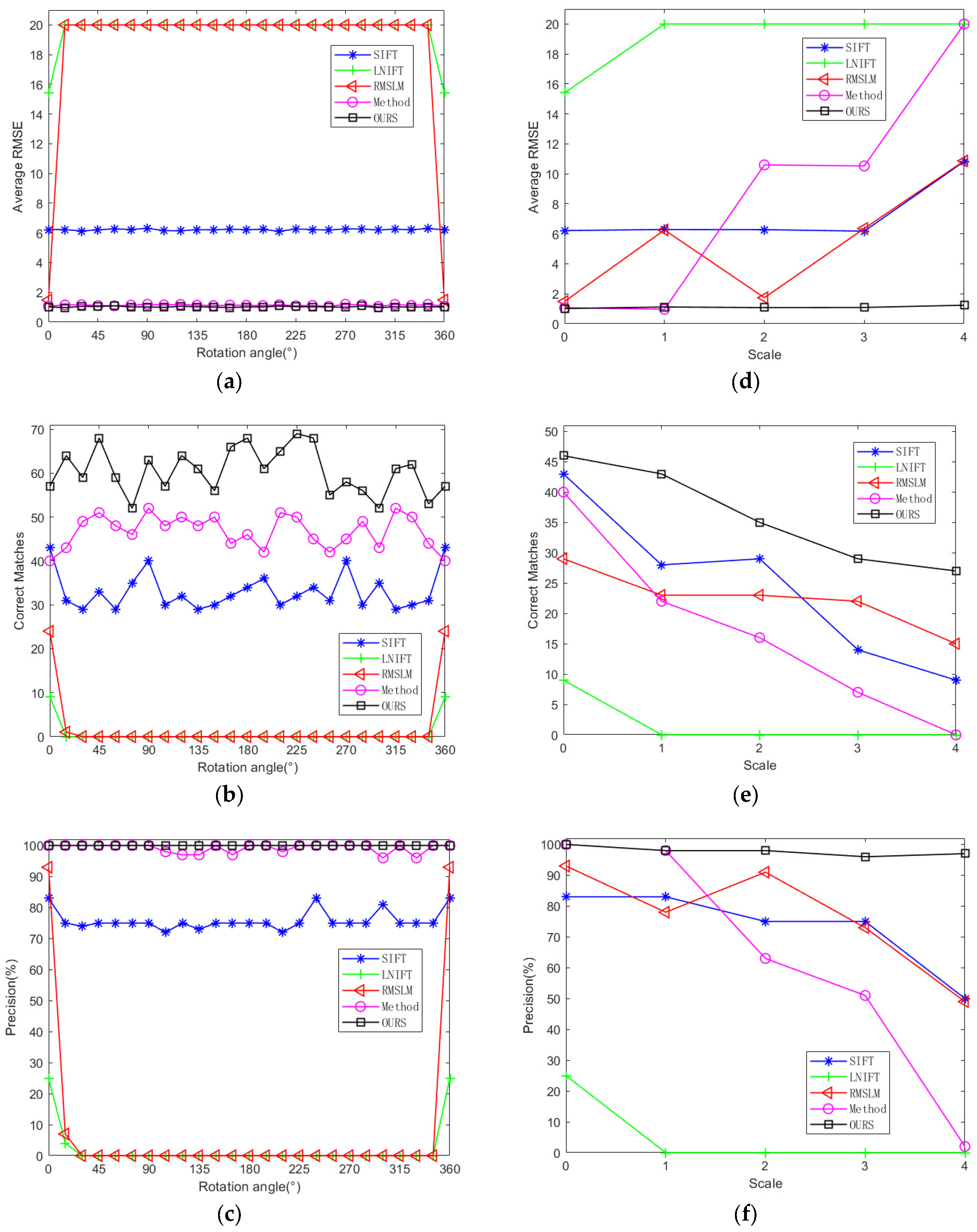
3.3.1. Experimental Results Applied to Dataset 1
3.3.2. Experimental Results Applied to Dataset 2
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lubin, A.; Saleem, A. Remote sensing-based mapping of the destruction to Aleppo during the Syrian Civil War between 2011 and 2017. Appl. Geogr. 2019, 108, 30–38. [Google Scholar] [CrossRef]
- Ning, X.; Zhang, H.; Zhang, R.; Huang, X. Multi-stage progressive change detection on high resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2024, 207, 231–244. [Google Scholar] [CrossRef]
- Hao, M.; Shi, W.; Zhang, H.; Li, C. Unsupervised Change Detection with Expectation-Maximization-Based Level Set. IEEE Geosci. Remote Sens. Lett. 2014, 11, 210–214. [Google Scholar] [CrossRef]
- Zhao, F.; Bao, J.; Ming, D. Battle Damage Assessment for Building based on Multi-feature. In Proceedings of the IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020. [Google Scholar]
- Oludare, V.; Kezebou, L.; Panetta, K.; Agaian, S. Semi-Supervised Learning for Improved Post-disaster Damage Assessment from Satellite Imagery. In Proceedings of the Conference on Image Exploitation and Learning, Online, 12–16 April 2021. [Google Scholar]
- Maes, F.; Collignon, A.; Vandermeulen, D. Multimodality image registration by maximization of mutual information. IEEE Transantions Med. Imaging 1997, 16, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded Up Robust Features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006. [Google Scholar]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A more distinctive representation for local image descriptors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Xiang, Y.; Wang, F.; You, H. A Robust SIFT-Like Algorithm for High-Resolution Optical-to-SAR Image Registration in Suburban Areas. IEEE Transanctions Geosci. Remote Sens. 2018, 56, 3078–3090. [Google Scholar] [CrossRef]
- Li, Q.; Han, G.; Liu, P.; Yang, H.; Luo, H.; Wu, J. An Infrared-Visible Image Registration Method Based on the Constrained Point Feature. Sensors 2021, 21, 1188. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, J. Image registration approach with scale-invariant feature transform algorithm and tangent-crossing-point feature. J. Electron. Imaging 2020, 29, 023010. [Google Scholar] [CrossRef]
- Si, S.; Li, Z.; Lin, Z.; Xu, X.; Zhang, Y.; Xie, S. 2-D/3-D Medical Image Registration Based on Feature-Point Matching. IEEE Trans. Instrum. Meas. 2024, 73, 5037609. [Google Scholar] [CrossRef]
- Li, J.Y.; Xu, W.Y.; Hu, Q.W.; Shi, P.C. Locally Normalized Image for Multimodal Feature Matching. IEEE Trans. Geosci. Remote Sens. 2022, 51, 5632314. [Google Scholar]
- Bodyr, M.; Milostnaya, N.; Khrapova, N. Approach to Detecting Pedestrian Movement Using the Method of Histograms of Oriented Gradients. Autom. Doc. Math. Linguist. 2025, 58, S169–S176. [Google Scholar]
- Yang, H.; Li, X.R.; Chen, S.H.; Zhao, L.Y. A Novel Coarse-to-Fine Scheme for RS Image Registration Based on SIFT and Phase Correlation. Remote Sens. 2017, 12, 1843. [Google Scholar]
- Tang, H.; Gao, Y.; Zhao, Z.; Bai, Z.; Yang, D. Homologous Image Registration Algorithm Based on Generalized Dual-Bootstrap Iterative Closest Point Algorithm. In Proceedings of the 4th International Conference on Intelligent Communications and Computing, Zhengzhou, China, 18–20 October 2024. [Google Scholar]
- Lu, J.; Hu, Q.; Zhu, R.; Jia, H. A High-Resolution Remote Sensing Image Registration Method Combining Object and Point Features. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4196–4213. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F.; Hu, Z. MSLD: A robust descriptor for line matching. Pattern Recognit. 2009, 42, 941–953. [Google Scholar] [CrossRef]
- Wu, L.; Wang, J.; Zhao, L.; Cheng, W.; Su, J. ISAR Image Registration Based on Line Features. J. Electromagn. Eng. Sci. 2024, 25, 225. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, J. Registration Method Based on Line-Intersection-Line for Remote Sensing Images of Urban Areas. Remote Sens. 2019, 11, 1400. [Google Scholar] [CrossRef]
- Sun, X.; Hu, C.; Yun, Z.; Yang, C.; Chen, H. Large scene sar image registration based on point and line matching network. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 7–12 July 2024. [Google Scholar]
- Lyu, C.; Jiang, J. Remote Sensing Image Registration with Line Segments and Their Intersections. Remote Sens. 2017, 9, 439. [Google Scholar] [CrossRef]
- Li, C.; Wang, B.; Zhou, Z.; Li, S.; Ma, J.; Tang, S. Image Registration through Self-correcting Based on Line Segments. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar]
- Fang, L.; Liu, Y.P.; Shi, Z.L.; Zhao, E.B.; Pang, M.Q.; Li, C.X. A general geometric transformation model for line-scan image registration. Eurasip J. Adv. Signal Process. 2024, 2023, 78. [Google Scholar] [CrossRef]
- Shi, X.L.; Jiang, J. Registration Method for Optical RS Images with Large Background Variations Using Line Segments. Remote Sens. 2017, 9, 436. [Google Scholar]
- Zhao, Y.; Chen, D.; Gong, J. A Line Feature-Based Rotation Invariant Method for Pre- and Post-Damage RS Image Registration. Remote Sens. 2025, 17, 184. [Google Scholar] [CrossRef]
- Jia, Q.; Fan, X.; Gao, X.; Yu, M.; Li, H.; Luo, Z. Line matching based on line-points invariant and local homography. Pattern Recognit. 2018, 81, 471–483. [Google Scholar] [CrossRef]
- Alrajeh, K.; Altameem, T. An Automated Medical Image Registration Algorithm Based on Straight-Line Segments. J. Med. Health Inform. 2016, 6, 1440–1444. [Google Scholar] [CrossRef]
- Fan, B.; Wu, F.; Hu, Z. Robust line matching through line-point invariants. Pattern Recognit. 2012, 45, 794–805. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Wang, W.; Zhu, Q. Robust line feature matching based on pair-wise geometric constraints and matching redundancy. ISPRS J. Photogramm. Remote Sens. 2020, 173, 42–58. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y. A Multi-source Image Registration Algorithm Based on Combined Line and Point Features. In Proceedings of the 20th International Conference on Information Fusion (Fusion), Montreal, QC, Canada, 10–13 July 2017. [Google Scholar]
- Yan, H.; Yang, S.; Li, Y.; Xue, Q.; Zhang, M. Multisource high-resolution optical remote sensing image registration based on point-line spatial geometric information. J. Appl. Remote Sens. 2021, 15, 036520. [Google Scholar]
- Li, Z.; Yue, J.; Fang, L. Adaptive Regional Multiple Features for Large-Scale High-Resolution Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5617313. [Google Scholar] [CrossRef]
- He, J.; Jiang, X.; Hao, Z.; Zhu, M.; Gao, W.; Liu, S. LPHOG: A Line Feature and Point Feature Combined Rotation Invariant Method for Heterologous Image Registration. Remote Sens. 2023, 15, 4548. [Google Scholar] [CrossRef]
- Lajili, M.; Belhachmi, Z.; Moakher, M.; Theljani, A. Unsupervised deep learning for geometric feature detection and multilevel-multimodal image registration. Appl. Intell. 2024, 54, 7878–7896. [Google Scholar] [CrossRef]
- Zhou, R.; Quan, D.; Wang, S.; Lv, C.; Cao, X.; Chanussot, J.; Li, Y.; Jiao, L. A Unified Deep Learning Network for Remote Sensing Image Registration and Change Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5101216. [Google Scholar] [CrossRef]
- Hong, X.; Tang, F.; Wang, L.; Chen, J. Unsupervised deep learning enables real-time image registration of fast-scanning optical-resolution photoacoustic microscopy. Photoacoustics 2024, 38, 100632. [Google Scholar] [CrossRef]
- Li, L.; Han, L.; Ding, M.; Liu, Z.; Cao, H. Remote Sensing Image Registration Based on Deep Learning Regression Model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8002905. [Google Scholar] [CrossRef]
- Li, L.; Han, L.; Ding, M.; Cao, H.; Hu, H. A deep learning semantic template matching framework for remote sensing image registration. ISPRS J. Photogramm. Remote Sens. 2021, 181, 205–217. [Google Scholar] [CrossRef]
- Wang, S.; Quan, D.; Liang, X.; Ning, M.; Guo, Y.; Jiao, L. A deep learning framework for remote sensing image registration. ISPRS J. Photogramm. Remote Sens. 2018, 145, 148–164. [Google Scholar] [CrossRef]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A Line Segment Detector. Image Process. Line 2012, 2, 35–55. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Gong, J.L.; Chen, D.R. A Multi-Feature Fusion-Based Method for Crater Extraction of Airport Runways in Remote-Sensing Images. Remote Sens. 2023, 15, 574. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, W.; Gong, M.; Su, L.; Jiao, L. A Novel Point-Matching Algorithm Based on Fast Sample Consensus for Image Registration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 43–47. [Google Scholar] [CrossRef]
- Ritwik, G.; Richard, H.; Sandra, S.; Nirav, P.; Bryce, G.; Jigar, D.; Eric, H.; Howie, C.; Matthew, G. Creating xBD: A Dataset for Assessing Building Damage from Satellite Imagery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Long Beach, CA, USA, 16–21 June 2019. [Google Scholar]














| Group | Image Pairs | Size | GSD (m) | Date | Status |
|---|---|---|---|---|---|
| Pre- and Post- attack | #1 | 720 × 437 | 0.6 | 2021 | Pre-attack |
| 716 × 431 | 0.6 | 2022 | Post-attack | ||
| #2 | 1024 × 701 | 0.5 | 2021 | Pre-attack | |
| 960 × 657 | 0.5 | 2022 | Post-attack | ||
| #3 | 1024 × 768 | 1.3 | 2022 | Pre-attack | |
| 1024 × 706 | 1.3 | 2022 | Post-attack | ||
| #4 | 1024 × 768 | 2.0 | 2023 | Pre-attack | |
| 1051 × 801 | 2.0 | 1999 | Post-attack | ||
| Pre- and Post- disaster | #5 | 1024 × 1024 | 0.5 | 2018 | Pre-hurricane |
| 1024 × 1024 | 0.5 | 2018 | Post-hurricane | ||
| #6 | 1024 × 1024 | 0.5 | 2019 | Pre-flood | |
| 1024 × 1024 | 0.5 | 2019 | Post-flood | ||
| #7 | 1024 × 1024 | 0.5 | 2018 | Pre-tsunami | |
| 1024 × 1024 | 0.5 | 2018 | Post-tsunami | ||
| #8 | 1024 × 1024 | 0.5 | 2018 | Pre-wildfire | |
| 1024 × 1024 | 0.5 | 2018 | Post-wildfire |
| Status | Indices | Method | ||||
|---|---|---|---|---|---|---|
| Method [7] | Method [14] | Method [26] | Method [27] | Ours | ||
| Scale_0 & Rot_0 | RMSE | 6.17 | 20.00 | 1.44 | 1.13 | 0.96 |
| NCM | 15 | 1 | 13 | 16 | 24 | |
| Precision | 75 | 13 | 88 | 97 | 100 | |
| Scale_2 & Rot_0 | RMSE | 6.03 | 20.00 | 6.23 | 5.97 | 1.09 |
| NCM | 10 | 0 | 12 | 7 | 20 | |
| Precision | 75 | 0 | 63 | 65 | 98 | |
| Scale_2 & Rot_45 | RMSE | 10.77 | 20 | 20 | 15.3 | 1.05 |
| NCM | 9 | 0 | 0 | 3 | 16 | |
| Precision | 56 | 0 | 0 | 25 | 98 | |
| Status | Indices | Method | ||||
|---|---|---|---|---|---|---|
| Method [7] | Method [14] | Method [26] | Method [27] | Ours | ||
| Scale_0 & Rot_0 | RMSE | 6.22 | 15.41 | 1.49 | 1.07 | 1.02 |
| NCM | 43 | 9 | 29 | 40 | 57 | |
| Precision | 83 | 25 | 93 | 100 | 100 | |
| Scale_2 & Rot_0 | RMSE | 6.28 | 20.00 | 1.74 | 10.6 | 1.08 |
| NCM | 29 | 0 | 23 | 16 | 35 | |
| Precision | 75 | 0 | 91 | 63 | 98 | |
| Scale_2 & Rot_45 | RMSE | 6.18 | 20 | 20 | 10.59 | 1.07 |
| NCM | 12 | 0 | 1 | 11 | 31 | |
| Precision | 75 | 0 | 5 | 50 | 98 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Chen, D.; Gong, J. A Spatial Point Feature-Based Registration Method for Remote Sensing Images with Large Regional Variations. Sensors 2025, 25, 6608. https://doi.org/10.3390/s25216608
Zhao Y, Chen D, Gong J. A Spatial Point Feature-Based Registration Method for Remote Sensing Images with Large Regional Variations. Sensors. 2025; 25(21):6608. https://doi.org/10.3390/s25216608
Chicago/Turabian StyleZhao, Yalun, Derong Chen, and Jiulu Gong. 2025. "A Spatial Point Feature-Based Registration Method for Remote Sensing Images with Large Regional Variations" Sensors 25, no. 21: 6608. https://doi.org/10.3390/s25216608
APA StyleZhao, Y., Chen, D., & Gong, J. (2025). A Spatial Point Feature-Based Registration Method for Remote Sensing Images with Large Regional Variations. Sensors, 25(21), 6608. https://doi.org/10.3390/s25216608





