The Task Dependency of Spontaneous Rhythmic Performance in Movements Beyond Established Biomechanical Models: An Inertial Sensor-Based Study
Highlights
- Spontaneous motor tempo (SMT) is task-dependent: Complex, full-body exercises have slower and more variable tempos compared to simple, established movements like walking, hopping, and tapping.
- Consistent Relative Timing: Despite variations in overall tempo, the relative duration of a movement cycle’s phases remains stable, typically at a 1:1 ratio. This points to a shared, underlying neural control mechanism.
- High Performance Stability: Individuals maintain a high degree of timing precision with low individual variability, even during complex, full-body exercises.
- Internal timing mechanisms are adaptable and adjust to task-specific biomechanical demands, providing insights into motor control beyond simple rhythmic movements.
- The findings provide a basis for designing personalized exercise and rehabilitation programs that account for an individual’s natural, task-specific rhythmic variability.
Abstract
1. Introduction
- Do individuals maintain an SMT during voluntary physical fitness exercise tasks performed without external pacing?
- How does SMT in such exercise tasks compare to that observed in established biomechanical model (EBM) tasks regarding temporal structure metrics and stability?
2. Materials and Methods
2.1. Participants
2.2. Experimental Procedure
2.2.1. Data Collection and Analysis
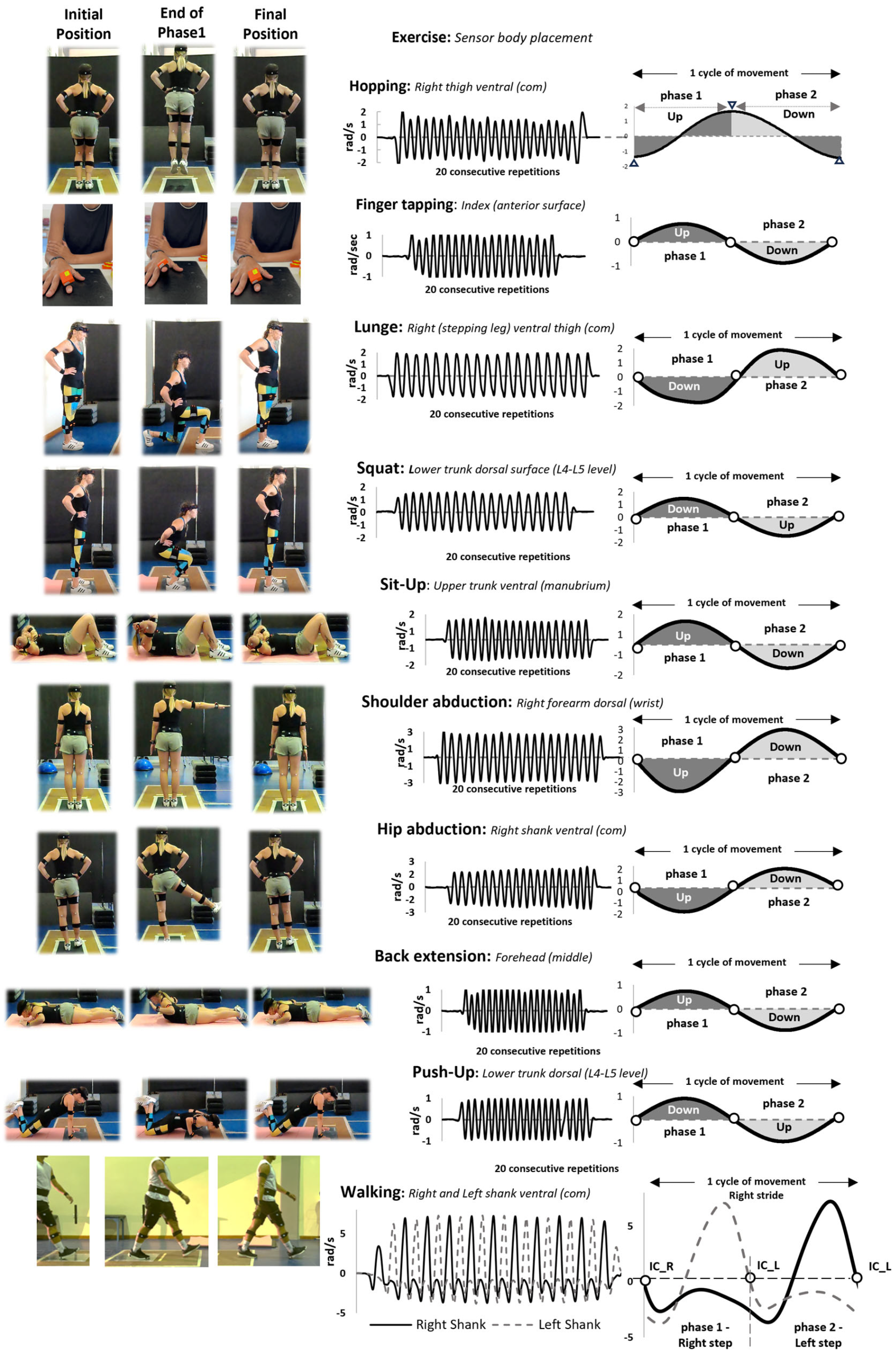
2.2.2. Extraction of Spontaneous Motor Performance Variables
Temporal Structure Metrics
Temporal Structure Stability
Selected Cycles and Reliability Assessment
- (a)
- The Intraclass Correlation Coefficient (ICC) using a two-way random-effects model for absolute agreement and average measures.
- (b)
- The Standard Error of Measurement (SEM) derived from the square root of the ANOVA residual mean square error (SEM = √S2error) and its relative form expressed as a percentage of the mean (SEM% = (SEM/) × 100).
- (c)
- The Minimal Detectable Change at 95% confidence (MDC95), calculated from the SEM as MDC95 = SEM × 1.96 × √2, and its relative form, expressed as a percentage of the mean (MDC95% = (MDC95/) × 100).
2.2.3. Statistical Analysis
3. Results
3.1. Task Dependency of Spontaneous Motor Tempo
3.2. Task Dependency of Temporal Structure
3.3. Task Dependency of Temporal Structure Stability
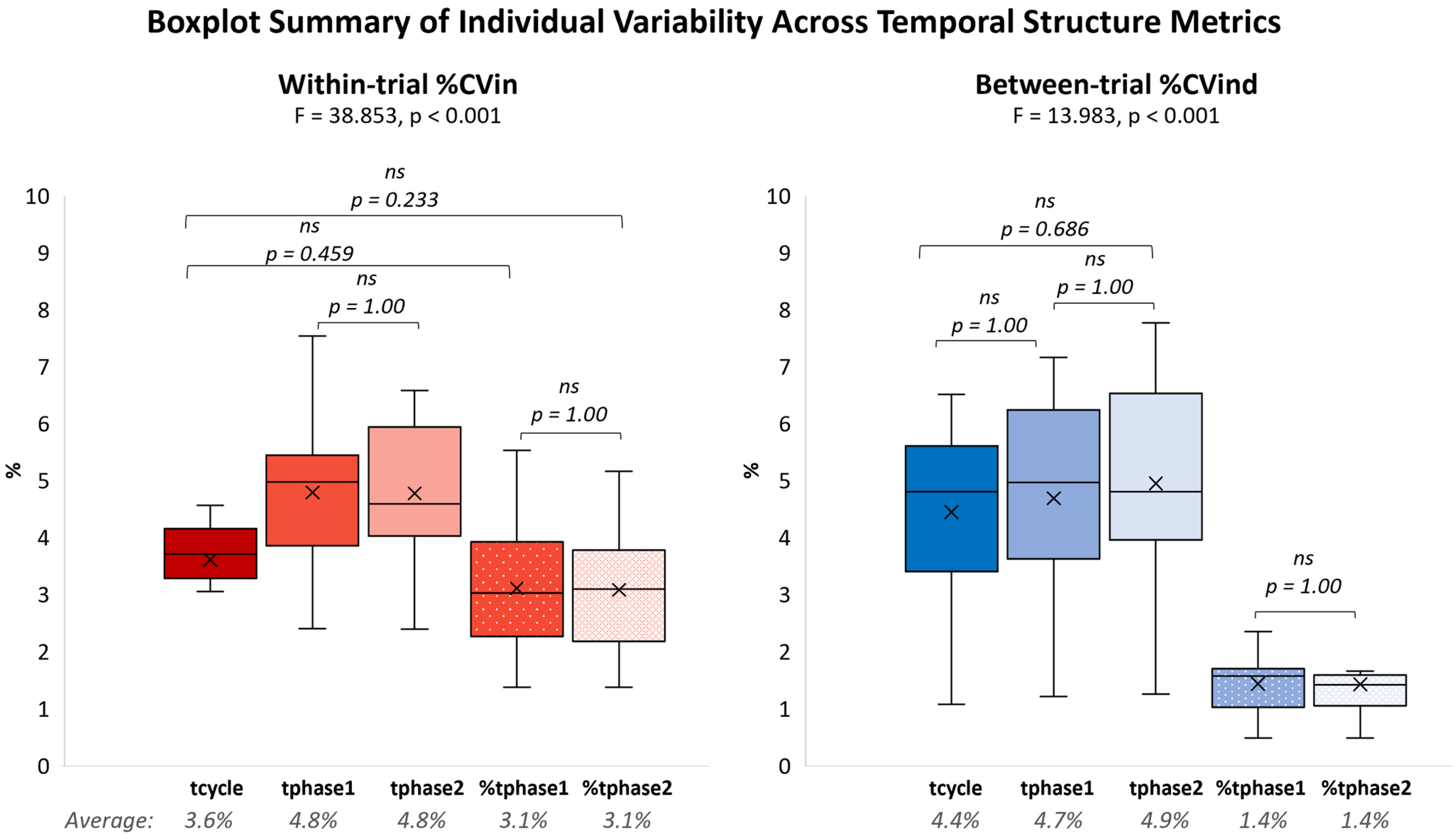
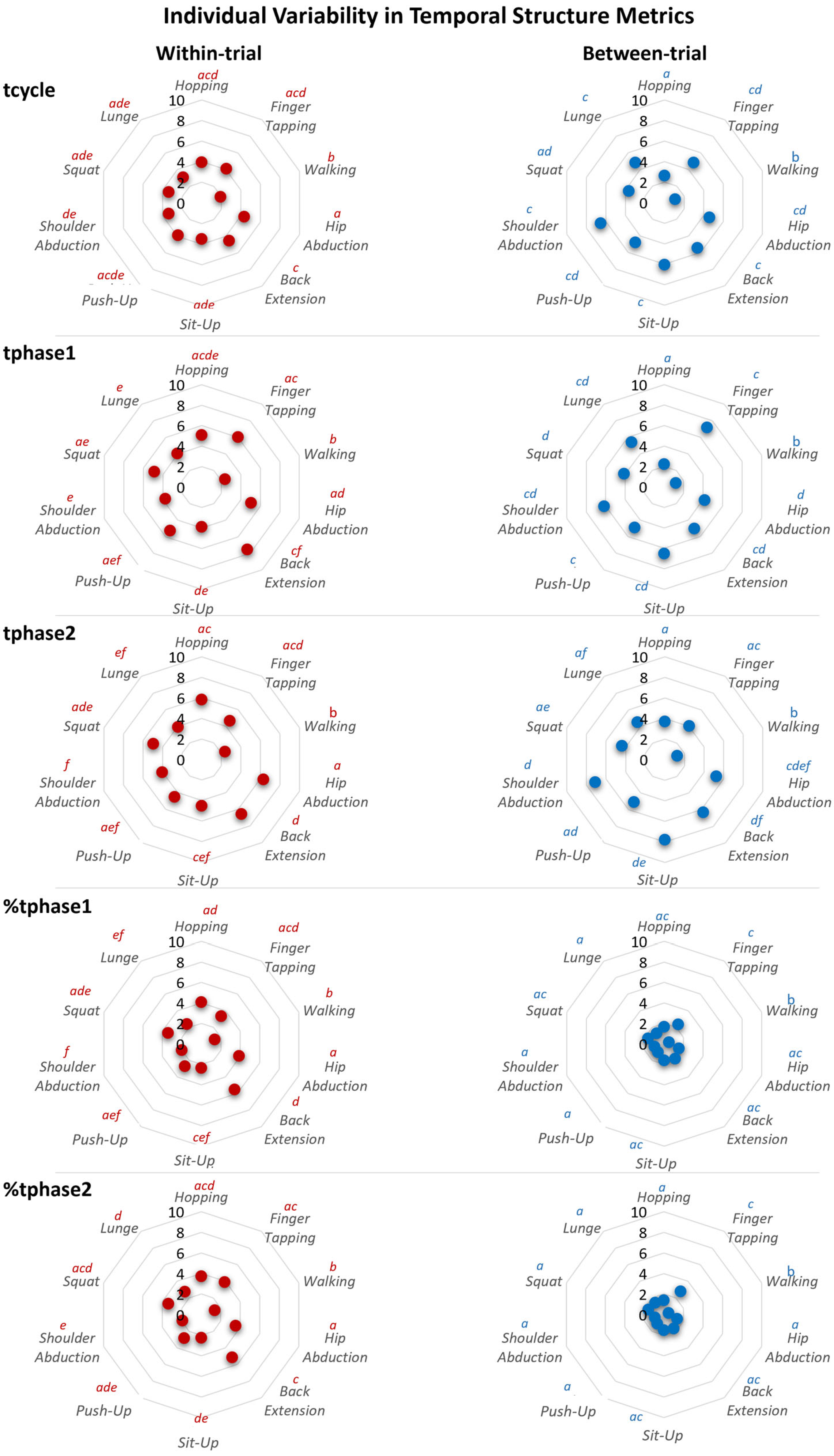
3.3.1. Overall Variability Tendency Across Temporal Structure Metrics
3.3.2. Within-Trial Individual Variability
3.3.3. Between-Trial Individual Variability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SMT | Spontaneous motor tempo |
| EBM | Established biomechanical Model |
| PFEs | Physical fitness exercise-based tasks |
| WALK | Walking |
| HOP | Two-leg hop in place |
| FT | Finger tapping |
| SQR | Squat |
| LNG | Lunge |
| PU | Push-up |
| SU | Sit-up |
| BE | Back extension |
| SA | Shoulder abduction |
| HA | Hip abduction |
Appendix A. Mean ± SD and ANOVA Results
| Temporal Structure Metrics | |||||
|---|---|---|---|---|---|
| Mean (SD) | |||||
| tcycle (s) | tphase1 (s) | tphase2 (s) | %tphase1 (%tcycle) | %tphase2 (%tcycle) | |
| EBM Tasks | |||||
| Hopping | 0.48 (0.05) | 0.22 (0.02) | 0.25 (0.04) | 47.16 (3.4) | 52.84 (3.4) |
| Finger Tapping | 0.53 (0.12) | 0.28 (0.07) | 0.24 (0.06) | 53.52 (3.16) | 46.48 (3.16) |
| Walking (stride) | 1.11 (0.06) | 0.55 (0.03) | 0.55 (0.03) | 50.1 (0.57) | 49.9 (0.57) |
| PFE Tasks | |||||
| Hip Abduction | 1.47 (0.28) | 0.7 (0.12) | 0.77 (0.16) | 47.64 (2.24) | 52.36 (2.24) |
| Back Extension | 1.51 (0.51) | 0.73 (0.22) | 0.78 (0.29) | 48.59 (1.92) | 51.41 (1.92) |
| Sit-Up | 1.62 (0.41) | 0.8 (0.2) | 0.82 (0.22) | 49.4 (1.98) | 50.6 (1.98) |
| Push-Up | 1.7 (0.34) | 0.87 (0.19) | 0.83 (0.16) | 51.05 (1.12) | 48.95 (1.12) |
| Shoulder Abduction | 1.8 (0.33) | 0.88 (0.15) | 0.92 (0.19) | 49.12 (1.56) | 50.88 (1.56) |
| Squat | 2.04 (0.37) | 1.01 (0.19) | 1.02 (0.19) | 49.8 (2.23) | 50.2 (2.23) |
| Lunge | 2.74 (0.56) | 1.46 (0.31) | 1.28 (0.27) | 53.33 (2.32) | 46.67 (2.32) |
| F-value | 158.94 | 177.50 | 126.11 | 28.04 | 28.04 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Partial η2 | 0.85 | 0.86 | 0.82 | 0.50 | 0.50 |
| Observed Power | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Within-Trial Individual Variability (%CVind) | |||||
|---|---|---|---|---|---|
| Mean (SD) | |||||
| tcycle (%) | tphase1 (%) | tphase2 (%) | %tphase1 (%) | %tphase2 (%) | |
| EBM Tasks | |||||
| Hopping | 4.0 (1.3) | 5.1 (2.7) | 5.8 (2.1) | 4.1 (1.9) | 3.7 (2.2) |
| Finger Tapping | 4.1 (1.3) | 6.0 (1.9) | 4.7 (1.7) | 3.3 (1.1) | 3.9 (1.5) |
| Walking (stride) | 1.9 (0.6) | 2.4 (0.6) | 2.4 (0.6) | 1.4 (0.3) | 1.4 (0.3) |
| PFE Tasks | |||||
| Hip Abduction | 4.3 (1.5) | 5.1 (1.5) | 6.3 (2.0) | 3.9 (1.2) | 3.5 (1.1) |
| Back Extension | 4.6 (1.3) | 7.5 (3.5) | 6.6 (3.0) | 5.5 (3.4) | 5.2 (3.0) |
| Sit-Up | 3.5 (1.1) | 3.9 (1.5) | 4.5 (1.5) | 2.4 (1.2) | 2.3 (1.1) |
| Push-Up | 3.9 (1.7) | 5.3 (3.5) | 4.5 (2.6) | 2.7 (1.9) | 2.8 (1.9) |
| Shoulder Abduction | 3.4 (1.0) | 3.7 (1.2) | 4.1 (1.2) | 2.0 (0.9) | 1.9 (0.7) |
| Squat | 3.4 (1.1) | 4.9 (1.5) | 5.0 (1.6) | 3.4 (1.5) | 3.4 (1.5) |
| Lunge | 3.1 (0.7) | 4.0 (0.9) | 3.9 (1.1) | 2.4 (0.5) | 2.7 (0.6) |
| F-value | 14.47 | 15.05 | 14.68 | 17.44 | 15.67 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Partial η2 | 0.34 | 0.35 | 0.34 | 0.38 | 0.36 |
| Observed Power | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Between-Trial Individual Variability (%Cvind) | |||||
|---|---|---|---|---|---|
| Mean (SD) | |||||
| tcycle (%) | tphase1 (%) | tphase2 (%) | %tphase1 (%) | %tphase2 (%) | |
| EBM Tasks | |||||
| Hopping | 2.6 (1.5) | 2.2 (1.9) | 3.7 (2.5) | 1.6 (2.1) | 1.4 (1.8) |
| Finger Tapping | 4.8 (3.1) | 7.2 (5.3) | 4.0 (3.4) | 2.4 (2.3) | 2.8 (2.5) |
| Walking (stride) | 1.1 (0.9) | 1.2 (0.9) | 1.3 (0.9) | 0.5 (0.3) | 0.5 (0.3) |
| PFE Tasks | |||||
| Hip Abduction | 4.6 (2.7) | 4.2 (2.5) | 5.3 (3.2) | 1.5 (0.9) | 1.4 (0.8) |
| Back Extension | 5.5 (3.4) | 5.0 (3.4) | 6.3 (4.2) | 1.8 (2.0) | 1.7 (1.8) |
| Sit-Up | 6.0 (6.1) | 6.5 (7.2) | 7.8 (8.8) | 1.6 (2.6) | 1.5 (2.4) |
| Push-Up | 4.8 (3.3) | 4.9 (2.6) | 5.1 (4.3) | 1.0 (1.5) | 1.1 (1.5) |
| Shoulder Abduction | 6.5 (5.8) | 6.1 (5.4) | 7.1 (6.2) | 1.0 (1.0) | 0.9 (1.0) |
| Squat | 3.7 (2.9) | 4.1 (2.9) | 4.4 (3.4) | 1.7 (1.9) | 1.6 (1.7) |
| Lunge | 4.8 (5.1) | 5.4 (5.6) | 4.5 (4.7) | 1.3 (1.0) | 1.4 (1.2) |
| F-value | 5.73 | 6.21 | 5.06 | 2.84 | 4.04 |
| p-value | <0.001 | <0.001 | 0.00 | 0.02 | 0.00 |
| Partial η2 | 0.17 | 0.18 | 0.15 | 0.09 | 0.13 |
| Observed Power | 0.99 | 0.99 | 0.97 | 0.79 | 0.92 |
Appendix B. Pairwise Comparisons
| p-Values of Temporal Structure Metrics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Task | HOP | FT | WALK | HA | BE | SU | PU | SA | SQR | |
| tcycle | FT | 1.000 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 0.000 | 0.000 | 0.000 | — | ||||||
| BE | 0.000 | 0.000 | 0.010 | 0.057 | — | |||||
| SU | 0.000 | 0.000 | 0.000 | 1.000 | 0.360 | — | ||||
| PU | 0.000 | 0.000 | 0.000 | 0.073 | 0.471 | 1.000 | — | |||
| SA | 0.000 | 0.000 | 0.000 | 0.004 | 0.360 | 0.602 | 1.000 | — | ||
| SQR | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.238 | — | |
| LNG | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| tphase1 | FT | 0.001 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 0.000 | 0.000 | 0.000 | — | ||||||
| BE | 0.000 | 0.000 | 0.012 | 0.010 | — | |||||
| SU | 0.000 | 0.000 | 0.000 | 0.575 | 0.002 | — | ||||
| PU | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.522 | — | |||
| SA | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.697 | 1.000 | — | ||
| SQR | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.053 | — | |
| LNG | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| tphase2 | FT | 1.000 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 0.000 | 0.000 | 0.000 | — | ||||||
| BE | 0.000 | 0.000 | 0.010 | 0.284 | — | |||||
| SU | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | — | ||||
| PU | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | — | |||
| SA | 0.000 | 0.000 | 0.000 | 0.079 | 1.000 | 0.771 | 0.630 | — | ||
| SQR | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 1.000 | — | |
| LNG | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| %tphase1 and %tphase2 | FT | 0.000 | — | |||||||
| WALK | 0.003 | 0.000 | — | |||||||
| HA | 1.000 | 0.000 | 0.000 | — | ||||||
| BE | 1.000 | 0.000 | 0.002 | 1.000 | — | |||||
| SU | 0.134 | 0.000 | 1.000 | 0.131 | 1.000 | — | ||||
| PU | 0.000 | 0.043 | 0.035 | 0.000 | 0.001 | 0.022 | — | |||
| SA | 0.407 | 0.000 | 0.243 | 0.284 | 1.000 | 1.000 | 0.001 | — | ||
| SQR | 0.078 | 0.001 | 1.000 | 0.069 | 0.725 | 1.000 | 0.435 | 1.000 | — | |
| LNG | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | |
| p-Values of Within-Trial Individual Variability | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Task | HOP | FT | WALK | HA | BE | SU | PU | SA | SQR | |
| tcycle | FT | 1.000 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 1.000 | 1.000 | 0.000 | — | ||||||
| BE | 1.000 | 1.000 | 0.000 | 0.010 | — | |||||
| SU | 1.000 | 1.000 | 0.000 | 0.450 | 0.020 | — | ||||
| PU | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | — | |||
| SA | 0.530 | 0.090 | 0.000 | 0.030 | 0.020 | 1.000 | 1.000 | — | ||
| SQR | 1.000 | 0.980 | 0.000 | 0.070 | 0.010 | 1.000 | 1.000 | 1.000 | — | |
| LNG | 0.040 | 0.030 | 0.000 | 0.000 | 0.000 | 1.000 | 0.370 | 1.000 | 1.000 | |
| tphase1 | FT | 1.000 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 1.000 | 1.000 | 0.000 | — | ||||||
| BE | 0.190 | 1.000 | 0.000 | 0.000 | — | |||||
| SU | 1.000 | 0.000 | 0.000 | 0.320 | 0.000 | — | ||||
| PU | 1.000 | 1.000 | 0.000 | 1.000 | 0.390 | 1.000 | — | |||
| SA | 0.270 | 0.000 | 0.000 | 0.010 | 0.000 | 1.000 | 0.960 | — | ||
| SQR | 1.000 | 0.530 | 0.000 | 1.000 | 0.020 | 0.580 | 1.000 | 0.130 | — | |
| LNG | 1.000 | 0.000 | 0.000 | 0.040 | 0.000 | 1.000 | 1.000 | 1.000 | 0.310 | |
| tphase2 | FT | 0.370 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 1.000 | 0.110 | 0.000 | — | ||||||
| BE | 1.000 | 0.250 | 0.000 | 0.010 | — | |||||
| SU | 0.530 | 1.000 | 0.000 | 0.010 | 0.070 | — | ||||
| PU | 1.000 | 1.000 | 0.000 | 0.020 | 0.090 | 1.000 | — | |||
| SA | 0.000 | 1.000 | 0.000 | 0.000 | 0.070 | 1.000 | 1.000 | — | ||
| SQR | 1.000 | 1.000 | 0.000 | 0.240 | 0.280 | 1.000 | 1.000 | 1.000 | — | |
| LNG | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 0.170 | |
| %tphase1 and %tphase2 | FT | 1.000 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 1.000 | 1.000 | 0.000 | — | ||||||
| BE | 1.000 | 0.140 | 0.000 | 0.000 | — | |||||
| SU | 0.010 | 0.130 | 0.000 | 0.000 | 0.000 | — | ||||
| PU | 0.450 | 1.000 | 0.020 | 0.200 | 0.010 | 1.000 | — | |||
| SA | 0.000 | 0.000 | 0.030 | 0.000 | 0.000 | 1.000 | 1.000 | — | ||
| SQR | 1.000 | 1.000 | 0.000 | 1.000 | 0.090 | 0.080 | 1.000 | 0.000 | — | |
| LNG | 0.000 | 0.020 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 0.060 | |
| p-Values of Between-Trial Individual Variability | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Task | HOP | FT | WALK | HA | BE | SU | PU | SA | SQR | |
| tcycle | FT | 0.001 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 0.000 | 0.755 | 0.000 | — | ||||||
| BE | 0.000 | 0.431 | 0.000 | 0.317 | — | |||||
| SU | 0.007 | 0.322 | 0.000 | 0.256 | 0.625 | — | ||||
| PU | 0.004 | 0.948 | 0.000 | 0.818 | 0.453 | 0.289 | — | |||
| SA | 0.002 | 0.172 | 0.000 | 0.143 | 0.625 | 0.746 | 0.230 | — | ||
| SQR | 0.099 | 0.181 | 0.000 | 0.163 | 0.036 | 0.046 | 0.182 | 0.030 | — | |
| LNG | 0.029 | 0.977 | 0.001 | 0.862 | 0.458 | 0.304 | 0.990 | 0.090 | 0.240 | |
| tphase1 | FT | 0.000 | — | |||||||
| WALK | 0.017 | 0.000 | — | |||||||
| HA | 0.000 | 0.005 | 0.000 | — | ||||||
| BE | 0.000 | 0.078 | 0.000 | 0.240 | — | |||||
| SU | 0.005 | 0.721 | 0.000 | 0.113 | 0.233 | — | ||||
| PU | 0.000 | 0.025 | 0.000 | 0.304 | 0.864 | 0.231 | — | |||
| SA | 0.001 | 0.474 | 0.000 | 0.099 | 0.233 | 0.804 | 0.326 | — | ||
| SQR | 0.009 | 0.017 | 0.000 | 0.904 | 0.170 | 0.072 | 0.272 | 0.109 | — | |
| LNG | 0.005 | 0.242 | 0.001 | 0.286 | 0.674 | 0.406 | 0.685 | 0.456 | 0.270 | |
| tphase2 | FT | 0.565 | — | |||||||
| WALK | 0.000 | 0.000 | — | |||||||
| HA | 0.036 | 0.155 | 0.000 | — | ||||||
| BE | 0.010 | 0.035 | 0.000 | 0.531 | — | |||||
| SU | 0.027 | 0.045 | 0.000 | 0.163 | 0.385 | — | ||||
| PU | 0.148 | 0.292 | 0.000 | 0.859 | 0.297 | 0.123 | — | |||
| SA | 0.015 | 0.027 | 0.000 | 0.199 | 0.385 | 0.688 | 0.206 | — | ||
| SQR | 0.418 | 0.758 | 0.000 | 0.303 | 0.040 | 0.050 | 0.486 | 0.049 | — | |
| LNG | 0.438 | 0.672 | 0.001 | 0.499 | 0.079 | 0.033 | 0.637 | 0.014 | 0.883 | |
| %tphase1 and %tphase2 | FT | 0.141 | — | |||||||
| WALK | 0.004 | 0.000 | — | |||||||
| HA | 0.715 | 0.066 | 0.000 | — | ||||||
| BE | 0.758 | 0.383 | 0.001 | 0.052 | — | |||||
| SU | 0.999 | 0.322 | 0.023 | 0.796 | 0.678 | — | ||||
| PU | 0.229 | 0.015 | 0.044 | 0.139 | 0.111 | 0.284 | — | |||
| SA | 0.136 | 0.008 | 0.024 | 0.074 | 0.678 | 0.121 | 0.839 | — | ||
| SQR | 0.967 | 0.246 | 0.004 | 0.698 | 0.680 | 0.957 | 0.207 | 0.112 | — | |
| LNG | 0.402 | 0.022 | 0.001 | 0.354 | 0.187 | 0.440 | 0.460 | 0.311 | 0.329 | |
Appendix C. Group-Level Variation in Temporal Structure Metrics
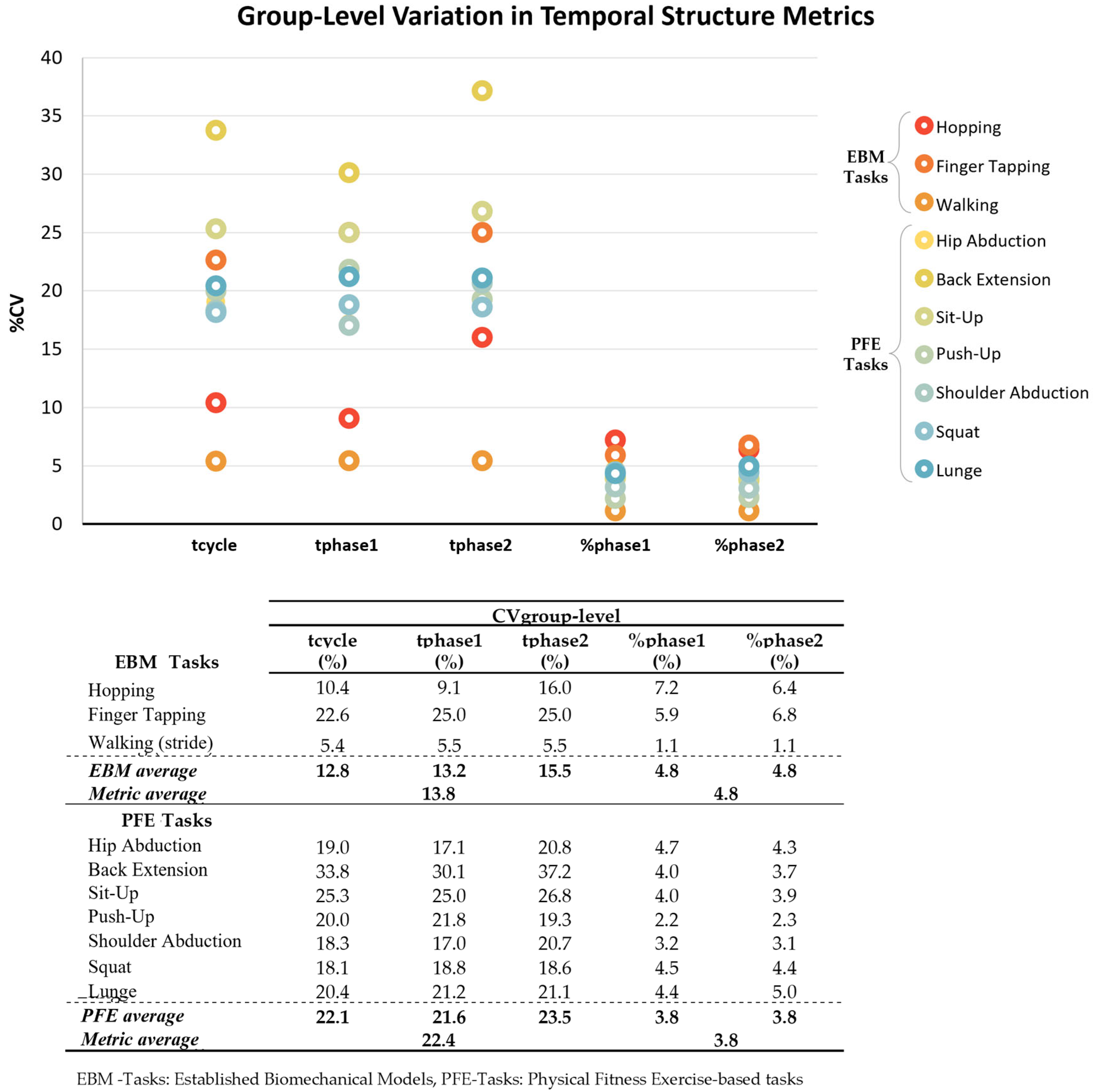
Appendix D
| Temporal Structure Metrics | |||||
|---|---|---|---|---|---|
| tcycle | tphase1 | tphase2 | %tphase1 | %tphase2 | |
| ICC (95% CI) | ICC (95% CI) | ICC (95% CI) | ICC (95% CI) | ICC (95% CI) | |
| HOP | 0.997 (0.995–0.998) | 0.985 (0.976–0.992) | 0.997 (0.995–0.998) | 0.990 (0.984–0.994) | 0.990 (0.984–0.994) |
| FT | 0.999 (0.998–0.999) | 0.998 (0.997–0.999) | 0.999 (0.998–0.999) | 0.992 (0.987–0.996) | 0.992 (0.987–0.996) |
| WALK | 0.994 (0.990–0.997) | 0.992 (0.986–0.995) | 0.993 (0.989–0.996) | 0.955 (0.928–0.975) | 0.955 (0.928–0.975) |
| BE | 0.999 (0.999–1.000) | 0.998 (0.997–0.999) | 0.999 (0.999–1.000) | 0.947 (0.915–0.971) | 0.947 (0.915–0.971) |
| HA | 0.998 (0.997–0.999) | 0.997 (0.996–0.999) | 0.997 (0.995–0.998) | 0.980 (0.968–0.989) | 0.980 (0.968–0.989) |
| SU | 0.999 (0.999–1.000) | 0.999 (0.998–0.999) | 0.999 (0.998–0.999) | 0.988 (0.981–0.994) | 0.988 (0.981–0.994) |
| PU | 0.997 (0.995–0.998) | 0.996 (0.993–0.998) | 0.994 (0.991–0.997) | 0.903 (0.841–0.948) | 0.903 (0.841–0.948) |
| SA | 0.999 (0.998–0.999) | 0.998 (0.997–0.999) | 0.999 (0.998–0.999) | 0.989 (0.982–0.994) | 0.989 (0.982–0.994) |
| SQR | 0.999 (0.998–0.999) | 0.998 (0.996–0.999) | 0.997 (0.996–0.999) | 0.981 (0.970–0.990) | 0.981 (0.970–0.990) |
| LNG | 0.999 (0.999–1.000) | 0.999 (0.998–0.999) | 0.999 (0.998–0.999) | 0.991 (0.986–0.995) | 0.991 (0.986–0.995) |
| Temporal Structure Metrics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| tcycle | tphase1 | tphase2 | %tphase1 | %tphase2 | ||||||
| SEM | SEM% | SEM | SEM% | SEM | SEM% | SEM | SEM% | SEM | SEM% | |
| HOP | 0.01 | 2.41 | 0.01 | 3.47 | 0.01 | 3.63 | 1.32 | 2.81 | 1.32 | 2.51 |
| FT | 0.01 | 2.83 | 0.01 | 3.88 | 0.01 | 3.40 | 1.10 | 2.05 | 1.10 | 2.36 |
| WALK | 0.02 | 1.43 | 0.01 | 1.77 | 0.01 | 1.65 | 0.47 | 0.93 | 0.47 | 0.93 |
| SQR | 0.05 | 3.13 | 0.03 | 4.63 | 0.03 | 4.02 | 1.70 | 3.49 | 1.70 | 3.30 |
| LNG | 0.04 | 2.88 | 0.02 | 3.40 | 0.03 | 4.26 | 1.21 | 2.55 | 1.21 | 2.32 |
| PU | 0.05 | 2.78 | 0.03 | 3.45 | 0.03 | 3.58 | 0.83 | 1.68 | 0.83 | 1.64 |
| SU | 0.06 | 3.39 | 0.04 | 4.26 | 0.03 | 4.12 | 1.05 | 2.06 | 1.05 | 2.15 |
| BE | 0.04 | 2.41 | 0.02 | 2.77 | 0.03 | 2.93 | 0.64 | 1.30 | 0.64 | 1.26 |
| SA | 0.05 | 2.47 | 0.03 | 3.40 | 0.04 | 3.66 | 1.17 | 2.36 | 1.17 | 2.34 |
| HA | 0.06 | 2.27 | 0.04 | 2.82 | 0.04 | 2.97 | 0.82 | 1.54 | 0.82 | 1.75 |
| Temporal Structure Metrics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| tcycle | tphase1 | tphase2 | %tphase1 | %tphase2 | ||||||
| MDC | MDC% | MDC | MDC% | MDC | MDC% | MDC | MDC% | MDC | MDC% | |
| HOP | 0.03 | 5.62 | 0.02 | 8.10 | 0.02 | 8.47 | 3.09 | 6.55 | 3.09 | 5.85 |
| FT | 0.03 | 6.59 | 0.03 | 9.05 | 0.02 | 7.94 | 2.56 | 4.78 | 2.56 | 5.50 |
| WALK | 0.04 | 3.34 | 0.02 | 4.12 | 0.02 | 3.84 | 1.09 | 2.17 | 1.09 | 2.18 |
| SQR | 0.11 | 7.31 | 0.08 | 10.81 | 0.07 | 9.39 | 3.96 | 8.14 | 3.96 | 7.70 |
| LNG | 0.10 | 6.72 | 0.06 | 7.94 | 0.08 | 9.94 | 2.83 | 5.94 | 2.83 | 5.41 |
| PU | 0.11 | 6.48 | 0.06 | 8.05 | 0.07 | 8.34 | 1.93 | 3.91 | 1.93 | 3.82 |
| SU | 0.13 | 7.90 | 0.09 | 9.94 | 0.08 | 9.61 | 2.45 | 4.81 | 2.45 | 5.01 |
| BE | 0.10 | 5.62 | 0.06 | 6.46 | 0.06 | 6.83 | 1.49 | 3.04 | 1.49 | 2.93 |
| SA | 0.12 | 5.76 | 0.08 | 7.93 | 0.09 | 8.54 | 2.74 | 5.50 | 2.74 | 5.46 |
| HA | 0.15 | 5.29 | 0.10 | 6.59 | 0.09 | 6.92 | 1.91 | 3.58 | 1.91 | 4.09 |
Appendix E
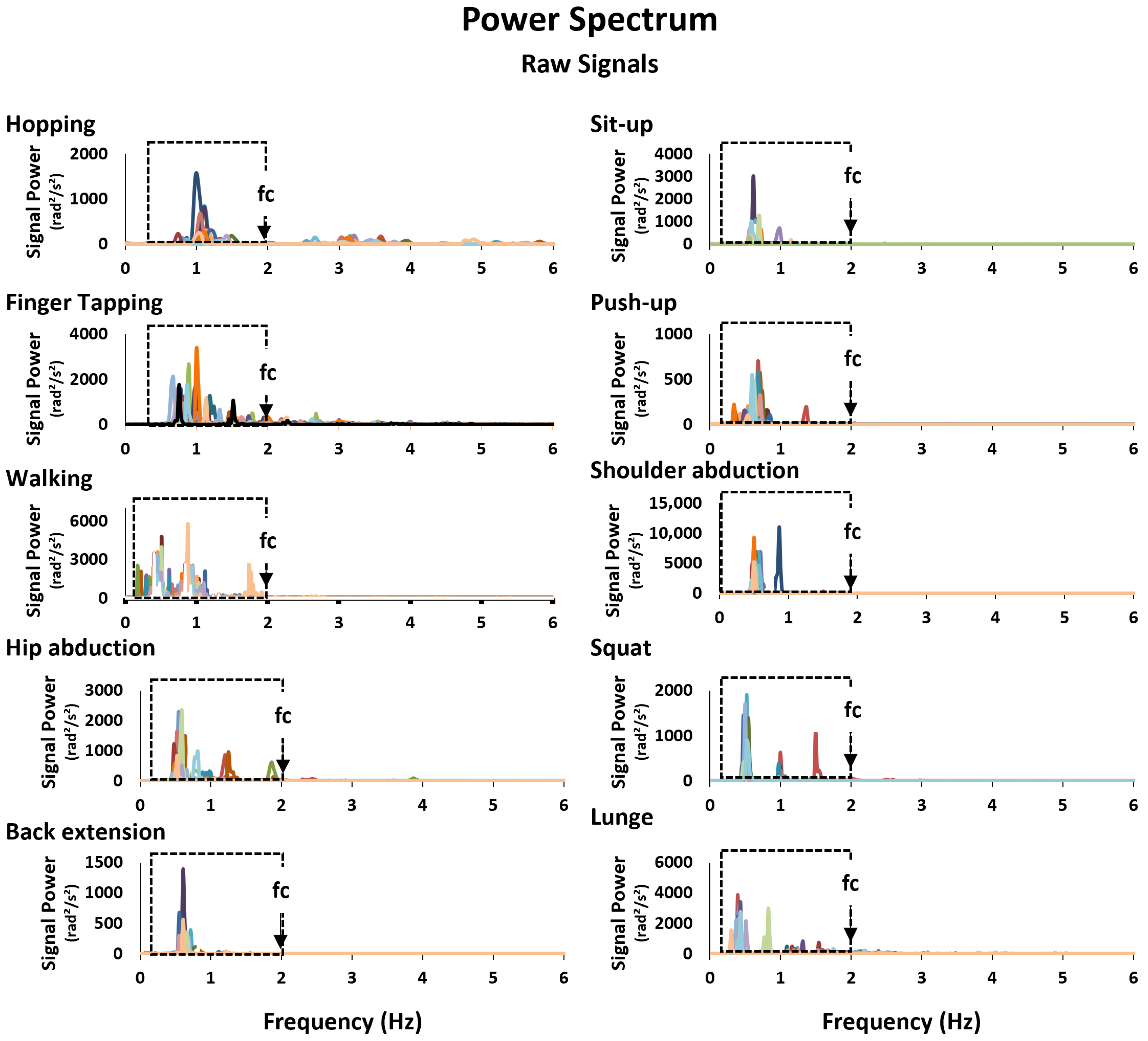
References
- Desbernats, A.; Martín, E.; Tallet, J. Which Factors Modulate Spontaneous Motor Tempo? A Systematic Review of Literature. Front. Psychol. 2023, 14, 1161052. [Google Scholar] [CrossRef]
- Hammerschmidt, D.; Frieler, K.; Wöllner, C. Spontaneous Motor Tempo: Investigating Psychological, Chronobiological, and Demographic Factors in a Large-Scale Online Tapping Experiment. Front. Psychol. 2021, 12, 677201. [Google Scholar] [CrossRef]
- Rose, D.; Cameron, D.J.; Lovatt, P.; Grahn, J.A.; Annett, L.E. Comparison of Spontaneous Motor Tempo during Finger Tapping, Toe Tapping and Stepping on the Spot in People with and without Parkinson’s Disease. J. Mov. Disord. 2020, 13, 47–56. [Google Scholar] [CrossRef]
- Rose, D.; Ott, L.; Guérin, S.M.; Annett, L.E.; Lovatt, P.; Delevoye-Turrell, Y.N. A General Procedure to Measure the Pacing of Body Movements Timed to Music and Metronome in Younger and Older Adults. Sci. Rep. 2021, 11, 3264. [Google Scholar] [CrossRef] [PubMed]
- Smoll, F.L. Preferred Tempo in Performance of Repetitive Movements. Percept. Mot. Ski. 1975, 40, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Smoll, F.L. Between-Days Consistency in Personal Tempo. Percept. Mot. Ski. 1975, 41, 731–734. [Google Scholar] [CrossRef]
- Engler, B.H.; Zamm, A.; Møller, C. Spontaneous Rates Exhibit High Intra-Individual Stability across Movements Involving Different Biomechanical Systems and Cognitive Demands. Sci. Rep. 2024, 14, 14876. [Google Scholar] [CrossRef]
- Fraisse, P. Rhythm and Tempo. In The Psychology of Music, 2nd ed.; Deutsch, D., Ed.; Academic Press: London, UK, 1982; pp. 149–180. [Google Scholar]
- Repp, B.H.; Su, Y.H. Sensorimotor Synchronization: A Review of Recent Research (2006–2012). Psychon. Bull. Rev. 2013, 20, 403–452. [Google Scholar] [CrossRef]
- Hansen, E.A. On Voluntary Rhythmic Leg Movement Behaviour and Control during Pedalling. Acta Physiol. 2015, 214, 1–18. [Google Scholar] [CrossRef]
- MacDougall, H.G.; Moore, S.T. Marching to the Beat of the Same Drummer: The Spontaneous Tempo of Human Locomotion. J. Appl. Physiol. 2005, 99, 1164–1173. [Google Scholar] [CrossRef]
- Rose, D.; Delevoye-Turrell, Y.; Ott, L.; Annett, L.E.; Lovatt, P.J. Music and Metronomes Differentially Impact Motor Timing in People with and without Parkinson’s Disease: Effects of Slow, Medium, and Fast Tempi on Entrainment and Synchronization Performances in Finger Tapping, Toe Tapping, and Stepping on the Spot Tasks. Park. Dis. 2019, 2019, 6530838. [Google Scholar] [CrossRef] [PubMed]
- Repp, B.H. Sensorimotor Synchronization: A Review of the Tapping Literature. Psychon. Bull. Rev. 2005, 12, 969–992. [Google Scholar] [CrossRef] [PubMed]
- Moelants, D. Preferred Tempo Reconsidered. In Proceedings of the 7th International Conference on Music Perception and Cognition, Sydney, Australia, 17–21 July 2002; pp. 1–4. Available online: http://hdl.handle.net/1854/LU-159578 (accessed on 15 September 2023).
- Delevoye-Turrell, Y.; Dione, M.; Agneray, G. Spontaneous Motor Tempo Is the Easiest Pace to Act Upon for Both the Emergent and the Predictive Timing Modes. Procedia Soc. Behav. Sci. 2014, 126, 121–122. [Google Scholar] [CrossRef]
- Collyer, C.E.; Broadbent, H.A.; Church, R.M. Preferred Rates of Repetitive Tapping and Categorical Time Production. Percept. Psychophys. 1994, 55, 443–453. [Google Scholar] [CrossRef]
- Rousanoglou, E.; Boudolos, K. Rhythmic Performance during a Whole Body Movement: Dynamic Analysis of Force–Time Curves. Hum. Mov. Sci. 2006, 25, 393–408. [Google Scholar] [CrossRef]
- Van Noorden, L.; Moelants, D. Resonance in the Perception of Musical Pulse. J. New Music Res. 1999, 28, 43–66. [Google Scholar] [CrossRef]
- Vanneste, V.; Pouthas, J.H.; Wearden, J. Temporal Control of Rhythmic Performance: A Comparison between Young and Old Adults. Exp. Aging Res. 2001, 27, 83–102. [Google Scholar] [CrossRef]
- Peckel, M.; Pozzo, T.; Bigand, E. The Impact of the Perception of Rhythmic Music on Self-Paced Oscillatory Movements. Front. Psychol. 2014, 5, 1037. [Google Scholar] [CrossRef]
- Styns, F.; Van Noorden, L.; Moelants, D.; Leman, M. Walking on Music. Hum. Mov. Sci. 2007, 26, 769–785. [Google Scholar] [CrossRef]
- Hammerschmidt, D.; Wöllner, C. Spontaneous Motor Tempo over the Course of a Week: The Role of the Time of the Day, Chronotype, and Arousal. Psychol. Res. 2023, 87, 327–338. [Google Scholar] [CrossRef]
- Stergiou, N.; Decker, L.M. Human Movement Variability, Nonlinear Dynamics, and Pathology: Is There a Connection? Hum. Mov. Sci. 2011, 30, 869–888. [Google Scholar] [CrossRef]
- Varlet, M.; Williams, R.A.; Keller, P.E. Effects of Pitch and Tempo of Auditory Rhythms on Spontaneous Movement Entrainment and Stabilisation. Psychol. Res. 2018, 84, 568–584. [Google Scholar] [CrossRef]
- Emmanouil, A.; Rousanoglou, E.; Georgaki, A.; Boudolos, K. When Musical Accompaniment Allows the Preferred Spatio-Temporal Pattern of Movement. Sports Med. Int. Open 2021, 5, E81–E90. [Google Scholar] [CrossRef]
- Coste, A.; Salesse, R.N.; Gueugnon, M.; Marín, L.; Bardy, B.G. Standing or Swaying to the Beat: Discrete Auditory Rhythms Entrain Stance and Promote Postural Coordination Stability. Gait Posture 2018, 59, 28–34. [Google Scholar] [CrossRef]
- Burger, B.; Thompson, M.; Luck, G.; Saarikallio, S.; Toiviainen, P. Influences of Rhythm- and Timbre-Related Musical Features on Characteristics of Music-Induced Movement. Front. Psychol. 2013, 4, 183. [Google Scholar] [CrossRef]
- Cudejko, T.; Button, K.; Al-Amri, M. Validity and Reliability of Accelerations and Orientations Measured Using Wearable Sensors during Functional Activities. Sci. Rep. 2022, 12, 18845. [Google Scholar] [CrossRef]
- Emmanouil, A.; Rousanoglou, E.; Boudolos, K. Two Repetitions May Be Enough! Reliability of Movement Timing in Physical Fitness Exercises Performed by Young, Trained Adults Using Inertial Sensors. Biomechanics 2024, 4, 84–108. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using IBM SPSS Statistics, 5th ed.; Sage Publications: London, UK, 2018. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- King, A.C.; Hannan, K.B. Segment Coordination Variability during Double Leg Bodyweight Squats at Different Tempos. Int. J. Sports Med. 2019, 40, 725–731. [Google Scholar] [CrossRef]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef]
- Iosa, M.; Fusco, A.; Marchetti, F.; Morone, G.; Caltagirone, C.; Paolucci, S.; Peppe, A. The Golden Ratio of Gait Harmony: Repetitive Proportions of Repetitive Gait Phases. BioMed Res. Int. 2013, 2013, 918642. [Google Scholar] [CrossRef]
- Winter, D.A.; Sienko, S.E. Biomechanics of Below-Knee Amputee Gait. J. Biomech. 1988, 21, 361–367. [Google Scholar] [CrossRef]
- Ivry, R.B.; Schlerf, J.E. Dedicated and Intrinsic Models of Time Perception. Trends Cogn. Sci. 2008, 12, 273–280. [Google Scholar] [CrossRef]
- Raffalt, P.C.; Alkjær, T.; Simonsen, E.B. Intra- and Inter-Subject Variation in Lower Limb Coordination during Countermovement Jumps in Children and Adults. Hum. Mov. Sci. 2016, 46, 63–77. [Google Scholar] [CrossRef]
- Kelso, J.A.S. Phase Transitions and Critical Behavior in Human Bimanual Coordination. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1984, 246, R1000–R1004. [Google Scholar] [CrossRef]
- Kelso, J.A.S.; Zanone, P.G. Coordination Dynamics of Learning and Transfer across Different Effector Systems. J. Exp. Psychol. Hum. Percept. Perform. 2002, 28, 776–797. [Google Scholar] [CrossRef]
- Schmidt, R.C.; Turvey, M.T. Phase-Entrainment Dynamics of Visually Coupled Rhythmic Movements. Biol. Cybern. 1994, 70, 369–376. [Google Scholar] [CrossRef]
- Wilson, A.D.; Collins, D.R.; Bingham, G.P. Perceptual Coupling in Rhythmic Movement Coordination: Stable Perception Leads to Stable Action. Exp. Brain Res. 2005, 164, 517–528. [Google Scholar] [CrossRef]
- Levy-Tzedek, S.; Ben Tov, M.; Karniel, A. Rhythmic Movements are Larger and Faster but with the Same Frequency on Removal of Visual Feedback. J. Neurophysiol. 2011, 106, 2120–2126. [Google Scholar] [CrossRef]
- Thaut, M.H.; McIntosh, G.C.; Rice, R.R. Rhythmic facilitation of gait training in hemiparetic stroke rehabilitation. J. Neurol. Sci. 1996, 151, 207–212. [Google Scholar] [CrossRef]
- Nombela, C.; Hughes, L.E.; Owen, A.M.; Grahn, J.A. Into the groove: Can rhythm influence Parkinson’s disease? Neurosci. Biobehav. Rev. 2013, 37 Pt 2, 2564–2570. [Google Scholar] [CrossRef]
- Fleiss, J.L. The Design and Analysis of Clinical Experiments; Willey: New York, NY, USA, 1986. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emmanouil, A.; Paderi, F.; Boudolos, K.; Rousanoglou, E. The Task Dependency of Spontaneous Rhythmic Performance in Movements Beyond Established Biomechanical Models: An Inertial Sensor-Based Study. Sensors 2025, 25, 6565. https://doi.org/10.3390/s25216565
Emmanouil A, Paderi F, Boudolos K, Rousanoglou E. The Task Dependency of Spontaneous Rhythmic Performance in Movements Beyond Established Biomechanical Models: An Inertial Sensor-Based Study. Sensors. 2025; 25(21):6565. https://doi.org/10.3390/s25216565
Chicago/Turabian StyleEmmanouil, Analina, Fani Paderi, Konstantinos Boudolos, and Elissavet Rousanoglou. 2025. "The Task Dependency of Spontaneous Rhythmic Performance in Movements Beyond Established Biomechanical Models: An Inertial Sensor-Based Study" Sensors 25, no. 21: 6565. https://doi.org/10.3390/s25216565
APA StyleEmmanouil, A., Paderi, F., Boudolos, K., & Rousanoglou, E. (2025). The Task Dependency of Spontaneous Rhythmic Performance in Movements Beyond Established Biomechanical Models: An Inertial Sensor-Based Study. Sensors, 25(21), 6565. https://doi.org/10.3390/s25216565







