Modality-Resilient Multimodal Industrial Anomaly Detection via Cross-Modal Knowledge Transfer and Dynamic Edge-Preserving Voxelization
Abstract
1. Introduction
- Integrated Cross-Modal Pre-training and Missing-Modal Resilient Inference Framework: Proposes a multimodal learning framework for industrial anomaly detection. During training, it fuses RGB and point cloud modalities to learn rich feature representations, while supporting missing-modal inputs during inference. This framework effectively addresses performance degradation caused by incomplete modalities in practical applications, substantially enhancing the robustness of anomaly detection.
- A dynamic voxel subsampling method with an edge-preserving strategy is designed for highly efficient feature extraction from large-scale point cloud data. It dynamically adjusts voxel subsampling ratios based on point cloud density while extracting structural features that preserve geometric edge information. This approach substantially reduces data volume and computational overhead while maintaining the ability to detect minute defects, laying the foundation for real-time 3D anomaly detection.
2. Related Work
2.1. Two-Dimensional Industrial Anomaly Detection
2.2. Three-Dimensional Industrial Anomaly Detection
2.3. Voxel-Based Point Cloud Downsampling
2.4. Cross-Modal Knowledge Distillation
3. Methodology
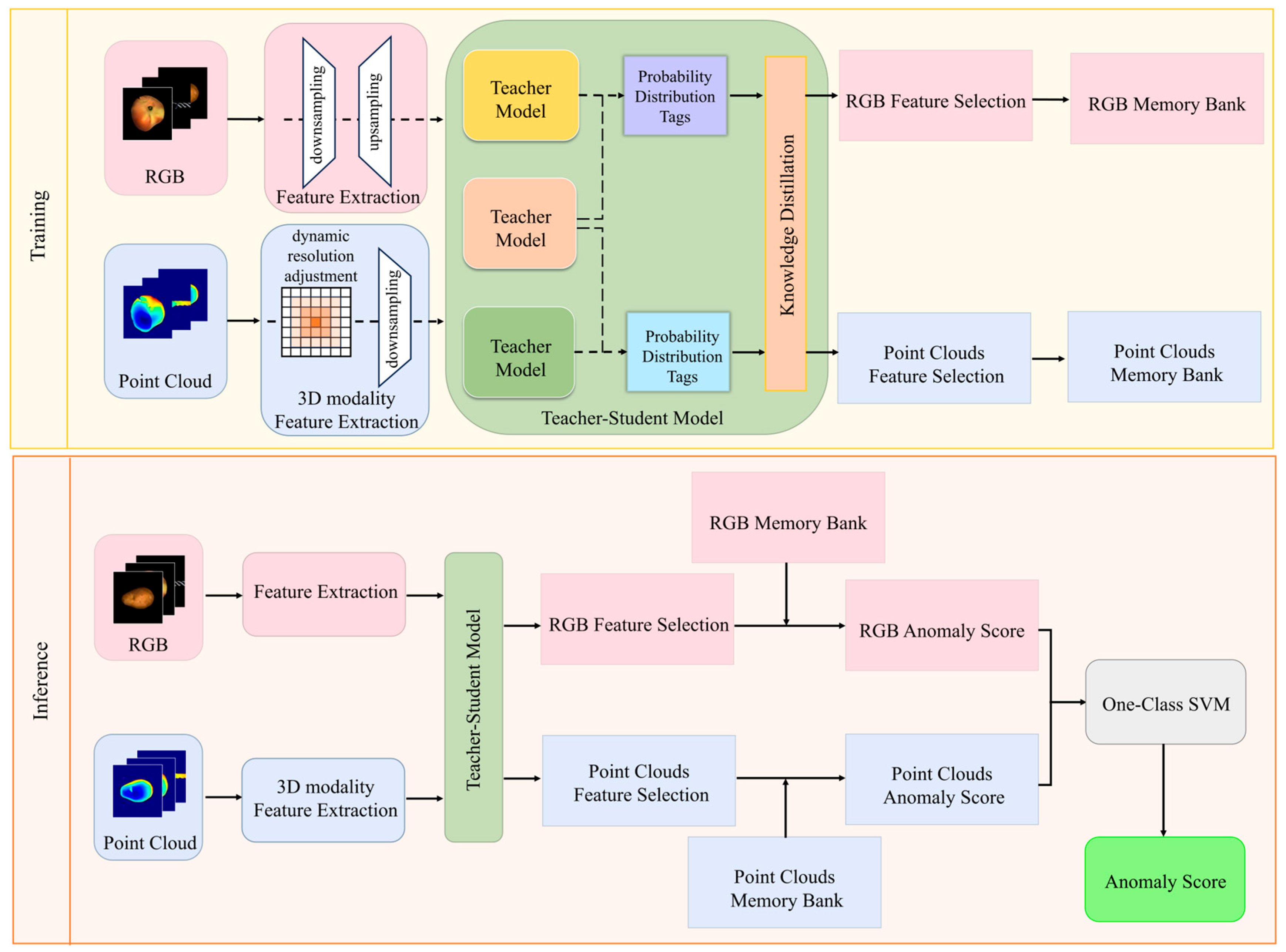
3.1. Overview
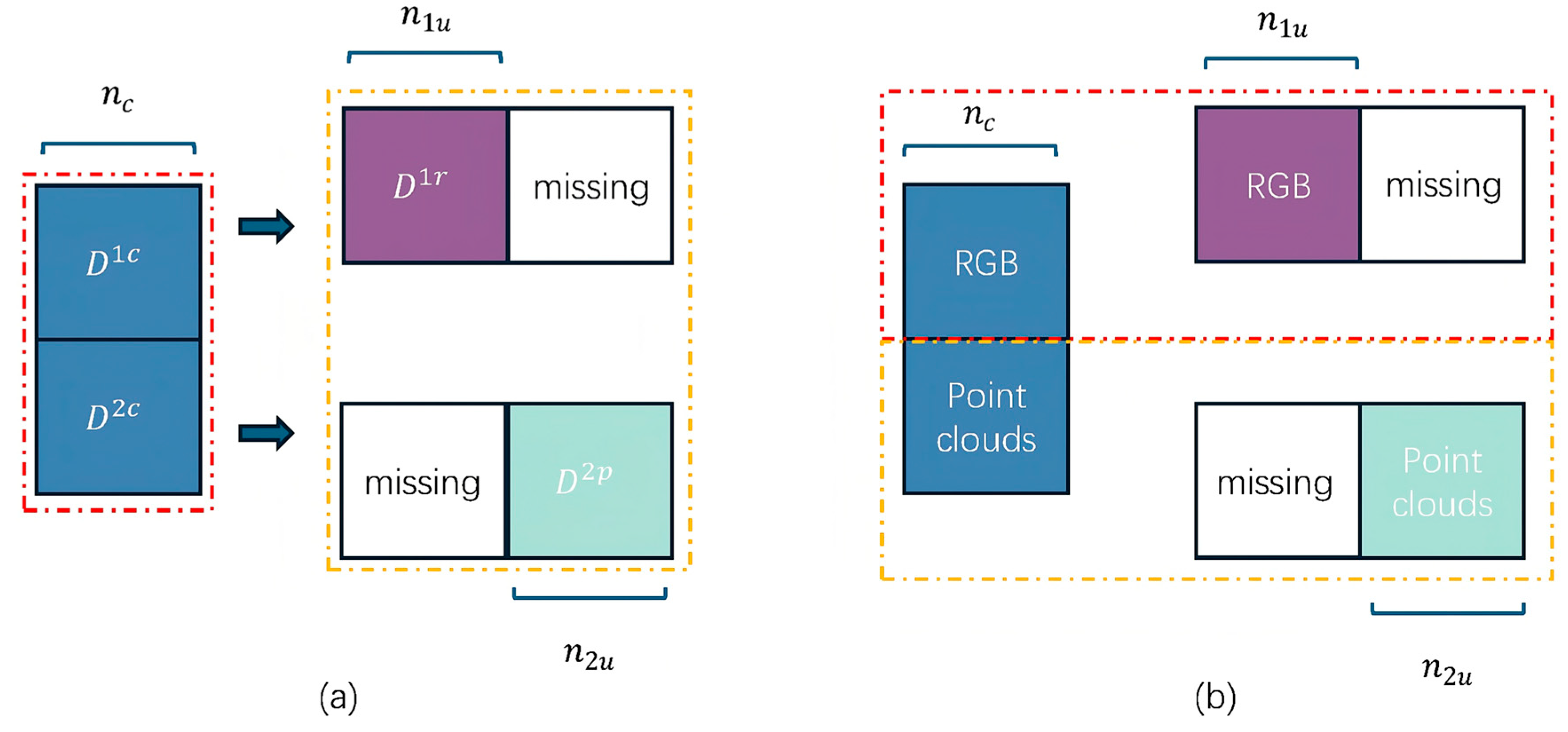
3.2. Integrated Framework for Cross-Modal Pre-Training and Elastic Inference Under Modal Deficiency
3.2.1. RGB Feature Extraction from
3.2.2. Three-Dimensional Point Cloud Feature Extraction
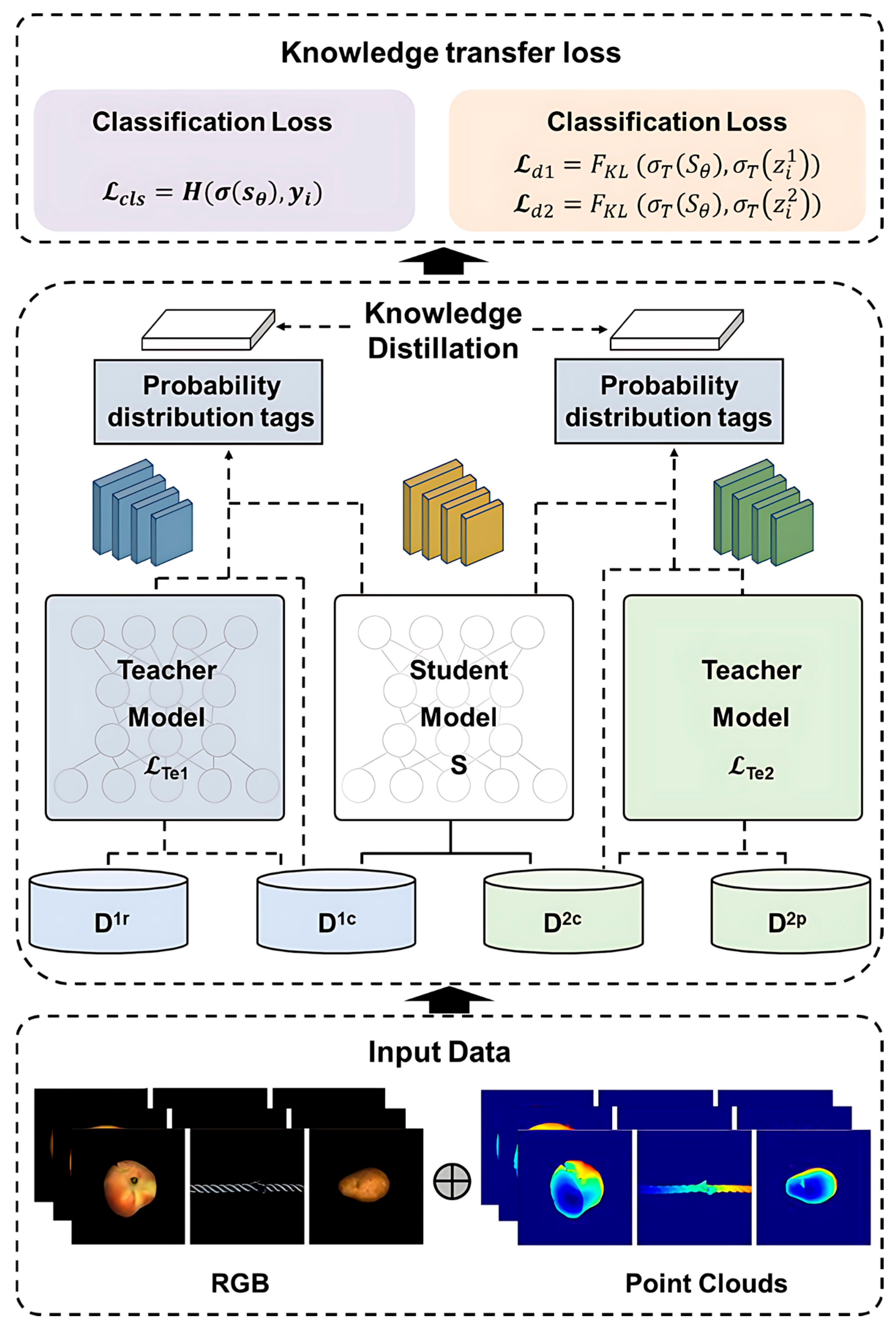
3.3. Cross-Distillation Mode
| Algorithm 1: Algorithm of the proposed method for two modalities. |
| , , , , , for each training iteration do Train teacher model with {[, ], [, ]} end for for each training iteration do Train teacher model with {[X2c, X2u], [,]} end for Label the samples to train student model with the teachers with Equation (14). for each training iteration do Train student model with Equation (15) end for |
3.4. Unsupervised Feature Fusion
3.4.1. Kernel Selection for Memory Repository Construction
- Apply the k-means clustering algorithm to partition into clusters
- For each cluster , select the sample closest to the cluster centre as its representative:where is the distance metric function. This metric should align with that used for calculating anomaly scores to ensure consistency between feature selection and anomaly detection processes.
- All selected representative points form the final core set
3.4.2. Decision Layer Fusion
- Classification Anomaly Score
- 2.
- Segmentation Anomaly Score
4. Experiments
4.1. Experimental Details
4.1.1. Dataset and Evaluation Metrics
4.1.2. Data Preprocessing
4.1.3. Experimental Implementation Details
4.2. Comparative Experiments
4.3. Melting Experiments
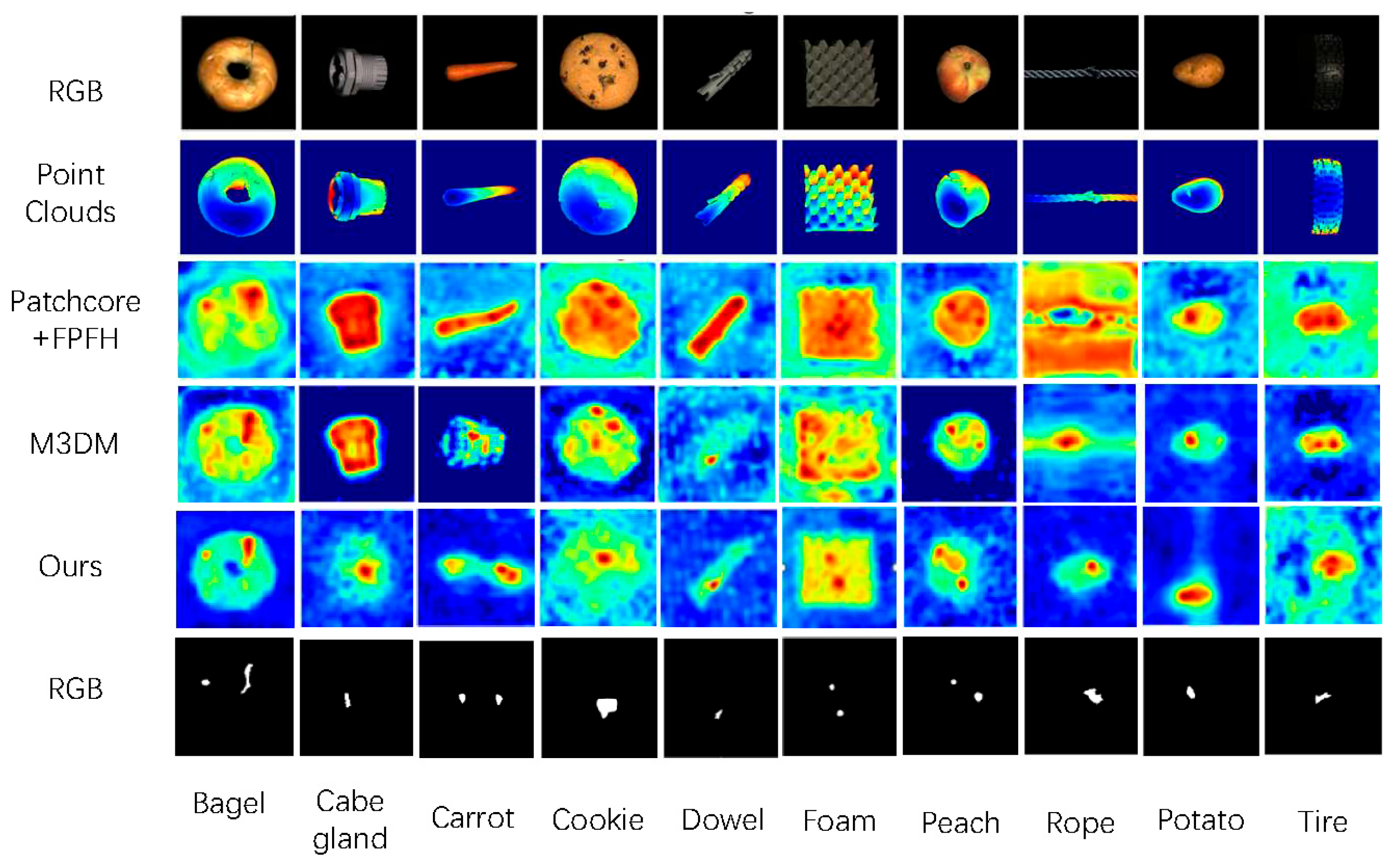
4.4. Visualisation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, J.; Huang, L. 3D ST-Net: A Large Kernel Simple Transformer for Brain Tumor Segmentation, and Cross-Modality Domain Adaptation for Medical Image Segmentation. In Brain Tumor Segmentation, and Cross-Modality Domain Adaptation for Medical Image Segmentation; Springer Nature: Cham, Switzerland, 2024; p. 106. [Google Scholar]
- Wang, Q.; Kim, M.K. Applications of 3D point cloud data in the construction industry: A fifteen-year review from 2004 to 2018. Adv. Eng. Inform. 2019, 39, 306–319. [Google Scholar] [CrossRef]
- Bergmann, P.; Jin, X.; Sattlegger, D.; Steger, C. The MVtec 3D-AD dataset for unsupervised 3D anomaly detection and localization. arXiv 2021, arXiv:2112.09045. [Google Scholar] [CrossRef]
- Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD—A Comprehensive Real-World Dataset for Unsupervised Anomaly Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9592–9600. [Google Scholar]
- Gong, D.; Liu, L.; Le, V.; Saha, B.; Mansour, M.R.; Venkatesh, S.; Hengel, A.V.D. Memorising Normality to Detect Anomaly: Memory-Augmented Deep Autoencoder for Unsupervised Anomaly Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1705–1714. [Google Scholar]
- Zavrtanik, V.; Kristan, M.; Skočaj, D. Reconstruction by inpainting for visual anomaly detection. Pattern Recognit. 2021, 112, 107706. [Google Scholar] [CrossRef]
- Deng, H.; Li, X. Anomaly detection via reverse distillation from one-class embedding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9737–9746. [Google Scholar]
- Nayar, S.K.; Sanderson, A.C.; Weiss, L.E.; Simon, D.A. Specular surface inspection s using structured highlight and Gaussian images. IEEE Trans. Robot. Autom. 1990, 6, 208–218. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, M.; Zhao, S. A review of deep learning-based approaches for defect detection in smart manufacturing. J. Opt. 2024, 53, 1345–1351. [Google Scholar] [CrossRef]
- Hattori, K.; Izumi, T.; Meng, L. Defect detection of apples using PatchCore. In Proceedings of the 2023 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, Australia, 4–7 September 2023; IEEE: New York, NY, USA; pp. 1–6. [Google Scholar]
- Liu, Y.; Zhang, C.; Dong, X. A survey of real-time surface defect inspection methods based on deep learning. Artif. Intell. Rev. 2023, 56, 12131–12170. [Google Scholar] [CrossRef]
- Perera, P.; Nallapati, R.; Xiang, B. Ocgan: One-Class Novelty Detection Using GANs with Constrained Latent Representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2898–2906. [Google Scholar]
- Liu, J.; Xie, G.; Chen, R.; Li, X.; Wang, J.; Liu, Y.; Wang, C.; Zheng, F. Real3d-ad: A dataset for point cloud anomaly detection. Adv. Neural Inf. Process. Syst. 2023, 36, 30402–30415. [Google Scholar]
- Zhu, H.; Xie, G.; Hou, C.; Shen, L. Towards High-resolution 3D Anomaly Detection via Group-Level Feature Contrastive Learning. In Proceedings of the 32nd ACM International Conference on Multimedia, Chicago, IL, USA, 28 October–1 November 2024; pp. 4680–4689. [Google Scholar]
- Zhao, B.; Xiong, Q.; Zhang, X.; Guo, J.; Liu, Q.; Xing, X.; Xu, X. Pointcore: Efficient unsupervised point cloud anomaly detector using local-global features. arXiv 2024, arXiv:2403.01804. [Google Scholar]
- Zhou, Z.; Wang, L.; Fang, N.; Wang, Z.; Qiu, L.; Zhang, S. R3D-AD: Reconstruction via Diffusion for 3D Anomaly Detection. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer Nature: Cham, Switzerland, 2024; pp. 91–107. [Google Scholar]
- Rusinkiewicz, S.; Hall-Holt, O.; Levoy, M. Real-time 3D model acquisition. ACM Trans. Graph. (TOG) 2002, 21, 438–446. [Google Scholar] [CrossRef]
- Sohail, S.S.; Himeur, Y.; Kheddar, H.; Amira, A.; Fadli, F.; Atalla, S.; Copiaco, A.; Mansoor, W. Advancing 3D point cloud understanding through deep transfer learning: A comprehensive survey. Inf. Fusion 2024, 113, 102601. [Google Scholar] [CrossRef]
- Lyu, W.; Ke, W.; Sheng, H.; Ma, X.; Zhang, H. Dynamic downsampling algorithm for 3D point cloud map based on voxel filtering. Appl. Sci. 2024, 14, 3160. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Zeng, H.; Zeng, Y.; Liu, Y. Svga-Net: Sparse Voxel-Graph Attention Network for 3D Object Detection from Point Clouds. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 870–878. [Google Scholar]
- Gelfand, N.; Ikemoto, L.; Rusinkiewicz, S.; Levoy, M. Geometrically stable sampling for the ICP algorithm. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modelling, 2003, 3DIM 2003, Banff, AB, Canada, 6–10 October 2003; IEEE: New York, NY, USA, 2003; pp. 260–267. [Google Scholar]
- Zhou, Q.; Sun, B. Adaptive K-means clustering-based under-sampling methods to solve the class imbalance problem. Data Inf. Manag. 2024, 8, 100064. [Google Scholar] [CrossRef]
- Yang, H.; Liang, D.; Zhang, D.; Liu, Z.; Zou, Z.; Jiang, X.; Zhu, Y. AVS-Net: Point sampling with adaptive voxel size for 3D scene understanding. arXiv 2024, arXiv:2402.17521. [Google Scholar] [CrossRef]
- Que, Z.; Lu, G.; Xu, D. Voxelcontext-Net: An Octree-Based Framework for Point Cloud Compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6042–6051. [Google Scholar]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud-Based 3D Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4490–4499. [Google Scholar]
- Vapnik, V.; Vashist, A. A new learning paradigm: Learning using privileged information. Neural Netw. 2009, 22, 544–557. [Google Scholar] [CrossRef]
- Garcia, N.C.; Morerio, P.; Murino, V. Modality Distillation with Multiple Stream Networks for Action Recognition. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 103–118. [Google Scholar]
- Huo, F.; Xu, W.; Guo, J.; Wang, H.; Guo, S. C2kd: Bridging the modality gap for cross-modal knowledge distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 16006–16015. [Google Scholar]
- Nugroho, M.A.; Woo, S.; Lee, S.; Kim, C. AHFu-Net: Align, Hallucinate, and Fuse Network for Missing Multimodal Action Recognition. In Proceedings of the 2023 IEEE International Conference on Visual Communications and Image Processing (VCIP), Jeju, Republic of Korea, 4–7 December 2023; pp. 1–5. [Google Scholar]
- Chu, Y.M.; Chieh, L.; Hsieh, T.I.; Chen, H.T.; Liu, T.L. Shape-guided dual-memory learning for 3D anomaly detection. In Proceedings of the ICML 2023, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Wang, H.; Ma, C.; Zhang, J.; Zhang, Y.; Avery, J.; Hull, L.; Carneiro, G. Learnable Cross-Modal Knowledge Distillation for Multi-Modal Learning with Missing Modality. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, BC, Canada, 8–12 October 2023; pp. 216–226. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Cohen, G.; Sapiro, G.; Giryes, R. DNN or k-NN: That is the generalize vs. memorize question. arXiv 2018, arXiv:1805.06822. [Google Scholar]
- Roy, S.; Butman, J.A.; Reich, D.S.; Calabresi, P.A.; Pham, D.L. Multiple sclerosis lesion segmentation from brain MRI via fully convolutional neural networks. arXiv 2018, arXiv:1803.09172. [Google Scholar] [CrossRef]
- Chen, F.W.; Liu, C.W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Sui, W.; Lichau, D.; Lefèvre, J.; Phelippeau, H. Incomplete Multimodal Industrial Anomaly Detection via Cross-Modal Distillation. arXiv 2024, arXiv:2405.13571. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, T.; Hospedales, T.M.; Lu, H. Deep Mutual Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4320–4328. [Google Scholar]
- Chen, Z.; Li, L.; Niu, K.; Wu, Y.; Hua, B. Pose measurement of non-cooperative spacecraft based on point cloud. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Thoker, F.M.; Gall, J. Cross-modal knowledge distillation for action recognition. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; IEEE: New York, NY, USA, 2019; pp. 6–10. [Google Scholar]
- Parker, G.J.M.; Haroon, H.A.; Wheeler-Kingshott, C.A.M. A framework for a streamline-based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements. J. Magn. Reson. Imaging Off. J. Int. Soc. Magn. Reson. Med. 2003, 18, 242–254. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhang, J.; Liu, Z.; Gu, J.; Liu, Y. Multimodal Industrial Anomaly Detection via Hybrid Fusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 8032–8041. [Google Scholar]
- Horwitz, E.; Hoshen, Y. Back to the Feature: Classical 3D Features are (Almost) All You Need for 3D Anomaly Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 2968–2977. [Google Scholar]
- Defard, T.; Setkov, A.; Loesch, A.; Audigier, R. PADIM: A Patch Distribution Modelling Framework for Anomaly Detection and Localisation. In Proceedings of the International Conference on Pattern Recognition, Milan, Italy, 10–15 January 2021; pp. 475–489. [Google Scholar]
- Roth, K.; Pemula, L.; Zepeda, J.; Schölkopf, B.; Brox, T.; Gehler, P. Towards Total Recall in Industrial Anomaly Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 14318–14328. [Google Scholar]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.R.; Guttag, J.; Dalca, A.V. Voxelmorph: A learning framework for deformable medical image registration. IEEE Trans. Med. Imaging 2019, 38, 1788–1800. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, F.; Liu, S.; Zhang, L.; Su, H.; Zhu, J.; Ni, L.M.; Shum, H.Y. Dino: Detr with improved denoising anchor-boxes for end-to-end object detection. arXiv 2022, arXiv:2203.03605. [Google Scholar]
- Bonfiglioli, L.; Toschi, M.; Silvestri, D.; Fioraio, N.; De Gregorio, D. The eyecandies dataset for unsupervised multimodal anomaly detection and localization. In Proceedings of the Asian Conference on Computer Vision, Macao, China, 4–8 December 2022; pp. 3586–3602. [Google Scholar]
- Klimke, J. Web-Based Provisioning and Application of Large-Scale Virtual 3D City Models. Ph.D. Thesis, Universität Potsdam, Potsdam, Germany, 2018. [Google Scholar]
- Kenyeres, M.; Kenyeres, J.; Hassankhani Dolatabadi, S. Distributed Consensus Gossip-Based Data Fusion for Suppressing Incorrect Sensor Readings in Wireless Sensor Networks. J. Low Power Electron. Appl. 2025, 15, 6. [Google Scholar] [CrossRef]
| System Environment | Version |
|---|---|
| ubuntu | 22.04 |
| cuda | 12.1 |
| python | 3.11 |
| pytorch | 2.2.0 |
| Method | Bagel | Cable Gland | Carrot | Cookie | Dowel | Foam | Peach | Potato | Rope | Tyre | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FPFH [43] | 0.825 | 0.551 | 0.952 | 0.797 | 0.883 | 0.582 | 0.758 | 0.889 | 0.929 | 0.653 | 0.782 |
| AST [30] | 0.881 | 0.576 | 0.965 | 0.957 | 0.679 | 0.797 | 0.990 | 0.915 | 0.956 | 0.611 | 0.833 |
| BTF [44] | 0.938 | 0.765 | 0.972 | 0.888 | 0.960 | 0.664 | 0.904 | 0.929 | 0.982 | 0.726 | 0.837 |
| Shape-guided [45] | 0.983 | 0.682 | 0.978 | 0.998 | 0.960 | 0.737 | 0.993 | 0.979 | 0.966 | 0.871 | 0.916 |
| M3DM [46] | 0.941 | 0.651 | 0.965 | 0.969 | 0.905 | 0.760 | 0.880 | 0.974 | 0.926 | 0.765 | 0.874 |
| Ours_single | 0.834 | 0.884 | 0.954 | 0.929 | 0.942 | 0.789 | 0.869 | 0.983 | 0.882 | 0.872 | 0.895 |
| Ours_F2F | 0.992 | 0.930 | 0.971 | 0.893 | 0.953 | 0.893 | 0.933 | 0.957 | 0.951 | 0.902 | 0.938 |
| Method | Bagel | Cable Gland | Carrot | Cookie | Dowel | Foam | Peach | Potato | Rope | Tyre | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FPFH | 0.973 | 0.879 | 0.982 | 0.906 | 0.892 | 0.735 | 0.977 | 0.982 | 0.956 | 0.961 | 0.924 |
| AST | 0.943 | 0.818 | 0.977 | 0.882 | 0.881 | 0.743 | 0.958 | 0.974 | 0.950 | 0.929 | 0.906 |
| BTF | 0.976 | 0.927 | 0.979 | 0.974 | 0.971 | 0.884 | 0.776 | 0.881 | 0.959 | 0.911 | 0.914 |
| Shape-guided | 0.947 | 0.826 | 0.977 | 0.882 | 0.881 | 0.767 | 0.967 | 0.978 | 0.947 | 0.940 | 0.911 |
| M3DM | 0.974 | 0.871 | 0.981 | 0.924 | 0.898 | 0.773 | 0.978 | 0.983 | 0.955 | 0.969 | 0.931 |
| Ours_single | 0.974 | 0.847 | 0.973 | 0.873 | 0.947 | 0.826 | 0.956 | 0.962 | 0.942 | 0.943 | 0.924 |
| Ours_F2F | 0.981 | 0.889 | 0.989 | 0.913 | 0.934 | 0.888 | 0.972 | 0.972 | 0.959 | 0.977 | 0.947 |
| Method | Bagel | Cable Gland | Carrot | Cookie | Dowel | Foam | Peach | Potato | Rope | Tyre | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Voxel VM | 0.553 | 0.772 | 0.484 | 0.701 | 0.751 | 0.578 | 0.480 | 0.466 | 0.689 | 0.611 | 0.609 |
| PADiM [47] | 0.975 | 0.775 | 0.698 | 0.582 | 0.959 | 0.663 | 0.858 | 0.535 | 0.832 | 0.760 | 0.764 |
| PatchCore | 0.876 | 0.880 | 0.791 | 0.682 | 0.912 | 0.701 | 0.695 | 0.618 | 0.841 | 0.702 | 0.770 |
| CS-Flow [48] | 0.941 | 0.930 | 0.827 | 0.795 | 0.990 | 0.886 | 0.731 | 0.471 | 0.986 | 0.745 | 0.830 |
| M3DM | 0.944 | 0.918 | 0.896 | 0.749 | 0.959 | 0.767 | 0.919 | 0.648 | 0.938 | 0.767 | 0.850 |
| AST | 0.983 | 0.873 | 0.976 | 0.971 | 0.932 | 0.885 | 0.974 | 0.091 | 0.832 | 0.797 | 0.825 |
| Ours_single | 0.932 | 0.938 | 0.888 | 0.739 | 0.969 | 0.797 | 0.920 | 0.624 | 0.949 | 0.771 | 0.853 |
| Ours_F2F | 0.992 | 0.930 | 0.971 | 0.893 | 0.953 | 0.893 | 0.933 | 0.957 | 0.951 | 0.902 | 0.938 |
| Method | Bagel | Cable Gland | Carrot | Cookie | Dowel | Foam | Peach | Potato | Rope | Tyre | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Voxel VM [49] | 0.510 | 0.331 | 0.413 | 0.715 | 0.680 | 0.279 | 0.300 | 0.507 | 0.611 | 0.366 | 0.471 |
| 3D-ST | 0.950 | 0.483 | 0.986 | 0.921 | 0.905 | 0.632 | 0.945 | 0.988 | 0.976 | 0.542 | 0.833 |
| CS-Flow | 0.855 | 0.919 | 0.958 | 0.867 | 0.969 | 0.500 | 0.889 | 0.935 | 0.904 | 0.919 | 0.871 |
| PatchCore | 0.901 | 0.949 | 0.928 | 0.877 | 0.892 | 0.563 | 0.904 | 0.932 | 0.908 | 0.906 | 0.876 |
| PADiM | 0.980 | 0.944 | 0.945 | 0.925 | 0.961 | 0.792 | 0.966 | 0.940 | 0.937 | 0.912 | 0.930 |
| M3DM | 0.952 | 0.972 | 0.973 | 0.891 | 0.932 | 0.843 | 0.970 | 0.956 | 0.968 | 0.966 | 0.942 |
| Ours_single | 0.953 | 0.982 | 0.969 | 0.903 | 0.947 | 0.860 | 0.966 | 0.959 | 0.969 | 0.965 | 0.946 |
| Ours_F2F | 0.981 | 0.889 | 0.989 | 0.913 | 0.934 | 0.888 | 0.972 | 0.972 | 0.959 | 0.977 | 0.947 |
| Methods | Number of Down-Sampled Points | Simplification Rate | Time (s) | Parameters |
|---|---|---|---|---|
| Voxel down-sampling | 104,356 | 0.5169 | 0.1025 | leafsize = 0.01 |
| 5225 | 0.9759 | 0.0125 | leafsize = 0.05 | |
| 1440 | 0.9934 | 0.0085 | leafsize = 0.1 | |
| Random down-sampling | 2170 | 0.9900 | 0.0143 | leafsize = 0.01 |
| 10,847 | 0.9500 | 0.0126 | leafsize = 0.05 | |
| 21,694 | 0.9000 | 0.0135 | leafsize = 0.1 | |
| Uniform down-sampling | 2177 | 0.9899 | 0.1129 | every_k_points = 100 |
| 8687 | 0.9599 | 0.3493 | every_k_points = 25 | |
| 21,694 | 0.9000 | 1.0615 | every_k_points = 10 | |
| FPS | 1000 | 0.9745 | 34.8717 | arget_number_of _triangles = 5000 |
| 5000 | 0.9490 | 65.9702 | arget_number_of _triangles = 10,000 | |
| 10,000 | 0.9235 | 109.9000 | arget_number_of _triangles =15,000 | |
| Our method | 17,557 | 0.9187 | 0.0139 |
| Pair | Mean Difference | Std. Deviation | Std. Error Mean | 95% CI Lower | 95% CI Upper | t | df | Sig. (2-Tailed) |
|---|---|---|---|---|---|---|---|---|
| FPFH | 0.155600 | 0.123984 | 0.039207 | 0.066907 | 0.244293 | 3.969 | 9 | 0.003 |
| AST | 0.104800 | 0.151272 | 0.047836 | 0.066870 | 0.213014 | 2.191 | 9 | 0.056 |
| BTF | 0.064700 | 0.090896 | 0.028744 | −0.000323 | 0.129723 | 2.251 | 9 | 0.051 |
| Shape-guided | 0.022800 | 0.103878 | 0.032849 | −0.051510 | 0.097110 | 0.694 | 9 | 0.505 |
| M3DM | 0.063900 | 0.098830 | 0.031253 | −0.006799 | 0.134599 | 2.045 | 9 | 0.071 |
| RGB-single | 0.043700 | 0.058631 | 0.018541 | 0.001758 | 0.085642 | 2.357 | 9 | 0.043 |
| Pair | Mean Difference | Std. Deviation | Std. Error Mean | 95% CI Lower | 95% CI Upper | t | df | Sig. (2-Tailed) |
|---|---|---|---|---|---|---|---|---|
| Ours_PC—Single_PC | 0.029500 | 0.052361 | 0.026180 | −0.053818 | 0.112818 | 1.127 | 3 | 0.342 |
| Ours_RGB—Single_RGB | 0.021250 | 0.035208 | 0.017604 | −0.034773 | 0.077273 | 1.207 | 3 | 0.314 |
| Dual_RGB—Single_PC | 0.027500 | 0.039408 | 0.019704 | −0.035207 | 0.090207 | 1.396 | 3 | 0.257 |
| Dual_RGB—Single_RGB | 0.042750 | 0.006397 | 0.003198 | 0.032572 | 0.052928 | 13.366 | 3 | 0.001 |
| Pair | Mean Difference | Std. Deviation | Std. Error Mean | 95% CI Lower | 95% CI Upper | t | df | Sig. (2-Tailed) |
|---|---|---|---|---|---|---|---|---|
| Ours_PC—Single_PC | 0.012750 | 0.005560 | 0.002780 | 0.003902 | 0.021598 | 4.586 | 3 | 0.019 |
| Ours_RGB—Single_RGB | 0.004750 | 0.004031 | 0.002016 | −0.001664 | 0.011164 | 2.357 | 3 | 0.100 |
| Dual_RGB—Single_PC | 0.010750 | 0.026663 | 0.013332 | −0.031677 | 0.053177 | 0.806 | 3 | 0.479 |
| Dual_RGB—Single_RGB | 0.021250 | 0.012971 | 0.006486 | 0.000610 | 0.041890 | 3.277 | 3 | 0.047 |
| Feature Extractors | Single PCs | Ours_PCs | Single RGB | Ours_RGB | Dual RGB + Principal Components |
|---|---|---|---|---|---|
| Swin Transformer + PointNet | 0.832 | 0.938 | 0.864 | 0.938 | 0.916 |
| 0.919 | 0.934 | 0.941 | 0.940 | 0.962 | |
| Swin Transformer + PointCNN | 0.908 | 0.898 | 0.893 | 0.896 | 0.932 |
| 0.863 | 0.874 | 0.905 | 0.098 | 0.911 | |
| DINO ViT-S/8 + PointNet | 0.863 | 0.882 | 0.831 | 0.833 | 0.869 |
| 0.893 | 0.912 | 0.851 | 0.860 | 0.891 | |
| DINO ViT-S/8 + PointCNN | 0.909 | 0.912 | 0.863 | 0.869 | 0.905 |
| 0.915 | 0.921 | 0.883 | 0.890 | 0.920 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Yuan, J.; Yang, M.; Yan, W. Modality-Resilient Multimodal Industrial Anomaly Detection via Cross-Modal Knowledge Transfer and Dynamic Edge-Preserving Voxelization. Sensors 2025, 25, 6529. https://doi.org/10.3390/s25216529
Xu J, Yuan J, Yang M, Yan W. Modality-Resilient Multimodal Industrial Anomaly Detection via Cross-Modal Knowledge Transfer and Dynamic Edge-Preserving Voxelization. Sensors. 2025; 25(21):6529. https://doi.org/10.3390/s25216529
Chicago/Turabian StyleXu, Jiahui, Jian Yuan, Mingrui Yang, and Weishu Yan. 2025. "Modality-Resilient Multimodal Industrial Anomaly Detection via Cross-Modal Knowledge Transfer and Dynamic Edge-Preserving Voxelization" Sensors 25, no. 21: 6529. https://doi.org/10.3390/s25216529
APA StyleXu, J., Yuan, J., Yang, M., & Yan, W. (2025). Modality-Resilient Multimodal Industrial Anomaly Detection via Cross-Modal Knowledge Transfer and Dynamic Edge-Preserving Voxelization. Sensors, 25(21), 6529. https://doi.org/10.3390/s25216529





