Enhancing Torque Output for a Magnetic Actuation System for Robotic Spinal Distraction
Abstract
1. Introduction
2. Theoretical Model
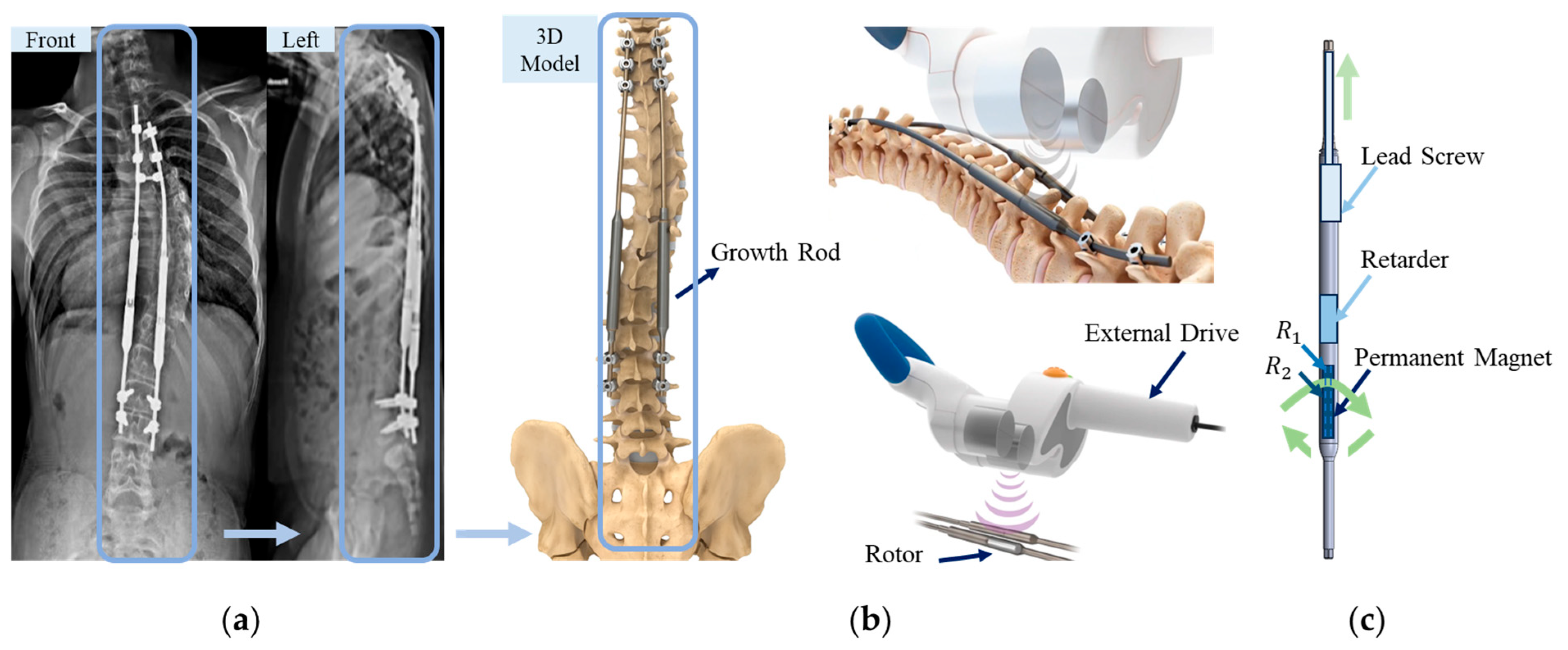
2.1. Overview of the MAGEC System for Spinal Growing Rod
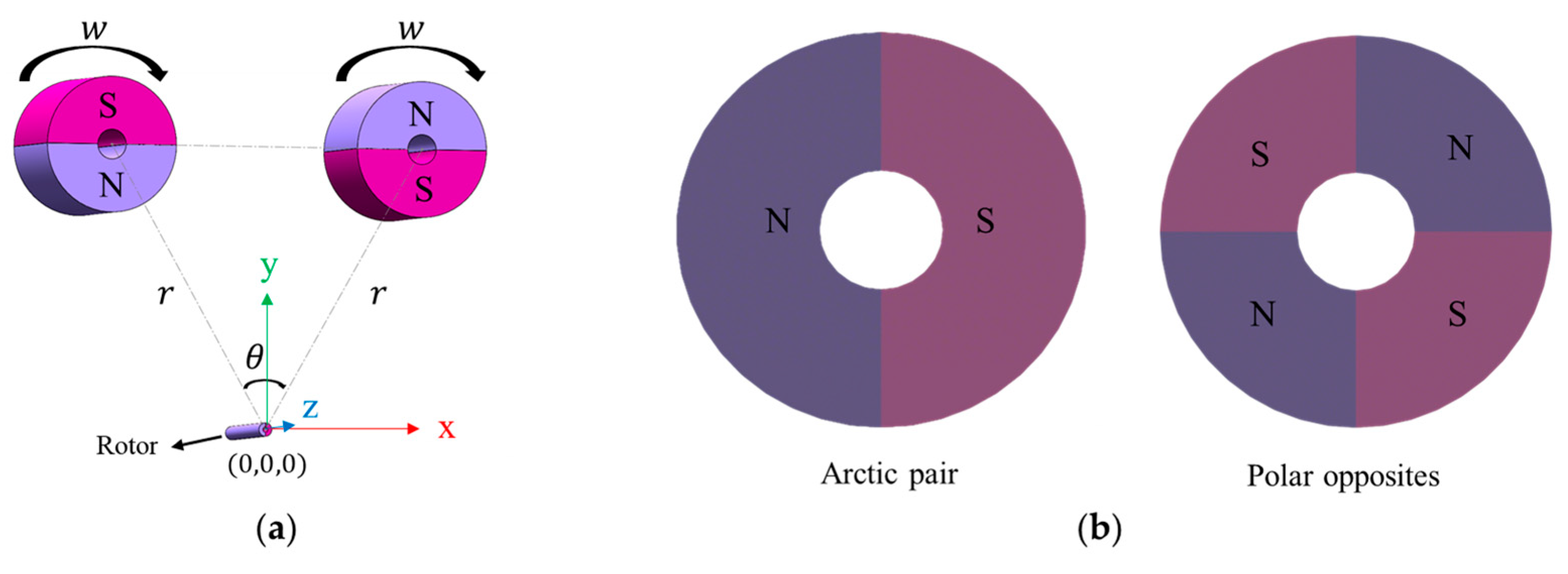
2.2. Mathematical Formulation of Magnetic Components
2.3. Governing Equation
2.4. Rotor Moment of Inertia
3. Magnetically Controlled Growth Bar System and Driven Permanent Magnet-Rotor Modeling
3.1. 3D Model Description
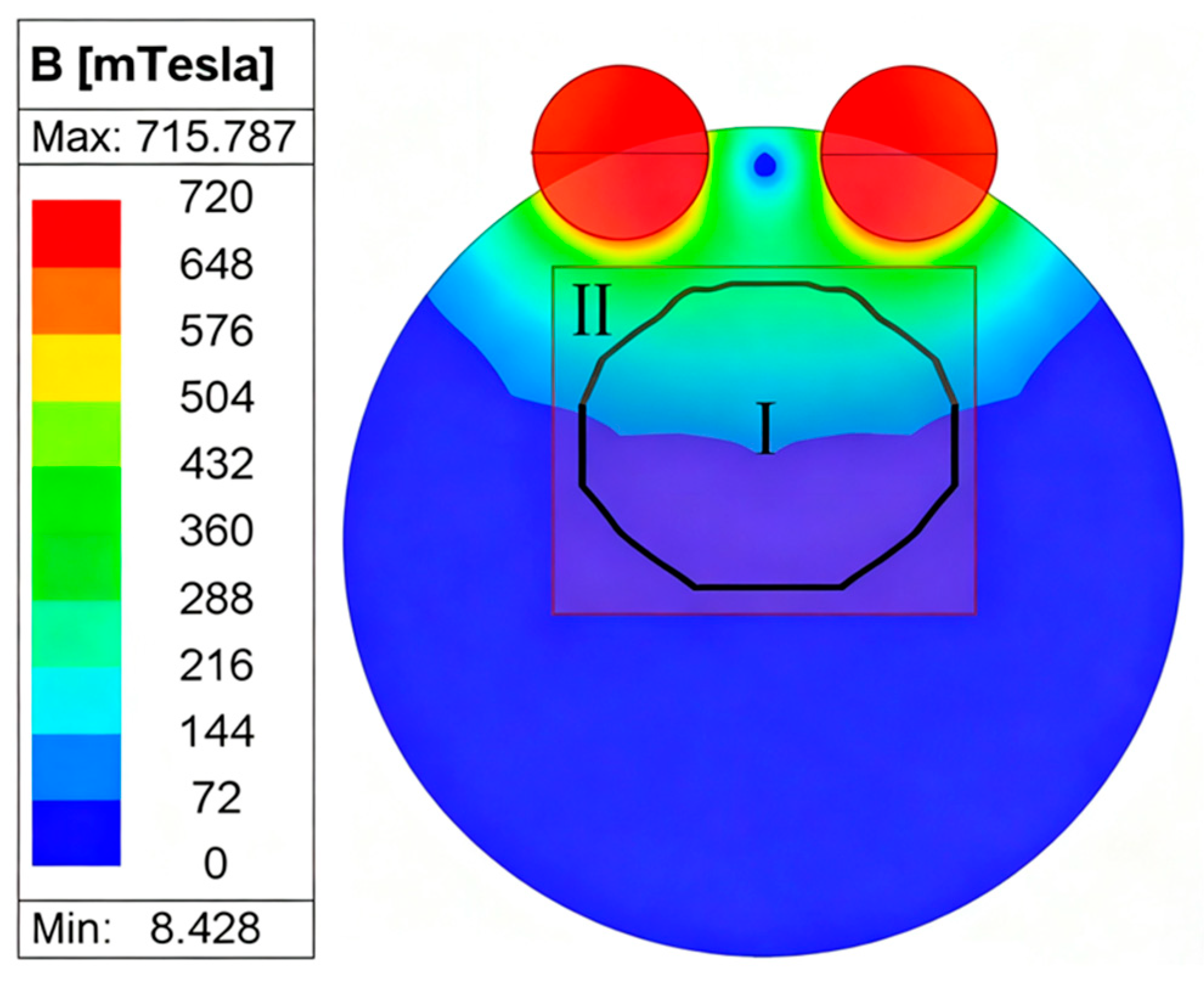
3.2. Magnetic Configuration and Simulation Domain
3.3. Model Parameters and Material Properties
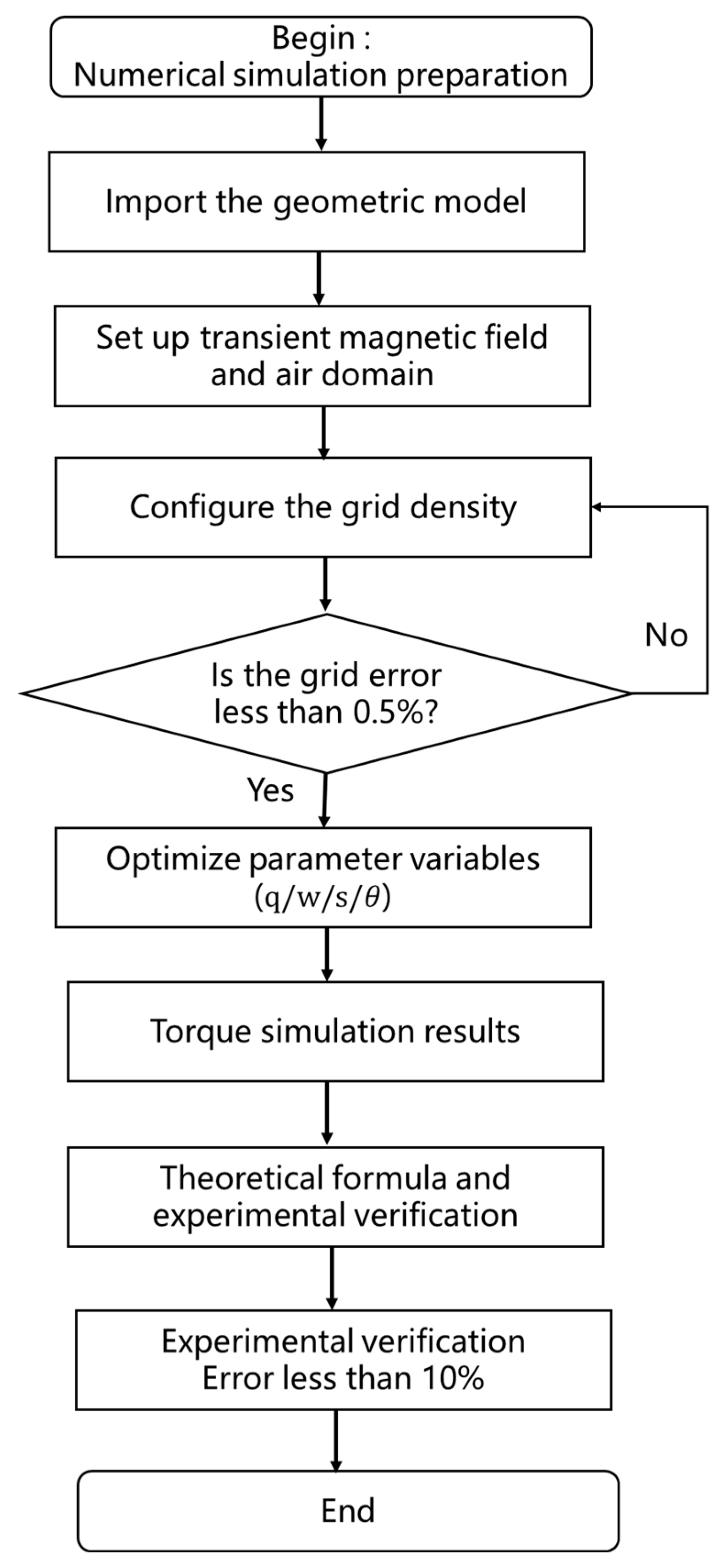
4. Simulation Results and Parameter Optimization Analysis
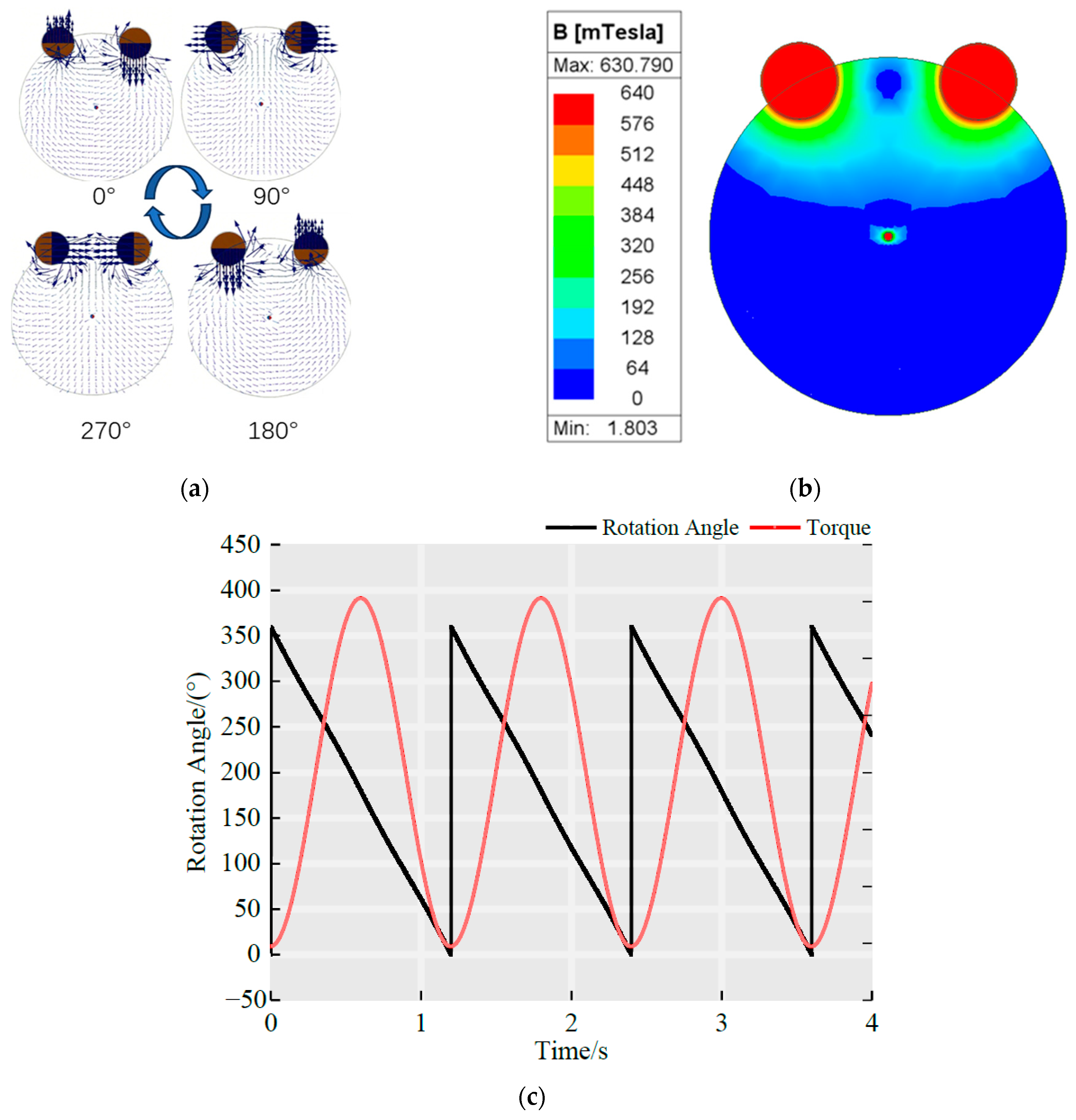
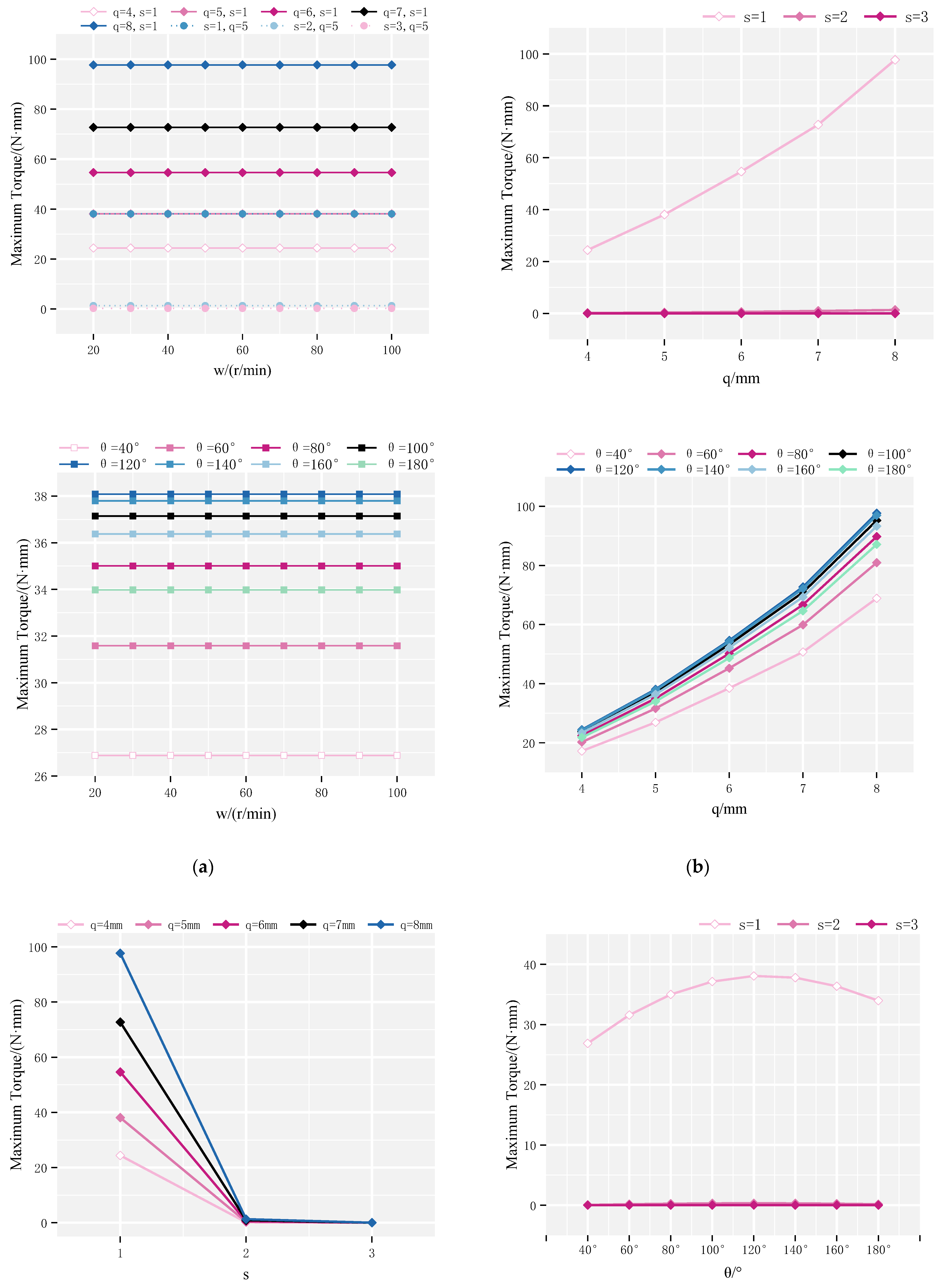
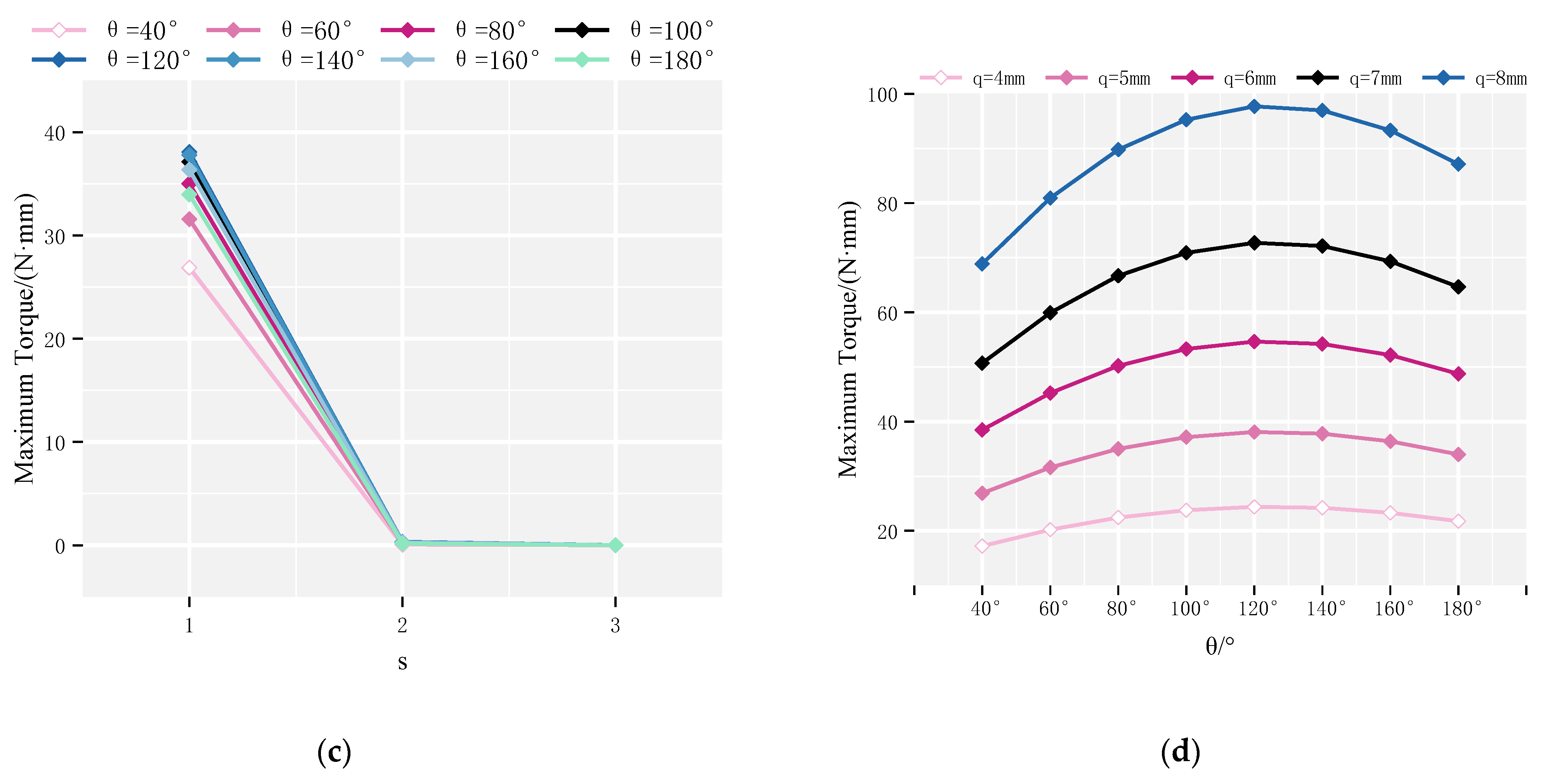
4.1. Maximum Rotor Torque
4.2. Continuous Rotation Domain of the Rotor
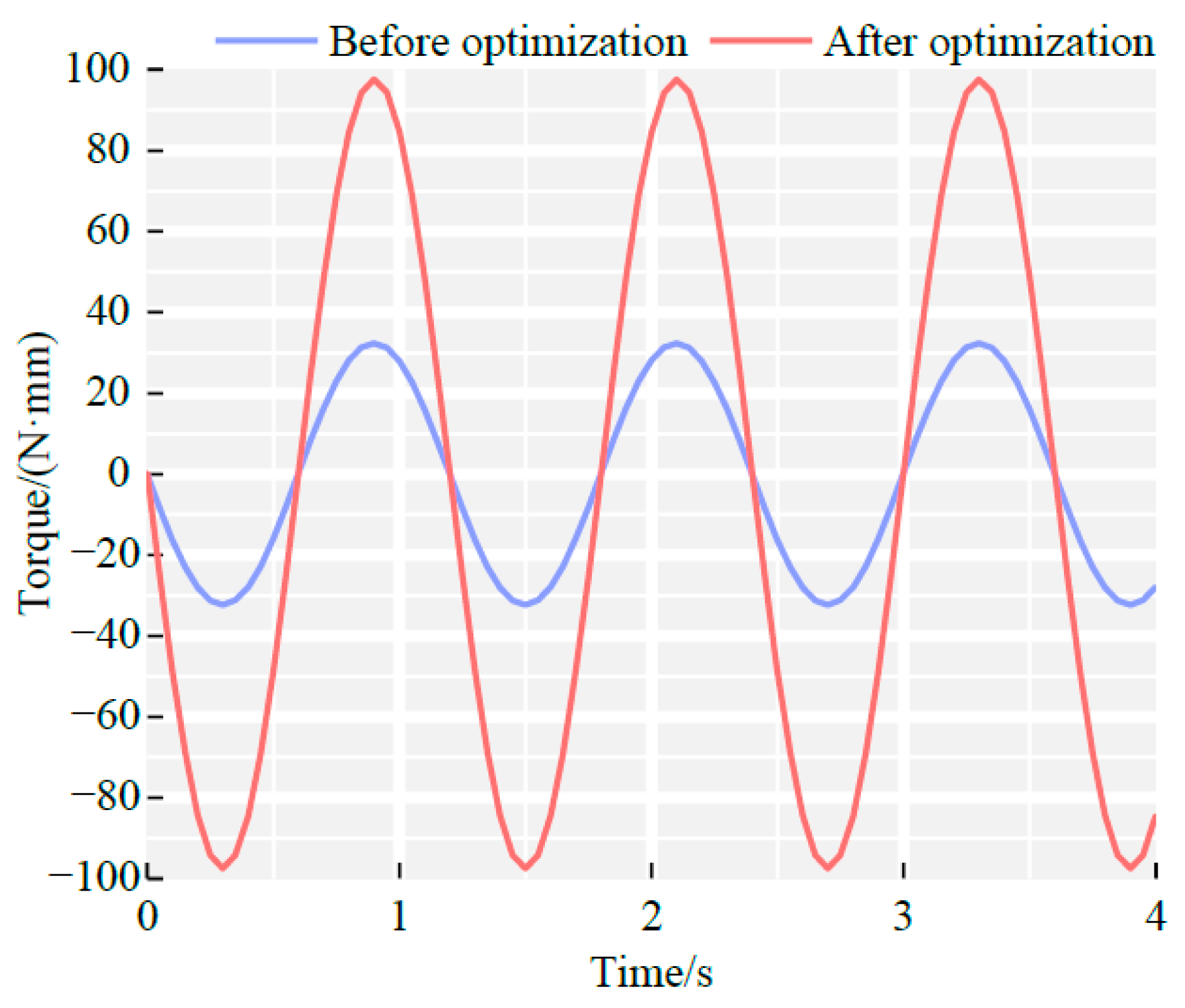
4.3. Optimization Analysis
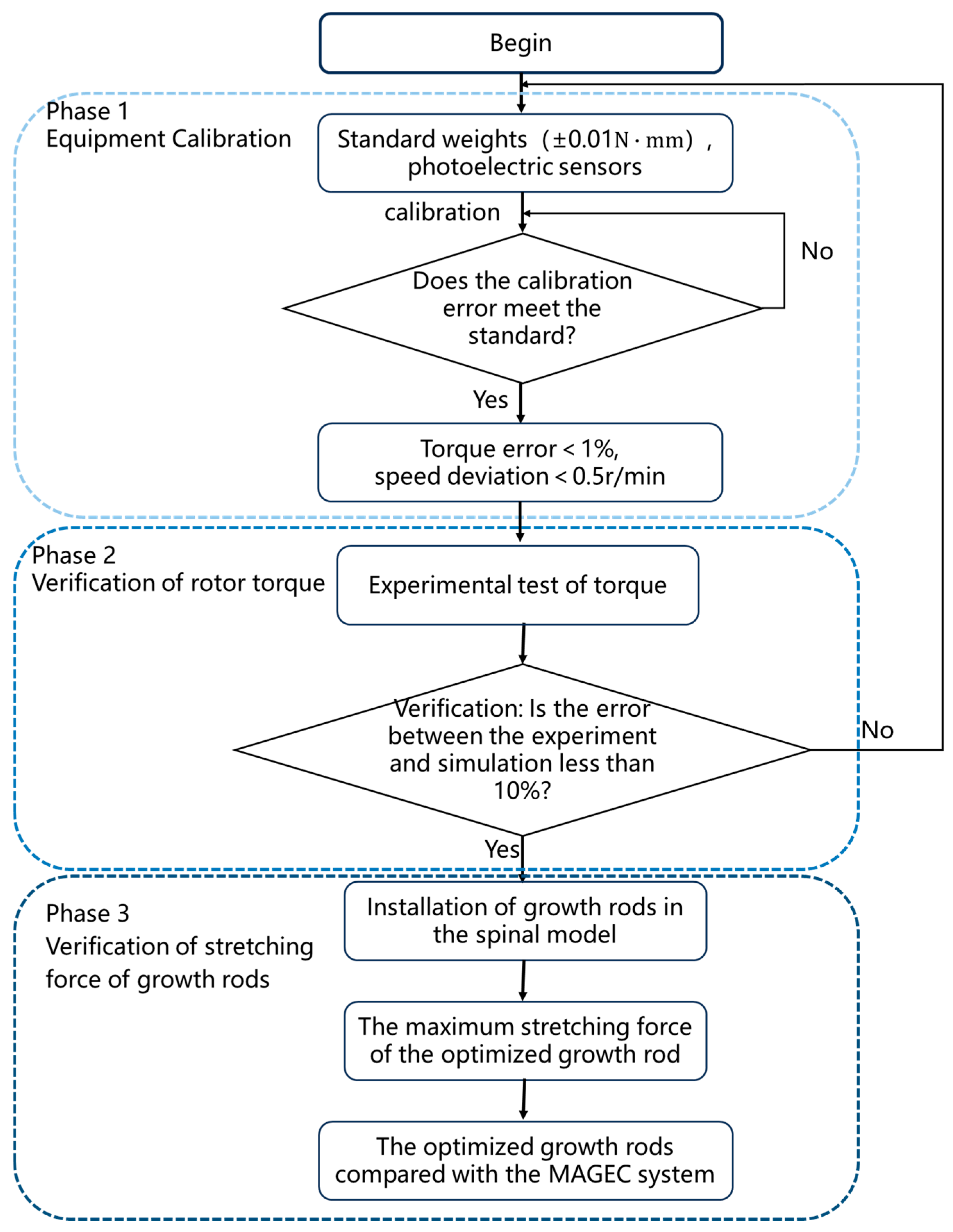
5. Experimental Verification of Magnetron Drives
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAGEC | MAGnetic Expansion Control |
| EOS | Early-onset scoliosis |
| PM | permanent magnet |
| PMSMs | permanent magnet synchronous motors |
| FEA | finite element analysis |
| FEM | finite element model |
Appendix A
| Parameter | Definition |
|---|---|
| Angular velocity of the driving magnet | |
| Rotor outer diameter | |
| Outer diameter of driving magnet | |
| Angle between driving magnet and rotor | |
| Number of pole pairs | |
| Coordinates on rotor end face | |
| Center-to-center distance (x–y plane) |
References
- Cruz-Medel, I.; Rodrigues-De-Souza, D.P.; Alburquerque-Sendín, F. Comprehensive Analysis of Pelvic Asymmetries in Low Back Pain, Scoliosis, Post-Traumatic Pelvic Dysfunctions and Obstetric Changes: A Narrative Review Focused on Clinical Relevance. Symmetry 2024, 16, 1304. [Google Scholar] [CrossRef]
- Grabara, M.; Witkowska, A. Sagittal spinal curvatures of young adults in the context of their self-reported physical activity and somatic parameters. Sci. Rep. 2024, 14, 12221. [Google Scholar] [CrossRef]
- Akbarnia, B.A.; Pawelek, J.B.; Cheung, K.; Demirkiran, G.; Elsebaie, H.B.; Emans, J.B.; Johnston, C.E.; Mundis, G.M.; Noordeen, H.; Skaggs, D.L.; et al. Traditional growing rods versus magnetically controlled growing rods for the surgical treatment of early-onset scoliosis: A case-matched 2-year study. Spine Deform. 2014, 2, 493–497. [Google Scholar] [CrossRef]
- Charroin, C.; Abelin-Genevois, K.; Cunin, V.; Berthiller, J.; Constant, H.; Kohler, R.; Aulagner, G.; Serrier, H.; Armoiry, X. Direct costs associated with the management of progressive early onset scoliosis: Estimations based on gold standard technique or with magnetically controlled growing rods. Orthop. Traumatol. Surg. Res. 2014, 100, 469–474. [Google Scholar] [CrossRef] [PubMed]
- Cheung, J.P.; Cahill, P.; Yaszay, B.; Akbarnia, B.A.; Cheung, K.M. Update on the magnetically controlled growing rod: Tips and pitfalls. J. Orthop. Surg. 2015, 23, 383–390. [Google Scholar] [CrossRef]
- Akbarnia, B.A.; Mundis, G.M., Jr.; Salari, P.; Yaszay, B.; Pawelek, J.B. Innovation in growing rod technique: A study of safety and efficacy of a magnetically controlled growing rod in a porcine model. Spine 2012, 37, 1109–1114. [Google Scholar] [CrossRef]
- Cheung, J.P.Y.; Cheung, K.M. Current status of the magnetically controlled growing rod in treatment of early-onset scoliosis: What we know after a decade of experience. J. Orthop. Surg. 2019, 27, 2309499019886945. [Google Scholar] [CrossRef]
- Jenks, M.; Craig, J.; Higgins, J.; Willits, I.; Barata, T.; Wood, H.; Kimpton, C.; Sims, A. The MAGEC System for Spinal Lengthening in Children with Scoliosis: A NICE Medical Technology Guidance. Appl. Heal. Econ. Heal. Policy 2014, 12, 587–599. [Google Scholar] [CrossRef]
- Andreozzi, V.; Princi, G.; Labianca, L.; Rinaldi, D.; Ferretti, A. Magnetically Controlled Growing Rods for Early Scoliosis Treatment in Coffin-Siris Syndrome: Case Report and Literature Review. Iowa Orthop. J. 2021, 41, 55–59. [Google Scholar] [PubMed]
- Lebel, D.E.; Rocos, B.; Helenius, I.; Sigal, A.; Struder, D.; Yazici, M.; Bekmez, S.; Hasler, C.C.; Pesenti, S.; Jouve, J.L.; et al. Magnetically Controlled Growing Rods Graduation: Deformity Control with High Complication Rate. Spine 2021, 46, E1105–E1112. [Google Scholar] [CrossRef]
- Falconi, B.A.; Remondino, R.G.; Piantoni, L.; Tello, C.A.; Galaretto, E.; Frank, S.; Noel, M.A. Magnetically-Controlled Growing Rods. Outcomes and Complications. Rev. Asoc. Argent. Ortop. Traumatol. 2023, 88, 302–313. [Google Scholar] [CrossRef]
- Tsirikos, A.I.; Roberts, S.B. Magnetic controlled growth rods in the treatment of scoliosis: Safety, efficacy and patient selection. Med. Devices Evid. Res. 2020, 13, 75–85. [Google Scholar]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Analysis and design optimization of a permanent magnet synchronous motor for a campus patrol electric vehicle. IEEE Trans. Veh. Technol. 2019, 68, 10535–10544. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, X.; Wu, W.; Xiang, Z.; Liu, Y.; Quan, L. Multi-objective optimization design of variable-saliency-ratio PM motor considering driving cycles. IEEE Trans. Ind. Electron. 2020, 68, 6516–6526. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Cai, Y.; Yang, Z.; Lei, G.; Guo, Y. Torque analysis and dynamic performance improvement of a PMSM for EVs by skew angle optimization. IEEE Trans. Appl. Supercond. 2018, 29, 0600305. [Google Scholar] [CrossRef]
- Bingi, K.; Prusty, B.R.; Kumra, A.; Chawla, A. Torque and temperature prediction for permanent magnet synchronous motor using neural networks. In Proceedings of the 2020 3rd International Conference on Energy, Power and Environment: Towards Clean Energy Technologies, Shillong, ML, India, 5–7 March 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Guemes, J.A.; Iraolagoitia, A.M.; Del Hoyo, J.I.; Fernández, P. Torque analysis in permanent-magnet synchronous motors: A comparative study. IEEE Trans. Energy Convers. 2010, 26, 55–63. [Google Scholar] [CrossRef]
- Usman, H.; Ikram, J.; Alimgeer, K.S.; Yousuf, M.; Bukhari, S.S.H.; Ro, J.-S. Analysis and optimization of axial flux permanent magnet machine for cogging torque reduction. Mathematics 2021, 9, 1738. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Torkaman, H.; Javadi, H. Simultaneous improvement of cogging torque and torque density in axial flux-switching permanent magnet motor. IET Electr. Power Appl. 2023, 18, 312–324. [Google Scholar] [CrossRef]
- Yan, D.; Yan, Y.; Cheng, Y.; Guo, L.; Shi, T. Research on cogging torque reduction method for permanent magnet synchronous motor accounting for the magnetic pole edge effect. IET Electr. Power Appl. 2023, 18, 64–75. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, G.; Du, G. An investigation into the pole–slot ratio and optimization of a low-speed and high-torque permanent magnet motor. Appl. Sci. 2024, 14, 3983. [Google Scholar] [CrossRef]
- Nobahari, A.; Vahedi, A.; Nasiri-Zarandi, R. A modified permanent magnet-assisted synchronous reluctance motor design for torque characteristics improvement. IEEE Trans. Energy Convers. 2021, 37, 989–998. [Google Scholar] [CrossRef]
- Cambiaghi, A. Biological Evaluation of Medical Devices as an Essential Part of the Risk Management Process: Updates and Challenges of ISO 10993-1: 2018; Eurofins Medical Device Testing: Lancaster, PA, USA, 2018; p. 6. [Google Scholar]
- Poon, S.; Nixon, R.; Wendolowski, S.; Gecelter, R.; Chen, Y.H.; DiMauro, J.P.; Amaral, T.; Graver, A.; Grande, D.A. A pilot cadaveric study of temperature and adjacent tissue changes after exposure of magnetic-controlled growing rods to MRI. Eur. Spine J. 2017, 26, 1618–1623. [Google Scholar] [CrossRef] [PubMed]
- Poon, S.; Chen, Y.H.; Wendolowski, S.F.; Graver, A.; Nixon, R.; Amaral, T.; DiMauro, J.P.; Walz, D.M.; Gecelter, R.C.; Grande, D.A. Cadaveric study of the safety and device functionality of magnetically controlled growing rods after exposure to magnetic resonance imaging. Spine Deform. 2018, 6, 290–298. [Google Scholar] [CrossRef] [PubMed]



| Parameters | Drive Permanent Magnets | Rotors |
|---|---|---|
| Inside diameter/ | 11 | 2 |
| External diameter/ | 50 | 5 |
| Thicknesses/ | 40 | 40 |
| Parameters | Numerical Value |
|---|---|
| Magnetic field strength/ ) | |
| Relative permeability/ | 1.100 |
| Electrical conductivity/ | |
| Density/ | |
| Remanent Flux Density/(T) | 1.30 |
| Operating Temperature Range | −40~80 °C |
| Curie Temperature/ (°C) | 310 °C |
| Magnet Grade | NdFeB 35 |
| Maximum Energy Product/(BH)max | 35 MGOe |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, Z.; Lu, D.; Peng, T.; Chen, Y.; Fu, G.; Nie, Z.; Wei, F. Enhancing Torque Output for a Magnetic Actuation System for Robotic Spinal Distraction. Sensors 2025, 25, 6497. https://doi.org/10.3390/s25206497
Li Y, Li Z, Lu D, Peng T, Chen Y, Fu G, Nie Z, Wei F. Enhancing Torque Output for a Magnetic Actuation System for Robotic Spinal Distraction. Sensors. 2025; 25(20):6497. https://doi.org/10.3390/s25206497
Chicago/Turabian StyleLi, Yumei, Zikang Li, Ding Lu, Tairan Peng, Yunzhi Chen, Gang Fu, Zhenguo Nie, and Fangyuan Wei. 2025. "Enhancing Torque Output for a Magnetic Actuation System for Robotic Spinal Distraction" Sensors 25, no. 20: 6497. https://doi.org/10.3390/s25206497
APA StyleLi, Y., Li, Z., Lu, D., Peng, T., Chen, Y., Fu, G., Nie, Z., & Wei, F. (2025). Enhancing Torque Output for a Magnetic Actuation System for Robotic Spinal Distraction. Sensors, 25(20), 6497. https://doi.org/10.3390/s25206497







