Probing a CNN–BiLSTM–Attention-Based Approach to Solve Order Remaining Completion Time Prediction in a Manufacturing Workshop
Abstract
1. Introduction
- (1)
- Through systematic data preprocessing, key patterns and hidden factors affecting processing cycle fluctuations are effectively identified, while noise reduction and missing value handling enhance data quality for more accurate and reliable analysis.
- (2)
- Utilizing deep learning to build predictive models enables workshop managers to explore production data more thoroughly, thereby uncovering complex relationships between various inputs (e.g., order data, workshop status, and machine conditions) and outputs (predicted remaining completion time).
- (3)
- By integrating CNN, BiLSTM, and Attention mechanism, this paper enhances the model ability to capture spatial patterns, temporal dependencies, and key contextual features in manufacturing processes, thereby achieving more accurate and reliable predictions of order remaining completion time.
2. Related Works
2.1. Workshop Remaining Completion Time Prediction
2.2. Deep Learning for Remaining Completion Time Prediction
2.3. Research Gaps and Methodology
- (1)
- Although deep learning models have been widely adopted, most studies have focused on isolated temporal or spatial feature extraction. For instance, traditional LSTM networks excel in capturing sequential dependencies but neglect local spatial patterns in manufacturing data. Conversely, CNN-based methods prioritize spatial correlations but fail to model long-term temporal dependencies, which leads to suboptimal predictions under complex multi-factor interactions.
- (2)
- The current approaches predominantly target static or idealized production conditions by relying on fixed input features and deterministic predictions. In real-world workshops with frequent disturbances, the correlation between input features and prediction targets shifts dynamically, which causes model performance degradation. Existing methods lack adaptive mechanisms to update feature relevance or adjust model structures in real time.
- (3)
- Although manufacturing systems generate high-dimensional heterogeneous data, most studies either adopt a simplistic feature selection or directly feed raw data into complex networks without optimizing the information density. This results in redundant computations and poor interpretability, particularly when handling sparse or noisy datasets.
- (1)
- Data collection and preprocessing. Using data collection methods such as RFID, PLC, and 5G, structured production data is extracted from multiple manufacturing information systems through extract, transform, and load technology. Then, original feature dataset is constructed by orders, work in process, and machine-level data. To ensure data quality, perform preprocessing on the dataset, including outlier handling, missing value imputation, and data normalization. This preprocessing stage ensures that the dataset is both representative and suitable for deep learning model training.
- (2)
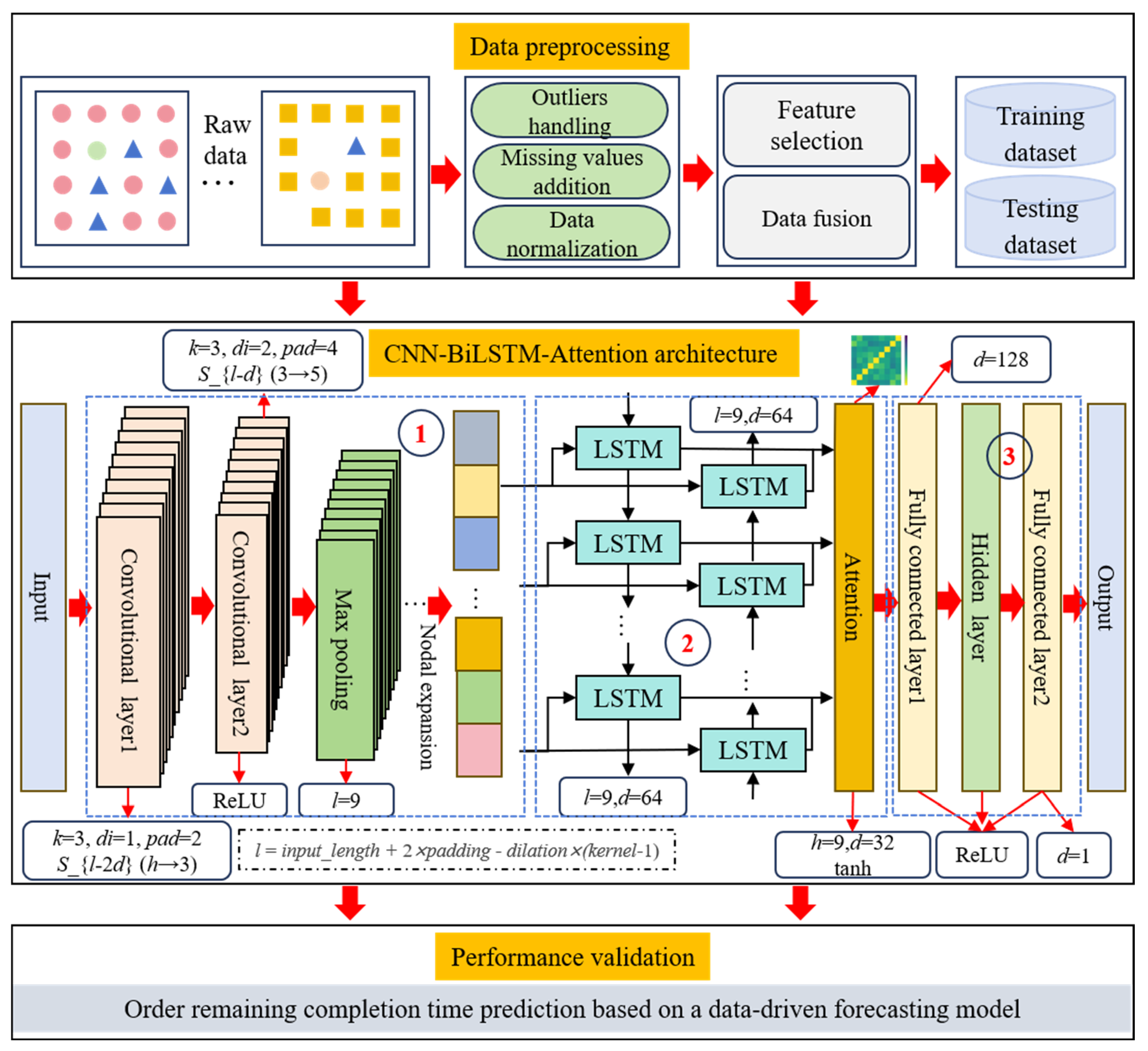
- Model design and implementation. To overcome the limitations of existing single-structure models, this paper develops a hybrid CNN–BiLSTM–Attention deep learning model. The CNN component is used to extract local spatial features from high-dimensional production data, while the BiLSTM layer captures bidirectional temporal dependencies to model sequential production patterns. The integrated Attention mechanism adaptively assigns weights to key features and time steps, enabling the model to emphasize critical information and reduce noise influence. This hybrid architecture facilitates comprehensive spatiotemporal feature learning for accurate order completion time prediction.
- (3)
- Experimental setup and validation. Experimental studies are conducted using real workshop data collected from a production line equipped with ten types of machining equipment. Multiple comparative methods, including Back Propagation (BP), Deep Belief Network (DBN), Convolutional Neural Network (CNN), Bidirectional Long Short-Term Memory (BiLSTM), CNN-LSTM and CNN-BiLSTM, are implemented to benchmark performance. Evaluation metrics such as mean absolute error, root mean square error, and R2 are employed to quantify prediction accuracy and generalization ability. Sensitivity and robustness analyses are also performed to verify the model’s adaptability under dynamic production conditions.
- (4)
- Result interpretation and analysis. Finally, the predictive performance and interpretability of the proposed model are analyzed through visual comparisons and statistical evaluations. The results demonstrate that the proposed CNN–BiLSTM–Attention model effectively captures spatiotemporal dependencies and outperforms baseline models in both accuracy and robustness, providing strong methodological support for data-driven decision-making in discrete manufacturing workshops.
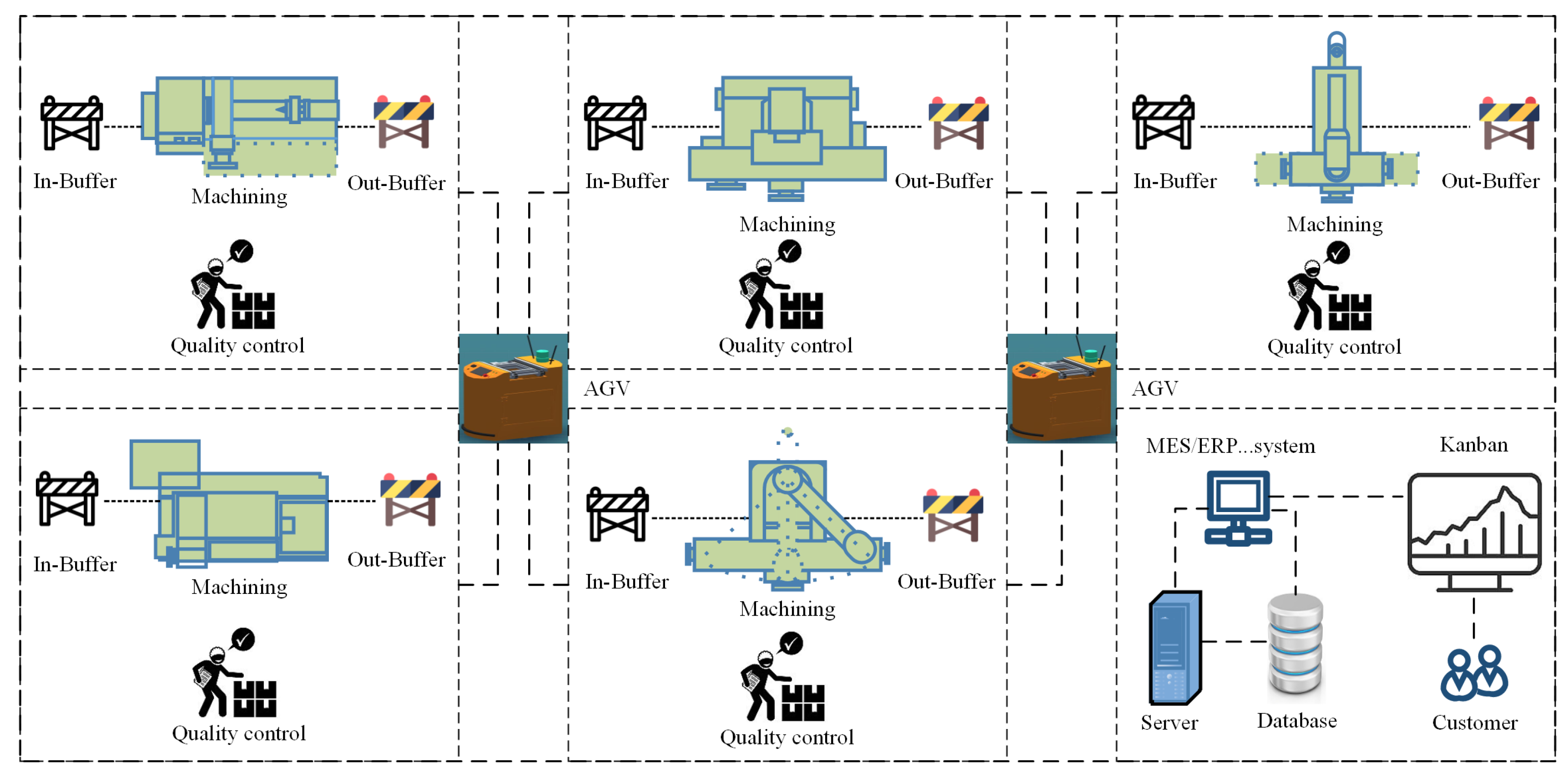
3. Feature Dataset Modeling
3.1. Problem Constraints
- (1)
- Resources constraint: Resources in discrete manufacturing workshops, including machines, human labor, and materials, play a crucial role in determining production efficiency. Their availability, allocation, and utilization directly influence both production performance and schedule feasibility. Material constraints often arise from shortages or delays in the supply of raw materials or semi-finished components. To address these issues, accurate procurement planning, dynamic inventory management, and real-time monitoring of material consumption are required to maintain the balance between supply and demand. Equipment constraints mainly stem from machine reliability issues and maintenance requirements. Unplanned downtime caused by equipment failures, as well as scheduled calibration or repairs, can disrupt production.To mitigate these risks, predictive maintenance strategies and the preparation of backup equipment should be integrated into the production system. Human resource constraints are reflected in limited labor availability, varying skill proficiency, and fluctuating operational efficiency. These challenges call for systematic solutions such as scientific shift scheduling, skill-based training programs, and workload balancing mechanisms to alleviate production bottlenecks. Together, these three dimensions, including materials, equipment, and human resources, form interdependent elements within the resource constraint framework. A systematic optimization approach is therefore required to achieve a dynamic balance between resource utilization efficiency and production rhythm.
- (2)
- Process and operational constraints: In discrete manufacturing workshops, a number of process and operational constraints inherently influence the execution of production tasks. Different products often follow distinct process routes and machining steps, and certain operations must be executed in a predefined order to ensure the accuracy and continuity of manufacturing processes. Each machine is capable of processing only one operation at a time, while the operations of each part must strictly comply with the process sequence specified in the production plan. In addition, the processing order of parts within in-buffer and out-buffer areas generally follows a first-in-first-out (FIFO) rule to maintain workflow stability and production efficiency.Violations of these process sequences may lead to machine idle time or production delays. Therefore, effective process modeling should explicitly account for task precedence rules, inter-task dependencies, and machine exclusivity constraints to ensure the feasibility and reliability of production schedules. These constraints are inherently embedded in the collected production data and are therefore implicitly reflected in the feature modeling stage. Consequently, the constructed feature dataset inherently captures such production logic, allowing the proposed CNN–BiLSTM–Attention model to learn temporal dependencies and operational behaviors under realistic manufacturing conditions.
3.2. Feature Dataset Construction
- (1)
- WIP status
- (2)
- Machine status
- (3)
- Order status
3.3. Data Preprocessing
4. Optimization Algorithm for Order Remaining Completion Time Prediction
- (1)
- Multi-dimensional feature extraction module
- (2)
- Attention-based key feature refinement module
- (3)
- High-precision linear prediction module
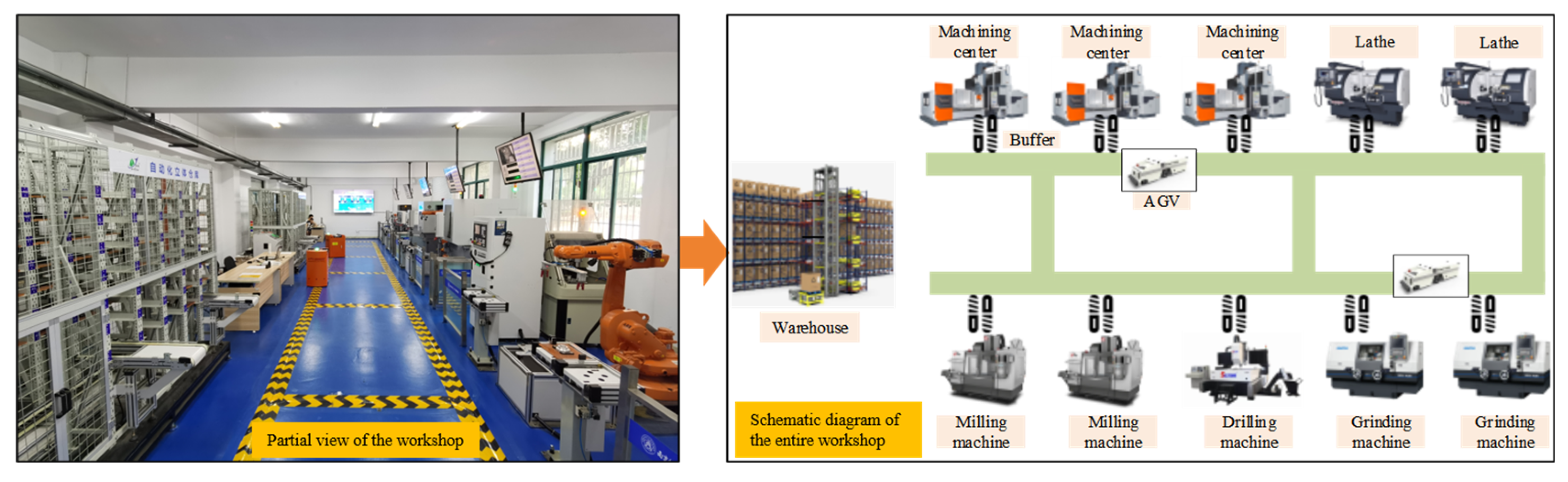
5. Experimental Studies
5.1. Experimental Environment
5.2. Analysis of Experimental Results
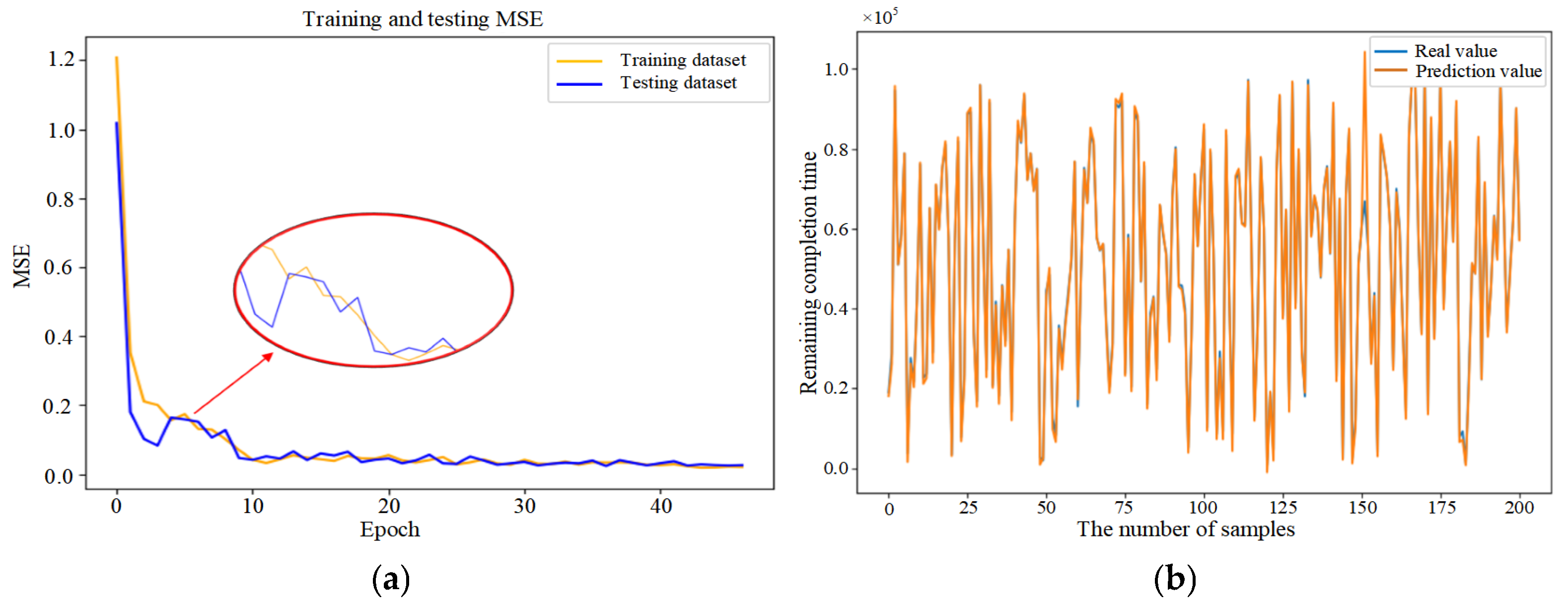
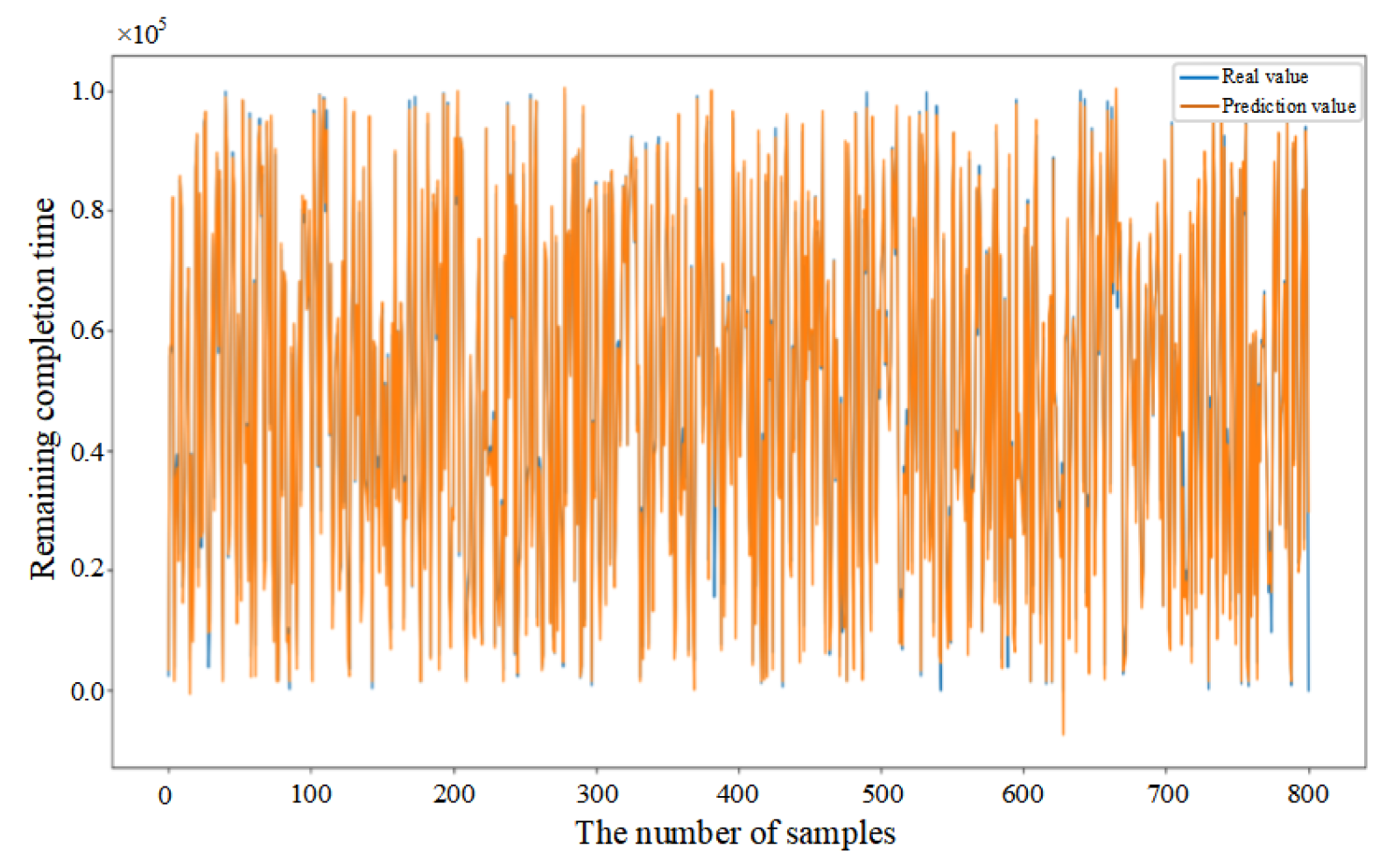
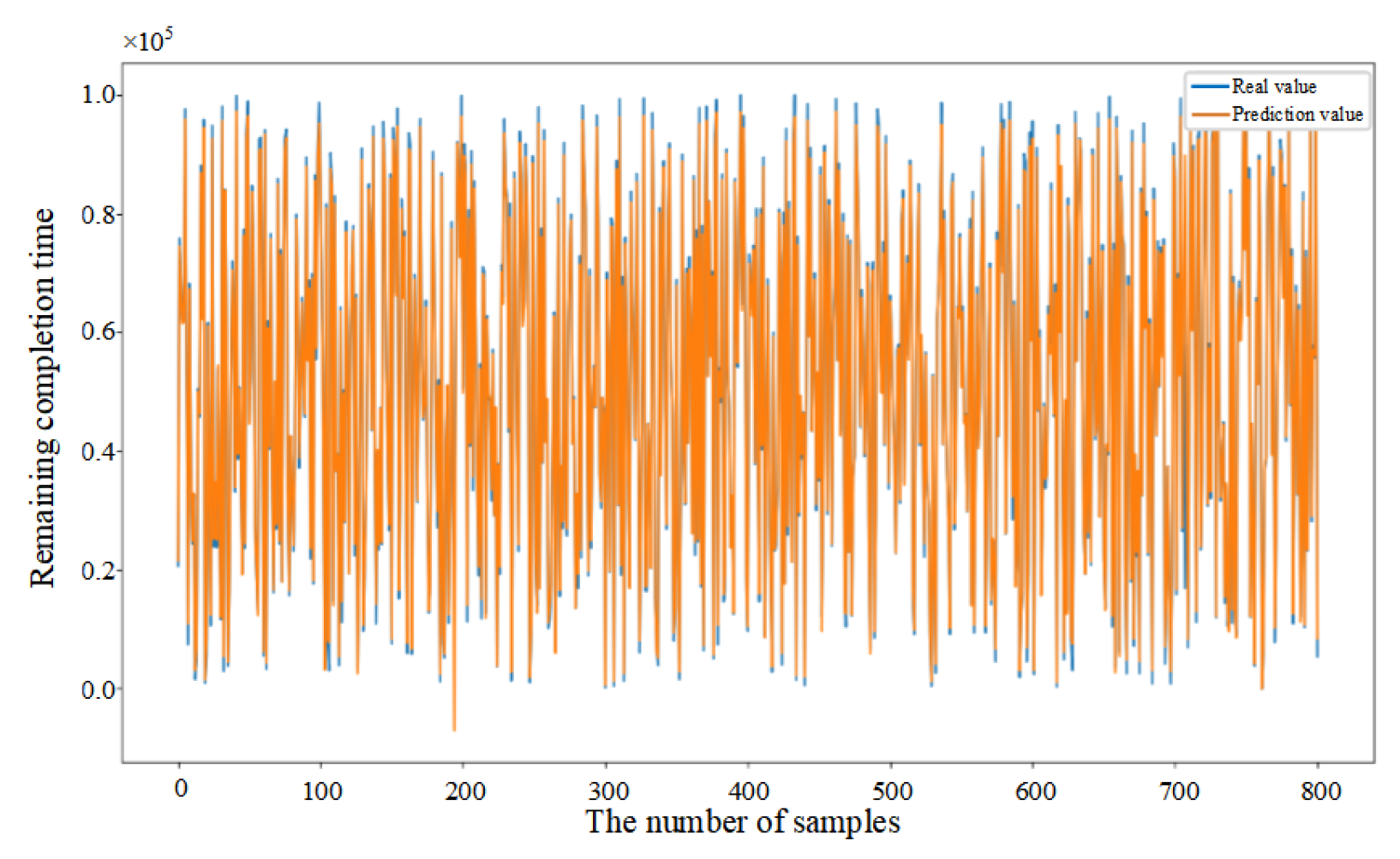
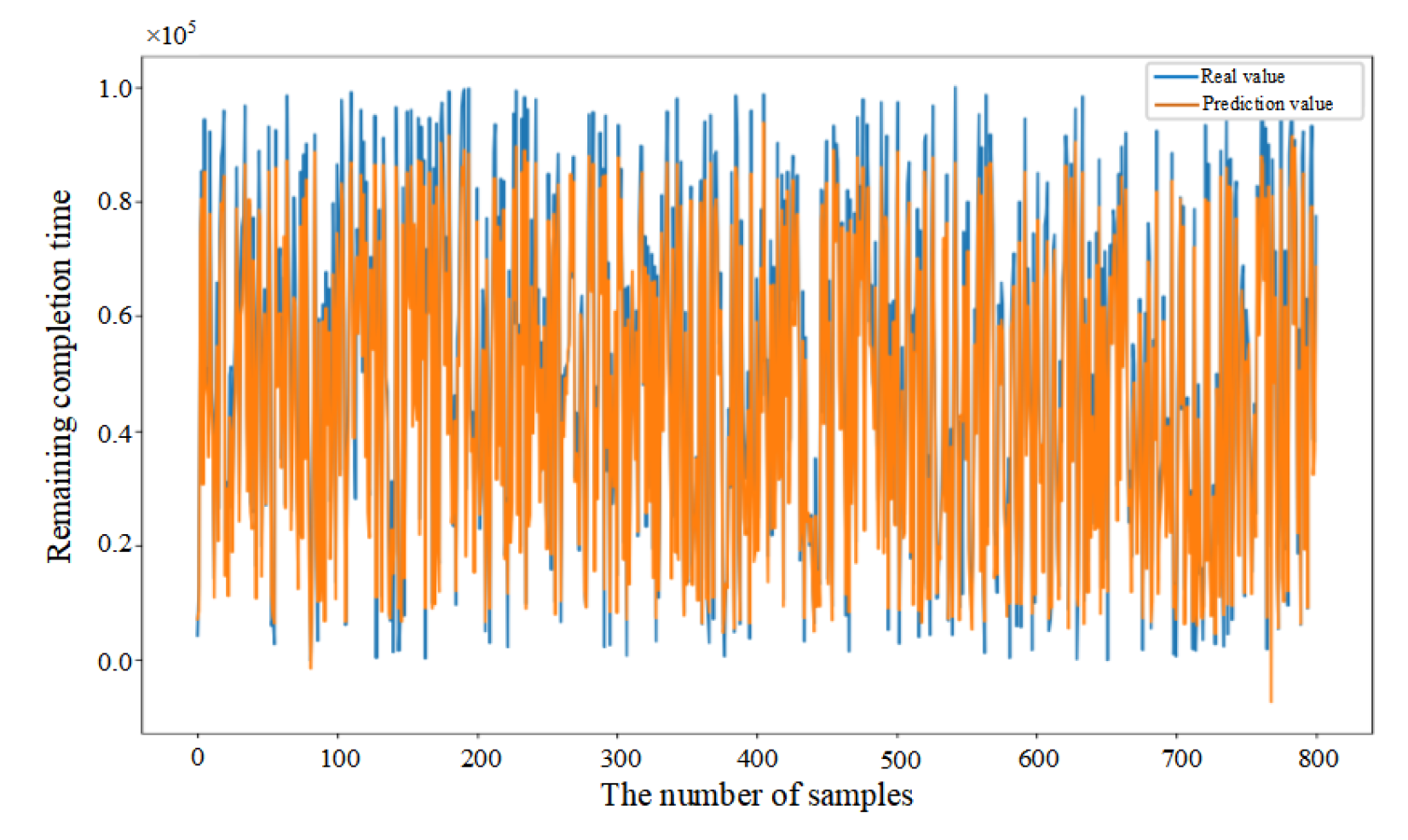
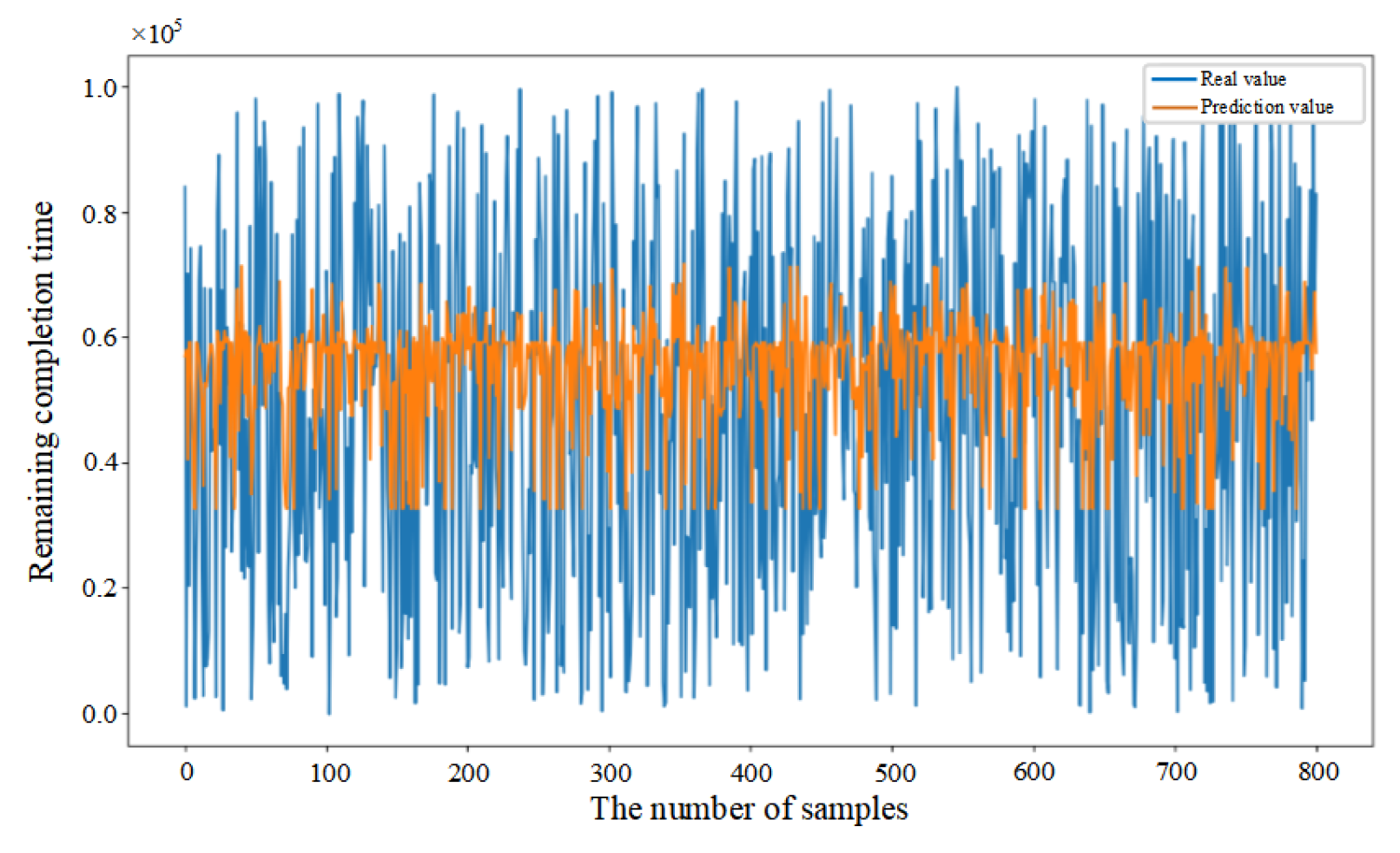
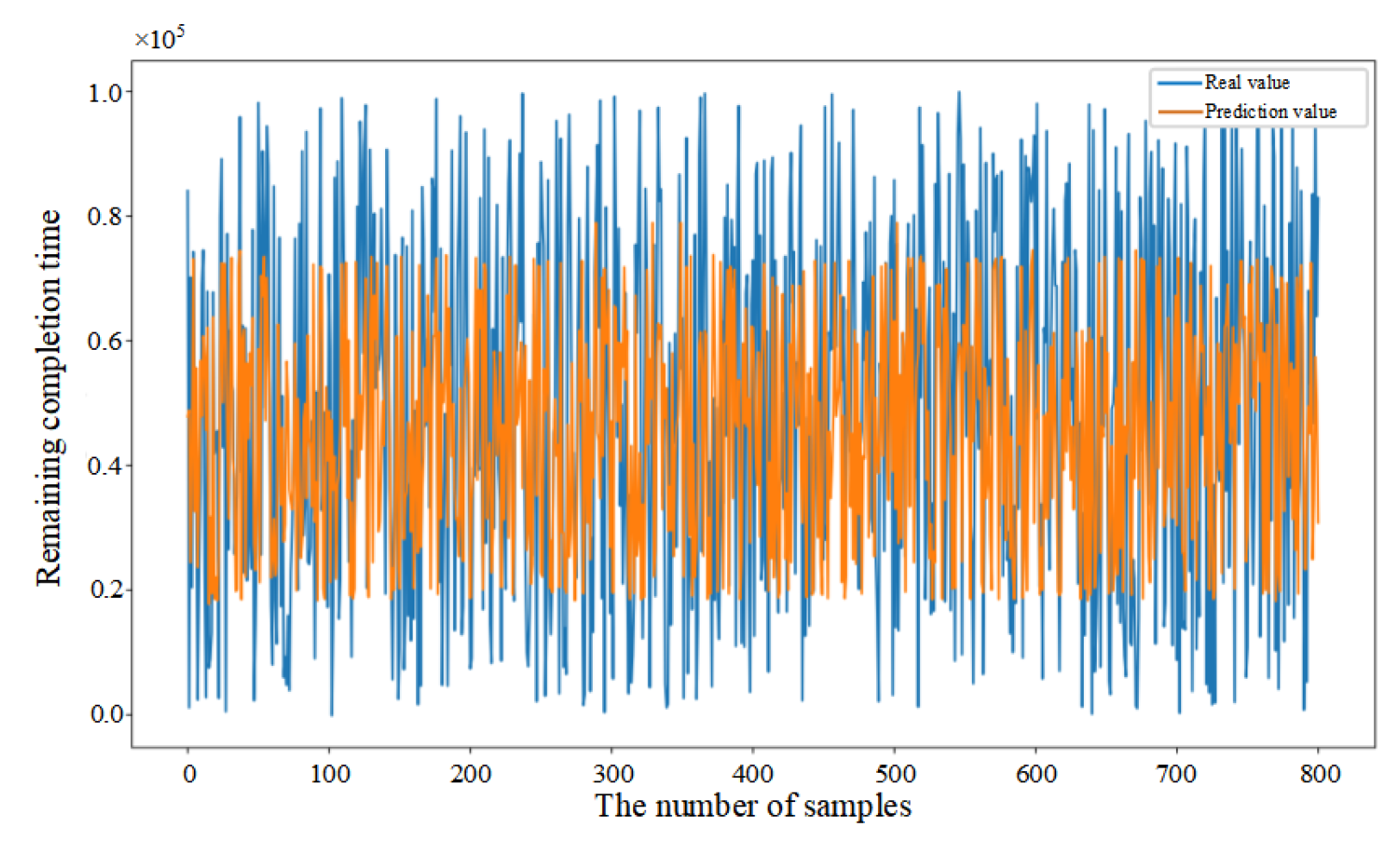
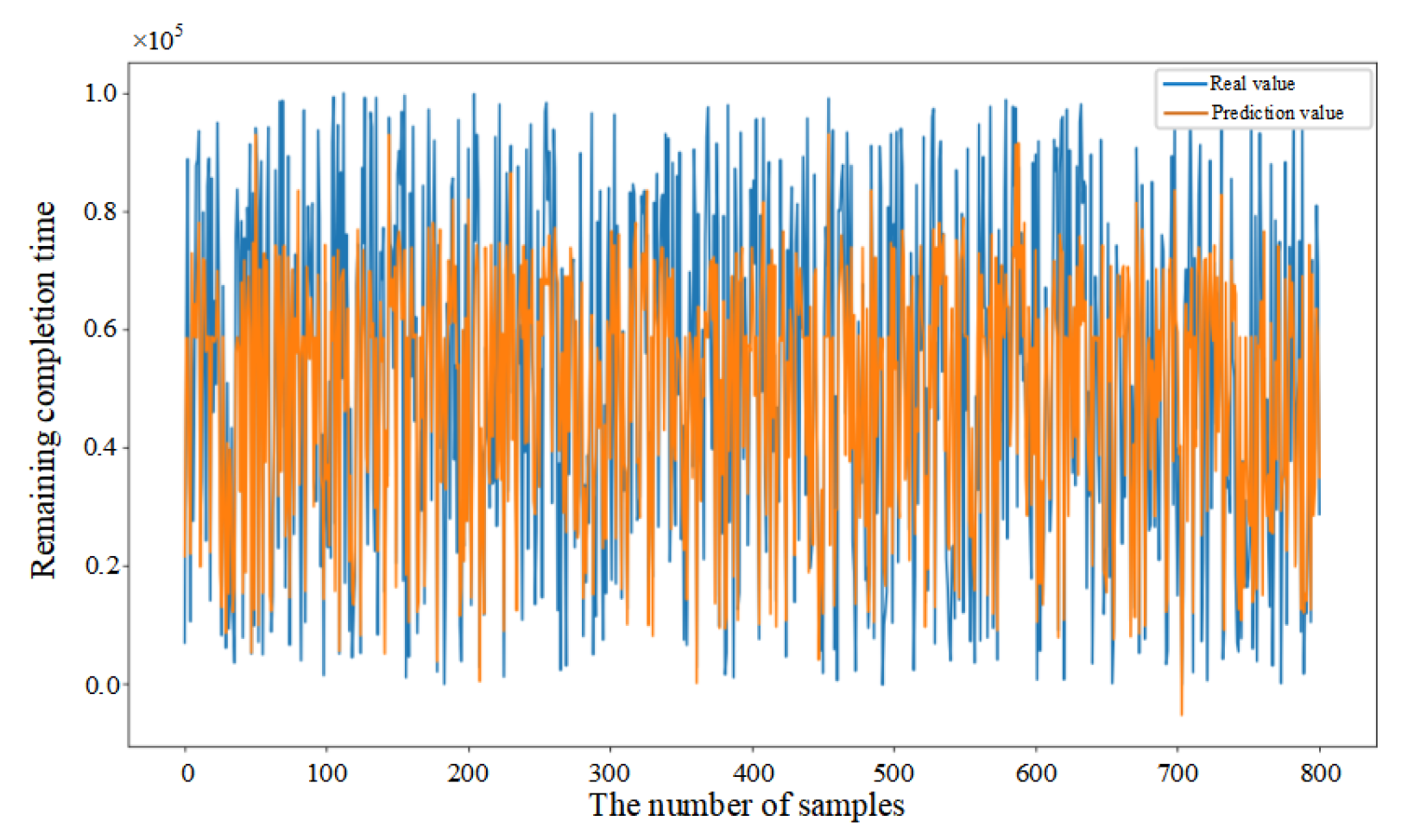
5.3. Comparative Analysis of Predictive Methods



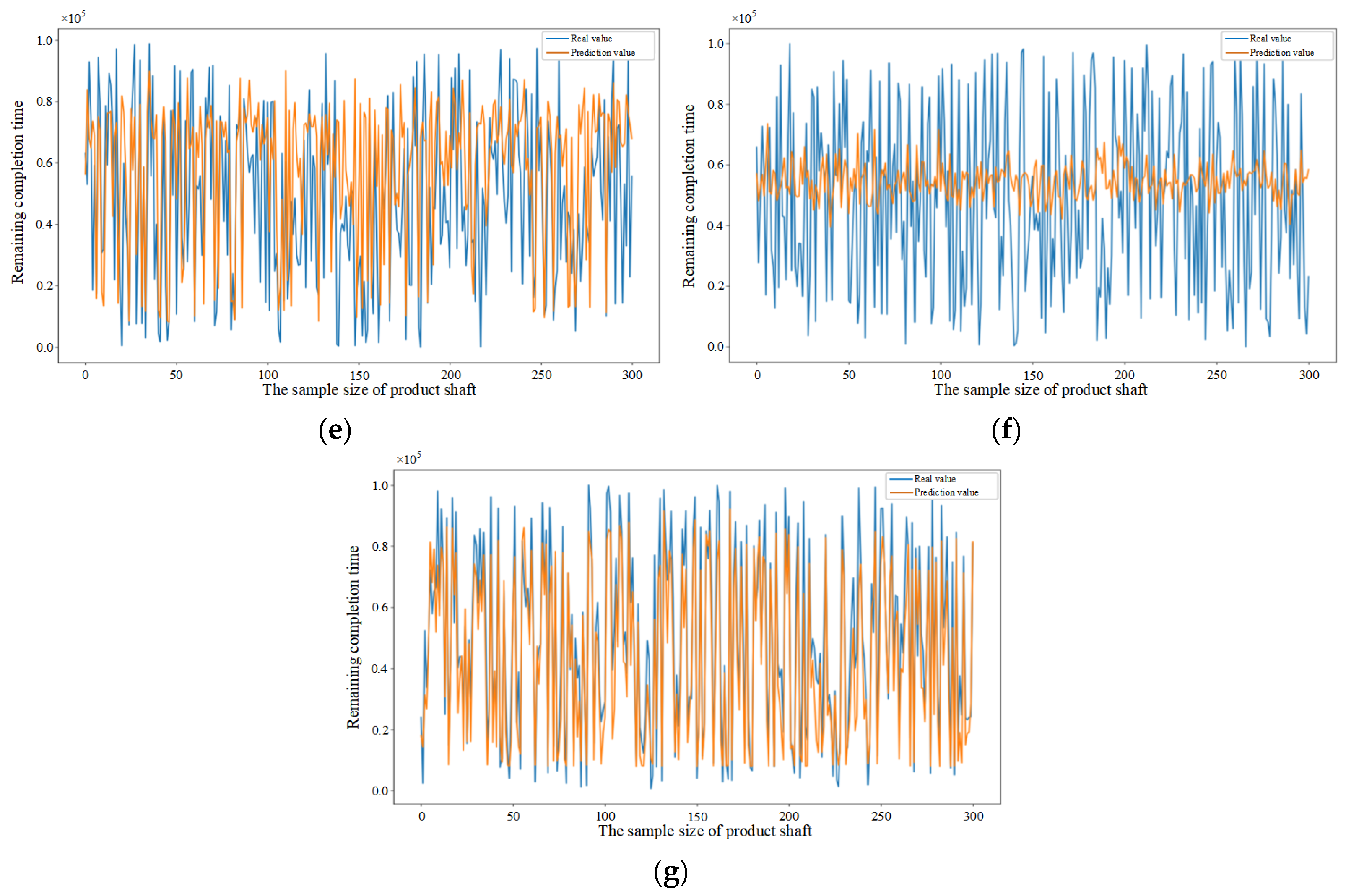
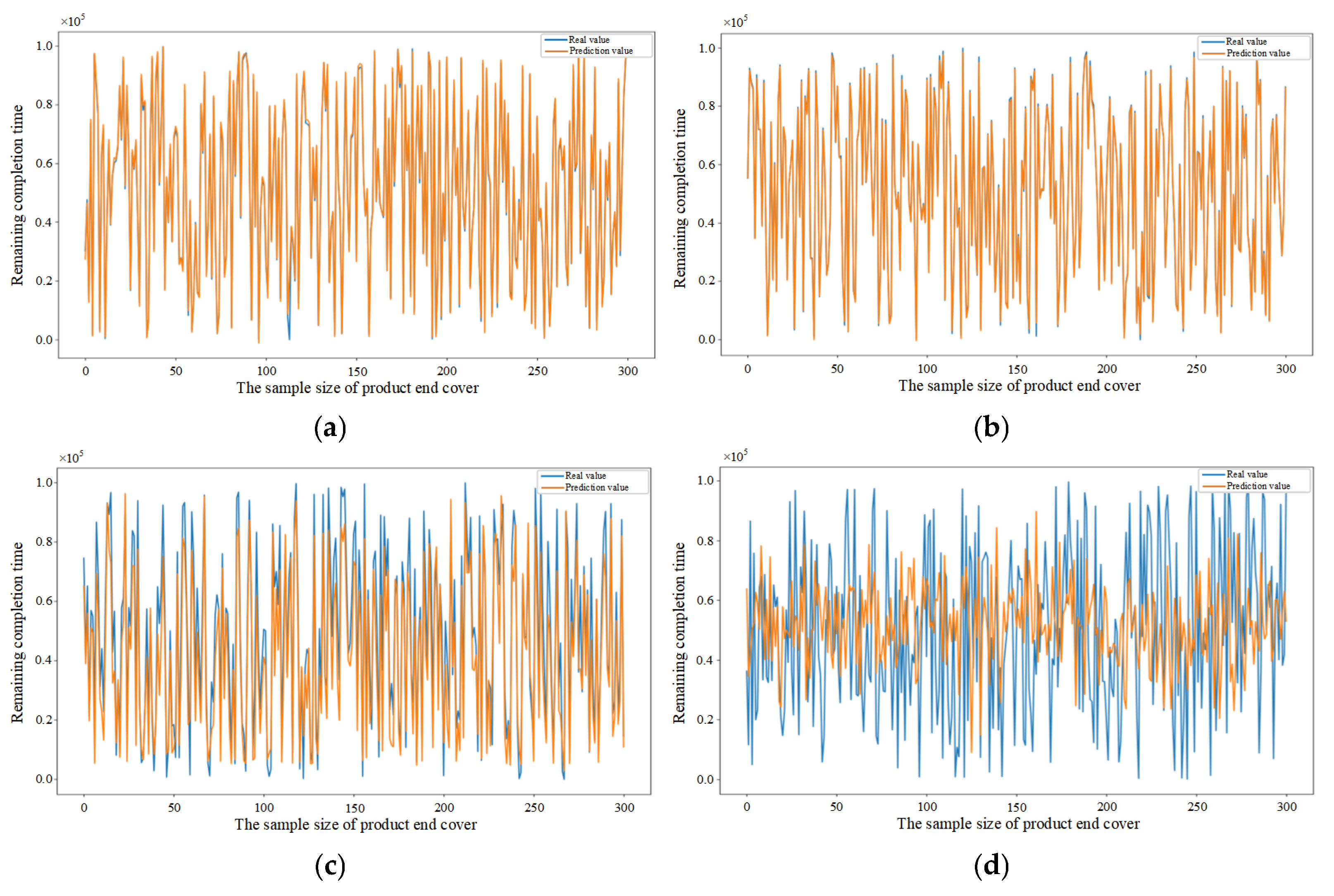
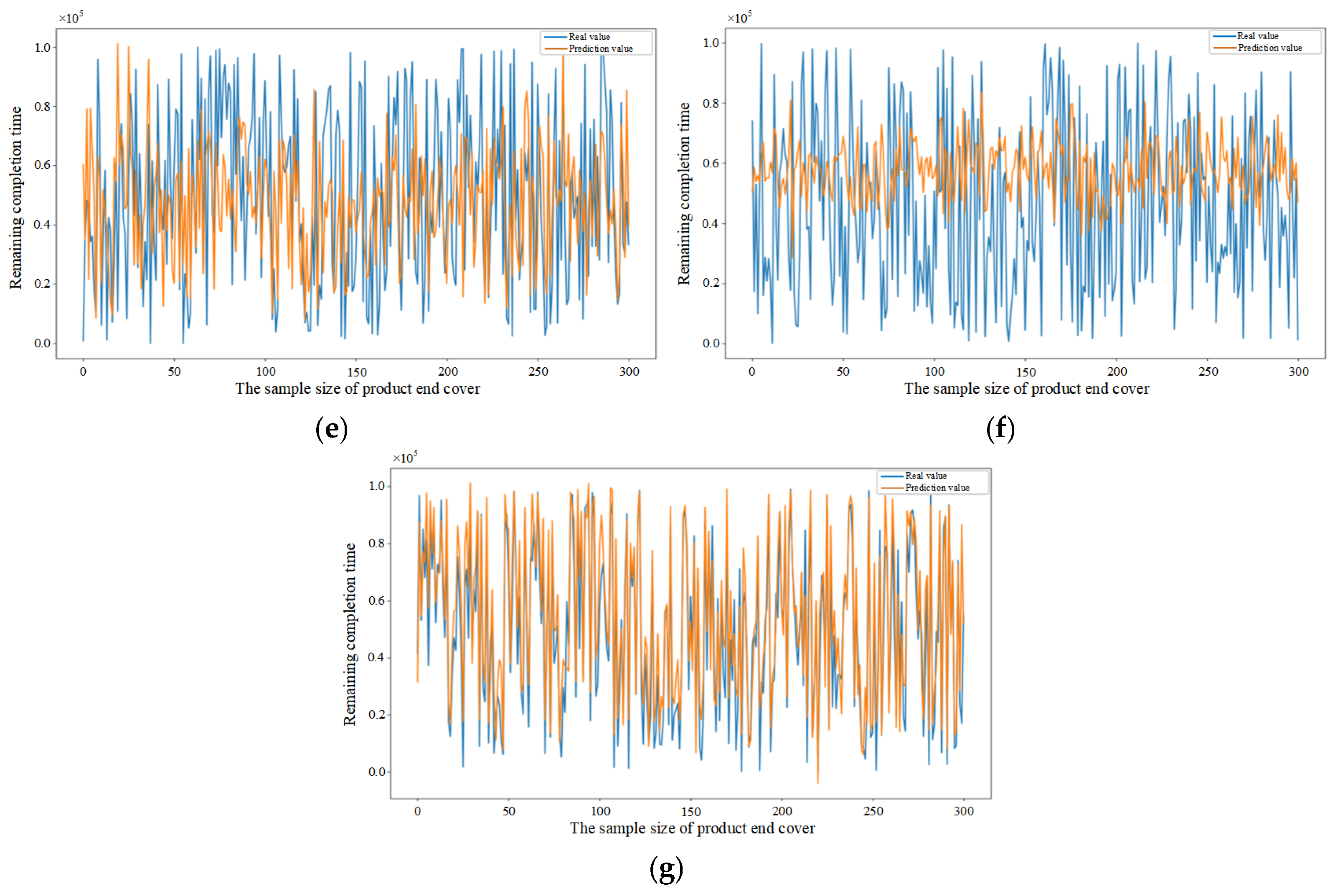
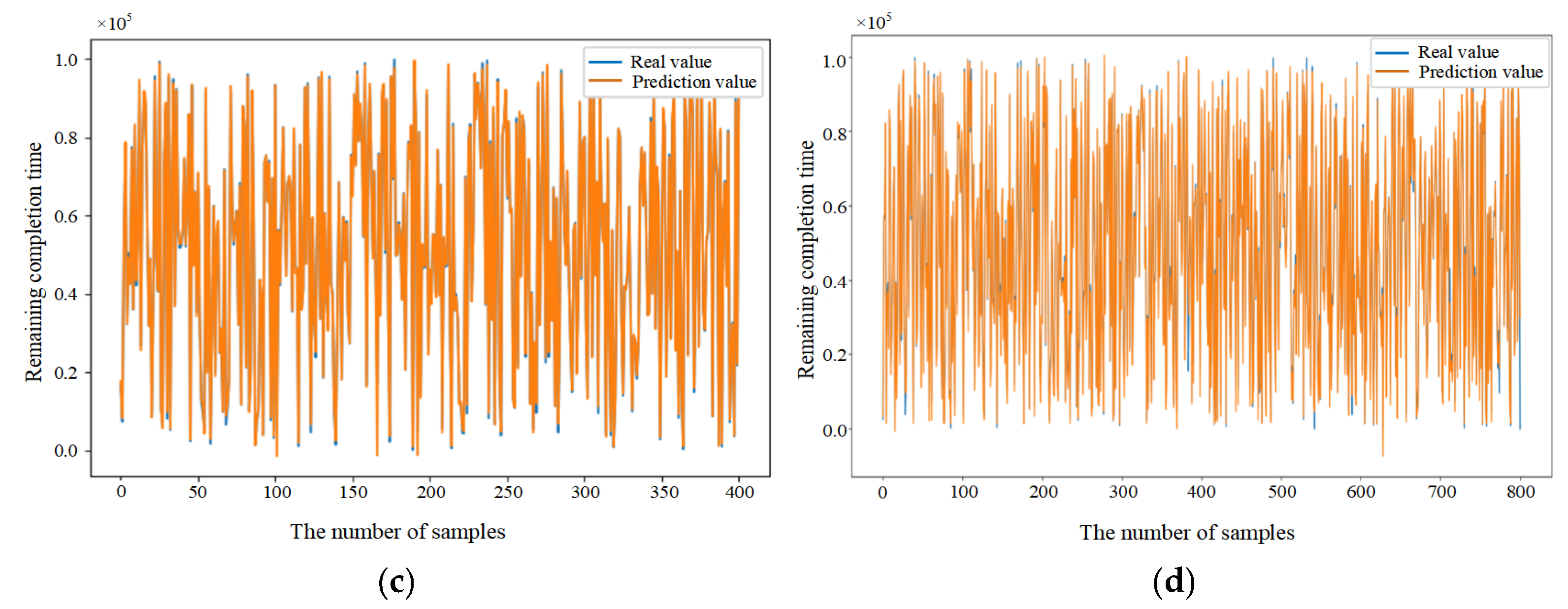
5.4. Performance Evaluation of Predictive Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruschel, E.; Rocha Loures, E.d.F.; Santos, E.A.P. Performance Analysis and Time Prediction in Manufacturing Systems. Comput. Ind. Eng. 2021, 151, 106972. [Google Scholar] [CrossRef]
- Mi Dahlgaard Park, S.; Dadfar, H.; Brege, S.; Sarah Ebadzadeh Semnani, S. Customer Involvement in Service Production, Delivery and Quality: The Challenges and Opportunities. Int. J. Qual. Serv. Sci. 2013, 5, 46–65. [Google Scholar] [CrossRef]
- Du, N.H.; Long, N.H.; Ha, K.N.; Hoang, N.V.; Huong, T.T.; Tran, K.P. Trans-Lighter: A Light-Weight Federated Learning-Based Architecture for Remaining Useful Lifetime Prediction. Comput. Ind. 2023, 148, 103888. [Google Scholar] [CrossRef]
- Rokoss, A.; Syberg, M.; Tomidei, L.; Hülsing, C.; Deuse, J.; Schmidt, M. Case Study on Delivery Time Determination Using a Machine Learning Approach in Small Batch Production Companies. J. Intell. Manuf. 2024, 35, 3937–3958. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, J.; Jiang, S.; Li, Y.; Long, T. A Novel Completion Status Prediction for the Aircraft Mixed-Model Assembly Lines: A Study in Dynamic Bayesian Networks. Adv. Eng. Inform. 2024, 62, 102701. [Google Scholar] [CrossRef]
- Shi, X.; Guo, W.; Wang, J.; Li, G.; Lu, H. Compilation of Load Spectrum of Loader Working Device and Application in Fatigue Life Prediction. Sensors 2025, 25, 5585. [Google Scholar] [CrossRef]
- Chen, T.; Wang, Y.-C. A Two-Stage Explainable Artificial Intelligence Approach for Classification-Based Job Cycle Time Prediction. Int. J. Adv. Manuf. Technol. 2022, 123, 2031–2042. [Google Scholar] [CrossRef]
- Liu, J.; Du, Y.; Wang, J.; Tang, X. A Large Kernel Convolutional Neural Network with a Noise Transfer Mechanism for Real-Time Semantic Segmentation. Sensors 2025, 25, 5357. [Google Scholar] [CrossRef]
- Lin, M.; Ye, Q.; Na, S.; Qin, D.; Gao, X.; Liu, Q. FDBRP: A Data–Model Co-Optimization Framework Towards Higher-Accuracy Bearing RUL Prediction. Sensors 2025, 25, 5347. [Google Scholar] [CrossRef]
- Uyanık, G.K.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia–Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Gansterer, M. Aggregate Planning and Forecasting in Make-to-Order Production Systems. Int. J. Prod. Econ. 2015, 170, 521–528. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q.; Liu, A.; Kusiak, A. Data-Driven Smart Manufacturing. J. Manuf. Syst. 2018, 48, 157–169. [Google Scholar] [CrossRef]
- Saberi, S.; Yusuff, R.M. Neural Network Application in Predicting Advanced Manufacturing Technology Implementation Performance. Neural Comput. Appl. 2012, 21, 1191–1204. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, M.; Cheng, T.C.E.; Wu, C.-C.; Cheng, S.-R. Four Single-Machine Scheduling Problems Involving Due Date Determination Decisions. Inf. Sci. 2013, 251, 164–181. [Google Scholar] [CrossRef]
- Chakravorty, S.S.; Atwater, J.B. Bottleneck Management: Theory and Practice. Prod. Plan. Control 2006, 17, 441–447. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, P. Deep Neural Networks Based Order Completion Time Prediction by Using Real-Time Job Shop RFID Data. J. Intell. Manuf. 2019, 30, 1303–1318. [Google Scholar] [CrossRef]
- Burggräf, P.; Wagner, J.; Koke, B.; Steinberg, F. Approaches for the Prediction of Lead Times in an Engineer to Order Environment—A Systematic Review. IEEE Access 2020, 8, 142434–142445. [Google Scholar] [CrossRef]
- Hsu, S.Y.; Sha, D.Y. Due Date Assignment Using Artificial Neural Networks under Different Shop Floor Control Strategies. Int. J. Prod. Res. 2004, 42, 1727–1745. [Google Scholar] [CrossRef]
- Vinod, V.; Sridharan, R. Simulation Modeling and Analysis of Due-Date Assignment Methods and Scheduling Decision Rules in a Dynamic Job Shop Production System. Int. J. Prod. Econ. 2011, 129, 127–146. [Google Scholar] [CrossRef]
- Brahimi, N.; Aouam, T.; Aghezzaf, E.-H. Integrating Order Acceptance Decisions with Flexible Due Dates in a Production Planning Model with Load-Dependent Lead Times. Int. J. Prod. Res. 2015, 53, 3810–3822. [Google Scholar] [CrossRef]
- Wang, H.; Peng, T.; Brintrup, A.; Wuest, T.; Tang, R. Dynamic Job Shop Scheduling Based on Order Remaining Completion Time Prediction. In Advances in Production Management Systems. Smart Manufacturing and Logistics Systems: Turning Ideas into Action; Kim, D.Y., von Cieminski, G., Romero, D., Eds.; Springer Nature: Cham, Switzerland, 2022; pp. 425–433. [Google Scholar]
- Choueiri, A.C.; Sato, D.M.V.; Scalabrin, E.E.; Santos, E.A.P. An Extended Model for Remaining Time Prediction in Manufacturing Systems Using Process Mining. J. Manuf. Syst. 2020, 56, 188–201. [Google Scholar] [CrossRef]
- Huang, J.; Chang, Q.; Arinez, J. Product Completion Time Prediction Using A Hybrid Approach Combining Deep Learning and System Model. J. Manuf. Syst. 2020, 57, 311–322. [Google Scholar] [CrossRef]
- Ahmed, T.; Hossain, S.M.; Hossain, M.d.A. Reducing Completion Time and Optimizing Resource Use of Resource-Constrained Construction Operation by Means of Simulation Modeling. Int. J. Constr. Manag. 2021, 21, 404–415. [Google Scholar] [CrossRef]
- Neu, D.A.; Lahann, J.; Fettke, P. A Systematic Literature Review on State-of-the-Art Deep Learning Methods for Process Prediction. Artif. Intell. Rev. 2022, 55, 801–827. [Google Scholar] [CrossRef]
- Meidan, Y.; Lerner, B.; Rabinowitz, G.; Hassoun, M. Cycle-Time Key Factor Identification and Prediction in Semiconductor Manufacturing Using Machine Learning and Data Mining. IEEE Trans. Semicond. Manuf. 2011, 24, 237–248. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Jana, C.; Pamucar, D.; Pedrycz, W. A Comprehensive Assessment of Machine Learning Models for Predictive Maintenance Using a Decision-Making Framework in the Industrial Sector. Alex. Eng. J. 2025, 120, 561–583. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.-C.; Chao, C.-C.; Huang, H.-J.; Wang, Y.-T.; Hsieh, K.-T. A Real-Time Diagnostic System Using a Long Short-Term Memory Model with Signal Reshaping Technology for Ship Propellers. Sensors 2025, 25, 5465. [Google Scholar] [CrossRef]
- Verenich, I.; Dumas, M.; Rosa, M.L.; Maggi, F.M.; Teinemaa, I. Survey and Cross-Benchmark Comparison of Remaining Time Prediction Methods in Business Process Monitoring. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–34. [Google Scholar] [CrossRef]
- Chen, T. A Hybrid Fuzzy-Neural Approach to Job Completion Time Prediction in a Semiconductor Fabrication Factory. Neurocomputing 2008, 71, 3193–3201. [Google Scholar] [CrossRef]
- Backus, P.; Janakiram, M.; Mowzoon, S.; Runger, C.; Bhargava, A. Factory Cycle-Time Prediction with a Data-Mining Approach. IEEE Trans. Semicond. Manuf. 2006, 19, 252–258. [Google Scholar] [CrossRef]
- Chien, C.-F.; Hsu, C.-Y.; Hsiao, C.-W. Manufacturing Intelligence to Forecast and Reduce Semiconductor Cycle Time. J. Intell. Manuf. 2012, 23, 2281–2294. [Google Scholar] [CrossRef]
- Lin, T.; Song, L.; Cui, L.; Wang, H. Advancing RUL Prediction in Mechanical Systems: A Hybrid Deep Learning Approach Utilizing Non-Full Lifecycle Data. Adv. Eng. Inform. 2024, 61, 102524. [Google Scholar] [CrossRef]
- Liu, C.-L.; Su, H.-C. Temporal Learning in Predictive Health Management Using Channel-Spatial Attention-Based Deep Neural Networks. Adv. Eng. Inform. 2024, 62, 102604. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, J.; Qin, S.; Zhang, K.; Wang, S.; Ding, G. A Multi-Target Regression-Based Method for Multiple Orders Remaining Completion Time Prediction in Discrete Manufacturing Workshops. Measurement 2025, 242, 116231. [Google Scholar] [CrossRef]
- Ding, K.; Jiang, P. RFID-Based Production Data Analysis in an IoT-Enabled Smart Job-Shop. IEEECAA J. Autom. Sin. 2018, 5, 128–138. [Google Scholar] [CrossRef]
- Fang, W.; Guo, Y.; Liao, W.; Ramani, K.; Huang, S. Big Data Driven Jobs Remaining Time Prediction in Discrete Manufacturing System: A Deep Learning-Based Approach. Int. J. Prod. Res. 2020, 58, 2751–2766. [Google Scholar] [CrossRef]
- Liu, D.; Guo, Y.; Huang, S.; Fang, W.; Tian, X. A Stacking Denoising Auto-Encoder with Sample Weight Approach for Order Remaining Completion Time Prediction in Complex Discrete Manufacturing Workshop. Int. J. Prod. Res. 2023, 61, 3246–3259. [Google Scholar] [CrossRef]
- Yuan, M.; Li, Z.; Zhang, C.; Zheng, L.; Mao, K.; Pei, F. Research on Real-Time Prediction of Completion Time Based on AE-CNN-LSTM. Comput. Ind. Eng. 2023, 185, 109677. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, H.; Tang, D.; Nie, Q.; Li, S.; Zhang, Y.; Liu, X. A Transfer Learning CNN-LSTM Network-Based Production Progress Prediction Approach in IIoT-Enabled Manufacturing. Int. J. Prod. Res. 2023, 61, 4045–4068. [Google Scholar] [CrossRef]
- Wang, C.; Du, W.; Zhu, Z.; Yue, Z. The Real-Time Big Data Processing Method Based on LSTM or GRU for the Smart Job Shop Production Process. J. Algorithms Comput. Technol. 2020, 14, 1748302620962390. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Wang, X. A Data Driven Cycle Time Prediction With Feature Selection in a Semiconductor Wafer Fabrication System. IEEE Trans. Semicond. Manuf. 2018, 31, 173–182. [Google Scholar] [CrossRef]
- Mirshekarian, S.; Šormaz, D.N. Correlation of Job-Shop Scheduling Problem Features with Scheduling Efficiency. Expert Syst. Appl. 2016, 62, 131–147. [Google Scholar] [CrossRef]



| Feature Type | Feature Description |
|---|---|
| Features of WIP | The number of operations Ni required for WIP i |
| The total processing time Ti of WIP i | |
| The longest processing time Tdi required for work in progress i on machine d | |
| Quality status Qi of WIP i | |
| The sum of the waiting times Wti of machine m on the processing path of WIP i | |
| The total quantity of WIP Si | |
| Work in process i completes processing process route Ri | |
| Features of machines | Processed part Pi on machine d |
| The number of parts to be processed Cdi queued up on machine d | |
| The total number of jobs Td currently being processed on machines 1, …, d | |
| The total remaining workload Rd of the machine 1, …, d processing operation | |
| The total processing time Td of machine 1, …, d | |
| Features of orders | Order O status So before arriving at the workshop |
| Priority Po of order O | |
| Quantity per order Os | |
| Order 1, …, n total workload On | |
| Average circulation time Ft of orders 1, …, n | |
| The sum of remaining processing times Ot for all orders in the workshop |
| Part Number | Part Type | Process Route | Processing Time (s) |
|---|---|---|---|
| 1 | Pipe | Lathing-Drilling-Grinding | 26-15-12 |
| 2 | Shaft | Lathing-Milling-Grinding | 18-16-12 |
| 3 | End cover | Machining center-Grinding | 26-28 |
| 4 | Plate | Machining center-Drilling-Grinding | 30-26-29 |
| 5 | Bracket | Machining center-Milling-Grinding | 24-19-27 |
| Model | Parameters | Value |
|---|---|---|
| CNN–BiLSTM–Attention | Number of convolution kernels in the first convolutional layer | 256 |
| Number of convolution kernels in the second convolutional layer | 256 | |
| Number of neurons in the BiLSTM layer | 128 | |
| Number of neurons in the first fully connected layer | 128 | |
| Number of neurons in the second fully connected layer | 1 | |
| Number of iterations | 1000 | |
| Learning rate | 0.001 | |
| Dropout rate | 0.2 | |
| Activation_CNN | ReLU | |
| Activation_BiLSTM | tanh | |
| Activation_Attention | tanh |
| Category | Data Characterization | Data Examples |
|---|---|---|
| WIP status | Number of processes | 2, 3, 2, 2, 3, … |
| Total processing time | 53, 46, 70, 54, 46, 85, … | |
| Maximum processing time | 26, 28, 30, 36, 41, … | |
| Product quality status | 0, 0, 0, 3, 0, 1, … | |
| Process route | 2, 3, 2, 3, 3, 2, … | |
| Waiting time | 12, 20, 14, 16, 36, … | |
| Total WIP | 252, 160, 350, 340, 150, … | |
| Machine status | Waiting queue length (per machine) | 3, 2, 2, 1, 0, 5, … |
| Remaining processing tasks | 10, 12, 8, 6, 13, … | |
| Total processing time | 230, 195, 250, 180, … | |
| Current state | 0, 0, 3, 1, 1, 0, 2, … | |
| Order status | Number of orders | 20, 15, 30, 20, … |
| Number of parts per order | 8, 10, 12, 15, 30, … | |
| Order priority | 1, 2, 3, 1, 1, … |
| Manufacturing Setting | Order | Part | Number |
|---|---|---|---|
| Manufacturing Setting 1 | Order 1 | Pipe | 50 |
| Order 2 | Pipe | 30 | |
| Order 3 | Pipe | 40 | |
| Manufacturing Setting 2 | Order 4 | Shaft | 60 |
| Order 5 | Shaft | 20 | |
| Order 6 | Shaft | 30 | |
| Manufacturing Setting 3 | Order 7 | End cover | 50 |
| Order 8 | End cover | 40 | |
| Order 9 | End cover | 40 |
| Model | R2 | MAE | RMSE | MAPE |
|---|---|---|---|---|
| DBN | 0.635 | 0.022 | 0.215 | 53.274% |
| BP | 0.386 | 0.351 | 0.362 | 133.413% |
| BiLSTM | 0.612 | 0.024 | 0.183 | 44.116% |
| CNN | 0.469 | 0.229 | 0.268 | 114.086% |
| CNN-LSTM | 0.728 | 0.0216 | 0.135 | 52.426% |
| CNN-BiLSTM | 0.967 | 0.015 | 0.061 | 21.898% |
| CNN–BiLSTM–Attention | 0.983 | 0.011 | 0.057 | 17.352% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Wang, L.; Liu, C.; Zhang, Z.; Tang, D. Probing a CNN–BiLSTM–Attention-Based Approach to Solve Order Remaining Completion Time Prediction in a Manufacturing Workshop. Sensors 2025, 25, 6480. https://doi.org/10.3390/s25206480
Chen W, Wang L, Liu C, Zhang Z, Tang D. Probing a CNN–BiLSTM–Attention-Based Approach to Solve Order Remaining Completion Time Prediction in a Manufacturing Workshop. Sensors. 2025; 25(20):6480. https://doi.org/10.3390/s25206480
Chicago/Turabian StyleChen, Wei, Liping Wang, Changchun Liu, Zequn Zhang, and Dunbing Tang. 2025. "Probing a CNN–BiLSTM–Attention-Based Approach to Solve Order Remaining Completion Time Prediction in a Manufacturing Workshop" Sensors 25, no. 20: 6480. https://doi.org/10.3390/s25206480
APA StyleChen, W., Wang, L., Liu, C., Zhang, Z., & Tang, D. (2025). Probing a CNN–BiLSTM–Attention-Based Approach to Solve Order Remaining Completion Time Prediction in a Manufacturing Workshop. Sensors, 25(20), 6480. https://doi.org/10.3390/s25206480







