Classification and Clustering of Fiber Break Events in Thermoset CFRP Using Acoustic Emission and Machine Learning
Abstract
1. Introduction
2. Background
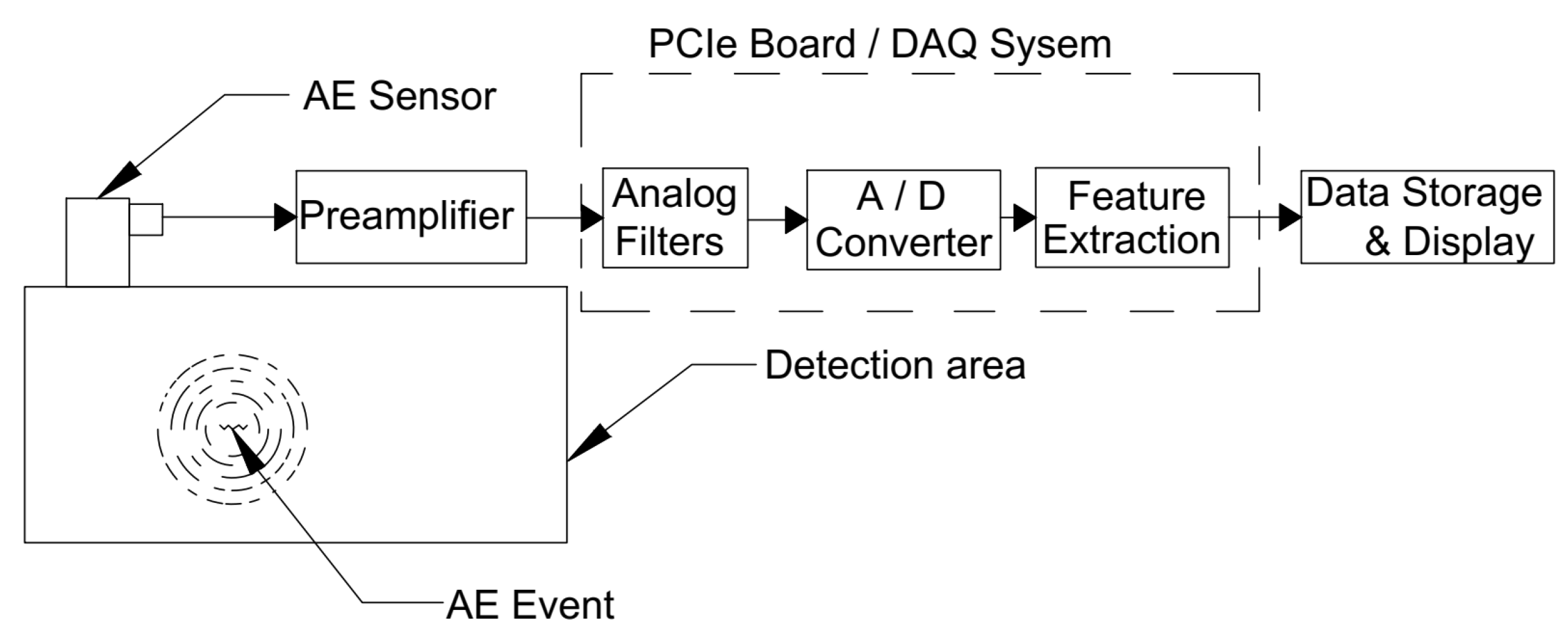
2.1. Acoustic Emission System
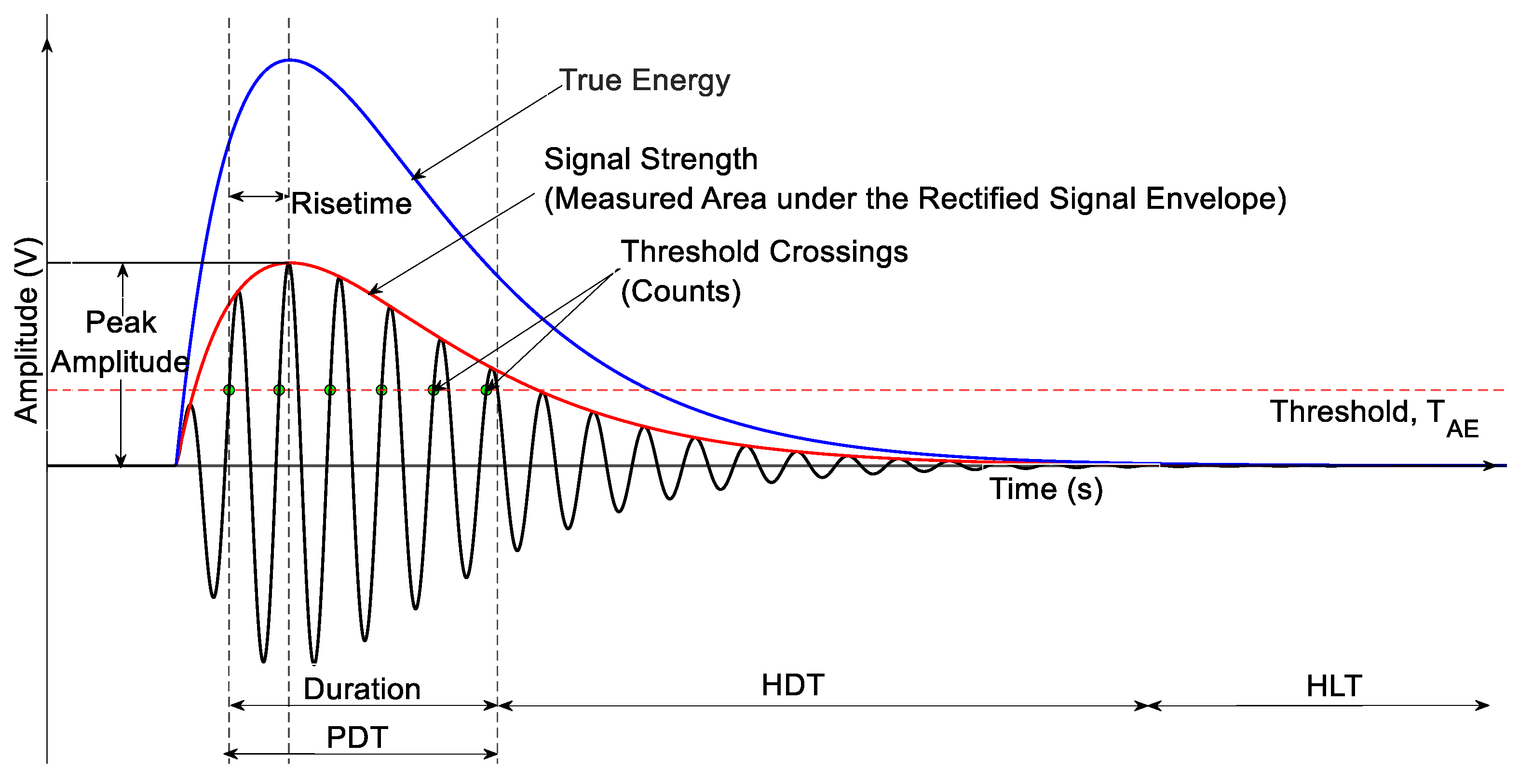
2.1.1. Conventional AE Parameters
- Threshold: Refers to the minimum amplitude level (usually expressed in decibels, dB) that an acoustic signal must exceed to be recognized and recorded by the AE system.
- Peak detection time (PDT): Defines the time window after the initial threshold crossing within which the system detects the peak amplitude of the AE hit.
- Hit definition time (HDT): Defines the minimum duration that the AE signal must remain below the threshold before the system considers the current AE hit to have ended.
- Hit lock time (HLT): Defines the fixed period after the end of a hit during which no new hits will be recognized, even if the signal exceeds the threshold again.
- Hit start: Sample point before the first point over threshold (V ≥ TAE).
- Hit end: Sample point after the last point over the threshold. (V < TAE).
- Duration: The time between the hit start and the hit end sample points.
- Counts: Refer to the number of times the AE signal crosses the set threshold level during a single AE hit.
- Amplitude: It is the maximum amplitude of the signal, detected within the PDT at the sensor, converted to dB, given by
- 6.
- Rise time: Defines the time from the hit start to the max amplitude sample point.
- 7.
- Counts to peak: Number of threshold crossings that occur between hit start and peak amplitude.
- 8.
- Signal strength: Defines the area under the rectified signal. It is given by the measured area under the rectified signal envelope (MARSE).
- 9.
- Absolute energy: Defines the true energy of the signal on a 10 k Ohm resistor computed at the sensor.
2.1.2. AE Waveforms and Failure Events in Composites
2.2. Machine Learning Algorithms
2.3. Performance Evaluation
2.3.1. Cross-Validation
2.3.2. Confusion Matrix
2.3.3. Precision
2.3.4. Recall
2.3.5. Accuracy
2.3.6. F1 Score
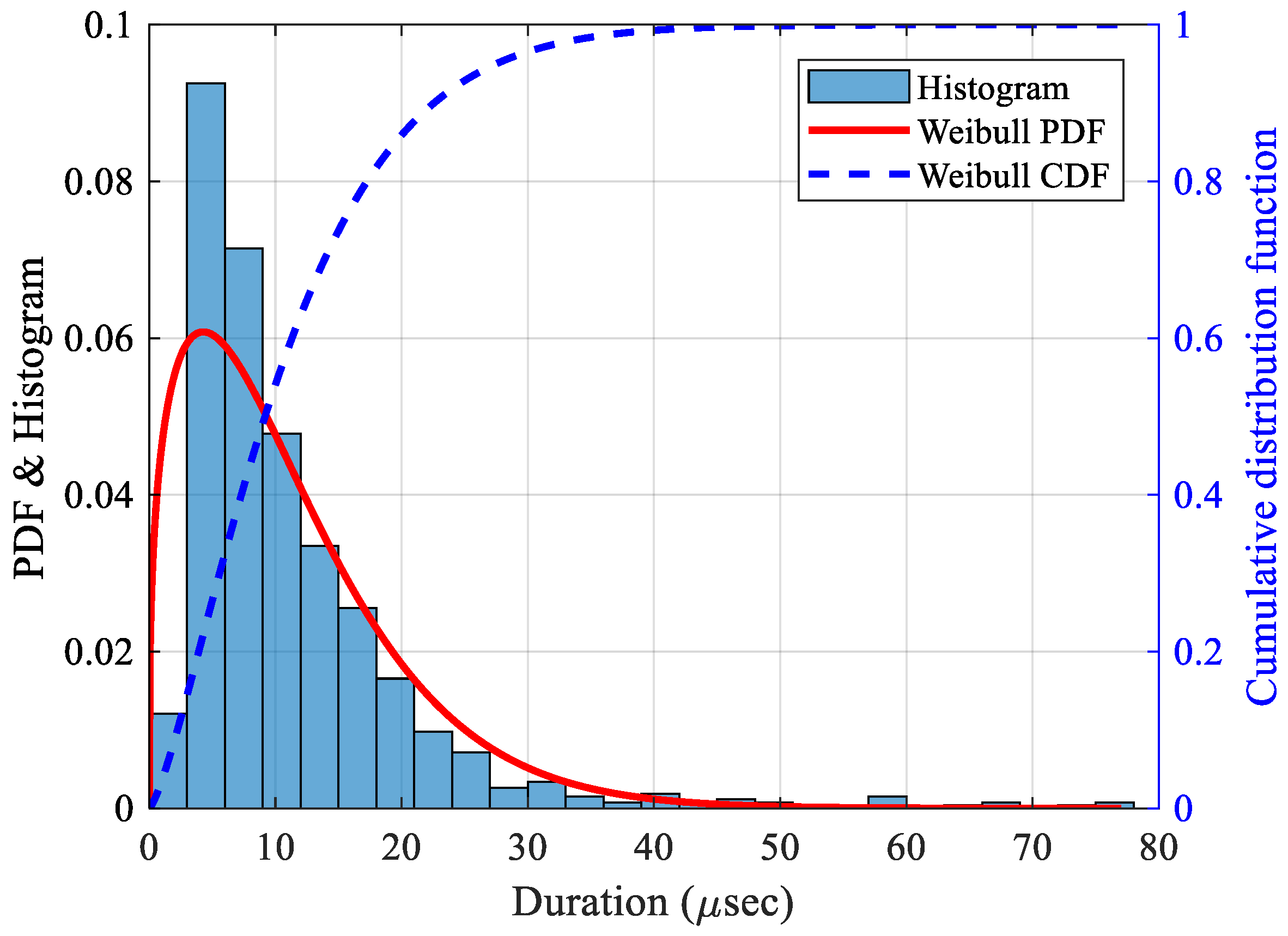
2.4. Cross-Correlation
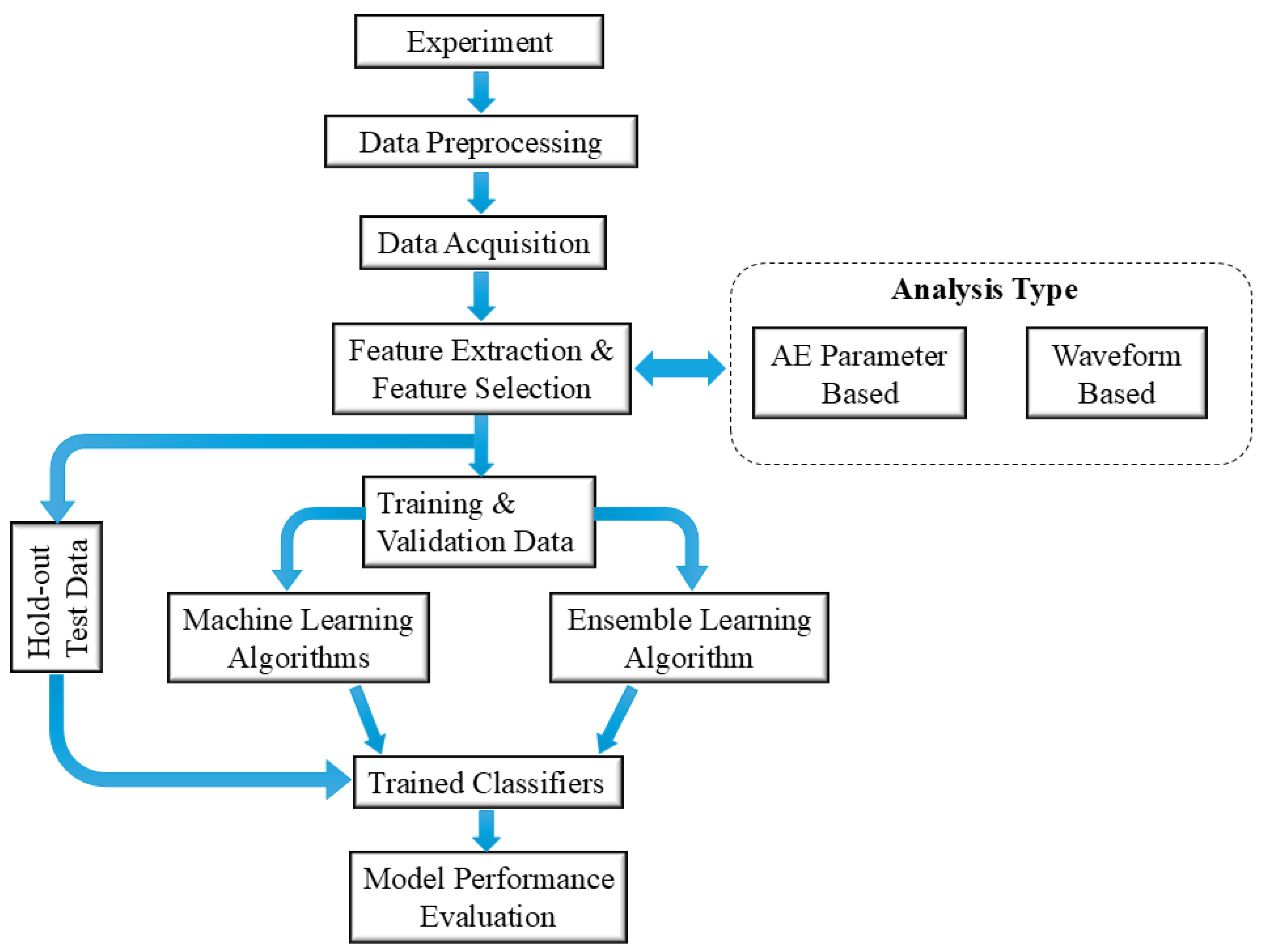
3. Materials and Methods
3.1. Experimental Procedures
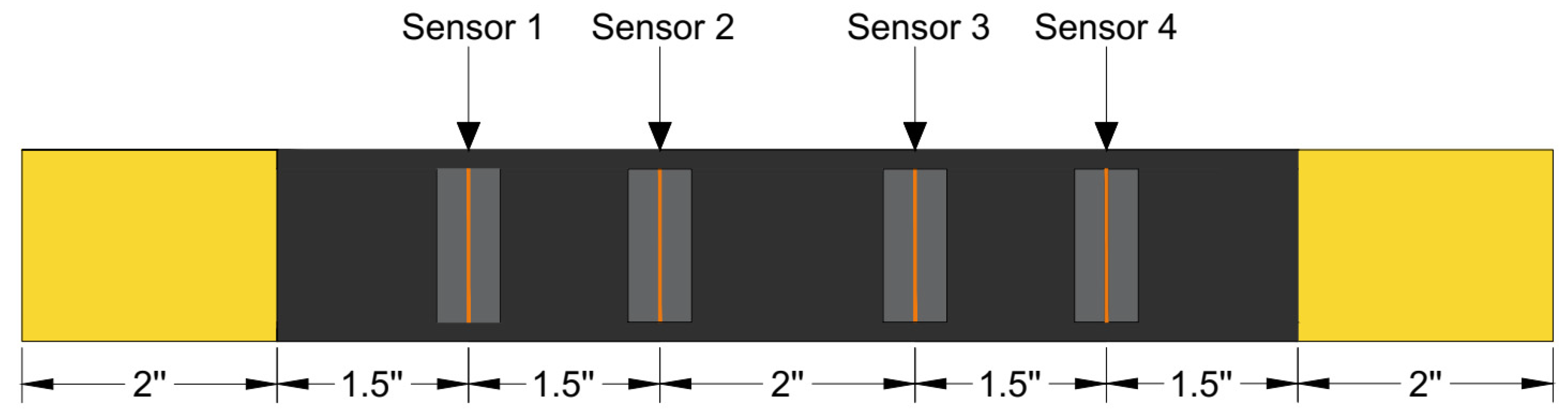
3.1.1. Sample Preparation
3.1.2. Instrumentation
3.1.3. Loading
3.2. Signal Preprocessing and Data Acquisition
3.3. Feature Extraction
3.3.1. Parameters-Based Feature Extraction
3.3.2. Waveform-Based Feature Extraction
3.4. Feature Selection
4. Results and Discussion
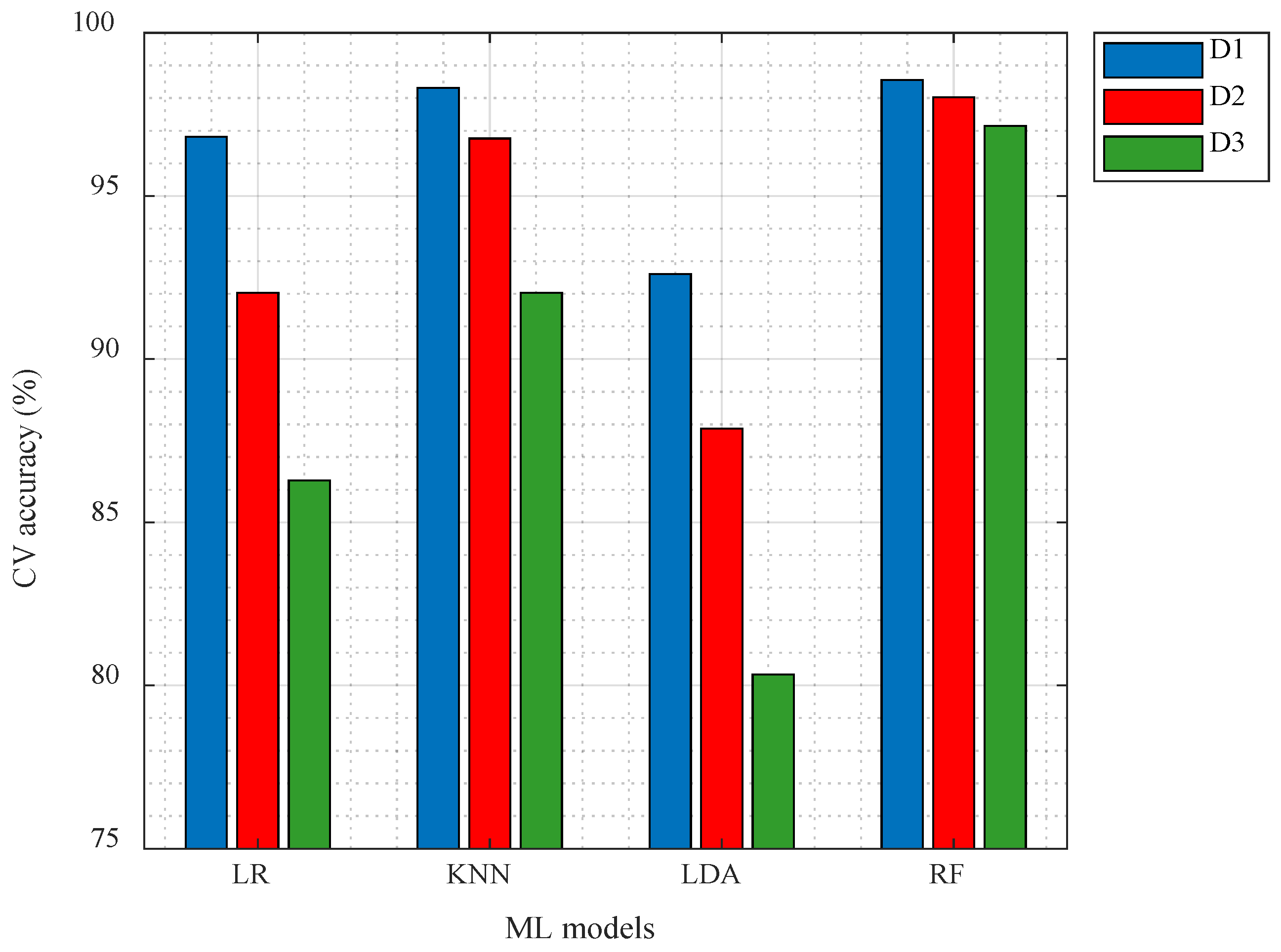
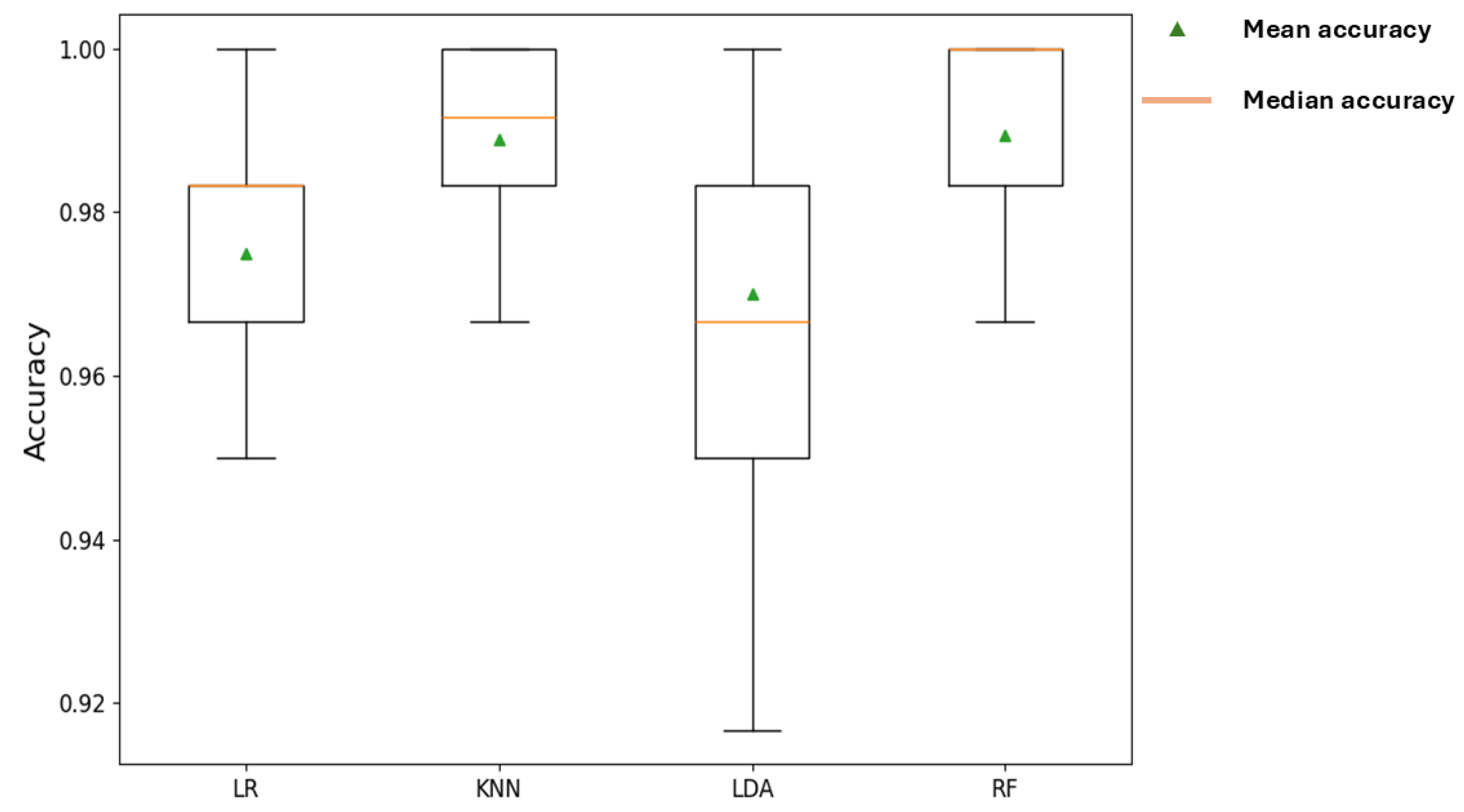
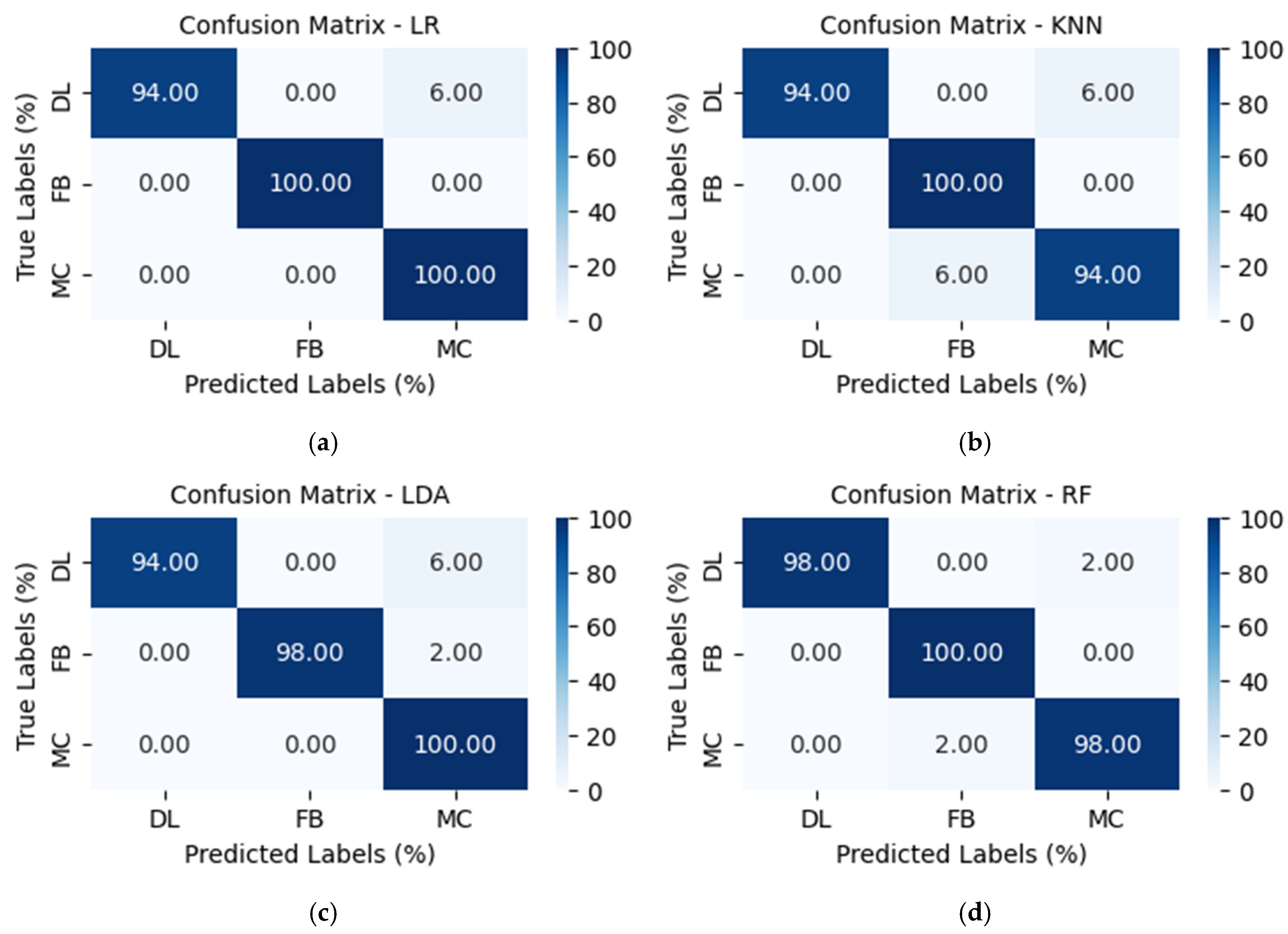
4.1. Classification Performance Using Conventional AE Parameters
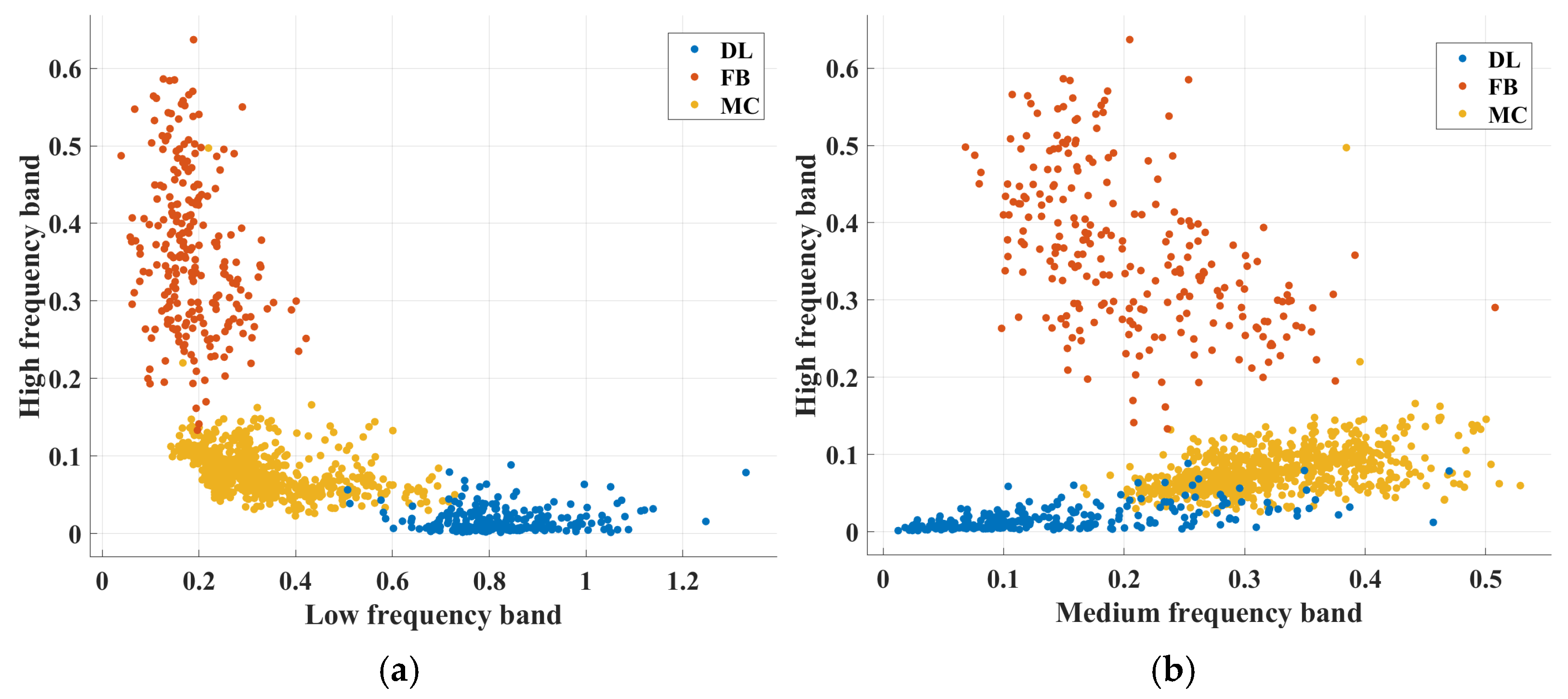
4.2. Classification Performance Using Waveform Analysis
4.3. Model Implementation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rahmat Rabi, R.; Monti, G. Genetic Algorithm-Based Model Updating in a Real-Time Digital Twin for Steel Bridge Monitoring. Appl. Sci. 2025, 15, 4074. [Google Scholar] [CrossRef]
- Monti, G.; Rabi, R.R.; Marella, L.; Proietti, S.T. Data-driven decision support system for the safety management of railway bridge networks. Reliab. Eng. Syst. Saf. 2025, 262, 111202. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Leman, Z.; Baharudin, B.T.H.T. A review of the application of acoustic emission technique in engineering. Struct. Eng. Mech. 2015, 54, 1075–1095. [Google Scholar] [CrossRef]
- Almeida, R.S.; Magalhães, M.D.; Nurul Karim, M.; Tushtev, K.; Rezwan, K. Identifying damage mechanisms of composites by acoustic emission and supervised machine learning. Mater. Des. 2023, 227, 111745. [Google Scholar] [CrossRef]
- Qiao, S.; Huang, M.; Liang, Y.; Zhang, S.; Zhou, W. Damage mode identification in carbon/epoxy composite via machine learning and acoustic emission. Polym. Compos. 2023, 44, 2427–2440. [Google Scholar] [CrossRef]
- Kundu, A.; Sikdar, S.; Eaton, M.; Navaratne, R. A Generic Framework for Application of Machine Learning in Acoustic Emission-Based Damage Identification. In Proceedings of the 13th International Conference on Damage Assessment of Structures, Porto, Portugal, 9–10 July 2019; Wahab, M., Ed.; Lecture Notes in Mechanical Engineering. Springer: Singapore, 2020. [Google Scholar]
- Mohammed, B.Y.; Tan, C.K.; Wilcox, S.J.; Chong, A.Z. Damage Characterisation of Carbon Fibre Reinforced Composite Plate Using Acoustic Emission. Key Eng. Mater. 2013, 558, 184–194. [Google Scholar] [CrossRef]
- Xue, S.; Wang, J.; Liang, Y.; Ma, L.; Zhou, W. Indentation damage identification of carbon fiber composite laminates based on modal acoustic emission and machine learning. Polym. Compos. 2025, 46, 6944–6955. [Google Scholar] [CrossRef]
- Dabetwar, S.; Ekwaro-Osire, S.; Dias, J.P. Damage Classification of Composites Based on Analysis of Lamb Wave Signals Using Machine Learning. ASME J. Risk Uncertain. Part B 2021, 7, 011002. [Google Scholar] [CrossRef]
- Dabetwar, S.; Ekwaro-Osire, S.; Dias, J.P. Damage Classification of Composites Using Machine Learning. In Proceedings of the ASME 2019 International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019. Volume 13: Safety Engineering, Risk, and Reliability Analysis. [Google Scholar]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Application of different acoustic emission descriptors in damage assessment of fiber reinforced plastics: A comprehensive review. Eng. Fract. Mech. 2020, 235, 107083. [Google Scholar] [CrossRef]
- Yokozeki, T.; Aoki, T.; Ogasawara, T.; Ishikawa, T. Effects of layup angle and ply thickness on matrix crack interaction in contiguous plies of composite laminates. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1229–1235. [Google Scholar] [CrossRef]
- Kashtalyan, M.; Soutis, C. Stiffness and fracture analysis of laminated composites with off-axis ply matrix cracking. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1262–1269. [Google Scholar] [CrossRef]
- Tessema, A.; Ravindran, S.; Kidane, A. Gradual damage evolution and propagation in quasi-isotropic CFRC under quasi-static loading. Compos. Struct. 2017, 185, 186–192. [Google Scholar] [CrossRef]
- Masters, J.E.; Reifsnider, K.L. An Investigation of Cumulative Damage Development in Quasi-Isotropic Graphite/Epoxy Laminates. In Damage in Composite Materials: Basic Mechanisms, Accumulation, Tolerance, and Characterization; ASTM International: West Conshohocken, PA, USA, 1982. [Google Scholar]
- Skinner, T.D.; Datta, S.; Chattopadhyay, A.; Hall, A. Biaxial Fatigue Damage in Quasi Isotropic Laminates. In Proceedings of the AIAA 2020-0475, AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Ujjin, R.; Crosky, A.; Schmidt, L.; Kelly, D.; Li, R.; Carr, D. Damage Development During Pin Loading of a Hole in a Quasi-Isotropic Carbon Fibre Reinforced Epoxy Composite. In Proceedings of the Structural Integrity and Fracture International Conference (SIF’04), Brisbane, Australia, 26–29 September 2004. [Google Scholar]
- Beaumont, P.W.R.; Dimant, R.A.; Shercliff, H.R. Failure processes in composite materials: Getting physical. J. Mater. Sci. 2006, 41, 6526–6546. [Google Scholar] [CrossRef]
- Pradhan, B.; Kumar, N.V.; Rao, N.S. Stiffness degradation resulting from 90 ply cracking in angle-ply composite laminates. Compos. Sci. Technol. 1999, 59, 1543–1552. [Google Scholar] [CrossRef]
- Kumar, M.S.; Raghavendra, K.; Venkataswamy, M.A.; Ramachandra, H.V. Fractographic analysis of tensile failures of aerospace grade composites. Mater. Res. 2012, 15, 990–997. [Google Scholar] [CrossRef]
- Scott, A.; Mavrogordato, M.; Wright, P.; Sinclair, I.; Spearing, S. In situ fibre fracture measurement in carbon-epoxy laminates using high resolution computed tomography. Compos. Sci. Technol. 2011, 71, 1471–1477. [Google Scholar] [CrossRef]
- Gutkin, R.; Green, C.; Vangrattanachai, S.; Pinho, S.; Robinson, P.; Curtis, P. On acoustic emission for failure investigation in CFRP: Pattern recognition and peak frequency analyses. Mech. Syst. Signal Process. 2011, 25, 1393–1407. [Google Scholar] [CrossRef]
- Berthelot, J.; Rhazi, J. Acoustic Emission in Carbon Fibre Composites. Compos. Sci. Technol. 1990, 37, 411–428. [Google Scholar] [CrossRef]
- Valentin, D.; Bonniau, P.; Bunsell, A. Failure mechanism discrimination in carbon fibre-reinforced epoxy composites. Composites 1983, 14, 345–351. [Google Scholar] [CrossRef]
- De Groot, P.J.; Wijnen, P.A.; Janssen, R.B. Real-time frequency determination of acoustic emission for different fracture mechanisms in carbon/epoxy composites. Compos. Sci. Technol. 1995, 55, 405–412. [Google Scholar] [CrossRef]
- Godin, N.; Huguet, S.; Gaertner, R.; Salmon, L. Clustering of acoustic emission signals collected during tensile tests on unidirectional glass/polyester composite using supervised and unsupervised classifiers. NDT E Int. 2004, 37, 253–264. [Google Scholar] [CrossRef]
- Surgeon, M.; Wevers, M. Modal analysis of acoustic emission signals from CFRP laminates. NDT E Int. 1999, 32, 311–322. [Google Scholar] [CrossRef]
- Baker, C.; Morscher, G.N.; Pujar, V.V.; Lemanski, J.R. Transverse cracking in carbon fiber reinforced polymer composites: Modal acoustic emission and peak frequency analysis. Compos. Sci. Technol. 2015, 116, 26–32. [Google Scholar] [CrossRef]
- Minhaj, T.B.; Amevorku, R.D.; Chaudhary, B.B.; Rijal, M.; Sundaresan, M.J. Assessment of damage evolution in thermoplastic composite using acoustic emission and deep learning models. In Proceedings of the SPE ACCE, Novi, MI, USA, 4–6 September 2024. [Google Scholar]
- Smolnicki, M.; Duda, S.; Stabla, P.; Zielonka, P.; Lesiuk, G. Acoustic emission with machine learning in fracture of composites: Preliminary study. Arch. Civ. Mech. Eng. 2023, 23, 254. [Google Scholar] [CrossRef]
- Muir, C.; Swaminathan, B.; Almansour, A.S.; Sevener, K.; Smith, C.; Presby, M.; Kiser, J.D.; Pollock, T.M.; Daly, S. Damage mechanism identification in composites via machine learning and acoustic emission. npj Comput. Mater. 2021, 7, 95. [Google Scholar] [CrossRef]
- Nasiri, A.; Bao, J.; Mccleeary, D.; Louis, S.Y.M.; Huang, X.; Hu, J. Online Damage Monitoring of SiCf-SiCm Composite Materials Using Acoustic Emission and Deep Learning. IEEE Access 2019, 7, 140534–140541. [Google Scholar] [CrossRef]
- Gholizadeh, S. Damage Analysis and Prediction in Glass Fiber Using Acoustic Emission and Machine Learning. Res. Sq. Reinf. Polyest. Compos. 2022, 3, 131–141. [Google Scholar]
- Gholizadeh, S.; Leman, Z.; Baharudin, B.T.H.T. State-of-the-art ensemble learning and unsupervised learning in fatigue crack recognition of glass fiber reinforced polyester composite (GFRP) using acoustic emission. Ultrasonics 2023, 132, 106998. [Google Scholar] [CrossRef]
- Mohammadi, R.; Najafabadi, M.A.; Saeedifar, M.; Yousefi, J.; Minak, G. Correlation of acoustic emission with finite element predicted damages in open-hole tensile laminated composites. Compos. Part B Eng. 2017, 108, 427–435. [Google Scholar] [CrossRef]
- Whitlow, T.; Sundaresan, M. Clustering of Fiber-Break Related Events in Carbon Fiber Reinforced Polymer Composites Using Acoustic Emission. J. Acoust. Emiss. 2017, 34, 52–63. [Google Scholar]
- Mills-Dadson, B.; Asamene, K.; Whitlow, T.; Sundaresan, M. Acoustic Emissions from Damage Mechanisms in Composites. Struct. Health Monit. 2015, 2015. [Google Scholar] [CrossRef]
- Rijal, M.; Obie-Rolle, T.; Sundaresan, M. Monitoring Damage Evolution in Carbon/Epoxy and Carbon/Thermoplastic Composites Using Acoustic Emission Technique. In Proceedings of the International Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2023. [Google Scholar]
- Yu, P.; Liu, W.; Gu, C.; Cheng, X.; Fu, X. Flexible piezoelectric tactile sensor array for dynamic three-axis force measurement. Sensors 2016, 16, 819. [Google Scholar] [CrossRef]
- Grosse, C.U.; Ohtsu, M.; Aggelis, D.G.; Shiotani, T. Acoustic Emission Testing Basics for Research-Applications in Engineering, 2nd ed.; Springer: Cham, Switzerland, 2022; Available online: http://www.springer.com/series/15088 (accessed on 25 March 2022).
- Grosse, C.U.; Ohtsu, M. Acoustic Emission Testing: Basics for Research-Applications in Civil Engineering, 1st ed.; Springer: Cham, Switzerland; Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- Ono, K. Acoustic Emission in Materials Research—A Review. J. Acoust. Emiss. 2011, 29, 284–309. [Google Scholar]
- Pollock, A.A. Material Brittleness and the Energetics of Acoustic Emission; Proulx, T., Ed.; Springer: New York, NY, USA, 2011; pp. 73–79. [Google Scholar]
- Rao, P.S.; Hardiman, M.; O’Dowd, N.P.; Sebaey, T.A. Comparison of progressive damage between thermoset and thermoplastic CFRP composites under in-situ tensile loading. J. Compos. Mater. 2021, 55, 1473–1484. [Google Scholar] [CrossRef]
- Komai, K.; Minoshima, K.; Shibutani, T. Investigations of the fracture mechanism of carbon/epoxy compo-sites by AE signal analyses. JSME Int. J. Ser. 1 Solid Mech. Strength Mater. 1991, 34, 381–388. [Google Scholar]
- Ono, K. Acoustic Emission Behavior of Flawed Unidirectional Carbon Fiber-Epoxy Composites. J. Rein-Forced Plast. Compos. 1988, 7, 90–105. [Google Scholar] [CrossRef]
- Malolan, V.; Wuriti, G.; Gopal, A.S.; Thomas, T. Comparison of acoustic emission parameters for fiber breakage and de-lamination failure mechanisms in carbon epoxy composites. J. Eng. Technol. 2016, 8, 21–30. [Google Scholar][Green Version]
- Rijal, M.; Amoateng-Mensah, D.; Sundaresan, M.J. Finite Element Simulation of Acoustic Emissions from Different Failure Mechanisms in Composite Materials. Materials 2024, 24, 6085. [Google Scholar] [CrossRef]
- Asamene, K.; Hudson, L.; Sundaresan, M. Influence of attenuation on acoustic emission signals in carbon fiber reinforced polymer panels. Ultrasonics 2015, 59, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Hu, K.; Xie, J.; Guo, Y.; Wu, H. Robust scientific text classification using prompt tuning based on data augmentation with L2 regularization. Inf. Process. Manag. 2024, 61, 103531. [Google Scholar] [CrossRef]
- Musa, A.B. Comparative study on classification performance between support vector machine and logistic regression. Int. J. Mach. Learn. Cybern. 2012, 4, 13–24. [Google Scholar] [CrossRef]
- Uddin, S.; Haque, I.; Lu, H.; Moni, M.A.; Gide, E. Comparative performance analysis of K-nearest neighbour (KNN) algorithm and its different variants for disease prediction. Sci. Rep. 2022, 12, 6256. [Google Scholar] [CrossRef]
- Amini, M.; Rahmani, A. Machine learning process evaluating damage classification of composites. Int. J. Sci. Adv. Technol. 2023, 9, 240–250. [Google Scholar]
- Balakrishnama, S.; Ganapathiraju, A. Linear discriminant analysis–A brief tutorial. Inst. Signal Inf. Process. 1998, 18, 1–8. [Google Scholar]
- Tharwat, A.; Gaber, T.; Ibrahim, A.; Hassanien, A.E. Linear discriminant analysis: A detailed tutorial. AI Commun. 2017, 30, 169–190. [Google Scholar] [CrossRef]
- Liu, R.; Qiao, S.; Li, C.-L.; Ma, L.-H.; Zhou, W.; Li, Q. An acoustic emission based approach for damage pattern recognition in composite using linear discriminant analysis. Compos. Adv. Mater. 2024, 33, 26349833241244403. [Google Scholar] [CrossRef]
- Milad, A.; Hussein, S.H.; Khekan, A.R.; Rashid, M.; Al-Msari, H.; Tran, T.H. Development of ensemble machine learning approaches for designing fiber-reinforced polymer composite strain prediction model. Eng. Comput. 2022, 38, 3625–3637. [Google Scholar] [CrossRef]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation, Encyclopedia of Database Systems; Springer: Tempe, AZ, USA, 2009; pp. 532–538. [Google Scholar]
- Düntsch, I.; Gediga, G. Confusion matrices and rough set data analysis. J. Phys. Conf. Series 2019, 1229, 012055. [Google Scholar] [CrossRef]
- Eaton, M.; Pullin, R.; Holford, K.; Evans, S.; Featherston, C.; Rose, A. Use of macro fibre composite transducers as acoustic emission sensors. Remote Sens. 2009, 1, 68–79. [Google Scholar] [CrossRef]
- ASTM D3039/D3039M-08; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2017.
- Bhuiyan, Y.; Lin, B.; Giurgiutiu, V. Characterization of piezoelectric wafer active sensor for acoustic emission sensing. Ultrasonics 2019, 92, 35–49. [Google Scholar] [CrossRef]
- Mills-Dadson, B.; Tran, D.; Asamene, K.; Whitlow, T.; Sundaresan, M. Acoustic emission monitoring of unstable damage growth in CFRP composites under tension. In Proceedings of the AIP Conference Proceedings, Atlanta, GA, USA, 17–22 July 2016. [Google Scholar]
- Chormunge, S.; Jena, S. Correlation based feature selection with clustering for high dimensional data. J. Electr. Syst. Inf. Technol. 2018, 5, 542–549. [Google Scholar] [CrossRef]
- Biesiada, J.; Duch, W. Feature Selection for High-Dimensional Data—A Pearson Redundancy Based Filter; Kacprzyk, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 2, pp. 242–249. [Google Scholar]
- Jiang, D.; Lin, W.; Raghavan, N. A novel framework for semiconductor manufacturing final test yield classification using machine learning techniques. IEEE Access 2020, 8, 197885–197895. [Google Scholar] [CrossRef]
- Tareen, A.D.K.; Nadeem, M.S.A.; Kearfott, K.J.; Abbas, K.; Khawaja, M.A.; Rafique, M. Descriptive analysis and earthquake prediction using boxplot interpretation of soil radon time series data. Appl. Radiat. Isot. 2019, 154, 108861. [Google Scholar] [CrossRef] [PubMed]
- Gómez, Y.M.; Gallardo, D.I.; Marchant, C.; Sánchez, L.; Bourguignon, M. An In-Depth Review of the Weibull Model with a Focus on Various Parameterizations. Mathematics 2023, 12, 56. [Google Scholar] [CrossRef]
- Bunsell, A.R.; Thionnet, A. Quantifiable analysis of the failure of advanced carbon fibre composite structures leading to improved safety factors. Prog. Mater. Sci. 2022, 123, 100753. [Google Scholar] [CrossRef]

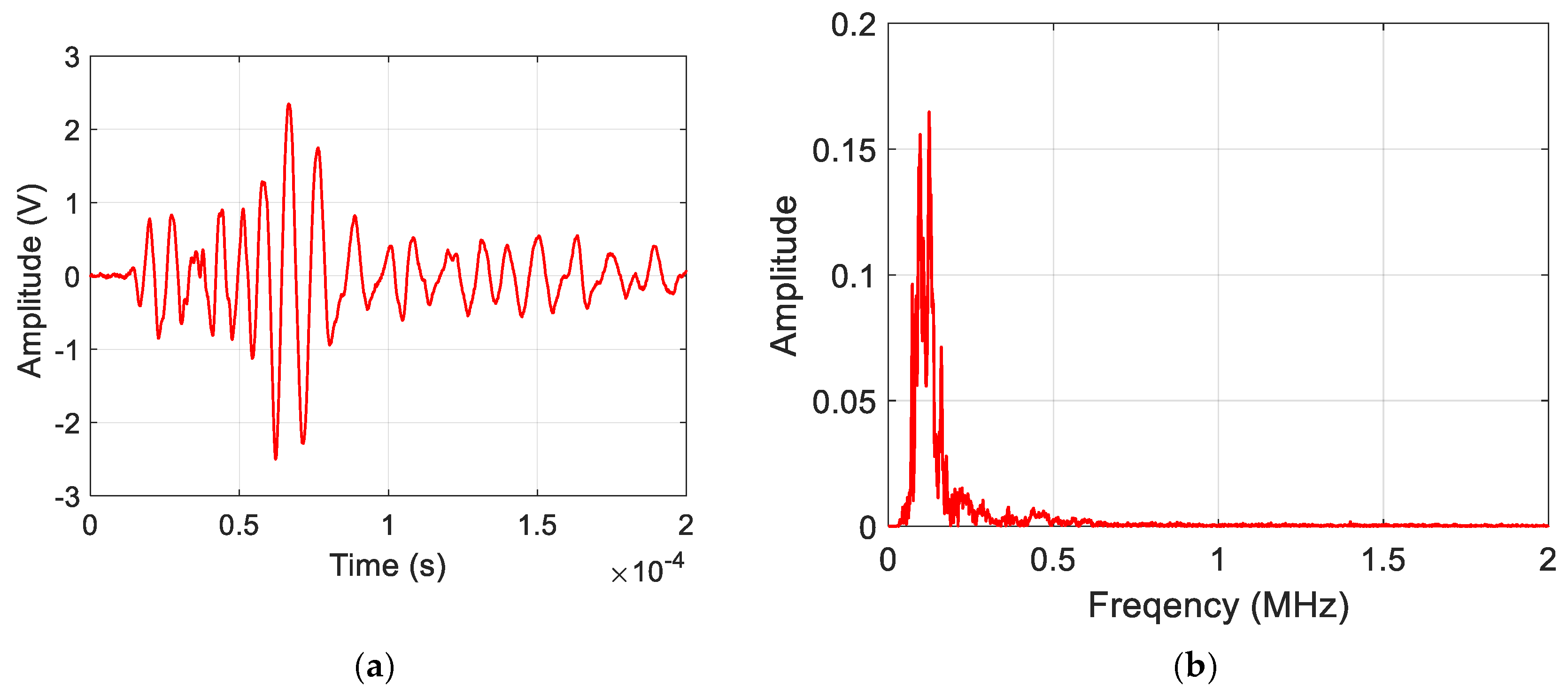
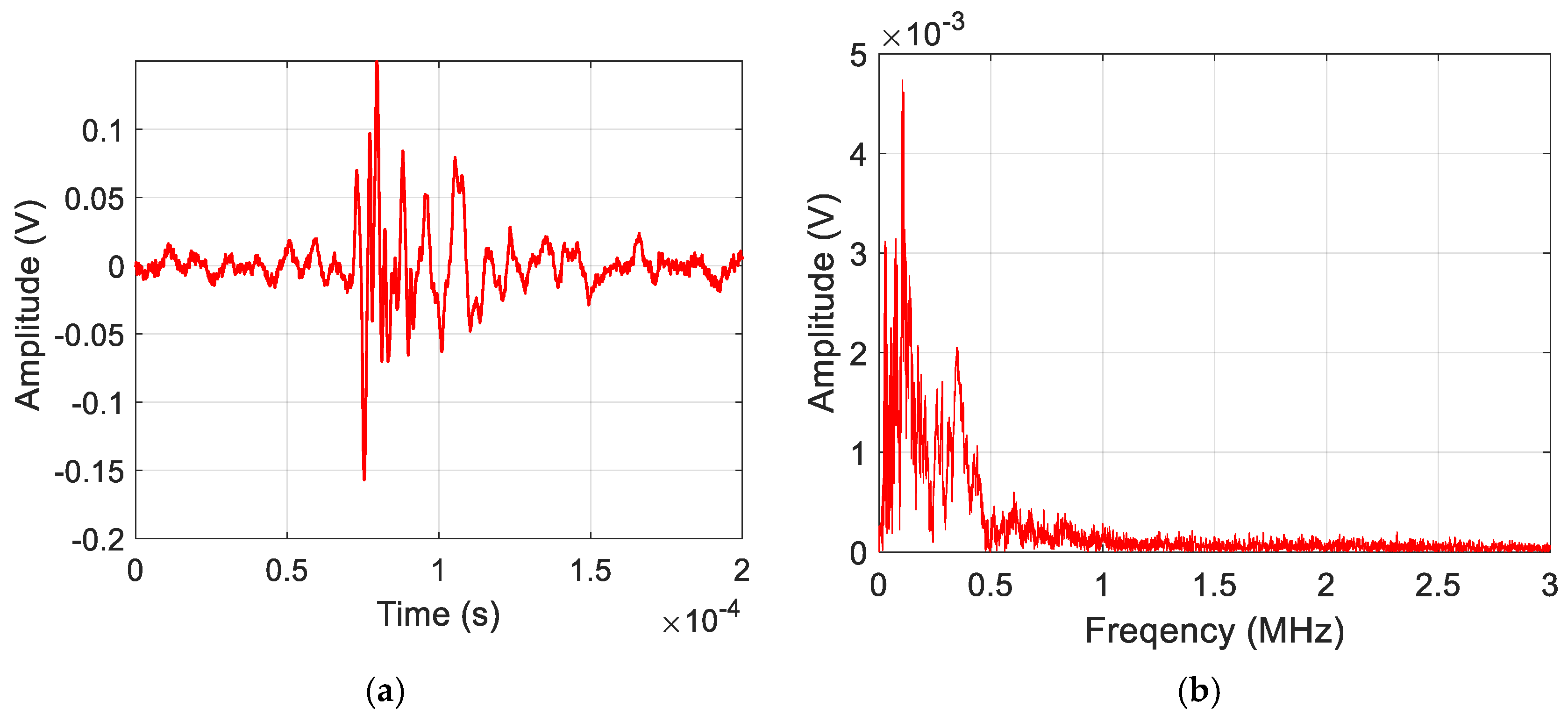
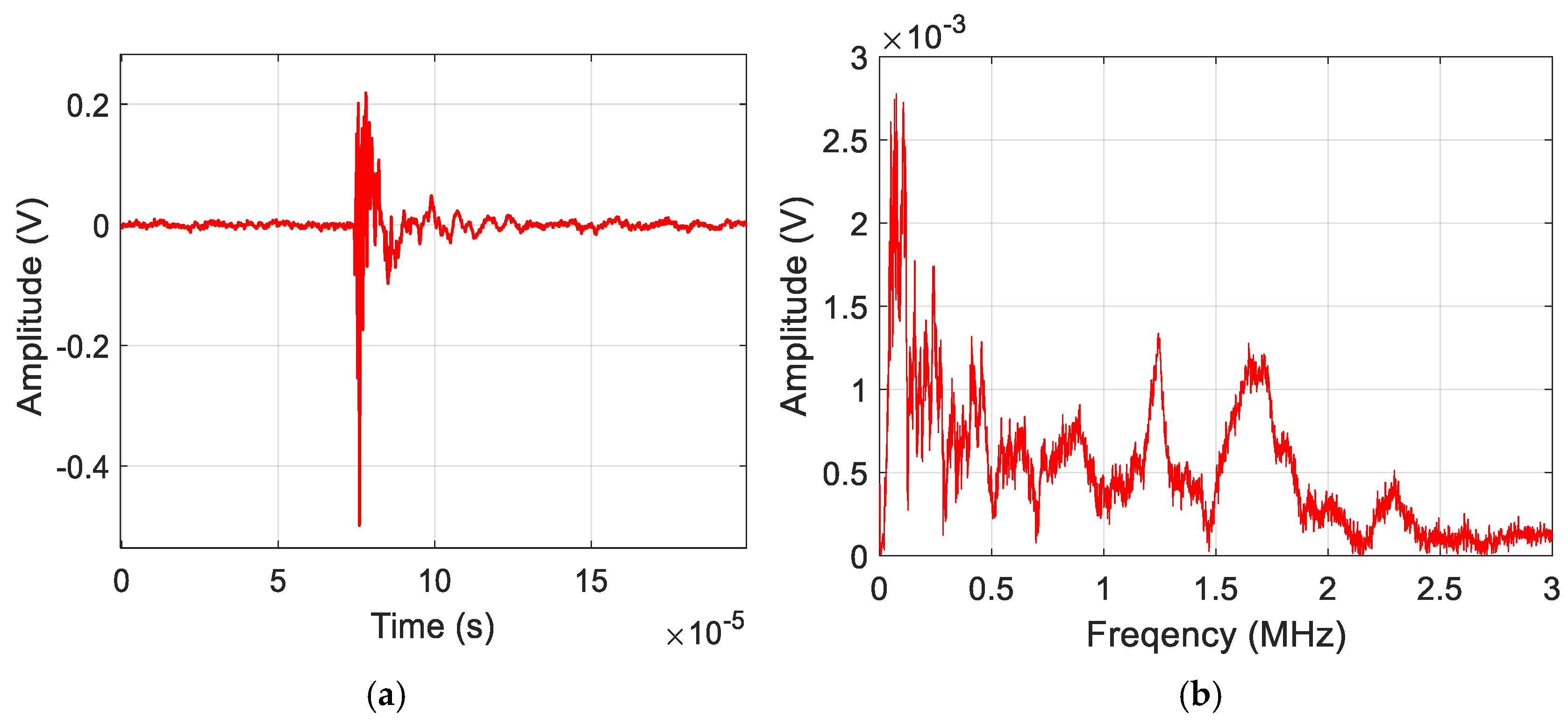
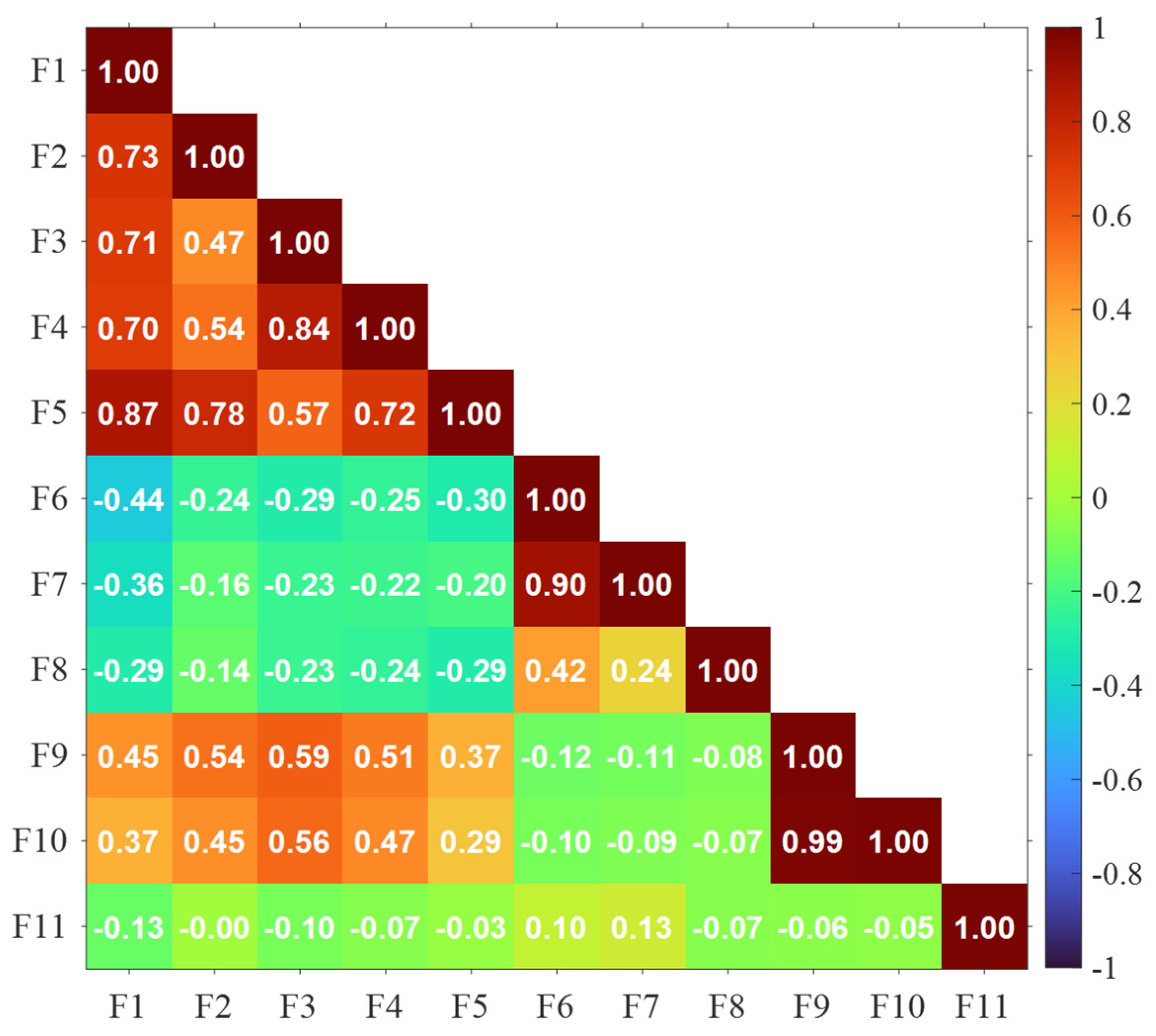
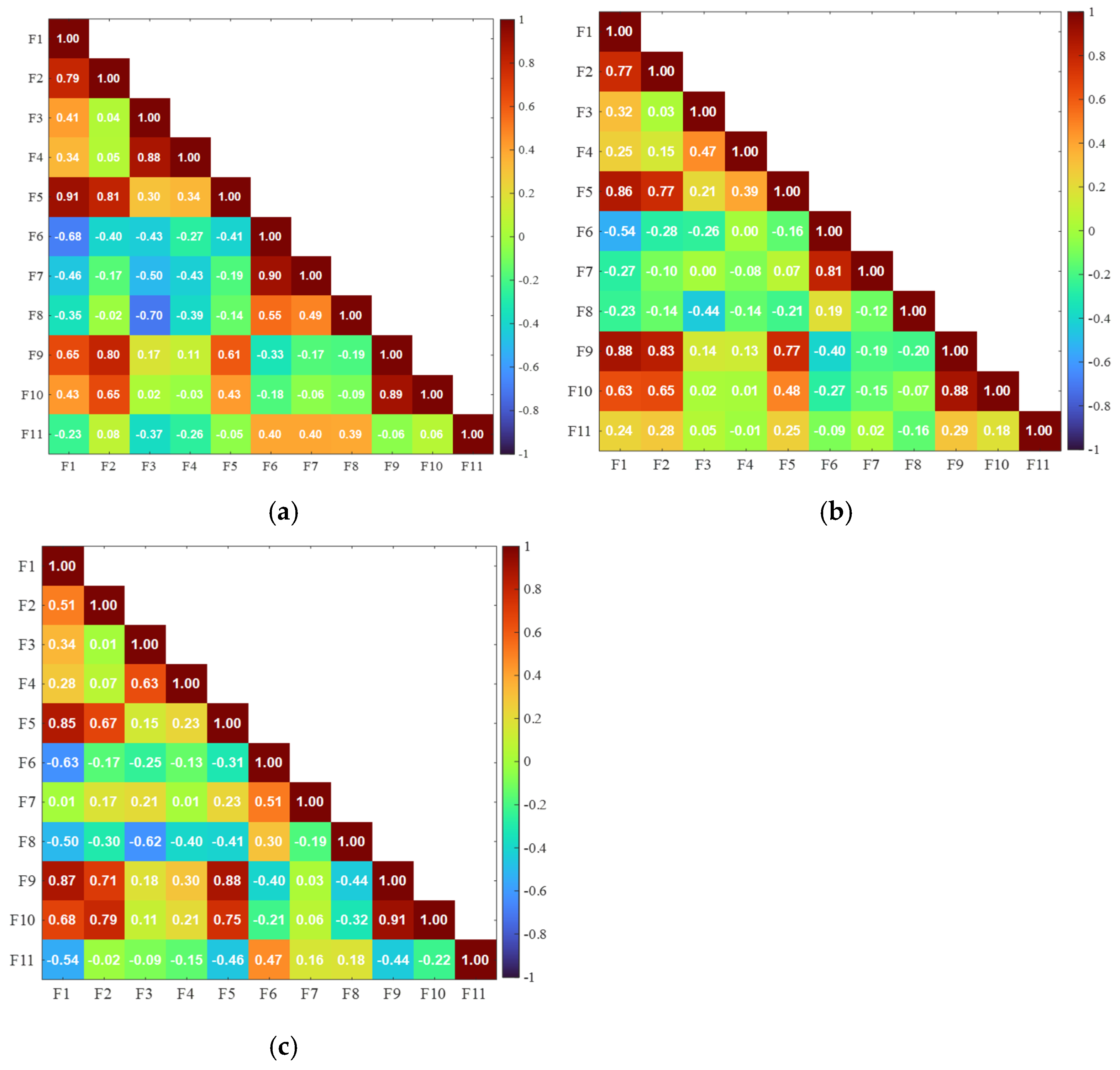
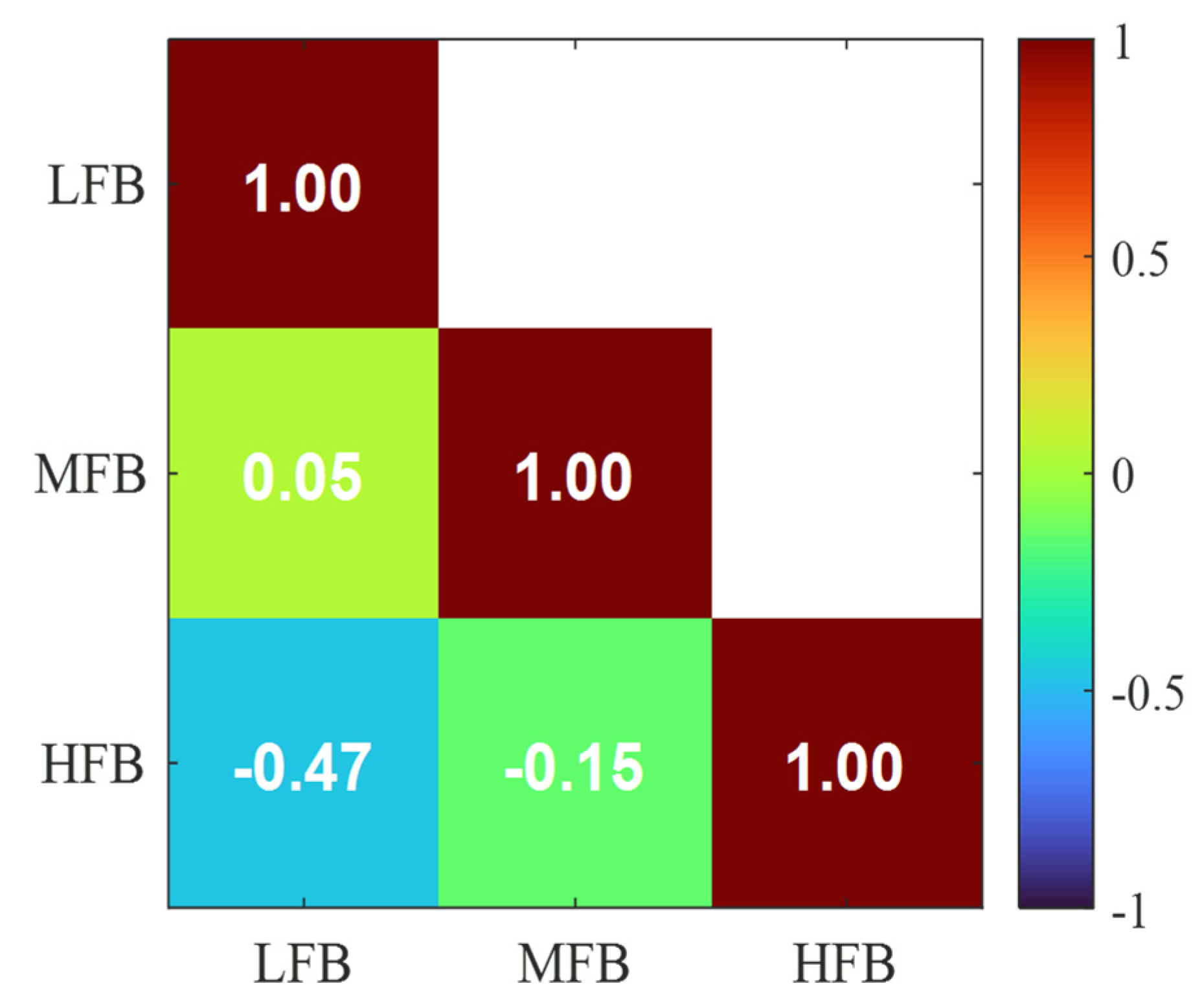
| Feature Name | Feature Number |
|---|---|
| Duration | F1 |
| Amplitude | F2 |
| Risetime | F3 |
| Counts to Peak | F4 |
| Counts | F5 |
| Average Frequency | F6 |
| Reverberation Frequency | F7 |
| Initiation Frequency | F8 |
| Signal Strength | F9 |
| Absolute Energy | F10 |
| Peak Frequency | F11 |
| Dataset | AE Threshold (dB) | PDT (µsec) | HDT (µsec) | HLT (µsec) |
|---|---|---|---|---|
| D1 | 32 | 100 | 200 | 700 |
| D2 | 35 | 100 | 300 | 600 |
| D3 | 40 | 100 | 400 | 500 |
| Frequency Band | Frequency Range (kHz) |
|---|---|
| Low-frequency band (LFB) | 25–225 |
| Mid-frequency band (MFB) | 250–650 |
| High-frequency band (HFB) | 700–3000 |
| AE Parameters |
|---|
| Duration |
| Amplitude |
| Risetime |
| Average Frequency |
| Initiation Frequency |
| Absolute Energy |
| Peak Frequency |
| Model | Accuracy |
|---|---|
| Logistic Regression (LR) | 97.50% |
| k-Nearest Neighbor (KNN) | 98.89% |
| Linear Discriminant Analysis (LDA) | 97.00% |
| Random Forest (RF) | 98.67% |
| Model | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| LR | 98% | DL: 100% FB: 100% MC: 94% | DL: 94% FB: 100% MC: 100% | DL: 97% FB: 100% MC: 97% |
| KNN | 96% | DL: 100% FB: 94% MC: 94% | DL: 94% FB: 100% MC: 94% | DL: 97% FB: 97% MC: 94% |
| LDA | 97% | DL: 100% FB: 100% MC: 93% | DL: 94% FB: 98% MC: 100% | DL: 97% FB: 99% MC: 96% |
| RF | 99% | DL: 100% FB: 98% MC: 98% | DL: 98% FB: 100% MC: 98% | DL: 99% FB: 99% MC: 98% |
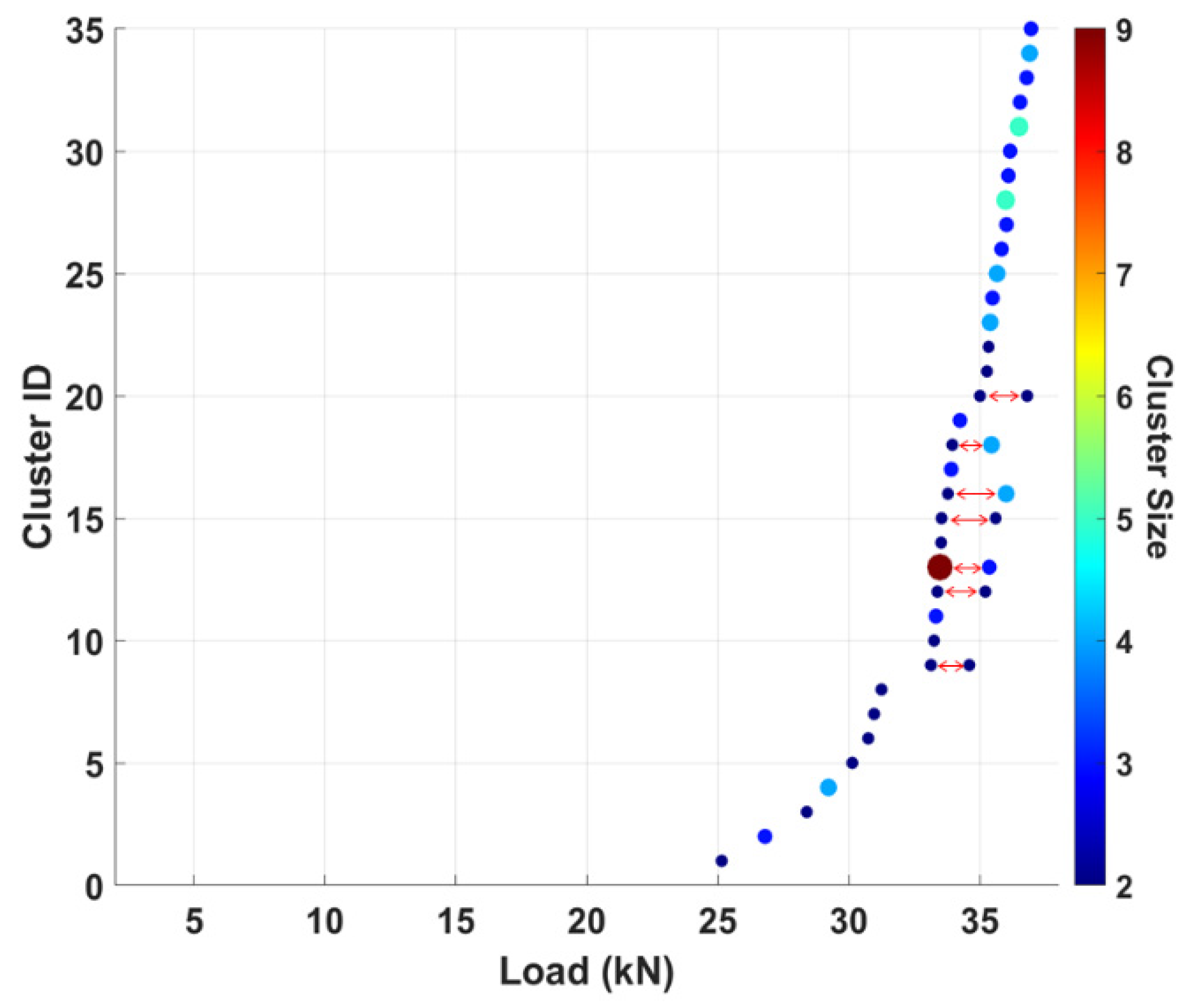
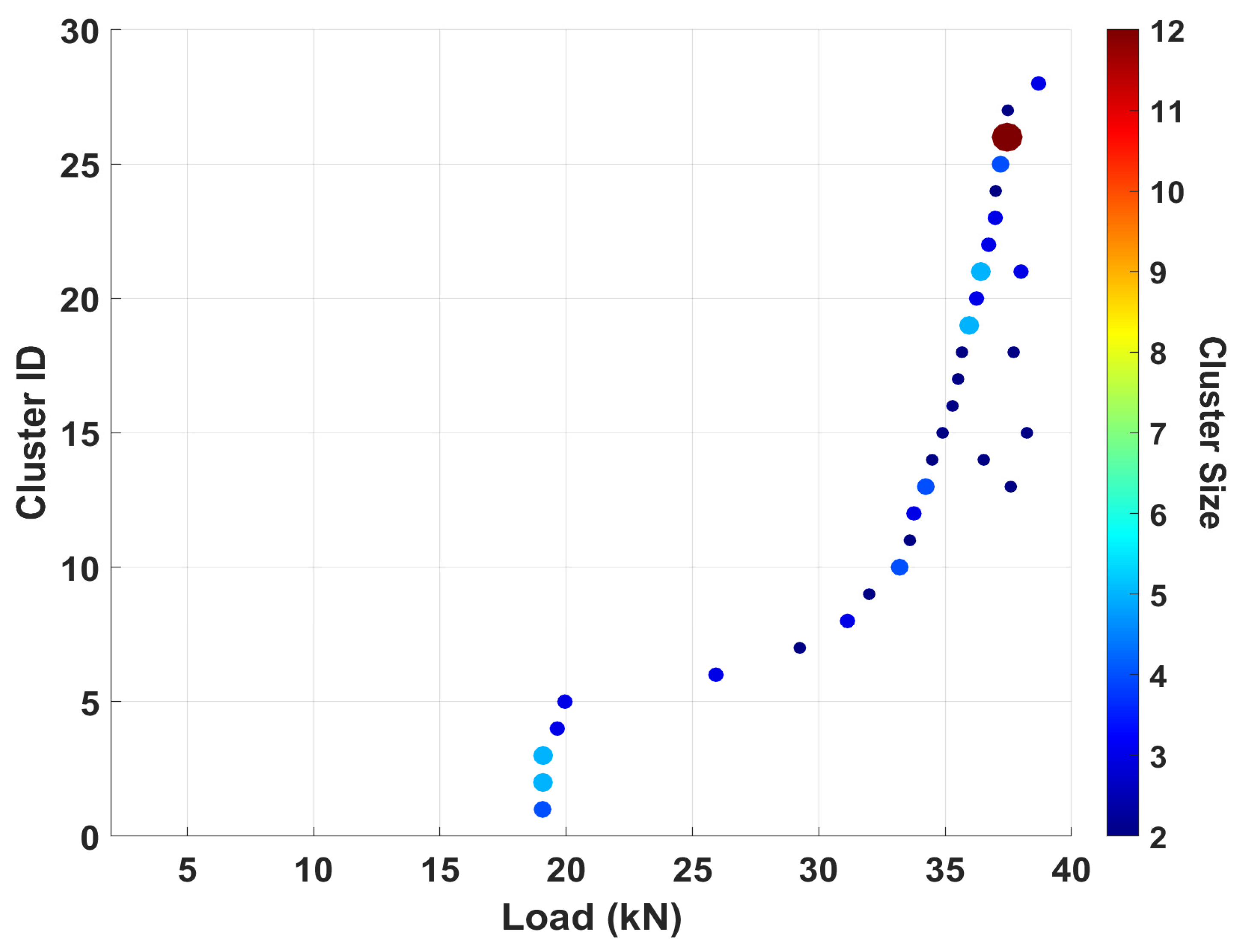
| Specimen | Unique Clusters | Total Clusters | Max. Cluster Size |
|---|---|---|---|
| 1 | 35 | 42 | 9 |
| 2 | 28 | 33 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amevorku, R.D.; Amoateng-Mensah, D.; Rijal, M.; Sundaresan, M.J. Classification and Clustering of Fiber Break Events in Thermoset CFRP Using Acoustic Emission and Machine Learning. Sensors 2025, 25, 6466. https://doi.org/10.3390/s25206466
Amevorku RD, Amoateng-Mensah D, Rijal M, Sundaresan MJ. Classification and Clustering of Fiber Break Events in Thermoset CFRP Using Acoustic Emission and Machine Learning. Sensors. 2025; 25(20):6466. https://doi.org/10.3390/s25206466
Chicago/Turabian StyleAmevorku, Richard Dela, David Amoateng-Mensah, Manoj Rijal, and Mannur J. Sundaresan. 2025. "Classification and Clustering of Fiber Break Events in Thermoset CFRP Using Acoustic Emission and Machine Learning" Sensors 25, no. 20: 6466. https://doi.org/10.3390/s25206466
APA StyleAmevorku, R. D., Amoateng-Mensah, D., Rijal, M., & Sundaresan, M. J. (2025). Classification and Clustering of Fiber Break Events in Thermoset CFRP Using Acoustic Emission and Machine Learning. Sensors, 25(20), 6466. https://doi.org/10.3390/s25206466





