Thermal Sensitivity of a Microoptoelectromechanical Evanescent-Coupling-Based Accelerometer
Abstract
1. Introduction
2. Experiments and Modeling of the Temperature Influence on the MOEM Accelerometer
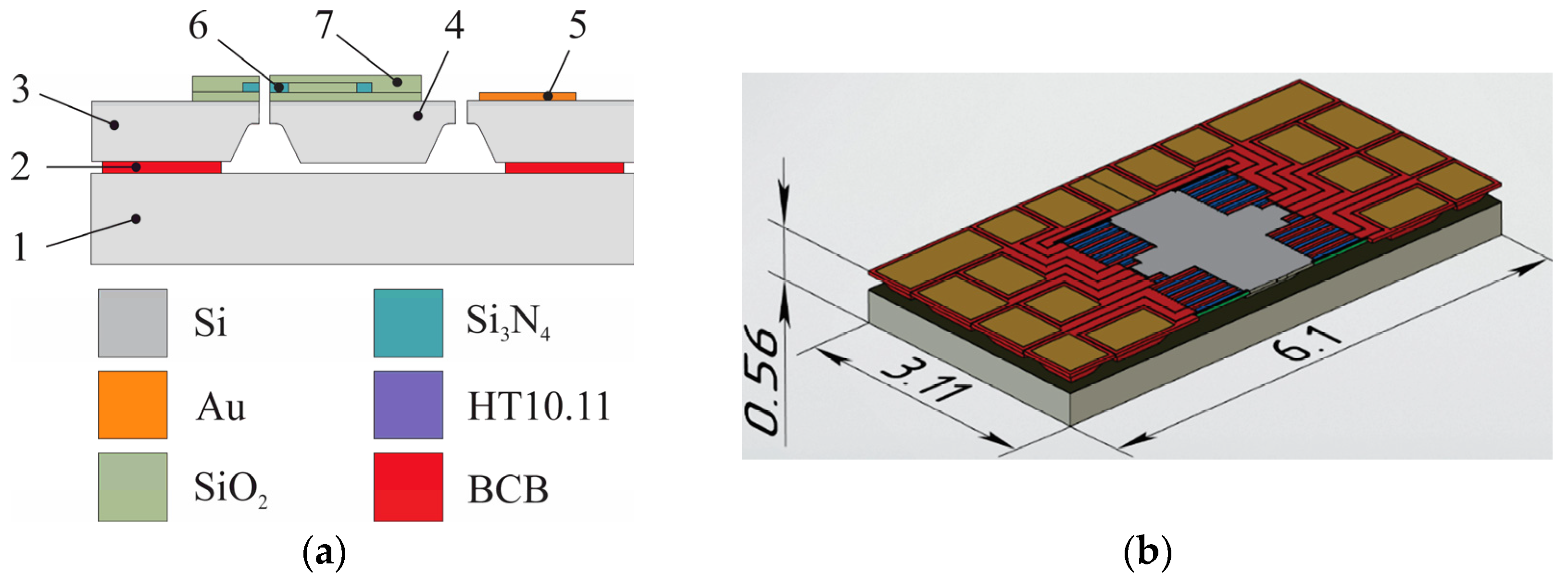
2.1. Functional Scheme of the Accelerometer
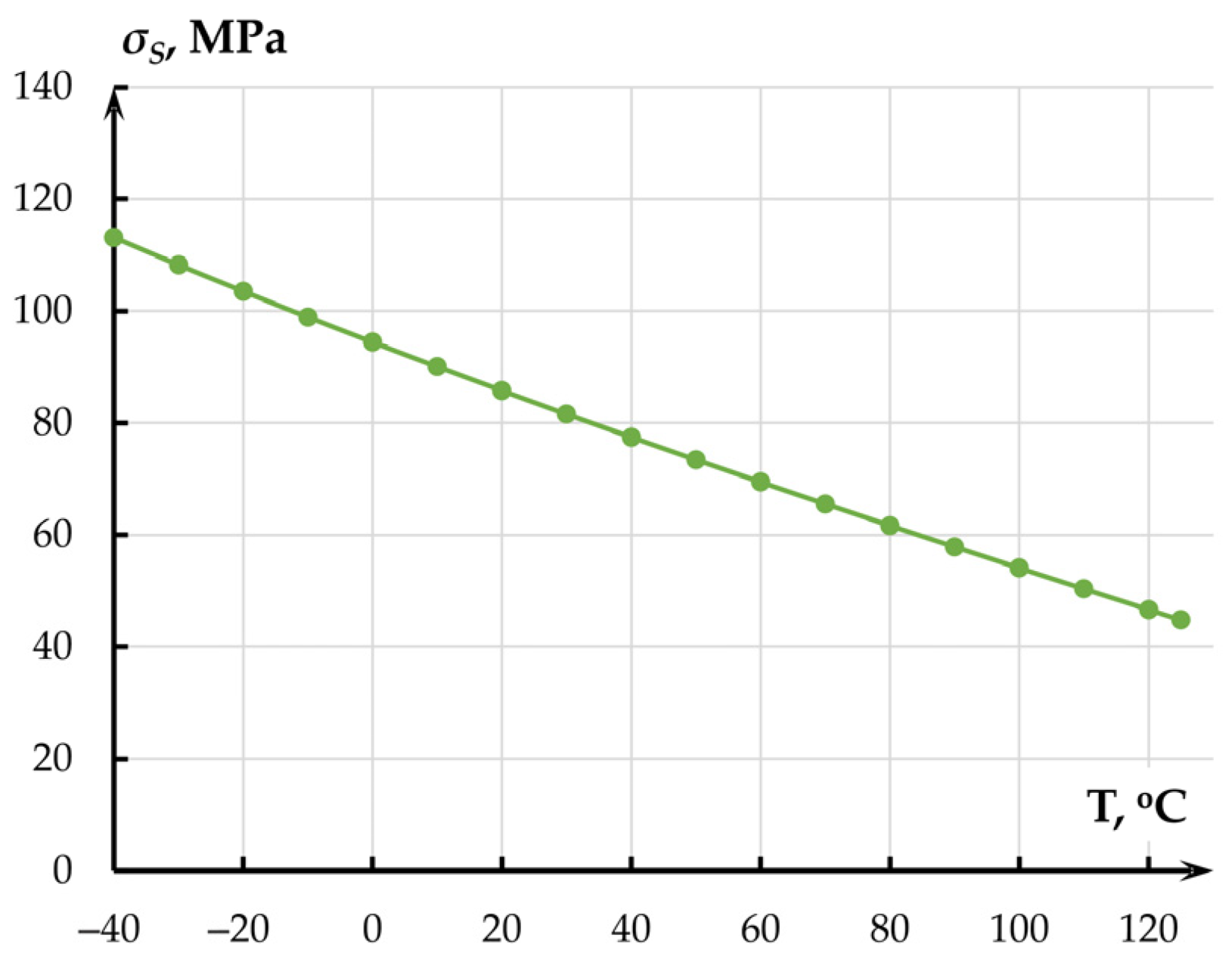
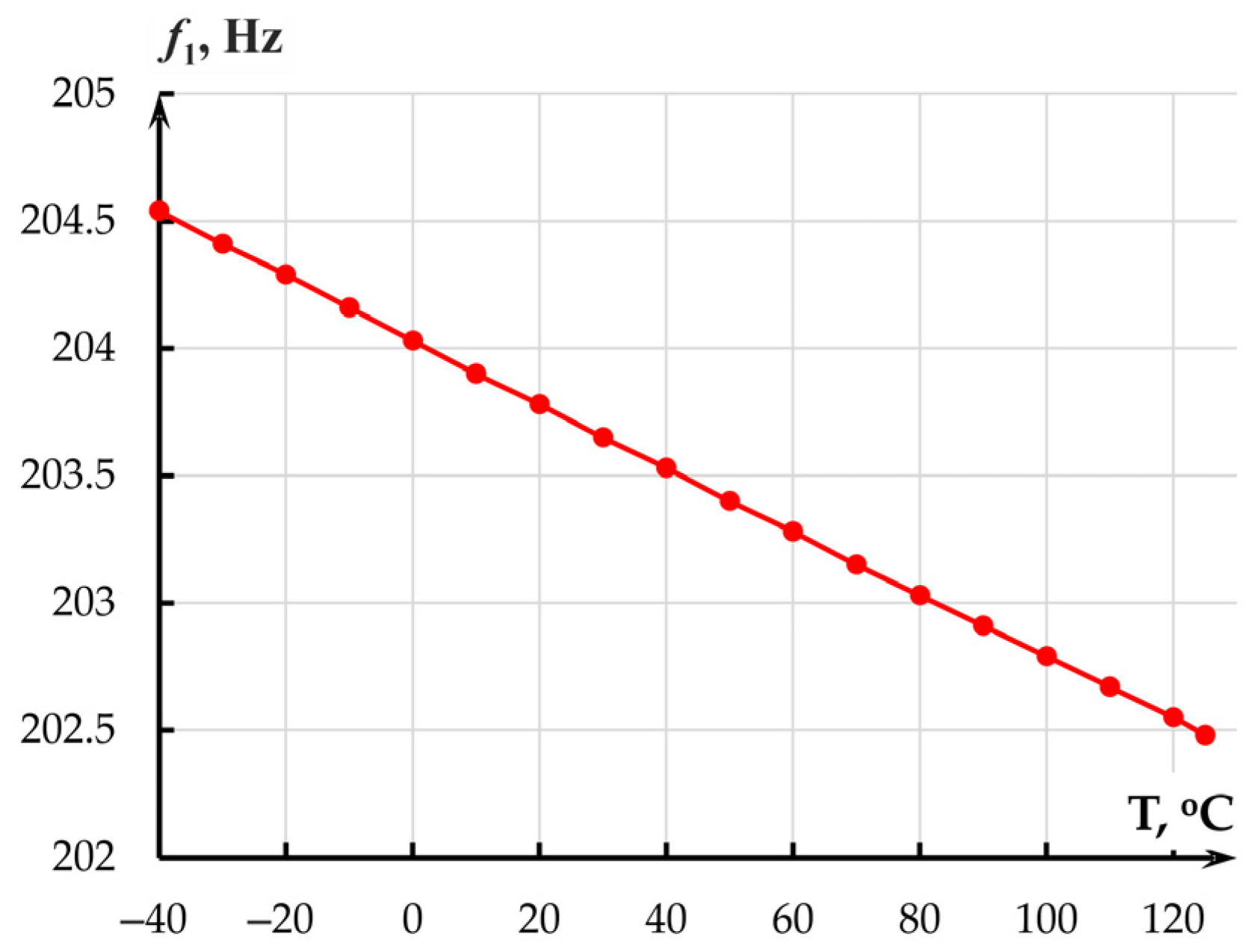
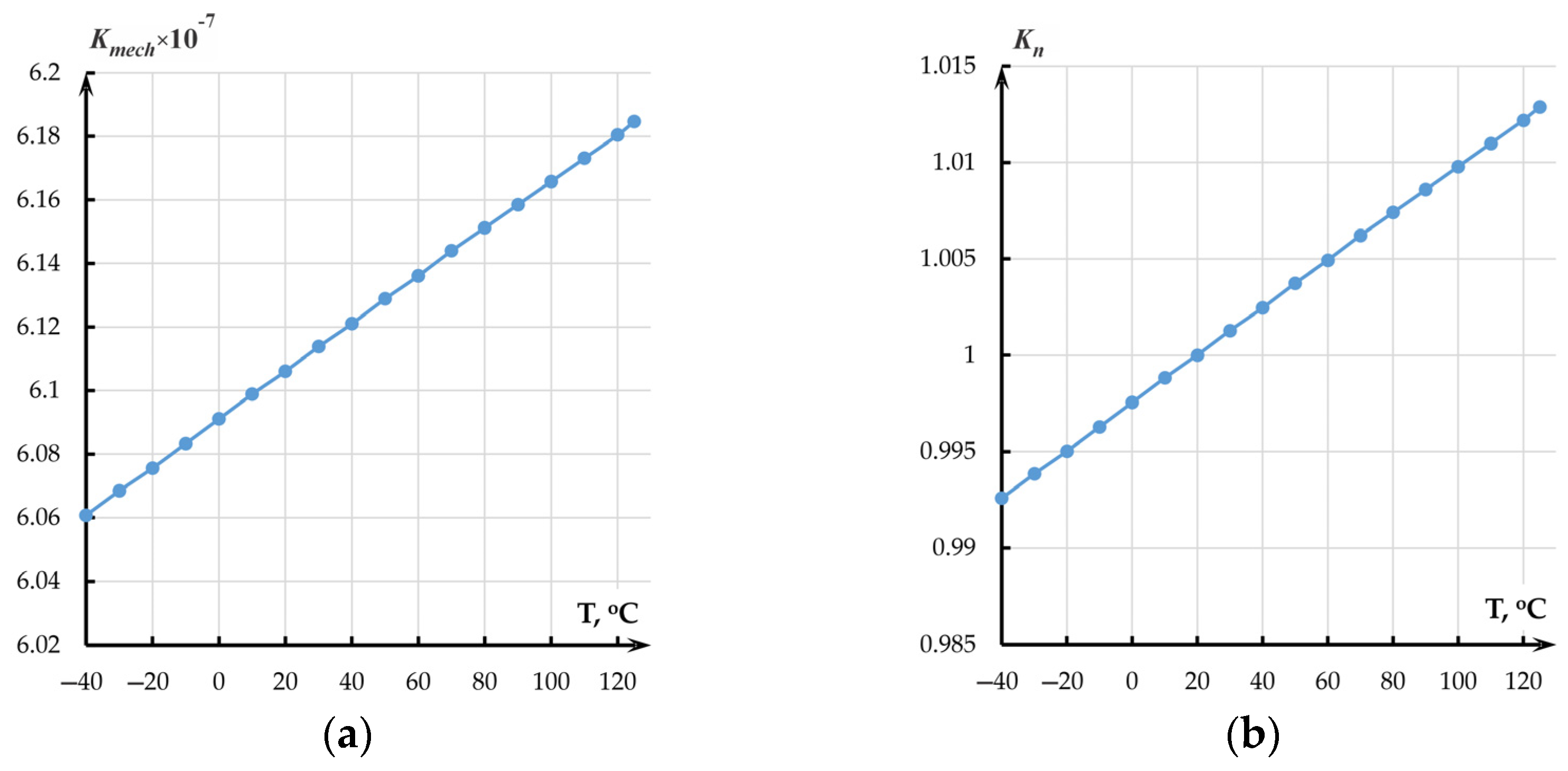
2.2. Temperature Influence on the Mechanical Transmission Coefficient of the Accelerometer
2.3. Temperature Influence on the Optical Measuring Transducer
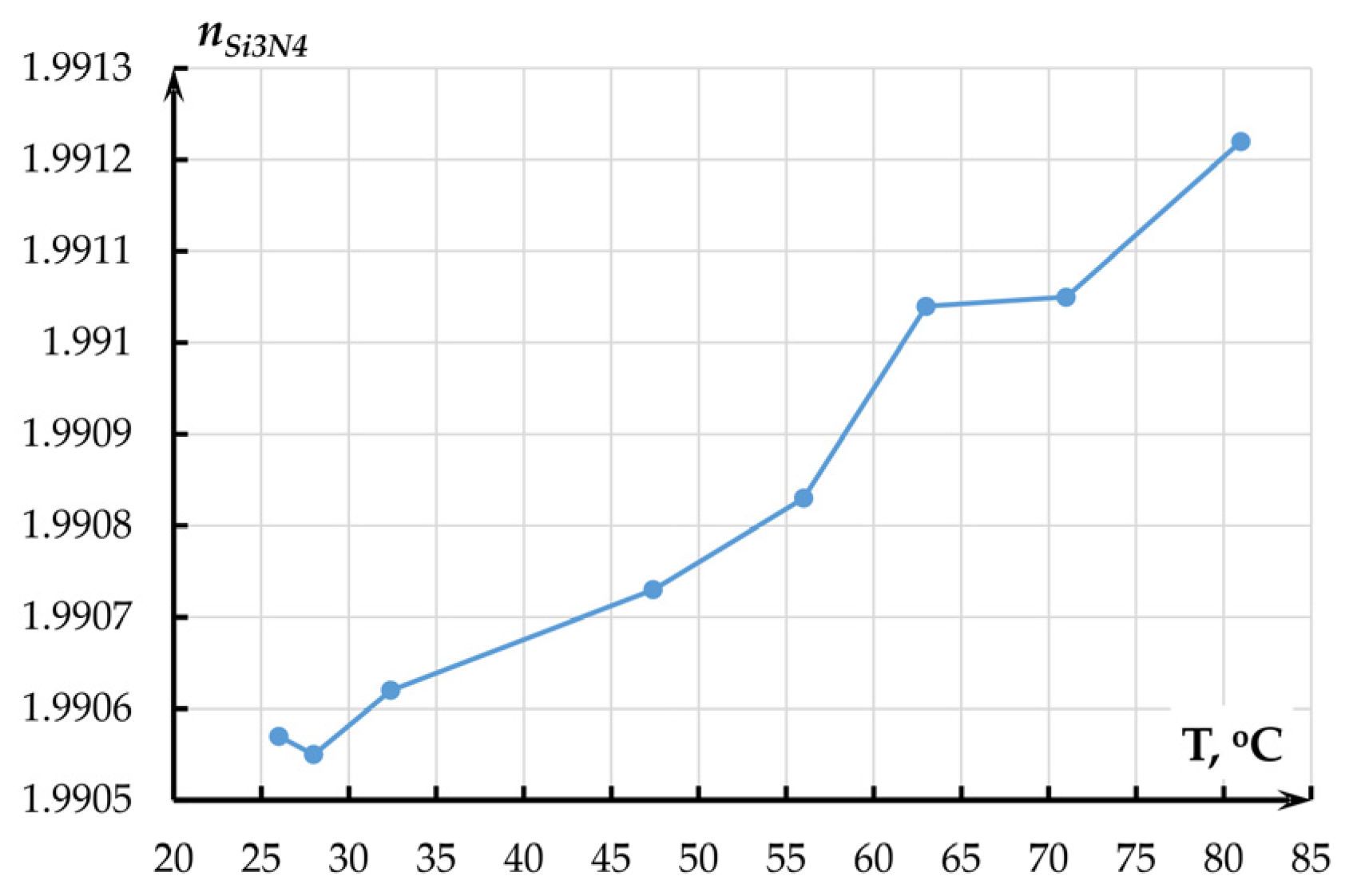
2.3.1. Experimental Determination of the Refraction Index of the Optical Waveguides
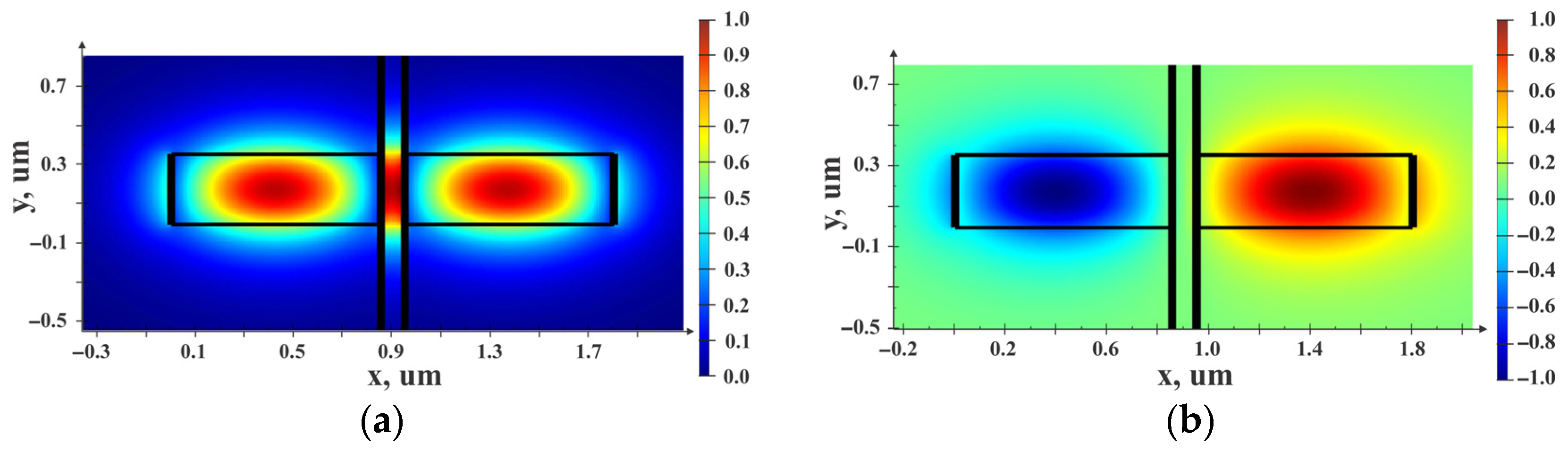
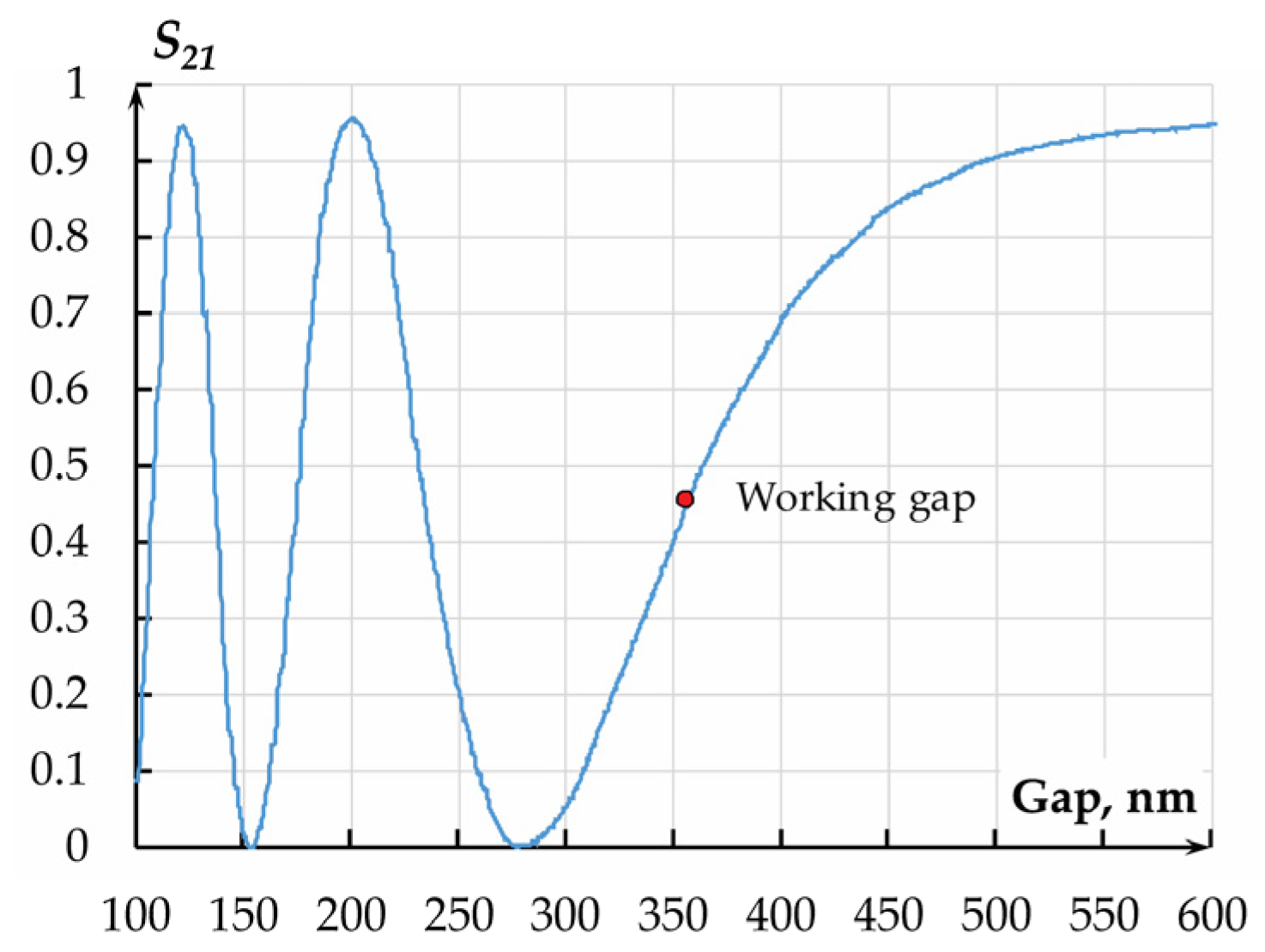
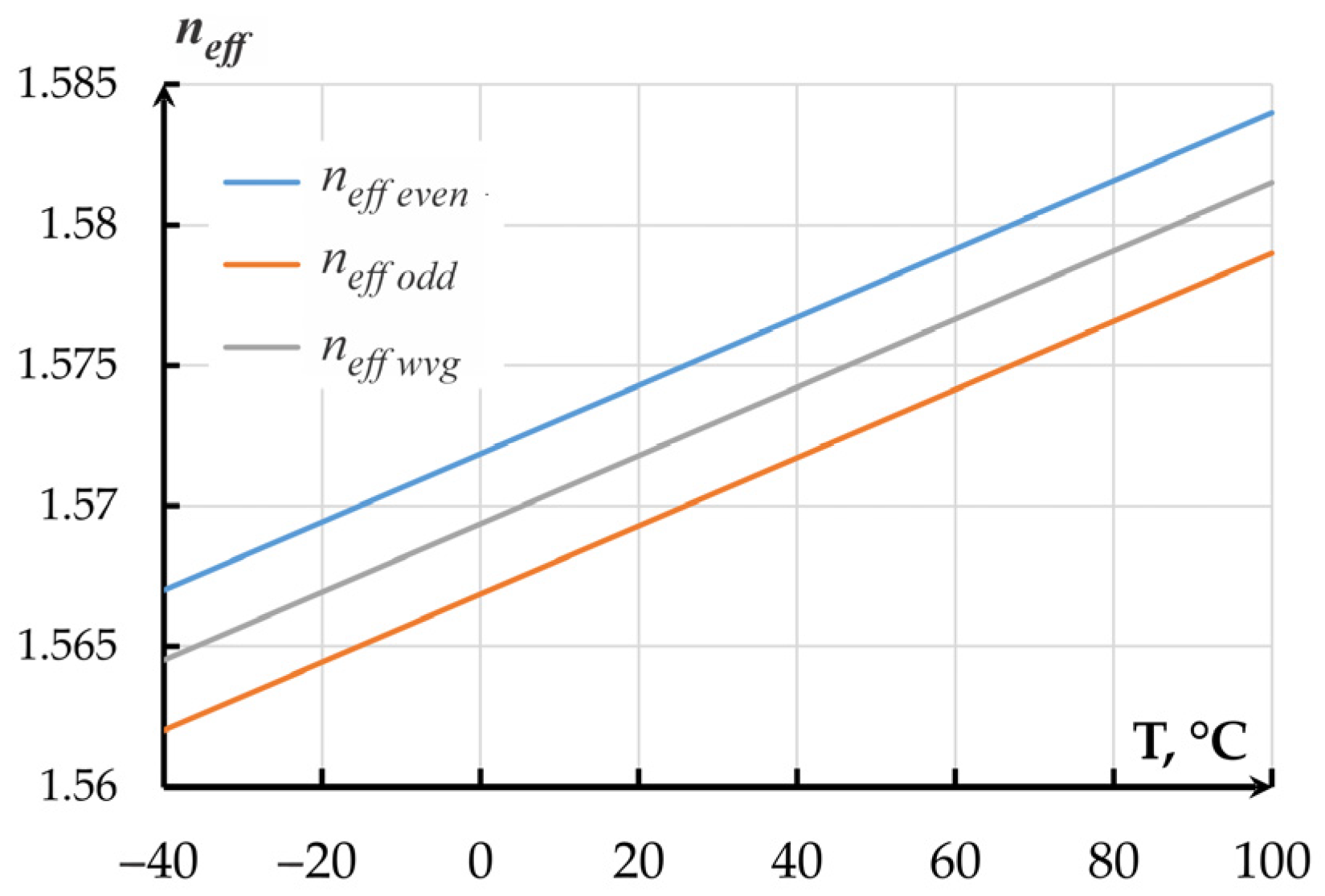
2.3.2. Measuring Transducer Based on a Directional Coupler
2.3.3. Measuring Transducer Based on a Resonator
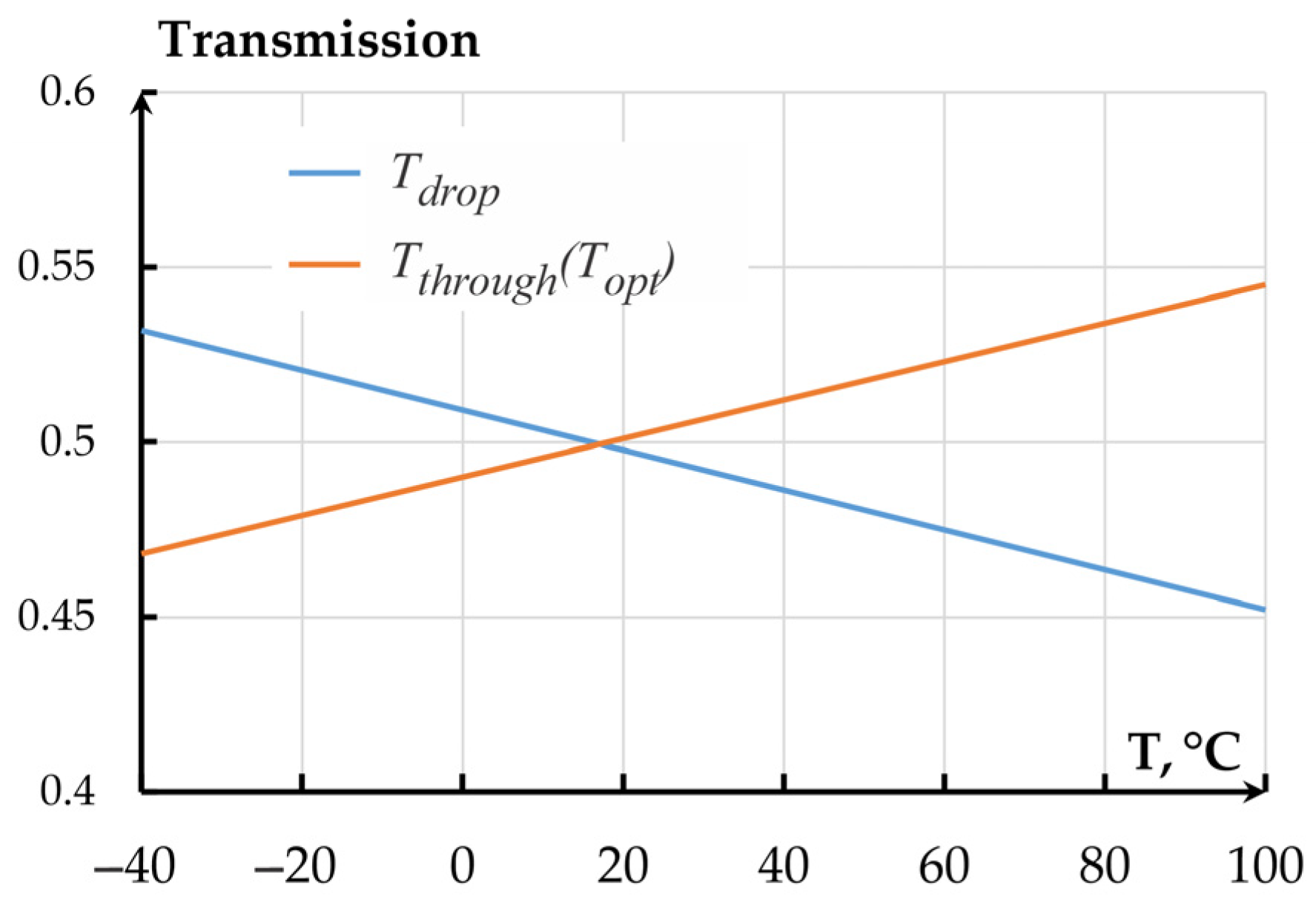
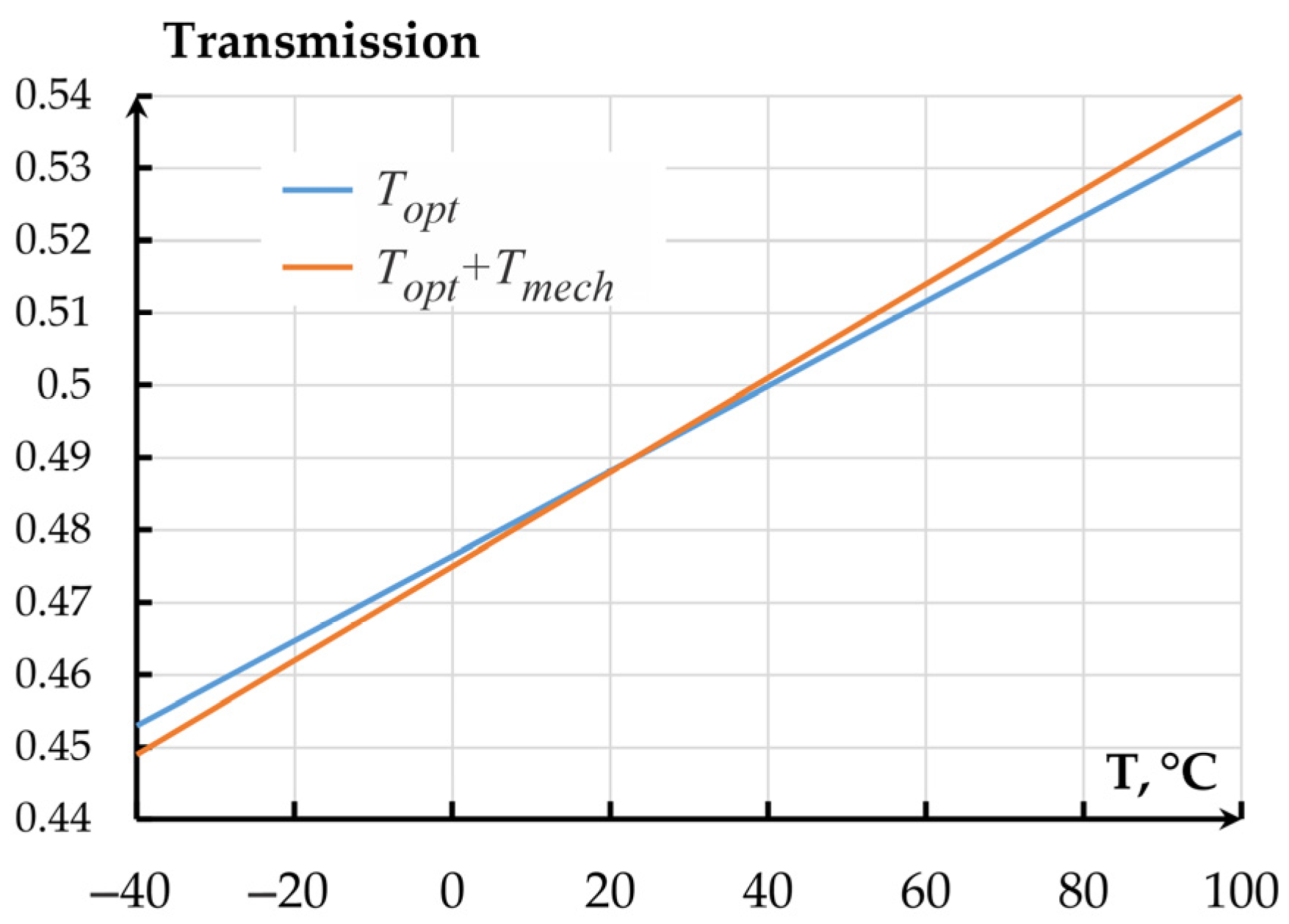
3. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MOEM | Microoptoelectromechanical |
| MEMS | Microelectromechanical system |
| PF | Proof mass |
| FBG | Fiber Bragg grating |
| MISO | Multi-input/single-output |
| GA | Genetic algorithm |
| TEC | Thermal expansion coefficient |
| PICs | Photonic integrated circuits |
| OMT | Optical measuring transducer |
| TTC | Total transmission coefficient |
| CLTE | Coefficients of linear temperature expansion |
| FEM | Finite element method |
| MOEMA | Microoptoelectromechanical accelerometer |
| OTC | Optical transmission coefficient |
| FDE | Finite-difference eigenmode |
| MTC | Mechanical transmission coefficient |
| FSR | Free spectral range |
References
- Solai, K.; Rathnasami, J.D.; Koilmani, S. SOI structure employed area dependent capacitive MEMS accelerometer with novel C–V converter. Microsyst. Technol. 2022, 5, 1191–1201. [Google Scholar] [CrossRef]
- Daeichin, M.; Miles, R.N.; Towfighian, S. Large-Stroke Capacitive MEMS Accelerometer Without Pull-In. IEEE Sens. J. 2021, 3, 3097–3106. [Google Scholar] [CrossRef]
- Lu, Q.; Bai, J.; Wang, K.; He, S. Design, Optimization, and Realization of a High-Performance MOEMS Accelerometer from a Double-Device-Layer SOI Wafer. J. Microelectromech. Syst. 2017, 26, 859–869. [Google Scholar] [CrossRef]
- Le, X.; Shi, Q.; Vachon, P.; Ng, E.J.; Lee, C. Piezoelectric MEMS—Evolution from sensing technology to diversified applications in the 5G/Internet of Things (IoT) era. J. Micromech. Microeng. 2022, 32, 014005. [Google Scholar] [CrossRef]
- Wang, C.; Hao, Y.; Sun, Z.; Zu, L.; Yuan, W.; Chang, H. Design of a Capacitive MEMS Accelerometer with Softened Beams. Micromachines 2022, 13, 459. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Scudero, S.; Vitale, G. A Review of the Capacitive MEMS for Seismology. Sensors 2019, 19, 3093. [Google Scholar] [CrossRef]
- Mo, Y.; Yang, J.; Peng, B.; Xie, G.; Tang, B. Design and verification of a structure for isolating stress in sandwich MEMS accelerometer. Microsyst. Technol. 2021, 27, 1943–1950. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, L.; Jiang, Z.; Ding, J.; Xu, T.; Zhao, Y. Analysis and design of a novel piezoresistive accelerometer with axially stressed self-supporting sensing beams. Sens. Actuators A Phys. 2016, 247, 1–11. [Google Scholar] [CrossRef]
- Timotijevic, B.; Petremand, Y.; Bayat, D.; Luetzelschwab, M.; Aebi, L.; Tormen, M. Compact optical MEMS accelerometers and temperature sensors. In Proceedings of the MOEMS and Miniaturized Systems XVI, San Francisco, CA, USA, 28 January–2 February 2017; Volume 101160G. [Google Scholar] [CrossRef]
- Hall, N.A.; Okandan, M.; Littrell, R.; Serkland, D.K.; Keeler, G.A.; Peterson, K.; Degertekin, F.L. Micromachined Accelerometers with Optical Interferometric Read-Out and Integrated Electrostatic Actuation. J. Microelectromech. Syst. 2008, 17, 37–44. [Google Scholar] [CrossRef]
- Davies, E.; George, D.S.; Gower, M.C.; Holmes, A.S. MEMS Fabry–Pérot optical accelerometer employing mechanical amplification via a V-beam structure. Sens. Actuators A Phys. 2014, 215, 22–29. [Google Scholar] [CrossRef]
- Davies, E.; George, D.S.; Holmes, A.S. Mechanically amplified MEMS optical accelerometer with FPI readout. In Proceedings of the SPIE MOEMS and Miniaturized Systems, San Francisco, CA, USA, 1–6 February 2014; Volume 8977. [Google Scholar] [CrossRef]
- Gerberding, O.; Guzmán Cervantes, F.; Melcher, J.; Pratt, J.R.; Taylor, J.M. Optomechanical reference accelerometer. Metrologia 2015, 52, 654–665. [Google Scholar] [CrossRef]
- Zandi, K.; Belanger, J.A.; Peter, Y.-A. Design and Demonstration of an In-Plane Silicon-on-Insulator Optical MEMS Fabry–Pérot-Based Accelerometer Integrated with Channel Waveguides. J. Microelectromech. Syst. 2012, 21, 1464–1470. [Google Scholar] [CrossRef]
- Krause, A.G.; Winger, M.; Blasius, T.D.; Lin, Q.; Painter, O. A high-resolution microchip optomechanical accelerometer. Nat. Photonics 2012, 6, 768–772. [Google Scholar] [CrossRef]
- Cui, R.; Xu, J.; Huang, B.; Xu, H.; Peng, M.; Yang, J.; Zhang, J.; Gu, Y.; Chen, D.; Li, H.; et al. A Temperature Compensation Approach for Micro-Electro-Mechanical Systems Accelerometer Based on Gated Recurrent Unit–Attention and Robust Local Mean Decomposition–Sample Entropy–Time-Frequency Peak Filtering. Micromachines 2024, 15, 483. [Google Scholar] [CrossRef]
- Yao, B.-Y.; Zhou, Z.; Feng, L.-S.; Wang, W.-P.; Wang, X. Structural Design of a Compact In-Plane Nano-Grating Accelerometer. Chin. Phys. Lett. 2012, 29, 118502. [Google Scholar] [CrossRef]
- Krishnamoorthy, U.; Olsson, R.H.; Bogart, G.R.; Baker, M.S.; Carr, D.W.; Swiler, T.P.; Clews, P.J. In-plane MEMS-based nano-g accelerometer with sub-wavelength optical resonant sensor. Sens. Actuators A Phys. 2008, 145, 283–290. [Google Scholar] [CrossRef]
- Sheikhaleh, A.; Abedi, K.; Jafari, K. An Optical MEMS Accelerometer Based on a Two-Dimensional Photonic Crystal Add-Drop Filter. J. Light. Technol. 2017, 35, 3029–3034. [Google Scholar] [CrossRef]
- Sheikhaleh, A.; Abedi, K.; Jafari, K.; Gholamzadeh, R. Micro-optoelectromechanical systems accelerometer based on intensity modulation using a one-dimensional photonic crystal. Appl. Opt. 2016, 55, 8993–8999. [Google Scholar] [CrossRef] [PubMed]
- Zotov, S.A.; Simon, B.R.; Trusov, A.A.; Shkel, A.M. High Quality Factor Resonant MEMS Accelerometer with Continuous Thermal Compensation. IEEE Sens. J. 2015, 15, 5045–5052. [Google Scholar] [CrossRef]
- Ruzza, G.; Guerriero, L.; Revellino, P.; Guadagno, F.M. Thermal Compensation of Low-Cost MEMS Accelerometers for Tilt Measurements. Sensors 2018, 18, 2536. [Google Scholar] [CrossRef]
- Shen, C.; Yang, J.; Tang, J.; Liu, J.; Cao, H. Note: Parallel processing algorithm of temperature and noise error for micro-electro-mechanical system gyroscope based on variational mode decomposition and augmented nonlinear differentiator. Rev. Sci. Instrum. 2018, 89, 076107. [Google Scholar] [CrossRef]
- Araghi, G.; Landry, R., Jr. Temperature compensation model of MEMS inertial sensors based on neural network. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 301–309. [Google Scholar] [CrossRef]
- Han, D.; Bai, J.; Lu, Q.; Lou, S.; Jiao, X.; Yang, G. The analysis of temperature effect and temperature compensation of MOEMS accelerometer based on a grating interferometric cavity. In Proceedings of the SPIE 9960, Interferometry XVIII, San Francisco, CA, USA, 28 August–1 September 2016; Volume 9960. [Google Scholar] [CrossRef]
- Fang, W.; Lu, Q.; Bai, J.; Han, D.; Chen, P. Thermal stress of MOEMS accelerometers based on grating interferometric cavity. In Proceedings of the Optical Design and Testing VIII, Beijing, China, 11–13 October 2018; Volume 10815. [Google Scholar] [CrossRef]
- Lu, Q.; Bai, J.; Wang, K.; Jiao, X.; Han, D.; Chen, P.; Liu, D.; Yang, Y.; Yang, G. Determination of thermally induced effects and design guidelines of optomechanical accelerometers. Meas. Sci. Technol. 2017, 28, 115201. [Google Scholar] [CrossRef]
- Fender, A.; MacPherson, W.N.; Maier, R.R.J.; Barton, J.S.; George, D.S.; Howden, R.I.; Smith, G.W.; Jones, B.J.S.; McCulloch, S.; Chen, X.; et al. Two-Axis Temperature-Insensitive Accelerometer Based on Multicore Fiber Bragg Gratings. IEEE Sens. J. 2008, 8, 1292–1298. [Google Scholar] [CrossRef]
- Fang, W.; Wang, C.; Bai, J.; Chen, J.; Yao, Y.; Lu, Q. Investigation of the thermal deformation of a chip-scale packaged optical accelerometer. Measurement 2020, 163, 108017. [Google Scholar] [CrossRef]
- Malayappan, B.; Poornalakshmi, U.; Pattnaik, P.K. Temperature insensitive waveguide grating based SOI MOEMS accelerometer. In Proceedings of the 2015 Workshop on Recent Advances in Photonics (WRAP), Bangalore, India, 16–17 December 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Malayappan, B.; Lakshmi, U.P.; Prabhakar Rao, B.V.V.S.N.; Ramaswamy, K.; Pattnaik, P.K. Sensing Techniques and Interrogation Methods in Optical MEMS Accelerometers: A Review. IEEE Sens. J. 2022, 22, 6232–6246. [Google Scholar] [CrossRef]
- Barbin, E.; Nesterenko, T.; Koleda, A.; Talovskaia, A.; Mokhovikov, D.; Kulinich, I. Temperature Effect on the Mechanical Transmission Coefficient of a Microoptoelectromechanical Accelerometer. In Proceedings of the 2024 IEEE 25th International Conference of Young Professionals in Electron Devices and Materials (EDM), Altai, Russia, 28 June–2 July 2024; pp. 290–294. [Google Scholar] [CrossRef]
- Baranov, P.; Nesterenko, T.; Barbin, E.; Koleda, A. Constructive approach to reduce the influence of temperature on spring suspension eigenfrequencies. Sens. Rev. 2020, 40, 297–309. [Google Scholar] [CrossRef]
- Huang, M.; Yan, X. Thermal-stress effects on the temperature sensitivity of optical waveguides. J. Opt. Soc. Am. B 2003, 20, 1326–1333. [Google Scholar] [CrossRef]
- Xiong, J.; Tang, J.; Chen, M.; Wang, T.; Cheng, Y.; Wen, H. Sensing performance of temperature insensitive microring resonators with double-layer U-shaped waveguide. Optik 2022, 262, 169236. [Google Scholar] [CrossRef]
- Zhang, C.; Kang, G.G.; Wang, J.; Wan, S.; Dong, C.H.; Pan, Y.J.; Qu, J.F. Photonic thermometer by silicon nitride microring resonator with milli-kelvin self-heating effect. Measurement 2021, 188, 110494. [Google Scholar] [CrossRef]
- Pavesi, L.; Guillot, G. Optical Interconnects: The Silicon Approach; Springer: Berlin/Heidelberg, Germany, 2006; p. 384. [Google Scholar] [CrossRef]
- Barbin, E.S.; Nesterenko, T.G.; Koleda, A.N.; Talovskaia, A.A.; Kulinich, I.V.; Mokhovikov, D.M. Temperature Effect on the Optical Characteristics of a Microoptoelectromechanical Accelerometer. In Proceedings of the 2024 IEEE 25th International Conference of Young Professionals in Electron Devices and Materials (EDM), Altai, Russia, 28 June–2 July 2024; pp. 40–44. [Google Scholar] [CrossRef]
- Shugurov, A.R.; Panin, A.V. Mechanisms of Stress Generation in Thin Films and Coatings. Tech. Phys. 2020, 65, 1881–1904. [Google Scholar] [CrossRef]
- Barbin, E.; Nesterenko, T.; Koleda, A.; Shesterikov, E.; Kulinich, I.; Kokolov, A.; Perin, A. The Design, Modeling and Experimental Investigation of a Micro-G Microoptoelectromechanical Accelerometer with an Optical Tunneling Measuring Transducer. Sensors 2024, 24, 765. [Google Scholar] [CrossRef] [PubMed]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbin, E.; Kulinich, I.; Nesterenko, T.; Koleda, A.; Myrzakhmetov, A.; Mokhovikov, D.; Vtorushin, S.; Talovskaia, A. Thermal Sensitivity of a Microoptoelectromechanical Evanescent-Coupling-Based Accelerometer. Sensors 2025, 25, 6388. https://doi.org/10.3390/s25206388
Barbin E, Kulinich I, Nesterenko T, Koleda A, Myrzakhmetov A, Mokhovikov D, Vtorushin S, Talovskaia A. Thermal Sensitivity of a Microoptoelectromechanical Evanescent-Coupling-Based Accelerometer. Sensors. 2025; 25(20):6388. https://doi.org/10.3390/s25206388
Chicago/Turabian StyleBarbin, Evgenii, Ivan Kulinich, Tamara Nesterenko, Alexei Koleda, Ayan Myrzakhmetov, Denis Mokhovikov, Sergey Vtorushin, and Alena Talovskaia. 2025. "Thermal Sensitivity of a Microoptoelectromechanical Evanescent-Coupling-Based Accelerometer" Sensors 25, no. 20: 6388. https://doi.org/10.3390/s25206388
APA StyleBarbin, E., Kulinich, I., Nesterenko, T., Koleda, A., Myrzakhmetov, A., Mokhovikov, D., Vtorushin, S., & Talovskaia, A. (2025). Thermal Sensitivity of a Microoptoelectromechanical Evanescent-Coupling-Based Accelerometer. Sensors, 25(20), 6388. https://doi.org/10.3390/s25206388






