Development and Modeling of a Novel Magnetorheological Elastomer Isolator in Hybrid Mode with a Compression–Shear Hybrid Fractional-Derivative Parametric Model
Abstract
1. Introduction
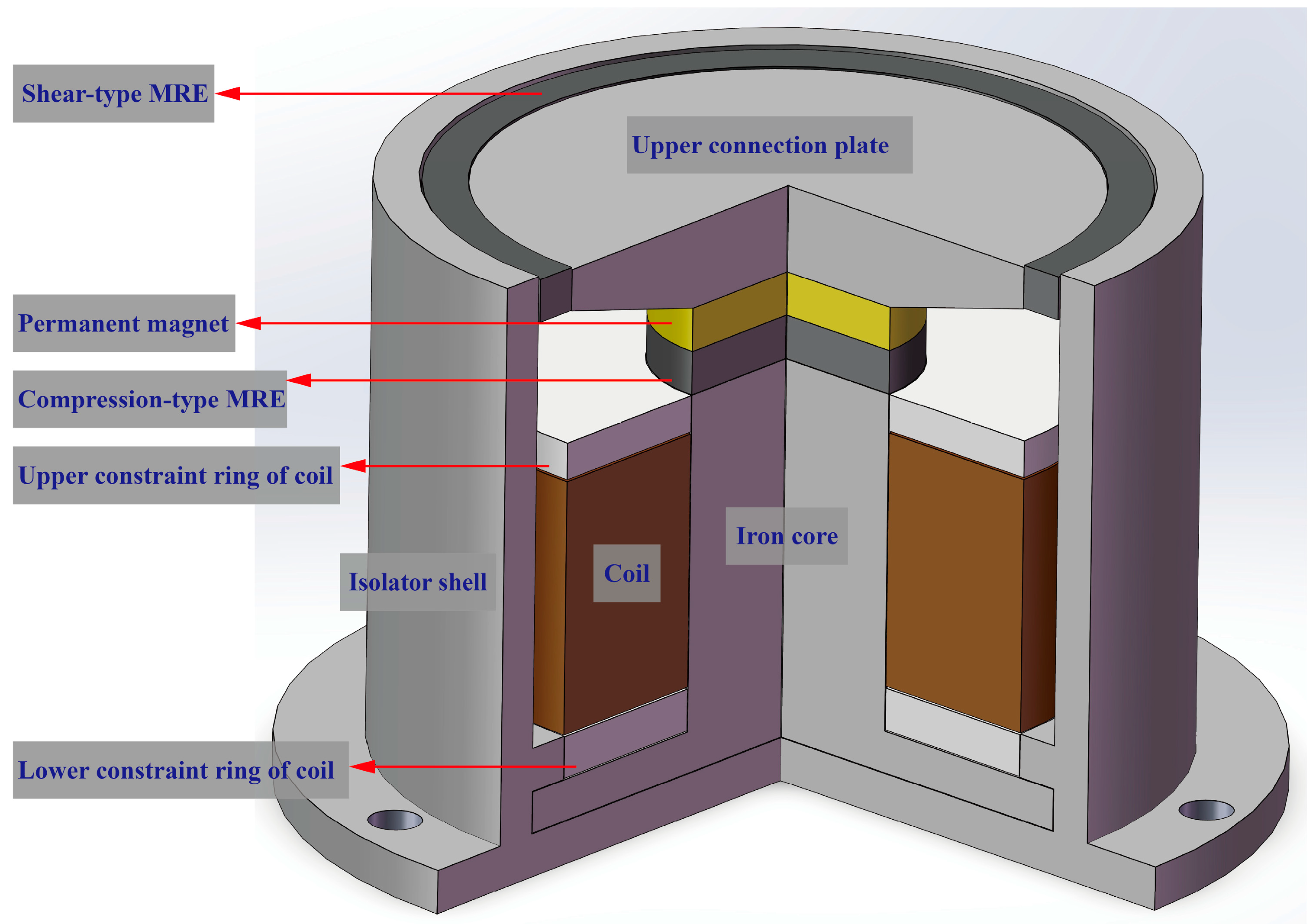
2. Manufacturing of the Compression–Shear Hybrid-Mode MRE Isolator
2.1. Preparation of MREs
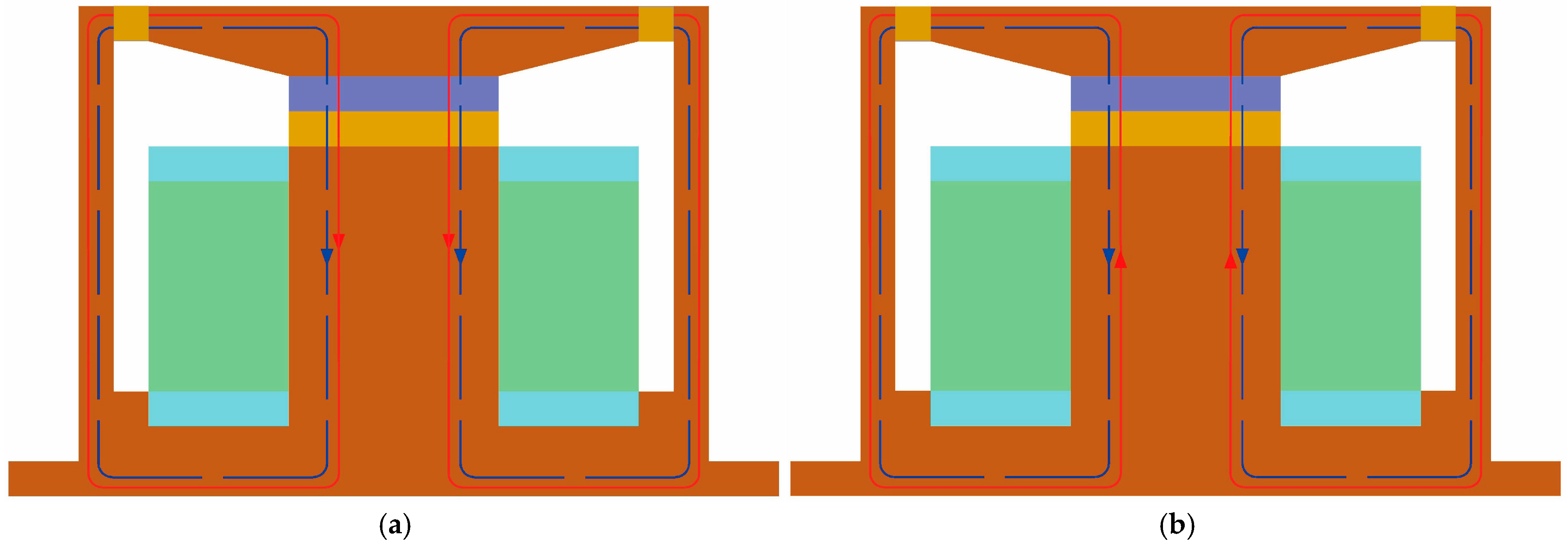
2.2. Preparation of the Compression–Shear Hybrid-Mode MRE Isolator
3. Experimental Analysis
3.1. Experimental Setup and Procedure
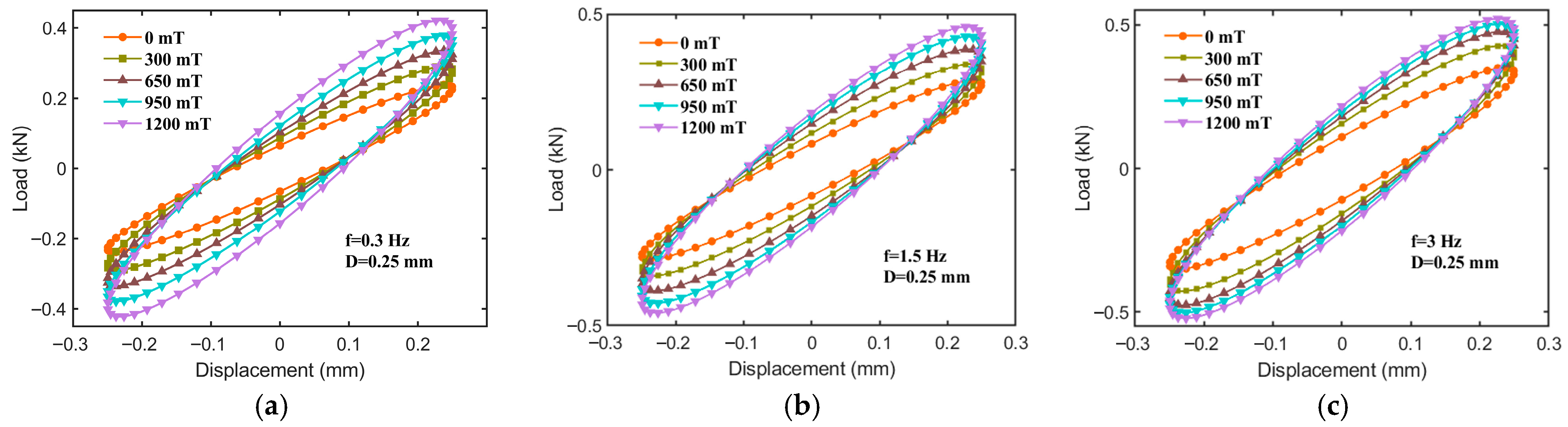
3.2. Results and Discussion
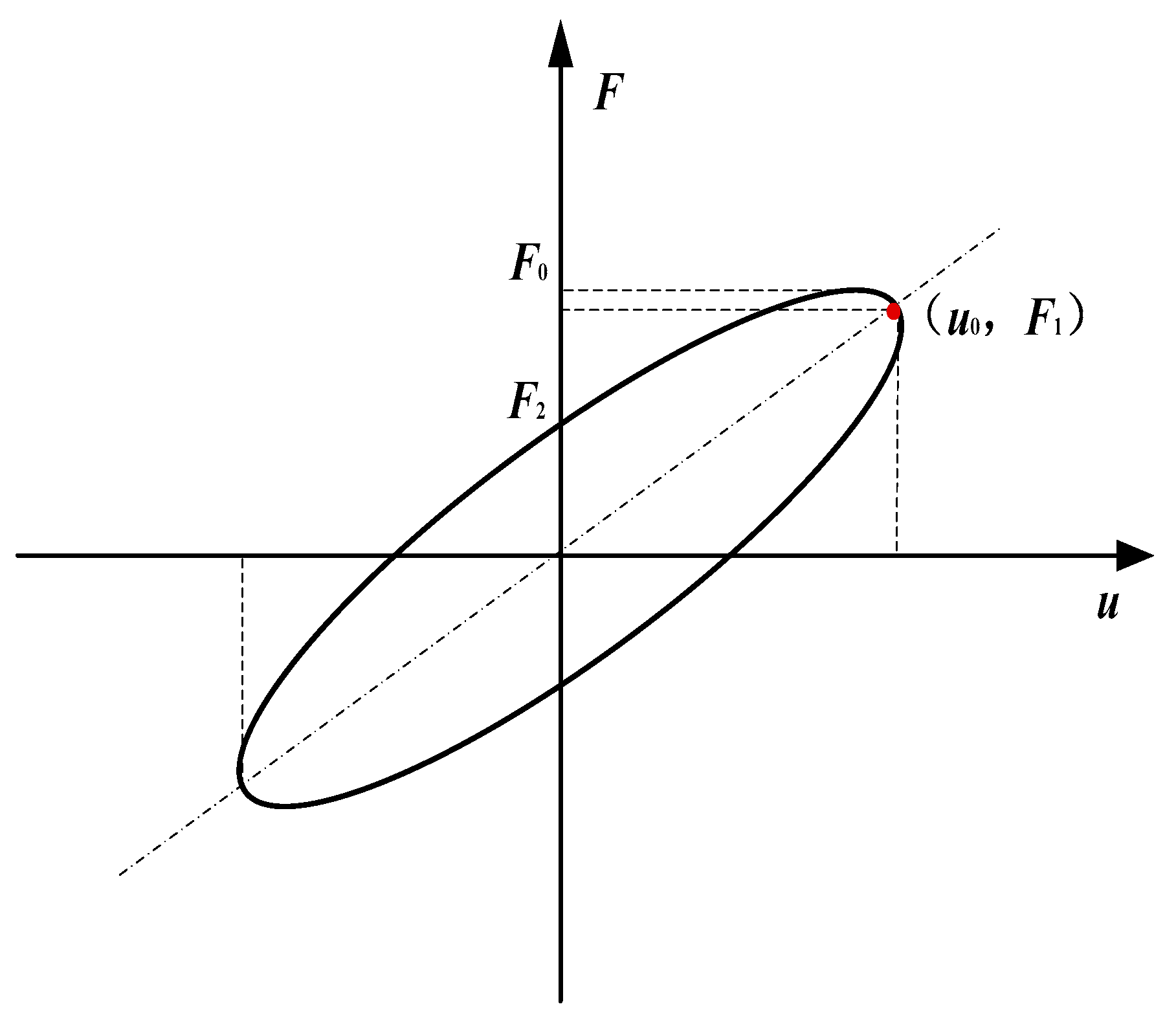
4. Mathematical Modeling
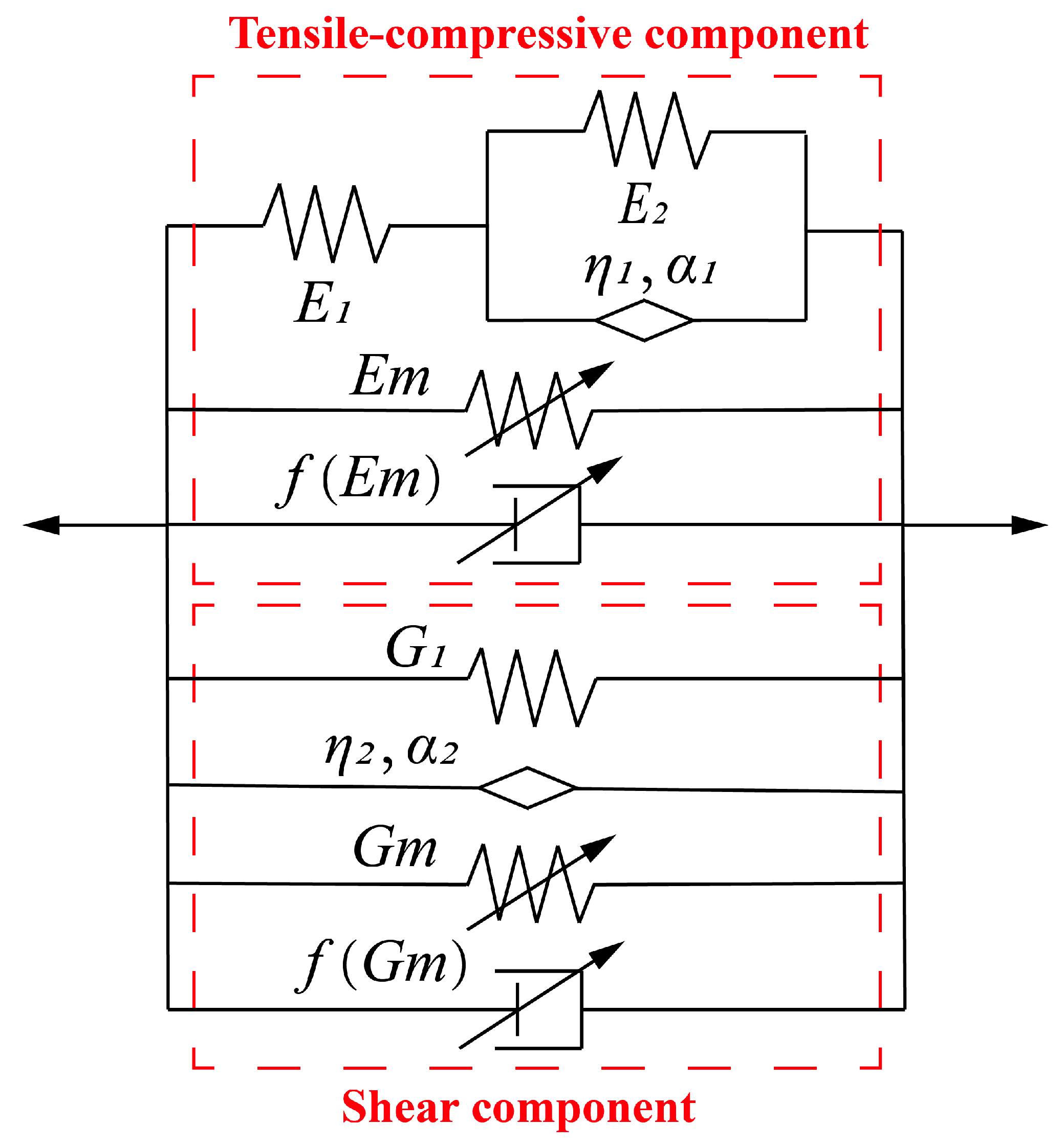
4.1. Compression–Shear Hybrid Fractional-Derivative Parametric Model
4.2. Parameter Identification
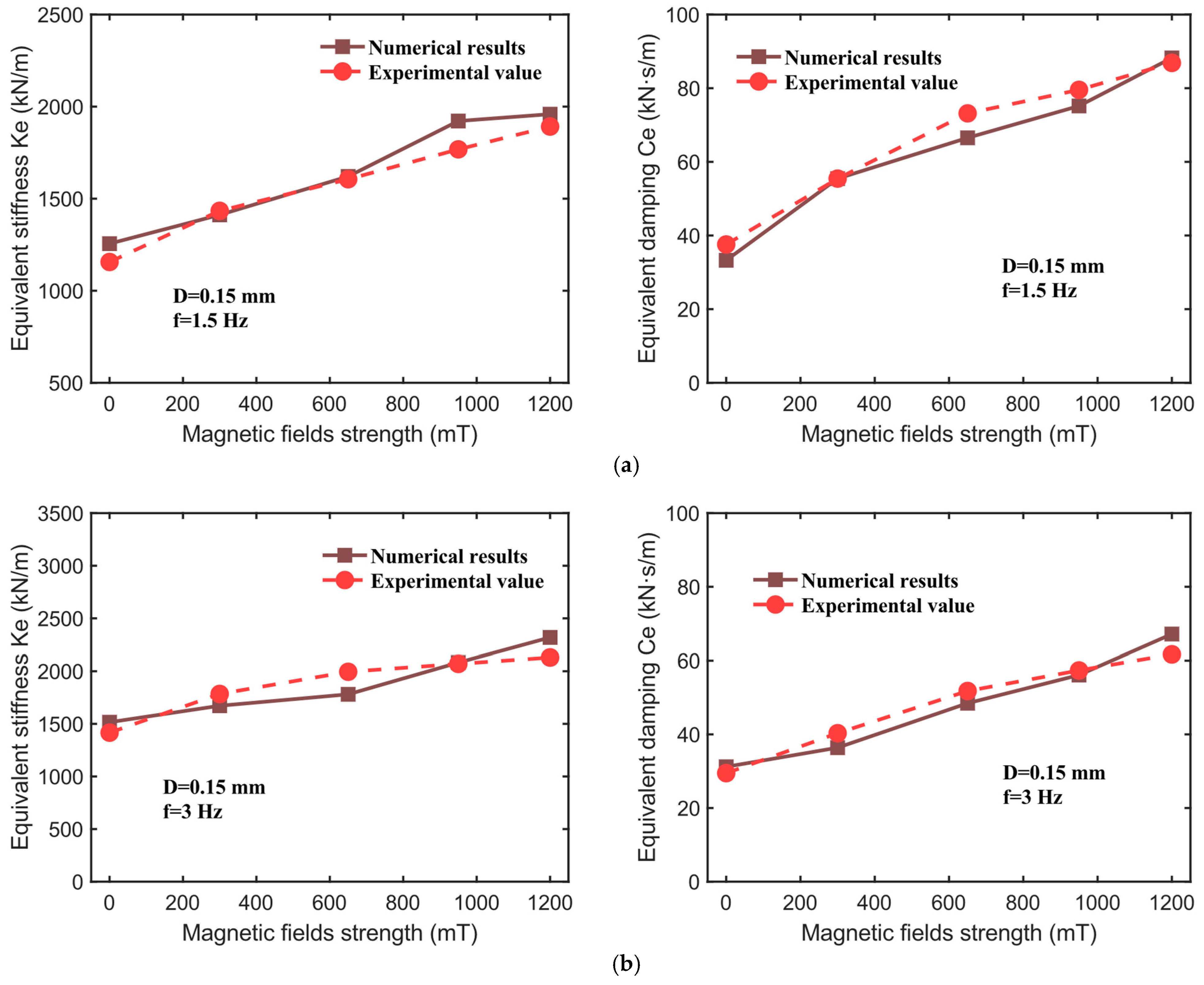
4.3. Comparison of Theoretical and Experimental Results
5. Conclusions
- (1)
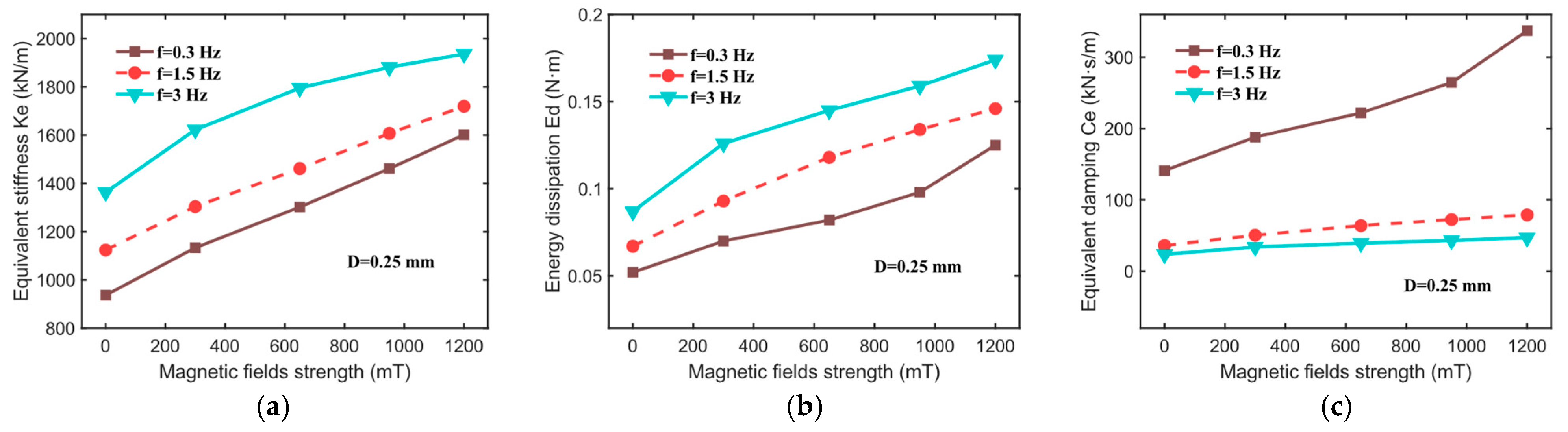
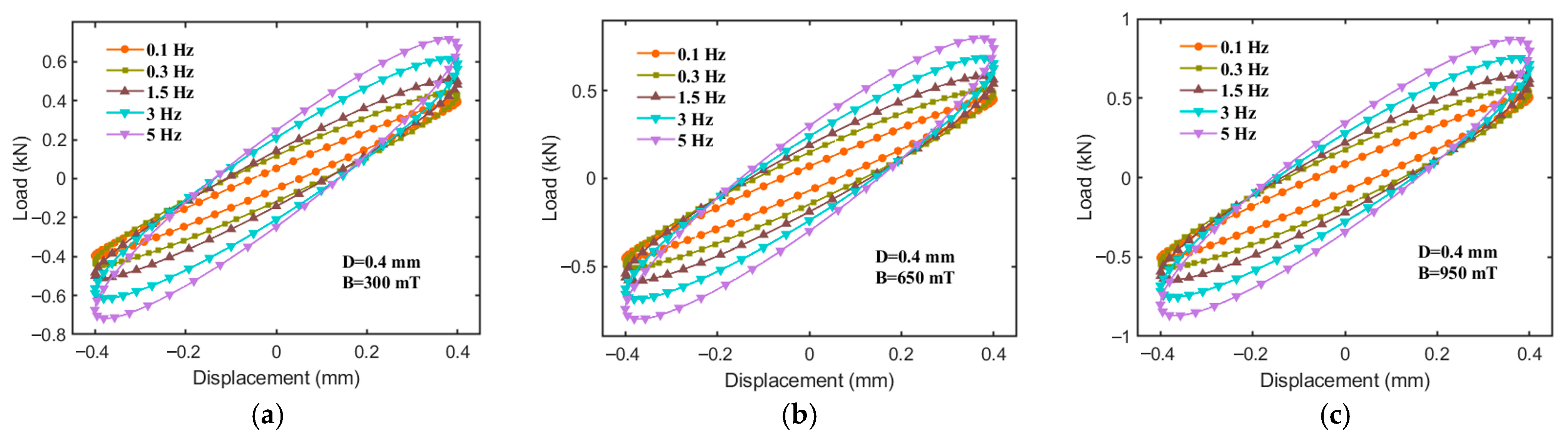
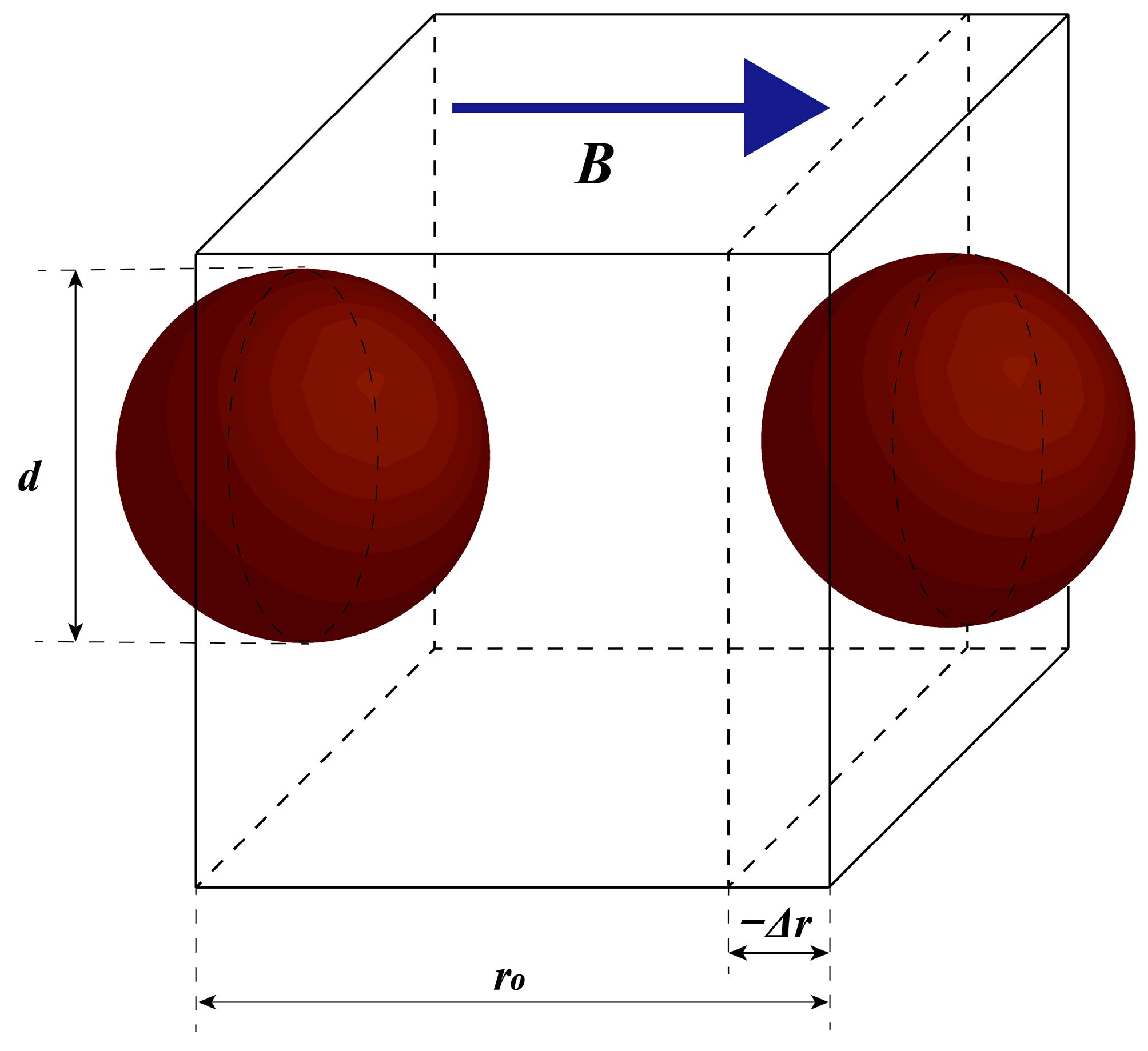
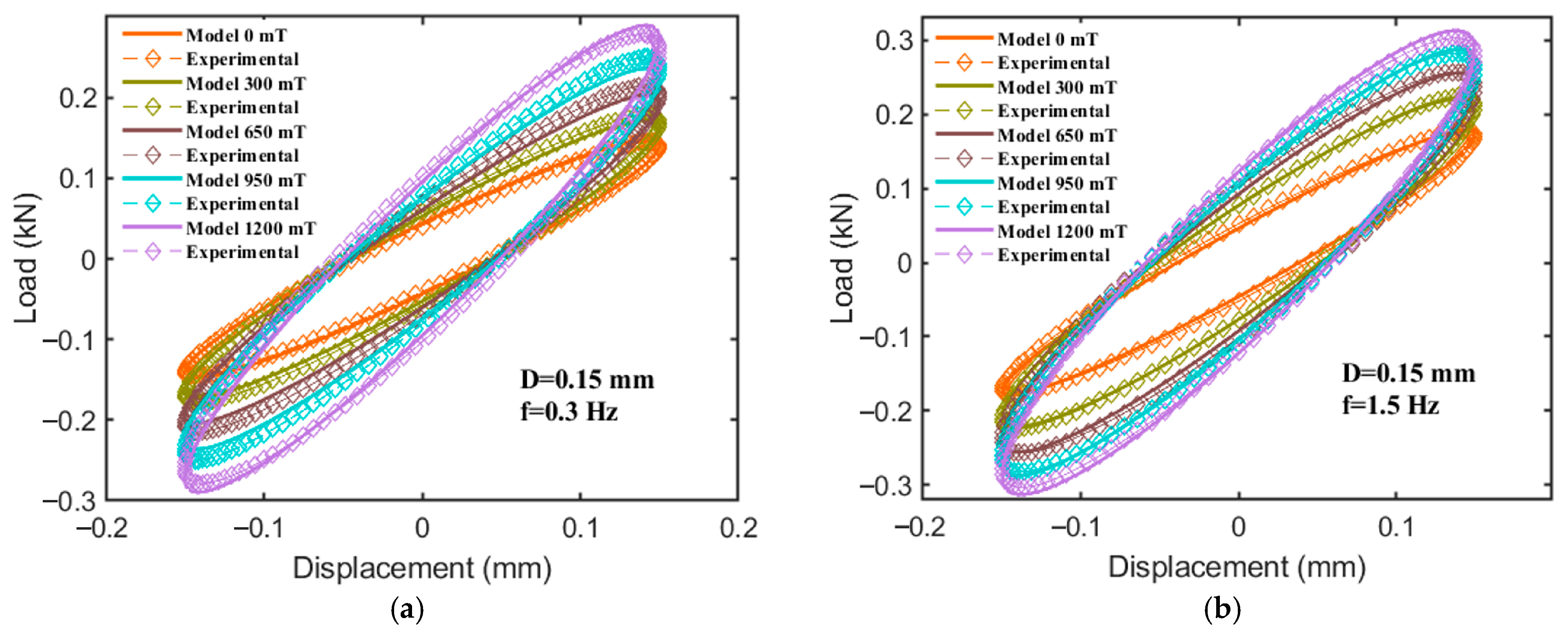
- Under varying excitation frequencies, when the applied magnetic field strength increases from 0 to 1200 mT, the force–displacement curve of the hybrid-mode MRE isolator exhibits a relatively regular elliptical shape. The slope, fullness, and area of the ellipse’s major axis increase significantly with the magnetic field strength, indicating that the fabricated MRE isolator demonstrates excellent magnetorheological (MR) effects, along with distinctly tunable stiffness and damping characteristics.
- (2)
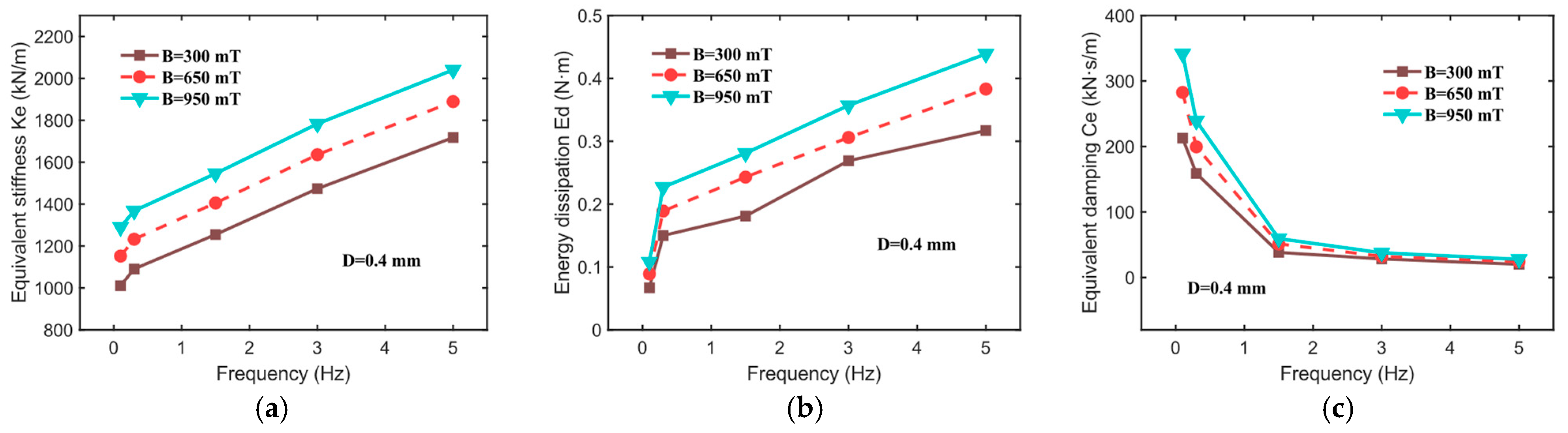
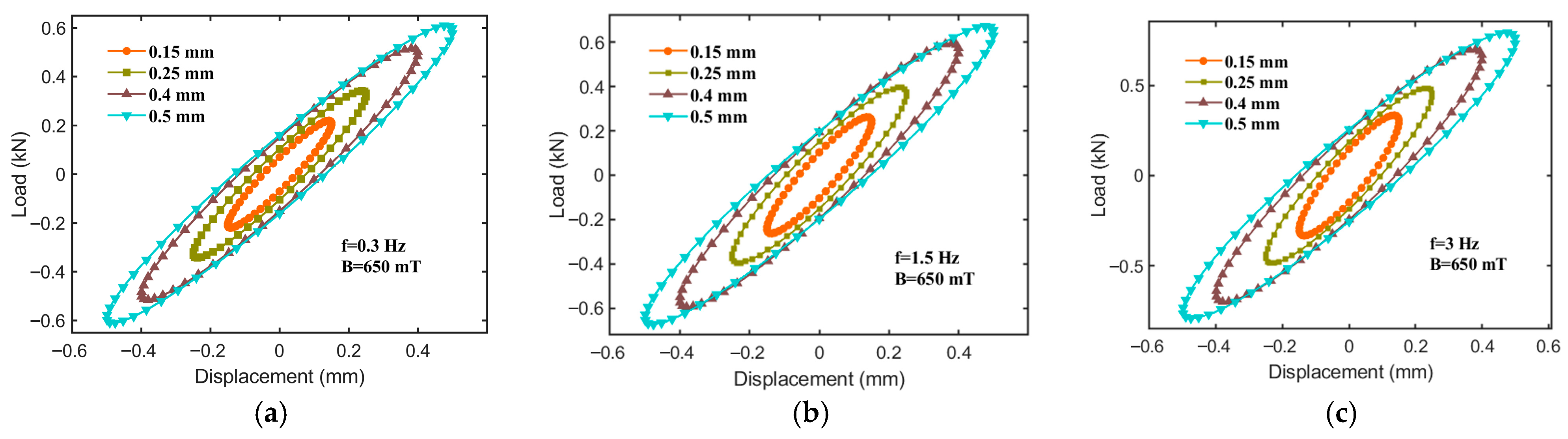
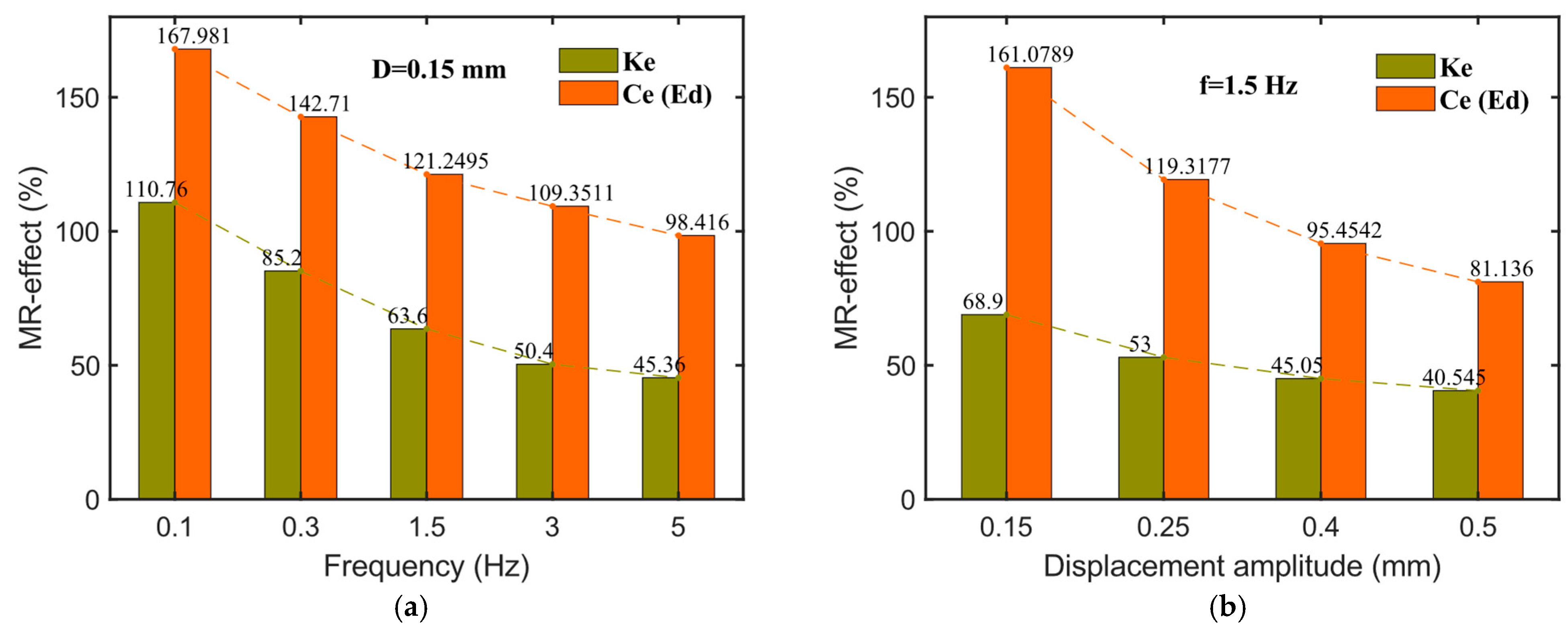
- The equivalent stiffness (), energy dissipation (), and equivalent damping () of the hybrid-mode MRE isolator are all influenced by factors such as the excitation frequency, displacement amplitude, and the applied magnetic field. Specifically, the values of all three parameters increase with the applied magnetic field strength. Both and increase with frequency, while decreases as frequency increases. Furthermore, and significantly decrease with an increasing displacement amplitude, whereas increases with displacement amplitude. Regarding the relative MR effect, the MR effects of all three parameters decrease markedly with increasing displacement amplitude and excitation frequency. The maximum MR effect of reaches 110.76%, and that of reaches 167.98%.
- (3)
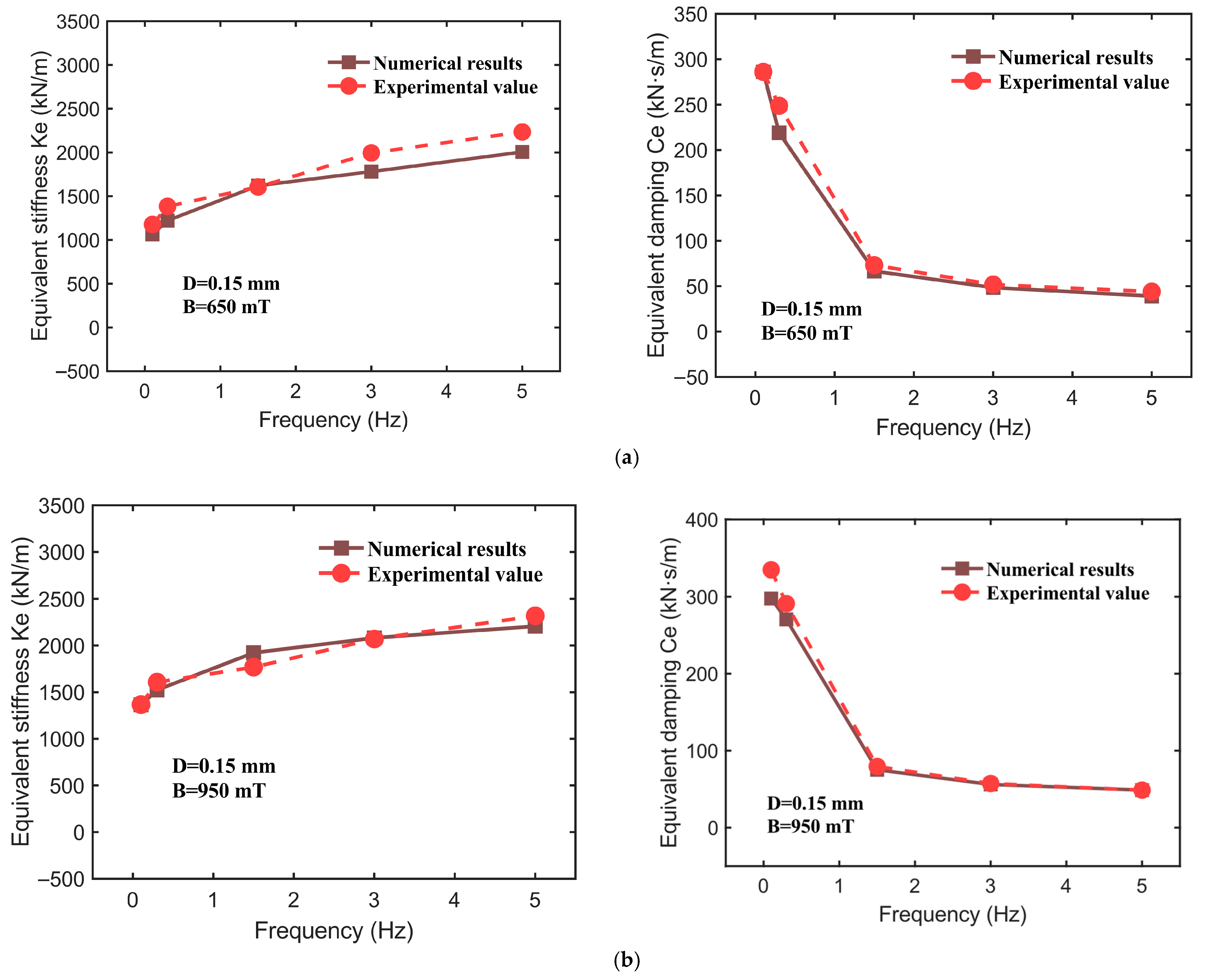
- Based on the experimental results, a compression–shear hybrid fractional-derivative parametric (CSHF) model is proposed. The numerical results closely align with the experimental findings, demonstrating the effectiveness of the model in describing the dynamic mechanical properties of the hybrid-mode MRE isolator under varying magnetic field strengths and excitation frequencies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, G.; Xiong, Y.; Li, Z.; Li, M.; Bai, X.F. A fractional-order model on the dynamic mechanical behavior of magnetorheological elastomers. Smart Mater. Struct. 2020, 29, 1345–1360. [Google Scholar] [CrossRef]
- Qi, S.; Yu, M.; Fu, J.; Li, P.D.; Zhu, M. Creep and recovery behaviors of magnetorheological elastomer based on polyurethane/epoxy resin IPNs matrix. Smart Mater. Struct. 2016, 25, 1389–1404. [Google Scholar] [CrossRef]
- Hermann, S.; Butaud, P.; Chevallier, G.; Manceau, J.F.; Espanet, C. Magnetic and dynamic mechanical properties of a highly coercive MRE based on NdFeB particles and a stiff matrix. Smart Mater. Struct. 2020, 29, 1188–1203. [Google Scholar] [CrossRef]
- Saharuddin, K.D.; Ariff, M.H.M.; Bahiuddin, I.; Ubaidillah, U.; Mazlan, S.A.; Aziz, S.A.A.; Nazmi, N.; Fatah, A.Y.A.; Shapiai, M.I. Non-parametric multiple inputs prediction model for magnetic field dependent complex modulus of magnetorheological elastomer. Sci. Rep. 2022, 12, 89–103. [Google Scholar] [CrossRef]
- Johari, M.A.F.; Mazlan, S.A.; Nasef, M.M.; Ubaidillah, U.; Nordin, N.A.; Aziz, S.A.A.; Johari, N.; Nazmi, N. Microstructural behavior of magnetorheological elastomer undergoing durability evaluation by stress relaxation. Sci. Rep. 2021, 11, 1589–1603. [Google Scholar] [CrossRef]
- Yang, J.; Gong, X.; Zong, L.; Peng, C.; Xuan, S. Silicon Carbide-Strengthened Magnetorheological Elastomer: Preparation and Mechanical Property. Polym. Eng. Sci. 2013, 53, 2615–2623. [Google Scholar] [CrossRef]
- Wang, P.; Yang, S.; Liu, Y.; Zhao, Y. Experimental study and fractional derivative model prediction for dynamic viscoelasticity of magnetorheological elastomers. J. Vib. Eng. Technol. 2022, 10, 1865–1881. [Google Scholar] [CrossRef]
- Xin, F.-L.; Bai, X.-X.; Qian, L.-J. Modeling and experimental verification of frequency-, amplitude-, and magneto-dependent viscoelasticity of magnetorheological elastomers. Smart Mater. Struct. 2016, 25, 105002. [Google Scholar] [CrossRef]
- Xu, Z.-D. Horizontal shaking table tests on structures using innovative earthquake mitigation devices. J. Sound Vib. 2009, 325, 34–48. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Guo, Y.-Q. Neuro-fuzzy control strategy for earthquake-excited nonlinear magnetorheological structures. Soil Dyn. Earthq. Eng. 2008, 28, 717–727. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Shen, Y.-P. Intelligent bi-State control for the structure with magnetorheological dampers. J. Intell. Mater. Syst. Struct. 2003, 14, 35–42. [Google Scholar] [CrossRef]
- Yang, J.; Du, H.; Li, W.; Li, Y.; Li, J.; Sun, S.; Deng, H.X. Experimental study and modeling of a novel magnetorheological elastomer isolator. Smart Mater. Struct. 2013, 22, 117001. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Tu, Q.; Guo, Y.-F. Experimental study on vertical performance of multidimensional earthquake isolation and mitigation devices for long-span reticulated structures. J. Vib. Control 2012, 18, 1971–1985. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Wu, K.-Y. Damage detection for space Truss structures based on strain mode under ambient excitation. J. Eng. Mech. 2012, 138, 1215–1223. [Google Scholar] [CrossRef]
- Ahmad Khairi, M.H.; Mazlan, S.A.; Ubaidillah, U.; Khaidir, R.E.M.; Nordin, N.A.; Johari, M.A.F.; Aziz, S.A.A.; Shilan, S.T.; Choi, S.-B. The effect of salt water ageing on the mechanical and rheological properties of magnetorheological elastomer. Sci. Rep. 2023, 13, 1289–1303. [Google Scholar] [CrossRef] [PubMed]
- Akbari, E.; Khajehsaeid, H. A continuum magneto-mechanical model for magnetorheological elastomers. Smart Mater. Struct. 2021, 30, 634–648. [Google Scholar] [CrossRef]
- Arani, A.G.; Eskandari, M.; Haghparast, E. The supersonic flutter behavior of sandwich plates with an magnetorheological elastomer core and gnp-reinforced face sheets. Int. J. Appl. Mech. 2022, 14, 09–18. [Google Scholar] [CrossRef]
- Saber, A.; Sedaghati, R. The modeling of magnetorheological elastomers: A state-of-the-art review. Adv. Eng. Mater. 2023, 25, 1438–1656. [Google Scholar] [CrossRef]
- Mukherjee, D.; Bodelot, L.; Danas, K. Microstructurally-guided explicit continuum models for isotropic magnetorheological elastomers with iron particles. Int. J. Non-Linear Mech. 2020, 120, 103380–103390. [Google Scholar] [CrossRef]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Modeling of particle interactions in magnetorheological elastomers. J. Appl. Phys. 2014, 116, 114904. [Google Scholar] [CrossRef]
- Hu, Z.; Xia, L.; Sun, L. Multiscale magneto-mechanical coupling of magnetorheological elastomer isolators. Finite Elem. Anal. Des. 2023, 224, 104003–104012. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Li, Y.; Li, S.; Li, H.; Wang, W. Comparative Investigation of Phenomenological Modeling for Hysteresis Responses of Magnetorheological Elastomer Devices. Int. J. Mol. Sci. 2019, 20, 3216. [Google Scholar] [CrossRef]
- Akhavan, H.; Ghadiri, M.; Zajkani, A. A new model for the cantilever MEMS actuator in magnetorheological elastomer cored sandwich form considering the fringing field and Casimir effects. Mech. Syst. Signal Process. 2019, 121, 551–561. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Komatsuzaki, T.; Iwata, Y.; Asanuma, H. Modeling and semi-active fuzzy control of magnetorheological elastomer-based isolator for seismic response reduction. Mech. Syst. Signal Process. 2018, 101, 449–466. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Komatsuzaki, T.; Iwata, Y.; Asanuma, H. Fuzzy Semiactive Vibration Control of Structures Using Magnetorheological Elastomer. Shock Vib. 2017, 2017, 1070–9622. [Google Scholar] [CrossRef]
- Fu, J.; Lai, J.; Yang, Z.; Bai, J.; Yu, M. Fuzzy-neural network control for a Magnetorheological elastomer vibration isolation system. Smart Mater. Struct. 2020, 29, 623–638. [Google Scholar] [CrossRef]
- Fu, J.; Bai, J.; Lai, J.; Li, P.; Yu, M.; Lam, H.-K. Adaptive fuzzy control of a magnetorheological elastomer vibration isolation system with time-varying sinusoidal excitations. J. Sound Vib. 2019, 456, 386–406. [Google Scholar] [CrossRef]
- Aguib, S.; Nour, A.; Benkoussas, B.; Tawfiq, I.; Djedid, T.; Chikh, N. Numerical simulation of the nonlinear static behavior of composite sandwich beams with a magnetorheological elastomer core. Compos. Struct. 2016, 139, 111–119. [Google Scholar] [CrossRef]
- Aguib, S.; Nour, A.; Zahloul, H.; Bossis, G.; Chevalier, Y.; Lancon, P. Dynamic behavior analysis of a magnetorheological elastomer sandwich plate. Int. J. Mech. Sci. 2014, 87, 118–136. [Google Scholar] [CrossRef]
- Lin, D.; Yang, F.; Gong, D.; Li, R. A new vibration isolator integrating tunable stiffness-damping and active driving properties based on radial-chains magnetorheological elastomer. Mech. Syst. Signal Process. 2023, 183, 456–469. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, T.; Ma, X.; Li, H.; Hu, J.; Liu, J.; Gao, Z. Complementary effects on vibration characteristics of functionally graded graphene reinforced magnetorheological elastomer sandwich plates. Eng. Struct. 2022, 270, 114864–114879. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Z.; Li, H.; Wong, P.K.; Xie, Z. Semi-active control for the nonlinear vibration suppression of square-celled sandwich plate with multi-zone MRE filler core. Mech. Syst. Signal Process. 2022, 172, 1502–1516. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Komatsuzaki, T.; Hoa Thi, T. Adaptive parameter identification of Bouc-wen hysteresis model for a vibration system using magnetorheological elastomer. Int. J. Mech. Sci. 2022, 213, 74–88. [Google Scholar] [CrossRef]
- Chen, V.W.; Arora, N.; Goshkoderia, A.; Willey, C.L.; Turgut, Z.; Buskohl, P.R.; Rudykh, S.; Juhl, A.T. Mechanical instability tuning of a magnetorheological elastomer composite laminate. Compos. Part B-Eng. 2023, 251, 1359–1365. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Wang, X.; Han, Q.; Liu, J.; Qin, Z.; Xiong, J.; Guan, Z. A nonlinear analytical model of composite plate structure with an MRE function layer considering internal magnetic and temperature fields. Compos. Sci. Technol. 2020, 200, 538–544. [Google Scholar] [CrossRef]
- Brancati, R.; Di Massa, G.; Pagano, S. Investigation on the Mechanical Properties of MRE Compounds. Machines 2019, 7, 36. [Google Scholar] [CrossRef]
- Shuib, R.K.; Pickering, K.L. Investigation and modelling of damping mechanisms of magnetorheological elastomers. J. Appl. Polym. Sci. 2016, 133, 43247. [Google Scholar] [CrossRef]
- Mukherjee, D.; Danas, K. A unified dual modeling framework for soft and hard magnetorheological elastomers. Int. J. Solids Struct. 2022, 257, 111513–111521. [Google Scholar] [CrossRef]
- Park, Y.-J.; Kim, B.-G.; Lee, E.-S.; Choi, S.-B. A Novel Tactile Sensing System Utilizing Magnetorheological Structures for Dynamic Contraction and Relaxation Motions. Sensors 2023, 23, 9035. [Google Scholar] [CrossRef]
- Park, Y.-J.; Choi, S.-B. Sensors and Sensing Devices Utilizing Electrorheological Fluids and Magnetorheological Materials—A Review. Sensors 2024, 24, 2842. [Google Scholar] [CrossRef]
- Erenchun, A.; Blanco, B.; Gil-Negrete, N.; Wang, B.; Kari, L. Effect of lubrication on the mechanical behavior of magnetorheological elastomers in compression mode. Polym. Test. 2022, 111, 765–779. [Google Scholar] [CrossRef]
- Shi, X.; Liu, S.; Zhao, D.; Zhao, Z.; Cui, J.; Wang, F. Effect of Electromagnetic Force on Dynamic Mechanical Properties of the Magnetorheological Elastomer Under Compression Mode. J. Eng. Mater. Technol.-Trans. Asme 2020, 142, 021004. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Z.-D.; Guo, Y.-Q.; Zhu, L.-H.; Dong, Y.-R.; Li, Q.-Q.; Hu, Z.-W.; Wei, Y.-X. Experimental and theoretical investigation on magnetorheological elastomers containing carbonyl iron particles coated with silane coupling agent. Smart Mater. Struct. 2024, 33, 732–747. [Google Scholar] [CrossRef]
- Park, Y.-J.; Choi, S.-B. A New Tactile Transfer Cell Using Magnetorheological Materials for Robot-Assisted Minimally Invasive Surgery. Sensors 2021, 21, 3034. [Google Scholar] [CrossRef]
- Bernat, J.; Gajewski, P.; Kapela, R.; Marcinkowska, A.; Superczyńska, P. Design, Fabrication and Analysis of Magnetorheological Soft Gripper. Sensors 2022, 22, 2757. [Google Scholar] [CrossRef]
- Li, H.-W.; Xu, Z.-D.; Wang, F.; Gai, P.-P.; Gomez, D.; Dyke, S.J. Development and Validation of a Nonlinear Model to Describe the Tension–Compression Behavior of Rubber-Like Base Isolators. J. Eng. Mech. 2023, 149, 04022104. [Google Scholar] [CrossRef]
- Mark, R.J.; Carlson, J.D.; Beth, C.M. A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 1996, 5, 834–849. [Google Scholar] [CrossRef]



| Order | Displacement (mm) | f (Hz) | B (mT) |
|---|---|---|---|
| 1 | 0.15 | 0.1, 0.3, 1.5, 3, 5 | 0, 300, 650, 950, 1200 |
| 2 | 0.25 | 0.1, 0.3, 1.5, 3, 5 | 0, 300, 650, 950, 1200 |
| 3 | 0.4 | 0.1, 0.3, 1.5, 3, 5 | 0, 300, 650, 950, 1200 |
| 4 | 0.5 | 0.1, 0.3, 1.5, 3, 5 | 0, 300, 650, 950, 1200 |
| Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| MRE isolator | 0.79 | 0.77 | 5.32 | 0.28 | 1.99 | 0.22 | 2.65 | 0.036 | 0.056 |
| H (mT) | f (Hz) | Equivalent Stiffness Ke (kN/m) | Equivalent Damping Ce (kN·s/m) | ||||
|---|---|---|---|---|---|---|---|
| Experimental Value | Numerical Results | Relative Error Value (%) | Experimental Value | Numerical Results | Relative Error Value (%) | ||
| 650 | 0.1 | 1177.272 | 1063.058 | 9.702 | 286.021 | 286.015 | 0.002 |
| 650 | 0.3 | 1385.025 | 1222.078 | 11.765 | 248.714 | 218.937 | 11.972 |
| 650 | 1.5 | 1605.662 | 1620.655 | 0.934 | 73.173 | 66.523 | 9.087 |
| 650 | 3 | 1994.980 | 1780.590 | 10.746 | 51.793 | 48.458 | 6.440 |
| 650 | 5 | 2234.377 | 2005.878 | 10.227 | 44.024 | 39.110 | 11.163 |
| 0 | 3 | 1415.944 | 1515.554 | 7.035 | 29.467 | 31.199 | 5.877 |
| 300 | 3 | 1784.648 | 1672.012 | 6.311 | 40.329 | 36.385 | 9.781 |
| 950 | 3 | 2069.592 | 2081.695 | 0.585 | 57.369 | 56.112 | 2.191 |
| 1200 | 3 | 2129.580 | 2318.870 | 8.889 | 61.690 | 67.162 | 8.871 |
| 950 | 0.1 | 1366.177 | 1364.164 | 0.147 | 334.727 | 297.670 | 11.071 |
| 950 | 0.3 | 1607.267 | 1523.183 | 5.231 | 291.067 | 270.591 | 7.035 |
| 950 | 1.5 | 1767.994 | 1921.760 | 8.697 | 79.565 | 75.178 | 5.514 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Hu, Z.; Guo, Y.; Zhu, L.; Dai, J.; Tao, Y.; Wang, X. Development and Modeling of a Novel Magnetorheological Elastomer Isolator in Hybrid Mode with a Compression–Shear Hybrid Fractional-Derivative Parametric Model. Sensors 2025, 25, 6376. https://doi.org/10.3390/s25206376
Tian Y, Hu Z, Guo Y, Zhu L, Dai J, Tao Y, Wang X. Development and Modeling of a Novel Magnetorheological Elastomer Isolator in Hybrid Mode with a Compression–Shear Hybrid Fractional-Derivative Parametric Model. Sensors. 2025; 25(20):6376. https://doi.org/10.3390/s25206376
Chicago/Turabian StyleTian, Yun, Zhongwei Hu, Yingqing Guo, Lihua Zhu, Jun Dai, Yuxuan Tao, and Xin Wang. 2025. "Development and Modeling of a Novel Magnetorheological Elastomer Isolator in Hybrid Mode with a Compression–Shear Hybrid Fractional-Derivative Parametric Model" Sensors 25, no. 20: 6376. https://doi.org/10.3390/s25206376
APA StyleTian, Y., Hu, Z., Guo, Y., Zhu, L., Dai, J., Tao, Y., & Wang, X. (2025). Development and Modeling of a Novel Magnetorheological Elastomer Isolator in Hybrid Mode with a Compression–Shear Hybrid Fractional-Derivative Parametric Model. Sensors, 25(20), 6376. https://doi.org/10.3390/s25206376







